6D Radar Sensing and Tracking in Monostatic Integrated Sensing and Communications System
Abstract
In this paper, we propose a novel scheme for six-dimensional (6D) radar sensing and tracking of dynamic target based on multiple input and multiple output (MIMO) array for monostatic integrated sensing and communications (ISAC) system. Unlike most existing ISAC studies believing that only the radial velocity of far-field dynamic target can be measured based on one single base station (BS), we find that the sensing echo channel of MIMO-ISAC system actually includes the distance, horizontal angle, pitch angle, radial velocity, horizontal angular velocity, and pitch angular velocity of the dynamic target. Thus we may fully rely on one single BS to estimate the dynamic target’s 6D motion parameters from the sensing echo signals. Specifically, we first propose the long-term motion and short-term motion model of dynamic target, in which the short-term motion model serves the single-shot sensing of dynamic target, while the long-term motion model serves multiple-shots tracking of dynamic target. As a step further, we derive the sensing channel model corresponding to the short-term motion. Next, for single-shot sensing, we employ the array signal processing methods to estimate the dynamic target’s horizontal angle, pitch angle, distance, and virtual velocity. By realizing that the virtual velocities observed by different antennas are different, we adopt plane fitting to estimate the radial velocity, horizontal angular velocity, and pitch angular velocity of dynamic target. Furthermore, we implement the multiple-shots tracking of dynamic target based on each single-shot sensing results and Kalman filtering. Simulation results demonstrate the effectiveness of the proposed 6D radar sensing and tracking scheme.
Index Terms:
6D MIMO radar, angular velocity estimation, integrated sensing and communications, dynamic target sensing, dynamic target tracking.I Introduction
In the past decade, the integration of wireless communications and radar sensing has promoted the researches on dual functions radar communications (DFRC) systems[1, 2]. With the further expansion of the connotation and extension of sensing, integrated sensing and communications (ISAC) that incorporates more diverse sensing technologies based on DFRC has been recognized as a promising air-interface technology for next-generation wireless networks[3, 4, 5]. Since ISAC allows sensing systems and communications systems to share spectrum resources, and can serve various intelligent applications, it has also been officially approved by ITU-R IMT 2030 as one of the six key usage scenarios for the sixth generation (6G) mobile communications[6, 7].
The ultimate functionality of sensing is to construct the mapping relationship from real physical world to digital twin world, where the former includes static environment (such as roads and buildings) and dynamic targets (such as pedestrians and vehicles). Therefore, realizing static environment reconstruction and dynamic target sensing is becoming one consensus among researchers. Specifically, dynamic target sensing, as a research focus, refers to the discovery, detection, parameters estimation, tracking, and recognition of target based on the radar sensing function of ISAC system.
On the other side, the base stations (BSs) in ISAC systems are usually stationary and are configured with massive multiple input and multiple output (MIMO) arrays. Depending on the number and location of BSs, the ISAC system can be divided into: 1) monostatic ISAC system (only one BS in the system); 2) bistatic ISAC system (two BSs in the system); and 3) multistatic ISAC system (multiple BSs in the system)[8, 9]. Among different ISAC architectures, monostatic ISAC system has received tremendous research attention due to low implementation complexity, as it does not require high-precision synchronization among BSs.
More relevant to this work, estimating the motion parameters of dynamic target with monostatic ISAC system has been well-investigated in the past few years. For example, X. Chen et. al. proposed a multiple signal classification based monostatic ISAC system that can attain high accuracy for target’s angle, distance, and radial velocity estimation[10]. W. Jiang et. al. proposed a model-driven ISAC scheme, which simultaneously accomplished tasks of demodulating uplink communications signals and estimating distance and radial velocity of dynamic target[11]. In order to track dynamic target, F. Liu et. al. investigated a sensing assisted predictive beamforming design for vehicle communications by exploiting ISAC technique[12]. On top of that, Z. Du et. al. proposed a tracking scheme for extended target based on extended Kalman filtering and beamwidth adjustment, which leveraged matched filtering and maximum likelihood estimation to obtain the angle, distance, and radial velocity of target, and then tracks the target[13]. It should be noted that all of these works adopt the traditional view in the field of radar sensing that only the radial velocity of dynamic target can be measured based on one single BS, while the angular velocity cannot be directly measured. Even in the field of radar sensing, the most advanced researches currently available suggest that the monostatic MIMO radar can and only can realize the 4D sensing of dynamic target, namely, measuring the dynamic target’s horizontal angle, pitch angle, distance, and radial velocity[14, 15]. However, by re-examining the relationship between the motion parameters of dynamic target and the sensing echo channel of MIMO system, one may realize that the sensing channel already encompasses the distance, horizontal angle, pitch angle, radial velocity, horizontal angular velocity, and pitch angular velocity of the dynamic target. As a consequence, it becomes possible to estimate the dynamic target’s 6D motion parameters from the echo signals based on one single BS.
Evidently, there are already some preliminary studies focusing on measuring the angular velocity based on monostatic radar system. J. A. Nanzer et. al. first proposed the theoretical method for measuring the angular velocity of moving object based on spatial interferometry using one single station radar system, which was later verified through hardware experiments[16, 17, 18, 19]. X. Wang et. al. extended this work to multiple targets angular velocities measurement scenarios through conceiving sophisticated algorithms[20, 21, 22]. However, all of these studies only considered the spatial interference effect between two or three antennas, resulting in severe sensing performance loss. To the best knowledge of the authors, estimating the angular velocity based on single station massive MIMO-OFDM system still remains widely unexplored.
In this paper, we attempt to fill in this research gap by proposing a novel scheme for 6D radar single-shot sensing and multiple-shots tracking of dynamic target based on massive MIMO array for monostatic ISAC system. The contributions of this paper are summarized as follows.
-
•
Based on the working pipeline of radar sensing in ISAC system, we construct the long-term motion and short-term motion model for dynamic target in 3D space, which correspond to multiple-shots tracking and single-shot sensing of dynamic target, respectively.
-
•
We re-examine the relationship between the 6D motion parameters of dynamic target and the sensing echo channel of MIMO-ISAC system, and reveal that the sensing channel actually includes the distance, horizontal angle, pitch angle, radial velocity, horizontal angular velocity, and pitch angular velocity of target, which enables us to estimate the dynamic target’s 6D motion parameters from echoes by solely relying on one single ISAC BS.
-
•
For single-shot sensing, we employ the array signal processing methods to estimate the dynamic target’s distance, horizontal angle, pitch angle, and virtual velocity. Then we show that the virtual velocities observed at different antennas are distinct from each other, allowing us to utilize plane fitting to estimate the radial velocity, horizontal angular velocity, and pitch angular velocity of the dynamic target.
-
•
Based on the single-shot 6D parameters sensing results, we further propose a multiple-shots tracking approach for dynamic target through Kalman filtering.
The remainder of this paper is organized as follows. In Section II, we propose the 6D motion model of dynamic target, and derive the corresponding sensing channel model. In Section III, we propose a novel 6D sensing and tracking scheme for dynamic target sensing. Simulation results and conclusions are given in Section IV and Section V, respectively.
Notation: Lower-case and upper-case boldface letters and denote a vector and a matrix; and denote the transpose and the conjugate transpose of vector , respectively; denotes the -th element of the vector ; denotes the -th element of the matrix ; is the submatrix composed of all columns elements in rows to of matrix ; is the submatrix composed of all rows elements in columns to of matrix ; represents the matrix eigenvalue decomposition function.
II System Model and Proposed ISAC Framework
In this section, we provide the generic model for massive MIMO based monostatic ISAC system, and propose the 6D motion model of dynamic target, as well as derive the sensing channel model of ISAC system.
II-A ISAC BS Model
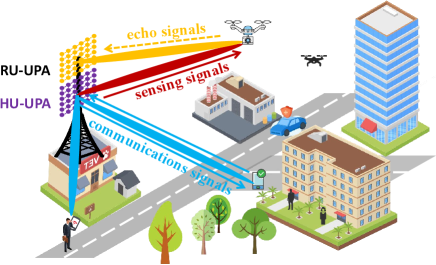
A massive MIMO based monostatic ISAC system operating in mmWave or Terahertz frequency bands with OFDM modulation is depicted in Fig. 1, which employs only one dual-functional BS for wireless communications and radar sensing at the same time. Generally, we consider that the BS consists of one hybrid unit (HU) and one radar unit (RU), where both the HU and the RU are configured with uniform planar arrays (UPAs). By designing the beamforming strategy, HU is responsible for transmitting downlink communications signals and receiving uplink communications signals, as well as transmitting downlink sensing signals to realize dynamic target sensing; while RU is responsible for receiving echo signals to realize dynamic target sensing.
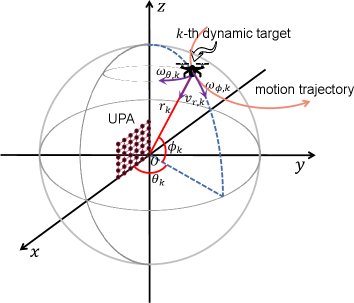
The HU and RU are each equipped with one UPA of and antenna elements, named as HU-UPA and RU-UPA, respectively. Assume that both the HU-UPA and the RU-UPA are vertically mounted on the 2D plane at BS side as shown in Fig. 2, and the antenna spacing between the antennas distributed along x-axis and z-axis are and , respectively, with being the wavelength. Without loss of generality, we denote the position of the -th antenna element in the HU-UPA as , where is the position of the reference element, and are the antenna indices. Here we use two types of index numbers to represent the same antenna, that is, the -th antenna may also be named as the -th antenna. Similarly, we denote the position of the -th antenna element in the RU-UPA as with and . Generally, according to the spatial consistency of the arrays, we further assume that the HU-UPA and RU-UPA are co-located and are parallel to each other, i.e., , such that they may see the targets at the same propagation directions111Since the normal communications and sensing distance is much longer than the protection distance between HU-UPA and RU-UPA, it can be considered that HU-UPA and RU-UPA are located in the same position.[23]. Besides, by balancing the hardware costs and system performance, we assume that the HU-UPA employs the hardware architecture based on phase shifter (PS) structure, in which a total of radio frequency (RF) chains are deployed, and each antenna is connected to a PS to realize beamforming. On the other side, we assume that the RU-UPA employs the fully-digital receiving array, with each antenna connected to one RF chain, to realize super-resolution sensing performance, which follows the setting in [10] and [23].
Suppose that the ISAC system emits OFDM signals with subcarriers, where the lowest frequency and the subcarrier interval of OFDM signals are and , respectively. Then the transmission bandwidth is , and the frequency of the -th subcarrier is , where . Further, we consider that an OFDM frame contains consecutive OFDM symbols, where the time interval between adjacent OFDM symbols is , with and being the OFDM symbol duration and guard interval, respectively.
We employ the spherical coordinates to represent one position in 3D space. As shown in Fig. 2, represents the polar distance with mathematical range of , represents the horizontal angle with mathematical range of , and represents the pitch angle with mathematical range of . Moreover, the spherical coordinate may be translated to its Cartesian counterpart through
| (1) |
Since BS is located at the origin of coordinate system, we denote the service area of BS as . Suppose that there are single-antenna communications users, dynamic targets, as well as widely distributed static environment within this service area. We assume that the 6D motion parameters of the -th dynamic target are , in which represents the position of the -th target, , and represent the radial velocity, horizontal angular velocity, and pitch angular velocity, respectively. Besides, we assume that the position of the -th user is , which are known and stationary to BS, due to the fact that they can be easily obtained through user reporting, or other techniques[24, 25, 26].
II-B The Proposed ISAC Framework
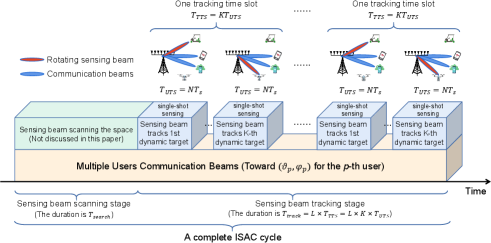
The task of ISAC system is to sense all dynamic targets while serving the communications of all users. As described in Fig. 3, the proposed ISAC framework consists of two stages: sensing beam scanning (SBS) stage and sensing beam tracking (SBT) stage. For the aspect of communications, BS continuously generates communications beams towards users to maintain communications service during both SBS stage and SBT stage. For the aspect of sensing, BS generates one sensing beam that can scan the service area during SBS stage, during which the BS may detect the targets and estimate their parameters. To proceed, BS generates a single sensing beam to track all dynamic targets in a time division manner during SBT stage, that is, the sensing beam may sequentially illuminate each target and continuously track them. In this work, we mainly focuses on the SBT stage, and refer readers to our previous work [27] for more details on the SBS stage.
Assume that dynamic targets possess different physical directions. At each direction, the BS may adopt one OFDM frame, i.e., consecutive OFDM symbols, to realize dynamic target sensing. As shown in Fig. 3, we divide the SBT stage into tracking time slots (TTSs), and each TTS lasts for a time duration of . Besides, each TTS is further divided into unit time slots (UTSs), and each UTS lasts for a time duration of . Clearly, there is . During consecutive TTSs, BS should track all dynamic targets using the methods such as Kalman filtering with as time step, which is named as multiple-shots tracking. To realize continuous target tracking and reliable users communications, in the -th UTS, BS needs to generate communications beams pointing to users and generate one sensing beam pointing to the sensing tracking direction from HU-UPA, where . The BS needs to update the motion parameter sensing results of the -th dynamic target within this UTS, known as single-shot sensing. Ideally, should be equal to the physical direction of the -th dynamic target in the -th UTS.
Here we assume that the transmission power of BS is , the energy of sensing beam is , and the remaining energy is evenly distributed among communications beams, where is the power distribution coefficient used in the -th UTS. Due to the short duration of one UTS, we keep the directions of transmitting beams unchanged within one UTS. Then the transmission signals from HU-UPA on the -th subcarrier of the -th symbol in the -th UTS should be represented as
| (2) |
where is the spatial-domain direction corresponding to the physical direction of the -th user, and is the spatial-domain direction corresponding to the sensing tracking direction . Besides, and are the communications beamforming vector for the -th user and the sensing beamforming vector for the sensing tracking direction, respectively, and is the array steering vector of HU-UPA with the form
| (3) |
where denotes the Kronecker product, and
| (4) | ||||
| (5) |
Moreover, and are communications signals for the -th user and sensing detection signals, respectively.
Based on (2), the BS may realize both communications function and sensing function by optimizing during each UTS, which may be conceived through the power allocation strategy proposed in [27], via maximizing the sensing performance while ensuring users communications performance. To that end, we only consider dynamic target sensing problem while omitting the design of communications function in this work. Consequently, there is always one beam towards the sensing tracking direction , and we can rewrite the transmission signals from the HU-UPA on the -th subcarrier of the -th OFDM symbol in the -th UTS as
| (6) |
where is the power allocated to direction, and is the signal transmitted to direction.
II-C The 6D Motion Model of Dynamic Target
The motion of dynamic target can be described from two levels: 1) long-term motion, and 2) short-term motion. Specifically, the dynamic target undergoes long-term motion within TTSs. Given the long tracking time of the target, the radial velocity and angular velocities of the target are susceptible to various disturbances. In long-term motion, the time interval for describing the target motion is . We refer to the 6D motion parameters of the -th target at the -th TTS as the state of this target, denoted as
| (7) |
where . Without loss of generality, during the motion process, the direction in which the polar distance decreases, the direction in which the horizontal angle value decreases, and the direction in which the pitch angle value decreases are taken as the positive directions for radial velocity, horizontal angular velocity, and pitch angular velocity, respectively. Then the 6D motion model of the -th dynamic target for long-term motion can be represented as
| (8) | ||||
| (9) | ||||
| (10) | ||||
| (11) | ||||
| (12) | ||||
| (13) |
where represents the random disturbance during the long-term motion.
In addition to sense the long-term motion, the BS needs to observe the -th dynamic target within the -th UTS. The dynamic target also undergoes short-term motion within this UTS. Due to the short duration of the short-term motion, one usually assumes that the velocities of the dynamic target remain constant within one UTS time, i.e., OFDM symbol times[10]. Then the 6D motion parameters of the -th dynamic target within the -th OFDM symbol time of the -th UTS can be expressed as
| (14) |
with , which satisfies
| (15) | ||||
| (16) | ||||
| (17) | ||||
| (18) | ||||
| (19) | ||||
| (20) |
Naturally, the long-term motion model corresponds to the multiple-shots tracking of dynamic target, while short-term motion model corresponds to single-shot sensing of dynamic target. The ISAC system needs to utilize as much as possible to sense and track of the -th dynamic target, that is, the ISAC system needs to utilize single-shot sensing to realize multiple-shots tracking.
II-D Sensing Channel Model of ISAC System
In the -th UTS, the BS transmits the detection signals through HU-UPA at the beginning of sensing, which will be reflected by dynamic targets and cause echoes. Then, the RU-UPA will receive the sensing echo signals. Let us define the path from the -th antenna of HU-UPA to the -th dynamic target and then back to the -th antenna of RU-UPA as the -th propagation path. Then we denote as the time delay of the -th propagation path in the -th OFDM symbol time during the -th UTS, where represents the speed of light, is the distance between the -th antenna of HU-UPA and the -th dynamic target, and is the distance between the -th antenna of RU-UPA and the -th dynamic target.
Suppose that the signal transmitted by the -th antenna of HU-UPA is , and the corresponding passband signal is . Then the echo signal will be a delayed version of the transmitting signal with amplitude attenuation. Specifically, the passband echo signal received by the -th antenna through the -th propagation path at the -th OFDM symbol during the -th UTS is . The corresponding baseband echo signal is , and the baseband equivalent channel is
| (21) |
where is the channel fading factor and denotes the Dirac delta function. Taking the Fourier transform of (21), the baseband frequency-domain channel response can be obtain as
| (22) |
Thus the frequency-domain sensing echo channel of the -th propagation path on the -th subcarrier of the -th OFDM symbol during the -th UTS is
| (23) |
Based on (1), the Taylor expansion approximation of can be expressed as . Similarly, can be approximated as . Let us denote
| (24) |
and then there is
| (25) |
Then (23) can be rewritten as
| (26) |
In narrowband OFDM systems, the Doppler squint effect and beam squint effect are typically negligible [28], and thus (26) can be further represented as
| (27) |
We denote as the overall frequency-domain sensing echo channel matrix on the -th subcarrier at the -th OFDM symbol within the -th UTS from the HU-UPA to the -th dynamic target and then back to the RU-UPA, whose -th element is . Moreover, the matrix can be decomposed as
| (28) |
where is the array steering vector for spatial-domain direction of RU-UPA with the form
| (29) |
Here denotes the Kronecker product, and
| (30) | ||||
| (31) |
Besides, is usually modeled as , and is the radar cross section (RCS) of the -th dynamic target. Without loss of generality, we assume that the RCS follows the Swerling model.
Based on (29), the sensing echo channel of all dynamic targets on the -th subcarrier of the -th OFDM symbol in the -th UTS can be represented as
| (32) |
In addition, since the real physical world is composed of dynamic targets and static environment, the RU-UPA will receive both the effective echoes caused by interested dynamic targets (dynamic target echoes) and the undesired echoes caused by uninterested background environment (clutter). Following our previous work [27], we model the static environmental clutter channel on the -th subcarrier of the -th OFDM symbol in the -th UTS as
| (33) |
where is the total number of static environmental clutter scattering units, , , is the position of the -th clutter scattering unit, is the channel fading factor, and is the RCS of the -th clutter scattering unit that also follows the Swerling model. Due to the random distribution of clutter scattering units in various directions and distances, when the number of clutter scattering units is large enough, can be considered as a random channel. Therefore, a low complexity clutter channel generation method is to directly approximate as
| (34) |
where is a complex Gaussian matrix with the dimension of , and is the clutter power regulation factor. Formulas (33) and (34) indicate that since the static clutter scattering unit remains stationary for OFDM symbol times, would remain unchanged for symbols.
Based on (32) and (34), the overall sensing echo channel of dynamic targets and static environment on the -th subcarrier of the -th OFDM symbol in the -th UTS is
| (35) |
III 6D Radar Sensing and Tracking
In this section, we provide the sensing echo signals model, and then propose a novel 6D sensing and tracking scheme for dynamic target sensing.
III-A Echo Signals Model
We design that the BS employs the Kalman filtering algorithm to track the dynamic targets within TTSs. Assume that the predicted value of the 6D parameters for the -th dynamic target within the -th TTS is . Then, the HUUPA of the BS needs to generate one sensing beam towards direction during the -th UTS to re-sense the -th target. Hence based on (6), the transmission signals of HU-UPA during the -th UTS can be expressed as
| (36) |
Then the sensing echo signals on the -th subcarrier of the -th OFDM symbol received by the RU-UPA in the -th UTS can be represented as
| (37) |
where is the zero-mean additive Gaussian noise with variance . Note that represents the echo signals received by all receiving antennas, and then we can reformat the vector into matrix form as
| (38) |
Furthermore, we can stack into one echoes tensor , whose -th element is .
Note that includes the sensing channel , transmitting beamforming, and transmission symbols , while targets sensing can be understood as an estimation of . However, random transmission symbols would affect the estimation of sensing channel, and thus we need to erase the transmission symbols from the received signals to obtain equivalent echo channel (EEC). Specifically, the EEC corresponding to can be obtained as . Then we can stack into an EEC tensor with .
III-B Static Environmental Clutter Filtering
It can be analyzed from (35) and (37) that the echo signals includes both dynamic target echoes and static environment echoes, and the EEC also includes both the EEC of dynamic targets (DT-EEC) and the EEC of static environment (SE-EEC). When we focus on dynamic target sensing, the SE-EEC in original echo signals would cause negative interference to dynamic target sensing, and thus SE-EEC can be referred to as clutter-EEC. To address this negative interference, we need to filter out the interference of clutter-EEC and to extract the effective DT-EEC from .
While the environmental clutter filtering is necessary in sensing processing, it is not the focus of this work. According to the clutter suppression method in [27], we may express the effective DT-EEC after static clutter filtering as , whose -th sub-matrix is with
| (39) |
where is the noise after static clutter filtering.
III-C Echo Signals Analysis
| (40) |
| (41) |
| (42) |
| (44) |
Based on (28), (32) and (36), in (39) can be calculated as (40) at the top of next page. When the Kalman filter predicts accurately, based on (16) and (17), there should be . Then in massive MIMO system, due to dynamic targets owning different directions, (40) can be calculated as (41) at the top of next page, where . Next, based on (41), the -th element in can be expressed as (42) at the top of next page.
To further simplify (42), we note that (based on (17)) and find that
| (43) |
Besides, we also note that (based on (16)). According to the definition and properties of directional derivatives of binary function, we compute as shown in (44) at the top of this page, where .
Based on (43) and (44), the -th element in , i.e., the in (42) can be calculated as shown in (45) at the top of this page. Formula (45) indicates that includes the distance term, pitch angle term, horizontal angle term, radial velocity term, pitch angular velocity term, and horizontal angular velocity term. Therefore, it is definite to estimate the 6D motion parameters of dynamic targets from DT-EEC and realize 6D radar sensing.
| (45) |
III-D Angle Direction and Distance Estimation
Let us transform into an -matrix with the dimension of . Based on (45), can be represented as
| (46) |
where , is defined as the second spatial-domain direction array steering vector, and . Since is the array signals form related to the second spatial-domain direction array, we can estimate from by utilizing array signal processing methods.
Here we adopt the estimating signal parameters via rotational variation techniques (ESPRIT) method for parameter estimation[29, 30, 31]. Specifically, the covariance matrix of can be calculated as . We perform eigenvalue decomposition of to obtain the diagonal matrix with eigenvalues ranging from large to small () and the corresponding eigenvector matrix (), that is, . Then the minimum description length (MDL) criterion is utilized to estimate the number of dynamic targets from as [32, 33]. We extract the parallel signal subspaces from as and compute . Then we perform eigenvalue decomposition of to obtain the diagonal matrix with eigenvalues ranging from large to small () and the corresponding eigenvector matrix (), that is, . We extract and , and we compute . Next, we perform eigenvalue decomposition of to obtain the diagonal matrix with eigenvalues ranging from large to small () and the corresponding eigenvector matrix (), that is, . We take out the elements on the main diagonal of to form one eigenvalues set as , and compute the space values as , where . Since only contains one dynamic target, there should be , and thus we abbreviate the space value corresponding to as . Then the second spatial-domain direction of the -th dynamic target within the -th TTS can be estimated as
| (47) |
Finally, the pitch angle of the -th dynamic target within the -th TTS can be estimated as
| (48) |
| (54) |
| (55) |
Similarly, let us transform into an -matrix with the dimension of . Based on (45), can be represented as
| (49) |
where , is defined as the first spatial-domain direction array steering vector, and . Since is the array signals form related to the first spatial-domain direction array, we can estimate from by utilizing array signal processing methods. Similarly, we can employ the ESPRIT method to obtain the space value corresponding to as . Then the first spatial-domain direction of the -th dynamic target within the -th TTS can be estimated as
| (50) |
Then the horizontal angle of the -th dynamic target within the -th TTS can be estimated as
| (51) |
To estimate the distance of the target, let us transform into a distance-matrix with the dimension of . Based on (45), can be represented as
| (52) |
where is defined as the distance array steering vector, and . Since is the array signals form related to the distance array, we can estimate from by utilizing array signal processing methods. Similarly, we can employ the ESPRIT method to obtain the space value corresponding to as . Then the polar distance of the -th dynamic target within the -th TTS can be estimated as
| (53) |
III-E Radial Velocity and Angular Velocities Estimation
It can be analyzed from (45) that each antenna observes one virtual-velocity composed of the radial velocity, horizontal angular velocity, and pitch angular velocity of the dynamic target. Note that the virtual-velocity observed by different antenna is different. We can design and derive the virtual-velocity of the -th dynamic target observed by the -th antenna within the -th TTS from (45) as , which is shown in (54) at the top of this page. Then (45) can be rewritten as (55) at the top of this page.
Next, we need to estimate the virtual-velocity observed by each antenna. We can extract the DT-EEC of the -th antenna on all subcarriers of all OFDM symbols from as
| (56) |
where , , , , and is defined as the virtual-velocity array steering vector. Since is the array signals form related to the virtual-velocity array, we can estimate from by utilizing array signal processing methods. Similarly, we can employ the ESPRIT method to obtain the space value corresponding to as . Then the virtual-velocity of the -th dynamic target observed by the -th antenna within the -th TTS can be estimated as
| (57) |
By traversing each antenna, we can obtain the virtual-velocity observed by each antenna, which is record as with and . Then we need to estimate the radial velocity, horizontal angular velocity, and pitch angular velocity of the target from these ternary pairs.
In fact, we can express as a binary function of . Based on (54), there is
| (58) |
where
| (59) |
| (60) |
| (61) |
Formula (58) indicates that ternary pairs could form a plane in three-dimensional space.
Therefore, we can use the least squares (LS) method for planar fitting of , and we record the parameter results of plane fitting as , and . Then based on (59), (60) and (61), the pitch angular velocity, horizontal angular velocity, and radial velocity of the -th dynamic target within the -th TTS can be sequentially estimated as
| (62) |
| (63) |
| (64) |
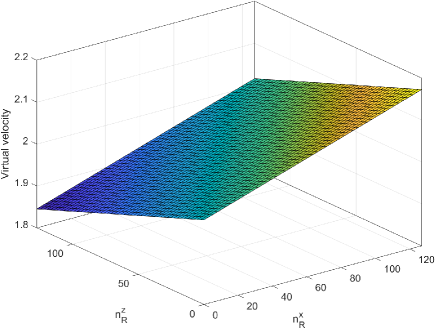
Based on (48), (51), (53), (62), (63) and (64), we have estimated the 6D motion parameters of the -th dynamic target within the -th TTS as .
Fig. 4 shows an example of virtual velocity estimation and fitting. It can be seen from the figure that different antennas have observed different virtual velocities for the same dynamic target, the 2D antenna index and virtual velocity form a plane in the 3D coordinate system, and thus we can recover the radial velocity, horizontal angular velocity, and pitch angular velocity of the target from these virtual velocities based on formulas from (58) to (64).
III-F Long-Term Motion Tracking
We consider the 6D motion parameters of the -th dynamic target as the state of one micro-system, and consider the obtained through the 6D sensing algorithm as the observation of this micro-system. Based on the formulas from (8) to (13), the state equation can be expressed as
| (65) |
where is state transition matrix, is disturbance driven matrix, is the state noise matrix and its covariance matrix is . Besides, the observation equation of the micro-system can be represented as
| (66) |
where is the observation matrix, is equivalent observation noise vector and its covariance matrix is . Then we can use Kalman filtering (KF) [34] to track the long-term motion of the -th dynamic target as follows:
1) Initialization: ISAC BS can obtain the 6D parameters estimation of the -th dynamic target through beam scanning during SBS stage. Next, to enter the SBT stage, we initialize the time as , the observation as , the state estimation as , and .
2) State prediction: Based on , the state prediction within the -th TTS can be calculated as .
3) Observation prediction: The observation prediction within the -th TTS can be computed as .
4) Calculate Kalman gain: Based on , we can compute . Then the Kalman gain can be obtained as .
5) State estimation update: The KF estimation of the 6D motion parameters can be updated and represented as . Besides, can be updated as .
Based on the above steps, we can continuously track the dynamic targets within TTS, and we employ as the final 6D motion parameters estimation result of the -th dynamic target within the -th TTS.
IV Simulation Results
In simulations, we set the lowest carrier frequency of the ISAC system as GHz, set the subcarrier frequency interval as kHz, and set the antenna spacing as . To succinctly display the simulation results, we set the horizontal angle and horizontal angular velocity of the dynamic target as and , and thus the dynamic target is fixed to move within a 2D plane. Then we focus on the sensing accuracy of the parameters of the dynamic target.
Specifically, for the aspect of evaluating 6D radar sensing, the root mean square error (RMSE) of distance sensing, angle sensing, radial velocity sensing and angular velocity sensing are defined as , , , and , where is the number of the Monte Carlo runs, the real parameters of the dynamic target is , and is the estimation parameters of the target.
IV-A The Performance of 6D Radar Single-Shot Sensing
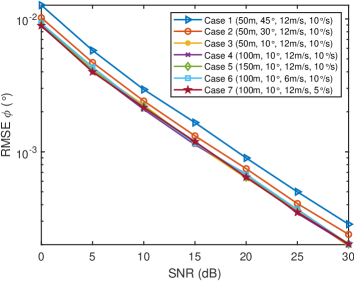
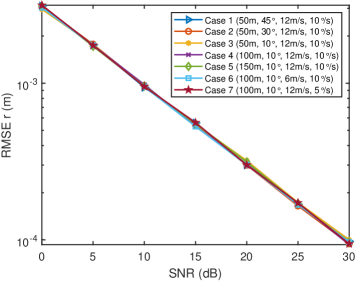
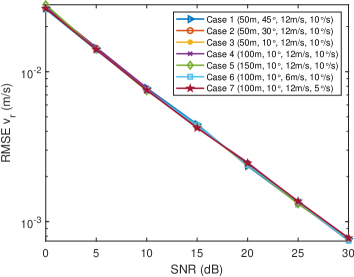
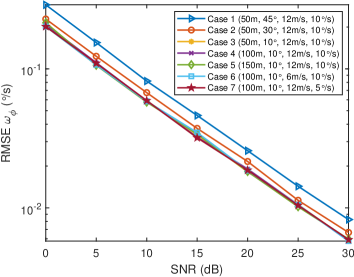
We set that the number of subcarriers is , the number of OFDM symbols is , the number of the antennas in HU-UPA is , the number of the antennas in RU-UPA is . Fig. 5 shows the single-shot sensing RMSE of the proposed scheme for different dynamic targets with different motion parameters versus SNR. It can be seen that the , , , and gradually decrease with the increase of SNR. When SNR dB, the average sensing RMSEs are , , , and . When SNR increases to dB, the average sensing RMSEs decrease to , , , and .
Unlike most existing ISAC studies believing that only the radial velocity of far-field dynamic target can be measured based on one single BS. These simulation results indicate that the proposed 6D radar sensing algorithm has high sensing accuracy, especially confirming that one single BS with MIMO array can effectively estimate the angular velocity of the dynamic target.
Besides, it is found from Fig. 5(b) and Fig. 5(c) that under the same system parameter settings, the distance sensing and radial velocity sensing performance of dynamic targets with different motion parameters are basically consistent. However, it is seen from Fig. 5(a) and Fig. 5(d) that under the same system parameter settings, the accuracy of dynamic target angle sensing and angular velocity senisng gradually improves as the target approaches , mainly because the MIMO array has narrower beamwidth near , thus improving the accuracy of angle sensing. Since the angular velocity sensing depends on the angle change of the target, the narrower beam near also brings higher angular velocity sensing accuracy.
IV-B The Impact of System Parameters on the Performance of 6D Radar Single-Shot Sensing
We take the sensing of the dynamic target with motion parameters (, , , ) as the example, and investigate the impact of system parameter settings on the performance of 6D radar single-shot sensing.
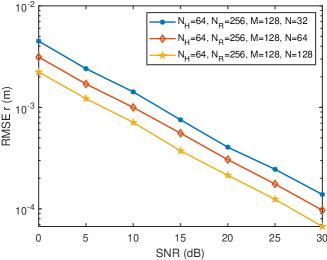
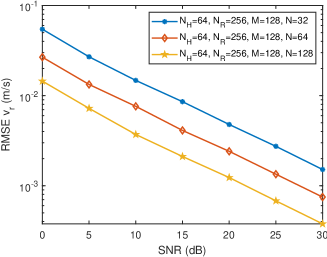
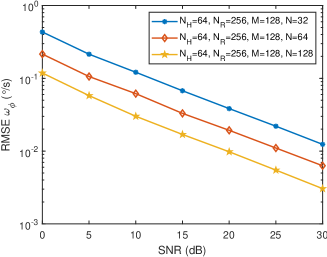
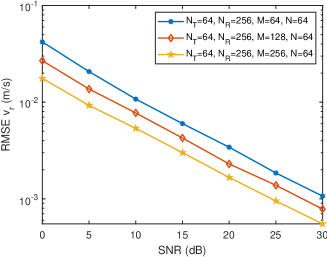
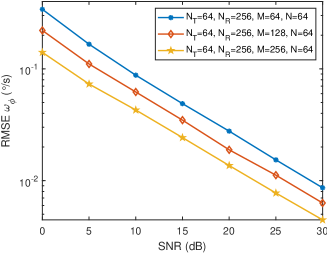
Fig. 6 shows the variation curves of distance sensing, radial velocity sensing, and angular velocity sensing versus SNR under different number of OFDM symbols. It can be seen from Fig. 6(a) that the gradually decreases as the number of OFDM symbols increases. This is because more OFDM symbols bring more observations to the distance array, making the estimation of the covariance matrix of the distance array more accurate, and thereby improving the accuracy of distance sensing. Besides, it can be found from Fig. 6(b) and Fig. 6(c) that the and the significantly decrease with the increase of . This is because more OFDM symbols form a larger virtual velocity array, making the sensing of radial velocity and angular velocity more accurate.
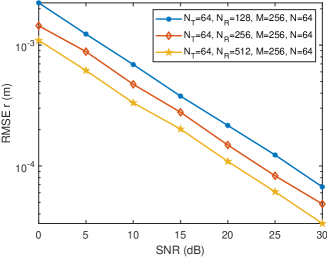
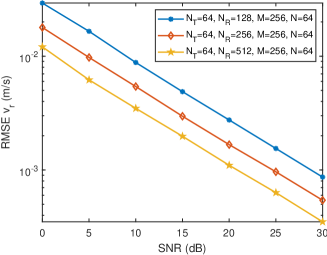
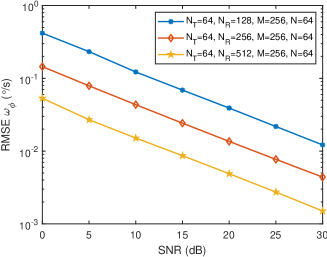
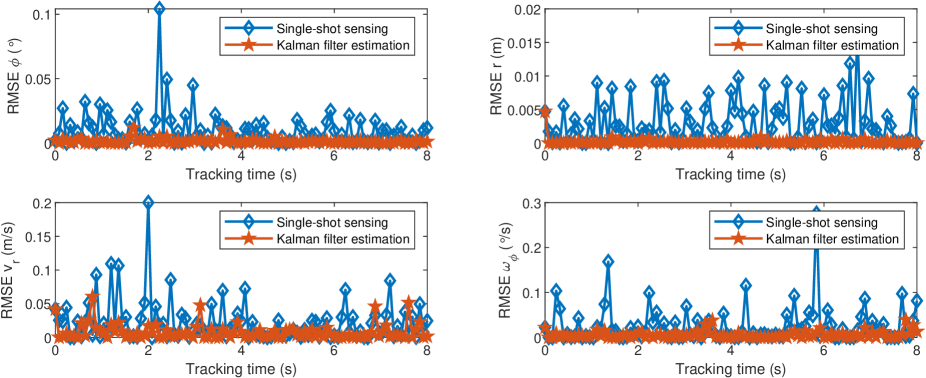
Fig. 7 shows the variation curves of sensing RMSEs versus SNR under different number of subcarriers. It can be seen from Fig. 7(a) that the gradually decreases with the increase of the number of subcarriers , because more subcarriers can form a larger distance array, thereby improving the accuracy of distance sensing. It can be found from Fig. 7(b) and Fig. 7(c) that the and the gradually decrease with the increase of . This is because more subcarriers bring more observations to the virtual velocity array, making the covariance matrix estimation of the virtual velocity array more accurate, thereby improving the sensing accuracy of radial velocity and angular velocity.
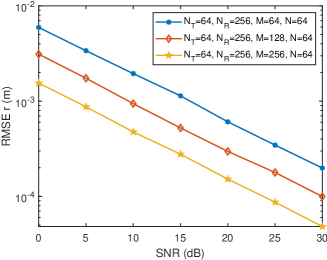
Fig. 8 shows the variation curves of sensing RMSEs versus SNR under different number of antennas. It can be seen from Fig. 8(a) that gradually decreases as the number of antennas increases. This is because more receiving antennas provide more observations for distance array, thereby improving the accuracy of distance sensing. More importantly, it can be observed from Fig. 8(b) and Fig. 8(c) that the and the gradually decrease with the increase of . This is because when there are more receiving antennas measuring the virtual velocity, the system can better fit the virtual velocity plane, thereby more accurately recovering the radial velocity and angular velocity of dynamic target.
IV-C The Performance of Multiple-Shots Tracking
We set the dynamic target with the initial motion parameter of , , , , and the BS needs to track this target within seconds. We set the system parameters as , , , and . Fig. 9 shows the tracking performance of multiple-shots tracking for dynamic target when SNR dB. It can be seen from the figure that the dynamic target tracking algorithm based on Kalman filtering can further improve the sensing accuracy of 6D radar single-shot sensing, especially the performance of angular velocity sensing. These simulation results verify the effectiveness of the proposed scheme.
V Conclusions
In this paper, we have proposed a novel scheme for 6D radar sensing and tracking of dynamic target based on MIMO array for monostatic ISAC system. We have re-examined and re-derived the relationship between 6D motion parameters of dynamic target and sensing echo channel of MIMO-ISAC system, and found that the sensing echo channel actually includes the distance, horizontal angle, pitch angle, radial velocity, horizontal angular velocity, and pitch angular velocity of dynamic target. Specifically, we have proposed the 6D long-term motion and short-term motion model of dynamic target. Then we have derived the sensing channel model corresponding to short-term motion. Next, for single-shot sensing, we employed the array signal processing methods to estimate the dynamic target’s distance, horizontal angle, pitch angle, and virtual velocity. Then we found that the virtual velocities observed by different antennas were different, which allowed us to utilize plane parameter fitting to estimate the radial velocity, horizontal angular velocity, and pitch angular velocity of the dynamic target. Furthermore, we have realized the multiple-shots tracking of dynamic target based on each single-shot sensing results and Kalman filtering. Simulation results have been provided to demonstrate the effectiveness of the proposed 6D radar sensing and tracking scheme.
References
- [1] A. Hassanien, M. G. Amin, E. Aboutanios, and B. Himed, “Dual-function radar communication systems: A solution to the spectrum congestion problem,” IEEE Signal Process. Mag., vol. 36, no. 5, pp. 115–126, Sep. 2019.
- [2] F. Liu, C. Masouros, A. P. Petropulu, H. Griffiths, and L. Hanzo, “Joint radar and communication design: Applications, state-of-the-art, and the road ahead,” IEEE Trans. Commun., vol. 68, no. 6, pp. 3834–3862, Feb. 2020.
- [3] F. Liu, Y. Cui, C. Masouros, J. Xu, T. X. Han, Y. C. Eldar, and S. Buzzi, “Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond,” IEEE J. Sel. Areas Commun., vol. 40, no. 6, pp. 1728–1767, Jun. 2022.
- [4] M. Giordani, M. Polese, M. Mezzavilla, S. Rangan, and M. Zorzi, “Toward 6G networks: Use cases and technologies,” IEEE Commun. Mag., vol. 58, no. 3, pp. 55–61, Mar. 2020.
- [5] Y. Cui, F. Liu, X. Jing, and J. Mu, “Integrating sensing and communications for ubiquitous IoT: Applications, trends, and challenges,” IEEE Network, vol. 35, no. 5, pp. 158–167, Nov. 2021.
- [6] C. Chaccour, M. N. Soorki, W. Saad, M. Bennis, P. Popovski, and M. Debbah, “Seven defining features of terahertz (THz) wireless systems: A fellowship of communication and sensing,” IEEE Commun. Surveys Tuts., vol. 24, no. 2, pp. 967–993, Jan. 2022.
- [7] Z. Wei, F. Liu, C. Masouros, N. Su, and A. P. Petropulu, “Toward multi-functional 6G wireless networks: Integrating sensing, communication, and security,” IEEE Commun. Mag., vol. 60, no. 4, pp. 65–71, Apr. 2022.
- [8] S. Lu, F. Liu, and L. Hanzo, “The degrees-of-freedom in monostatic ISAC channels: NLoS exploitation vs. reduction,” IEEE Trans. Veh. Technol., vol. 72, no. 2, pp. 2643–2648, Feb. 2023.
- [9] Z. Han, L. Han, X. Zhang, Y. Wang, L. Ma, M. Lou, J. Jin, and G. Liu, “Multistatic Integrated Sensing and Communication System in Cellular Networks,” arXiv e-prints, p. arXiv:2305.12994, May 2023.
- [10] X. Chen, Z. Feng, Z. Wei, X. Yuan, P. Zhang, J. Andrew Zhang, and H. Yang, “Multiple signal classification based joint communication and sensing system,” IEEE Trans. Wireless Commun., pp. 1–1, 2023.
- [11] W. Jiang, D. Ma, Z. Wei, Z. Feng, and P. Zhang, “ISAC-NET: Model-driven deep learning for integrated passive sensing and communication,” arXiv e-prints, p. arXiv:2307.15074, July 2023.
- [12] F. Liu, W. Yuan, C. Masouros, and J. Yuan, “Radar-assisted predictive beamforming for vehicular links: Communication served by sensing,” IEEE Trans. Wireless Commun., vol. 19, no. 11, pp. 7704–7719, Nov. 2020.
- [13] Z. Du, F. Liu, W. Yuan, C. Masouros, Z. Zhang, S. Xia, and G. Caire, “Integrated sensing and communications for v2i networks: Dynamic predictive beamforming for extended vehicle targets,” IEEE Trans. Wireless Commun., vol. 22, no. 6, pp. 3612–3627, Jun. 2023.
- [14] S. Sun and Y. D. Zhang, “4D automotive radar sensing for autonomous vehicles: A sparsity-oriented approach,” IEEE J. Sel. Topics Signal Process., vol. 15, no. 4, pp. 879–891, Jun. 2021.
- [15] M. Lei, D. Yang, and X. Weng, “Integrated sensor fusion based on 4D MIMO radar and camera: A solution for connected vehicle applications,” IEEE Veh. Technol. Mag., vol. 17, no. 4, pp. 38–46, Dec. 2022.
- [16] J. A. Nanzer, “Millimeter-wave interferometric angular velocity detection,” IEEE Trans. Microw. Theory Techn., vol. 58, no. 12, pp. 4128–4136, Dec. 2010.
- [17] J. A. Nanzer, K. Kammerman, and K. S. Zilevu, “A 29.5 GHz radar interferometer for measuring the angular velocity of moving objects,” in Proc. IEEE Int. Microwave Symp. Digest, pp. 1–3, Jun. 2013.
- [18] J. A. Nanzer and K. S. Zilevu, “Time-frequency measurement of moving objects using a 29.5GHz dual interferometric-Doppler radar,” in Proc. IEEE Antennas and Propagation Soc. Int. Symp., pp. 830–831, Jul. 2013.
- [19] J. A. Nanzer, “On the resolution of the interferometric measurement of the angular velocity of moving objects,” IEEE Trans. Antennas Propag., vol. 60, no. 11, pp. 5356–5363, Nov. 2012.
- [20] X. Wang, P. Wang, and V. C. Chen, “Simultaneous measurement of radial and transversal velocities using a dual-frequency interferometric radar,” in Proc. IEEE RadarConf, pp. 1–6, Apr. 2019.
- [21] X. Wang, P. Wang, and V. C. Chen, “Simultaneous measurement of radial and transversal velocities using interferometric radar,” IEEE Trans. Aerosp. Electron. Syst., vol. 56, no. 4, pp. 3080–3098, Aug. 2020.
- [22] P. Wang, H. Liang, X. Wang, and E. Aboutanios, “Transversal velocity measurement of multiple targets based on spatial interferometric averaging,” in Proc. IEEE Int. Radar Conf. (RADAR), pp. 709–713, Apr. 2020.
- [23] Z. Gao, Z. Wan, D. Zheng, S. Tan, C. Masouros, D. W. K. Ng, and S. Chen, “Integrated sensing and communication with mmWave massive MIMO: A compressed sampling perspective,” IEEE Trans. Wireless Commun., vol. 22, no. 3, pp. 1745–1762, Mar. 2023.
- [24] H. Chen, H. Sarieddeen, T. Ballal, H. Wymeersch, M.-S. Alouini, and T. Y. Al-Naffouri, “A tutorial on terahertz-band localization for 6G communication systems,” IEEE Commun. Surveys Tuts., vol. 24, no. 3, pp. 1780–1815, May 2022.
- [25] H. Luo, F. Gao, W. Yuan, and S. Zhang, “Beam squint assisted user localization in near-field integrated sensing and communications systems,” IEEE Trans. Wireless Commun., pp. 1–1, Oct. 2023.
- [26] Z. Lin, T. Lv, J. A. Zhang, and R. P. Liu, “3D wideband mmwave localization for 5G massive MIMO systems,” in Proc. IEEE Global Commun. Conf. (GLOBECOM), Waikoloa, HI, USA, Dec. 2019, pp. 1–6.
- [27] H. Luo, Y. Wang, J. Zhao, H. Wu, S. Ma, and F. Gao, “Integrated sensing and communications in clutter environment,” arXiv e-prints, p. arXiv:2311.01674, Nov. 2023.
- [28] H. Luo, F. Gao, H. Lin, S. Ma, and H. V. Poor, “YOLO: An efficient terahertz band integrated sensing and communications scheme with beam squint,” arXiv e-prints, p. arXiv:2305.12064, May 2023.
- [29] R. Roy and T. Kailath, “ESPRIT-estimation of signal parameters via rotational invariance techniques,” IEEE Trans. Acoust., Speech, Signal Process., vol. 37, no. 7, pp. 984–995, Jul. 1989.
- [30] R. Roy, A. Paulraj, and T. Kailath, “ESPRIT–a subspace rotation approach to estimation of parameters of cisoids in noise,” IEEE Trans. Acoust., Speech, Signal Process., vol. 34, no. 5, pp. 1340–1342, Oct. 1986.
- [31] A. Paulraj, R. Roy, and T. Kailath, “Estimation of signal parameters via rotational invariance techniques- esprit,” in Nineteeth Asilomar Conference on Circuits, Systems and Computers, 1985., pp. 83–89, Nov. 1985.
- [32] M. Wax and T. Kailath, “Detection of signals by information theoretic criteria,” IEEE Trans. Acoust., Speech, Signal Process., vol. 33, no. 2, pp. 387–392, Apr. 1985.
- [33] A. Barron, J. Rissanen, and B. Yu, “The minimum description length principle in coding and modeling,” IEEE Trans. Inf. Theory, vol. 44, no. 6, pp. 2743–2760, Oct. 1998.
- [34] H. Ma, L. Yan, Y. Xia, and M. Fu, Introduction to Kalman Filtering, pp. 3–9. Singapore: Springer Singapore, 2020.