⁷⁷Se NMR measurements of the $\pi-d$ exchange field in the organic conductor $\lambda-$(BETS)₂FeCl₄

Correlations between conduction electrons and local magnetic moments in condensed matter physics are of considerable interest in situations where the properties of the conduction electrons are significantly tuned by the internal field generated by the local magnetic moments. These interactions can lead to a rich variety of phases, including superconductivity, density waves, and magnetic ordering. Many examples include low-dimensional organic conductors that have been synthesized in recent decades day ; coronado ; uji1 ; kobayashi1 . It is widely accepted that their physical properties are largely determined by the interaction between the donor HOMO (highest occupied molecular orbitals) band molecules and the anions mori1 ; ruderman ; mori2 .

An important example is the quasi-two dimensional (2D) triclinic (space group P$\bar{1}$) salt, $\lambda$-(BETS)₂FeCl₄, where BETS is bis(ethylenedithio)tetraselenafulvalene (C₁₀S₄Se₄H₈) uji1 ; kobayashi1 ; tokumoto ; brossard ; akutsu1 . Below an applied magnetic field ($\bf{B}$₀) of about 11 T, as the temperature ($T$) is lowered it has a transition from a paramagnetic metal (PM) to an antiferromagnetic insulating (AFI) phase. At higher fields and low $T$ there is a PM to field-induced superconducting (FISC) phase uji1 ; kobayashi1 ; tokumoto ; brossard .

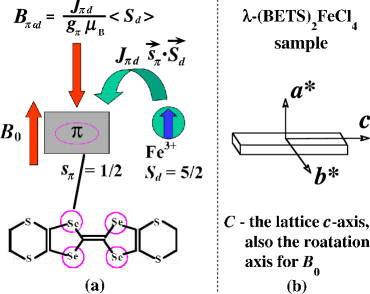
A mechanism proposed for the FISC phase in $\lambda$-(BETS)₂FeCl₄ is the Jaccarino-Peter (J-P) compensation effect jaccarino operating in a two-dimensional (2D) system uji1 ; balicas1 ; balicas2 , as illustrated in Fig. 1 (a) hiraki . In this model, the total (negative) exchange interaction ($\pi-$d interaction, exchange constant $J_{\pi d}$) between the paramagnetic 3d Fe³⁺ moments ($g\mu_{B}\bf{S}$_d) ($g$ is the Landé $g$-factor of the Fe³⁺ and $\mu_{B}$ is the Bohr magneton) and the conduction $\pi$-electrons at the Se sites in the BETS molecule uji1 ; akutsu1 generates a large exchange field ($\bf{B}$_πd) at the Se electrons aligned opposite to $\bf{B}$₀ given by

where $<\bf{S}$${}_{d}>$ is the average value of the Fe³⁺ spin polarization, and $g_{\pi}$ is the Landé $g$-factor for the $\pi$-electrons. When $\bf{B}$₀ is aligned parallel to the $ac$ plane, the orbital pair breaking effect for the $\pi$-electrons is minimized. At low $T$ ($T$ $<$ 5 K) for 17 T $<$ $\bf{B}$₀ $<$ 45 T [in the FISC phase] uji1 , $<\bf{S}$${}_{d}>$ is nearly saturated and it is expected that $|$$\bf{B}$${}_{\pi d}|$ $\simeq$ 33 T balicas1 . Thus, the magnitude of the effective field at the Se electrons, $|\bf{B}$₀ $-$ $\bf{B}$${}_{\pi d}|$ = $|\bf{B}$${}_{0}|$ $-$ 33 T, is small enough to permit the FISC phase. Also, for $|\bf{B}$${}_{0}|$ $<$ $|\bf{B}$${}_{\pi d}|$ and $|\bf{B}$${}_{0}|$ $>$ $|\bf{B}$${}_{\pi d}|$ the spin polarization of the conduction electrons is respectively antiparallel and parallel to $\bf{B}$₀, a feature that can be probed by the hyperfine frequency shift of the ⁷⁷Se NMR signal.

This description in terms of the J-P mechanism is supported by the fact that its iso-structural nonmagnetic and non-3d-electron analog $\lambda$-(BETS)₂GaCl₄ exhibits a behavior kobayashi2 ; kobayashi3 that is completely different from that of $\lambda$-(BETS)₂FeCl₄. Even though the above model of FISC in $\lambda$-(BETS)₂FeCl₄ is widely accepted, it needs further experimental confirmation.

Nuclear magnetic resonance (NMR) is a versatile local probe that is capable of directly measuring the distribution of internal magnetic field and the electron spin dynamics on the atomic scale. Thus, it can be used as a tool to test the validity of the J-P mechanism for FISC in $\lambda$-(BETS)₂FeCl₄.

⁷⁷Se-NMR measurments hiraki1 have been reported for a single crystal of $\lambda$-(BETS)₂FeCl₄ with $\bf{B}$₀ = 14.5 T aligned in the $ac$ plane (PM phase) uji1 . But the value obtained for $|\bf{B}$${}_{\pi d}|$ is 23 T, which is $\sim$ 30$\%$ smaller than the 33 T predicted by the electricial resistivity measurements uji2 ; balicas1 and a theoretical estimate mori2 . Also, these measurements do not include other alignments for $\bf{B}$₀.

In this paper, we report ⁷⁷Se-NMR spectrum and frequency shift measurements in a single crystal of $\lambda$-(BETS)₂FeCl₄, for 2.5 K $\leq$ $T$ $\leq$ 30 K over a range of alignments of $\bf{B}$₀ = 9 T in the plane $\perp$ to the $c$-axis. At this value of $\bf{B}$₀, the PM-AFI transition is at 3.5 K. Analysis of these results gives $|\bf{B}$${}_{\pi d}|$ = (32.7 $\pm$ 1.5) T aligned opposite to $\bf{B}$₀ at low $T$ and $B_{0}$ $\geq$ 9 T where the Fe³⁺ magnetization is almost fully saturated (the saturation value of $<S_{d}>$ is slightly less than 2.5 at 9 T due to Fe³⁺ $-$ Fe³⁺ antiferromagnetic interaction guoqing ), consistent with the predicted value 33 T uji2 ; balicas1 ; mori2 . It supports the J-P compensation as the mechanism for the FISC phase in $\lambda$-(BETS)₂FeCl₄. An important input for this work is the Fe³⁺ magnetization that obtained from proton NMR measurements on $\lambda$-(BETS)₂FeCl₄ guoqing , which are not sensitive to conduction electron contributions.

The sample used for these measurements was grown using a standard method kobayashi1 without ⁷⁷Se enrichment (⁷⁷Se natural abundance = 7.5$\%$). Its dimensions are $a^{\ast}$ $\times$ $b^{\ast}$ $\times$ $c$ = 0.09 mm $\times$ 0.04 mm $\times$ 0.80 mm [Fig. 1 (b)], corresponding to a mass of $\sim$ 7 $\mu g$ with $\sim$ 2.0 $\times$ 10^{15 77}Se nuclei. Because of the small number of spins, a small microcoil with a filling factor ($\sim$ 0.4) was used. For most acquisitions, 10⁴-10⁵ averages were used on a time scale of $\sim$ 5 min for 10⁴ averages. The gyromagnetic ratio of ⁷⁷Se, $\gamma$ = 8.131 MHz/T, is used for data analysis. The sample and coil were rotated on a goniometer (rotation angle $\phi$) whose rotation axis is along the lattice $c$-axis (needle direction), which is $\perp$ $\bf{B}$₀. Based on the crystal structure kobayashi1 , the direction of the Se $p_{z}$ orbital is 76.4^∘ from the $c$-axis guoqing1 . Then, the minimum angle between $p_{z}$ and $\bf{B}$₀ during the rotation of the goniometer is $\phi_{\text{min}}$ = 13.6^∘.

Figure 2 shows the ⁷⁷Se-NMR absorption spectrum ($\chi^{\prime\prime}$) of $\lambda$-(BETS)₂FeCl₄, plotted as a function of the frequency shift $\nu$ $-$ $\nu_{0}$ ($\nu_{0}$ = 72.90 MHz) at a few $T$ from 30 to 2.5 K with $\bf{B}$₀ = 9 T $\parallel$ $\bf{a}$^′, where $\nu$ $-$ $\nu_{0}$ has a weak $T$-dependence as discussed in more detail later.

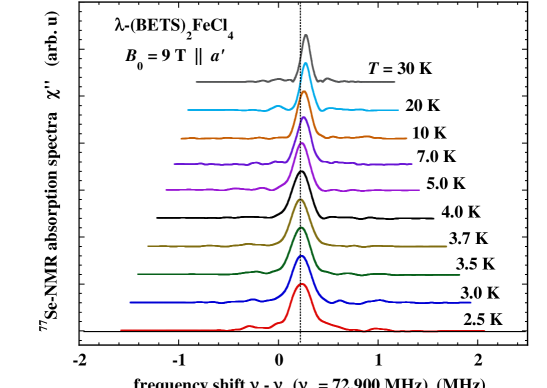
These spectra measure the distribution of the local magnetic field at the different ⁷⁷Se nuclei in the sample. As discussed in more detail later, the local field responsible for this distribution is dominated by the sum of $\bf{B}$₀, the dipole field from the Fe³⁺ spins ($\bf{B}$_dip), and the hyperfine field from the Se conduction electrons, whose polarization is strongly influenced by $\bf{B}$_πd. The spectra are characterized by (1) the full width at half maximum (FWHM) linewidth ($\Delta f$) which represents the internal magnetic field distribution, and (2) the frequency ($\nu$) of the center of $\chi^{\prime\prime}$ which measures the average of the hyperfine field from the conduction electrons that coupled to the Fe³⁺ ions.

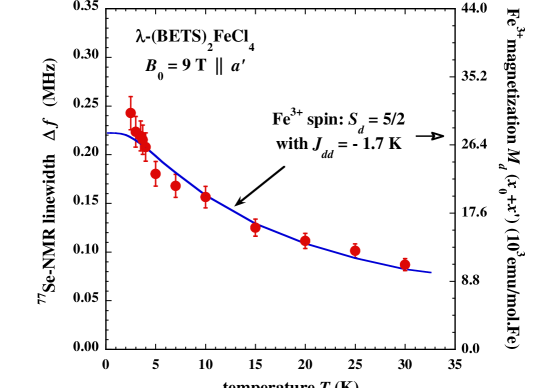
Figure 3 shows $\Delta f$ as a function of $T$ for $\bf{B}$₀ = 9 T $\parallel$ $a^{\prime}$. Also shown is a fit to the Fe³⁺ magnetization $M_{d}(x_{0}+x^{\prime})$ [unit: 10³ emu/mol.Fe] provided by the modified Brillouin function guoqing $B_{JM}(x)$ = $B_{J}(x_{0}+x^{\prime})$, where $B_{J}(x)$ is the standard Brillouin function ashcroft , $J$ = $S_{d}$ = 5/2, $x_{0}$ = $\frac{Jg\mu_{B}B_{0}}{k_{B}T}$, $x^{\prime}$ = $-\frac{Jg\mu_{B}B^{\prime}}{k_{B}T}$, the $d$-$d$ Fe³⁺ exchange field $B^{\prime}$ $\simeq$ $\frac{|J_{dd}|Jk_{\rm{B}}}{g\mu_{\rm{B}}}B_{J}(x_{0})$, and $J_{dd}$ = $-$1.7 K is the $d$-$d$ exchange parameter. The fit parameters for $B_{JM}(x)$ are obtained from proton NMR measurements guoqing . In Fig. 3, $\Delta f(T)$ increases from $\sim$ 90 kHz to $\sim$ 200 kHz as $T$ is lowered from 30 to 5 K. Also, $M_{d}(x_{0}+x^{\prime})$ provides a good fit. Since the susceptibility of the BETS molecules is small and nearly independent of $T$, $M_{d}$ is the main source of $\Delta f(T)$ in the PM phase. The size of $\Delta f(T)$ is attributed to a distribution of $\bf{B}$_dip and the hyperfine field of the Fe³⁺ across the different Se sites. Since measurements of the ⁷⁷Se-NMR spin-echo decay indicate a homogeneous linewidth of $\sim$ 10 kHz guoqing , it follows that $\chi^{\prime\prime}$ is strongly inhomogeneously broadened.

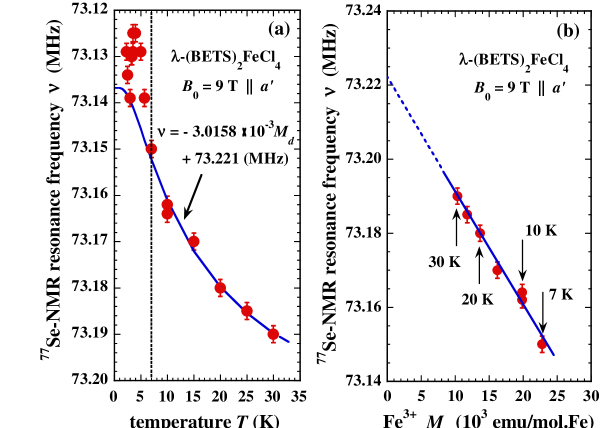
A similar $T-$dependence is also observed in $\nu$, which is plotted as a function of $T$ in Fig. 4 (a) and $M_{d}(x_{0}+x^{\prime})$ in Fig. 4 (b). In the PM state above $\sim$ 7 K, a good fit to $\nu$ (uncertainty $\pm$ 3 kHz) is obtained using

This result is a strong indication that the $T-$dependence of $\nu$ is dominated by the hyperfine field from the Fe³⁺ magnetization. The negative sign of the contribution from $M_{d}$ is very important. It indicates that the hyperfine field from the Fe³⁺ magnetization is negative, i.e., opposite to $\bf{B}$₀, as needed for the J-P comensation mechanism.

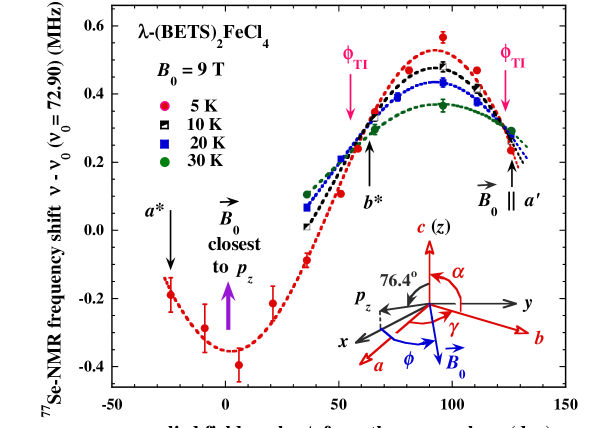
A more informative result is shown in Fig. 5, where $\nu$ $-$ $\nu_{0}$ ($\nu_{0}$ = 72.90 MHz) is plotted as a function of both $\phi$ and $T$. As shown in the lower right of Fig. 5, the $z$-axis is chosen to be parallel to the $c$-axis, $p_{z}$ is the $z$-component of the BETS $\pi$-electron orbital moment, the $x$-axis is in the the $c$-$p_{z}$ plane, and $\bf{B}$₀ is in the $xy$-plane ($\perp$ $c$) rotated by $\phi$ from the $x$-axis. The angle $\phi$ = 0^∘ corresponds to $\bf{B}$₀ $\parallel$ the $c$-$p_{z}$ plane and the minimum angle between $\bf{B}$₀ and $p_{z}$ is $\phi_{\rm{min}}$ = 13.6^∘. The solid lines are a fit to the following theoretical model based upon the hyperfine coupling to the BETS Se $\pi$-electrons whose polarization is affected by the exchange field from the Fe³⁺ magnetization.

According to NMR theory slichter , the contributions to the Hamiltonian ($H_{I}$) of the ⁷⁷Se nuclear spins can be expressed as

where $H_{IZ}$ is the Zeeman Hamiltonian of the ⁷⁷Se nuclei in $\bf{B}$₀, $H_{II}$ is the ${}^{77}Se-^{77}$Se dipole-dipole interaction Hamiltonian, $H_{I\pi}^{\rm{hf}}$ is the direct hyperfine coupling of the ⁷⁷Se nucleus to the BETS $\pi$-electrons generated by $\bf{B}$₀, $H_{Id}^{\rm{hf}}$ is the indirect hyperfine coupling via the $\pi$-electrons to the 3d Fe³⁺ spins (field $\bf{B}$_πd), and $H_{d}^{\rm{dip}}$ is the dipolar coupling to the Fe³⁺ which gives $\bf{B}$_dip. Here, $\bf{B}$_dip is calculated guoqing1 using the sum of the near dipole, the bulk demagnetization and the Lorentz contributions slichter ; carter . All of these terms contribute to the static local magnetic field at the ⁷⁷Se sites and all but the first cause the ⁷⁷Se-NMR frequency shifts.

Based upon the lattice structure and the shape and size of the sample, we calculated the angular dependence of $\bf{B}$_dip and estimated guoqing1 that the contributions of $H_{II}$ is negligible. Thus,

and the corresponding value of $\nu$ is hiraki1

where $\phi^{\prime}$ is the angle between $\bf{B}$₀ and the $p_{z}$ direction, and $K_{c}$ and $K_{s}$ are respectively the (orbital) chemical shift and the (spin) Knight shift of the BETS Se $\pi$-electrons. The approximation in the second line corresponds to dropping the terms $B_{\rm{dip}}(B_{0},T)[K_{C}+K_{S}(\phi^{\prime})]$, which are the product of small quantities. It can be shown hiraki1 ; metzger ; takagi ; guoqing1 that for rotation of the sample about the $c$-axis with $\bf{B}$₀ in the plane $\perp$ $c$, $K_{s}(\phi^{\prime})$ is given by

where $K_{\rm{iso}}$ and $K_{\rm{an}}(\phi)$ are the isotropic (independent of $\phi$) and axial (anisotropic) parts of the Knight shift, respectively. $K_{\rm{iso}(\rm{ax})}$ is a constant determined by the isotropic (axial) hyperfine field $[A_{\rm{iso}(\rm{ax})}]$ produced by the 4$p_{\pi}$ spin polarization of the BETS Se $\pi$-electrons hiraki1 .

The quantities that determine $K_{\rm{ax}}$ are

where $\chi_{\rm{BETS}}$ = 4.5 $\times$ 10^-4 emu/mol is the BETS $\pi$-electron susceptibility tanaka , $g_{\pi}$ = 2, $N_{A}$ is the Avogadro’s number, and $A_{\rm{ax}}$ = + 38.6 kOe/$\mu_{B}$ reported by S. Takagi $et~al.$ takagi . This value of $A_{\rm{ax}}$ is based on theoretical calculations $<r^{-3}>_{4p}$ = 9.28 $a_{0}^{-3}$ ($a_{0}$ = 0.529 $\AA$, the Bohr radius) fraga , and $\sigma_{\rm{Se}}$ = 0.166 takagi1 obtained for $\lambda$-(BETS)₂GaCl₄, which has essentially the same BETS-molecules as $\lambda$-(BETS)₂FeCl₄. By using these values, one obtains $K_{\rm{ax}}$ = 15.3 $\times$ 10^-4. Its uncertainty is not known to us and is not included in our analysis.

The angular dependence of the shift in $K_{s}(\phi)$ [Eqs. (7)-(8)] has been used for the fit of the 5 K data shown in Fig. 5 using the relation $\nu$ $-$ $\nu_{0}$ = $a_{1}[3\cos^{2}\phi\cos^{2}13.6^{\circ}$ $-$ 1] + $b_{1}$, with the fit values $a_{1}$ = $-$ 313 kHz and $b_{1}$ = + 221 kHz (uncertainty $\pm$ 8 kHz).

From Eqs. (6)$-$(8), the formula for $B_{\pi,d}$ at a fixed $B_{0}$ and $T_{0}$ from the difference in $\nu$ ($\Delta\nu$) at the two angles $\phi_{1}$ and $\phi_{2}$ is

where

The conditions $T$ = 5 K, $\phi_{1}$ = 90^∘, and $\phi_{2}$ = 0^∘ give $\Delta\nu$(5K, 90^∘, 0^∘) = 880 $\pm$ 26 kHz (from Fig. 5) and $\Delta K_{\rm{an}}$ = 4.42 $\times$ 10^-3 (estimated error $\pm$ 3$\%$). Our calculated value of $B_{\rm{dip}}(0^{\circ})$ $-$ $B_{\rm{dip}}$(90^∘) at 5 K is 3.63$\times$10^-3 T and the field used was $B_{0}$ = 9.0006 T. These values then give $B_{\it{\pi d}}$ = $-$ 32.7 $\pm$ 1.5 T at 5 K (aligned opposite to $B_{0}$ = 9.0006 T), which is very close to the expected value of $-$ 33 T obtained from the electrical resistivity measurement uji2 ; balicas1 and the theoretical estimate mori2 . Also, a small increase in $<\bf{S}$${}_{d}>$ is expected as $B_{0}$ is increased from 9 T to 33 T at 5 K. From the modified Brillouin function analysis used for the proton NMR linewidth guoqing , we expect this increase in $<\bf{S}$${}_{d}>$ to be a factor 1.05 $\pm$ 0.05, which corresponds to an adjustment to $B_{\pi d}(33$ T, 5 K$)$ = $-$ 34.3 $\pm$ 2.4 T.

Similar results for the exchange field $B_{\pi d}$ can also be obtained from the $T$-dependence of $\nu$ at a fixed $\phi$ with the data in Figs. 4 and 5 using the same kind of fit as Eq. (2). But the uncertainty in the value obtained for $B_{\pi d}$ with this type of analysis is large enough that we do not present it here. An important test we plan to do in the future is to extend the measurements to $B_{0}$ $>$ $|B_{\pi d}|$ to find the value of $B_{0}$ = $|B_{\pi d}|$, where the angular dependence in Fig. 5 disappears [Eqs. (6)$-$(8)] and above which the sign of $K_{s}(\phi^{\prime})$ changes from negative to positive.

Figure 5 shows two values of $\phi$ ($\phi_{\rm{TI1}}$ and $\phi_{\rm{TI2}}$) where $\nu$ becomes independent of $T$. The measured difference $\phi_{\rm{TI1}}$ $-$ $\phi_{\rm{TI2}}$ = 65.0^∘ $\pm$ 2.0^∘, which should be symmetric around 90^∘, or $\phi_{\rm{TI1}}$ = 57.5^∘ $\pm$ 1.0^∘ and $\phi_{\rm{TI2}}$ = 122.5^∘ $\pm$ 1.0^∘. By using Eqs. (6) and (8) and neglecting the very small contribution from $B_{\rm{dip}}$ ($B_{\rm{dip}}$ $<<$ $|B_{\pi d}|$), it can be shown that the condition for $\phi_{\rm{TI\it{i}}}$ ($i$ = 1 , 2) is $K_{\rm{iso}}$ + $K_{\rm{ax}}[3\cos^{2}\phi_{\rm{TIi}}\cos^{2}\phi_{\rm{min}}$ $-$ 1] = 0. From this relation, the measured values of $\phi_{\rm{TI1}}$ and $\phi_{\rm{TI2}}$, and $K_{\rm{ax}}$ = 15.3 $\times$ 10^-4, one obtains $K_{\rm{iso}}$ = (2.8 $\pm$ 0.7) $\times$ 10^-4, or $K_{\rm{iso}}/K_{\rm{ax}}$ = 1/(5.5 $\pm$ 1.4).

In summary, our results of ⁷⁷Se-NMR spectrum and frequency shift measurements in $\lambda-$(BETS)₂FeCl₄ indicate that the Fe³⁺ spins have a strong antiferromagnetic coupling to the BETS $\pi$-electrons, and we determined the $\pi-d$ exchange field to be $B_{\pi d}$ = $J_{\pi d}<S_{d}>/g\mu_{B}$ = $-$ 32.7 $\pm$ 1.5 T at $B_{0}$ = 9 T and 5 K, with an expected value of $-$ 34.3 $\pm$ 2.4 T at $B_{0}$ $\simeq$ 33 T and 5 K. This large negative value of $B_{\pi d}$ (or $J_{\pi d}$) is consistent with that predicted by the resistivity measurements, and supports the Jaccarino-Peter internal field-compensation mechanism being responsible for the origin of the FISC phase in $\lambda-$(BETS)₂FeCl₄.

This work at UCLA is supported by NSF Grants DMR-0334869 (W.G.C.) and 0520552 (S.E.B.), and work at NHMFL is supported by NSF under Cooperative Agreement No. DMR-0084173 and the State of Florida.