A 4/3-approximation for TSP on cubic 3-edge-connected graphs
1 Introduction
We consider the travelling salesman problem on metrics which can be viewed as the shortest path metric of an undirected graph with unit edge-lengths. Finding a TSP tour in such a metric is then equivalent to finding a connected Eulerian subgraph in the underlying graph. Since the length of the tour is the number of edges in this Eulerian subgraph our problem can equivalently be stated as follows: Given an undirected, unweighted graph find a connected Eulerian subgraph, with the fewest edges. Note that could be a multigraph.
In this paper we consider the special case of the problem when is 3-regular (also called cubic) and 3-edge-connected. Note that the smallest Eulerian subgraph contains at least edges. In fact, in the shortest path metric arising out of such a graph the Held-Karp bound for the length of the TSP tour would also be . This is because we can obtain a fractional solution to the sub-tour elimination LP (which is equivalent to the Held-Karp bound) of value by assigning 2/3 to every edge in .
Improving the approximation ratio for metric-TSP beyond 3/2 is a long standing open problem. For the metric completion of cubic 3-edge connected graphs Gamarnik et.al. [1] obtained an algorithm with an approximation guarantee slightly better than 3/2. The main result of this paper is to improve this approximation guarantee to 4/3 by giving a polynomial time algorithm to find a connected Eulerian subgraph with at most 4n/3 edges. This matches the conjectured integrality gap for the sub-tour elimination LP for the special case of these metrics.
2 Preliminaries
Let be the number of vertices of the given graph G. Let denote the degree of x. A 2-factor in is a subset of edges such that every vertex has degree 2 in . Let denote the minimum size of components of X. Given two distinct edges and incident on a vertex , let denote the graph obtained by replacing by the edge . The vertex is said to be split off. We call a cut essential when both and contain at least one edge each.
We will need the following results for our discussion
Lemma 1 (Peterson[4]).
Every bridgeless cubic graph has a 2-factor.
Lemma 2 (Mader[3]).
Let be a -edge-connected graph, with . Then there exists edges such that is homeomorphic to a -edge-connected graph.
Lemma 3 (Jackson, Yoshimoto[2]).
Let be a 3-edge-connected graph with vertices. Then has a spanning even subgraph in which each component has at least vertices.
3 Algorithm
Our algorithm can be broadly split into three parts. We first find a 2-factor of the cubic graph that has no 3-cycles and 4-cycles. Next, we compress the 5-cycles into ‘super-vertices’ and split them using Lemma 2 to get a cubic 3-edge-connected graph again. Repeatedly applying the first part on and compressing the five cycles gives a 2-factor with no 5-cycle on the vertices of the original graph. We ‘expand’ back the super-vertices to form that is a subgraph of G. We finally argue that can be modified to get a connected spanning even multi-graph using at most 4/3(n) edges.
The starting point of our algorithm is Theorem 3 [2]. In fact [2] proves the following stronger theorem.
Theorem 1.
Let be a 3-edge-connected graph with vertices, be a vertex of with , and be edges of . (it may be the case that ). Then has a spanning even subgraph with and .
The proof of this theorem is non-constructive. We refer to the edges in the statement of the theorem as “required edges”. We now discuss the changes required in the proof given in [2] to obtain a polynomial time algorithm which gives the subgraph with the properties as specified in Theorem 1. Note that we will be working with a 3-regular graph (as against an arbitrary graph of min degree 3 in [2]) and hence the even subgraph we obtain will be a 2-factor.
-
1.
If contains a non-essential 3-edge cut then we proceed as in the proof of Claim 2 in [2]. This involves splitting into 2 graphs and suitably defining the required edges for these 2 instances so that the even subgraphs computed in these 2 graphs can be combined. This step is to be performed whenever the graph under consideration has an essential 3-edge cut.
-
2.
Since is 3-regular we do not require the argument of Claim 6.
-
3.
Since has no essential 3-edge cut and is 3-regular, a 3-cycle in implies that is . In this case we can find a spanning even subgraph containing any 2 required edges.
-
4.
The process of eliminating 4-cycles in the graph involves a sequence of graph transformations. The transformations are as specified in [2] but the order in which the 4-cycles are considered depends on the number of required edges in the cycle. We first consider all such cycles which do not have any required edges, then cycles with 2 required edges and finally cycles which have one required edge.
Since with each transformation the number of edges and vertices in the graph reduces we would eventually terminate with a graph, say , with girth 5. We find a 2-factor in , say and undo the transformations (as specified in [2]) in the reverse order in which they were done to obtain a 2-factor in the original graph which has the properties of Theorem 1.
Suppose the 2-factor obtained contains a 5-cycle . We compress the vertices of into a single vertex, say , and remove self loops. has degree 5 and we call this vertex a super-vertex. We now use Lemma 2 to replace two edges and incident at with the edge while preserving 3-edge connectivity. The edge is called a super-edge. Since the graph obtained is cubic and 3-edge connected we can once again find a 2-factor, each of whose cycles has length at least 5. If there is a 5-cycle which does not contain any super-vertex or super-edge we compress it and repeat the above process. We continue doing this till we obtain a 2-factor, say , each of whose cycles is either of length at least 6 or contains a super-vertex or a super-edge.
In the 2-factor we replace every super-edge with the corresponding edges. For instance the super-edge would get replaced by edges and where is a super-vertex obtained by collapsing the vertices of a cycle . After this process is no more a 2-factor but an even subgraph. However, the only vertices which have degree more than 2 are the super-vertices and they can have a maximum degree 4. Let denote this even subgraph.
Consider some connected component of . We will show how to expand the super-vertices in into 5-cycles to form an Eulerian subgraph with at most edges, where is number of vertices in the expanded component. For each component we will use 2 more edges to connect this component to the other components to obtain a connected Eulerian subgraph with at most edges. Note that the subgraph we obtain may use an edge of the original graph at most twice.
We now consider two cases depending on whether contains a super-vertex.
-
1.
has no super-vertices. Then, is a cycle with at least 6 vertices and hence Eulerian. Since the claim follows.
-
2.
has at least one super-vertex, say . We will discuss the transformations for a single super-vertex and this will be repeated for the other super-vertices. Note that has degree 2 or 4.
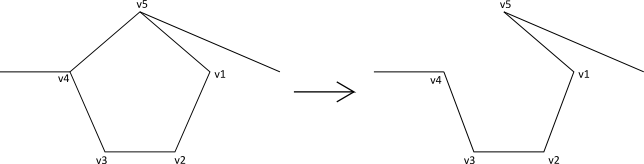
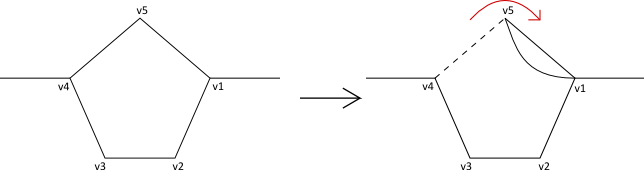
Figure 1: On Expanding a super-vertex with degree 2 If has degree 2, then the 2 edges incident on the 5-cycle corresponding to would be as in Figure 1. In both cases we obtain an Eulerian subgraph. By this transformation we have added 4 vertices and at most 5 edges to the subgraph .
Suppose the super-vertex has degree 4 in the component . may not necessarily be a component of the subgraph as it might have been obtained after expanding a few super-vertices, but that will not effect our argument. Let be the 5-cycle corresponding to this super-vertex and let be the vertices on (in order). Further let be the vertex not in adjacent to . Let be the edge incident on that is not in the subgraph .
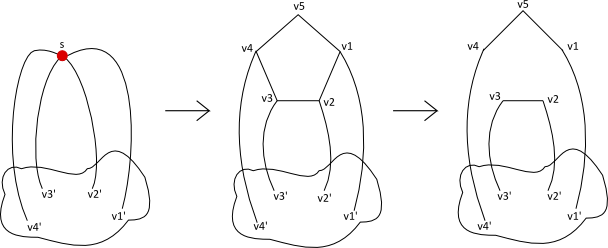
Figure 2: Expanding a super-vertex with degree 4 when and do not form a 2-edge-cut of the sub-graph constructed till now. 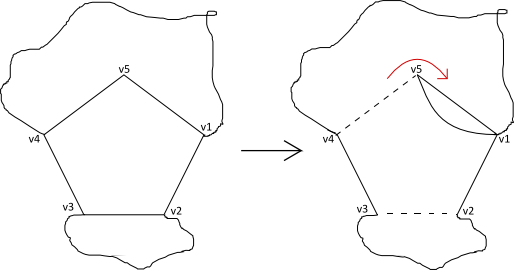
Figure 3: Expanding a super-vertex with degree 4 when and form a 2-edge-cut. We replace the vertex in with the cycle and let be the resulting subgraph. Note that by dropping edges and from we obtain an Eulerian subgraph which includes all vertices of . However, this subgraph may not be connected as it could be the case that edges and form an edge-cut in . If this is the case then we apply the transformation as shown in Figure 3. This ensures that remains connected and is Eulerian. Note that as a result of this step we have added 4 vertices and at most 4 edges to the subgraph .
Let be the component obtained by expanding all the super-vertices in . Suppose initially, component had super-vertices of degree 2, super-vertices of degree 4 and vertices of degree 2. This implies had + 2 + edges. On expanding a super-vertex of degree 2, we add 5 edges in the worst case. On expanding a super-vertex of degree 4, we add 4 edges in the worst case. So, the total number of edges in is at most while the number of vertices in is exactly . Note that and if then . Hence, and this implies that the number of edges in is at most .
4 Conclusions
We show that any cubic 3-edge connected graph contains a connected Eulerian subgraph with at most 4n/3 edges. It is tempting to conjecture the same for non-cubic graphs especially since the result in [2] holds for all 3-edge connected graphs. The example of a demonstrates that this conjecture would be false. A is 3-edge connected and any connected Eulerian subgraph contains at least edges.
References
- [1] David Gamarnik, Moshe Lewenstein, and Maxim Sviridenko. An improved upper bound for the tsp in cubic 3-edge-connected graphs. Oper. Res. Lett.
- [2] Bill Jackson and Kiyoshi Yoshimoto. Spanning even subgraphs of 3-edge-connected graphs. Journal of Graph Theory, 62(1):37–47, 2009.
- [3] W. Mader. A reduction method for edge-connectivity in graphs. Ann. Discrete Math, 3:145–164, 1978.
- [4] J. Petersen. Die theorie der regularen graphen. Acta Math., 15:193–220, 1891.