A brief account of Steven Weinberg’s legacy in ab initio many-body theory

On July 23, 2021, by the time we were completing this manuscript, Nobel laureate Steven Weinberg died at the age of 88 The University of Texas at Austin: UT News (2021). With his passing the physics community has lost one of its greatest minds, a co-founder of the Standard Model, and the father of nuclear Effective Field Theory (EFT)—in particular, chiral EFT, for which his seminal papers Weinberg (1990, 1991, 1992) in the early 1990s laid the groundwork.

In this contribution to the special issue “Celebrating 30 years of Steven Weinberg’s papers on Nuclear Forces from Chiral Lagrangians,” we honor Weinberg’s scientific achievements by emphasizing the important role chiral EFT has played in leading nuclear physics into a precision era Epelbaum (2016). But where to begin? And where to end—given the wide range of keywords in Figure 1 that is associated with Weinberg’s legacy? To this end, we share here our personal view on only a few recent advances made in ab initio calculations of nuclear structure and nuclear matter, which have been fueled by several key advantages that chiral EFT offers over older phenomenological nuclear approaches:

• •

  Nuclear forces and currents can be consistently derived based on the symmetries of low-energy quantum chromodynamics (QCD) and then used to make predictions for nuclear observables from first principles (i.e., ab initio calculations). Three-nucleon (3N) forces appear naturally and at a higher order in the chiral expansion than the leading nucleon-nucleon (NN) forces.

• •

  Chiral NN and 3N potentials are relatively soft, which leads to important computational simplifications in most many-body calculations. The hard core (i.e., strong short-range repulsion) typically found in phenomenological potentials is suppressed in chiral potentials by regulator functions with moderate momentum cutoffs.

• •

  Theoretical uncertainties can be rigorously quantified by order-by-order calculations combined with Bayesian statistical methods. Chiral EFT predicts the momentum scale at which it breaks down.

This article is organized as follows. In Sections 2 to 4 we will point out the importance of each of those (interrelated) advantages using recent many-body applications as examples. We also discuss promising new tools that will shed light on some of the issues inherent in chiral EFT with Weinberg power counting. The article concludes with a brief summary in Section 5.

For more details on the broad subjects covered in this article, we share here our (incomplete) personal hot list of interesting articles with the reader:

• •

  (chiral) EFT in general Epelbaum et al. (2020); Hammer et al. (2020); Machleidt and Entem (2011); Epelbaum et al. (2009)

• •

  implementation and importance of chiral 3N interactions Hebeler (2021); Hebeler et al. (2015)

• •

  Renormalization Group methods in low-energy nuclear physics Bogner et al. (2010); Furnstahl et al. (2014)

• •

  nuclear equation of state and astrophysical applications Lattimer (2021); Drischler et al. (2021a); Tews (2020)

• •

  current status of ab initio nuclear structure calculations Hergert (2020); Stroberg et al. (2019)

• •

  Bayesian methods Sivia and Skilling (2006) for uncertainty quantification Melendez (2020); Phillips et al. (2021); Melendez et al. (2019); Furnstahl et al. (2015)

• •

  eigenvector continuation Sarkar and Lee (2021); Frame et al. (2018) and applications of emulators Melendez et al. (2021); Wesolowski et al. (2021); Miller et al. (2021a); Furnstahl et al. (2020); Ekström and Hagen (2019); König et al. (2020)

• •

  applications of delta-full chiral EFT Jiang et al. (2020); Piarulli and Tews (2020); Ekström et al. (2018)

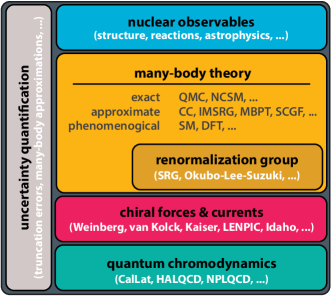
Figure 2 illustrates our conception of an idealized workflow for ab initio many-body calculations in modern nuclear theory. The difficult task here is to make accurate predictions of nuclear observables with quantified and controllable theoretical uncertainties (blue box). Ideally, these predictions are directly derived from the theory of strong interactions, QCD, e.g., through lattice QCD calculations (turquoise box) Drischler et al. (2021b). But at the low-energy scales and finite densities relevant to nuclear physics, such direct calculations are, if possible at all, extremely challenging due to the nonperturbative nature of QCD and the fermion sign problem—even in the foreseeable future.

Nuclear calculations with direct connection to QCD, nonetheless, have become within reach thanks to Weinberg’s seminal papers in the early 1990s. Nowadays, chiral EFT with pion and nucleon degrees of freedom—supplemented with a truncation scheme known as Weinberg power counting—is the dominant microscopic approach to deriving nuclear forces and currents consistent with the symmetries of low-energy QCD (red box). The unresolved short-distance physics is expressed in terms of contact interactions with low-energy couplings fitted to experimental or lattice data.

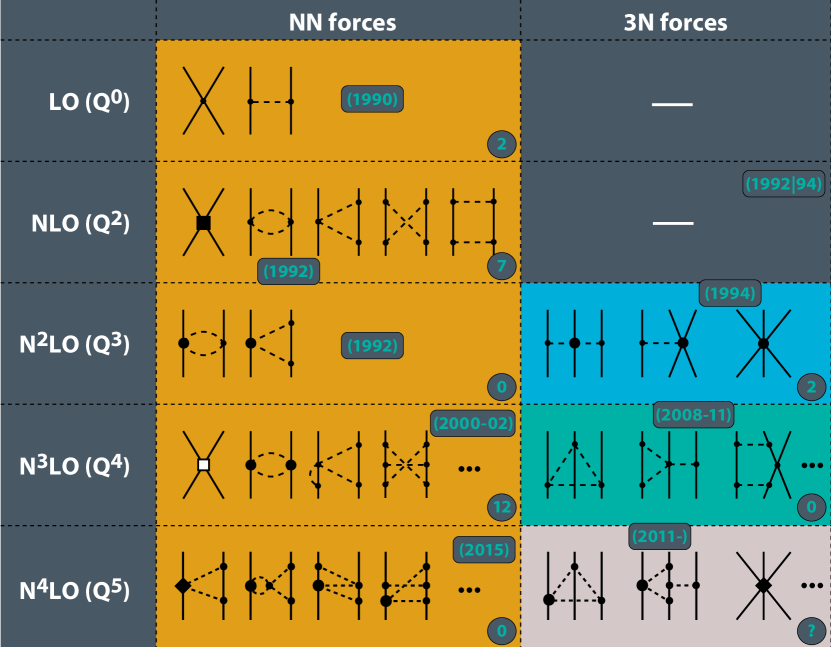
Figure 3 shows the hierarchy of chiral nuclear forces up to fifth order, or $\mathrm{N}^{4}\mathrm{LO}$, in Weinberg power counting. Four-nucleon forces start contributing at $\mathrm{N}^{3}\mathrm{LO}$ but are omitted for brevity. The boxed numbers represent the years in which the contributions were derived, and the circled numbers count the short-range contact low-energy couplings. In recent years, significant progress has been made (e.g., by LENPIC Low Energy Nuclear Physics International Collaboration (2021) (LENPIC)) in constructing nuclear potentials up to a high order in the chiral expansion as well as exploring novel regularization schemes.

Given a chiral potential at some order and resolution scale, a computational framework is used to determine the nuclear observable of interest by solving the many-body Schrödinger equation (light-orange box in Figure 2). Roughly, these many-body frameworks can be categorized into three categories (for a review, e.g., see Ref. Hergert (2020)):

1. 1.

   Methods that obtain (in principle) numerically exact solutions, such as Quantum Monte Carlo (QMC) methods and the No Core Shell Model (NCSM), and are therefore limited to light nuclei due to their exponential scaling.

2. 2.

   Approximate but systematically improvable methods based on many-body expansions, such as Coupled Cluster (CC) theory, In-Medium Similarity Renormalization Group (IMSRG), Many-Body Perturbation Theory (MBPT), and Self-Consistent Green’s Functions (SCGF) method. These methods scale polynomially and can reach well into the medium-mass region.

3. 3.

   Phenomenological frameworks such as the Shell Model (SM) and Density Functional Theory (DFT), which together cover nearly the entire mass table and are the traditional workhorses for interpreting data and guiding experiments, but the connection to the underlying microscopic physics is unclear.

All of these frameworks have their own advantages, limitations, and numerical approximations associated. The strength of modern many-body theory lies in the ability to compare results for nuclear observables obtained in different frameworks to assess the underlying (many-body) approximations.

The Renormalization Group (RG) Bogner et al. (2010) is a versatile tool to systematically modify the resolution scale of nuclear interactions while keeping observables invariant (dark-orange box in Figure 2). Softening interactions using RG methods (as a preprocessing step) accelerates the rate of convergence of approximate many-body frameworks, but comes at the expense of inducing many-body forces—independent of the truncation level of the unevolved Hamiltonian.

In recent years, the similarity RG (SRG) Bogner et al. (2010) has been the method of choice for decoupling the high-to-low-momentum components of the nuclear interaction due to the strong short-range repulsion and tensor force. Nuclear matrix elements are driven band- or block-diagonal in momentum space as the resolution scale is lowered through continuous infinitesimal unitary transformations dictated by the SRG flow equations. In practice, induced many-body forces have to be truncated, e.g., at the three-body level. The SRG is only approximately unitary in these cases, and thus nuclear observables in systems with particle number greater than the truncation level will artificially depend on the resolution scale. One way to efficiently control the proliferation of induced many-body interactions is to use normal-ordering with respect to an $A$-particle “reference state”. This is the idea behind the IMSRG Hergert et al. (2016)—truncating terms in the flow equations to $n$-body normal-ordered operators defines the IMSRG($n$) approximation. In contrast to “free-space” SRG evolution, the IMSRG can be used as an ab initio many-body method in and of itself. When starting from relatively soft NN and 3N interactions, the IMSRG($2$) already gives an excellent approximation for many nuclei, with controlled approximations to the IMSRG($3$) possible Morris (2016); Heinz et al. (2021).

The Weinberg eigenvalue analysis has provided invaluable insights into RG methods acting in different partial-wave channels and nuclear potentials in general. Weinberg (and others) developed this useful technique Weinberg (1963) in the early 1960s while he was at University of California, Berkeley, to understand how divergent Born series can be cured by introducing quasi-particles. More recent applications of the Weinberg eigenvalue analysis include studies of the (rate of) convergence of perturbation expansions, both in free space (Born series) Hoppe et al. (2017) and in medium (MBPT) Bogner et al. (2010), pairing instabilities Ramanan et al. (2007); Srinivas and Ramanan (2016), and the construction of improved chiral NN potentials Reinert et al. (2018).

Theoretical uncertainties arise at all layers shown in Figure 2 and need to be quantified (gray box) for meaningful comparisons with, e.g., competing theories and constraints from nuclear experiment—where the latter typically are provided with a confidence interval. The main sources of uncertainties in EFT calculations Furnstahl et al. (2015) are due to the truncation of the EFT expansion at a finite order (i.e., the truncation error), fits of the low-energy couplings to experimental (or lattice) data, and approximations applied in the computational framework, e.g., to keep the numerical calculations tractable (see also Section 4).

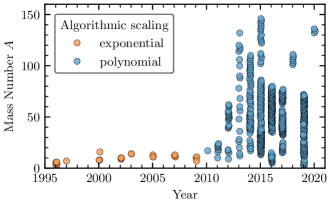
Figure 4 summarizes the progress in microscopic nuclear structure calculations over the past 25 years. Until about 2010, the (approximately) linear increase in the highest mass number $A$ reachable in those calculations was determined by Moore’s law and the exponential scaling of exact many-body methods (orange dots). Since 2010, approximate but systematically improvable many-body methods with polynomial scaling in $A$ (see Section 3) have pushed the frontier of state-of-the-art microscopic calculations to significantly higher mass numbers (blue dots) Hergert (2020).

Why did it take so long for these polynomially scaling methods to gain a foothold in nuclear many-body theory? The primary reason is that prior to the introduction of chiral EFT, phenomenological nuclear force models were rather hard, utilizing ultraviolet cutoffs or resolution scales on the order of several GeV or higher. Since these approximate many-body methods rely on expanding various quantities (e.g., two-body matrix elements of the NN potential) in a single-particle basis, it is essential that basis expansions converge rapidly for calculations to be tractable. For instance, the lowest non-trivial truncations of CC and IMSRG scale roughly as $N^{6}$, where $N$ is the number of included single-particle orbitals. Demanding that the single-particle basis is sufficiently extended in coordinate space to capture the spatial extent of the nucleus, and sufficiently extended in momentum space to capture relevant momentum modes up to the resolution scale in the nuclear potentials, one can use semi-classical arguments to show that $N$ scales as $\Lambda^{3}$, with the resolution scale $\Lambda$.

The bottom line is that even a modest reduction in $\Lambda$, such as that in going from the hard phenomenological nuclear force models to the softer chiral interactions, can have a profound impact on the viability of these approximate many-body methods. The impressive progress shown in Figure 4 would not have been possible without the computational simplifications afforded by soft (and even softer RG-evolved) chiral interactions. That said, it is ironic that the softness that has been so central to the many-body progress is a consequence of inconsistencies in Weinberg power counting that prevent one from taking the cutoff to larger values—see the discussion in Ref. van Kolck (2021).

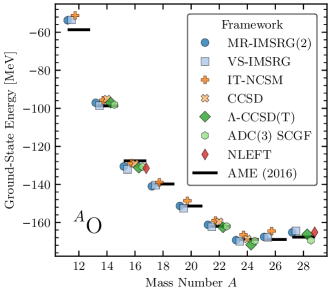
The advancement of ab initio theory well into the medium-mass region is an impressive feat, but the physics value lies in the fact that such calculations are becoming increasingly precise. Figure 5 is one such illustration, where a wide variety of many-body methods starting from the same SRG-evolved chiral NN and 3N potential are in good agreement with experiment and each other for the oxygen isotopes. Note that “good agreement” in the present context is somewhat ill-defined since the calculations do not come with error bars reflecting the uncertainties in the input chiral interactions and the subsequent many-body approximations.

For the time being, we content ourselves with the following comments. First, while the many-body truncation errors of the different methods in Figure 5 are not rigorously quantified, there is numerical evidence that they are significantly smaller than the uncertainties associated with the input chiral interactions. Therefore, the urgent task from the perspective of UQ is to propagate the chiral EFT uncertainties through the many-body calculations. See Ref. Maris et al. (2021) where impressive progress has been made in carrying out a comprehensive error analysis for ab initio calculations of light nuclei. Second, the “good agreement” with experiment tends to degrade substantially for total energies and radii as one moves to heavier nuclei for nearly all chiral NN and 3N interactions on the market. This deficiency is the primary obstacle to precision calculations in microscopic nuclear structure theory, though as discussed in Section 4, the recent development of accurate and efficient emulators for UQ holds much promise in addressing this issue.

The phenomenological shell model has enjoyed tremendous success as the main workhorse of nuclear structure theory, but it requires an abundance of data in the mass region of interest in order to pin down the effective valence Hamiltonian. As nuclear physics shifts its focus to the study of rare isotopes in unexplored regions of the nuclear chart, this places a strain on data-driven approaches like the phenomenological shell model, requiring microscopic approaches to play a greater role.

Along these lines, an important recent development in ab initio theory is the controlled derivation of shell model Hamiltonians and effective operators, starting from chiral NN and 3N interactions Bogner et al. (2014); Stroberg et al. (2017); Sun et al. (2021). While there had been previous efforts that enjoyed some quantitative success dating back to the 1960s, they were plagued with convergence issues that trace back to the high resolution scales of the pre-chiral EFT NN interactions. The shell model is an intrinsically low-resolution description since the underlying picture of a dominant attractive mean field plus a weak residual interaction implies a decoupling of high- and low-momentum modes in the Hamiltonian. In this sense, chiral NN and 3N interactions give a much closer starting point to this picture, and the subsequent transformations to decouple the valence nucleons are easier to treat with controlled approximations.

Another difficulty with the older efforts to derive shell model Hamiltonians is that very little was known about the impact of 3N interactions. This was in part because of the computational difficulties of including them, but also because there was no underlying framework that said they needed to be included at a given level of description as in chiral EFT—they were merely asserted to be small and usually neglected. Indeed, the empirical adjustments that need to be made to the older microscopically derived shell model Hamiltonians, such as the “monopole correction” of Zuker, are thought to mock up the effects of neglected 3N forces. As discussed in Ref. Stroberg et al. (2019), the valence-space IMSRG (VS–IMSRG) explicitly demonstrates that this is indeed the case. More generally, the inclusion of chiral 3N interactions has been shown to play a crucial role in accurately describing the evolution of structure along isotopic chains Hebeler et al. (2015).

Perhaps one of the more impressive applications of the new generation of ab initio shell model Hamiltonians is the recent work of Stroberg et al. Stroberg et al. (2021) that computed ground-state and separation energies of nearly 700 isotopes, in what is arguably the first ab initio mass table calculation up to the iron isotopes. Performing a Bayesian linear regression analysis for the residual of the various separation energies, Stroberg et al.were then able to predict the location of the neutron and proton driplines probabilistically. They used the softest of the interactions by Hebeler et al. Hebeler et al. (2011), where the chiral NN interaction is softened by SRG evolution, and the leading chiral 3N forces are fit to reproduce the \isotope[3]H ground-state energy and \isotope[4]He charge radius. While inconsistent from an EFT perspective, this interaction gives a strikingly good description of nuclear matter saturation properties Hebeler et al. (2011); Drischler et al. (2019) and ground- and excited-state energies well into the medium-mass region Simonis et al. (2017), and is informally referred to as the “magic” interaction. Radii likewise are closer to experiment than most chiral interactions, though the systematic underprediction remains.

We have only scratched the surface of a very deep and rapidly evolving area of research. Recent advances not covered here include the explanation of the quenching of $g_{A}$ in medium-mass nuclei as an interplay of correlation effects and two-body currents Gysbers et al. (2019), the first ab initio calculations of neutrinoless double beta decay matrix elements Yao et al. (2020); Belley et al. (2021), and many more.

Quantifying theoretical uncertainties is an integral component of the ab initio workflow depicted in Figure 2. The focus has recently shifted from probing uncertainties by simple (somewhat arbitrary) parameter variations toward systematic studies of EFT truncation errors Furnstahl et al. (2015). Epelbaum et al. Epelbaum et al. (2015a, b) introduced an implementation of the standard EFT uncertainty that assumes that the truncation error of an observable is uncorrelated and dominated by the first chiral order in Figure 3 not included in the many-body calculations. This “EKM uncertainty” has been extensively studied in ab initio calculations of atomic nuclei Binder et al. (2016); Epelbaum et al. (2020) and nuclear matter Drischler et al. (2019); Lonardoni et al. (2020). Furthermore, the Bayesian UQ: Errors in Your EFT (BUQEYE) Collaboration BUQEYE collaboration (2020) has been developing advanced statistical methods for rigorous quantification and propagation of (correlated) theoretical uncertainties, including the inference of to-all-orders EFT truncation errors and breakdown scales, via order-by-order calculations, e.g., of scattering and nuclear matter observables Melendez et al. (2017, 2019); Drischler et al. (2020a).

The progress in applying statistical methods, such as Bayesian parameter estimation Wesolowski et al. (2019), model comparison Phillips et al. (2021), and sensitivity analysis Ekström and Hagen (2019), is apparent in the successful Information and Statistics in Nuclear Experiment and Theory (ISNET) workshops Ireland and Nazarewicz (2015); Information and Statistics in Nuclear Experiment and Theory Series website(2021) (ISNET). Since 2012 these annual workshops bring nuclear physicists and statisticians together to learn and discuss statistical methods and their applications to nuclear physics problems in an inclusive scientific environment. The pedagogical lectures during the workshops, hosted by the Bayesian Analysis for Nuclear Dynamics (BAND) Framework Collaboration Bayesian Analysis of Nuclear Dynamics Framework project(2020) (BAND), are an excellent way of getting starting with Bayesian methods.

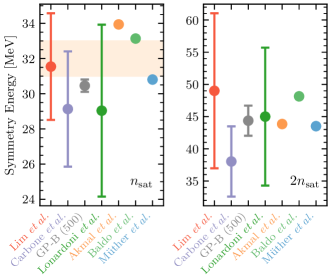
Let us use nuclear matter as an example to highlight UQ in chiral EFT calculations. A recent review of the nuclear EOS with UQ and astrophysical applications can be found in Ref. Drischler et al. (2021a). Figure 6 compares microscopic constraints (error bars) on the nuclear symmetry energy—a key quantity in nuclear (astro)physics—obtained with different many-body frameworks and chiral NN and 3N interactions at $n=n_{\text{sat}}$ (left panel) and $2n_{\text{sat}}$ (right panel). See the caption of Figure 6 for more details on the calculations. Only because uncertainties were estimated can one judge how well (in this case) the symmetry energy is determined microscopically: overall, within the relatively large uncertainties, the different constraints are consistent with one another, and the symmetry energy is predicted in the range $E_{\text{sym}}(n_{\text{sat}})\approx 24.1-34.6\,\text{MeV}$ and $E_{\text{sym}}(2n_{\text{sat}})\approx 32.5-61.1\,\text{MeV}$, respectively, as shown in Figure 6. On the other hand, the older phenomenological calculations—how accurate those may or may not be—only provide point estimates (dots), while the underlying uncertainties are unknown, and thus do not allow for such an interpretation. However, we stress that the methods used for estimating the uncertainties in Figure 6 are conceptually different, ranging from parameter variations in the nuclear interactions to truncation error studies. Rigorously quantifying all theoretical uncertainties available within a comprehensive statistical framework to constrain the nuclear EOS (not only the symmetry energy) from different many-body methods and chiral interactions is an important avenue for the future. This will require the development of improved order-by-order NN and 3N interactions Hüther et al. (2020). The Bayesian framework for quantifying EFT truncation errors introduced by the BUQEYE Collaboration Drischler et al. (2020b, a) (and applied to the structure of neutron stars Drischler et al. (2021c)) is the first step in this direction.

These full Bayesian analyses typically are computationally demanding and thus prohibitively slow in most cases—or so one might have thought. However, emulators for nuclear observables—where applicable—have overcome this computational limitation by providing highly accurate approximations to exact solutions (e.g., of the Schrödinger equation) fast and reliably. But applications of these powerful new tools reach way beyond that. Several methods have been used to implement emulators, with eigenvector continuation (EC) Frame et al. (2018) being one of the promising methods. For instance, EC-driven emulators have been demonstrated to be remarkably efficient in emulating, e.g., ground-state energies and charge radii Ekström and Hagen (2019); König et al. (2020); Wesolowski et al. (2021). Furthermore, the EC concept has been extended to emulate two-body scattering observables using the variational principles due to Kohn Furnstahl et al. (2020); Drischler et al. (2021d) and Newton Melendez et al. (2021), respectively, while the first application to three-body scattering—where the emulators’ efficacies are put to a real display—is already encouraging for systematic studies of emulated three- and higher-body scattering observables in the future Zhang and Furnstahl . A fast & accurate emulator for few-body bound-state properties was recently key to constructing the first set of order-by-order chiral NN and 3N interactions (up to $\mathrm{N}^{2}\mathrm{LO}$) with theoretical uncertainties fully quantified Wesolowski et al. (2021). The task now is to bridge the developments in Bayesian methods and emulator technology toward a full UQ in microscopic calculations of nuclear matter and atomic nuclei across the nuclear chart.

For nuclear matter, such a rigorous UQ has never been more important than today given the great variety of empirical constraints on the nuclear EOS recently obtained or anticipated soon. These constraints include tidal deformabilities of neutron stars inferred from direct gravitational-wave detection by the LIGO-Virgo scientific collaboration (now joined by the KAGRA observatory) Abbott et al. (2018); De et al. (2018); Capano et al. (2020), simultaneous mass-radius measurements of neutron stars by the NICER telescope Miller et al. (2021b); Riley et al. (2021), and neutron skins, e.g., measured by the second \isotope[208]Pb Radius EXperiment (PREX–II) at Jefferson Lab Adhikari et al. (2021); Reed et al. (2021). Statistically meaningful comparisons of EOS constraints from observation and experiment with chiral EFT predictions, especially at $n\approx 1-2\,n_{\text{sat}}$, shed light on strongly interacting matter under extreme conditions and, through the ab initio workflow in Figure 2, also on the underlying microscopic nuclear interactions. This has been, and will continue to be, an exciting era for nuclear (astro)physics—about 30 years after Weinberg’s seminal papers were published.

Celebrating Weinberg’s scientific achievements, we argued that nuclear physics has recently entered a precision era thanks to chiral EFT, for which his seminal papers Weinberg (1990, 1991, 1992) in the early 1990s laid the groundwork. Specifically, we pointed out chiral EFT’s advantages over previous phenomenological nuclear approaches and shared our perspective on some of the recent advances made in ab initio calculations of nuclear structure and nuclear matter observables, as well as the quantification of EFT truncation errors.

With increasingly accurate and efficient many-body frameworks available, however, long-lasting formal issues in chiral EFT (e.g., with the power counting) resurface as the uncertainties from the chiral interactions gradually become more important than those from the many-body frameworks. These issues were discussed in the recent INT Program Nuclear Structure at the Crossroads (INT–19–2a) and summarized in the organizers’ contribution to this special issue Furnstahl et al. (2021). From this perspective, despite all the progress in many-body calculations because of chiral EFT, it seems as if nuclear theory is indeed at the crossroads with unknown roads ahead. Bayesian methods combined with emulators for nuclear observables (see Section 4) will provide invaluable guidance along the way, though.

In his contribution to this special issue van Kolck (2021), Bira van Kolck vividly tells an anecdote of encountering an agitated Steven Weinberg after he had called Gerry Brown sometime in 1990. Weinberg wanted to pick Gerry’s brain because he knew him to be one of the leading experts on nuclear forces and nuclear physics at that time. The phone call must have been confusing and agitating for both sides. Despite the fact that they shared a common conviction of the central role of chiral symmetry in understanding nuclear forces—indeed, Gerry and collaborators wrote several papers in which they forcefully made this point ten years prior—they spoke different scientific languages and had different points of emphasis that clashed with each other. Weinberg was frustrated because Gerry stubbornly kept on emphasizing fitting data and the importance of keeping the rho meson as an explicit degree of freedom, in part because it is needed to cancel the “unphysical” large attractive tensor force of the one-pion exchange potential at short distances. And Gerry was equally frustrated that Weinberg refused to treat the rho meson as a low-energy degree of freedom due to its large mass near the EFT breakdown scale.

About ten years later, when one of us (S.B.) was a wide-eyed graduate student at Stony Brook together with Achim Schwenk, who would turn out to be the thesis advisor for another one of us (C.D.), Gerry regaled us about the infamous phone call. It’s worth mentioning that Gerry told the story with a wry smile on his face, and seemed to take special delight in the fact that he had made Weinberg so mad!¹¹1Gerry was such a masterful storyteller that S.B. always wondered if he was taking a bit of artistic license for comic effect in his recollection of the phone call. Several years later—it might have been over pints in Trento or Seattle during some long-forgotten conference—Bira ended any lingering doubts by basically telling the anecdote that is in his contribution. It’s also worth mentioning that Gerry was, apart from his unwavering feelings about the rho meson, a strong supporter of the EFT ideology in general, and he had tremendous respect for Weinberg’s seminal work in this area. We can only speculate what Gerry had exactly in mind during this contentious phone call. But as Bira wrote in his contribution van Kolck (2021), it may very well be that Gerry’s deep intuition for nuclear forces let him anticipate some of the issues that we are still facing in chiral EFT with Weinberg power counting. However, beyond speculation we are confident that, no matter what quantum state Steven Weinberg and Gerry Brown may be in together now, they will not run out of interesting physics questions to discuss anytime soon. In memory of Steven Weinberg (1933–2021) and Gerry Brown (1926–2013).