11email: {liqing, huangsiyuan, yininghong}@ucla.edu, 11email: sczhu@stat.ucla.edu
A Competence-aware Curriculum for Visual Concepts Learning via Question Answering
Abstract
Humans can progressively learn visual concepts from easy to hard questions. To mimic this efficient learning ability, we propose a competence-aware curriculum for visual concept learning in a question-answering manner. Specifically, we design a neural-symbolic concept learner for learning the visual concepts and a multi-dimensional Item Response Theory (mIRT) model for guiding the learning process with an adaptive curriculum. The mIRT effectively estimates the concept difficulty and the model competence at each learning step from accumulated model responses. The estimated concept difficulty and model competence are further utilized to select the most profitable training samples. Experimental results on CLEVR show that with a competence-aware curriculum, the proposed method achieves state-of-the-art performances with superior data efficiency and convergence speed. Specifically, the proposed model only uses 40% of training data and converges three times faster compared with other state-of-the-art methods.
Keywords:
Visual Question Answering, Visual Concept Learning, Curriculum Learning, Model Competence1 Introduction
Humans excel at learning visual concepts and their compositions in a question-answering manner [16, 10, 18], which requires a joint understanding of vision and language. The essence of such learning skill is the superior capability to connect linguistic symbols (words/phrases) in question-answer pairs with visual cues (appearance/geometry) in images. Imagine a person without prior knowledge of colors is presented with two contrastive examples in Figure 1-I. The left images are the same except for color, and the right question-answer pairs differ only in the descriptions about color. By assuming that the differences in the question-answer pairs capture the differences in appearances, he can learn the concept of color and the appearance of specific colors (i.e., red and green). Besides learning the basic unary concepts from contrastive examples, compositional relations from complex questions consisting of multiple concepts can be further learned, as shown in Figure 1-II and -III.

Another crucial characteristic of the human learning process is to start small and learn incrementally. More specifically, the human learning process is well-organized with a curriculum that introduces concepts progressively and facilitates the learning of new abstract knowledge by exploiting learned concepts. A good curriculum serves as an experienced teacher. By ranking and selecting examples according to the learning state, it can guide the training process of the learner (student) and significantly increase the learning speed. This idea is originally examined in animal training as shaping [52, 46, 32] and then applied to machine learning as curriculum learning [13, 7, 20, 21, 44].
Inspired by the efficient curriculum, Mao et al. [41] proposes a neural-symbolic approach to learn visual concepts with a fixed curriculum. Their approach learns from image-question-answer triplets and does not require annotation on images or programs generated from questions. The model is trained with a manually-designed curriculum that includes four stages: (1) learning unary visual concepts; (2) learning relational concepts; (3) learning more complex questions with visual perception fixed; (4) joint fine-tuning all modules. They select questions for each stage by the depths of the latent programs. Their curriculum heavily relies on the manually-designed heuristic that measures the question difficulty and discretizes the curriculum. Such heuristic suffers from three limitations. First, it ignores the variance of difficulties for questions with the same program depths, where different concepts might have various difficulties. Second, the manually-designed curriculum relies on strong human prior knowledge for the difficulties, while such prior may conflict with the inherent difficulty distribution of the training examples. Last but most importantly, it neglects the progress of the learner that evolves along with the training process. More specifically, the order of training samples in the curriculum is nonadjustable based on the model state. This scheme is in stark contrast to the way that humans learn – by actively selecting learning samples based on our current learning state, instead of passively accepting specific training samples. A desirable learning system should be capable of automatically adjusting the curriculum during the learning process without requiring any prior knowledge, which makes the learning procedure more efficient with less data redundancy and faster convergence speed.
To address these issues and mimic human ability in adaptive learning, we propose a competence-aware curriculum for visual concept learning via question answering, where competence represents the capability of the model to recognize each concept. The proposed approach utilizes multi-dimensional Item Response Theory (mIRT) to estimate the concept difficulty and model competence at each learning step from accumulated model responses. Item Response Theory (IRT) [5, 6] is a widely adopted method in psychometrics that estimates the human ability and the item difficulty from human responses on various items. We extend the IRT to a mIRT that matches the compositional nature of visual reasoning, and apply variational inference to get a Bayesian estimation for the parameters in mIRT. Based on the estimations of concept difficulty and model competence, we further define a continuous adaptive curriculum (instead of a discretized fixed regime) that selects the most profitable training samples according to the current learning state. More specifically, the learner can filter out samples with either too naive or too challenging questions. These questions bring either negligible or sharp gradients to the learner, which makes it slower and harder to converge.
With the proposed competence-aware curriculum, the learner can address the aforementioned limitations brought by a fixed curriculum with the following advantages:
-
1.
The concept difficulty and the model competence at each learning step can be inferred effectively from accumulated model responses. It enables the model to distinguish difficulties among various concepts and be aware of its own capability for recognizing these concepts.
-
2.
The question difficulty can be calculated with the estimated concept difficulty and model competence without requiring any heuristics.
-
3.
The adaptive curriculum significantly contributes to the improvement of learning efficiency by relieving the data redundancy and accelerating the convergence, as well as the improvement of the final performance.
We explore the proposed method on the CLEVR dataset [29], an artificial universe where visual concepts are clearly defined and less correlated. We opt for this synthetic environment because there is little prior work on curriculum learning for visual concepts and there lacks a clear definition of visual concepts in real-world setting. CLEVR allows us to perform controllable diagnoses of the proposed mIRT model in building an adaptive curriculum. Section 5 further discusses the potentials and challenges of generalizing our method to other domains such as real-world images and natural language processing.
Experimental results show that the visual concept learner with the proposed competence-aware curriculum converges three times faster and consumes only of the training data while achieving similar or even higher accuracy compared with other state-of-the-art models. We also evaluate individual modules in the proposed method and demonstrate their efficacy in Section 4.
2 Related Work
2.1 Neural-symbolic Visual Question Answering
Visual question answering (VQA) [39, 56, 48, 29, 17] is a popular task for gauging the capability of visual reasoning systems. Some recent studies [2, 3, 24, 30, 59] focus on learning the neural module networks (NMNs) on the CLEVR dataset. NMNs translate questions into programs, which are further executed over image features to predict answers. The program generator is typically trained on human annotations. Several recent works target on reducing the supervision or increasing the generalization ability to new tasks in NMNs. For example, Johnson et al. [30] replaces the hand-designed syntactic parsers by a learned program generator. Neural-Symbolic VQA [60] explores an object-based visual representation and uses a symbolic executor for inferring the answer. Neural-symbolic concept learner [41] uses a symbolic reasoning process and manually-defined curriculum to bridge the learning of visual concepts, words, and the parsing of questions without explicit annotations. In this paper, we build our model on the neural-symbolic concept learner [41] and learn an adaptive curriculum to select the most profitable training samples.
Learning-by-asking (LBA) [42] proposes an interactive learning framework that allows the model to actively query an oracle and discover an easy-to-hard curriculum. LBA uses the expected accuracy improvement over candidate answers as an informativeness measure to pick questions. However, it is costly to compute the expected accuracy improvement for sampled questions since it requires to process all the questions and images through a VQA model. Moreover, the expected accuracy improvement cannot help to learn which specific component of the question contributes to the performance, especially while learning from the answers with little information such as “yes/no”. In contrast, we select questions by explicitly modeling the difficulty of visual concepts, combined with model competence to infer the difficulty of each question.
2.2 Curriculum Learning and Machine Teaching
The competence-aware curriculum in our work is related to curriculum learning [7, 53, 55, 20, 51, 44, 21, 47] and machine teaching [61, 62, 38, 11, 40, 15, 58]. Curriculum learning is firstly proposed by Bengio et al. [7] and demonstrates that a dataset order from easy instances to hard ones benefits learning process. The measures of hardness in curriculum learning approaches are usually determined by hand-designed heuristics [53, 55, 51, 41]. Graves et al. [20] explore learning signals based on the increase rates in prediction accuracy and network complexity to adjust data distributions along with training. Self-paced learning [33, 27, 28, 51] quantifies the sample hardness by the training loss and formulates curriculum learning as an optimization problem by jointly modeling the sample selection and the learning objective. These hand-designed heuristics are usually task-specific without any generalization ability to other domains.
Machine teaching [61, 62, 38] introduces a teacher model that receives feedback from the student model and guides the learning of the student model accordingly. Zhu et al. [61, 62] assume that the teacher knows the ground-truth model (i.e., the Oracle) beforehand and constructs a minimal training set for the student model. The recent works learning to teach [15, 58] break this strong assumption of the existence of the oracle model and endow the teacher with the capability of learning to teach via a reinforcement learning framework.
Our work explores curriculum learning in visual reasoning, which is highly compositional and more complex than tasks studied before. Different from previous works, our method requires neither hand-designed heuristics nor an extra teacher model. We combine the idea of competence with curriculum learning and propose a novel mIRT model that estimates the concept difficulty and model competence from accumulated model responses.
3 Methodology
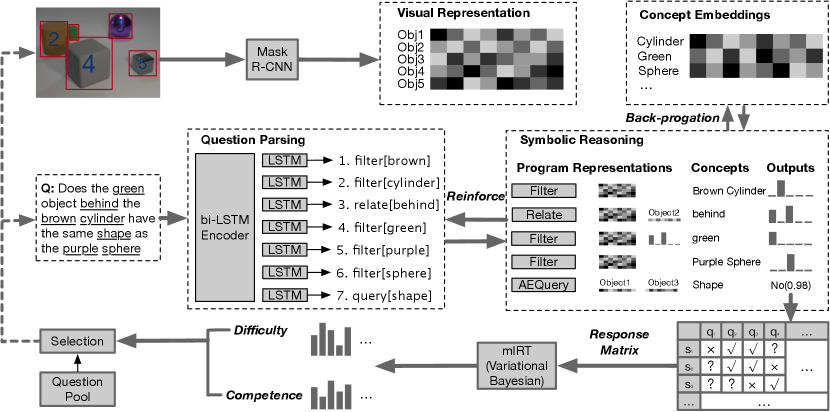
In this section, we will discuss the proposed competence-aware curriculum for visual concept learning, as also shown in Figure 2. We first describe a neural-symbolic approach to learn visual concepts from image-question-answer triplets. Next, we introduce the background of IRT model and discuss how we derive a mIRT model for estimating concept difficulty and model competence. Finally, we present how to select training samples based on the estimated concept difficulty and model competence to make the training process more efficient.
3.1 Neural-Symbolic Concept Learner
We briefly describe the neural-symbolic concept learner. It uses a symbolic reasoning process to bridge the learning of visual concepts and the semantic parsing of textual questions without any intermediate annotations except for the final answers. We refer readers to [41, 60] for more details on this model.
Scene Parsing. A scene parsing module develops an object-based representation for each image. Concretely, we adopt a pre-trained Mask R-CNN [22] to generate object proposals from the image. The detected bounding boxes with the original image are sent to a ResNet-34 [23] to extract the object-based features.
Concept Embeddings. By assuming each visual attribute (e.g., shape) contains a set of visual concepts (e.g., cylinder), the extracted visual features are embedded into concept spaces by learnable neural operators of the attributes.
Question Parsing. The question parsing module translates a question in natural language into an executable program in a domain-specific language designed for VQA. The question parser generates the latent program from a question in a sequence-to-sequence manner. A bi-directional LSTM is used to encode the input question into a fixed-length representation. The decoder is an attention-based LSTM, which produces the operations in the program step-by-step. Some operations take concepts as their parameters, such as Filter[Cube] and Relate[Left]. These concepts are selected from the concepts appearing in the question by the attention mechanism.
Symbolic Reasoning. Given the latent program, the symbolic executor runs the operations in the program with the object-based image representation to derive an answer for the input question. The execution is fully differentiable with respect to the concept embeddings since the intermediate results are represented in a probabilistic manner. Specifically, we keep an attention mask on all object proposals, with each element in the mask denoting the probability that the corresponding object contains certain concepts. The attention mask is fed into the next operation, and the execution continues. The final operation predicts an answer to the question. We refer the readers to the supplementary materials for more details and examples of the symbolic execution process.
Joint Optimizing. We formulate the problem of jointly learning the question parser and the concept embeddings without the annotated programs. Suppose we have a training sample consisting of image , question , and answer , and we do not observe the latent program . The goal of training the whole system is to maximize the following conditional probability:
| (1) |
where is parametrized by the question parser with the parameters and is parametrized by the concept embeddings (there are no learnable parameters in the symbolic reasoning module). Considering the expectation over the program space in Eq. 1 is intractable, we approximate the expectation with Monte Carlo sampling. Specifically, we first sample a program from the question parser and then apply to obtain a probability distribution over possible answers
Recalling the program execution is fully differentiable w.r.t. the concept embeddings, we learn the concept embeddings by directly maximizing using gradient descent and the gradient can be calculated through back-propagation. Since the hard selection of through Monte Carlo sampling is non-differentiable, the gradients of the question parser cannot be computed by back-propagation. Instead we optimize the question parser using the REINFORCE algorithm [57]. The gradient of the reward function over the parameters of the policy is:
| (2) |
where denotes the reward. Defining the reward as the log-probability of the correct answer and again, we rewrite the intractable expectation with one Monte Carlo sample :
| (3) |
where is the exponential moving average of , serving as a simple baseline to reduce the variance of gradients. Therefore, the update to the question parser at each learning step is simply the gradient of the log-probability of choosing the program, multiplied by the probability of the correct answer using that program.
3.2 Background of Item Response Theory (IRT)
Item response theory (IRT) [5, 6] was initially created in the fields of educational measurement and psychometrics. It has been widely used to measure the latent abilities of subjects (e.g., human beings, robots or AI models) based on their responses to items (e.g., test questions) with different levels of difficulty. The core idea of IRT is that the probability of a correct response to an item can be modeled by a mathematical function of both individual ability and item characteristics. More formally, if we let be an individual and be an item, then the probability that the individual answers the item correctly can be modeled by a logistic model as:
| (4) |
where is the latent ability of the individual and are the characteristics of the item . The item parameters can be interpreted as changing the shape of the standard logistic function: (the discrimination parameter) controls the slope of the curve; (the difficulty parameter) is the ability level, it is the point on where the probability of a correct response is the average of (min) and 1 (max), also where the slope is maximized; (the guessing parameter) is the asymptotic minimum of this function, which accounts for the effects of guessing on the probability of a correct response for a multi-choice item. Equation 4 is often referred to as the three-parameter logistic (3PL) model since it has three parameters describing the characteristics of items. We refer the readers to [5, 6, 14] for more background and details on IRT.
3.3 Multi-dimensional IRT using Model Responses
Traditional IRT is proposed to model the human responses to several hundred items. However, datasets used in machine learning, especially deep neural networks, often consist of hundreds of thousands of samples or even more. It is costly to collect human responses for large datasets, and more importantly, human responses are not distinguishable enough to estimate the sample difficulties since samples in machine learning datasets are usually straightforward for humans. Lalor et al. [34, 35] empirically shows on two NLP tasks that IRT models can be fit using machine responses by comparing item parameters learned from the human responses and the responses from an artificial crowd of thousands of machine learning models.
Similarly, we propose to fit IRT models with accumulated model responses (i.e., the predictions of model snapshots) from the training process. Considering the compositional nature of visual reasoning, we propose a multi-dimensional IRT (mIRT) model to estimate the concept difficulty and model competence (corresponding to the subject ability in original IRT), from which the question difficulty can be further calculated.
Formally, we have concepts, model snapshots saved from all time steps, and questions. Let , where is the -th snapshot’s competence on the -th concept, and , where is the difficulty of the -th concept, , where is the number of the -th concept in the -th question and is the probability of guessing the correct answer to the -th question, , where be the response of the -th snapshot to the -th question ( if the model answers the question correctly and otherwise). The probability that the snapshot can correctly recognize the concept is formulated by a logistic function:
| (5) |
Then the probability that the snapshot answers the question correctly is calculated as:
| (6) |
The probability that the snapshot answers the question incorrectly is:
| (7) |
The total data likelihood is:
3.4 Variational Bayesian Inference for mIRT
The goal of fitting an IRT model on observed responses is to estimate the latent subject abilities and item parameters. In traditional IRT, the item parameters are usually estimated by Marginal Maximum Likelihood (MML) via an Expectation-Maximization (EM) algorithm [9], where the subject ability parameters are randomly sampled from a normal distribution and marginalized out. Once the item parameters are estimated, the subject abilities are scored by maximum a posterior (MAP) estimation based on their responses to items. However, the EM algorithm is not computational efficient on large datasets. One feasible way for scaling up is to perform variational Bayesian inference on IRT [43, 35]. The posterior probability of the parameters in mIRT can be written as:
| (9) |
where are the priors distribution of and . The integral over the parameter space in Eq 9 is intractable. Therefore, we approximate it by a factorized variational distribution on top of an independence assumption of and :
| (10) |
where and denote Gaussian distributions for model competences and concept difficulties, respectively. We adopt the Kullback-Leibler divergence (KL-divergence) to measure the distance of from , which is defined as:
| (11) |
where is still intractable. We can further decompose the KL-divergence as:
| (12) |
In other words, we also have:
| (13) | ||||
| (14) |
As the log evidence is fixed with respect to , maximizing the final term minimizes the KL divergence of from . And since is a parametric distribution we can sample from, we can use Monte Carlo sampling to estimate this quantity. Since the KL-divergence is non-negative, is an evidence lower bound (ELBO) of . By maximizing the ELBO with an Adam optimizer [31] in Pyro [8], we can estimate the parameters in mIRT.
3.5 Training Samples Selection Strategy
The proposed model can estimate the question difficulty for the current model competence without looking at the ground-truth images and answers. It facilitates the active selection for future training samples. More specifically, we can easily calculate the probability that the model answers a given question correctly from Eq. 5 and Eq. 6 (without guessing) using estimated and . This probability serves as an indicator of the question difficulty for the learner in each stage. The higher the probability, the easier the question. To select appropriate training samples, we rank the questions and filter out the hardest questions by setting a probability lower bound (LB) and the easiest questions by a probability upper bound (UB). Algorithm 1 summarizes the overall training process. We will discuss the influence of LB and UB on the learning process in Section 4.5.
4 Experiments
4.1 Experimental Setup
Dataset. We evaluate the proposed method on the CLEVR dataset [29], which consists of a training set of 70k images and 700k questions, and a validation set of 15k images and 150k questions. The proposed model selects questions from the training set during learning, and we evaluate our model on the entire validation set.
Models. To analyze the performance of the proposed approach, We conduct experiments by comparing with several model variants:
-
•
FiLM-LBA: the best model from [42].
-
•
NSCL: the neural-symbolic concept learner [41] without using any curriculum. Questions are randomly sampled from the training set.
-
•
NSCL-Fixed: NSCL following a manually-designed discretized curriculum.
-
•
NSCL-mIRT: NSCL following a continuous curriculum built by the proposed mIRT estimator.
Please refer to the supplementary materials for detailed model settings and learning techniques during training.
4.2 Training Process & Model Performance
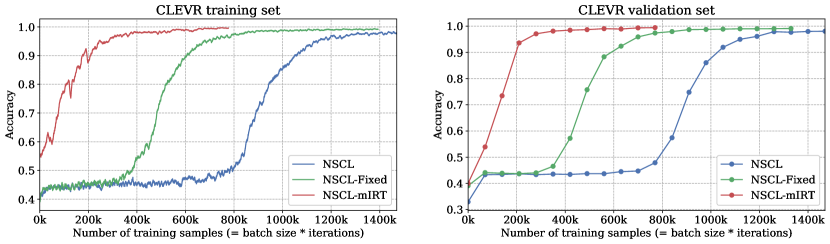
Figure 3 shows the accuracies of the model variants at different timesteps on the training set (left) and validation set (right). Notably, the proposed NSCL-mIRT converges almost 2 times faster than NSCL-Fixed and 3 times faster than NSCL (i.e., 400k v.s. 800k v.s. 1200k). Although NSCL-mIRT spends extra time to estimate the parameters of the mIRT model, such time cost is negligible compared to other time spent in training (less than 1%). From Table 2, we can see that NSCL-mIRT consistently outperforms FilM-LBA at various iterations, which demonstrates the preeminence of mIRT in building an adaptive curriculum.
Besides, NSCL-mIRT consumes less than 300k unique questions for training when it converges. It indicates that NSCL-mIRT saves about 60% of the training data, which largely eases the data redundancy problems. It provides a promising direction for designing a data-efficient curriculum and helping current data-hungry deep learning models save time and money cost during data annotation and model training.
Moreover, NSCL-mIRT obtains even higher accuracy than NSCL and NSCL-Fixed. This indicates that the adaptive curriculum built by the multi-dimensional IRT model not only remarkably increases the speed of convergence and reduces the data consumption during the training process, but also leads to better performance, which also verifies the hypothesis made by Bengio et al. [7].
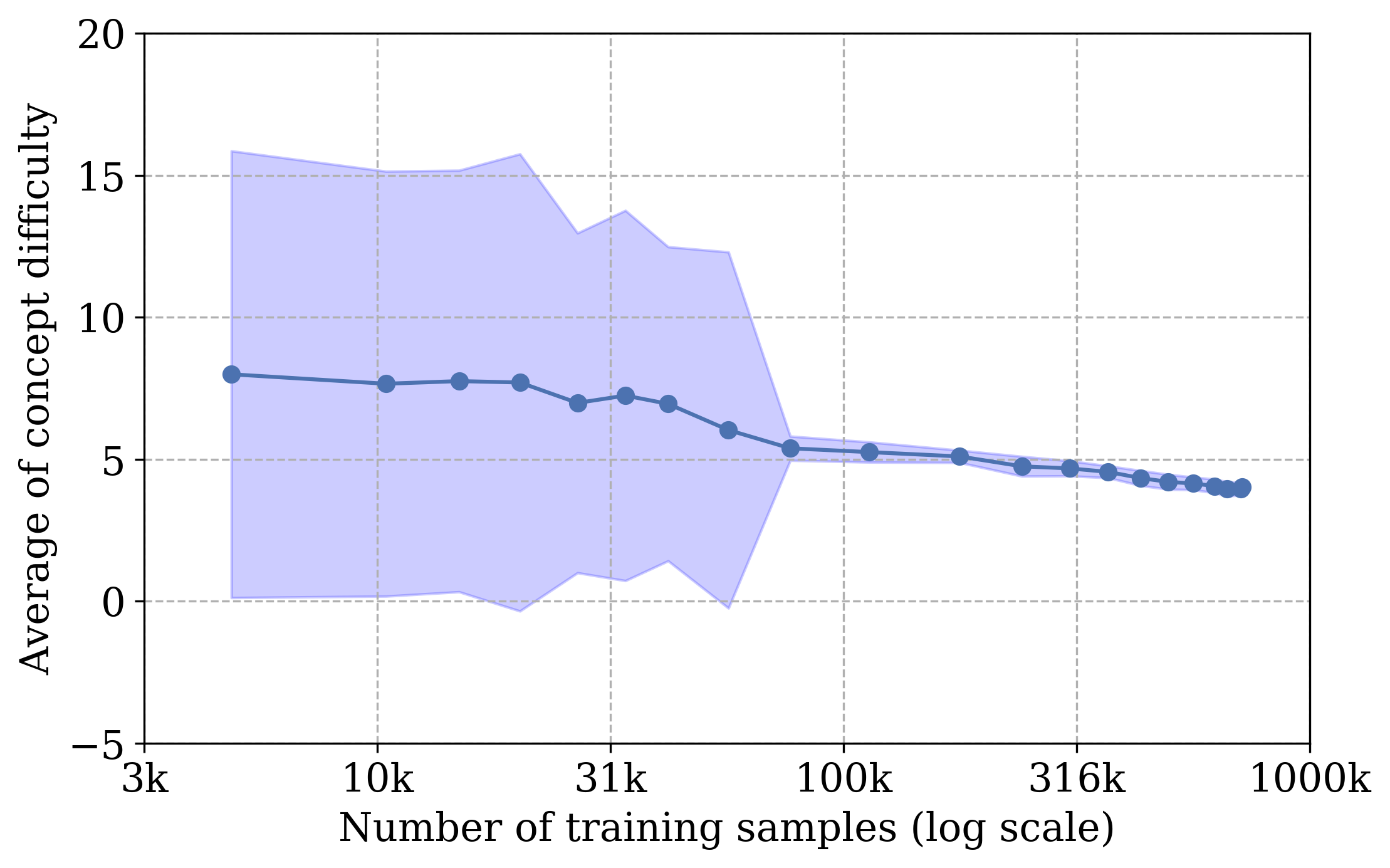
4.3 Multi-dimensional IRT
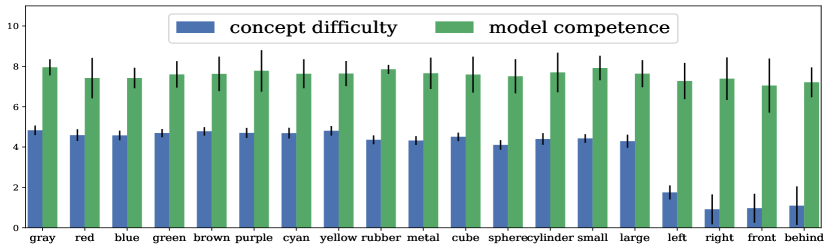
The estimated concept difficulty and model competence after converging is shown in Figure 4 for studying the performance of the mIRT model. Several critical observations are: (1) The spatial relations (i.e., left/right/front/behind) are the easiest concepts. It satisfies our intuition since the model only needs to exploit the object positions to determine their spatial relations without dealing with appearance. The spatial relations are learned during the late stages since they appear more frequently in complex questions to connect multiple concepts. (2) Colors are the most difficult concepts. The model needs to capture the subtle differences in the appearance of objects to distinguish eight different colors. (3) The model competence scores surpass the concept difficulty scores for all the concepts. This result corresponds to the nearly perfect accuracy () on all questions and concepts.
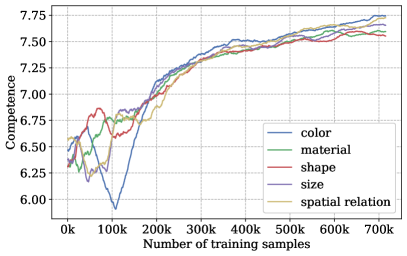
Figure 5 shows the estimation of the model competence for each attribute type at various iterations. We can observe that model competence consistently increases throughout the training. Figure 5 shows the estimations of the concept difficulty at different learning steps. As the training progresses, the estimations become more stable with smaller variance since more model responses are accumulated.
4.4 Concept Learner
| Models | 70k | 140k | 280k | 420k | 630k | 700k |
|---|---|---|---|---|---|---|
| FiLM-LBA [42] | 51.2 | 76.2 | 92.9 | 94.8 | 95.2 | 97.3 |
| NSCL | 43.3 | 43.4 | 43.3 | 43.4 | 44.5 | 44.7 |
| NSCL-Fixed | 44.1 | 43.9 | 44.0 | 57.2 | 92.4 | 95.9 |
| NSCL-mIRT | 53.9 | 73.4 | 97.1 | 98.5 | 98.9 | 99.3 |
| Model | Overall | Count |
|
Exist |
|
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Human | 92.6 | 86.7 | 86.4 | 96.6 | 95.0 | 96.0 | ||||||
| IEP [29] | 96.9 | 92.7 | 98.7 | 97.1 | 98.1 | 98.9 | ||||||
| FiLM [45] | 97.6 | 94.5 | 93.8 | 99.2 | 99.2 | 99.0 | ||||||
| MAC [25] | 98.9 | 97.2 | 99.4 | 99.5 | 99.3 | 99.5 | ||||||
| NSCL [41] | 98.9 | 98.2 | 99.0 | 98.8 | 99.3 | 99.1 | ||||||
| NS-VQA [60] | 99.8 | 99.7 | 99.9 | 99.9 | 99.8 | 99.8 | ||||||
| NSCL-mIRT | 99.5 | 98.9 | 99.0 | 99.7 | 99.7 | 99.6 |
| (LB,UB) | 70k | 140k | 210k | 280k | 560k | 770k |
|---|---|---|---|---|---|---|
| (-10, 0) | 44.39 | 52.01 | 63.04 | 73.5 | 97.93 | 99.01 |
| (-5, 0) | 53.75 | 69.55 | 82.44 | 95.31 | 98.92 | 99.27 |
| (-3, 0) | 51.38 | 55.97 | 58.33 | 65.11 | 69.57 | 70.01 |
| (-5, -0.5) | 42.06 | 52.67 | 80.46 | 95.54 | 98.41 | 99.06 |
| (-5, -0.75) | 53.91 | 73.42 | 93.6 | 97.07 | 99.04 | 99.50 |
| (-5, -1) | 44.57 | 63.65 | 82.95 | 94.38 | 99.15 | 99.48 |
We apply the count-based concept evaluation metric proposed in [41] to measure the performance of the concept learner, which evaluates the visual concepts on synthetic questions with a single concept such as “How many red objects are there?” Table 2 presents the results by comparing with several state-of-the-art methods, which includes methods based on neural module network with programs (IEP [29]) and neural attentions without programs (MAC [24]). Our model achieves nearly perfect performance across visual concepts and outperforms all other approaches. This means the model can learn visual concepts better with an adaptive curriculum. Our model can also be applied to the VQA. Table 4 summarizes the VQA accuracy on the CLEVR validation split. Our approach achieves comparable performance with state-of-the-art methods.
4.5 Question Selection strategy
The question selection strategy is controlled by two hyper-parameters: the lower bound (LB) and upper bound (UB). We conduct experiments by learning with different LBs and UBs, and Table 4 shows the VQA accuracy at various iterations. It reveals that the proper lower bound can effectively filter out too hard questions and accelerate the learning at the early stage of the training, as shown in the first three rows. Similarly, a proper upper bound helps to filter out too easy questions at the late stage of the training when the model has learned most concepts. Please refer to the supplementary material for the visualization of selected questions at various iterations.
5 Conclusions and Discussions
We propose a competence-aware curriculum for visual concepts learning via question answering. We design a multi-dimensional IRT model to estimate concept difficulty and model competence at each training step from the accumulated model responses generated by different model snapshots. The estimated concept difficulty and model competence are further used to build an adaptive curriculum for the visual concept learner. Experiments on the CLEVR dataset show that the concept learner with the proposed competence-aware curriculum converges three times faster and consumes only of the training data while achieving similar or even higher accuracy compared with other state-of-the-art models.
In the future, our work can be potentially applied to real-world images like GQA [26] and VQA-v2 [19] datasets, by explicitly modeling the relationship among visual concepts. However, there are still unsolved challenges for real-world images. Specifically, compared with synthetic images in CLEVR, real-world images have a much larger vocabulary of visual concepts. For example, as shown in [1], there are over 2,000 visual concepts in MSCOCO images. Usually, these concepts are automatically mined from image captions and scene graphs. Thus some of them are highly correlated like “huge” and “large”, and some of them are very subjective like “busy” and “calm”. Such a large and noisy vocabulary of visual concepts is challenging for the mIRT model since current visual concepts are assumed to be independent. It also requires a much longer time to converge when maximizing the ELBO to fit the mIRT model with more concepts. A potential solution is to consider the hierarchical structure of visual concept space and correlations among the concepts and incorporate commonsense knowledge to handle subjective concepts.
More importantly, the competence-aware curriculum can be adapted to other domains that possess compositional structures such as natural language processing. Specifically, in neural machine translation task [54, 4], mIRT can be used to model the difficulty and competence of translating different words/phrases and build a curriculum to increase learning speed and data efficiency. mIRT can also be used in the task of semantic parsing [12, 36, 37] that transforms natural language sentences (e.g., instructions or queries) into logic forms (e.g., lambda-calculus or SQL). The difficulty and competence of different logic predicates can also be estimated by the mIRT model.
Acknowledgements.
We thank Yixin Chen from UCLA for helpful discussions. This work reported herein is supported by ARO W911NF1810296, DARPA XAI N66001-17-2-4029, and ONR MURI N00014-16-1-2007.
References
- [1] Anderson, P., He, X., Buehler, C., Teney, D., Johnson, M., Gould, S., Zhang, L.: Bottom-up and top-down attention for image captioning and visual question answering. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 6077–6086 (2018)
- [2] Andreas, J., Rohrbach, M., Darrell, T., Klein, D.: Neural module networks. Conference on Computer Vision and Pattern Recognition (CVPR) pp. 39–48 (2015)
- [3] Andreas, J., Rohrbach, M., Darrell, T., Klein, D.: Learning to compose neural networks for question answering. In: Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (2016)
- [4] Bahdanau, D., Cho, K., Bengio, Y.: Neural machine translation by jointly learning to align and translate. ICLR (2015)
- [5] Baker, F.B.: The basics of item response theory. ERIC (2001)
- [6] Baker, F.B., Kim, S.H.: Item response theory: Parameter estimation techniques. CRC Press (2004)
- [7] Bengio, Y., Louradour, J., Collobert, R., Weston, J.: Curriculum learning. In: International Conference on Machine Learning (ICML) (2009)
- [8] Bingham, E., Chen, J.P., Jankowiak, M., Obermeyer, F., Pradhan, N., Karaletsos, T., Singh, R., Szerlip, P., Horsfall, P., Goodman, N.D.: Pyro: Deep Universal Probabilistic Programming. Journal of Machine Learning Research (2018)
- [9] Bock, R.D., Aitkin, M.: Marginal maximum likelihood estimation of item parameters: Application of an em algorithm. Psychometrika (1981)
- [10] Chrupała, G., Kádár, A., Alishahi, A.: Learning language through pictures. Association for Computational Linguistics(ACL) (2015)
- [11] Dasgupta, S., Hsu, D., Poulis, S., Zhu, X.: Teaching a black-box learner. In: ICML (2019)
- [12] Dong, L., Lapata, M.: Language to logical form with neural attention. ACL (2016)
- [13] Elman, J.L.: Learning and development in neural networks: The importance of starting small. Cognition (1993)
- [14] Embretson, S.E., Reise, S.P.: Item response theory. Psychology Press (2013)
- [15] Fan, Y., et al.: Learning to teach. ICLR (2018)
- [16] Fazly, A., Alishahi, A., Stevenson, S.: A probabilistic computational model of cross-situational word learning. Annual Meeting of the Cognitive Science Society (CogSci) (2010)
- [17] Gan, C., Li, Y., Li, H., Sun, C., Gong, B.: Vqs: Linking segmentations to questions and answers for supervised attention in vqa and question-focused semantic segmentation. In: ICCV. pp. 1811–1820 (2017)
- [18] Gauthier, J., Levy, R., Tenenbaum, J.B.: Word learning and the acquisition of syntactic-semantic overhypotheses. Annual Meeting of the Cognitive Science Society (CogSci) (2018)
- [19] Goyal, Y., Khot, T., Summers-Stay, D., Batra, D., Parikh, D.: Making the v in vqa matter: Elevating the role of image understanding in visual question answering. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. pp. 6904–6913 (2017)
- [20] Graves, A., Bellemare, M.G., Menick, J., Munos, R., Kavukcuoglu, K.: Automated curriculum learning for neural networks. In: International Conference on Machine Learning (ICML) (2017)
- [21] Guo, S., Huang, W., Zhang, H., Zhuang, C., Dong, D., Scott, M.R., Huang, D.: Curriculumnet: Weakly supervised learning from large-scale web images. ArXiv abs/1808.01097 (2018)
- [22] He, K., Gkioxari, G., Dollár, P., Girshick, R.: Mask r-cnn. In: Conference on Computer Vision and Pattern Recognition (CVPR) (2017)
- [23] He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: Conference on Computer Vision and Pattern Recognition (CVPR) (2016)
- [24] Hu, R., Andreas, J., Rohrbach, M., Darrell, T., Saenko, K.: Learning to reason: End-to-end module networks for visual question answering. International Conference on Computer Vision (ICCV) pp. 804–813 (2017)
- [25] Hudson, D.A., Manning, C.D.: Compositional attention networks for machine reasoning. In: International Conference on Learning Representations (ICLR) (2018)
- [26] Hudson, D.A., Manning, C.D.: Gqa: A new dataset for real-world visual reasoning and compositional question answering. CVPR (2019)
- [27] Jiang, L., et al.: Self-paced learning with diversity. In: NIPS (2014)
- [28] Jiang, L., et al.: Self-paced curriculum learning. In: AAAI (2015)
- [29] Johnson, J., Hariharan, B., van der Maaten, L., Fei-Fei, L., Lawrence Zitnick, C., Girshick, R.: Clevr: A diagnostic dataset for compositional language and elementary visual reasoning. In: Conference on Computer Vision and Pattern Recognition (CVPR) (2017)
- [30] Johnson, J., Hariharan, B., van der Maaten, L., Hoffman, J., Li, F.F., Zitnick, C., Girshick, R.: Inferring and executing programs for visual reasoning. In: International Conference on Computer Vision (ICCV) (2017)
- [31] Kingma, D., Ba, J.: Adam: A method for stochastic optimization. In: International Conference on Learning Representations (ICLR) (2015)
- [32] Krueger, K.A., Dayan, P.: Flexible shaping: How learning in small steps helps. Cognition (2009)
- [33] Kumar, M.P., et al.: Self-paced learning for latent variable models. In: NIPS (2010)
- [34] Lalor, J.P., Wu, H., Yu, H.: Building an evaluation scale using item response theory. Conference on Empirical Methods in Natural Language Processing (EMNLP) (2016)
- [35] Lalor, J.P., Wu, H., Yu, H.: Learning latent parameters without human response patterns: Item response theory with artificial crowds. Conference on Empirical Methods in Natural Language Processing (EMNLP) (2019)
- [36] Liang, C., Berant, J., Le, Q., Forbus, K.D., Lao, N.: Neural symbolic machines: Learning semantic parsers on freebase with weak supervision. In: ACL (2016)
- [37] Liang, C., Norouzi, M., Berant, J., Le, Q., Lao, N.: Memory augmented policy optimization for program synthesis and semantic parsing. In: NIPS (Jul 2018)
- [38] Liu, W., Dai, B., Humayun, A., Tay, C., Yu, C., Smith, L.B., Rehg, J.M., Song, L.: Iterative machine teaching. In: Proceedings of the 34th International Conference on Machine Learning-Volume 70. pp. 2149–2158. JMLR. org (2017)
- [39] Malinowski, M., Fritz, M.: A multi-world approach to question answering about real-world scenes based on uncertain input. In: Advances in Neural Information Processing Systems (NeurIPS) (2014)
- [40] Mansouri, F., Chen, Y., Vartanian, A., Zhu, X., Singla, A.: Preference-based batch and sequential teaching: Towards a unified view of models. In: NeurIPS (2019)
- [41] Mao, J., Gan, C., Kohli, P., Tenenbaum, J.B., Wu, J.: The neuro-symbolic concept learner: Interpreting scenes, words, and sentences from natural supervision. International Conference on Learning Representations (ICLR) (2019)
- [42] Misra, I., Girshick, R.B., Fergus, R., Hebert, M., Gupta, A., van der Maaten, L.: Learning by asking questions. Conference on Computer Vision and Pattern Recognition (CVPR) (2017)
- [43] Natesan, P., Nandakumar, R., Minka, T., Rubright, J.D.: Bayesian prior choice in irt estimation using mcmc and variational bayes. Frontiers in psychology (2016)
- [44] Pentina, A., Sharmanska, V., Lampert, C.H.: Curriculum learning of multiple tasks. Conference on Computer Vision and Pattern Recognition (CVPR) pp. 5492–5500 (2014)
- [45] Perez, E., Strub, F., de Vries, H., Dumoulin, V., Courville, A.C.: Film: Visual reasoning with a general conditioning layer. In: AAAI Conference on Artificial Intelligence (AAAI) (2017)
- [46] Peterson, G.B.: A day of great illumination: Bf skinner’s discovery of shaping. Journal of the experimental analysis of behavior (2004)
- [47] Platanios, E.A., Stretcu, O., Neubig, G., Póczos, B., Mitchell, T.M.: Competence-based curriculum learning for neural machine translation. In: North American Chapter of the Association for Computational Linguistics(NAACL-HLT) (2019)
- [48] Qi, H., Wu, T., Lee, M.W., Zhu, S.C.: A restricted visual turing test for deep scene and event understanding. arXiv preprint arXiv:1512.01715 (2015)
- [49] Reckase, M.D.: The difficulty of test items that measure more than one ability. Applied psychological measurement (1985)
- [50] Reckase, M.D.: Multidimensional item response theory models. In: Multidimensional item response theory (2009)
- [51] Sachan, M., et al.: Easy questions first? a case study on curriculum learning for question answering. In: ACL (2016)
- [52] Skinner, B.F.: Reinforcement today. American Psychologist (1958)
- [53] Spitkovsky, V.I., Alshawi, H., Jurafsky, D.: From baby steps to leapfrog: How less is more in unsupervised dependency parsing. In: Human Language Technologies: The 2010 Annual Conference of the North American Chapter of the Association for Computational Linguistics. pp. 751–759. Association for Computational Linguistics (2010)
- [54] Sutskever, I., Vinyals, O., Le, Q.V.: Sequence to sequence learning with neural networks. In: Advances in neural information processing systems. pp. 3104–3112 (2014)
- [55] Tsvetkov, Y., Faruqui, M., Ling, W., MacWhinney, B., Dyer, C.: Learning the curriculum with bayesian optimization for task-specific word representation learning. ACL (2016)
- [56] Tu, K., Meng, M., Lee, M.W., Choe, T.E., Zhu, S.C.: Joint video and text parsing for understanding events and answering queries. IEEE MultiMedia (2014)
- [57] Williams, R.J.: Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning (1992)
- [58] Wu, L., et al.: Learning to teach with dynamic loss functions. In: NeurIPS (2018)
- [59] Yi, K., Gan, C., Li, Y., Kohli, P., Wu, J., Torralba, A., Tenenbaum, J.B.: Clevrer: Collision events for video representation and reasoning. ICLR (2020)
- [60] Yi, K., Wu, J., Gan, C., Torralba, A., Kohli, P., Tenenbaum, J.: Neural-symbolic vqa: Disentangling reasoning from vision and language understanding. In: Advances in Neural Information Processing Systems (2018)
- [61] Zhu, X.: Machine teaching: An inverse problem to machine learning and an approach toward optimal education. In: Twenty-Ninth AAAI Conference on Artificial Intelligence (2015)
- [62] Zhu, X., Singla, A., Zilles, S., Rafferty, A.N.: An overview of machine teaching. arXiv preprint arXiv:1801.05927 (2018)