A Consistent Diffusion-Based Algorithm for Semi-Supervised Classification on Graphs

Nathan de Lara Thomas Bonald
Télécom Paris, Institut Polytechnique de Paris
{nathan.delara, thomas.bonald}@telecom-paris.fr

Abstract

Semi-supervised classification on graphs aims at assigning labels to all nodes of a graph based on the labels known for a few nodes, called the seeds. The most popular algorithm relies on the principle of heat diffusion, where the labels of the seeds are spread by thermo-conductance and the temperature of each node is used as a score function for each label. Using a simple block model, we prove that this algorithm is not consistent unless the temperatures of the nodes are centered before classification. We show that this simple modification of the algorithm is enough to get significant performance gains on real data.

1 Introduction

Heat diffusion, describing by the evolution of temperature $T$ in an isotropic material, is governed by the heat equation:

\dfrac{\partial T}{\partial t}=\alpha\Delta T,

(1)

where $\alpha$ is the thermal conductivity of the material and $\Delta$ is the Laplace operator. In steady state, this equation simplifies to $\Delta T=0$ and the function $T$ is said to be harmonic. The Dirichlet problem consists in finding the equilibrium in the presence of boundary conditions, that is when the temperature $T$ is fixed on the boundary of the region of interest.

The principle of heat diffusion has proved instrumental in graph mining, using a discrete version of the heat equation (1) (Kondor and Lafferty, 2002). It has been applied for many different tasks, including pattern matching (Thanou et al., 2017), ranking (Ma et al., 2008, 2011), embedding (Donnat et al., 2018), clustering (Tremblay and Borgnat, 2014) and classification (Zhu, 2005; Merkurjev et al., 2016; Berberidis et al., 2018; Li et al., 2019). In this paper, we focus on the classification task: given labels known for some nodes of the graph, referred to as the seeds, how to infer the labels of the other nodes? The number of seeds is typically small compared to the total number of nodes (e.g., 1%), hence the name of semi-supervised classification.

The most popular algorithm for semi-supervised classification in graphs is based on a discrete version of the Dirichlet problem, the seeds playing the role of the “boundary” of the Dirichlet problem (Zhu et al., 2003). Specifically, one Dirichlet problem is solved per label, setting the temperature of the corresponding seeds at 1 and the temperature of the other seeds as 0. Each node is then assigned the label with the highest temperature over the different Dirichlet problems. In this paper, we prove on a simple block model that this vanilla algorithm is not consistent, unless the temperatures are centered before classification. Experiments show that this simple modification of the algorithm significantly improves classification scores on real datasets.

The rest of this paper is organized as follows. In section 2, we introduce the Dirichlet problem on graphs. Section 3 describes our algorithm for node classification. The analysis showing the consistency of our algorithm on a simple block model is presented in section 4. Section 5 presents the experiments and section 6 concludes the paper.

2 Dirichlet problem on graphs

In this section, we introduce the Dirichlet problem on graphs and characterize the solution, which will be used in the analysis.

2.1 Heat equation

Consider a graph $G$ with $n$ nodes indexed from $1$ to $n$ . Denote by $A$ its adjacency matrix. This is a symmetric, binary matrix. Let $d=A\mathbf{1}$ be the degree vector, which is assumed positive, and $D=\text{diag}(d)$ . The Laplacian matrix is defined by

L=D-A.

Now let $S$ be some strict subset of $\{1,\dots,n\}$ and assume that the temperature of each node $i\in S$ is set at some fixed value $T_{i}$ . We are interested in the evolution of the temperatures of the other nodes. Heat exchanges occur through each edge of the graph proportionally to the temperature difference between the corresponding nodes. Then,

\forall i\notin S,\quad\dfrac{dT_{i}}{dt}=\underset{j=1}{\overset{n}{\sum}}A_{ij}(T_{j}-T_{i}),

that is

\forall i\notin S,\quad\dfrac{dT_{i}}{dt}=-(LT)_{i},

where $T$ is the vector of temperatures. This is the heat equation in discrete space, where $-L$ plays the role of the Laplace operator in (1). At equilibrium, $T$ satisfies Laplace’s equation:

\forall i\notin S,\quad(LT)_{i}=0.

(2)

We say that the vector $T$ is harmonic. With the boundary conditions $T_{i}$ for all $i\in S$ , this defines a Dirichlet problem in discrete space. Observe that Laplace’s equation (2) can be written equivalently:

\forall i\notin S,\quad T_{i}=(PT)_{i},

(3)

where $P=D^{-1}A$ is the transition matrix of the random walk in the graph.

2.2 Solution to the Dirichlet problem

We now characterize the solution to the Dirichlet problem in discrete space. Without any loss of generality, we assume that nodes with unknown temperatures (i.e., not in $S$ ) are indexed from 1 to $n-s$ so that the vector of temperatures can be written

T=\begin{bmatrix}X\\ Y\end{bmatrix},

where $X$ is the unknown vector of temperatures at equilibrium, of dimension $n-s$ . Writing the transition matrix in block form as

P=\begin{bmatrix}Q&R\\ \cdot&\cdot\end{bmatrix},

it follows from (3) that:

\quad X=QX+RY,

(4)

so that:

\quad X=(I-Q)^{-1}RY.

(5)

Note that the inverse of the matrix $I-Q$ exists whenever the graph is connected, which implies that the matrix $Q$ is sub-stochastic with spectral radius strictly less than 1 (Chung, 1997).

The exact solution (5) requires to solve a (potentially large) linear system. In practice, a very good approximation is provided by a few iterations of (4), the rate of convergence depending on the spectral radius of the matrix $Q$ . The small-world property of real graphs suggests that a few iterations are enough in practice (Watts and Strogatz, 1998). This will be confirmed by the experiments.

2.3 Extensions

The results apply to weighted graphs, with a positive weight assigned to each edge. This weight can then be interpreted as the thermal conductivity of the edge in the diffusion process. Interestingly, the results also apply to directed graphs. Indeed, a directed graph $G$ of $n$ nodes, with adjacency matrix $A$ , can be considered as a bipartite graph of $2n$ nodes, with adjacency matrix:

\begin{bmatrix}0&A\\ A^{T}&0\end{bmatrix}

The diffusion can be applied to this bipartite graph, which is undirected. Observe that each node of the directed graph $G$ is duplicated in the bipartite graph and is thus characterized by 2 temperatures, one as heat source (for outgoing edges) and one as heat destination (for incoming edges). It is not necessary for the directed graph to be strongly connected; only the associate bipartite graph needs to be connected.

3 Node classification algorithm

In this section, we introduce a node classification algorithm based on the Dirichlet problem. The objective is to infer the labels of all nodes given the labels of a few nodes called the seeds. Our algorithm is a simple modification of the popular method proposed by Zhu et al. (2003). Specifically, we propose to center temperatures before classification.

3.1 Binary classification

When there are only two different labels, the classification can be done by solving one Dirichlet problem. The idea is to use the seeds with label 1 as hot sources, setting their temperature at $1$ , and the seeds with label 2 as cold sources, setting their temperature at $0$ . The solution to this Dirichlet problem gives temperatures between 0 and 1, as illustrated by Figure 1.

A natural approach, proposed by Zhu et al. (2003), consists in assigning label 1 to all nodes with temperature above 0.5 and label 2 to other nodes. The analysis of section 4 suggests that it is preferable to set the threshold to the mean temperature,

\bar{T}=\frac{1}{n}\sum_{i=1}^{n}T_{i}.

Specifically, all nodes with temperature above $\bar{T}$ are assigned label 1, the other are assigned label 2. Equivalently, temperatures are centered before classification: after centering, nodes with positive temperature are assigned label 1, the others are assigned label 2.

Note that the temperature of each node can be used to assess the confidence in the classification: the closer the temperature to the mean, the lower the confidence. This is illustrated by Figure 1 (the lighter the color, the lower the confidence). In this case, only one node is misclassified and has indeed a temperature close to the mean.

3.2 Multi-class classification

In the presence of more than 2 labels, we use a one-against-all strategy: the seeds of each label alternately serve as hot sources (temperature 1) while all the other seeds serve as cold sources (temperature 0). After centering the temperatures (so that the mean temperature of each diffusion is equal to 0), each node is assigned the label that maximizes its temperature. This algorithm, we refer to as Dirichlet classifier, is parameter-free.

Algorithm 1 Dirichlet classifier

0: Seed set

S

and associated labels

y\in\{1,\ldots,K\}

1: for

k

\{1,\ldots,K\}

T^{S}=0

3: for

i\in S

4: if

y_{i}=k

then

T^{S}_{i}=1

6: end if

7: end for

T^{(k)}\leftarrow\text{Dirichlet}(S,T^{S})

\Delta^{(k)}\leftarrow T^{(k)}-\text{mean}({T}^{(k)})

10: end for

11: for

i\not\in S

12:

x_{i}=\operatorname*{arg\,max}_{k=1,\ldots,K}(\Delta^{(k)}_{i})

13: end for

14: return

x

, labels of nodes outside

S

The key difference with the vanilla method lies in temperature centering (line 9 of the algorithm). Another variant proposed by Zhu et al. (2003) consists in rescaling the temperature vector by the weight of the considered label in the seeds (see equation (9) in their paper).

3.3 Time complexity

The time complexity depends on the algorithm used to solve the Dirichlet problem. We here focus on the approximate solution by successive iterations of (4). Let $m$ be the number of edges of the graph. Using the Compressed Sparse Row format for the adjacency matrix, each matrix-vector product has a complexity of $O(m)$ . The complexity of Algorithm 1 is then $O(NKm)$ , where $N$ is the number of iterations. Note that the $K$ Dirichlet problems are independent and can thus be computed in parallel.

4 Analysis

In this section, we prove the consistency of Algorithm 1 on a simple block model. In particular, we highlight the importance of temperature centering in the analysis.

4.1 Block model

Consider a graph of $n$ nodes consisting of $K$ blocks of respective sizes $n_{1},\ldots,n_{K}$ , forming a partition of the set of nodes. There are $s_{1},\ldots,s_{K}$ seeds in these blocks, which are respectively assigned labels $1,\ldots,K$ . Intra-block edges have weight $p$ and inter-block edges have weight $q$ . We expect the algorithm to assign label $k$ to all nodes of block $k$ whenever $p>q$ , for all $k=1,\ldots,K$ .

4.2 Dirichlet problem

Consider the Dirichlet problem when the temperature of the $s_{1}$ seeds of block 1 is set to 1 and the temperature of the other seeds is set to 0. We have an explicit solution to this Dirichlet problem, whose proof is provided in the appendix.

Lemma 1.

Let $T_{k}$ be the temperature of non-seed nodes of block $k$ at equilibrium. We have:

	$\displaystyle(s_{1}(p-q)+nq)T_{1}$	$\displaystyle=s_{1}(p-q)+n\bar{T}q,$
	$\displaystyle(s_{k}(p-q)+nq)T_{k}$	$\displaystyle=n\bar{T}q\quad\quad k=2,\ldots,K,$

where $\bar{T}$ is the average temperature, given by:

\bar{T}=\left(\frac{s_{1}}{n}\frac{n_{1}(p-q)+nq}{s_{1}(p-q)+nq}\right)/\left(1-\sum_{k=1}^{K}\frac{(n_{k}-s_{k})q}{s_{k}(p-q)+nq}\right).

4.3 Classification

We now state the main result of the paper: the Dirichlet classifier is a consistent algorithm for the block model, in the sense that all nodes are correctly classified whenever $p>q$ .

Theorem 1.

If $p>q$ , then $x_{i}=k$ for all non-seed nodes $i$ of each block $k$ , for any parameters $n_{1},\ldots,n_{K}$ (block sizes) and $s_{1},\ldots,s_{K}$ (numbers of seeds).

Proof.

Let $\delta^{(1)}_{k}=T_{k}-\bar{T}$ be the deviation of temperature of non-seed nodes of block $k$ for the Dirichlet problem associated with label 1. In view of Lemma 1, we have:

	$\displaystyle(s_{1}(p-q)+nq)\delta^{(1)}_{1}$	$\displaystyle=s_{1}(p-q)(1-\bar{T}),$
	$\displaystyle(s_{k}(p-q)+nq)\delta^{(1)}_{k}$	$\displaystyle=-s_{k}(p-q)\bar{T}\quad\quad k=2,\ldots,K,$

For $p>q$ , using the fact that $\bar{T}\in(0,1)$ , we get $\delta^{(1)}_{1}>0$ and $\delta^{(1)}_{k}<0$ for all $k=2,\ldots,K$ . By symmetry, for each label $l=1,\ldots,K$ , $\delta^{(l)}_{l}>0$ and $\delta^{(l)}_{k}<0$ for all $k\neq l$ . We deduce that for each block $k$ , $x_{i}=\arg\max_{l}\delta^{(l)}_{k}=k$ for all non-seed nodes $i$ of block $k$ . ∎

Observe that the temperature centering is critical for consistency. In the absence of centering, non-seed nodes of block 1 are correctly classified if and only if their temperature is the highest in the Dirichlet problem associated with label 1. In view of Lemma 1, this means that for all $k=2,\ldots,K$ ,

\displaystyle s_{1}q\frac{n_{1}(p-q)+nq}{s_{1}(p-q)+nq}+s_{1}(p-q)\left(1-\sum_{j=1}^{K}\frac{(n_{j}-s_{j})q}{s_{j}(p-q)+nq}\right)>s_{k}q\frac{n_{k}(p-q)+nq}{s_{k}(p-q)+nq}.

This condition might be violated even if $p>q$ , depending on the parameters $n_{1},\ldots,n_{K}$ and $s_{1},\ldots,s_{K}$ . In the practically interesting case where $s_{1}<<n_{1},\ldots,s_{K}<<n_{K}$ for instance (low fractions of seeds), the condition requires:

s_{1}(n_{1}(p-q)+nq)>s_{k}(n_{k}(p-q)+nq).

For blocks of same size, this means that only blocks with the largest number of seeds are correctly classified. The classifier is biased towards labels with a large number of seeds. This sensitivity of the vanilla algorithm to the label distribution of seeds will be confirmed in the experiments on real graphs.

5 Experiments

In this section, we show the impact of temperature centering on the quality of classification using both synthetic and real data. We do not provide a general benchmark of classification methods as the focus of the paper is on the impact of temperature centering in heat diffusion methods. We focus on 3 algorithms: the vanilla algorithm (without temperature centering), the weighted version proposed by (Zhu et al., 2003) (also without temperature centering) and our algorithm (with temperature centering).

All datasets and codes are available online¹¹1https://github.com/nathandelara/Dirichlet, making the experiments fully reproducible.

5.1 Synthetic data

We first use the stochastic block model (SBM) (Airoldi et al., 2008) to generate graphs with an underlying structure in clusters. This is the stochastic version of the block model used in the analysis. There are $K$ blocks of respective sizes $n_{1},\ldots,n_{K}$ . Nodes of the same block are connected with probability $p$ while nodes in different blocks are connected probability $q$ . We denote by $s_{k}$ the number of seeds in block $k$ and by $s$ the total number of seeds.

We first compare the performance of the algorithms on a binary classification task ( $K=2$ ) for a graph of $n=10\,000$ nodes with $p=10^{-3}$ and $q=10^{-4}$ , in two different settings:

•

Seed asymmetry: Both blocks have the same size $n_{1}=n_{2}=5000$ but different numbers of seeds, with $s_{1}/s_{2}\in\{1,2,\dots,10\}$ and $s_{2}=250$ (5% of nodes in block 2).
•

Block size asymmetry: The blocks have different sizes with ratio $n_{1}/n_{2}\in\{1,2,\dots,10\}$ and seeds in proportion to these sizes, with a total of $s=1\,000$ seeds ( $10\%$ of nodes).

For each configuration, the experiment is repeated 10 times. Randomness comes both from the generation of the graph and from the selection of the seeds. We report the F1-scores in Figure 2 (average $\pm$ standard deviation). Observe that the variability of the results is very low due to the relatively large size of the graph. As expected, the centered version is much more robust to both types of asymmetry. Besides, in case of asymmetry in the seeds, the weighted version of the algorithm tends to amplify the bias and leads to lower scores than the vanilla version.

We show in Figure 3 the same type of results for $K=10$ blocks and $p=5.10^{-2}$ . For the block size asymmetry, the size of blocks $2,\ldots,10$ is set to $1\,000$ .

5.2 Real data

We use datasets from the NetSet²²2https://netset.telecom-paris.fr/ and SNAP³³3https://snap.stanford.edu/data/ collections (see Table 1).

Table 1: Datasets.

dataset	# nodes	# edges	# classes	$(\%)$ labeled
CO	$2\ 708$	$10\ 556$	7	100
CS	$3\ 264$	$9\ 072$	6	100
WS	$4\ 403$	$112\ 834$	16	100
WV	$10\ 012$	$792\ 091$	11	100
WL	$3\ 210\ 346$	$67\ 196\ 296$	10	100
DBLP	$317\ 080$	$2\ 099\ 732$	5000	29
Amazon	$334\ 863$	$1\ 851\ 744$	5000	5

These datasets can be categorized into 3 groups:

•

Citations networks: Cora (CO) and CiteSeer (CS) are citation networks between scientific publications. These are standard datasets for node classification (Fey et al., 2018; Huang et al., 2018; Wijesinghe and Wang, 2019).
•

Wikipedia graphs: Wikipedia for schools (WS) (Haruechaiyasak and Damrongrat, 2008), Wikipedia vitals (WV) and Wikilinks (WL) are graphs of hyperlinks between different selections of Wikipedia pages. In WS and WV, pages are labeled by category (People, History, Geography…). For WL, pages are labeled through clusters of words used in these articles. As these graphs are directed, we use the extension of the algorithm described in §2.3, with nodes considered as heat sources.
•

Social networks: DBLP and Amazon are social networks with partial ground-truth communities (Leskovec and Krevl, 2014). As nodes are partially labeled and some nodes have several labels, the results for these datasets are presented separately, with specific experiments based on binary classification.

For the citation networks and the Wikipedia graphs, we compare the classification performance of the algorithms in terms of macro-F1 score and two seeding policies:

•

Uniform sampling, where seeds are sampled uniformly at random.
•

Degree sampling, where seeds are sampled in proportion to their degrees.

In both cases, the seeds represent $1\%$ of the total number of nodes in the graph. The process is repeated 10 times for each configuration. We defer the results for the weighted version of the algorithm to the supplementary material as they are very close to those obtained with the vanilla algorithm.

We report the results in Tables 2 and 3 for uniform sampling and degree sampling, respectively. We see that centered version outperforms the vanilla one by a significant margin.

Table 2: Macro-F1 scores (mean

\pm

standard deviation) with uniform seed sampling.

algorithm	CO	CS	WS	WV	WL
Vanilla	$0.19\pm 0.12$	$0.17\pm 0.04$	$0.04\pm 0.02$	$0.09\pm 0.04$	$0.19\pm 0.01$
Centered	$\mathbf{0.42\pm 0.18}$	$\mathbf{0.36\pm 0.04}$	$\mathbf{0.16\pm 0.11}$	$\mathbf{0.55\pm 0.03}$	$\mathbf{0.51\pm 0.01}$

Table 3: Macro-F1 scores (mean

\pm

standard deviation) with degree seed sampling.

algorithm	CO	CS	WS	WV	WL
Vanilla	$0.30\pm 0.08$	$0.16\pm 0.07$	$0.02\pm 0.01$	$0.10\pm 0.04$	$0.34\pm 0.00$
Centered	$\mathbf{0.51\pm 0.08}$	$\mathbf{0.26\pm 0.13}$	$\mathbf{0.06\pm 0.04}$	$\mathbf{0.48\pm 0.02}$	$\mathbf{0.45\pm 0.00}$

For the social networks, we perform independent binary classifications for each of the 3 dominant labels and average the scores. As these datasets have only a few labeled nodes, we consider the most favorable scenario where seeds are sampled in proportion to the labels. Seeds still represent $1\%$ of the nodes. The results are shown in Table 4.

Table 4: Macro-F1 scores (mean

\pm

standard deviation) with balanced seed sampling.

algorithm	DBLP	Amazon
Vanilla	$0.04\pm 0.00$	$0.05\pm 0.01$
Centered	$\mathbf{0.19\pm 0.01}$	$\mathbf{0.18\pm 0.02}$

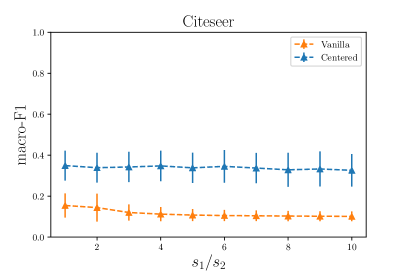
Finally, we assess the classification performance of the algorithms in the case of seed asymmetry. Specifically, we first sample $s=1\%$ of the nodes uniformly at random and progressively increase the number of seeds for the dominant class of each dataset, say label 1.

The process is repeated 10 times for each configuration. Figure 4 shows the macro-F1 scores. We see that the performance of the centered algorithm remains steady in the presence of seed asymmetry.

6 Conclusion

We have proposed a novel approach to node classification based on heat diffusion. Specifically, we propose to center the temperatures of each solution to the Dirichlet problem before classification. We have proved the consistency of this algorithm on a simple block model and we have shown that it drastically improves classification performance on real datasets with respect to the vanilla version.

In future work, we plan to extend this algorithm to soft classification, using the centered temperatures to get a confidence score for each node of the graph. Another interesting research perspective is to extend our proof of consistency of the algorithm to stochastic block models.

References

Airoldi et al. [2008] Edoardo M Airoldi, David M Blei, Stephen E Fienberg, and Eric P Xing. Mixed membership stochastic blockmodels. Journal of machine learning research, 9(Sep):1981–2014, 2008.
Berberidis et al. [2018] Dimitris Berberidis, Athanasios N Nikolakopoulos, and Georgios B Giannakis. Adadif: Adaptive diffusions for efficient semi-supervised learning over graphs. In 2018 IEEE International Conference on Big Data (Big Data), pages 92–99. IEEE, 2018.
Chung [1997] Fan RK Chung. Spectral graph theory. American Mathematical Soc., 1997.
Donnat et al. [2018] Claire Donnat, Marinka Zitnik, David Hallac, and Jure Leskovec. Learning structural node embeddings via diffusion wavelets. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pages 1320–1329. ACM, 2018.
Fey et al. [2018] Matthias Fey, Jan Eric Lenssen, Frank Weichert, and Heinrich Müller. Splinecnn: Fast geometric deep learning with continuous b-spline kernels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 869–877, 2018.
Haruechaiyasak and Damrongrat [2008] Choochart Haruechaiyasak and Chaianun Damrongrat. Article recommendation based on a topic model for wikipedia selection for schools. In International Conference on Asian Digital Libraries, pages 339–342. Springer, 2008.
Huang et al. [2018] Wenbing Huang, Tong Zhang, Yu Rong, and Junzhou Huang. Adaptive sampling towards fast graph representation learning. In Advances in Neural Information Processing Systems, pages 4558–4567, 2018.
Kondor and Lafferty [2002] Risi Imre Kondor and John Lafferty. Diffusion kernels on graphs and other discrete structures. In Proceedings of the 19th international conference on machine learning, volume 2002, pages 315–322, 2002.
Leskovec and Krevl [2014] Jure Leskovec and Andrej Krevl. SNAP Datasets: Stanford large network dataset collection. http://snap.stanford.edu/data, June 2014.
Li et al. [2019] Qilin Li, Senjian An, Ling Li, and Wanquan Liu. Semi-supervised learning on graph with an alternating diffusion process. CoRR, abs/1902.06105, 2019.
Ma et al. [2008] Hao Ma, Haixuan Yang, Michael R Lyu, and Irwin King. Mining social networks using heat diffusion processes for marketing candidates selection. In Proceedings of the 17th ACM conference on Information and knowledge management, pages 233–242. ACM, 2008.
Ma et al. [2011] Hao Ma, Irwin King, and Michael R Lyu. Mining web graphs for recommendations. IEEE Transactions on Knowledge and Data Engineering, 24(6):1051–1064, 2011.
Merkurjev et al. [2016] Ekatherina Merkurjev, Andrea L Bertozzi, and Fan Chung. A semi-supervised heat kernel pagerank MBO algorithm for data classification. Technical report, University of California, Los Angeles Los Angeles United States, 2016.
Thanou et al. [2017] Dorina Thanou, Xiaowen Dong, Daniel Kressner, and Pascal Frossard. Learning heat diffusion graphs. IEEE Transactions on Signal and Information Processing over Networks, 3(3):484–499, 2017.
Tremblay and Borgnat [2014] Nicolas Tremblay and Pierre Borgnat. Graph wavelets for multiscale community mining. IEEE Transactions on Signal Processing, 62(20):5227–5239, 2014.
Watts and Strogatz [1998] Duncan J Watts and Steven H Strogatz. Collective dynamics of small-world networks. Nature, 1998.
Wijesinghe and Wang [2019] Asiri Wijesinghe and Qing Wang. Dfnets: Spectral cnns for graphs with feedback-looped filters. In Advances in Neural Information Processing Systems, pages 6007–6018, 2019.
Zachary [1977] Wayne W Zachary. An information flow model for conflict and fission in small groups. Journal of anthropological research, 33(4):452–473, 1977.
Zhu et al. [2003] Xiaojin Zhu, Zoubin Ghahramani, and John D Lafferty. Semi-supervised learning using gaussian fields and harmonic functions. In Proceedings of the 20th International conference on Machine learning (ICML-03), pages 912–919, 2003.
Zhu [2005] Xiaojin Zhu. Semi-supervised learning with graphs. PhD thesis, Carnegie Mellon University, 2005.

Appendix: Proof of Lemma 1

Proof.

In view of (2), we have:

	$\displaystyle(n_{1}(p-q)+nq)T_{1}=s_{1}p+(n_{1}-s_{1})pT_{1}+\sum_{j\neq 1}(n_{j}-s_{j})qT_{j},$
	$\displaystyle(n_{k}(p-q)+nq)T_{k}=s_{1}q+(n_{k}-s_{k})pT_{k}+\sum_{j\neq k}(n_{j}-s_{j})qT_{j},\quad k=2,\ldots,K.$

We deduce:

	$\displaystyle(s_{1}(p-q)+nq)T_{1}$	$\displaystyle=s_{1}p+Vq,$
	$\displaystyle(s_{k}(p-q)+nq)T_{k}$	$\displaystyle=s_{1}q+Vq\quad\quad k=2,\ldots,K.$

with

V=\sum_{j=1}^{K}(n_{j}-s_{j})T_{j}.

The proof then follows from the fact that

n\bar{T}=s_{1}+\sum_{j=1}^{K}(n_{j}-s_{j})T_{j}=s_{1}+V.

∎