A Deterministic Sampling Method via Maximum Mean Discrepancy Flow with Adaptive Kernel

The core idea of VI is to minimize a user-specified dissimilarity functional that measures the difference between two distributions. Many dissimilarity functionals, such as Kullback-Leibler (KL-)divergence and the more general $f$-divergence (Csiszár et al., 2004; Zhang et al., 2019), Wasserstein distance (Villani, 2021), kernel stein discrepancy (KSD) (Liu et al., 2016; Chen et al., 2018b), and kernel discrepancy, have been used in the literature.

If the target distribution is known up to the intractable normalizing constant, KL-divergence is commonly used (Liu and Wang, 2016; Blei et al., 2017; Ma et al., 2019; Heng et al., 2021). For example, the Langevin Monte Carlo (LMC) (Welling and Teh, 2011; Cheng et al., 2018; Bernton, 2018) and the Stein Variational Gradient Descent (SVGD) (Liu and Wang, 2016) can be considered as a discretization of the Wasserstein gradient flow (Jordan et al., 1998) of the KL-divergence. However, KL-divergence is only suitable for the target distribution whose density function takes the form $\frac{1}{Z}\exp(-V({\bm{x}}))$. Moreover, the KL-divergence-based algorithms require repeated evaluation of the gradient of the target distribution, which can be computationally costly if the target distribution is complicated to compute.

Kernel discrepancy is another popular dissimilarity functional. In machine learning, kernel discrepancy is better known as Maximum Mean Discrepancy or MMD. It is suitable for the case where the target distribution is compactly supported. Unlike KL-divergence, MMD does not have the “$\log 0$” issue which can occur when the density values are really small at certain particles. What is more, it is easy to compute the MMD for the two-sample problems (Li et al., 2015, 2017), in which the target distribution is the empirical distribution of training data. For these reasons, we choose kernel discrepancy or MMD as the objective functional. We defer the detailed review of kernel discrepancy/MMD and its related literature in Section 2.

Another important aspect of a VI approach is the minimization method. As reviewed by Blei et al. (2017), the complexity of the minimization is largely decided by the distribution family $\mathcal{Q}$, i.e., the set of feasible distributions to approximate the target distribution. It can be a family of parametric distributions. But sometimes, the parametric distribution is too restrictive, and thus flow-based VI methods have been created, in which $\mathcal{Q}$ consists of distributions obtained by a series of smooth transformations from a tractable initial reference distribution. Examples include normalizing flow VI methods (Rezende and Mohamed, 2015; Kingma et al., 2016; Salman et al., 2018) and particle-based VI methods (ParVIs) (Liu and Wang, 2016; Liu, 2017; Liu and Zhu, 2017; Chen et al., 2018a; Liu et al., 2019; Chen et al., 2019; Wang et al., 2021). Our proposed approach belongs to the ParVIs category. Among all the ParVIs, SVGD (Liu, 2017) is one of the most popular early works. We compare the proposed approach with some other ParVI methods, including SVGD.

In this paper, we propose a deterministic sampling method by minimizing the kernel discrepancy or MMD via the general energetic variational inference (EVI) framework (Wang et al., 2021). The EVI transforms the minimization problem into a dynamic system, which can be solved by many numerical schemes, including the implicit Euler method as demonstrated in this paper. We name it EVI-MMD algorithm.

Compared to some existing works that also minimize MMD, the proposed approach applies to many scenarios, including the cases when the target distribution is fully known and empirically given by the data, whereas most existing MMD methods (Gretton et al., 2012; Li et al., 2015; Liu et al., 2016; Li et al., 2017; Mak and Joseph, 2018; Cheng and Xie, 2021; Hofert et al., 2021) focus on the two-sample problem. Besides, the proposed EVI-MMD method is much simpler considering it does not need to construct any deep neural network as the flow map. The implicit Euler is stable because the MMD is guaranteed to be decreased in each iteration (Section 2.2). More importantly, we propose a novel way to specify the bandwidth dynamically. It overcomes a long-existing issue of bandwidth selection for the Gaussian kernel in many ParVI methods. Through a comprehensive numerical study, we show the proposed adaptive bandwidth significantly improves the EVI-MMD algorithm.

The rest of the paper is organized as follows. Section 2 gives the necessary background on the kernel discrepancy and the general deterministic sampling method by the EVI framework. In Section 3, we apply the general EVI framework to minimize the kernel discrepancy and discuss the practical issues of EVI-MMD, including the specification of adaptive bandwidth and other tuning parameters. In Section 4, three groups of examples are used to compare the EVI-MMD algorithm with some alternative methods. We conclude the paper in Section 5.

Before its wide recognition in machine learning as MMD, kernel discrepancy has been an important concept in QMC literature and was promoted as a goodness-of-fit statistic and a quality measure for statistical experimental design (Hickernell, 1998, 1999; Fang et al., 2000; Fang and Mukerjee, 2000; Fang et al., 2002; Hickernell and Liu, 2002). Kernel discrepancy can be interpreted in different ways. Hickernell (2016) and Li et al. (2020) explained three identities of kernel discrepancy. First, it can be considered as a norm on a Hilbert space of measures, which has to include the Dirac measure. Second, it is commonly used as a deterministic cubature error bound for Monte Carlo methods. Third, it is the root mean squared cubature error, where the kernel function is also the covariance function for a stochastic process. Here we review it using the second identity and then generalize it and connect it with MMD.

Let $\Omega\subset\mathbb{R}^{d}$ be the domain of a probability measure $\mu$, which has density $\rho(\bm{x})$ and cumulative distribution function $F(\bm{x})$. The three concepts, measure, density, and CDF, are used interchangeably in the rest of the paper to refer to distribution. Let $(\mathcal{H},\left\langle\cdot,\cdot\right\rangle_{\mathcal{H}})$ be a reproducing kernel Hilbert space (RKHS) of functions $f:\Omega\rightarrow\mathbb{R}$. By definition, the reproducing kernel, $K$, is the unique function defined on $\Omega\times\Omega$ with the properties that $K(\cdot,\bm{x})\in\mathcal{H}$ for any $\bm{x}\in\Omega$ and $f(\bm{x})=\left\langle K(\cdot,\bm{x}),f\right\rangle_{\mathcal{H}}$. The second property implies that $K$ reproduces function values via the inner product. It can be verified that $K$ is symmetric in its arguments and positive definite.

A cubature method approximates the integral $I=\int_{\Omega}f(\bm{x})\rho(\bm{x})\mathrm{d}\bm{x}=\mathbb{E}_{\bm{x}\sim\mu}[f(\bm{X})]$ of an $f\in\mathcal{H}$ by the sample mean

Let $\mathcal{X}=\{\bm{x}_{i}\}_{i=1}^{N}$ be the set of the i.i.d. samples following $F(\bm{x})$ distribution. To measure the quality of the approximation, define the cubature error as

where $F_{\mathcal{X}}$ is the empirical CDF based on the sample $\mathcal{X}$. Under modest assumptions of the reproducing kernel, based on Cauchy-Schwarz inequality, the tight error bound is

where $\|f\|_{\mathcal{H}}$ is the norm of the function $f$ based on the inner product of the RKHS $\mathcal{H}$ and $D(\mathcal{X},F,K)$ is the kernel discrepancy whose square is equal to

Recall that the kernel discrepancy is also the norm on a Hilbert space of measures, i.e., the first identity mentioned earlier. More specifically, this Hilbert space of measures, denoted by $\mathcal{M}$, is the closure of the pre-Hilbert space and its inner product is defined as

For the given kernel $K$, the Hilbert space contains all measures such that $\|\nu\|_{\mathcal{M}}$ is bounded. Please see Hickernell (2016) or Li et al. (2020) for the detailed definitions of the RKHS $\mathcal{H}$, $\mathcal{M}$, and the derivation of (1). The kernel discrepancy can be more generally defined by

measuring the difference between any $\nu_{1},\nu_{2}\in\mathcal{M}$. Gretton et al. (2012) defined the maximum mean discrepancy (MMD) as

and under the same definition of $\mathcal{H}$ and $\mathcal{M}$, the square of MMD is

which is equivalent to $D^{2}(\nu_{1},\nu_{2},K)$ in (2). Therefore, in the rest of the paper, we use kernel discrepancy and MMD interchangeably.

Kernel discrepancy has many desirable properties, one of which is measuring the difference between distributions. In fact, $\text{MMD}(\mathcal{H},\nu_{1},\nu_{2})=0$ if and only if $\nu_{1}=\nu_{2}$, provided that $\Omega$ is a compact metric space and more importantly, $K$ is a universal kernel and thus $\mathcal{H}$ is a universal RKHS (Gretton et al., 2012). Simply put, universal kernel (Micchelli et al., 2006) means that $K$ has to be complex enough such that $\mathcal{H}$ and $\mathcal{M}$ are sufficiently big. Lower-order polynomial kernels, such as linear and second-order polynomials are not universal. MMD induced by the second-order polynomial kernel can distinguish two distributions in terms of mean and variance, and the linear kernel can only do so in terms of the mean. On the other hand, the Gaussian kernel is universal and thus the MMD based on it can be used as a metric for measures (Micchelli et al., 2006; Fukumizu et al., 2007). Therefore, with a proper kernel, if $D^{2}(\mathcal{X}_{N},F,K)\rightarrow 0$ as $N\rightarrow\infty$, then $F_{\mathcal{X}_{N}}\rightarrow F$. For fixed $N$, if $D^{2}(\mathcal{X},F,K)\rightarrow 0$ as $n\rightarrow\infty$ ($n$ is the notation for iteration of algorithm), then $F_{\mathcal{X}}\rightarrow F$. Kernel discrepancy is also related to energy distance (Székely and Rizzo, 2013) and support points (Mak and Joseph, 2018). If set $K(\bm{x},\bm{y})=-\|\bm{x}-\bm{y}\|_{2}^{2}$, then the kernel discrepancy becomes energy distance. For the two-sample problem, the energy distance is given by

Motivated by the energetic variational approaches for modeling the dynamics of non-equilibrium thermodynamical systems (Giga et al., 2017), the energetic variational inference (EVI) framework uses a continuous energy-dissipation law to specify the dynamics of minimizing the objective function in machine learning problems. Under the EVI framework, a practical algorithm can be obtained by introducing a suitable discretization to the continuous energy-dissipation law. This idea was introduced and applied to variational inference by Wang et al. (2021). It can also be applied to other machine learning problems similar to Trillos and Sanz-Alonso (2020) and E et al. (2020).

We first introduce the EVI using the continuous formulation. Let $\bm{\phi}_{t}$ be the dynamic flow map $\bm{\phi}_{t}:\mathbb{R}^{d}\rightarrow\mathbb{R}^{d}$ that continuously transforms the $d$-dimensional distribution from an initial distribution toward the target one and we require the map $\bm{\phi}_{t}$ to be smooth and one-to-one. Let $\rho_{[\bm{\phi}_{t}]}$ denote the probability density that is transformed by ${\bm{\phi}}_{t}$ from an initial distribution. For a given target distribution $\rho^{*}$, one can define a functional $\mathcal{F}(\bm{\phi}_{t})=D(\rho_{[\bm{\phi}]_{t}}||\rho^{*})$, where $D$ is the user-specified dissimilarity functional, such as the KL-divergence in Wang et al. (2021). Taking the analogy of a thermodynamics system, $\mathcal{F}(\bm{\phi}_{t})$ can be viewed as the Helmholtz free energy. Following the First and Second Law of thermodynamics (Giga et al., 2017) (kinetic energy is set to be zero), one can impose the following energy-dissipation

to describe a dynamics of minimizing $\mathcal{F}(\bm{\phi}_{t})$. Here $\triangle(\bm{\phi}_{t},\dot{\bm{\phi}}_{t})$ is a user-specified functional representing the rate of energy dissipation, and $\dot{\bm{\phi}}_{t}$ is the derivative of $\bm{\phi}_{t}$ with time $t$. So $\dot{\bm{\phi}}_{t}$ can be interpreted as the “velocity” of the transformation. Each variational formulation gives a natural path of decreasing the objective functional $\mathcal{F}(\bm{\phi}_{t})$ toward an equilibrium (Trillos and Sanz-Alonso, 2020).

The dissipation functional should satisfy $\triangle(\bm{\phi}_{t},\dot{\bm{\phi}}_{t})\geq 0$ so that $\mathcal{F}(\bm{\phi}_{t})$ decreases with time. As discussed in Wang et al. (2021), there are many ways to specify $\triangle(\bm{\phi}_{t},\dot{\bm{\phi}}_{t})$ and the simplest among them is a quadratic functional in terms of $\dot{\bm{\phi}}_{t}$,

where $\rho_{[\bm{\phi}_{t}]}$ denotes the pdf of the current distribution which is the initial distribution transformed by $\bm{\phi}_{t}$, $\eta(\cdot)$ is a user-specified positive function of $\rho_{[\bm{\phi}_{t}]}$, $\Omega_{t}$ is the current support, and $\|{\bm{a}}\|_{2}=\sqrt{{\bm{a}}^{\top}{\bm{a}}}$ for $\forall{\bm{a}}\in\mathbb{R}^{d}$.

With the specified energy-dissipation law (4), the energy variational approach derives the dynamics of the systems through two variational procedures, the Least Action Principle (LAP) and the Maximum Dissipation Principle (MDP), which leads to

The approach is motivated by the seminal works of Raleigh (Rayleigh, 1873) and Onsager (Onsager, 1931a, b). Using the quadratic $\triangle(\bm{\phi}_{t},\dot{\bm{\phi}}_{t})$ (5), the dynamics of decreasing $\mathcal{F}$ is

In general, this continuous formulation is difficult to solve, since the manifold of $\bm{\phi}_{t}$ is of infinite dimension. Naturally, there are different approaches to approximating an infinite-dimensional manifold by a finite-dimensional manifold. One such approach, as used in Wang et al. (2021), is to use particles (or samples) to approximate the continuous distribution $\rho_{[\bm{\phi}_{t}]}$ with kernel regularization. If this approximation applies to (6), after the LAP and MDP variational steps, we call it the “variation-then-approximation” approach. If this approximation is applied to (4) directly, before any variational steps, we call it the “approximation-then-variation” approach. The latter leads to a discrete version of the energy-dissipation law, i.e.,

Here $\{\bm{x}_{i}(t)\}_{i=1}^{N}$ are the locations of $N$ particles at time $t$ and $\dot{\bm{x}}_{i}(t)$ is the derivative of $\bm{x}_{i}$ with $t$, and thus is the velocity of the $i$th particle as it moves toward the target distribution. The functional $\mathcal{F}_{h}$ and $\triangle_{h}$ are the discretized free energy and dissipation by the $N$ particles. The subscript $h$ of $\mathcal{F}_{h}$ and $\triangle$ denotes the bandwidth parameter of the kernel function used in the kernelization operation. Applying the variational steps to (7), we obtain the dynamics of decreasing $\mathcal{F}$ at the particle level,

This leads to an ODE system of $\{\bm{x}_{i}(t)\}_{i=1}^{N}$ that can be solved by different numerical schemes. The solution of the ODE system is the particles approximating the target distribution. Using the dissipation $\triangle(\bm{\phi}_{t},\dot{\bm{\phi}}_{t})=G\int_{\Omega_{t}}\rho_{[\bm{\phi}_{t}]}\|\dot{\bm{\phi}}_{t}\|_{2}^{2}\mathrm{d}\bm{x}$, the discretized dissipation is $\triangle_{h}=-\frac{G}{N}\sum_{i=1}^{N}\|\dot{{\bm{x}}}_{i}(t)\|_{2}^{2},$ where $G$ is a positive constant. Then (8) becomes

The most straightforward way to solve (8) is the explicit Euler method, which is equivalent to minimizing $\mathcal{F}_{h}$ using the gradient descent method. Another approach is to adopt the implicit Euler scheme to solve the ODE system. This is done by discretizing the left-hand side of (8) in time $t$ and replacing the $\{\bm{x}_{i}\}_{i=1}^{N}$ by $\{\bm{x}_{i}^{n+1}\}_{i=1}^{N}$ for $i=1,\ldots,N$ in the right-hand side, i.e.,

Note that if $\{\bm{x}_{i}\}_{i=1}^{N}$ is replaced by $\{\bm{x}_{i}^{n}\}_{i=1}^{N}$, it leads to the explicit Euler scheme. It is easy to show that a solution of the nonlinear system (10) can be obtained by solving an optimization problem

where

We can therefore define the general EVI Algorithm 1. It shares some resemblance in structure with the proximal point algorithm (Rockafellar, 1976). The advantage of the implicit method is the stability even with a large step size $\tau$. Indeed, it can be shown that (Wang et al., 2021)

So the set of particles always reduces $\mathcal{F}_{h}(\{{\bm{x}}_{i}\}_{i=1}^{N})$ in each iteration. Many other novel approaches can be proposed by applying different numerical algorithms to solve (8) and/or by transforming the original optimization problem into a differential equation system.

The first challenge is how to estimate the free energy $D^{2}(\{{\bm{x}}_{i}(t)\}_{i=1}^{N},F,K)$ efficiently. There are three terms in $D^{2}(\{{\bm{x}}_{i}(t)\}_{i=1}^{N},F,K)$ in (1). The first term $\int_{\Omega\times\Omega}K(\bm{x},\bm{y})\mathrm{d}F(\bm{x})\mathrm{d}F(\bm{y})$ only depends on the target distribution and does not affect the minimization with respect to the particles. So we do not need to compute it in the optimization procedure. The third term $\frac{1}{N^{2}}\sum_{i,j=1}^{N}K(\bm{x}_{i},\bm{x}_{j})$ is easily calculated based on the particles $\{\bm{x}_{i}(t)\}_{i=1}^{N}$, which we call “square-term”. Assume $\rho^{*}(\bm{y})$ is the probability density function associated with the target CDF $F(\bm{x})$. The main challenge is how to compute the “cross-term” in (1), i.e.,

Since it is difficult to sample from $\rho^{*}(y)$ directly, one cannot use any standard Monte Carlo integration. Fortunately, using the Gaussian kernel $K(\bm{x}_{i},\bm{x}_{j})=\exp\left(-\frac{\|\bm{x}_{i}-\bm{x}_{j}\|_{2}^{2}}{2h^{2}}\right)$, one can estimate this integration by generating samples from a Gaussian distribution. Indeed, for the Gaussian kernel, the cross-term can be estimated by

where $\{\bm{\xi}_{l}\}_{l=1}^{L}$ are sampled from the $d$-dimensional standard normal $\mathcal{N}({\bm{0}},\bm{I}_{d})$ and $C_{h}=(2\pi)^{d/2}h^{d}$ is the normalizing constant. The gradient of the cross-term with respect to ${\bm{x}}_{i}$ is also easy to compute based on the approximation (14), i.e.,

Other than the Gaussian kernel, any other positive kernel function that is proportional to a certain density function and easy to be sampled from can be used here. In this paper, we use the Gaussian kernel when the target distribution is fully specified. Theoretically, it is unclear if the error in estimating the cross-term will significantly affect the final performance of EVI-MMD. In the numerical examples in Section 4 we set $L=100$ or $500$ depending on the scale of the problem and the computational cost. It is shown to achieve a good numerical performance.

If the target distribution is an empirical one and only available from the training data $\{\bm{y}_{i}\}_{i=1}^{M}$ with sample size $M$, i.e., the two-sample problem, it is easy to estimate the cross-term by

To reduce computation for large data, we can use the mini-batch procedure, which means randomly drawing a subset of samples $\{\bm{y}_{i}\}_{i=1}^{L}$ from $\{\bm{y}_{i}\}_{i=1}^{M}$ to compute (16) in each iteration. For the two-sample problem, we can use kernels other than the Gaussian kernel. In Section 4, we also use the kernel $K(\bm{x},\bm{y})=-\|\bm{x}-\bm{y}\|_{2}$ which leads to the energy distance and compare it with the Gaussian kernel using the EVI-MMD algorithm.

The parameter $\tau$ is interpreted as the time step size in the implicit Euler in (10). The positive constant $G$ is to scale the dissipation law to suit the chosen free energy. It is easy to see from Algorithm 1 that only the ratio $\tau^{*}=\tau/G$ affects the implicit Euler procedure, so we consider how to choose $\tau^{*}$. Notice that

which indicates

The above inequality shows that, in each iteration, the displacement of the particles, i.e., the left-hand side of the inequality, is bounded above by the change of $\mathcal{F}_{h}$. For Gaussian kernel, the scale of $|\mathcal{F}_{h}(\{\bm{x}_{i}^{(n)}\}_{i=1}^{N})-\mathcal{F}_{h}(\{\bm{x}_{i}^{(n+1)}\}_{i=1}^{N})|$ is almost independent with the dimension. As a result, the convergence of the algorithm can be extremely slow for high-dimensional problems because $\sum_{i=1}^{N}\|\bm{x}_{i}^{(n+1)}-\bm{x}_{i}^{(n)}\|_{2}^{2}$ can be small if $\tau^{*}$ is small. This observation motivates us to pick a relatively large $\tau^{*}$ to balance the scale of the first and second terms in $J_{n}(\{{\bm{x}}_{i}^{n+1}\}_{i=1}^{N})$. We have done extensive numerical experiments and they suggest taking $\tau^{*}\approx d$, which is the dimension of $\bm{x}$. More detailed discussions on tuning parameters are in Section 3.4.

Kernel selection is an important component in any MMD-based algorithm. The key question is how to choose the bandwidth since it is much easier to select the proper kernel function based on the problem. Bandwidth parameter significantly affects the efficiency and robustness of the algorithm (Briol et al., 2019). Although some approaches have been proposed in the literature (Bińkowski et al., 2018; Briol et al., 2019; Li et al., 2017), a satisfactory and universal solution is still not achieved yet.

In this paper, we propose a new adaptive bandwidth selection for the Gaussian kernel $K({\bm{x}},y)=\exp\left(-\|x-y\|^{2}/2h^{2}\right)$. We have done extensive numerical studies and observed the following trend. If the bandwidth $h$ is too small, there will be outliers that converge too slowly toward the target distribution, whereas if $h$ is too large, all the particles will eventually collapse to the same location as the algorithm iterates.

To illustrate this point, we construct a toy example to demonstrate different patterns of the decreasing ${\rm MMD}^{2}$ curves with different bandwidth settings. For a given $\theta\in[0,2]$, we generate samples $\{\bm{x}_{i}^{\theta}\}_{i=1}^{N}$ from the model $\bm{x}_{i}^{\theta}=\bm{y}_{i}+(2-\theta)\bm{z}_{i}$, where $\bm{z}_{i}$ is sampled from a two-dimensional standard Gaussian distribution and $\bm{y}_{i}$ is sampled from the fully specified target distribution, an eight-component Gaussian mixture distribution (the second toy example in Section 4.1). It is obvious that as $\theta\rightarrow 2$, $\{\bm{x}_{i}^{\theta}\}_{i=1}^{N}$ converges to the target distribution. Indeed, in the right panel of Figure 1, the samples $\{\bm{x}_{i}^{\theta}\}^{N}$ (red dots) are closer to the Gaussian mixture distribution (green contour plot) as $\theta\rightarrow 2$. Using the Gaussian kernel, we compute ${\rm MMD}^{2}(\{\bm{x}_{i}^{\theta}\}_{i=1}^{N},\{\bm{y}_{i}\}_{i=1}^{N})$ for different $\theta$ and $h$ values. It is expected that all MMD² curves decrease to zero as $\theta\rightarrow 2$ as shown in the left panel of Figure 1. But they have very different decreasing patterns. For $h=0.5,1,2,4$, the ${\rm MMD}^{2}$ decreases very fast initially when $\theta$ is small but much slower when $\theta$ is close to $2$. For $h=0.05,0.1,0.2$, the trend of ${\rm MMD}^{2}$ is completely opposite. The curves are flat initially for $\theta$ in the range of $(0,1.75)$ and drop to zero very fast near the end.

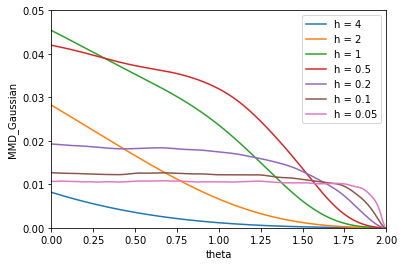
In this toy example, samples $\{\bm{x}_{i}^{\theta}\}_{i=1}^{N}$ of different $\theta$ values mimic the particles that are evolving toward the target distribution in the EVI-MMD algorithm. Generalizing this observation to any MMD-based algorithm, the convergence of the particles is not at the optimal speed if $h$ is fixed throughout the algorithmic iteration. Therefore, we should choose a relatively large $h$ at the beginning of the iteration and gradually decrease $h$. In this way, we can take advantage of the fast decent of MMD² both at the early and end stages of the algorithm and avoid the plateau. The idea behind such an operation is “exploration v.s. exploitation”. In the early stage, with a large $h$, the particles would explore a large neighborhood to find the region with a higher density of the target distribution. As the algorithm proceeds, when most particles are already at the region with a high probability density, the particles only need to exploit their close neighborhood and adjust their positions relative to other particles. As a result, the particles appear to align more regularly as shown in the toy examples in Section 4.1

Based on this idea, we propose to specify the bandwidth as follows,

where $n$ is the iteration index and $a$, $b$, and $c$ are three user-specified parameters. Among them, $a=h_{0}-b$ and we set it to be the median of the pairwise distance between the initial particles. In our examples, the initial distribution is a uniform distribution with a proper domain. The domain is obtained from the fully specified target distribution or from the training data in two-sample problems. The parameter $b>0$ is a regulatory parameter, which serves as a lower bound of $h_{n}$. It is not very influential to the algorithm since it is only to stop $h_{n}$ from becoming zero. For lower-dimensional problems, such as the examples in Section 4.1 and 4.2, we set $b=0.01$. For high-dimensional problems, such as the image data in Section 4.3, we set $b=1$. In fact, in all our examples, when $n=\texttt{maxIter}$ (in Algorithm 2), $h_{n}$ is still significantly larger than $b$, and the largest maxIter we have used is 5000 (in this case $a$ is also very large). The parameter $c>0$ decides the rate of decrease of the bandwidth with respect to $n$. More discussion about the tuning parameters is in Section 3.4

We summarize the EIV-MMD method using the Gaussian kernel and the adaptive bandwidth selection in Algorithm 2. For the problem with a fully specified target distribution, the free energy is

For the two-sample problem (training data size is $M$), the free energy is

The constant term (first term) in the free energy is not relevant to the optimization with respect to the particles and thus they are not computed in the optimization. For the large two-sample problems, the cross term and square term (the second and third term) are computed using the mini-batch procedure to save computation. There are many methods available to solve the proximal point minimization in each iteration. We have chosen the L-BFGS method (Liu and Nocedal, 1989) and it performs adequately.

In Appendix A1, we use the eight-component Gaussian mixture as the target distribution and show the performance of Algorithm 2. Different combination of $a$, $c$, and $\tau^{*}$ are used. From this example and many other simulation studies we have done, we recommend the following settings for all the tuning parameters.

• •

  $\tau^{*}\approx d$

• •

  $a$ is the median of all the pairwise distances between the initial particles.

• •

  $b$ is 0.01 or 1 depending on the dimension of the problem.

• •

  $c$ is mostly selected by trial-and-error and the usual candidates we have tried are $c=0.1,0.2,0.5$.

• •

  $L$ is set based on the dimension of the problem as well as the constraint of the computation cost. In general, a bigger $L$ value leads to more accurate estimations of the free energy and its derivative.

• •

  maxIter should be large enough to ensure the convergence of MMD² and the particles.

• •

  $N$ is largely based on consideration of the computational cost.

Although we recommend these rules-of-thumb on the tuning parameters, users should still run multiple trials to select the best possible combination of the tuning parameters for their problems in practice.

We test the Algorithm 2 in three toy examples where the target distributions are listed below.

1. 1.

   Star-shaped five-component Gaussian mixture distribution:

   $$\rho({\bm{x}})=\frac{1}{5}\sum_{i=1}^{5}N(\bm{x}|\bm{\mu}_{i},\bm{\Sigma}_{i}),$$

   where for $i=1,\ldots,5$,

   $$\bm{\mu}_{i}=\left[\begin{array}[]{rr}\cos\left(\frac{2\pi}{5}\right),&-\sin\left(\frac{2\pi}{5}\right)\\ \sin\left(\frac{2\pi}{5}\right),&\cos\left(\frac{2\pi}{5}\right)\end{array}\right]^{i-1}\left[\begin{array}[]{c}1.5\\ 0\end{array}\right],\quad\bm{\Sigma}_{i}=\left[\begin{array}[]{rr}\cos\left(\frac{2\pi}{5}\right),&-\sin\left(\frac{2\pi}{5}\right)\\ \sin\left(\frac{2\pi}{5}\right),&\cos\left(\frac{2\pi}{5}\right)\end{array}\right]^{i-1}\left[\begin{array}[]{cc}1,&0\\ 0,&0.01\end{array}\right].$$

2. 2.

   Eight-component Gaussian mixture distribution:

   $$\rho({\bm{x}})=\frac{1}{8}\sum_{i=1}^{8}N(\bm{x}|\bm{\mu}_{i},\bm{\Sigma}),$$

   where $\bm{\mu}_{1}=(0,4)$, $\bm{\mu}_{2}=(2.8,2.8)$, $\bm{\mu}_{3}=(4,0)$, $\bm{\mu}_{4}=(-2.8,2.8)$, $\bm{\mu}_{5}=(-4,0)$, $\bm{\mu}_{6}=(-2.8,-2.8)$, $\bm{\mu}_{7}=(0,-4)$, $\bm{\mu}_{8}=(2.8,-2.8)$, and $\bm{\Sigma}=\left[\begin{array}[]{rr}0.2,&0\\ 0,&0.2\end{array}\right]$.

3. 3.

   Wave-shaped distribution:

   $$\rho({\bm{x}})=9.93^{-1}\exp\left(-0.1x_{1}^{2}-(x_{2}-\sin(\pi x_{1}))^{2}\right).$$

Although the first two distributions are both Gaussian mixture distributions, the eight-component Gaussian mixture distribution is more challenging since the effective support region for each Gaussian component is not connected, unlike the star-shaped distribution.

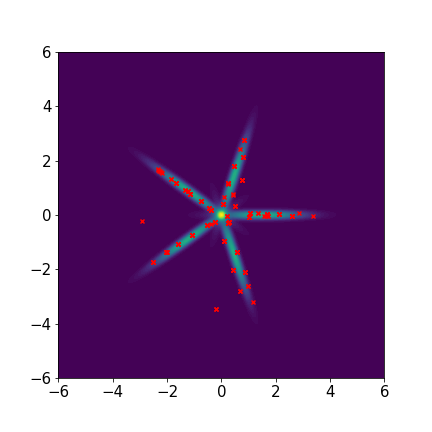
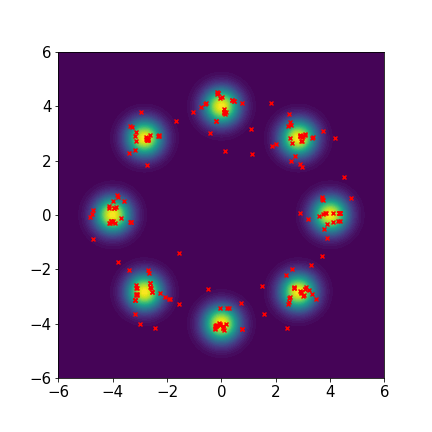
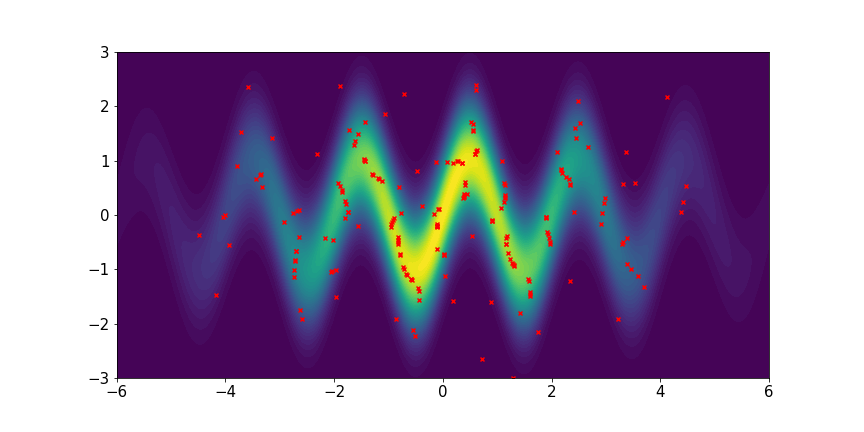
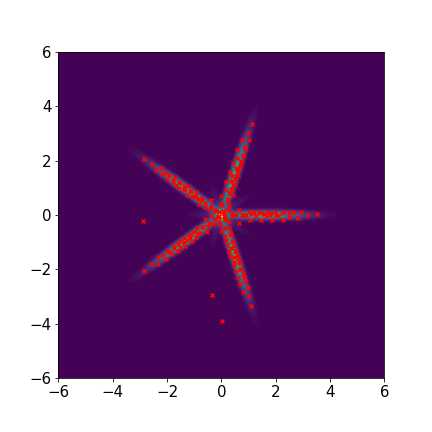
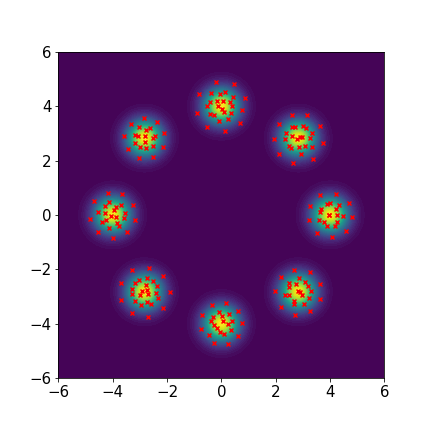
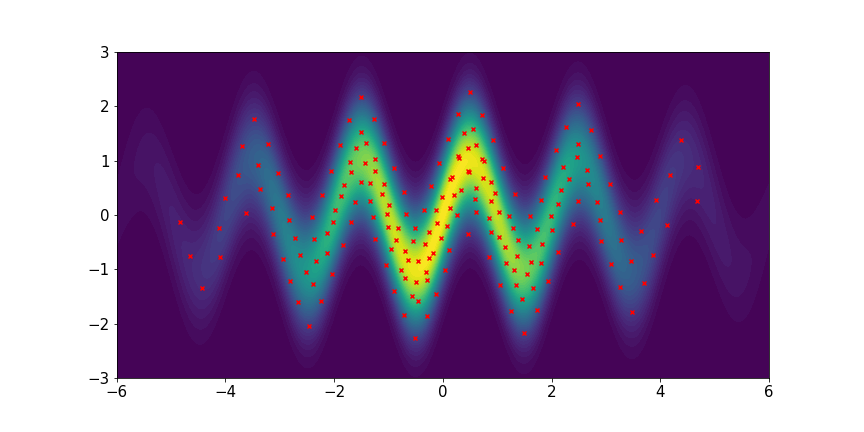
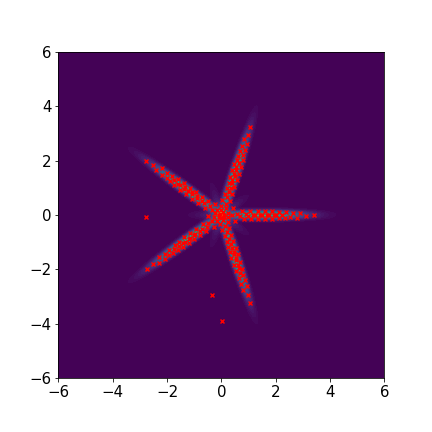
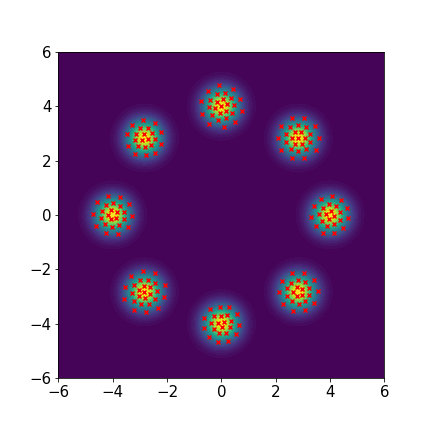
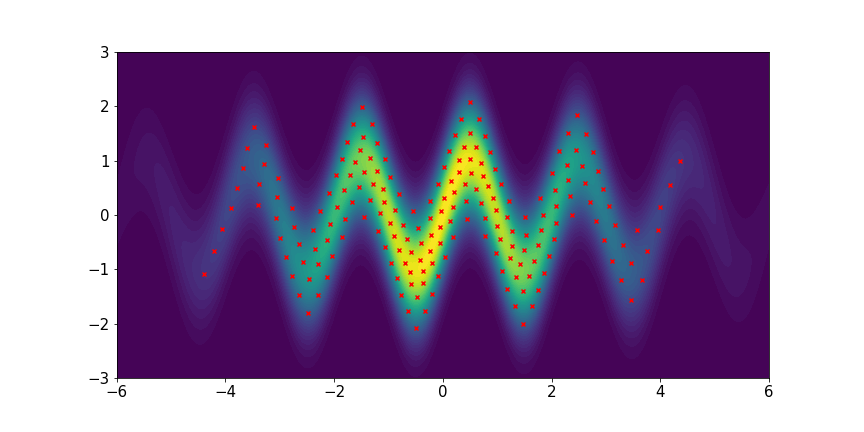
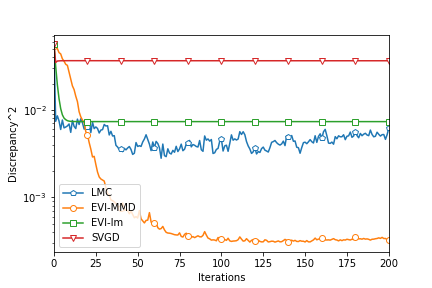
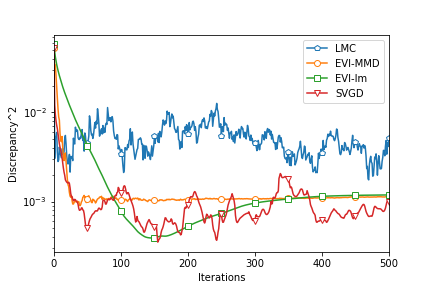
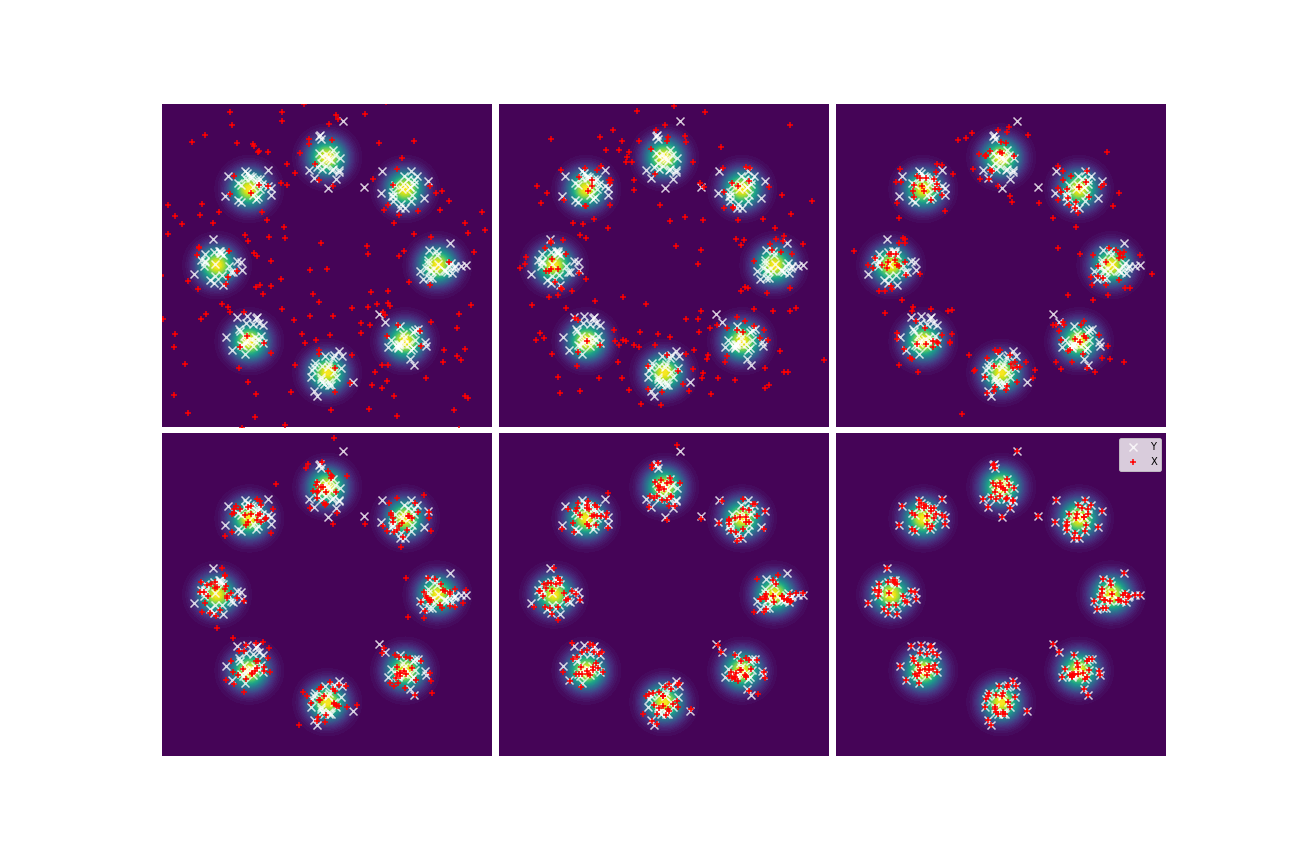
We set $N=200$ and maxIter=5000 for all three examples. The initial distributions are Uniform$[-2,2]$, Uniform$[-4,4]$, and Uniform$[-3,3]$, respectively. The three rows of sub-figures in Figure 2 show the particles at the 50th, 500th, and 5000th iteration. We see that most particles have been moved to the high-density region around the 500th iteration. At the 5000th iteration, all particles have been aligned quite regularly and the algorithm definitely reaches convergence.

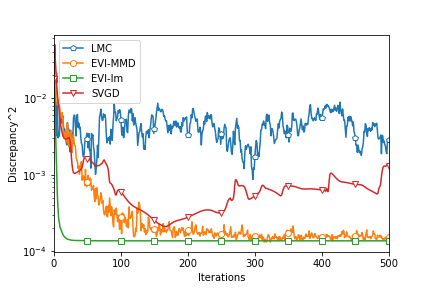
We compare the proposed Algorithm 2 with other similar methods, including the EVI-Im by Wang et al. (2021), SVGD by Liu (2017), and Langevin Monte Carlo (LMC) by Rossky et al. (1978). For the EVI-Im and SVGD methods, we set the step size $\eta_{0}=0.1$ and a fixed bandwidth $h=0.1$ for the Gaussian kernel. The tuning parameters of LMC are $a=0.1$, $b=1$, and $c=0.55$, which decides the step size of LMC by the equation $\eta_{0}=a(b+n)^{-c}$ (different from the proposed algorithm).

To fairly compare the four algorithms, we compute the MMD² criterion using a fixed bandwidth $h=0.5$. So this MMD² is not the objective function of any algorithms in this comparison. Figure 3 shows the decreasing MMD² with respect to iterations of all the algorithms. Since both EVI-Im and EVI-MMD use the implicit Euler scheme, it is reasonable to compare the MMD² in each iteration. The two methods have two embedded loops in Algorithm 1. The outer loop is indexed by $n$ and it is for each complete update of all particles. The inner loop is to minimize the objective function $J_{n}(\{\bm{x}_{i}\}_{i=1}^{N})$ using L-BFGS. But SVGD and LMC only have a single loop. So we compare every 100 iterations of SVGD and LMC with 1 iteration (outer iteration indexed by $n$) of EVI-Im and EVI-MMD. This actually favors SVGD and LMC because the inner loop of EVI-Im and EVI-MMD is usually much less than 100 iterations. From Figure 3 we can see that the EVI-MMD has the fastest descent in the second and third examples and only second to EVI-Im in the first example. Both EVI-MMD and EVI-Im are more stable than SVGD and LMC.

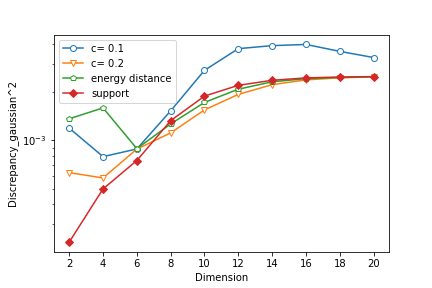
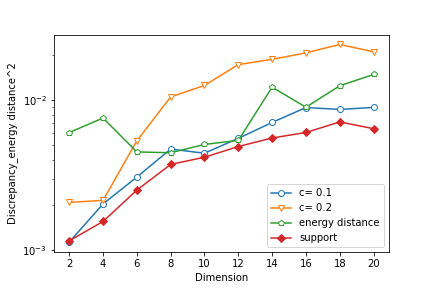
In this example, we study the performance of the proposed algorithm with respect to the increasing dimension. We compare the EVI-MMD with the adaptive bandwidth for the Gaussian kernel with two alternative methods:

• •

  Energy-Distance: this method means that we set the free energy in Algorithm 1 to be the energy distance in (3) proposed in Székely and Rizzo (2013), i.e., $\mathcal{F}(\{\bm{x}_{i}\}_{i=1}^{n})=E(F_{n},F)$.

• •

  Support-Points: this method is proposed by Mak and Joseph (2018), which minimizes the same energy distance by a combination of the convex-concave procedure (CCP) with the resampling method.

The Energy-Distance method and the Support-Points method both minimize the same objective function but use different minimization methods. The EVI-MMD method and the Energy-Distance method minimize different objective functions but use the same implicit method.

We sample the training data of size $M=50,000$ from a standard Gaussian distribution with $d=2,4,\ldots,20$. For all three methods, we set the size of the particles $N=500$ and the initial distribution is Uniform$[-2,2]$. For EVI-MMD and Energy-Distance, we set $\texttt{maxIter}=5000$ and use the mini-batch size of $L=500$. Only for EVI-MMD, we have tried $c=0.1$ and $c=0.2$. For Support-Points, the default settings suggested by Mak and Joseph (2018) are used, except for the initial distribution. Figure 4 compares the MMD² (Gaussian kernel with fixed $h=1$) and energy distance by (3) of the final particles returned by the three methods for $d=2,\ldots,20$. It is not surprising that both criteria become larger as the dimension increases whereas the sample size $N$ is fixed at 500, and the increasing trend is not linear but concave instead. Judging based on the MMD² criterion, the EVI-MMD with $c=0.2$ has a similar performance with the two alternative methods. If using the energy distance criterion, the EVI-MMD with $c=0.1$ is comparable to the Support-Points method. Note that the y-axis is in log-scale, so the differences between these methods are not significant.

Generative learning models have been widely used in various machine learning applications. They can solve supervised and unsupervised learning problems. Simply put, the generative learning model generates new samples based on the training data. More advanced generative learning models are combined with deep neural networks (Jabbar et al., 2021), Naive Bayes, Gaussian mixture model, hidden Markov model, etc. (Harshvardhan et al., 2020). In this example, we use the simplest nonparametric generative learning setup and apply the EVI-MMD to three benchmark image datasets, MNIST (LeCun et al., 1998), Fashion-MNIST (Xiao et al., 2017), and Cifar10 (Krizhevsky and Hinton, 2009).

For the MNIST and Fashion-MNIST datasets, each data point is a grey image of $d=28\times 28=784$ size of pixels. For the Cifar10 dataset, each data point is a full-color image of $d=32\times 32\times 3=3072$ size of pixels. One pixel value is in $[0,1]$. All three are extremely high-dimensional two-sample problems. For the MNIST and Fashion-MNIST datasets, we use the whole dataset of size $M=60,000$ as the training data and resample a mini-batch of $L=100$ samples in each iteration. However, for the Cifar10 dataset, due to the extremely high dimension, we randomly choose a subset of $M=5000$ images as the training data and also use the mini-batch of the size of $L=100$. We choose $L=100$, which is relatively small considering the dimension, is mainly due to the limited computing resources, but it has been proved to be sufficient.

We generate $N=100$ new imagines using the EVI-MMD method and the Energy-Distance method defined in Section 4.2¹¹1We do not include the Support-Points method in this comparison because some issues with the R codes by Mak and Joseph (2018). We are not sure the reason but the returned results do not show any sign of convergence.. The initial particles are sampled from a uniform distribution in $[0,1]^{d}$. We terminate both algorithms at $\texttt{maxIter}=500$ for the EVI-MMD method. Figure 5 compares side-by-side 100 training data randomly chosen from the original training data (left column), new images generated by EVI-MMD (middle column), and Energy-Distance (right column). Both the training and new images are put into a $10\times 10$ panel. We can see the new images generated by both methods are very similar to the training data, and the EVI-MMD returns slightly sharper images than the Energy-Distance method.

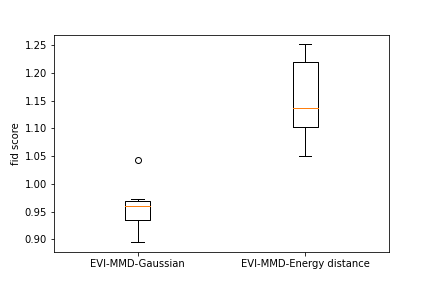
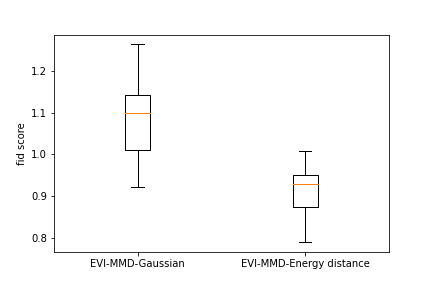
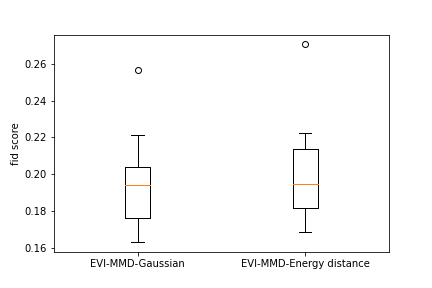
To provide a numerical comparison of the two methods, we calculate the FID score (Heusel et al., 2017) of the generated images. Due to the high computational cost, we randomly sample a subset of 500 images from the training data and calculate the FID score between the new images and the subset of training images. Repeating this 10 times we obtain 10 FID scores for each example. Figure 6 shows the boxplots of all the FID scores for the two methods for all three examples. We can see that both methods have a comparable FID score and the EVI-MMD outperforms the Energy-Distance in the MNIST and Cifar10 examples, which is consistent with the visual comparison in Figure 5.

We also provide the trajectory of the EVI-MMD method in Figure 7. It shows the evolution of some randomly picked particles from static images to the final sharp images. Interestingly, some images are switched directions in the middle of their trajectories. For example, in the second row of the middle panel, the image suddenly switched from a top to a dress then to a pair of pants. This is because when we resample a mini-batch in each iteration. New images can appear in the mini-batch while some old images are not selected, causing the particles to constantly change to approximate the mini-batch data. Note that the EVI-MMD is by no means the best approach for the MNIST benchmark example. Readers can find many more sophisticated generative learning approaches that return better results. However, the EVI-MMD is probably the simplest by comparison and its results are adequate.