A Dual Iterative Refinement Method for Non-rigid Shape Matching
Abstract
In this work, a robust and efficient dual iterative refinement (DIR) method is proposed for dense correspondence between two nearly isometric shapes. The key idea is to use dual information, such as spatial and spectral, or local and global features, in a complementary and effective way, and extract more accurate information from current iteration to use for the next iteration. In each DIR iteration, starting from current correspondence, a zoom-in process at each point is used to select well matched anchor pairs by a local mapping distortion criterion. These selected anchor pairs are then used to align spectral features (or other appropriate global features) whose dimension adaptively matches the capacity of the selected anchor pairs. Thanks to the effective combination of complementary information in a data-adaptive way, DIR is not only efficient but also robust to render accurate results within a few iterations. By choosing appropriate dual features, DIR has the flexibility to handle patch and partial matching as well. Extensive experiments on various data sets demonstrate the superiority of DIR over other state-of-the-art methods in terms of both accuracy and efficiency.
1 Introduction
Nonrigid shape matching is one of the most basic and important tasks in computer vision and shape analysis, e.g., shape registration, comparison, recognition, and retrieval. Different from 2D images, shapes are usually represented as 2-dimensional manifolds embedded in . Many challenges for nonrigid shape matching come from embedding ambiguities, i.e. shapes sharing the same metric (isometry) or very similar metrics (nearly isometry) can have drastically different xyz-coordinates representations in .
To overcome these representation ambiguities, one of the commonly used strategies is to extract features which are isometrically invariant and robust to small perturbations. Along with the idea, many successful and popular approaches are based on spectral geometry [40, 30, 53, 11, 27, 44]. Theoretically, the Laplace-Beltrami (LB) operator is isometrically invariant. As a generalization of Fourier basis functions from Euclidean domains to manifolds, the eigensystem of LB operator provides complete intrinsic spectral information of the underlying manifold. Moreover, from lower eigen-modes to higher eigen-modes, LB eigen-functions also provide a multi-scale characterization of the underlying manifold from coarse to fine resolution. Although using spectral geometry removed possible non-rigid embedding ambiguities, new ambiguities emerge in the spectral domain due to non-uniqueness of the LB eigen-system, e.g., sign ambiguity for eigen-functions, the ambiguity of choosing a basis for the LB eigen-space corresponding to a non-simple LB eigen-value (due to symmetry), the ambiguity of ordering for close eigen-values (due to small perturbations). To handle these ambiguities and use spectral features accurately and robustly, a proper linear transformation (a rigid transformation for exact isometry) needs to be found to align the spectral modes between two shapes first. This linear transformation is typically computed through some matching/correlation based on given (prior) correspondence, e.g., landmarks [35, 2, 28]. Moreover, to resolve fine details and acquire accurate correspondence between two shapes, high eigen-modes need to be used. However, the use of higher eign-modes will not only require more computation costs, but, more importantly, can also cause instability with respect to small perturbations.
To tackle the instability issue of using high eigen-modes directly, one natural multi-scale approach is to start from a correspondence at a coarse scale using a few low modes and iteratively refine the correspondence at a finer and finer scale by adding more and more higher modes gradually. The main motivation is that the linear transformation (a small matrix) on a coarse scale between two truncated spectral spaces spanned by a few low eigen-modes can be determined efficiently and stably from an initial approximate or limited correspondence. Once low eigen-modes are aligned well, an improved correspondence, especially between smooth parts of the two shapes, is likely obtained. The improved correspondence is then used to determine the linear transformation for the next iteration which involves more and higher LB eigen-modes. Such a multi-scale idea for shape correspondence has been proposed in [28] for multi-scale registration using rotation-invariant sliced-Wasserstein distance and in [34] as a Zoom-out process. However, for the above straightforward multi-scale approach in the spectral domain, there are two key issues. First, in each iteration, the determination of the linear transformation between the truncated spectral embedding of two shapes using current correspondence of all points, many of which are incorrect, indiscriminately might be problematic. In Theorem 1, we show that the linear transformation between two spectral spaces determined using all points from an inaccurate correspondence will most likely lead to errors. These errors could be very significant and can cause either a failure for later refinement or slow convergence shown in the supplementary material. The other issue is the lack of a systematic and data-adaptive way to determine how many eigen-modes can be aligned accurately and stably by the current correspondence. Thus, it is hard to decide the appropriate jump in the number of eigen-modes for the next refinement after each iteration to achieve fast convergence. Previously, an increment of one mode was typically used in Zoom-Out [34], while a prefixed sequence of eigenmodes was proposed in [28] based on the rule of thumb.
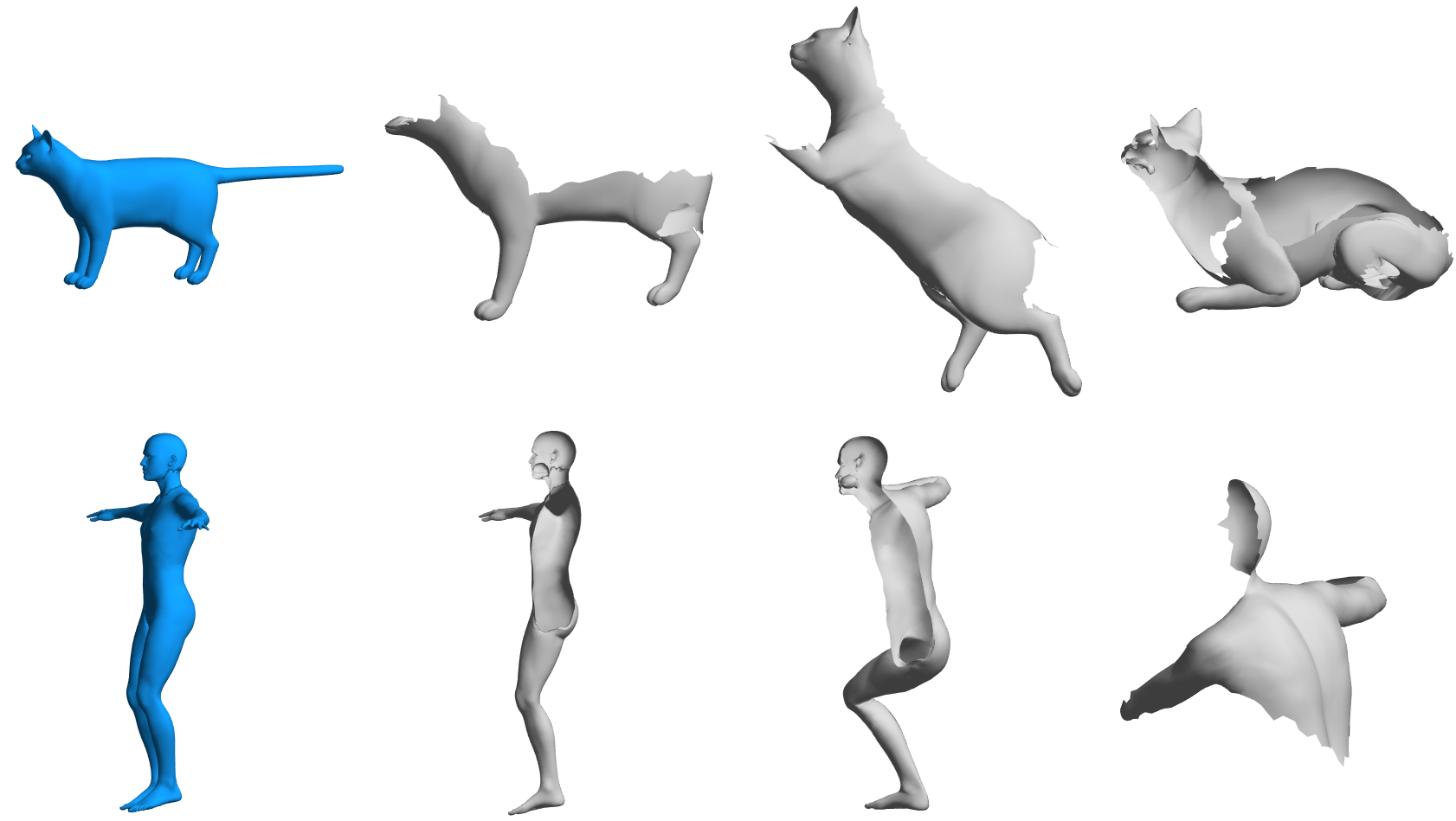
In this work, we propose a simple and efficient dual iterative refinement strategy. This method combines complementary information, such as spatial and spectral, or local and global, to simultaneously refine the correspondence between approximately isometric shapes in an effective way. More specifically, spatial matching via local mapping distortion (see Definition 1) is applied point-wisely to choose well-matched correspondence – anchor pairs, at the current stage. Once anchor pairs are selected, they are used to find 1) the maximal dimension of spectral space that can be robustly and accurately determined by these anchor pairs based on their distribution, and 2) the linear transformation that aligns spectral basis at next scale which will lead to a more refined correspondence at next stage. This remarkable simple strategy addresses the aforementioned two critical issues in previous multi-scale approaches using only spectral matching and allows one to utilize all well-matched pairs from the current step to jump to the next step in an accurate, efficient, stable, and data-adaptive way. We use extensive numerical experiments to show that our simple strategy, DIR, outperforms start-of-the-art model-based methods in terms of both accuracy and efficiency markedly. By choosing appropriate and application-specific dual features, DIR enjoys the flexibility to handle different scenarios, such as raw point clouds, patch and partial matching (as illustrated in Figure 1). We defer a detailed explanation of this Figure in Section 5.
Contributions. We summarize our main contributions as follows:
-
•
By combining spatial matching via local mapping distortion and spectral matching via LB eigen-basis, the proposed DIR goes from coarse to fine resolution stably and effectively in a data-adaptive way which overcomes the main challenges in spectral matching.
-
•
By generalizing this dual refinement strategy to other local and global features such as local mapping distortion and global geodesic distance, DIR handles patch and partial matching.
The rest of this paper is organized as follows. In Section 2, we give a brief review of some related work. Then we present our proposed method, DIR, in detail followed by a discussion about a few possible extensions of our method in Section 3. After that, we conduct extensive experiments on various benchmark data sets and compare DIR to other state-of-the-art methods in terms of both accuracy and efficiency in Section 5. We conclude the paper in Section 6.
2 Related work
Deigning effective shape descriptors is crucial for shape registration or correspondence. In general, descriptors can be categorized as pointwise or pairwise. Extrinsic pointwise descriptors [50, 20, 15, 41] are easy to compute but usually not very accurate, especially when non-rigid transformation is involved. To deal with non-rigid transformation, different intrinsic descriptors either in spatial domain, such as geodesics distance signatures [54], heat kernel signatures [48] and wave kernel signatures [4], or in spectral domain using eigensystem of LB operator [30, 53, 11, 27, 35, 28], are proposed. Then various nearest neighbor searching or linear assignment methods are used in the descriptor space to find the dense point correspondence. For point-wise descriptors in spectral domain, such as functional map [35], a proper linear transformation is needed to align spectral basis to remove ambiguities in the eigensystem of LB operator. The determination of the linear transformation itself is typically based on some prior knowledge, e.g., given landmarks, region correspondence or orientation preserving properties [39], and can be challenging to achieve good accuracy especially when the dimension of spectral embedding is high, which is needed to resolve fine shape features to achieve accurate correspondence. On the other hand, spatial domain pointwise descriptors are usually defined smoothly on shapes which is difficult to provide accurate correspondence as well. Our method aims at tackling these issues raised in aligning shapes using pointwise descriptors.
Intrinsic pairwise descriptors, such as pairwise geodesic distance [7, 10, 56] and kernel functions [32, 46, 55] have also been proposed for non-rigid shape correspondence problems. Although the matching of pairwise descriptors is stricter and may be more robust and accurate, it requires to solve a quadratic assignment problem (QAP) which is NP-hard. Various methods have been proposed to solve the QAP approximately in a more computational tractable way e.g sub-sampling [49], coarse-to-fine [57], geodesic distance sparsity enforcement methods [18] and various relaxation approaches [1, 8, 24, 29, 13, 16]. One popular approach is to relax the nonconvex permutation matrix (representing pointwise correspondence) constraint in the QAP to a doubly stochastic matrix (convex) constraint [1, 13]. However, both the pairwise descriptors and the doubly stochastic matrix are dense matrices, which make the relaxed QAP still challenging to solve even for a modest size problem. Recently, a novel local pairwise descriptor and a simple, effective iterative method to solve the resulting quadratic assignment through sparsity control was proposed in [58] for shape correspondence between two approximately isometric surfaces.
3 Dual Iterative Refinement Method
3.1 Functional map
Spectral geometry is widely used in shape analysis [40, 30, 53, 11, 27, 35, 28, 45, 21]. Leveraging by spectral presentation, functional map is introduced in [35] to solve non-rigid shape correspondence problem. It improves earlier point-based spectral methods [22, 23, 33, 36] which directly matches the spectral embeddings of shapes. We provide a brief introduction to the concept of functional map which is used in our multi-scale DIR process.
Given as a closed 2-dimensional Riemannian manifold, the LB operator uniquely determines the underlying manifold up to isometry [6]. Eigen-functions of LB operator form an orthonormal basis on the underlying manifold and can be used as intrinsic and multi-scale descriptors for shapes. In discrete setting, the manifold is usually represented as a triangulated mesh with vertices . The LB matrix is given by [37], where is the diagonal element area matrix of and is the standard cotangent weight matrix. The discrete truncated -dimensional spectral embedding of can be expressed as a matrix whose rows are the first LB eigen-functions evaluated at each point. Similarly, we can define the first LB eigen-embedding for as .
The key idea of functional map is to lift a shape correspondence to a linear map, functional map, between the function spaces and . The functional map for a given correspondence can be represented as a linear transformation between two given bases of and , which becomes a matrix when the shapes are discretized and bases are truncated. In practice, LB eigen-functions are commonly used as the basis for the function space. For example, given a permutation matrix representing a point-to-point map from to , the functional map is defined as:
| (1) |
Theoretically, if and are isometric, then the corresponding LB eigen-functions are the same up to possible ambiguities caused by sign switch and non-simple eigen-values, which form an orthonormal group. This motivates a constrained version of the following functional map [28]
| (2) |
where denotes the set of orthonormal matrices and the projection to is provided as with the singular value decomposition (SVD) of . Since this paper aims at tackling nearly isometric shape matching problem, we adopt (2) which is equivalent to (1) for the isometric case.
Typically, the functional map is obtained via a least square optimization with various constraints and regularizations, such as preservation of given landmarks, communitivity with LB operator, and sparsity [46, 39]. Once the optimized functional map is computed, for any , the correspondence can be obtained by solving the following spectral matching problem:
| (3) |
However, determination of an accurate functional map can be difficult when limited prior knowledge or a poor correspondence is used. On the one hand, it becomes harder when more eigen-modes are involved since the degrees of freedom of the functional map grow quadratically in terms of the eigen-modes involved and, moreover, high eigen-modes are less computationally stable with respect to perturbations or noises. On the other hand, confining to low eigen-modes limits resolution of the spectral representation and hence the accuracy of shape correspondence. A natural multi-scale idea is to start the functional map from a coarse resolution involving a few low eigen-modes and construct a coarse correspondence . Then the coarse correspondence is used to help determining the functional map at a finer scale and hence a more refined correspondence. This process can be iterated until a fine enough resolution is achieved. The main motivation is that the functional map at a coarse scale – a small matrix, can be determined efficiently and stably from an initial approximate or limited correspondence, which is then used to improve the correspondence at next iteration. This strategy leads to iteratively computing (2) and (3), or (1) and (3), which is the key idea proposed in [28] using rotation-invariant sliced Wasserstein distance and in the Zoom-out process [34]. As a crucial component of these iterative refinement methods, the new functional map is obtained from the current correspondence of all points. Since intermediate correspondence, especially at the beginning, can be quite inaccurate, this naive strategy may lead to significant errors.
Next, we provide both theoretical and experimental evidences on the effect of correspondence error of in (2). This can be problematic for any iterative refinement procedure based on spectral geometry. Assume we have two perfectly isometric manifold and their corresponding discrete truncated spectral embedding . Without loss of generality, we assume is the ground truth correspondence between and (otherwise, we can shuffle row vectors of according to the ground truth correspondence). The ground truth functional map is an orthonormal matrix , i.e. and .
Theorem 1.
Given with . Let’s assume a one-to-one correspondence is an inaccurate correspondence which maps a portion of accurately to the corresponding part of , while the rest part of is inaccurate. Without loss of generality, we write and where and . We let for a permutation matrix . Let . Then it is most likely that the spectral norm with probability at least with .
Notice that decreases rapidly as grows. For example, when , . We provide a detailed proof of this theorem in the supplementary material where we also numerically verify that using points from an inaccurate correspondence may lead to significant errors in the functional map. This can cause failure for iterative refinement.
Another critical issue for multi-scale approach in spectral domain is how to iteratively increase the resolution, i.e., the dimension of spectral embedding, in an accurate, stable and data adaptive way. Most approaches [55, 28, 34] just adopt an empirical or prefixed increasing sequence.
Motivated from the above difficulties and limitations of iterative refinement approaches in spectral domain, we propose a dual iterative refinement method which iteratively updates on the spatial and spectral domains. The first key idea is to choose well-matched pairs using local spatial matching from current correspondence, called anchor pairs, and only use them to determine the functional map which helps to construct a much more improved correspondence for the next iteration. In order to choose high-quality anchor pairs from a given correspondence, we zoom in at each corresponding pair and measure local mapping distortion. This step integrates local spatial information in the spectral refinement process. The second key idea is to find the maximal dimension of spectral embedding that can be robustly and accurately determined by these anchor pairs according to their distribution in spectral domain using singular value analysis on their correlation matrix.
3.2 Local mapping distortion
In order to choose well-matched anchor pairs, or to filter out bad correspondences, to compute the functional map more accurately, we use the following local mapping distortion (LMD) introduced in [58] to measure the matching quality of a given correspondence pair and choose those pairs with small LMD. Without relying on any information of the ground truth correspondence, this distortion provides a quantitative measurement to check the accuracy of the map through its continuity and local distance preservation,
Definition 1 (Local mapping distortion (LMD)).
Let be a map between two manifolds. For any point , consider its -geodesic ball in as . LMD of at is defined as:
| (4) |
where and is the volume of .
Based on the above definition of LMD, it is straightforward to check if is an isometric map, then . Conversely, if for some , then is isometric.
In discrete setting, equation (4) can be approximated by:
| (5) |
where is the area element of the mesh representing .
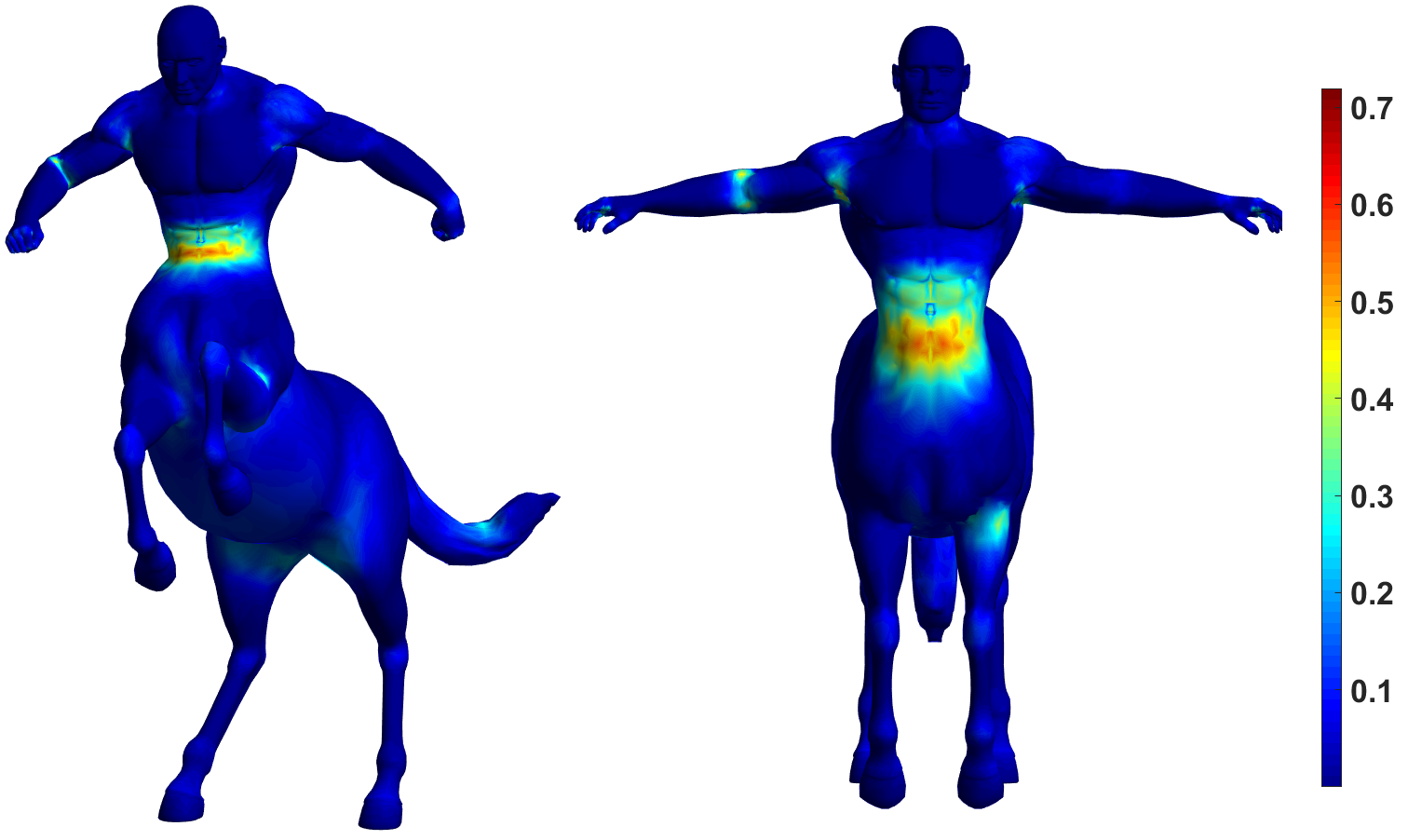
By normalizing the distance with respect to , LMD is robust to global scaling as well as local sampling variation. Figure 2 shows that, for the ground truth correspondence, LMD is very small almost everywhere except in regions where non-isometric distortion is large. Hence the proposed LMD also serves as a good unsupervised error metric when ground truth is not available.
3.3 Our Method
We first precompute leading LB eigen-functions for each shape. Here can be determined by computation cost limitation, the noise level in the data, or desired accuracy of the correspondence. In any case, it should not exceed what the mesh resolution can support for the discretized shape, i.e., a few mesh points are needed in each nodal domain.
Our method can start with an initial correspondence provided by SHOT [50] based on extrinsic point-wise features, or a few given landmarks used as initial anchor pairs which can be fixed or updated in later refinement, or by any other (fast but not necessary very accurate) methods. Then we start DIR which includes the following three simple steps: ① Choose anchor pairs from current correspondence using LMD criterion; ② Determine the spectral dimension and the corresponding functional map based on the selected anchor pairs; ③ Update the correspondence using the current functional map. In addition, we enforce two stopping criteria, the total number of iterations and the spectral dimension supported by anchor pairs reaches , whichever is satisfied first. Here are more detailed descriptions of each step.
Step 1: Selecting anchor pairs.
By setting a proper LMD threshold , the set of pairs are selected as anchor pairs from the current correspondence which will be used to guide next refinement. It is important to note that both the threshold and anchor pairs are updated in later refinement. By decreasing with iterations, the quality of anchor pairs is also improved.
Step 2: There are two components described as follows.
(1) Determining the proper spectral dimension based on anchor pairs. Given a set of anchor pairs, an important question is to find a proper spectral dimension that can be determined accurately and stably according to the distribution of the anchor pairs in spectral embedding. Due to possible degeneracy of the distribution, the dimension can be quite smaller than the number of anchor pairs. We use singular value decomposition (SVD) [51], a.k.a principal component analysis, to find the dimension well expanded by a set of anchor pairs in spectral domain.
| (6) |
We threshold the singular values to determine the proper dimension. One can use a simple thresholding strategy. In our implementation, we adopt a normalization strategy to make the threshold adaptive to the data and noise level. After normalizing all singular values by the mean of 10 largest singular values, the dimension cut is set at where the sum of ten consecutive normalized singular values is smaller than a threshold (0.1 for all our tests). We point out that since the spectral embedding is defined by each eigen-function of the LB operator, instead of the collectively spanned space, the accuracy and stability of each singular vectors is more relevant in our case. For example, perturbation analysis for SVD can be found in [31].
(2) Computing functional map based on anchor pairs. Once the proper spectral dimension, , is determined by the selected anchor pairs , we compute the functional map for dimensional spectral embedding only based on the anchor pairs as follows:
| (7) |
This restricted version to compute a functional map minimizes possible corruption from inaccurate correspondence and leads to a more accurate estimation of the functional map as discussed in the Section 3.1 and supplementary material. Meanwhile, it also reduces the computation cost.
Step 3: Construct the new correspondence. Using the functional map computed from selected anchor pairs in the properly enlarged spectral embedding space, a refined correspondence is constructed by solving the assignment problem (3), where a KNN search method is applied.
We summarize the full procedure in Algorithm 1.
Computation complexity The complexity for computing leading eigen-vectors of a sparse matrix corresponding to the discretized LB operator is . The complexity for checking LMD is since geodesic distance is only computed in a fixed neighborhood, e.g., first ring or second ring, at each point. To compute the functional map, the complexity of matrix multiplication is at most and SVD decomposition is at most since the number of anchor pairs is at most and the spectral dimension is at most which is prefixed and far less than . KNN search used to solve Equation (3) has a complexity of [52]. Hence, our method is of complexity altogether. It is still using other global features such as geodesic distance to anchor points since we limit the maximal number of anchor points (as the number of LB eigen-functions). The complexity of computing geodesic distance and solving the resulting assignment problem is still .
4 Discussion
In this section, we discuss other possible extensions of our approach and a few specific applications.
Combination of local and global features. For shape correspondence problem, an efficient and robust approach should use both local and global features. So far we have mainly talked about using spatial and spectral features, which are perfectly complementary in the sense of local and global information. Anchor pair selection by the LMD criterion is based on local spatial features while the spectral features are global. We would like to point out that the proposed strategy of DIR process can be extended to other combinations of appropriate local and global features in different applications. For examples, one may alternatively use Heat Kernel Signature [12], Wave Kernel Signature [4] or Geodesic Distance Signature (GDS) [54] as global features. For shapes with holes and boundaries, we choose GDS which is less sensitive to local mesh distortions and boundaries for most interior points. However, if accurate spectral information is available, taking advantage of the multi-scale representation in spectral embedding leads to better accuracy and efficiency according to our tests.
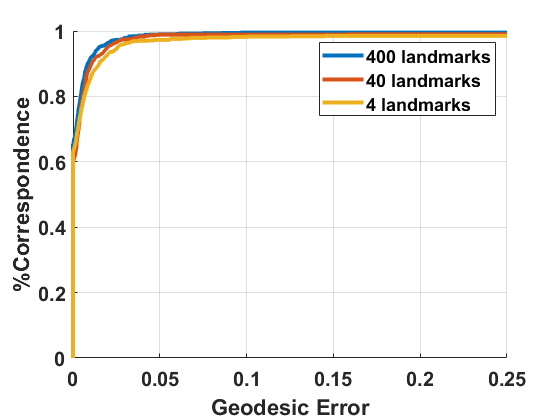
DIR with limited initial landmarks. In our previous discussion, the first collection of anchor pairs is selected from a given initial correspondence such as the one obtained from comparing SHOT features. Our method does enjoy the flexibility to incorporate given landmarks. This is applauded in applications like shape matching in the morphological study in medical imaging where landmarks could be annotated based on specific tasks [19]. Once a few human-annotated and required landmarks are given, which are taken as the initial anchor pairs and fixed in later iterations, DIR will converge to a stable solution. The fewer landmarks are provided, the more iterations are usually needed. The final convergence performance of our numerical tests, as shown in Figure 6, indicates that DIR can provide accurate correspondence based on only four landmarks and it is stable with respect to different initialization.
Matching of point clouds without mesh. In real applications, point clouds with well-constructed global triangulation is usually hard to obtain. For point clouds without global mesh, we use the local mesh method to compute the LB eigenvalues and LMD [26, 58]. DIR works well on matching raw point clouds as shown in section 5.
Patch/partial matching. Patch/partial matching often comes with difficulties due to artificial boundaries, different sizes and topological perturbations. Spectral information is either unavailable or unreliable to use. However, our local feature, LMD, is not affected by the above difficulties at interior points. By replacing spectral features with geodesic distance to anchor points, which is global and less sensitive to the above difficulties for most interior points, DIR can handle patch or partial matching well as shown in our numerical experiments.
5 Experiments
In this section, we conduct comprehensive experiments to evaluate the performance of our method on various benchmark data sets. In all experiments, no pre-processing, such as a low resolution model or pre-computing the geodesic distance matrix, is required in our algorithm. Raw point clouds (with or without meshes) are directly used. In our comparisons, all geodesic errors from existing methods are obtained from the associated error curve data appeared in the papers. Computation using ZoomOut is produced from the code on GitHub shared by the authors [34](3 to 150 spectral basis). All experiments using our methods are conducted in Matlab with 16GB RAM and Intel i7-6800k CPU.
Error Metric. We use the geodesic error as our error metric in most experiments. Suppose the constructed correspondence maps to while the true correspondence is is to , we measure the quality of our result by computing the geodesic error defined as , where is the geodesic diameter of .
Hyperparameters. We use the second ring neighborhood size for LMD criterion; maximum iteration number is 10 with the LMD threshold as . The initial correspondence is given by the KNN search result based on SHOT features [50]. These hyperparameters, especially the LMD, are not sensitive to different data sets. We use the same hyperparameters on TOSCA and SCAPE data sets. For SHREC’16 and patch matching, we set the maximum 800 anchor pairs served as the reference points for geodesic distance features.
TOSCA [9], SCAPE [3]. TOSCA data set consists of 76 shapes in 8 different categories ( human and animal shapes) with vertex numbers ranging from 4k to 50k. We present the results of our method using mesh structure with the maximal spectral dimension as 1000 and 500 respectively. We also apply our method using only point clouds (no mesh) with the maximal spectral dimension as 1000 (using local mesh method [26]). We perform the same experiments on SCAPE data set which has 72 shapes (12,500 vertices for each) of the same person with different poses.
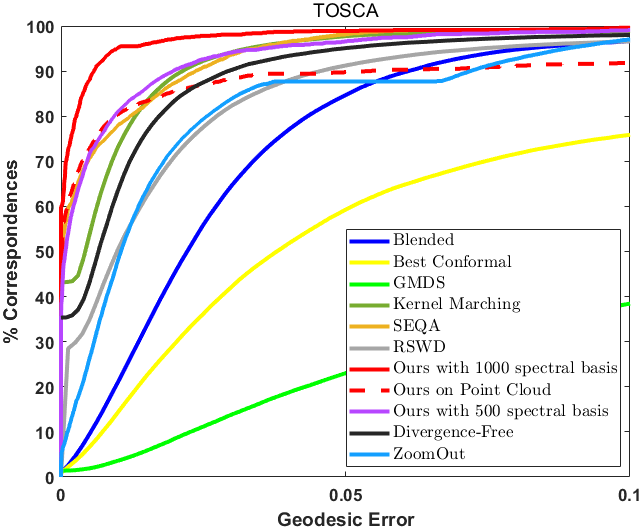
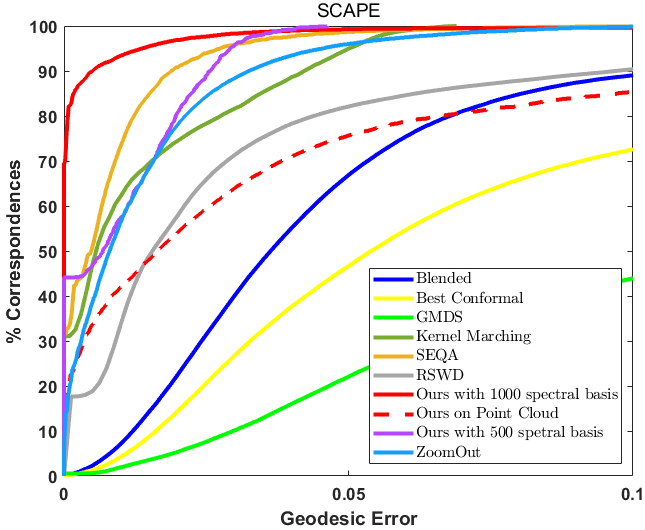
In Figure 3, We compare our method with the following methods: Blended [25], Best Conformal [25], GMDS [8], Kernel Marching [55], SEQA [58], RSWD [28], ZoomOut [34], Divergence-Free Shape Interpolation [17], SRFM [38] and BCICP [39]. Our method with 1000 spectral basis outperforms all methods, our method with 500 spectral basis outperforms almost all methods, and our method on purely point cloud inputs still achieves good performance.
Table 1 indicates the computation efficiency of our methods by showing the average run time on several examples from TOSCA including shapes with vertices ranging from 4k to 50k. CUP time of our method reports total time of all steps including computation of LB eigenfunctions. As discussed in Section 3.3, the complexity of our method is . But in practice, when computing shapes with more than 20,000 vertices, our computer suffers a computation speed slow-down from the vast RAM usage because of our limited RAM capacity. Hence, for Cat and David shape from TOSCA, the run time is higher than expected. Most state-of-the-art approaches have a computation complexity of and do not report run time for shapes over 10,000 vertices. Our method is very efficient compared with state-of-the-art methods which report computation time.
| Model | Wolf | Centaur | Horse | Cat | David | ||
| Number of Vertices | 4344 | 15768 | 19248 | 27894 | 52565 | ||
| SEQA (s) | 59 | 531 | 801 | 929 | 1681 | ||
| Kernel Matching (s) | 60 | NA | NA | NA | NA | ||
| ZoomOut(3-150 spectral basis) (s) | 25 | 277 | 449 | 1267 | 4312 | ||
| Consistent Shape Matching (s) | 483 | NA | 2118 | 3299 | NA | ||
|
36 | 144 | 191 | 474 | 1774 | ||
|
19 | 106 | 131 | 330 | 1301 |
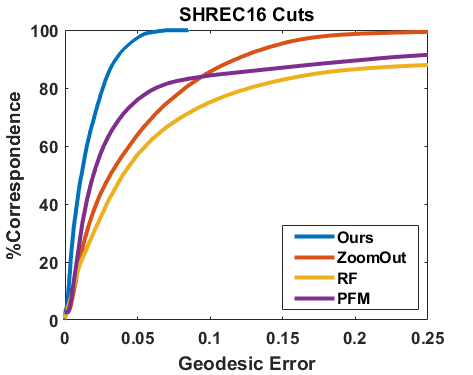
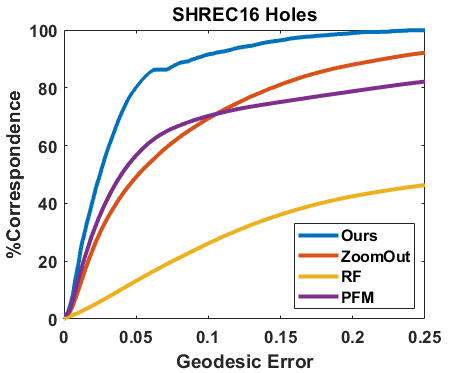
SHREC’16 [14] SHREC’16 Partial Correspondence benchmark data set consists of 8 types of isometric human or animal shapes in different poses with regular ‘cuts’ and irregular ‘holes’. We test our method by matching each partial shape to the corresponding full shape. Since spectral basis is sensitive to mesh ’cuts’ and ’holes’, we use geodesic distance to anchor points as global features. We still use SHOT for the initialization. In Figure 1, We compare our method with ZoomOut [34], Partial Functional Maps [42] and Random Forests [43]. The results show that our method is quite flexible and robust to handle shape matching for different scenarios. It again outperforms other state-of-the-art methods markedly and achieves high accuracy on this challenging data set.
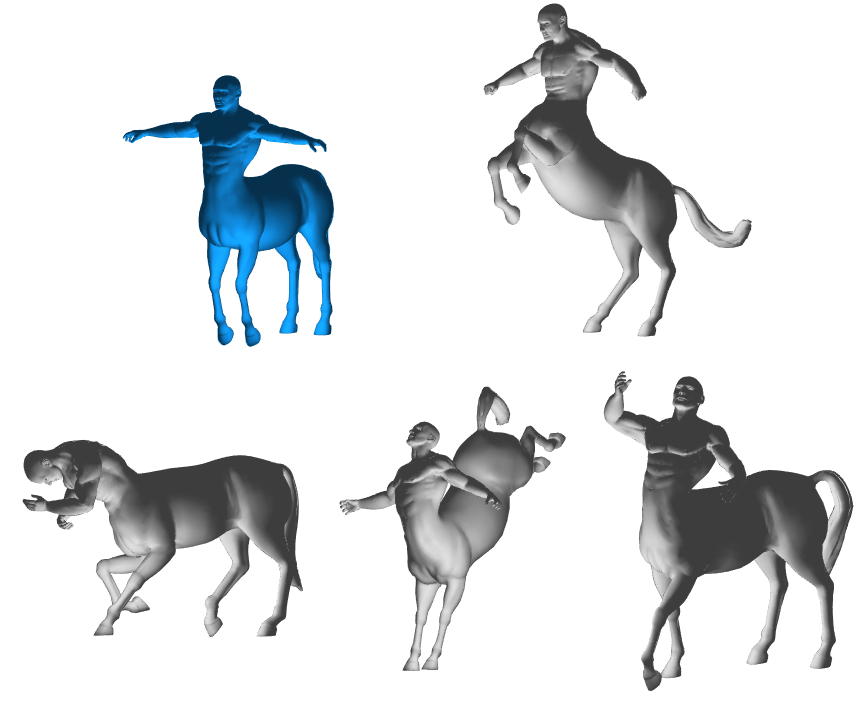
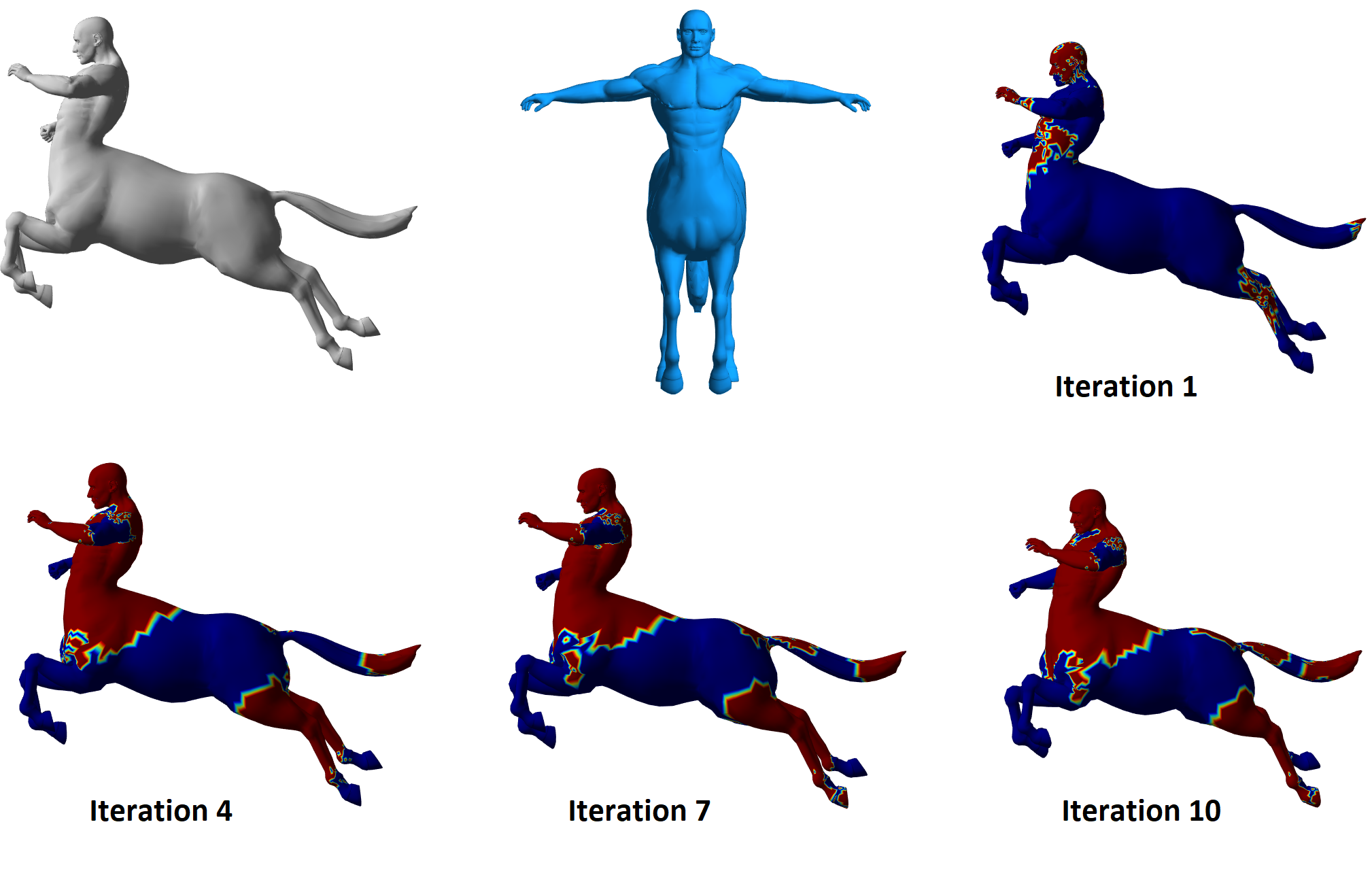
Patch Matching. Since there is no standard data set for patch matching, so instead we report several experiments using patches cut from TOSCA data set. The first case contains two examples with artificial boundaries, different sizes (partial patching) and topological changes simultaneously. In the first example, we take a portion of an arm (finger tips also removed) from one of two nearly isometric centaur shapes, and then map the partial arm onto the other entire centaur. In the second example, we map a body patch onto the whole shape. The original centaur is a closed mesh surface with no holes, while the arm and the body patch are not closed and have holes and boundaries. Our method performs quite well even for this challenging example as shown in Figure 4.
The second case is matching two patches containing both overlap and non-overlap parts. We match an arm without the hand to a portion of an arm with the hand, where forearm is the common part. Since there is no correspondence between the non-overlap parts, a post LMD test is added to prune out those points. The result is shown in Figure 5. Again our method performs quite well. These experiments indicate that our method is robust to size differences, artificial boundaries and topological changes.


Experiments Using Limited Landmarks. We select 4 pairs of centaur shapes from TOSCA, initialize our method with different number of randomly chosen landmark pairs (without using SHOT for initialization) and then plot the average geodesic error curve. These landmark pairs are fixed and always belong to our selected anchors pairs in later iterations. After different number of iterations, the final performance is illustrated in Figure 6. Even with four initial random landmarks, the performance is excellent although more iterations are needed. It shows stability and robustness of our method with respect to initial correspondence.
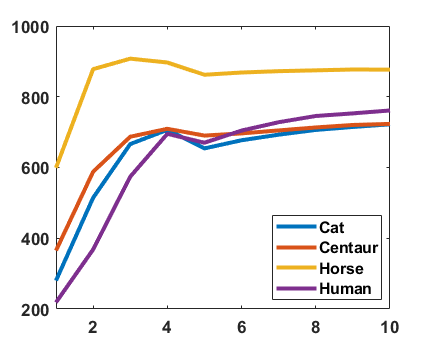
Growth of Anchor Pairs and Spectral Dimensions. One key feature of our method is the selection of well matched pairs used to determine spectral dimension and the corresponding functional map at next iteration in an automatic and data-adaptive way. A steady growth and improvement (by decreasing the mapping distortion threshold with iterations) of anchor pairs (updated in each iteration) means a steady growth of the spectral dimension and increase of resolution which leads to an effective and fast refinement of the correspondence. The left image in Figure 7 shows the average spectral dimensions for several class of shapes from TOSCA or SPACE data set. The right image in Figure 7 shows the growth pattern of anchor pairs. These indicate that our method can extract anchor pairs and increase spectral resolution in a steady and efficient way.
6 Conclusion
We propose a simple and efficient iterative refinement strategy utilizing dual features, spatial and spectral or local and global. By only relying on selected well-matched pairs to guide the next refinement, our proposed method combines complementary information in an optimal and data-adaptive way. Our method shows superior performance on extensive tests compared to other state-of-the-arts methods in terms of accuracy, efficiency and stability.
Acknowledgement
R. Lai is supported in part by an NSF Career Award DMS–1752934, and H. Zhao is supported by an NSF Award DMS-1821010.
References
- [1] Yonathan Aflalo, Alexander Bronstein, and Ron Kimmel. On convex relaxation of graph isomorphism. Proceedings of the National Academy of Sciences, 112(10):2942–2947, 2015.
- [2] Yonathan Aflalo, Anastasia Dubrovina, and Ron Kimmel. Spectral generalized multi-dimensional scaling. International Journal of Computer Vision, 118(3):380–392, 2016.
- [3] Dragomir Anguelov, Praveen Srinivasan, Hoi-Cheung Pang, Daphne Koller, Sebastian Thrun, and James Davis. The correlated correspondence algorithm for unsupervised registration of nonrigid surfaces. In Advances in neural information processing systems, pages 33–40, 2005.
- [4] Mathieu Aubry, Ulrich Schlickewei, and Daniel Cremers. The wave kernel signature: A quantum mechanical approach to shape analysis. In Computer Vision Workshops (ICCV Workshops), 2011 IEEE International Conference on, pages 1626–1633. IEEE, 2011.
- [5] Omri Azencot, Anastasia Dubrovina, and Leonidas Guibas. Consistent shape matching via coupled optimization. In Computer Graphics Forum, volume 38, pages 13–25. Wiley Online Library, 2019.
- [6] Pierre Bérard, Gérard Besson, and Sylvain Gallot. Embedding riemannian manifolds by their heat kernel. Geometric & Functional Analysis GAFA, 4(4):373–398, 1994.
- [7] Alex Bronstein, Michael Bronstein, and Ron Kimmel. Generalized multidimensional scaling: a framework for isometry-invariant partial surface matching. Proceedings of the National Academy of Sciences, 103(5):1168–1172, 2006.
- [8] Alexander M Bronstein, Michael M Bronstein, and Ron Kimmel. Generalized multidimensional scaling: a framework for isometry-invariant partial surface matching. Proceedings of the National Academy of Sciences, 103(5):1168–1172, 2006.
- [9] Alexander M Bronstein, Michael M Bronstein, and Ron Kimmel. Numerical geometry of non-rigid shapes. Springer Science & Business Media, 2008.
- [10] Alexander M Bronstein, Michael M Bronstein, Ron Kimmel, Mona Mahmoudi, and Guillermo Sapiro. A gromov-hausdorff framework with diffusion geometry for topologically-robust non-rigid shape matching. International Journal of Computer Vision, 89(2-3):266–286, 2010.
- [11] M. M. Bronstein and I. Kokkinos. Scale-invariant heat kernel signatures for non-rigid shape recognition. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 1704–1711, 2010.
- [12] Michael M Bronstein and Iasonas Kokkinos. Scale-invariant heat kernel signatures for non-rigid shape recognition. In 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pages 1704–1711. IEEE, 2010.
- [13] Qifeng Chen and Vladlen Koltun. Robust nonrigid registration by convex optimization. In Proceedings of the IEEE International Conference on Computer Vision, pages 2039–2047, 2015.
- [14] Luca Cosmo, Emanuele Rodolà, Jonathan Masci, Andrea Torsello, and Michael Bronstein. Matching deformable objects in clutter. In 3D Vision (3DV), 2016 Fourth International Conference on, pages 1–10. IEEE, 2016.
- [15] Anastasia Dubrovina and Ron Kimmel. Approximately isometric shape correspondence by matching pointwise spectral features and global geodesic structures. Advances in Adaptive Data Analysis, 3(01n02):203–228, 2011.
- [16] Nadav Dym, Haggai Maron, and Yaron Lipman. Ds++: A flexible, scalable and provably tight relaxation for matching problems. arXiv preprint arXiv:1705.06148, 2017.
- [17] Marvin Eisenberger, Zorah Lähner, and Daniel Cremers. Divergence-free shape interpolation and correspondence. arXiv preprint arXiv:1806.10417, 2018.
- [18] Andrea Gasparetto, Luca Cosmo, Emanuele Rodola, Michael Bronstein, and Andrea Torsello. Spatial maps: From low rank spectral to sparse spatial functional representations. In 2017 International Conference on 3D Vision (3DV), pages 477–485. IEEE, 2017.
- [19] Xianfeng Gu, Yalin Wang, Tony F Chan, Paul M Thompson, and Shing-Tung Yau. Genus zero surface conformal mapping and its application to brain surface mapping. IEEE transactions on medical imaging, 23(8):949–958, 2004.
- [20] Stefan Gumhold, Xinlong Wang, and Rob S MacLeod. Feature extraction from point clouds. In IMR. Citeseer, 2001.
- [21] Li Han, Shuning Liu, Bing Yu, Shengsi Xu, and Rui Xiang. Orientation-preserving spectral correspondence for 3d shape analysis. Journal of Imaging Science and Technology, 2019.
- [22] Varun Jain and Hao Zhang. Robust 3d shape correspondence in the spectral domain. In Shape Modeling and Applications, 2006. SMI 2006. IEEE International Conference on, pages 19–19. IEEE, 2006.
- [23] Varun Jain, Hao Zhang, and Oliver van Kaick. Non-rigid spectral correspondence of triangle meshes. International Journal of Shape Modeling, 13(01):101–124, 2007.
- [24] Itay Kezurer, Shahar Z Kovalsky, Ronen Basri, and Yaron Lipman. Tight relaxation of quadratic matching. In Computer Graphics Forum, volume 34, pages 115–128. Wiley Online Library, 2015.
- [25] Vladimir G Kim, Yaron Lipman, and Thomas Funkhouser. Blended intrinsic maps. In ACM Transactions on Graphics (TOG), volume 30, page 79. ACM, 2011.
- [26] Rongjie Lai, Jiang Liang, and Hongkai Zhao. A local mesh method for solving pdes on point clouds. Inverse Problems & Imaging, 7(3), 2013.
- [27] Rongjie Lai, Yonggang Shi, Kevin Scheibel, Scott Fears, Roger Woods, Arthur W Toga, and Tony F Chan. Metric-induced optimal embedding for intrinsic 3d shape analysis. In 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pages 2871–2878. IEEE, 2010.
- [28] Rongjie Lai and Hongkai Zhao. Multiscale nonrigid point cloud registration using rotation-invariant sliced-wasserstein distance via laplace–beltrami eigenmap. SIAM Journal on Imaging Sciences, 10(2):449–483, 2017.
- [29] Marius Leordeanu and Martial Hebert. A spectral technique for correspondence problems using pairwise constraints. In Tenth IEEE International Conference on Computer Vision (ICCV’05) Volume 1, volume 2, pages 1482–1489. IEEE, 2005.
- [30] B. Levy. Laplace-beltrami eigenfunctions: Towards an algorithm that understands geometry. IEEE International Conference on Shape Modeling and Applications, invited talk, 2006.
- [31] Jun Liu, Xiangqian Liu, and Xiaoli Ma. First-order perturbation analysis of singular vectors in singular value decomposition. IEEE Transactions on Signal Processing, 56(7):3044–3049, 2008.
- [32] Xiuwen Liu, Arturo Donate, Matthew Jemison, and Washington Mio. Kernel functions for robust 3d surface registration with spectral embeddings. In 2008 19th International Conference on Pattern Recognition, pages 1–4. IEEE, 2008.
- [33] Diana Mateus, Radu Horaud, David Knossow, Fabio Cuzzolin, and Edmond Boyer. Articulated shape matching using laplacian eigenfunctions and unsupervised point registration. In Computer Vision and Pattern Recognition, 2008. CVPR 2008. IEEE Conference on, pages 1–8. IEEE, 2008.
- [34] Simone Melzi, Jing Ren, Emanuele Rodolà, Abhishek Sharma, Peter Wonka, and Maks Ovsjanikov. Zoomout: Spectral upsampling for efficient shape correspondence. ACM Transactions on Graphics (TOG), 38(6):155, 2019.
- [35] Maks Ovsjanikov, Mirela Ben-Chen, Justin Solomon, Adrian Butscher, and Leonidas Guibas. Functional maps: a flexible representation of maps between shapes. ACM Transactions on Graphics (TOG), 31(4):30:1–30:11, 2012.
- [36] Maks Ovsjanikov, Quentin Merigot, Facundo Memoli, and Leonidas Guibas. One point isometric matching with the heat kernel. CGF, 29(5):1555–1564, 2010.
- [37] Ulrich Pinkall and Konrad Polthier. Computing Discrete Minimal Surfaces and their Conjugates. Experimental mathematics, 2(1):15–36, 1993.
- [38] Jing Ren, Mikhail Panine, Peter Wonka, and Maks Ovsjanikov. Structured regularization of functional map computations. In Computer Graphics Forum, volume 38, pages 39–53. Wiley Online Library, 2019.
- [39] Jing Ren, Adrien Poulenard, Peter Wonka, and Maks Ovsjanikov. Continuous and orientation-preserving correspondences via functional maps. ACM Transactions on Graphics (TOG), 37(6), 2018.
- [40] M. Reuter, F.E. Wolter, and N. Peinecke. Laplace-Beltrami spectra as Shape-DNA of surfaces and solids. Computer-Aided Design, 38:342–366, 2006.
- [41] Emanuele Rodola, Alex M Bronstein, Andrea Albarelli, Filippo Bergamasco, and Andrea Torsello. A game-theoretic approach to deformable shape matching. In 2012 IEEE Conference on Computer Vision and Pattern Recognition, pages 182–189. IEEE, 2012.
- [42] Emanuele Rodolà, Luca Cosmo, Michael Bronstein, Andrea Torsello, and Daniel Cremers. Partial functional correspondence. Computer Graphics Forum, 36(1):222–236, 2017.
- [43] Emanuele Rodolà, Samuel Rota Bulò, Thomas Windheuser, Matthias Vestner, and Daniel Cremers. Dense non-rigid shape correspondence using random forests. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 4177–4184. IEEE, 2014.
- [44] Raif M Rustamov. Laplace-beltrami eigenfunctions for deformation invariant shape representation. In Proceedings of the fifth Eurographics symposium on Geometry processing, pages 225–233. Eurographics Association, 2007.
- [45] Stefan C Schonsheck, Michael M Bronstein, and Rongjie Lai. Nonisometric surface registration via conformal laplace-beltrami basis pursuit. arXiv preprint arXiv:1809.07399, 2018.
- [46] Alon Shtern and Ron Kimmel. Iterative closest spectral kernel maps. In 2014 2nd International Conference on 3D Vision, volume 1, pages 499–505. IEEE, 2014.
- [47] S Skiena. Involutions. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica, pages 32–33, 1990.
- [48] Jian Sun, Maks Ovsjanikov, and Leonidas Guibas. A concise and provably informative multi-scale signature based on heat diffusion. Computer graphics forum, 28(5):1383–1392, 2009.
- [49] Art Tevs, Alexander Berner, Michael Wand, Ivo Ihrke, and H-P Seidel. Intrinsic shape matching by planned landmark sampling. In Computer Graphics Forum, volume 30, pages 543–552. Wiley Online Library, 2011.
- [50] Federico Tombari, Samuele Salti, and Luigi Di Stefano. Unique signatures of histograms for local surface description. In European conference on computer vision, pages 356–369. Springer, 2010.
- [51] Lloyd N Trefethen and David Bau III. Numerical linear algebra, volume 50. Siam, 1997.
- [52] Pravin M Vaidya. An o (n logn) algorithm for the all-nearest-neighbors problem. Discrete & Computational Geometry, 4(2):101–115, 1989.
- [53] B. Vallet and B. Levy. Spectral geometry processing with manifold harmonics. Computer Graphics Forum (Proceedings Eurographics), 2008.
- [54] Oliver Van Kaick, Hao Zhang, Ghassan Hamarneh, and Daniel Cohen-Or. A survey on shape correspondence. Computer Graphics Forum, 30(6):1681–1707, 2011.
- [55] Matthias Vestner, Zorah Lähner, Amit Boyarski, Or Litany, Ron Slossberg, Tal Remez, Emanuele Rodolà, Alex Bronstein, Michael Bronstein, and Ron Kimmel. Efficient deformable shape correspondence via kernel matching. In 3D Vision (3DV), 2017 International Conference on, pages 517–526. IEEE, 2017.
- [56] Matthias Vestner, Roee Litman, Emanuele Rodolà, Alex Bronstein, and Daniel Cremers. Product manifold filter: Non-rigid shape correspondence via kernel density estimation in the product space. In Proc. CVPR, pages 6681–6690, 2017.
- [57] Chaohui Wang, Michael M Bronstein, Alexander M Bronstein, and Nikos Paragios. Discrete minimum distortion correspondence problems for non-rigid shape matching. In International Conference on Scale Space and Variational Methods in Computer Vision, pages 580–591. Springer, 2011.
- [58] Rui Xiang, Rongjie Lai, and Hongkai Zhao. Efficient and robust shape correspondence via sparsity-enforced quadratic assignment. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 9513–9522, 2020.
Appendix A The Effect of Correspondence Error on Spectral Alignment
Proof of Theorem 1 We first show that a necessary condition for is that permutation is an involution, i.e. symmetric matrix.
Since , we have . It is clear that . Assume that there is a SVD decomposition . Then we have a SVD decomposition because is an orthonormal matrix. Therefore, . This yields
Thus, implies . This leads to is symmetric. From the fact that there are permutation matrix of size and there are symmetric permutation matrix of size [47]. This concludes the proof.
One obvious observation is that decreases rapidly as grows. For example, when , . However, to give a more quantitative characterization of the perturbation for an arbitrary shuffling is difficult since it depends not only on but also on and . Instead, we conduct a few numerical experiments to demonstrate how an inaccurate correspondence will affect the correlation matrix , which is the essential information to align spectral basis, e.g., functional map, between two shapes.
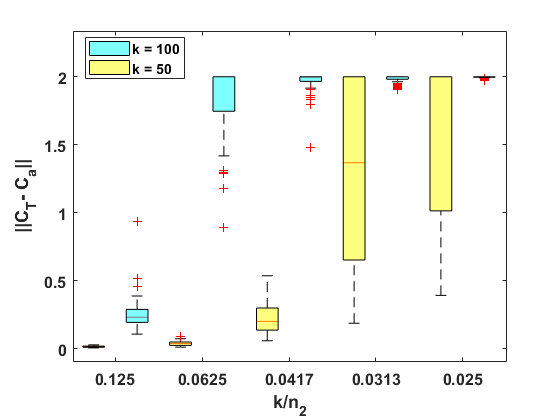
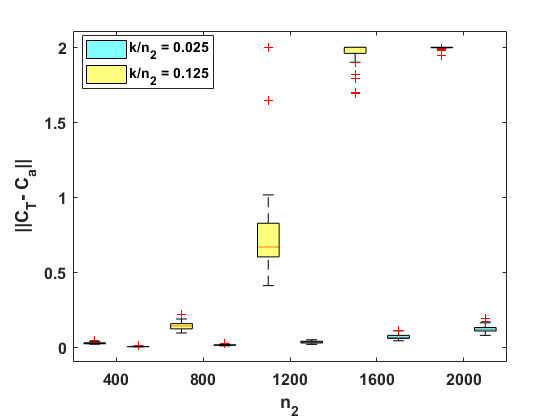
In our experiments, , where is the total number of points and is the spectral dimension. We map a human shape with 12,500 vertices to itself, which is a perfect isometric shape correspondence problem with identity map as the ground truth. Theoretically, , since both and are orthonormal. The first experiment tests the behavior of with respect to the ratio of for two fixed spectral dimension, and ; second experiments tests the behavior of with respect to for two fixed ratio. A random permutation is imposed on to compute , and we independently run 50 trails for each parameter combination. Box-plots are used to illustrate the statistics of our computation in Figure 8. The experiments indicate that using inaccurate correspondences at the current step will introduce error to the estimation of functional map at the next step and the error can be quite significant (as big as the worst case, ). This could cause a failure or slow convergence for an iterative refinement strategy.

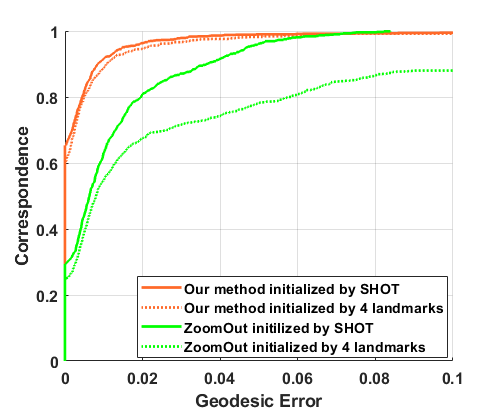
We further test a real example on one pair of shapes from TOSCA data set using ZoomOut [34], which is a simple iterative refinement method based on functional map in spectral domain. A fixed increment of spectral dimension is pre-specified for each iteration. Due to the use of current correspondence at all points to construct the functional map, the following iterative refinements may not lead to a satisfactory result in the end. In this test, we use 1000 LB eigen-functions for ZoomOut (and our method) with two different initial setups: (1) correspondence provided by SHOT, or (2) 4 given landmarks. For ZoomOut, we first compute a functional map for the first 4 spectral modes from the initial correspondence and then use the code provided by the authors on GitHub to run the experiment. Test results are plotted in Figure 9. These experiment further verify our analysis on possible issues using simple iterative spectral refinement without filtering out bad correspondences.