A fixed-time inverse-free dynamical system for solving the system of absolute value equations
Abstract: In this paper, an inverse-free dynamical system with fixed-time convergence is presented to solve the system of absolute value equations (AVEs). Under a mild condition, it is proved that the solution of the proposed dynamical system converges to the solution of the AVEs. Moreover, in contrast to the existing inverse-free dynamical system [2], a conservative settling-time of the proposed method is given. Numerical simulations illustrate the effectiveness of the new method.
Keywords: Absolute value equation; Fixed-time convergence; Inverse-free; Dynamical system; Numerical simulation.
1 Introduction
To solve the system of absolute value equations (AVEs) is to find an such that
| (1.1) |
where , and represents the componentwise absolute value of the unknown vector . The AVEs (1.1) is a special case of the generalized absolute value equations (GAVEs)
| (1.2) |
where , and . The GAVEs (1.2) is originally introduced by Rohn in [23] and further investigated in [14, 21, 6] and the references therein. Over the past two decades, the AVEs (1.1) has been widely studied in the optimization community because of its relevance to many mathematical programming problems, such as the linear complementarity problem (LCP) [21, 14, 16, 8], the horizontal LCP (HLCP) [19], the generalized LCP (GLCP) [16] and others, see e.g. [21, 16, 15] and the references therein. In addition, the AVEs (1.1) is closely related to the system of linear interval equations [22].
In general, it has been shown in [14] that solving the GAVEs (1.2) is NP-hard. Moreover, if the GAVEs (1.2) is solvable, it follows from [21] that checking whether the GAVEs (1.2) has a unique solution or multiple solutions is NP-complete. Throughout this paper, we assume that is invertible and , and thus the AVEs (1.1) has a unique solution for any [16]. For more discussions about the unique solvability of the AVEs (1.1), see e.g. [28, 19, 24, 27, 7] and the references therein.
In this paper, we focus on further studying the continuous solution schemes for solving the AVEs (1.1). We briefly introduce some existing works in the following. To this end, we recall two reformulations of the AVEs (1.1).
The AVEs (1.1) is equivalent with the following GLCP [16]:
| (1.3) |
Furthermore, if is not an eigenvalue of , then the AVEs (1.1) can be reformulated as the following LCP [16]:
| (1.4) |
with
| (1.5) |
It follows from (1.4) and (1.5) that if is a solution of the LCP (1.4), then is a solution of the AVEs (1.1).
By utilizing the reformulation (1.4) with (1.5) of the AVEs (1.1), some dynamical systems are constructed to solve the AVEs (1.1). For instance, the following dynamical model
is used by Mansoori, Eshaghnezhad and Effati [18] to solve the AVEs (1.1), where , , and
Huang and Cui [10] use the following dynamical system
to solve the AVEs (1.1) and Mansoori and Erfanian [17] suggest the following dynamical system
to solve the AVEs (1.1), where is the convergence rate. Recently, Ju, Li, Han and He [11] develop a fixed-time dynamical system for solving the AVEs (1.1). Based on the relation with HLCP, the following dynamical system is proposed in [4] to solve AVEs (1.1):
where is a scaling constant. Obviously, all of the above mentioned dynamical systems involve the inversion of the matrix or . In order to avoid the inversion, based on (1.3), Chen, Yang, Yu and Han [2] develop the following inverse-free dynamical system
| (1.6) |
where is the convergence rate parameter. The dynamical system (1.6) can trace back to [29, 13, 9, 3]. Subsequently, an inertial version of (1.6) is developed in [31]. Other inverse-free dynamical system appears in [25, 26, 30], in which the smoothing technique is used.
It is known that the finite-time convergence proposed in [1] is of practical interests than the classic asymptotical stability or exponential stability over infinite time [11]. To overcome the limitation that the settling-time of the finite-time model is initial condition dependent, the concept of the so-called fixed-time convergence [20] is developed. Inspired by the works of [2, 11], we will develop a fixed-time inverse-free dynamical system for solving the AVEs (1.1). The main features of our method can be summarized as follows.
- (a)
-
(b)
Comparing with the method proposed in [11], the proposed method is inverse-free.
- (c)
- (d)
The rest of this paper is organized as follows. In section 2 we state a few basic results on the AVEs (1.1) and the autonomous system, relevant to our later developments. The fixed-time inverse-free dynamical system to solve the AVEs (1.1) is developed in section 3 and its convergence analysis is also given there. Numerical simulations are given in section 4. Conclusions are made in section 5.
Notation. We use to denote the set of all real matrices and . We use to denote the nonnegative reals. is the identity matrix with suitable dimension. denotes absolute value for real scalar. The transposition of a matrix or vector is denoted by . The inner product of two vectors in is defined as and denotes the -norm of vector . denotes the spectral norm of and is defined by the formula . The smallest singular value and the smallest eigenvalue of are denoted by and , respectively. denotes a matrix that has as the subdiagonal, main diagonal and superdiagonal entries in the matrix, respectively. The projection mapping from onto , denoted by , is defined as .
2 Preliminaries
In this section, we collect a few important results on the autonomous system and the AVEs (1.1), which lay the foundation of our later arguments.
Before talking something about the autonomous system, we give the definition of Lipschitz continuity.
Definition 2.1.
The function is said to be Lipschitz continuous with Lipschitz constant if
Consider the autonomous system
| (2.1) |
where is a function from to . Throughout this paper, denote the solution of (2.1) determined by the initial value condition .
Lemma 2.1.
([12]) Assume that is a continuous function, then for arbitrary , there exists a local solution for some . Furthermore, if is locally Lipschitz continuous at , then the solution is unique; and if is Lipschitz continuous in , then can be extended to .
Definition 2.2.
Lemma 2.2.
Definition 2.3.
Definition 2.4.
Lemma 2.3.
Before ending this section, we will give some properties of the AVEs (1.1).
3 The new dynamical system and its convergence analysis
In this section, inspired by the works of [2, 11], we present a fixed-time inverse-free dynamical system for solving the AVEs (1.1).
The developed fixed-time inverse-free dynamical system is as follows:
| (3.1) |
where , , and .
Theorem 3.1.
Proof.
If is an equilibrium point of (3.1), then
Since is invertible, the above equation implies that
from which we have
both of which mean that is a solution of the AVEs (1.1).
The other direction is trivial. ∎
Lemma 3.1.
Theorem 3.2.
For a given initial value , there exists a unique solution for the dynamical system (3.1).
Now we are in the position to explore the convergence of the proposed model (3.1).
Theorem 3.3.
Proof.
Remark 3.1.
It follows from [32] that the smaller settling-time often implies the faster convergent rate of a given fixed-time dynamical system. Hence, it concludes from (3.2), (3.3) and (3.4) that the larger , or is, the smaller the upper bound of the settling-time or the faster convergence rate of the dynamical system (3.1) is. In addition, is also dependent on the parameters and . See the next section for more details.
4 Numerical simulations
In this section, we will present one example to illustrate the effectiveness of the proposed method. All experiments are implemented in MATLAB R2018b with a machine precision on a PC Windows 10 operating system with an Intel i7-9700 CPU and 8GB RAM. The ODE solver used is “ode23”. Concretely, the MATLAB expression
is used, which integrates the system of differential equations from to with . Here, “odefun” is a function handle.
Example 4.1 ([5]).
In this example, we have and thus the AVEs (1.1) has a unique solution for any . Equivalently, the dynamical model (3.1) has a unique equilibrium point and it is globally fixed-time stable.
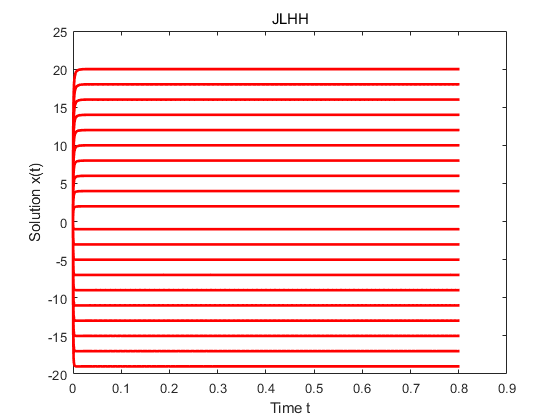
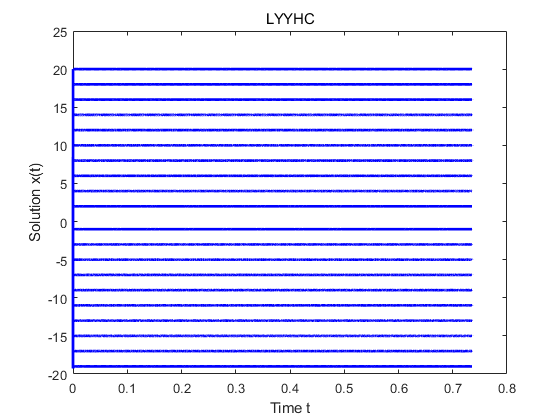
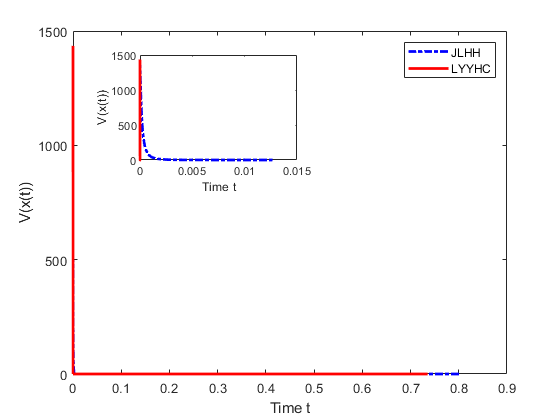
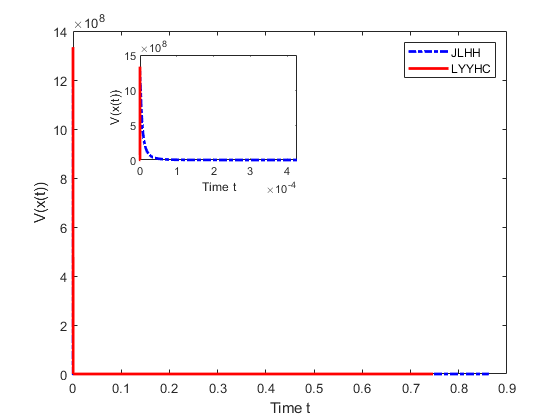
Since we are interested in the fixed-time stable dynamical systems, in the first stage, we only compare our method (denoted by ‘LYYHC’) with the method (denoted by ‘JLHH’) proposed in [11]. For both methods, we set , , . For LYYHC, and For JLHH, , is selected such that and . When , we have and numerical simulations are shown in Figure 1 and Figure 2. When , we have and numerical simulations are shown in Figure 2. Under the setting of these parameters, numerical results show that LYYHC is superior to JLHH.
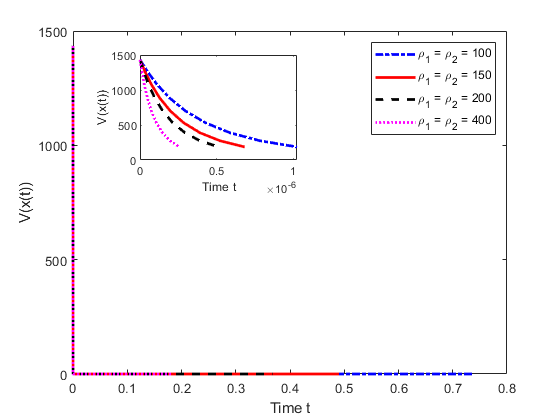
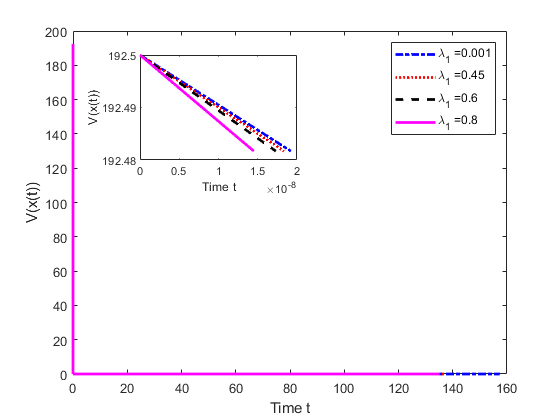
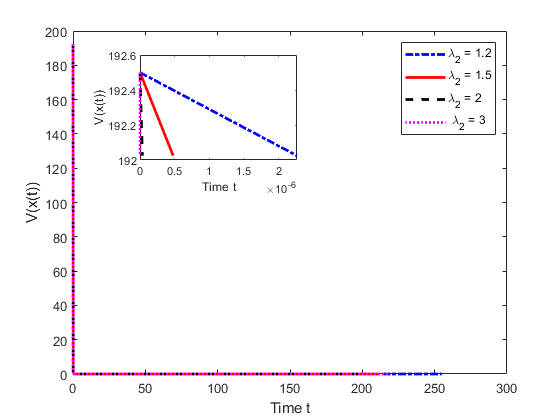
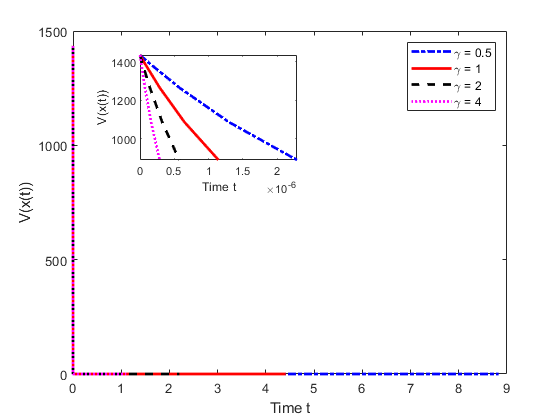
In the second stage, we show the influence of the tunable parameters for LYYHC. Firstly, we fix . Secondly, we freeze . Thirdly, we fix . Finally, we set and alter . Numerical results are shown in Figure 3 and Table 1, for this example, from which we can observe that the settling-time of LYYHC is decreasing with increased value of parameters . However, the influence of the parameters and on or the convergence rate of (3.1) is more complicated.
|
|
|
|
|
|
|
|
|
5 Conclusion
In this paper, a fixed-time dynamical system is proposed to solve the AVEs (1.1). Theoretical results show that the presented model is globally convergent and has a conservative settling-time. Numerical comparison with the method proposed in [11] shows that our method is preferred, at least in the sense that our method is inverse-free.
References
- [1] S. P. Bhat, D. S. Bernstein. Finite-time stability of continuous autonomous ststems, SIAM J. Control Optim., 38: 751–766, 2000.
- [2] C.-R. Chen, Y.-N. Yang, D.-M. Yu, D.-R. Han. An inverse-free dynamical system for solving the absolute value equations, Appl. Numer. Math., 168: 170–181, 2021.
- [3] X.-B. Gao. A neural network for a class of extended linear variational inequalities, Chin. J. Electron., 10: 471–475, 2001.
- [4] X.-B. Gao, J. Wang. Analysis and application of a one-layer neural network for solving horizontal linear complementarity problems, Int. J. Conput. Int. Sys., 7: 724–732, 2014.
- [5] P. Guo, S.-L Wu, C.-X Li. On the SOR-like iteration method for solving absolute value equations, Appl. Math. Lett., 97: 107–113, 2019.
- [6] M. Hladík. Bounds for the solutions of absolute value equations, Comput. Optim. Appl., 69: 243–266, 2018.
- [7] M. Hladík, H. Moosaei. Some notes on the solvability conditions for absolute value equations, Optim. Lett., 2022. https://doi.org/10.1007/s11590-022-01900-x.
- [8] S.-L. Hu, Z.-H. Huang. A note on absolute value equations, Optim. Lett., 4: 417–424, 2010.
- [9] X.-L. Hu, J. Wang. A recurrent neural network for solving a class of general variational inequalities, IEEE Trans. Syst., Man, Cybern. B, Cybern., 37: 528–539, 2007.
- [10] X.-J. Huang, B.-T. Cui. Neural network-based method for solving absolute value equations, ICIC-EL, 11: 853–861, 2017.
- [11] X.-X. Ju, C.-D. Li, X. Han, X. He. Neurodynamic network for absolute value equations: A fixed-time convergence technique, IEEE T. Circuits-II, 69: 1807–1811, 2022.
- [12] H.K. Khalil. Nonlinear Systems, Prentice-Hall, Michigan, NJ, 1996.
- [13] Q.-S. Liu, J.-D. Cao. A recurrent neural network based on projection operator for extended general variational inequalities, IEEE Trans. Syst., Man, Cybern. B, Cybern., 40: 928–938, 2010.
- [14] O.L. Mangasarian. Absolute value programming, Comput. Optim. Appl., 36: 43–53, 2007.
- [15] O.L. Mangasarian. Knapsack feasibility as an absolute value equation solvable by successive linear programming, Optim. Lett., 3: 161–171, 2009.
- [16] O.L. Mangasarian, R.R. Meyer. Absolute value equations, Linear Algebra Appl., 419: 359–367, 2006.
- [17] A. Mansoori, M. Erfanian. A dynamic model to solve the absolute value equations, J. Comput. Appl. Math., 333: 28–35, 2018.
- [18] A. Mansoori, M. Eshaghnezhad, S. Effati. An efficient neural network model for solving the absolute value equations, IEEE T. Circuits-II, 65: 391–395, 2017.
- [19] F. Mezzadri. On the solution of general absolute value equations, Appl. Math. Lett., 107: 106462, 2020.
- [20] A. Polyakov. Nonlinear feedback design for fixed-time stabilization of linear control systems, IEEE Trans. Autom. Control, 57: 2106–2110, 2011.
- [21] O. Prokopyev. On equivalent reformulations for absolute value equations, Comput. Optim. Appl., 44: 363–372, 2009.
- [22] J. Rohn. Systems of linear interval equations, Linear Algebra Appl., 126: 39–78, 1989.
- [23] J. Rohn. A theorem of the alternatives for the equation , Linear Multilinear Algebra, 52: 421–426, 2004.
- [24] J. Rohn, V. Hooshyarbakhsh, R. Farhadsefat. An iterative method for solving absolute value equations and sufficient conditions for unique solvability, Optim. Lett., 8: 35–44, 2014.
- [25] B. Saheya, C. T. Nguyen, J.-S. Chen. Neural network based on systematically generated smoothing functions for absolute value equation, J. Appl. Math. Comput., 61: 533–558, 2019.
- [26] F.-R. Wang, Z.-S. Yu, C. Gao. A smoothing neural network algorithm for absolute value equations, Engineering, 7: 567–576, 2015.
- [27] S.-L. Wu, P. Guo. On the unique solvability of the absolute value equation, J. Optim. Theory Appl., 169: 705–712, 2016.
- [28] S.-L. Wu, C.-X. Li. The unique solution of the absolute value equations, Appl. Math. Lett., 76: 195–200, 2018.
- [29] Y. Xia, J. Wang. A general projection neural network for solving monotone variational inequalities and related optimization problems, IEEE Trans. Neural Netw., 15: 318–328, 2004.
- [30] L.-Q. Yong. Neural network method for absolute value equation and linear complementarity problem, Journal of Shaanxi University of Technology (Natural Science Edition), 36: 72–81, 2020 (in Chinese).
- [31] D.-M. Yu, C.-R. Chen, Y.-N. Yang, D.-R. Han. An inertial inverse-free dynamical system for solving absolute value equations, J. Ind. Manag. Optim., 2022. doi:10.3934/jimo.2022055.
- [32] Z. Zuo, Q.-L. Han, B. Ning, X. Ge, X.-M. Zhang. An overview of recent advances in fixed-time cooperative control of multiagent systems, IEEE Trans. Ind. Informat., 14: 2322–2334, 2018.