A Fundamental Analysis of the Impact on Traffic Assignment
by Toll System of Electric Road System

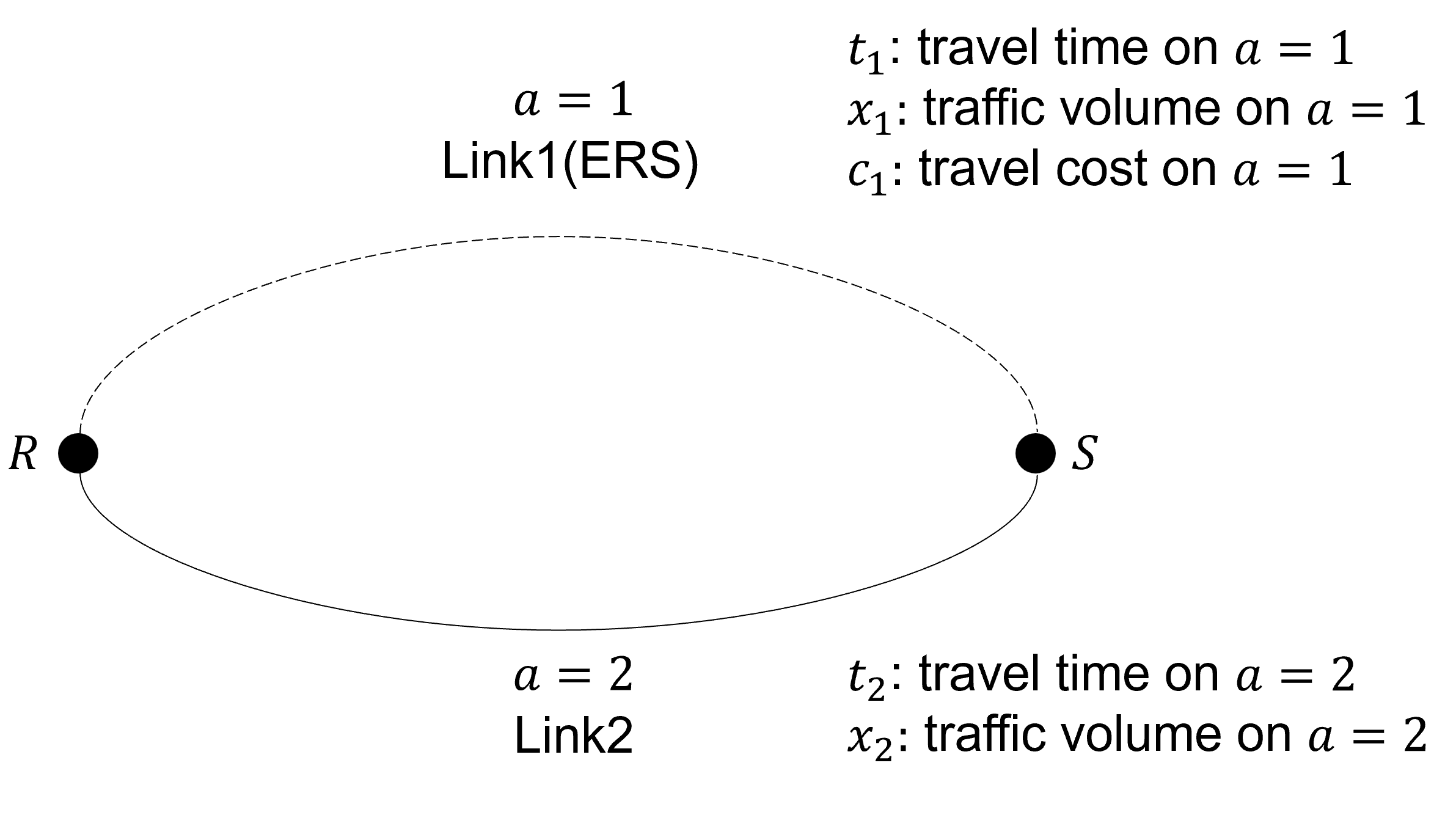
$\mathcal{D}$ and $\mathcal{O}$ represent a set of DWPT-EVs and OTHER-Vs, respectively. Total number of vehicles is denoted as $N$ and DWPT-ratio as $r,\ 0<r<1$; the number of DWPT-EVs is $rN$. DWPT-EV’s traffic volume on $a$ is denoted as $x_{a}^{D}$, and Other-V’s traffic volume on $a$ as $x_{a}^{O}$.

Then, some properties of DWPT-EVs are assumed as follows.

• •

  Battery capacity is represented in units of electric energy (e.g., [kWh]), which is the product of electric power and time.

• •

  The amount of battery consumed by a DWPT while driving is calculated by dividing the distance traveled (e.g., [km]) by the electric cost consumption (e.g., [km/kWh]). The amount a DWPT can charge while driving on the ERS is calculated by multiplying the travel time, $t$ (e.g., [h]), by the output of the ERS, $W$ (e.g., [kW]).

• •

  State of charge (SoC) is defined as the ratio of the remaining battery level to the battery capacity.

• •

  For simplicity, $i\in\mathcal{D}$ is always charged while driving on ERS.

Each vehicle deterministically chooses one of the links (i.e., $a=1$ or $2$) to maximize its utility as in a deterministic user equilibrium assignment. The utility functions of a vehicle are described by the weighted sum of the following three components.

1. i)

   Travel time disutility.
   Travel time on link $a$, $t_{a}$, is described by a monotonically increasing function of traffic volume on link $a$, $x_{a}$ (e.g., The Bureau of Public Roads (BPR) function).

2. ii)

   Travel cost disutility.
   Travel cost on link $a$ is denoted as $c_{a}$. Only $c_{1}$ in fixed-toll system is defined in this paper.

3. iii)

   Charging utility.
   This is only applied to DWPT-EVs. The more electicity a DWPT-EV $i$ can charge, the larger this utility is. We denote SoC of $i$ at $R$ as $s_{i}$ and assume $0<s_{i}<1$ for simplicity. Then, we model this utility as $(1/s_{i}-1)$.

In this system, all vehicles use ERS for free. This means that ERS is built and operated by taxes. The utility functions are defined as Eqs.(1–4).

Here, $V_{a,i}^{D}$ and $V_{a,j}^{O}$ represent the utility of $i\in\mathcal{D}$ and $j\in\mathcal{O}$ to choose link $a$, respectively. $\beta_{t}$ and $\beta_{s}$ are the parameters of travel time disutility and charging utility, respectively. $\beta_{t}<0$ and $\beta_{s}>0$ are assumed.

In this system, vehicles can use ERS for a fixed toll of $c_{1}=C$ (constant). In particular, we consider that only $i\in\mathcal{D}$ uses $a=1$ should pay the toll. This is the simplest implementation of the policy that any vehicles should pay about their “fee for electricity” (Gustavsson \BOthers., \APACyear2021). The utility functions are defined as Eqs.(5–8).

Here, $\beta_{c}$ is the parameter of travel cost disutility. $\beta_{c}<0$ is assumed. Also, $\beta_{t}/\beta_{c}$ and $-\beta_{s}/\beta_{c}$ represents VoT and VoE, respectively.

1. A-i.:

   when $r<0.5$.
   As mentioned above, $x_{1}=x_{2}$ and $t_{1}=t_{2}$ hold. All $i\in\mathcal{D}$ choose $a=1$ ($x_{1}^{D}=rN$) since $V_{1,i}^{D}-V_{2,i}^{D}=\beta_{s}({1}/{s_{i}}-1)>0$. Also, $0.5N$ of OTHER-Vs choose $a=2$ and the rest choose $a=1$.

   In this case,

   • •

     TTT is calculated as $x_{1}t_{1}+x_{2}t_{2}=Nt_{1}$ and is minimised. In conventional transportation network analyses, minimizing TTT is the most popular measure to determine social optimum (SO). In this sense, we refer to an assignment as “conventional SO” if TTT is minimised.

   • •

     TCV is calculated as $rNWt_{1}$. Once traffic volume (and hence, travel time) is given and fixed, this is the possible maximum charged volume. We refer to such assignments as “ERS-Optimum”. As $i$ cannot be charged beyond the battery capacity in the acutal situation, the precise calculation should be carried out in future work.

   • •

     Revenue is 0.

2. A-ii.:

   when $r\geq 0.5$.
   In this case, $x_{1}^{D}\geq 0.5N$. This can be checked by supposing the case $x_{1}^{D}<0.5N$, which means $x_{1}=x_{2}$ and both DWPT-EVs and OTHER-Vs choose both $a=1$ and $2$. Although details are omitted due to space limitations, this is not a stable state. In a stable state, all $j\in\mathcal{O}$ should choose $a=2$ and $i\in\mathcal{D}$ chooses the link so that the travel time disutility and the charging utility are balanced. From Eq.(1), $i\in\mathcal{D}$ chooses $a=1$ in increasing order of $s_{i}$. Then, a threshold of $s_{i}$ that DWPT-EVs with smaller SoC than this value choose $a=1$ exists. We denote this SoC as $s_{thres}$ and the number of DWPT-EVs with $s_{i}<s_{thres}$ as $N_{thres}$.

   In this case,

   • •

     TTT is calculated as $x_{1}t_{1}+x_{2}t_{2}=N_{thres}t_{1}+(N-N_{thres})t_{2}=N_{thres}(t_{1}-t_{2})+Nt_{2}$. This is minimised at the special case of $t_{1}=t_{2}$, which means $N_{thres}=0.5N$ (i.e., $x_{1}=x_{2}$). Otherwise, generally, this case is not conventional SO.

   • •

     TCV is calculated as $N_{thres}Wt_{1}$, and this is ERS-optimum. Nonetheless, TCV is maximised at the special case of $N_{thres}=rN$ (i.e., all $i\in\mathcal{D}$ choose $a=1$) and not otherwise.

   • •

     Revenue is 0.

1. B-i.:

   when $r<0.5$.
   The assignment of $j\in\mathcal{O}$ is uniquely determined to achieve $x_{1}=x_{2}$ once the assignment of $i\in\mathcal{D}$ is determined. Thus, we first consider the assignment of DWPT-EVs. The following three patterns are possible.

   1. B-i.(a)

      Only $a=1$ is chosen by all $i\in\mathcal{D}$.
      This pattern occurs when even a DWPT-EV with maximum $s_{i}$ will pay the toll and charge its battery (i.e., $s_{\max}<s_{thres}$ where $s_{\max}$ represents the maximum $s_{i}$). Naturally, $x_{2}^{O}=0.5N$ and $x_{1}^{O}=(0.5-r)N$. Note that $t_{1}=t_{2}$, from Eqs.(5-6), the cost condition for this pattern is

      $\displaystyle C<-\frac{\beta_{s}}{\beta_{c}}(\frac{1}{s_{\max}}-1).$

      (9)

   2. B-i.(b)

      Only $a=2$ is chosen by all $i\in\mathcal{D}$.
      This pattern occurs when even a DWPT-EV with minimum $s_{i}$ will not pay the toll and not charge its battery (i.e., $s_{thres}\leq s_{\min}$ where $s_{\min}$ represents the minimum $s_{i}$). Naturally, $x_{1}^{O}=0.5N$ and $x_{2}^{O}=(0.5-r)N$. Similarly, the cost condition for this pattern is

      $\displaystyle C\geq-\frac{\beta_{s}}{\beta_{c}}(\frac{1}{s_{\min}}-1).$

      (10)

   3. B-i.(c)

      Both $a=1$ and $2$ are chosen by $i\in\mathcal{D}$.
      This pattern occurs when some DWPT-EVs will pay the toll and charge its battery while others will not (i.e., $s_{\min}<s_{thres}\leq s_{\max}$). $j\in\mathcal{O}$ chooses both $a=1$ and $2$ to realize $x_{1}=x_{2}$. Therefore, in this pattern, both DWPT-EVs and OTHER-Vs choose both links. Similarly, the cost condition for this pattern is

      $\displaystyle-\frac{\beta_{s}}{\beta_{c}}(\frac{1}{s_{\min}}-1)\leq C<-\frac{\beta_{s}}{\beta_{c}}(\frac{1}{s_{\max}}-1).$

      (11)

   In this case,

   • •

     TTT is $Nt_{1}$, which means Conventional SO.

   • •

     TCV is calculated as $N_{thres}Wt_{1}$. This is maximised at the special case of $N_{thres}=rN$: pattern (a). Also, ERS-optimum is only achieved in pattern (a). Otherwise, TCV is not maximised and the assignments are not ERS-Optimum. In particular, TCV becomes 0 in (b).

   • •

     Revenue is calculated as $N_{thres}C$.

2. B-ii.:

   when $r\geq 0.5$.
   As for $i\in\mathcal{D}$, the same three assignment patterns as B-i. can be done as follows. Corresponding assignment patterns for $j\in\mathcal{O}$ are also described.

   1. B-ii.(a)

      Only $a=1$ is chosen by all $i\in\mathcal{D}$.
      Here, all $j\in\mathcal{O}$ choose $a=2$. At this point, $x_{1}=rN>x_{2}=(1-rN)$ and hence, $t_{1}>t_{2}$. Then, if no DWPT-EV has a motivation to change its link choice under this $t_{1}$ and $t_{2}$ (i.e., a DWPT-EV with $s_{\max}$ still chooses $a=1$), this is a stable assignment. From Eqs.(5-6), the cost condition for this pattern is

      $\displaystyle C<\frac{\beta_{t}}{\beta_{c}}(t_{1}-t_{2})-\frac{\beta_{s}}{\beta_{c}}(\frac{1}{s_{\max}}-1).$

      (12)

   2. B-ii.(b)

      Only $a=2$ is chosen by all $i\in\mathcal{D}$.
      Here, all $j\in\mathcal{O}$ choose $a=1$. At this point, $x_{1}=(1-rN)<x_{2}=rN$ and hence, $t_{1}<t_{2}$. Then, if no DWPT-EV has a motivation to change its link choice under this $t_{1}$ and $t_{2}$ (i.e., a DWPT-EV with $s_{\min}$ still chooses $a=2$), this is a stable assignment. Similarly, the cost condition for this pattern is

      $\displaystyle C\geq\frac{\beta_{t}}{\beta_{c}}(t_{1}-t_{2})-\frac{\beta_{s}}{\beta_{c}}(\frac{1}{s_{\min}}-1).$

      (13)

   3. B-ii.(c)

      Both $a=1$ and $2$ are chosen by $i\in\mathcal{D}$.
      (c1) Suppose $x_{1}=x_{2}$ after all $j\in\mathcal{O}$ choose the links. Then, this is similar to B-i.(c). Both DWPT-EVs and OTHER-Vs choose both links except the special cases of exactly $0.5N$ of DWPT-EVs choose $a=1$ or $2$.
      (c2) Suppose $x_{1}>x_{2}$ after all $j\in\mathcal{O}$ choose the links. This occurs only if all $j\in\mathcal{O}$ choose $a=2$ and $N_{thres}>0.5N$ holds.
      (c3) Suppose $x_{1}<x_{2}$ after all $j\in\mathcal{O}$ choose the links. This occurs only if all $j\in\mathcal{O}$ choose $a=1$ and $(rN-N_{thres})>0.5N$ holds.
      The cost condition common to (c1-3) is

      $\displaystyle\frac{\beta_{t}}{\beta_{c}}(t_{1}-t_{2})-\frac{\beta_{s}}{\beta_{c}}(\frac{1}{s_{\min}}-1)\leq C<\frac{\beta_{t}}{\beta_{c}}(t_{1}-t_{2})-\frac{\beta_{s}}{\beta_{c}}(\frac{1}{s_{\max}}-1).$

      (14)

   In this case,

   • •

     TTT is only minimised in (c1) and not otherwise.

   • •

     TCV is calculated as $N_{thres}Wt_{1}$. This is maximised at $N_{thres}=rN$ in (a) and not otherwise. In particular, TCV becomes 0 in (b). ERS-optimum is achieved in pattern (a), a special case of (c1), and (c2).

   • •

     Revenue is $N_{thres}C$.

When $r<0.5$, toll-free system (A-i.) is less problematic except for the beneficiary-pay perspective. This assignment is social optimum in the conventional meaning, and is maximising charged volume, if the policy that ERS construction and operating cost are covered by taxes is acceptable. On the other hand, the biggest problem in fixed-toll system (B-i.) is that ERS may not be utilised by DWPT-EVs depending on the price $C$. Some DWPT-EVs avoid ERS to avoid paying toll (B-i.(c)). Furthermore, in the worst situation, no DWPT-EV uses ERS and no revenue is obtained (B-i.(b)). Even in the simple example of this paper, a beneficiary-pay-oriented system may lead to such meaningless and undesirable situations. Numerical examples are shown in the next subsection. Of course, if we could specify an appropriate price $C$, the resulting assignment has no problem (Eq.(9)). However, this seems to be completely difficult because the upper bound of $C$ is a function of $s_{\max}$, $\beta_{s}$ and $\beta_{c}$. First of all, we cannot expect $s_{\max}$ to be constant or stable, either for within-day or day-to-day variations. In addition, $\beta_{s}$ is not always stable and is assumed to vary over time in accordance with electricity prices (U.S. Department of Energy, \APACyear2006).

When $r\geq 0.5$, the biggest problem common to A-ii. and B-ii. is that TTT is not generally minimised. If spread of ERS and DWPT-EVs results in increased TTT, they are counterproductive to CO₂ emission reductions. Therefore, the case $r\geq 0.5$ is more difficult than the case $r<0.5$ in that the toll system must be designed in such a way that TTT does not increase inadvertently. Also, the same problem as $r<0.5$ that ERS is not fully utilised exists. Of course, theoretically, $C$ could be determined to minimise TTT or to achieve ERS-optimum. However, this is difficult because of the same reason as $r<0.5$.

Finally, a numerical example is shown by taking case B-i. as an example. Some values assuming Japanese current market are determined (Table 1). Travel time is calculated by BPR function, $t_{a}=t_{a0}(1+\alpha{x_{a}}/{Q_{a}})^{\beta}$.

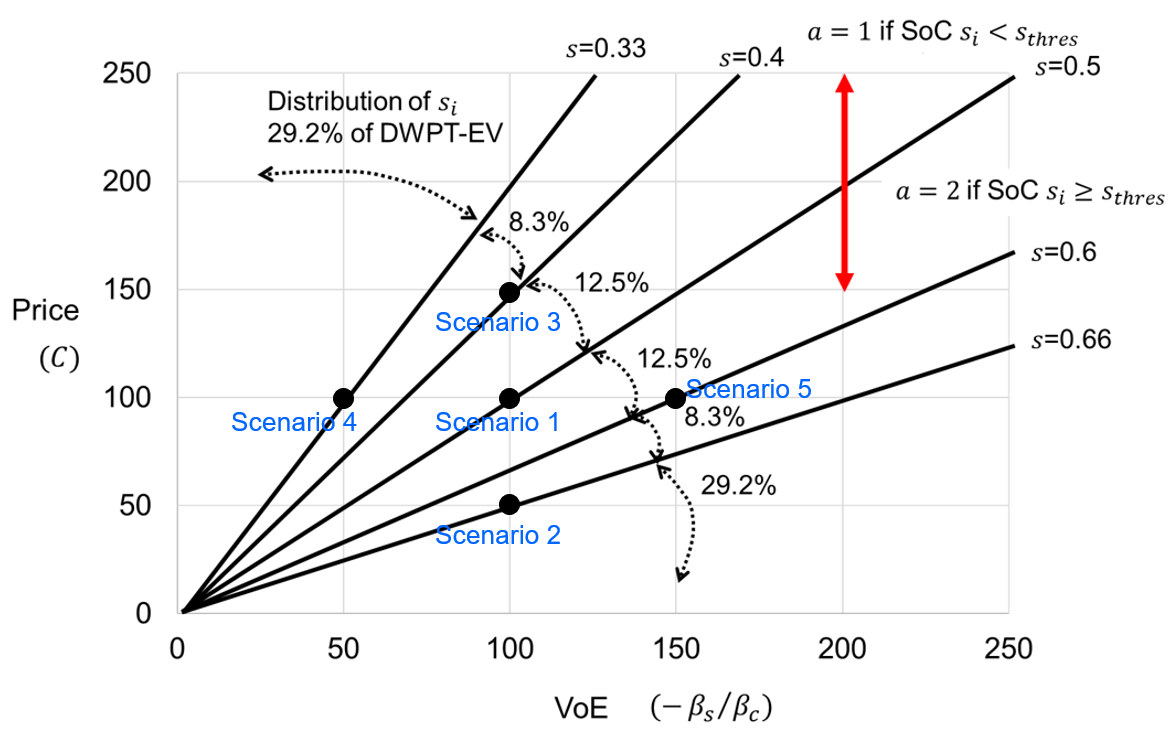
The results of five scenarios are shown in Table 2. They differ in VoE and $C$: Scenario 1 is the base case; Scenarios 2 to 5 are those with VoE or $C$ multiplied by 1.5 or halved. VoE $=100$ and and the price $C=100$ [JPY] are assumed by standard VoT (50 [JPY/min]) and the output of quick charger (around 120 [kW]). Since the charging utility is defined in a non-linear way, VoE cannot be directly interpreted as the price of electricity, but it can vary in such degrees. Fig. 2 is the illustration of Eq.(11). $s_{thres}$ is the value of $s_{i}$ when $V_{1,i}^{D}=V_{2,i}^{D}$ (Eq.(5-6)) holds, and is calculated from VoE and $C$.

As a result, changes in both price $C$ (from Scenarios 1–3) and VoE (Scenarios 1, 4, 5) made a difference of several tens of per cent of DWPT-EVs in ERS utilisation. Also, the significant changes in ERS utilisation for different SoC distributions can also be easily confirmed by considering the scenarios where the values on Fig. 2 are changed. For example, if $s_{\min}>0.4$ in Scenario 3, no DWPT-EV choose $a=1$, which is the worst pattern.