A general Multidimensional Monte Carlo Approach for Dynamic Hedging under stochastic volatility
Abstract.
In this work, we introduce a Monte Carlo method for the dynamic hedging of general European-type contingent claims in a multidimensional Brownian arbitrage-free market. Based on bounded variation martingale approximations for Galtchouk-Kunita-Watanabe decompositions, we propose a feasible and constructive methodology which allows us to compute pure hedging strategies w.r.t arbitrary square-integrable claims in incomplete markets. In particular, the methodology can be applied to quadratic hedging-type strategies for fully path-dependent options with stochastic volatility and discontinuous payoffs. We illustrate the method with numerical examples based on generalized Föllmer-Schweizer decompositions, locally-risk minimizing and mean-variance hedging strategies for vanilla and path-dependent options written on local volatility and stochastic volatility models.
Key words and phrases:
Martingale representation, hedging contingent claims, path dependent options1991 Mathematics Subject Classification:
Primary: C02; Secondary: G121. Introduction
1.1. Background and Motivation
Let be a financial market composed by a continuous -semimartingale which represents a discounted risky asset price process, is a filtration which encodes the information flow in the market on a finite horizon , is a physical probability measure and is the set of equivalent local martingale measures. Let be an -measurable contingent claim describing the net payoff whose the trader is faced at time . In order to hedge this claim, the trader has to choose a dynamic portfolio strategy.
Under the assumption of an arbitrage-free market, the classical Galtchouk-Kunita-Watanabe (henceforth abbreviated by GKW) decomposition yields
| (1.1) |
where is a -local martingale which is strongly orthogonal to and is an adapted process.
The GKW decomposition plays a crucial role in determining optimal hedging strategies in a general Brownian-based market model subject to stochastic volatility. For instance, if is a one-dimensional Itô risky asset price process which is adapted to the information generated by a two-dimensional Brownian motion , then there exists a two-dimensional adapted process such that
which also realizes
| (1.2) |
In the complete market case, there exists a unique and in this case, , is the unique fair price and the hedging replicating strategy is fully described by the process . In a general stochastic volatility framework, there are infinitely many GKW orthogonal decompositions parameterized by the set and hence one can ask if it is possible to determine the notion of non-self-financing optimal hedging strategies solely based on the quantities (1.2). This type of question was firstly answered by Föllmer and Sonderman [9] and later on extended by Schweizer [23] and Föllmer and Schweizer [8] through the existence of the so-called Föllmer-Schweizer decomposition which turns out to be equivalent to the existence of locally-risk minimizing hedging strategies. The GKW decomposition under the so-called minimal martingale measure constitutes the starting point to get locally risk minimizing strategies provided one is able to check some square-integrability properties of the components in (1.1) under the physical measure. See e.g [12] and [26] for details and other references therein. Orthogonal decompositions without square-integrability properties can also be defined in terms of the the so-called generalized Föllmer-Schweizer decomposition (see e.g Schweizer [24]).
In contrast to the local-risk minimization approach, one can insist in working with self-financing hedging strategies which give rise to the so-called mean-variance hedging methodology. In this approach, the spirit is to minimize the expectation of the squared hedging error over all initial endowments and all suitable admissible strategies :
| (1.3) |
The nature of the optimization problem (1.3) suggests to work with the subset . Rheinlander and Schweizer [22], Gourieroux, Laurent and Pham [10] and Schweizer [25] show that if and then the optimal quadratic hedging strategy exists and it is given by , where
| (1.4) |
Here is computed in terms of , the so-called variance optimal martingale measure, realizes
| (1.5) |
and is the value option price process under . See also Cerný and Kallsen [4] for the general semimartingale case and the works [16], [18] and [19] for other utility-based hedging strategies based on GKW decompositions.
Concrete representations for the pure hedging strategies can in principle be obtained by computing cross-quadratic variations for . For instance, in the classical vanilla case, pure hedging strategies can be computed by means of the Feynman-Kac theorem (see e.g Heath, Platen and Schweizer [12]). In the path-dependent case, the obtention of concrete computationally efficient representations for is a rather difficult problem. Feynman-Kac-type arguments for fully path-dependent options mixed with stochastic volatility typically face not-well posed problems on the whole trading period as well as highly degenerate PDEs arise in this context. Generically speaking, one has to work with non-Markovian versions of the Feynman-Kac theorem in order to get robust dynamic hedging strategies for fully path dependent options written on stochastic volatility risky asset price processes.
In the mean variance case, the only quantity in (1.4) not related to GKW decomposition is which can in principle be expressed in terms of the so-called fundamental representation equations given by Hobson [14] and Biagini, Guasoni and Pratelli [2] in the stochastic volatility case. For instance, Hobson derives closed form expressions for and also for any type of -optimal measure in the Heston model [13]. Recently, semi-explicit formulas for vanilla options based on general characterizations of the variance-optimal hedge in Cerný and Kallsen [4] have been also proposed in the literature which allow for a feasible numerical implementation in affine models. See Kallsen and Vierthauer [17] and Cerný and Kallsen [5] for some results in this direction. A different approach based on backward stochastic differential equations can also be used in order to get useful characterizations for the optimal mean variance hedging strategies. See e.g Jeanblanc, Mania, Santacrose and Schweizer [15] and other references therein.
1.2. Contribution of the current paper.
In spite of deep characterizations of optimal quadratic hedging strategies and concrete numerical schemes available for vanilla-type options, to our best knowledge no feasible approach has been proposed to tackle the problem of obtaining dynamic optimal quadratic hedging strategies for fully path dependent options written on a generic multidimensional Itô risky asset price process. In this work, we attempt to solve this problem with a probabilistic approach. The main difficulty in dealing with fully path dependent and/or discontinuous payoffs is the non-Markovian nature of the option value and a priori lack of path smoothness of the pure hedging strategies. Usual numerical schemes based on PDE and martingale techniques do not trivially apply to this context.
The main contribution of this paper is the obtention of flexible and computationally efficient multidimensional non-Markovian representations for generic option price processes which allow for a concrete computation of the associated GKW decomposition for -square integrable payoffs with . We provide a Monte Carlo methodology capable to compute optimal quadratic hedging strategies w.r.t general square-integrable claims in a multidimensional Brownian-based market model.
This article provides a feasible and constructive method to compute generalized Föllmer-Schweizer decompositions under full generality. As far as the mean variance hedging is concerned, we are able to compute pure optimal hedging strategies for arbitrary square-integrable payoffs. Hence, our methodology also applies to this case provided one is able to compute the fundamental representation equations in Hobson [14] and Biagini, Guasoni and Pratelli [2] which is the case for the classical Heston model. In mathematical terms, we are able to compute -GKW decompositions under full generality so that the results of this article can also be used to other non-quadratic hedging methodologies where orthogonal martingale representations play an important role in determining optimal hedging strategies.
The starting point of this article is based on weak approximations developed by Leão and Ohashi [20] for one-dimensional Brownian functionals. They introduced a one-dimensional space-filtration discretization scheme constructed from suitable waiting times which measure the instants when the Brownian motion hits some a priori levels. In this work, we extend [20] to the multidimensional case as follows: More general and stronger convergence results are obtained in order to recover incomplete markets with stochastic volatility. Hitting times induced by multidimensional noises which drive the stochastic volatility are carefully analyzed in order to obtain -GKW decompositions under rather weak integrability conditions for any . Moreover, a complete analysis is performed w.r.t weak approximations for gain processes by means of suitable non-antecipative discrete-time hedging strategies for square-integrable payoffs, including path-dependent ones.
It is important to stress that the results of this article can be applied to both complete and incomplete markets written on a generic multidimensional Itô risky asset price process. One important restriction of our methodology is the assumption that the risky asset price process has continuous paths. This is a limitation that we hope to overcome in a future work.
Numerical results based on the standard Black-Scholes, local-volatility and Heston models are performed in order to illustrate the theoretical results and the methodology of this article. In particular, we briefly compare our results with other prominent methodologies based on Malliavin weights (complete market case) and PDE techniques (incomplete market case) employed by Bernis, Gobet and Kohatsu-Higa [1] and Heath, Platen and Schweizer [12], respectively. The numerical experiments suggest that pure hedging strategies based on generalized Föllmer-Schweizer decompositions mitigate very well the cost of hedging of a path-dependent option even if there is no guarantee of the existence of locally-risk minimizing strategies. We also compare hedging errors arising from optimal mean variance hedging strategies for one-touch options written on a Heston model with nonzero correlation.
The remainder of this paper is structured as follows. In Section 2, we fix the notation and we describe the basic underlying market model. In Section 3, we provide the basic elements of the Monte Carlo methodology proposed in this article. In Section 4, we formulate dynamic hedging strategies starting from a given GKW decomposition and we translate our results to well-known quadratic hedging strategies. The Monte Carlo algorithm and the numerical study are described in Sections 5 and 6, respectively. The Appendix presents more refined approximations when the martingale representations admit additional hypotheses.
2. Preliminaries
Throughout this paper, we assume that we are in the usual Brownian market model with finite time horizon equipped with the stochastic basis generated by a standard -dimensional Brownian motion starting from . The filtration is the -augmentation of the natural filtration generated by . For a given -dimensional vector , we denote by the diagonal matrix whose -th diagonal term is . In this paper, for all unexplained terminology concerning general theory of processes, we refer to Dellacherie and Meyer [6].
In view of stochastic volatility models, let us split into two multidimensional Brownian motions as follows and . In this section, the market consists of assets : one riskless asset given by
and a -dimensional vector of risky assets which satisfies the following stochastic differential equation
Here, the real-valued interest rate process , the vector of mean rates of return and the volatility matrix are assumed to be predictable and they satisfy the standard assumptions in such way that both and are well-defined positive semimartingales. We also assume that the volatility matrix is non-singular for almost all . The discounted price follows
where is a d-dimensional vector with every component equal to . The market price of risk is given by
where we assume
In the sequel, denotes the set of -equivalent probability measures such that the respective Radon-Nikodym derivative process is a martingale and the discounted price is a -local martingale. Throughout this paper, we assume that . In our setup, it is well known that is given by the subset of probability measures with Radon-Nikodym derivatives of the form
for some -valued adapted process such that a.s.
Example: The typical example studied in the literature is the following one-dimensional stochastic volatility model
| (2.1) |
where and are correlated Brownian motions with correlation , and are suitable functions such that is a well-defined two-dimensional Markov process. All continuous stochastic volatility model commonly used in practice fit into the specification (2.1). In this case, and we recall that the market is incomplete where the set is infinity. The dynamic hedging procedure turns out to be quite challenging due to extrinsic randomness generated by the non-tradeable volatility, specially w.r.t to exotic options.
2.1. GKW Decomposition
In the sequel, we take and we set and where
| (2.2) |
is a standard -dimensional Brownian motion under the measure and filtration generated by . In what follows, we fix a discounted contingent claim . Recall that the filtration is contained in , but it is not necessarily equal. In the remainder of this article, we assume the following hypothesis.
(M) The contingent claim is also -measurable.
Remark 2.1.
Assumption (M) is essential for the approach taken in this work because the whole algorithm is based on the information generated by the Brownian motion (defined under the measure and filtration ). As long as the numeraire is deterministic, this hypothesis is satisfied for any stochastic volatility model of the form (2.1) and a payoff where is a Borel map and is the usual space of continuous paths on . Hence, (M) holds for a very large class of examples founded in practice.
For a given -square integrable claim , the Brownian martingale representation (computed in terms of ) yields
where is a -dimensional -predictable process. In what follows, we set , and
| (2.3) |
The discounted stock price process has the following -dynamics
and therefore the -GKW decomposition for the pair of locally square integrable local martingales is given by
| (2.4) |
where
| (2.5) |
The -dimensional process which constitutes (2.3) and (2.5) plays a major role in several types of hedging strategies in incomplete markets and it will be our main object of study.
Remark 2.2.
If we set for and the correspondent density process is a martingale then the resulting minimal martingale measure yields a GKW decomposition where is still a -local martingale orthogonal to the martingale component of under . In this case, it is also natural to implement a pure hedging strategy based on regardless the existence of the Föllmer-Schweizer decomposition. If this is the case, this hedging strategy can be based on the generalized Föllmer-Schweizer decomposition (see e.g Th.9 in [24]).
3. The Random Skeleton and Weak Approximations for GKW Decompositions
In this section, we provide the fundamentals of the numerical algorithm of this article for the obtention of hedging strategies in complete and incomplete markets.
3.1. The Multidimensional Random Skeleton
At first, we fix once and for all and a -square-integrable contingent claim satisfying (M). In the remainder of this section, we are going to fix a -Brownian motion and with a slight abuse of notation all -expectations will be denoted by . The choice of is dictated by the pricing and hedging method used by the trader.
In the sequel, denotes the usual quadratic variation between semimartingales and the usual jump of a process is denoted by where is the left-hand limit of a cadlag process . For a pair , we denote and . Moreover, for any two stopping times and , we denote the stochastic intervals , and so on. Throughout this article, denotes the Lebesgue measure on the interval .
For a fixed positive integer and for each we define a.s. and
| (3.1) |
where is the -dimensional -Brownian motion as defined in (2.2).
For each , the family is a sequence of -stopping times where the increments is an i.i.d sequence with the same distribution as . In the sequel, we define as the -dimensional step process given componentwise by
where
| (3.2) |
for and . We split into where is the -dimensional process constituted by the first components of and the remainder -dimensional process. Let be the natural filtration generated by . One should notice that is a discrete-type filtration in the sense that
where and for and . Here, denotes the smallest sigma-algebra generated by the union. One can easily check that and hence
With a slight abuse of notation we write to denote its -augmentation satisfying the usual conditions.
Let us now introduce the multidimensional filtration generated by . Let us consider where for . Let be the order statistics obtained from the family of random variables . That is, we set ,
| (3.3) |
for . In this case, is the partition generated by all stopping times defined in (3.1). The finite-dimensional distribution of is absolutely continuous for each and therefore the elements of are almost surely distinct for every . Moreover, the following result holds true.
Lemma 3.1.
For every , the set is an exhaustive sequence of -stopping times such that in probability as .
Proof.
The following obvious estimate holds
in probability as and a.s as for each . Let us now prove that is a sequence of -stopping times. In order to show this, we write in a different way. This sequence can be defined recursively as follows
where denotes the -maximum norm. Therefore, is an -stopping time. Next, let us define a family of -random variables related to the index which realizes the hitting time as follows
for any . Then, we shift as follows
for . In this case, we conclude that is adapted to the filtration , the hitting time
is a -stopping time and is a -stopping time. In the sequel, we define a family of -random variables related to the index which realizes the hitting time as follows
for . If we denote , we shift as follows
for every . In this case, we conclude that is adapted to the filtration , the hitting time
is an -stopping time and is a -stopping time. By induction, we conclude that is a sequence of -stopping times. ∎
With Lemma 3.1 at hand, we notice that the filtration is a discrete-type filtration in the sense that
for and . Itô representation theorem yields
where is a -dimensional -predictable process such that
The payoff induces the -square-integrable -martingale . We now embed the process into the quasi left-continuous filtration by means of the following operator
Since is a -martingale, then the usual optional stopping theorem yields the representation
Therefore, is indeed a -square-integrable -martingale and we shall write it as
Remark 3.1.
Similar to the univariate case, one can easily check that weakly and since has continuous paths then uniformly in probability as . See Remark 2.1 in [20].
Based on the Dirac process , we denote
In order to work with non-antecipative hedging strategies, let us now define a suitable -predictable version of as follows
One can check that is -predictable. See e.g [11], Ch.5 for details.
Example: Let be a contingent claim satisfying (M). Then for a given , we have
| (3.5) |
One should notice that (3.5) is reminiscent from the usual delta-hedging strategy but the price is shifted on the level of the sigma-algebras jointly with the increments of the driving Brownian motion instead of the pure spot price. For instance, in the one-dimensional case , we have
and hence a natural procedure to approximate pure hedging strategies is to look at at time zero. In the incomplete market case, additional randomness from e.g stochastic volatilities are encoded by where is determined not only by the hitting times coming from the risky asset prices but also by possibly Brownian motion hitting times coming from stochastic volatility.
3.2. Weak approximation for the hedging process
| (3.6) |
In order to shorten notation, we do not write in (3.6). The main goal of this section is the obtention of bounded variation martingale weak approximations for both the gain and cost processes, given respectively, by
We assume the trader has some knowledge of the underlying volatility so that the obtention of will be sufficient to recover . The typical example we have in mind are generalized Föllmer-Schweizer decompositions, locally-risk minimizing and mean variance strategies as explained in the Introduction. The scheme will be very constructive in such way that all the elements of our approximation will be amenable to a feasible numerical analysis. Under very mild integrability conditions, the weak approximations for the gain process will be translated into the physical measure.
The weak topology. In order to obtain approximation results under full generality, it is important to consider a topology which is flexible to deal with nonsmooth hedging strategies for possibly non-Markovian payoffs and at the same time justifies Monte Carlo procedures. In the sequel, we make use of the weak topology of the Banach space constituted by -optional processes such that
where and such that . The subspace of the square-integrable -martingales will be denoted by . It will be also useful to work with -topology given in [20]. For more details about these topologies, we refer to the works [6, 7, 20]. It turns out that and are very natural notions to deal with generic square-integrable random variables as described in [20].
In the sequel, we recall the following notion of covariation introduced in [20].
Definition 3.1.
Let be a sequence of square-integrable -martingales. We say that has -covariation w.r.t jth component of if the limit
exists weakly in for every .
Lemma 3.2.
Let be a sequence of stochastic integrals and . Assume that
Then exists weakly in for each with if, and only if, admits -covariation w.r.t jth component of . In this case,
for .
Proof.
The proof follows easily from the arguments given in the proof of Prop. 3.2 in [20] by using the fact that is an independent family of Brownian motions, so we omit the details. ∎
In the sequel, we present a key asymptotic result for the numerical algorithm of this article.
Theorem 3.1.
Let be a -square integrable contingent claim satisfying (M). Then
| (3.7) |
and
| (3.8) |
weakly in . In particular,
| (3.9) |
weakly in for each
Proof.
We divide the proof into three steps. Throughout this proof is a generic constant which may defer from line to line.
STEP1. We claim that
| (3.10) |
for each . In order to prove (3.10), we begin by noticing that Lemma 3.1 states that the elements of are -stopping times. By assumption, is -square integrable martingale and hence one may use similar arguments given in the proof of Lemma 3.1 in [20] to safely state that the following estimate holds
| (3.11) |
Now, we notice that the sequence converges weakly to , is continuous and therefore uniformly in probability (see Remark 3.1). Since , then a simple application of Burkhölder inequality allows us to state that converges strongly in and a routine argument based on the definition of the -weak topology yields
| (3.13) |
holds weakly in for each and due to the pairwise independence of . Summing up (3.11) and (3.13), we shall apply Lemma 3.2 to get (3.10).
STEP 2. In the sequel, let and be the optional and predictable projections w.r.t , respectively. Let us consider the -martingales given by
where
We claim that . One can check that a.s for each and (see e.g chap.5, section 5 in [11]). Moreover, by the very definition
| (3.14) |
Therefore, Jensen inequality yields
| (3.15) | |||||
where in (3.15) we have used (3.14) and the fact that a.s for each and . We shall write in a slightly different manner as follows
| (3.16) |
| (3.17) |
STEP 3. We claim that for a given , and we have
| (3.18) |
By using the fact that is -optional and is -predictable, we shall use duality of the -optional projection to write
In order to prove (3.18), let us check that
| (3.19) |
and
as because has continuous paths (see Remark 3.1). This proves (3.19). Now, in order to shorten notation let us denote by the expectation in (3.20). Cauchy-Schwartz and Burkholder-Davis-Gundy inequalities jointly with (3.17) and (3.11) yield
| (3.21) |
We shall proceed similar to Lemma 4.1 in [20] to safely state that as and from (3.21) we conclude that (3.20) holds. Summing up Steps 1, 2 and 3, we shall use Lemma 3.2 to conclude that (3.7) and (3.8) hold true. It remains to show (3.9) but this is a straightforward consequence of (3.18) together with a similar argument given in the proof of Theorem 4.1 and Remark 4.2 in [20], so we omit the details. This concludes the proof of the theorem. ∎
Stronger convergence results can be obtained under rather weak integrability and path smoothness assumptions for representations . We refer the reader to the Appendix for further details.
4. Weak dynamic hedging
In this section, we apply Theorem 3.1 for the formulation of a dynamic hedging strategy starting with a given GKW decomposition
| (4.1) |
where is a -square integrable European-type option satisfying (M) for a given . The typical examples we have in mind are quadratic hedging strategies w.r.t a fully path-dependent option. We recall that when is the minimal martingale measure then (4.1) is the generalized Föllmer-Schweizer decomposition so that under some -square integrability conditions on the components of (4.1), is the locally risk minimizing hedging strategy (see e.g [12], [24]). In fact, GKW and Föllmer-Schweizer decompositions are essentially equivalent for the market model assumed in Section 2. We recall that decomposition (4.1) is not sufficient to fully describe mean variance hedging strategies but the additional component rests on the fundamental representation equations as described in Introduction. See also expression (6.4) in Section 6.
For simplicity of exposition, we consider a financial market driven by a two-dimensional Brownian motion and a one-dimensional risky asset price process as described in Section 2. We stress that all results in this section hold for a general multidimensional setting with the obvious modifications.
In the sequel, we denote
where for .
Corollary 4.1.
For a given , let be a -square integrable claim satisfying (M). Let
be the correspondent GKW decomposition under . If and
| (4.2) |
then
in the -topology under .
Proof.
We have . To shorten notation, let and for Let be an arbitrary -stopping time bounded by and let be an essentially -bounded random variable and -measurable. Let be a continuous linear functional given by the purely discontinuous -optional bounded variation process
where the duality action is given by . See [20] for more details. Then Theorem 3.1 and the fact yield
as . By the very definition,
Then from the definition of the -topology based on the physical measure , we shall conclude the proof. ∎
Remark 4.1.
Corollary 4.1 provides a non-antecipative Riemman-sum approximation for the gain process in a multi-dimensional filtration setting where none path regularity of the pure hedging strategy is imposed. The price we pay is a weak-type convergence instead of uniform convergence in probability. However, from the financial point of view this type of convergence is sufficient for the implementation of Monte Carlo methods in hedging. More importantly, we will see that can be fairly simulated and hence the resulting Monte Carlo hedging strategy can be calibrated from market data.
Remark 4.2.
If one is interested only at convergence at the terminal time , then assumption (4.2) can be weakened to . Assumption is essential to change the -convergence into the physical measure . One should notice that the associated density process is no longer a -local-martingale and in general such integrability assumption must be checked case by case. Such assumption holds locally for every underlying Itô risky asset price process. Our numerical results suggest that this property behaves well for a variety of spot price models.
Of course, in practice both the spot prices and trading dates are not observable at the stopping times so we need to translate our results to a given deterministic set of rebalancing hedging dates.
4.1. Hedging Strategies
In this section, we provide a dynamic hedging strategy based on a refined set of hedging dates . For this, we need to introduce some objects. For a given , we set for . Of course, by the strong Markov property of the Brownian motion, we know that is an -Brownian motion for each and independent from , where for . Similar to Section 3.1, we set and
For a given and , we define as the sigma-algebra generated by and . We then define the following discrete jumping filtration
In order to deal with fully path dependent options, it is convenient to introduce the following augmented filtration
for . The bidimensional information flows are defined by and for . We set . We shall assume that they satisfy the usual conditions. The piecewise constant martingale projection based on is given by
We set as the order statistic generated by the stopping times similar to (3.3).
If and , then we define
so that the related derivative operators are given by
where
An -predictable version of is given by
In the sequel, we denote
| (4.4) |
where is the volatility process driven by the shifted filtration and is the risky asset price process driven by the shifted Brownian .
We are now able to present the main result of this section.
Corollary 4.2.
For a given , let be a -square integrable claim satisfying (M). Let
be the correspondent GKW decomposition under . If and
then for any set of trading dates , we have
| (4.5) |
weakly in under .
Proof.
Let be any set of trading dates. To shorten notation, let us define
| (4.6) |
for and . At first, we recall that is an i.i.d sequence with absolutely continuous distribution. In this case, the probability of the set is always strictly positive for every and . Hence, is a non-degenerate subset of random variables. By making a change of variable on the Itô integral, we shall write
| (4.7) |
Let us fix . By the very definition,
Now we notice that Theorem 3.1 holds for the two-dimensional Brownian motion , for each with the discretization of the Brownian motion given by . Moreover, using the fact that and repeating the argument given by (4) restricted to the interval , we have
| (4.8) | |||||
weakly in for each . This concludes the proof.
∎
Remark 4.3.
In practice, one may approximate the gain process by a non-antecipative strategy as follows: Let be a given set of trading dates on the interval so that is small. We take a large and we perform a non-antecipative buy and hold-type strategy among the trading dates in the full approximation (4.6) which results
| (4.9) |
Convergence (4.5) implies that the approximation (4.9) results in unavoidable hedging errors w.r.t the gain process due to the discretization of the dynamic hedging, but we do not expect large hedging errors provided is large and small. Hedging errors arising from discrete hedging in complete markets are widely studied in literature. We do not know optimal rebalancing dates in this incomplete market setting, but simulation results presented in Section 6 suggest that homogeneous hedging dates work very well for a variety of models with and without stochastic volatility. A more detailed study is needed in order to get more precise relations between and the stopping times, a topic which will be further explored in a forthcoming paper.
Let us now briefly explain how the results of this section can be applied to well-known quadratic hedging methodologies.
Generalized Föllmer-Schweizer: If one takes the minimal martingale measure , then in (4.1) is a -local martingale and orthogonal to the martingale component of . Due this orthogonality and the zero mean behavior of the cost , it is still reasonable to work with generalized Föllmer-Schweizer decompositions under without knowing a priori the existence of locally-risk minimizing hedging strategies.
Local Risk Minimization: One should notice that if , under and , then is the locally risk minimizing trading strategy and (4.1) is the Föllmer-Schweizer decomposition under .
Mean Variance hedging: If one takes , then the mean variance hedging strategy is not completely determined by the GKW decomposition under . Nevertheless, Corollary 4.2 still can be used to approximate the optimal hedging strategy by computing the density process based on the so-called fundamental equations derived by Hobson [14]. See (1.4) and (1.5) for details. For instance, in the classical Heston model, Hobson derives analytical formulas for . See (6.4) in Section 6.
Hedging of fully path-dependent options: The most interesting application of our results is the hedging of fully path-dependent options under stochastic volatility. For instance, if then Corollary 4.2 and Remark 4.3 jointly with the above hedging methodologies allow us to dynamically hedge the payoff based on (4.9). The conditioning on the information flow in the hedging strategy encodes the continuous monitoring of a path-dependent option. For each hedging date , one has to incorporate the whole history of the price and volatility until such date in order to get an accurate description of the hedging. If is not path-dependent then the information encoded by in is only crucial at time .
Next, we provide the details of the Monte Carlo algorithm for the approximating pure hedging strategy .
5. The algorithm
In this section we present the basic algorithm to evaluate the hedging strategy for a given European-type contingent claim satisfying assumption (M) for a fixed at a terminal time . The structure of the algorithm is based on the space-filtration discretization scheme induced by the stopping times . From the Markov property, the key point is the simulation of the first passage time for each for which we refer the work of Burq and Jones [3] for details.
(Step 1) Simulation of .
-
(1)
One chooses which represents the level of discretization of the Brownian motion.
-
(2)
One generates the increments according to the algorithm described by Burq and Jones [3].
-
(3)
One simulates the family independently from . This family must be simulated according to the Bernoulli random variable with parameter for . This simulates the jump process for .
The next step is the simulation of where the conditional expectations in (3.5) play a key role. For this, we need to simulate based on as follows.
(Step 2) Simulation of the risky asset price process .
-
(1)
Generate a sample of according to Step 1 for a fixed .
-
(2)
With the partition at hand, we can apply some appropriate approximation method to evaluate the discounted price. Generally speaking, we work with some Itô-Taylor expansion method.
The multidimensional setup requires an additional notation as follows. In the sequel, denotes the realization of the by means of Step 1, denotes the realization of based on the finest random partition . Moreover, any sequence encodes the information generated by the realization of until the first hitting time of the -th partition. In addition, we denote as the last time in the finest partition previous to . Let be the pair which realizes
Based on this quantities, we define as the realization of the random variable . Recall expression (3.2).
(Step 3) Simulation of the stochastic derivative .
Based on Steps 1 and 2, for each one simulates as follows. In the sequel, denotes the conditional expectation computed in terms of the Monte Carlo method:
| (5.1) |
where with a slight abuse of notation, in (5.1) denotes the realization of the Bernoulli variable . Then we define
| (5.2) |
The correspondent simulated pure hedging strategy is given by
| (5.3) |
(Step 4) Simulation of .
Repeat these steps several times and
| (5.4) |
The quantity (5.4) is a Monte Carlo estimate of .
Remark 5.1.
In order to compute the hedging strategy over a trading period , one perform the algorithm described above but based on the shifted filtration and the Brownian motions for as described in Section 4.1.
Remark 5.2.
In practice, one has to calibrate the parameters of a given stochastic volatility model based on liquid instruments such as vanilla options and volatility surfaces. With those parameters at hand, the trader must follow the steps (5.1) and (5.4). The hedging strategy is then given by calibration and the computation of the quantity (5.4) over a trading period.
6. Numerical Analysis and Discussion of the Methods
In this section, we provide a detailed analysis of the numerical scheme proposed in this work.
6.1. Multidimensional Black-Scholes model
At first, we consider the classical multidimensional Black-Scholes model with as many risky stocks as underlying independent random factors to be hedged . In this case, there is only one equivalent local martingale measure, the hedging strategy is given by (3.6) and the cost is just the option price. To illustrate our method, we study a very special type of exotic option: a BLAC (Basket Lock Active Coupon) down and out barrier option whose payoff is given by
It is well-known that for this type of option, there exists a closed formula for the hedging strategy. Moreover, it satisfies the assumptions of Theorem 7.2. See e.g Bernis, Gobet and Kohatsu-Higa [1] for some formulas.
For comparison purposes with Bernis, Gobet and Kohatsu-Higa [1], we consider underlying assets, for the interest rate and year for the maturity time. For each asset, we set initial values and we compute the hedging strategy with respect to the first asset with discretization level and simulations.
Following the work [1], we consider the volatilities of the assets given by , , , and , the correlation matrix defined by for , where and we use the barrier level . Table 1 provides the numerical results based on the algorithm described in Section 5 for the pointwise hedging strategy . Due to Theorem 7.2, we expect that when the discretization level increases, we obtain results closer to the true value and this is what we find in our Monte Carlo experiments. The standard deviation and percentage error in Table 1 are related to the average of the hedging strategies calculated by Monte Carlo and the difference between the true and the estimated hedging value, respectively.
| k | Result | St. error | True value | Diference | error | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
In Figure 1, we plot the average hedging estimates with respect to the number of simulations. One should notice that when increases, the standard error also increases, which suggests more simulations for higher values of .
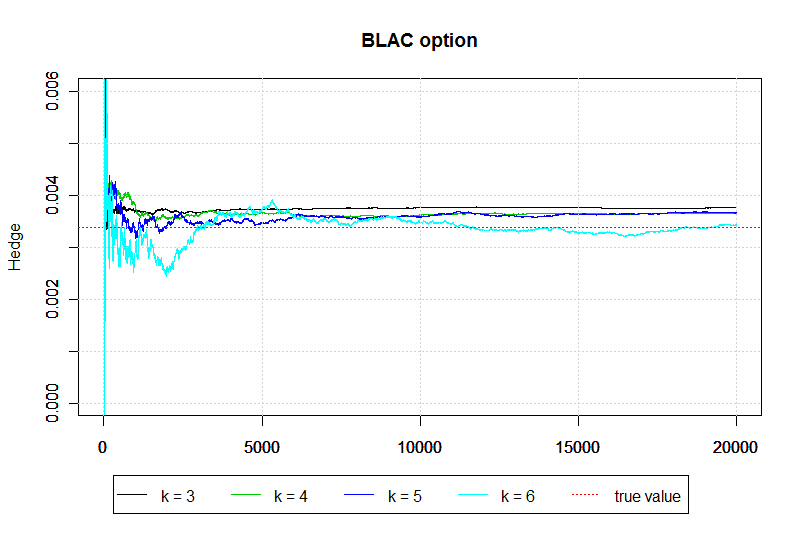
6.2. Hedging Errors.
Next, we present some hedging error results for two well-known non-constant volatility models: The constant elasticity of variance (CEV) model and the classical Heston stochastic volatility model [13]. The typical examples we have in mind are the generalized Föllmer-Schweizer, local risk minimization and mean variance hedging strategies, where the optimal hedging strategies are computed by means of the minimal martingale measure and the variance optimal martingale measure, respectively. We analyze digital and one-touch one-dimensional European-type contingent claims as follows
By using the algorithm described in Section 5, we compute the error committed by approximating the payoff by . This error will be called hedging error. The computation of this error is summarized in the following steps:
-
(1)
We first simulate paths under the physical measure and compute the payoff .
-
(2)
Then, we consider some deterministic partition of the interval [0,T] into points such that , for .
- (3)
-
(4)
We simulate by means of the shifting argument based on the strong Markov property of the Brownian motion as described in Section 4.1.
-
(5)
We compute by
(6.1) -
(6)
Finally, the hedging error estimate and the percentual error are given by and , respectively.
Remark 6.1.
When no locally-risk minimizing strategy is available, we also expect to obtain low hedging errors when dealing with generalized Föllmer-Schweizer decompositions due to the orthogonal martingale decomposition. In the mean variance hedging case, two terms appear in the optimal hedging strategy: the pure hedging component of the GKW decomposition under the optimal variance martingale measure and as described by (1.4) and (1.5). For the Heston model, was explicitly calculated by Hobson [14]. We have used his formula in our numerical simulations jointly with under in the calculation of the mean variance hedging errors. See expression (6.4) for details.
6.2.1. Constant Elasticity of Variance (CEV) model
The discounted risky asset price process described by the CEV model under the physical measure is given by
| (6.2) |
where is a -Brownian motion. The instantaneous sharpe ratio is such that the model can be rewritten as
| (6.3) |
where is a -Brownian motion and is the equivalent local martingale measure. For both the digital and one-touch options, we consider the parameters for the interest rate, (month) for the maturity time, , and such that the constant of elasticity is . We simulate the hedging error along considering discretization levels , and and hedging strategies per day, which means approximately and hedging strategies, respectively, along the interval . From Corollary 4.2, we know that this procedure is consistent. For the digital option, we also recall that the hedging strategy has continuous paths up to some stopping time (see Zhang [27]) so that Theorem 7.2 and Remark 7.2 apply accordingly. The hedging error results for the digital and one-touch options are summarized in Tables 2 and 3, respectively. The standard deviations are related to the hedging errors.
| Simulations | k | Hedges/day | Hedging error | St. dev. | Price | % Error | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simulations | k | Hedges/day | Hedging error | St. dev. | Price | % Error | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
6.2.2. Heston’s Stochastic Volatility Model
Here we consider two types of hedging methodologies: Local-risk minimization and mean variance hedging strategies as described in the Introduction and Remark 6.1. The Heston dynamics of the discounted price under the physical measure is given by
where , , with two independent -Brownian motions and are suitable constants in order to have a well-defined Markov process (see e.g Heston [13]). Alternatively, we can rewrite the dynamics as
where and .
Local-Risk Minimization. For comparison purposes with Heath, Platen and Schweizer [12], we consider the hedging of a European put option written on a Heston model with correlation parameter . We set , strike price , (month) and we use discretization levels and . We set the parameters , , , , and . In this case, the hedging strategy based on the local-risk-minimization methodology is bounded with continuous paths so that Theorem 7.2 applies to this case. Moreover, as described by Heath, Platen and Schweizer [12], can be obtained by a PDE numerical analysis.
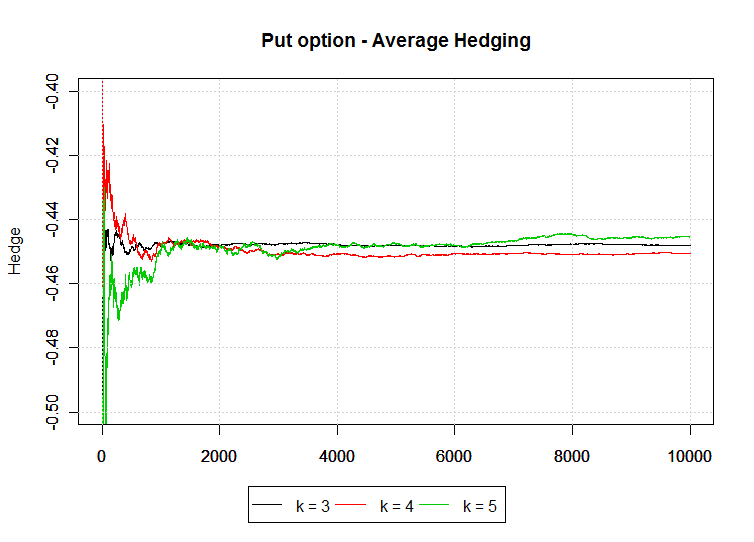
Table 4 presents the results of the hedging strategy by using the algorithm described in Section 5. Figure 2 provides the Monte Carlo hedging strategy with respect to the number of simulations of order . We notice that our results agree with the results obtained by Heath, Platen and Schweizer [12] by PDE methods. In this case, the true value of the hedging at time is approximately . The standard errors in Table 4 are related to the hedging and prices computed, respectively, from the Monte Carlo method described in Section 5.
| k | Hedging | Standard error | Monte Carlo price | Standard error | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
Hedging with generalized Föllmer-Schweizer decomposition for one-touch option. Based on Corollary 4.2, we also present the hedging error associated to one-touch options for a Heston model with non-zero correlation. We simulate the hedging error along the interval using as discretization levels and and hedging strategies per day with parameters , , , , , , and where the barrier is . The hedging error result for the one-touch option is summarized in Table 5. The standard deviations in Table 5 are related to the hedging error.
To our best knowledge, there is no result about the existence of locally-risk minimizing hedging strategies for one-touch options written on a Heston model with nonzero correlation. As pointed out in Remark 6.1, it is expected that pure hedging strategies based on the generalized Föllmer-Schweizer decomposition mitigate very-well the hedging error. This is what we get in the simulation results.
| Simulations | k | Hedges/day | Hedging error | St. dev. | Price | % error | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Mean variance hedging strategy. Here we present the hedging errors associated to one-touch options written on a Heston model with non-zero correlation under the mean variance methodology. Again, we simulate the hedging error along the interval using as discritization levels and and hedging strategies per day with parameters , , , , , , and with barrier 105. The computation of the optimal hedging strategy follows from Remark 6.1. The quantity is not related to the GKW decomposition but it is described by Theorem 1.1 in Hobson [14] as follows. The process appearing in (1.4) and (1.5) is given by
| (6.4) |
where is given by (see case 2 of Prop. 5.1 in Hobson [14])
with , and where . The initial condition is given by
The hedging error results are summarized in Table 6 where the standard deviations are related to the hedging error. In comparison with the local-risk minimization methodology, the results show smaller percentual errors when increases. Also, in all the cases, we had smaller values of the standard deviation which suggests the mean variance methodology provides more accurate values of the hedging strategy.
| Simulations | k | Hedges/day | Hedging error | St. dev. | Price | % error | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
7. Appendix
This appendix provides a deeper understanding of the Monte Carlo algorithm proposed in this work when the representation in (3.6) admits additional integrability and path smoothness assumptions. We present stronger approximations which complement the asymptotic result given in Theorem 3.1. Uniform-type weak and strong pointwise approximations for are presented and they validate the numerical experiments in Tables 1 and 4 in Section 6. At first, we need of some technical lemmas.
Lemma 7.1.
Suppose that is a -dimensional progressive process such that . Then, the following identity holds
| (7.1) |
Proof.
It is sufficient to prove for since the argument for easily follows from this case. Let be the linear space constituted by the bounded -valued -progressive processes such that (7.1) holds with where . Let be the class of stochastic intervals of the form where is a -stopping time. We claim that for every -stopping times and . In order to check (7.1) for such , we only need to show for since the argument for is the same. With a slight abuse of notation, any sub-sigma algebra of of the form will be denoted by where is the trivial sigma-algebra on the first copy .
At first, we split and we make the argument on the sets . In this case, we know that a.s and
The independence between and and the independence of the Brownian motion increments yield
on the set . We also have,
on the set . By construction a.s and again the independence between and yields
on . Similarly,
on . By assumption is an -stopping time, where is a product filtration. Hence, a.s on .
Summing up the above identities, we shall conclude . In particular, the constant process and if is a sequence in such that a.s with bounded, then a routine application of Burkhölder inequality shows that . Since generates the optional sigma-algebra then we shall apply the monotone class theorem and, by localization, we may conclude the proof.
∎
Lemma 7.2.
Let be a one-dimensional Brownian motion and with , . If is an absolutely continuous and non-negative adapted process then there exists a deterministic constant which does not depend on such that
Proof.
For given , Young inequality and integration by parts yield
for some constant which does not depend on . ∎
Lemma 7.3.
Assume that for some . Then there exists a constant such that
Proof.
By repeating the argument employed in Lemma 7.1 for , and , we shall write
Doob maximal inequalities combined with Jensen inequality yield
| (7.2) |
for and for some positive constant . Now, we need a path-wise argument in order to estimate the right-hand side of (7.2). For this, let us define
Lemma 7.2 and the fact that yield
| (7.3) |
where is the constant in Lemma 7.2. Now, by applying Lemma 2.4 in Nutz [21], the estimate (7.3) and a routine localization procedure, the following estimate holds
and therefore
The following result allows us to get a uniform-type weak convergence of under very mild integrability assumption.
Theorem 7.1.
Let be a -square integrable contingent claim satisfying assumption (M) and assume that admits a representation such that for some . Then
weakly in .
Proof.
Let us fix . From Lemma 7.3, we know that is bounded in and therefore this set is weakly relatively compact in . By Eberlein Theorem, we also know that it is -weakly relatively sequentially compact. From Theorem 3.1,
weakly in and since is stronger than , we necessarily have the full convergence
in . ∎
Next, we analyze the pointwise strong convergence for our approximation scheme.
7.1. Strong Convergence under Mild Regularity
In this section, we provide a pointwise strong convergence result for GKW projectors under rather weak path regularity conditions. Let us consider the stopping times
and we set
Here, if satisfies we set and for simplicity we assume that .
Theorem 7.2.
If is a -square integrable contingent claim satisfying (M) and there exists a representation of such that for some and the initial time is a Lebesgue point of , then
| (7.5) |
Proof.
In the sequel, will be a constant which may differ from line to line and let us fix . For a given , it follows from Lemma 7.1 that
| (7.6) |
We recall that so that we shall apply the Burkholder-Davis-Gundy and Cauchy-Schwartz inequalities together with a simple time change argument on the Brownian motion to get the following estimate
| (7.7) |
Therefore, the right-hand side of (7.1) vanishes if, and only if, is a Lebesgue point of , i.e.,
| (7.8) |
The estimate (7.1), the limit (7.8) and the weak convergence of to the initial sigma-algebra yield
strongly in . Since then we conclude the proof. ∎
Remark 7.1.
At first glance, the limit (7.5) stated in Theorem 7.2 seems to be rather weak since it is not defined in terms of convergence of processes. However, from the purely computational point of view, we shall construct a pointwise Monte Carlo simulation method of the GKW projectors in terms of given by (3.5). This substantially simplifies the algorithm introduced by Leão and Ohashi [20] for the unidimensional case under rather weak path regularity.
Remark 7.2.
For each , let us define
One can show by a standard shifting argument based on the Brownian motion strong Markov property that if there exists a representation such that is cadlag for a given then one can recover pointwise in -strong sense the -th GKW projector for that . We notice that if belongs to and it has cadlag paths then is cadlag for each , but the converse does not hold. Hence the assumption in Theorem 7.2 is rather weak in the sense that it does not imply the existence of a cadlag version of .
References
- [1] G. Bernis, E. Gobet, and A. Kohatsu-Higa. Monte carlo evaluation of greeks for multidimensional barrier and lookback options. Mathematical Finance, 13(1):99–113, 2003.
- [2] F. Biagini, P. Guasoni, and M. Pratelli. Mean-variance hedging for stochastic volatility models. Mathematical Finance, 10(2):109–123, 2000.
- [3] Z. A. Burq and O. D. Jones. Simulation of brownian motion at first-passage times. Mathematics and Computers in Simulation, 77(1):64–71, 2008.
- [4] A. Černỳ and J. Kallsen. On the structure of general mean-variance hedging strategies. The Annals of probability, 35(4):1479–1531, 2007.
- [5] A. Černỳ and J. Kallsen. Mean–variance hedging and optimal investment in heston’s model with correlation. Mathematical Finance, 18(3):473–492, 2008.
- [6] C. Dellacherie and P.-A. Meyer. Probabilities and Potential, volume B. Amsterdam, North-Holland, 1982.
- [7] C. Dellacherie, P.-A. Meyer, and M. Yor. Sur certaines proprietes des espaces de banach et bmo. Séminaire de Probabiltés, XII (Univ. Strasbourg, Strasbourg 1976/1977), 649:98–113, 1978.
- [8] H. Föllmer and M. Schweizer. Hedging of contingent claims under incomplete information. Applied Stochastic Analysis, Stochastic Monographs, 5:389–414, 1991.
- [9] H. Föllmer and D. Sondermann. Hedging of non-redundant contingent claims. Contributions to Mathematical Economics, pages 205–223.
- [10] C. Gourieroux, J. P. Laurent, and H. Pham. Mean-variance hedging and numéraire. Mathematical Finance, 8(3):179–200, 1998.
- [11] Sheng-wu He, Chia-kang Wang, and Jia-an Yan. Semimartingale theory and stochastic calculus. 1992.
- [12] D. Heath, E. Platen, and M. Schweizer. A comparison of two quadratic approaches to hedging in incomplete markets. Mathematical Finance, 11(4):385–413, 2001.
- [13] S. L. Heston. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Review of financial studies, 6(2):327–343, 1993.
- [14] D. Hobson. Stochastic volatility models, correlation, and the q-optimal measure. Mathematical Finance, 14(4):537–556, 2004.
- [15] M. Jeanblanc, M. Mania, M. Santacroce, and M. Schweizer. Mean-variance hedging via stochastic control and bsdes for general semimartingales. The Annals of Applied Probability, 22(6):2388–2428, 2012.
- [16] J. Kallsen, J. Muhle-Karbe, and R. Vierthauer. Asymptotic power utility-based pricing and hedging. Mathematics and Financial Economics, pages 1–28, 2009.
- [17] J. Kallsen and R. Vierthauer. Quadratic hedging in affine stochastic volatility models. Review of Derivatives Research, 12(1):3–27, 2009.
- [18] D. Kramkov and M. Sirbu. Sensitivity analysis of utility-based prices and risk-tolerance wealth processes. The Annals of Applied Probability, 16(4):2140–2194, 2006.
- [19] D. Kramkov and M. Sirbu. Asymptotic analysis of utility-based hedging strategies for small number of contingent claims. Stochastic Processes and their Applications, 117(11):1606–1620, 2007.
- [20] D. Leão and A. Ohashi. Weak approximations for wiener functionals. The Annals of Applied Probability, 23(4):1660–1691, 2013.
- [21] M. Nutz. Pathwise construction of stochastic integrals. Electronic Communications in Probabilidy, 17(24):1–7, 2012.
- [22] T. Rheinländer and M. Schweizer. On -projections on a space of stochastic integrals. The Annals of Probability, 25(4):1810–1831, 1997.
- [23] M. Schweizer. Option hedging for semimartingales. Stochastic Processes and their Applications, 37:339–363, 1991.
- [24] M. Schweizer. On the minimal martingale measure and the föllmer-schweizer decomposition. Stochastic Analysis and Applications, pages 573–599, 1995.
- [25] M. Schweizer. Approximation pricing and the variance-optimal martingale measure. The Annals of Probability, 24(1):206–236, 1996.
- [26] M. Schweizer. A guided tour through quadratic hedging approaches. Option Pricing, Interest Rates and Risk Management, In Jouini, E. Cvitanic, J. and Musiela, M. (Eds.), pages 538–574, 2001.
- [27] J. Zhang. Representation of solutions to bsdes associated with a degenerate fsde. The Annals of Applied Probability, 15(3):1798–1831, 2005.