A graph discretization of vector Laplace operator

In Mathematics and Physics, Laplace’s equation is one of the most famous differential equation named after Pierre-Simon de Laplace, who firstly presented and investigated its properties. In general, this is often written as

where $\nabla^{2}$ is the Laplace operator (or Laplacian) operating a scalar function $f$. With that in mind, the Laplacian is also referred to as scalar Laplacian. In the context of real space $\mathbb{R}^{3}$ and rectangular coordinates, then

where $\operatorname{div}=\nabla\cdot$ and $\operatorname{grad}=\nabla$ are respectively the divergence and gradient operators. Recall,

where $\mathbf{F}$ is a vector field.

In the setting of Graph Theory, the scalar Laplacian $\nabla^{2}=-{\rm div\!~{}grad}$ gives the celebrated Laplacian matrix of a graph [8, Lemma 5.6, eg.], defined by

where $D(G)={\rm diag}(d(v_{1}),d(v_{2}),\cdots,d(v_{n}))$ is the degree diagonal matrix with $d(v)$ being the degree of vertex $v$ and $A(G)=(a_{ij})$ is the adjacency matrix of $G$ in which $a_{ij}=1$ if $v_{i}v_{j}\in E(G)$ and $0$ otherwise. Proverbially, the graph Laplacian has been studied extensively in Spectral Graph Theory and has so much influence on many areas. For good survey articles on the graph Laplacian the reader is referred to [10, 11].

We here pay attention to the vector Laplacian. In $\mathbb{R}^{3}$, the curl of a vector field $\mathbf{F}$ is defined to be

Then the vector Laplace equation is defined as

A straightforward calculation shows that

which is called vector Laplace operator (or vector Laplacian [12]) or Helmholtz operator [6];.

What is clear from the literature is that the operators involving $\nabla^{2}=\nabla\cdot\nabla$ on a vector function start back in 1911 [3, p133]. However, the difference between the scalar and vector Laplacians was not unrecognized in a long period, which caused that the progress in this direction had been hampered. The meaning of the vector Laplacian was not clear untill 1953, credit to Moon and Spencer [12], who developed a general equation for the vector Laplacian in any orthogonal, curvilinear coordinate system. Remark that the scalar and vector Laplacians are special cases of Hodge Laplacians, named from the Hodge theory on graphs [8], and that the Laplace equation and vector Laplace equation are respectively the special cases of Helmholtz equations

in which $\theta$ is a scalar function or a vector field.

For the purpose here, we consider the adjoint operators of $\operatorname{grad}$ and $\operatorname{curl}$ denoted by $\operatorname{grad}^{*}$ and $\operatorname{curl}^{*}$ respectively. Due to $\operatorname{div}=-\operatorname{grad}^{*}$ and $\operatorname{curl}=\operatorname{curl}^{*}$ [16, pp. 207], then an equivalent expression of (2) is shown as follows

In this paper, we fucus on the graph-theoretic analogues of vector Laplacian and vector Laplace equation. In Section 2 we determine the graph matrix representation, Helmholzian matrix, of vector Laplacian, which put the way for establish a spectral graph theory based on this new matrix. In Section 3 we identify the dimension of solution space of vector Laplace equation on graphs. As a corollary, the number of triangles in a graph is also obtained. In Section 4 we give some remarks and point out some potential applications of the results obtained in this paper.

Let $G=(V(G),E(G))$ be an undirected simple graph with vertex set $V(G)=\{v_{1},v_{2},\cdots,v_{n}\}$ and edge set $E(G)=\{e_{1},e_{2},\cdots,e_{m}\}$, where its order is $n=|V(G)|$ and its size is $m=|E(G)|$. Let $T$ be the set of triangles in $G$. We define the real valued functions on its vertex set $\phi:V\rightarrow R$. Moreover, we request the real valued functions on $E$ and $T$ to be alternating. By an alternating function on $E$, we mean a function of the form $\varphi:V\times V\rightarrow\mathbb{R}$, where

An alternating function on $T$ is one of the form $\psi:V\times V\times V\rightarrow\mathbb{R}$, where

From the topological point of view, the functions $\phi,\varphi$ and $\psi$ are called 0-, 1-, 2-cochains, which are discrete analogues of differential forms on manifolds [17]. Let the Hilbert spaces of $0$-, $1$- and $2$-cochains be respectively $L^{2}(V)$, $L^{2}_{\wedge}(E)$ and $L^{2}_{\wedge}(T)$ with $\wedge$ indicating alternating and with standard $L^{2}$-inner products defined by

We describe the graph-theoretic analogues of $\operatorname{grad}$, $\operatorname{curl}$, and $\operatorname{div}$ in multivariate calculus [8]. The gradient is the linear operator grad: $L^{2}(V)\rightarrow L_{\wedge}^{2}(E)$ defined by

for all $\{i,j\}\in E$ and zero otherwise. The curl is the linear operator curl: $L_{\wedge}^{2}(E)\rightarrow L_{\wedge}^{2}(T)$ defined by

for all $\{i,j,k\}\in T$ and zero otherwise. The divergence is the linear operator div: $L_{\wedge}^{2}(E)\rightarrow L^{2}(V)$ defined by

for all $i\in V$. Then the graph-theoretic analogue of the vector Laplacian, called graph Helmholtzian, is defined by $\Lambda=-\operatorname{grad}\operatorname{div}+\operatorname{curl^{\ast}}\operatorname{curl}$ [8, pp. 692]. From $\operatorname{div}=-\operatorname{grad^{\ast}}$ [8, Lemma 5.4] it follows that $\Lambda$ can be expressed as

Note, Helmholtz Decomposition Theorem for the clique complex of a graph correlates closely with the kernel of graph Helmholtzian $\Lambda$ [6, Theorem 2]. In addition, the graph Helmholtzian is a special case of Hodge Laplacians, a higher-order generalization of the graph Laplacian, due to Lim [8].

We emphatically derive a graph matrix representation of graph Helmholtzian. Given arbitrary orientations to the edges and triangles of $G$, the trail and the head of an oriented edge $e$ are respectively marked by $e^{-}$ and $e^{+}$. Set $\mathcal{V}(e)=\{e^{-},e^{+}\}$. If there is a directed edge from $u$ to $v$, then we write $u\rightarrow v$. If two vertices $u$ and $v$ are adjacent, then we write $u\sim v$, and $u\nsim v$ otherwise. Therefore, $u\sim v$ implies either $u\rightarrow v$ or $v\rightarrow u$. If a vertex $v$ satisfies $v\in\mathcal{V}(e)$, then we write $v\in e$. Furthermore, set $v\rightarrow e$ if $v=e^{-}$, and $e\rightarrow v$ if $v=e^{+}$. For two edges $e_{1}$ and $e_{2}$, let $e_{1}\sim e_{2}$ if $\mathcal{V}(e_{1})\cap\mathcal{V}(e_{2})\neq\emptyset$. Put $e_{1}\rightarrow e_{2}$ if $e_{1}^{+}=e_{2}^{-}$, $e_{1}\overset{+}{\sim}e_{2}$ if $e_{1}^{+}=e_{2}^{+}$, and $e_{1}\overset{-}{\sim}e_{2}$ if $e_{1}^{-}=e_{2}^{-}$. Denote by $e_{1}\leftrightarrow e_{2}$ if either $e_{1}\rightarrow e_{2}$ or $e_{2}\rightarrow e_{1}$, and denote by $e_{1}\overset{\pm}{\sim}e_{2}$ if either $e_{1}\overset{+}{\sim}e_{2}$ or $e_{1}\overset{-}{\sim}e_{2}$. Set $e_{1}\vartriangle e_{2}$ if $e_{1}$ and $e_{2}$ are in a same triangle. For an edge $e$ and a triangle $\vartriangle$, write $e\in\vartriangle$ if $e$ is an edge of $\vartriangle$. Furthermore, if the orientation of $e$ is coincident with that of $\vartriangle$ then we write $e\in\vartriangle^{+}$, and $e\in\vartriangle^{-}$ otherwise. To make the symbols more clear, we collect them in Tab. 1.

For an edge $e\in E(G)$, the triangle degree of $e$, denoted by $\triangle_{G}(e),$ is the number of triangles containing $e$, that is,

The edge-vertex incidence matrix $\mathcal{B}(G)=(b_{ev})_{m\times n}$ and triangle-edge incidence matrix $\mathcal{C}(G)=(c_{\vartriangle e})_{t\times m}$ are severally defined by

whose examples are given in Fig. 1.

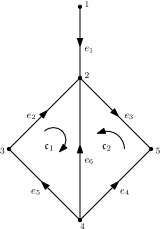
The lemma below indicates the relations among the operators and matrices mentioned above.

Clearly, the graph-theoretic analogue of vector Laplace equation (2) is

Hereafter, we determine the dimension $\dim{\mathcal{V}_{0}}$ of solution space $\mathcal{V}_{0}$ of (7). Since $\mathcal{H}(G)$ is diagonalizable, then $\dim{\mathcal{V}_{0}}$ is equal to the algebraic multiplicity of eigenvalues $0$, which is said to be nullity of a graph $G$. Denoted by $\eta_{M}(G)$ the nullity of a graph $G$ with respect to a graph matrix $M(G)$. For the adjacency matrix $A(G)$, Collatz and Sinogowitz [4] first posed the problem of characterizing all graphs with $\eta_{A}(G)>0$. This question has strong chemical background, because $\eta(G)=0$ is a necessary condition for a so-called conjugated molecule to be chemically stable, where $G$ is the graph representing the carbon-atom skeleton of this molecule. For the Laplacian matrix $L(G)$, it is well-known that the nullity of a graph is exactly the number of its connected components.

We next determine $\eta_{\mathcal{H}}(G)$ involving the order, the size and the number of triangles of $G$.

Note that ${\rm rank}(\mathcal{B}^{\top}(G))={\rm rank}(\mathcal{B}(G))$ and ${\rm rank}(\mathcal{C}(G))=t_{G}(\triangle)$, the number of triangles in $G$. Thus we get the following result immediately.

For a vertex $v$ of a graph $G$, let $N_{G}(v)$ denote the set of the neighbours of $v$. If $e=uv$ such that $N_{G}(u)\cap N_{G}(v)=\emptyset$, the contraction of $e$ is the replacement of $u$ and $v$ with a single vertex whose incident edges are the edges other than $e$ that are incident to $u$ or $v$, and the resulting graph is denoted by $G/e$.

The following result follows from the above lemma.

The next result follows from the fact that each edge of a tree is a cut-egde and using Corollary 3.5 repeatedly.

Our main result in this subsection is shown as follows.