High-order, conservative local time-stepping W. Throwe and S. A. Teukolsky
A high-order, conservative integrator with local time-stepping††thanks: Submitted to the editors 10 October 2019. \funding This work was supported in part by the Sherman Fairchild Foundation and NSF grants PHY-1606654 and ACI-1713678 at Cornell.
Abstract
We present a family of multistep integrators based on the Adams-Bashforth methods. These schemes can be constructed for arbitrary convergence order with arbitrary step size variation. The step size can differ between different subdomains of the system. It can also change with time within a given subdomain. The methods are linearly conservative, preserving a wide class of analytically constant quantities to numerical roundoff, even when numerical truncation error is significantly higher. These methods are intended for use in solving conservative PDEs in discontinuous Galerkin formulations or in finite-difference methods with compact stencils. A numerical test demonstrates these properties and shows that significant speed improvements over the standard Adams-Bashforth schemes can be obtained.
keywords:
local time-stepping, multirate time integration, Adams methods, adaptive time stepping, conservation laws65L06, 65L60, 65M20, 65M60, 65Z05
1 Introduction
A common problem in computational fields is to find approximate solutions to partial differential equations (PDEs). For hyperbolic PDEs, where a solution typically describes an evolution of one or more fields through time, the most common approach is to apply the method of lines, where the spatial coordinates in the PDE are discretized, producing a large system of coupled ordinary differential equations (ODEs) with one degree of freedom per variable per grid point. These systems of equations can then be discretized in time and solved using standard explicit integration schemes.
In order to obtain an accurate solution, it is a necessary condition that the time discretization must be fine enough for the integration to be stable. For a method-of-lines system, this limit is primarily because of the Courant-Friedrichs-Lewy (CFL) condition, which limits the step size to approximately the information propagation time between grid points. The resulting step size can show large variation across the spatial domain because of changes in the propagation speed or, more commonly, because of changes in the spacing of the evaluation points. It is often desirable to increase the density of points in some regions to resolve rapidly varying parts of the solution, but this then restricts the step size allowed for stability. Furthermore, in order to evaluate the system right-hand side, it is necessary to know the entire state of the system at the time of interest. The time step for the whole system is then set by the most restrictive of the conditions over the entire domain. If the problematic points make up a small fraction of the system, then the forced evaluations at the remaining points can dominate the computational expense.
To reduce the computational cost of finding these solutions, we would like to evaluate each point at intervals set by its own stability limit, rather than the smallest limit for all the points. A method allowing this is known as a local time-stepping (LTS) (or multirate) method, as opposed to a global time-stepping (GTS) method. Such a method must describe an update scheme for the frequently evaluated degrees of freedom that does not require knowing the full state of the system.
Modifying a GTS method into an LTS one can have significant drawbacks. The individual steps near locations of time step changes are typically more expensive than for a GTS method, so the benefit of fewer derivative evaluations must outweigh this overhead. Care must be taken when calculating the CFL limit near step size changes to take into account variations in the characteristic speeds of the system in the neighborhood of the element. [13] Furthermore, modifying the GTS scheme can destroy numerically desirable properties of the integrator, such as a high convergence order. LTS schemes also do not naturally provide exact conservation of linear conserved quantities [25], a property usually guaranteed by GTS integrators. In a physical system, errors accumulated in these quantities (which can represent, for example, total mass) can produce an approximate solution qualitatively different from the true solution.
Early LTS schemes (for example [4, 12]) typically used GTS integrators with different time steps and performed interpolation to obtain data at times at which it was not produced directly. Such schemes are easy to adapt to arbitrary mesh configurations and can be constructed to obtain the same convergence order as the underlying GTS method, but they do not preserve conserved quantities of the system. Corrections to more accurately treat conservation laws were developed [3], but still only resulted in approximate conservation.
More recently, many methods have been investigated as starting points for more sophisticated LTS methods, including both substep [21, 11, 14, 10, 17, 2] and multistep [25, 16, 29] integrators and also less common methods such as leapfrog [16, 15], Richardson extrapolation [8], ADER [27], and implicit methods [6]. Demirelet al. [9] have even explored LTS schemes constructed from multiple unrelated GTS integrators. Recently, Günther and Sandu [17] presented a very general family of multirate Runge-Kutta-like methods based on the GARK family of integrators [26] that unifies many of the previous Runge-Kutta-based LTS schemes. These methods are applicable to any problem and can be constructed to have any order of accuracy, but they are not conservative. Sandu and Constantinescu [25] presented an Adams-Bashforth-based scheme based on evaluating the right-hand side of the evolution equations using a combination of data at different times. This system is conservative and applicable to any system of equations, but the method is limited to second-order accuracy at times at which all degrees of freedom are evaluated and first-order accuracy at intermediate times.
LTS integrators for the special case of linear systems have been developed based on Adams-Bashforth [16], Runge-Kutta [14, 2], and leapfrog [16, 15] schemes. Of particular interest here, starting from the Adams-Bashforth methods, Grote and Mitkova [16] found a family of high-order, conservative methods for integer ratios between step sizes on different degrees of freedom. These methods use the linearity of the system to split the equations into a form resembling multiple copies of the standard Adams-Bashforth method.
Some authors have derived methods specialized to the discontinuous Galerkin or finite volume formalisms. The structure of elements coupled comparatively weakly in a standard way by exchange of fluxes allows for some simplifications to the problem. Winters and Kopriva [29] presented a scheme using dense output of the integrators for each element to calculate fluxes at intermediate times. This scheme is high-order and allows for arbitrary step ratios and varying time steps, but it sacrifices the conservative nature of its parent scheme. Gassneret al. [11] presented a similar method, but restored conservation by treating the element and flux terms as a predictor and corrector. Krivodonova [21] constructed a method based on a Runge-Kutta integrator which, while not naturally conservative, was made so by adding a correction to cancel any error in conservation whenever neighboring cells are aligned in time. Cavalcantiet al. [5] considered the addition of nonlinear operations, such as slope limiting, to the integration step.
In this paper we present a high-order, conservative scheme based on the Adams-Bashforth family of explicit multistep methods capable of solving any explicit initial value problem. The method uses the idea of performing single right-hand side evaluations using values from different times, in a similar manner to previous work presented by Sandu and Constantinescu [25]. The scheme is conservative and has the same convergence order as the Adams-Bashforth integrator it is based on. The method allows for generic ratios of step sizes between different degrees of freedom, as well as for arbitrarily varying the time steps of the individual degrees of freedom. The applications discussed here are to discontinuous Galerkin methods, but the method can also be applied to finite-difference schemes with compact stencils. (Although the method is in principle fully general for any explicit initial value problem for a set of coupled ODEs, in practice it becomes extremely inefficient if the spatial couplings are non-local.) When applied to a linear system with integer step size ratios, this scheme reduces to the Adams-Bashforth-based scheme presented by Grote and Mitkova [16].
Throughout this work, we refer to approximations with leading order error proportional to as “order-” approximations or as “accurate to order .” Thus, a single step of order- Adams-Bashforth is an order- approximation of the new value.
The remainder of this paper is structured as follows: Section 2 presents a derivation of the integration scheme. Section 3 discusses simplifications that are applicable when the method is applied to some common special cases. Section 4 applies the method to numerical test cases. Appendices A and B demonstrate the consistency of the method and compute the leading order error term. Appendix C provides a method of writing common GTS integrators in a form mathematically similar to the LTS integrator presented here. Finally, Appendix D lists specific formulas for methods of order 2, 3, and 4.
2 The method
2.1 Adams-Bashforth methods
Suppose we wish to numerically solve a set of coupled first-order ordinary differential equations
| (1) |
with at some initial time . Here , the time-derivative operator, is the right-hand side evaluated when the system is in state . (Throughout this work we will restrict our attention to autonomous systems. As any non-autonomous system can be recast in an autonomous form (see, for example, Section II.2 of [18]) we lose no generality from this restriction.) A common method is to solve for the variables at a (monotonic) sequence of times using a th-order Adams-Bashforth method
| (2) |
with , and the coefficients corresponding to the step given by [29]
| (3) |
Here
| (4) |
are Lagrange polynomials. The values required for evaluating the first step can be obtained using a standard Adams-Bashforth GTS self-start procedure [23], after which the step sizes can be adjusted to the desired ratio.
If different degrees of freedom require different time steps for stability, it may be desirable to evaluate these variables at different frequencies, in order to avoid unnecessary computations for the more stable variables. Suppose we divide the components of into sets , each of which is a collection of degrees of freedom that are always evaluated at the same times, . We can then split (1) into an equation for each of these sets:
| (5) |
where is the result of restricted to the set . Any attempt to use this equation to perform an LTS evolution immediately encounters the problem that evaluating its right-hand side requires knowing the entire state of the system, which conflicts with the goal of independent evaluation times for different degrees of freedom.
2.2 Conserved quantities
A linear conserved quantity is a quantity expressible as an inner product of a vector with the evolved variables (treated as a vector)
| (6) |
with
| (7) |
for all values of . Such a quantity is constant under exact integration of the system and under integration using Euler’s method. An integrator is called (linearly) conservative if all such quantities remain constant when integrating a system using it [28]. It is desirable for an integrator to keep such quantities precisely constant (up to roundoff error) rather than merely constant up to the truncation error of the scheme. Such quantities often have an intuitive physical meaning, and frequently even a small rate of drift can cause qualitative changes in the evolution of the system.
When solving a PDE representing a physical system, the most common linear conserved quantities are integrals over the computational domain of fields representing densities. The vector in these cases is the vector of coefficients necessary to perform a numerical integral. In a discontinuous Galerkin scheme these coefficients would combine quadrature weights on the elements and factors arising from coordinate mappings of the elements relative to their canonical shapes.
2.3 Second-order stepping
Let us first consider as an example the case of a second-order scheme on two sets, and , with being evaluated twice as often as . Call their step sizes and . This step pattern is shown in Figure 1, where for simplicity we consider the steps starting from leading up to . There are three types of steps to consider: the large step on set , labeled , and the first and second halves of that step on set , labeled and . This case is considered in Sandu and Constantinescu [25], but the method presented there only provides a second-order value when sets have stepped to the same time; intermediate values are only accurate to first order.
We will start with the small step . For a GTS Adams-Bashforth method, this step would be given by
| (8) |
where is an approximation to the derivative at time that we will now construct.
At time we have values for the entire system, so we can obtain a derivative by applying the derivative operator to the initial data, so we take . We cannot evaluate in this manner, however, because we do not have data for at , so we must construct it from the values at and . Up through this point, the derivation matches the results of Sandu and Constantinescu [25], but they now choose to use the known value of to evaluate the derivative, while we will search for a more accurate approximation. There are two reasonable choices of how to do this: average the known values of to get a value at the desired time and use that to apply the derivative operator, or apply the derivative operator at both times (using the value of at both times) and average the results. We choose the latter, taking , so (8) becomes
| (9) |
The error in averaging the derivatives is of order , so it introduces an error of order in the value after the step, preserving the second-order quality of the base GTS method.
The second small step, , proceeds similarly, except that we now use a derivative at instead of . Instead of averaging the derivatives at different we must therefore perform a (linear) extrapolation to obtain our approximate derivative . Thus, we obtain the rule
| (10) |
We could use the same procedure to evaluate the large step , but, as this would not take into account the value used for taking the second small step, there is no way this procedure could be conservative. This, however, gives us a hint as to how to proceed: we treat the large step as having two internal steps, one for balancing each of the small steps. In fact, in order to remain conservative, we must take each of these internal steps using the same scheme as for the corresponding small step, except using the part of the derivative corresponding to set . This can be seen by considering a generic pair of methods for a step: , where the are given coefficients and the are vectors obtained in some manner from the known values of . The change in a linear conserved quantity during that step is
| (11) | ||||
| (12) |
The first term vanishes by (7), so the only way for two sets to take equal-sized steps in a conservative manner is if they use the same step rule. The procedure for the large step can therefore be found by summing (9) and (10), giving
| (13) |
Note that the coefficients have changed by a factor of compared to the previous equations because of the change of the leading coefficient to . As the two small steps were accurate to second order and this is effectively their concatenation, it is also accurate to second order. A detailed analysis of the consistency and convergence of the general method described below, of which this is a special case, is presented in Appendix A.
2.4 Conservative time steppers
Let us turn now to the task of finding a general conservative, high-order LTS integrator. First, we will consider the implications of requiring an Adams-Bashforth-like LTS scheme to be conservative. For such a scheme it only makes sense to evaluate (6) at times at which all the degrees of freedom are evaluated. We therefore introduce a new quantity that is defined for the entire set of degrees of freedom for each time at which any set is evaluated, and is equal to the (as yet unknown) complete numerical solution at all grid points wherever it exists. If we provide a rule to compute from earlier values then, as long as portions of that do not correspond to values in one of the are never used, we can obtain an LTS method by summing the between evaluations. Furthermore, if the step from to is conservative, then the implied full method will be as well.
The condition for this small step to be conservative is
| (14) |
This is satisfied if we evaluate using a standard Adams-Bashforth method, but that would require values of that are not included in any of the . Comparing (7) and (14), we see that we will obtain a conservative method if we take
| (15) |
for some coefficients . The choices of these coefficients are not unique, but there is a natural choice. We evaluate each step using a standard order- Adams-Bashforth scheme, but instead of using the derivatives of the function that we cannot evaluate, we use approximate derivatives . As long as these are accurate to order , we will lose no formal accuracy for the step. We evaluate by treating as a function of the times independently, and then performing a multidimensional interpolation from the known values in the space of the evaluation times on each set. To obtain the required accuracy, we must use evaluations from at least times from each set, and it is natural to choose the most recent values. The known values of then form a lattice in the multidimensional space. Multidimensional interpolation from such a lattice is not unique, but a natural choice is to perform it as a series of one-dimensional interpolations.111This freedom arises from the fact that the system of equations defining this interpolation is underdetermined for and greater than 1: we must find fitting coefficients but there are only monomial terms of degree less than (which are the ones relevant for an order fit). A general choice of interpolation coefficients will result in an interpolating polynomial containing all terms of degree less than in each of the individually. We therefore have the freedom to modify the interpolation coefficients as long as the modification alters only terms in the interpolating polynomial of total degree at least . This freedom could be used, for example, to set certain coefficients to zero to reduce the number of computations required or to decrease the effect of terms where the times on different sets have large mismatches. In the case where the step size on each set is constant, the alternative sets of interpolation coefficients can be obtained by adding high-order products of discrete Chebyshev polynomials [7] to the coefficients in (19). In the general case we know of no simple method to calculate alternative coefficients. We have not investigated the use of such alternative coefficients in either of these cases. Combining all these ideas, we have
| (16) |
where are Adams-Bashforth coefficients corresponding to the sequence of times and is defined by , i.e., it is the index of the last evaluation on set that can influence the step (see Figure 2). The interpolation coefficients are given by
| (17) |
For computational purposes, it is useful to rewrite these steps as
| (18) |
where the coefficient is
| (19) |
The full change in the value of a given set of degrees of freedom over an entire step can then be obtained by summing the contributions of all these small steps. This will give for each set of degrees of freedom an equation of the form
| (20) |
for some coefficients . Setting (20) equal to this sum over (18) gives the coefficients
| (21) |
3 Application to nearest-neighbor couplings
3.1 Element splitting
The equations (20) involve many more evaluations of the derivative than the standard GTS Adams-Bashforth method, so in this form the LTS method is unlikely to be more efficient. However, if the couplings between the sets of degrees of freedom are inexpensive to calculate compared to the interactions within each set, then the required number of evaluations can be reduced.. Let us suppose that the derivative on set is split into a “volume” portion depending only on set itself and a “boundary” portion encoding the coupling to other sets:
| (22) |
These names are motivated by finite volume and discontinuous Galerkin methods, where the terms from the interior and boundaries of elements split in this manner. Substituting (22) into (18) and summing over the small steps, the volume contribution to the full step on set is
| (23) |
where is defined by (see Figure 2). This is the same form as the GTS Adams-Bashforth method (2) using the bracketed expression as coefficients (absorbing the factor). The bracketed expression does not depend on the form of the derivative, so to evaluate it we can take the boundary coupling to be zero, in which case this is the only contribution to the step. As this is then a th-order GTS method and the Adams-Bashforth method is the unique th-order method of this form, the bracketed quantity must be the standard Adams-Bashforth coefficient. Returning to the general case with a coupling, this shows that a set of degrees of freedom can be evolved using the standard Adams-Bashforth method for the volume portion with only the coupling terms evaluated using (18).
This simplification applies in intermediate cases as well: if the full derivative can be split into portions each of which depends on only some of the degree-of-freedom sets, each of those contributions to the step can be calculated independently using (18) ignoring non-contributing sets. In calculations where the sets are only coupled pairwise, this implies that only the case need be considered.
3.2 Two-set case
As mentioned previously, a major intended application of this time-stepping scheme is to evolution of PDEs using discontinuous Galerkin methods. In such a method, the sets of degrees of freedom are only coupled pairwise and the update method reduces to a collection of standard Adams-Bashforth methods and LTS methods with . For the two-set case, we call the sets and and define the selection functions , , and to be one if is an evaluation time for only set , only set , or both sets, respectively. By construction, a time evaluated on neither set can never occur. These selection functions sum to one, so we can write with
| (24) |
By the definition of , is not older than , so, from the construction of the we see that . This implies that if is an evaluation time for either set, it is one of the control points in the corresponding Lagrange polynomial. We can therefore collapse those polynomials to obtain
| (25) | ||||
| (26) | ||||
and . The expressions should be taken to be zero when the conditionals on the right are not satisfied. Some example values are shown in Tables 1 and 2. The meaning of, for example, the first entry for (a) in Table 1 is that in (20) the coefficient (where we have chosen to number the steps starting from so the step on set at is step 1), so the equation for this step begins
| (27) |
Similarly, the lower-left entry for (c) in Table 2 indicates that one term in the second small step is
| (28) |
Additional tables of coefficients can be found in Appendix D.
(a) (b) (c)
(a) (b) (c)
4 Numerical results
We tested this scheme on a set of field equations evaluated using discontinuous Galerkin methods. In a DG formulation, the domain of evolution is divided into elements, with each element containing a collection of nodes. The evolution equations are evaluated locally within each element and this collection of partial solutions is coupled by adding additional terms at the element boundaries obtained from comparison with neighboring elements. The problem therefore naturally splits as described in Section 3.1, with each element being evolved using a standard GTS method and the couplings using the LTS equations.
4.1 Convergence
For our first test problem, we wanted a simple nonlinear problem to test the convergence and conservation properties of the method. Accordingly, we evolved the Burgers equation:
| (29) |
The DG elements were coupled using the numerical flux of Harten, Lax, and van Leer [19]. In the common case where the solution has the same sign on both sides of the interface between two elements, this reduces to an upwind flux. For this PDE, the spatial integral of the field is a linear conserved quantity, and this carries over to the discretized system when using a DG scheme.
For our first test, we considered the exact solution
| (30) |
We used the analytic value of as an initial condition and evolved from to on the interval , with free boundary conditions. The interval was divided into 16 elements of equal size, each of which contained 10 nodes distributed as Legendre-Gauss-Lobatto points. These values reduce the spatial truncation error to approximately , smaller than the floating-point roundoff error, so it can be ignored for this analysis.
To simplify bookkeeping, the size of each time step was restricted to be a power of two, but each element was allowed to independently adjust its step size to conform to the CFL limit. We found that increasing the step size too rapidly led to a growth in the error, so each step size increase was limited to a factor of two and an increase was only allowed if the previous steps were all of the same size, where is the integration order. All elements were initialized with a very small time step of . Figure 3 shows a typical step pattern.
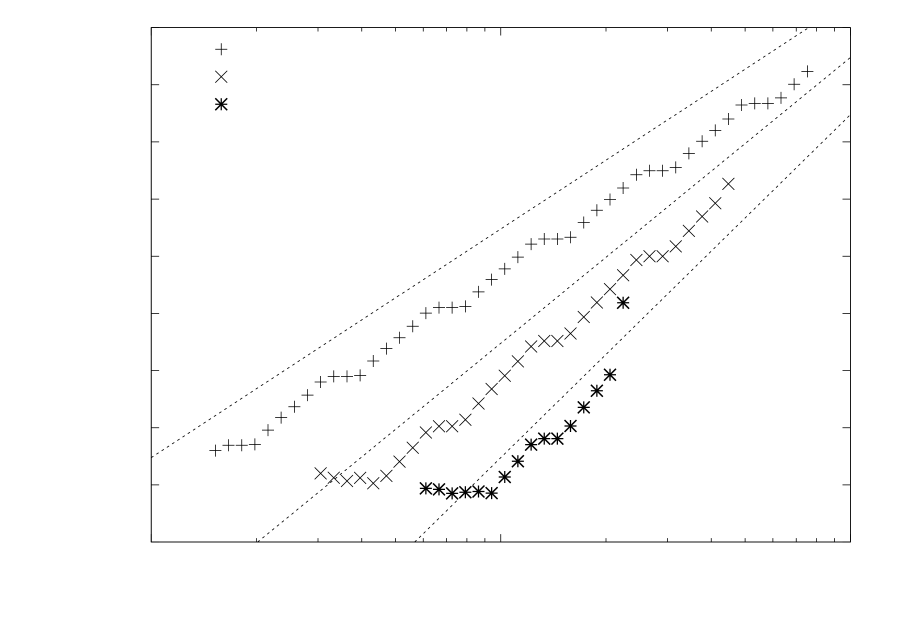
The sole characteristic speed in the Burgers system is , so the CFL condition predicts that the stable step size will be proportional to . The coefficient of proportionality can be estimated from the point distribution and properties of the time stepper, but in order to investigate the convergence of the method we kept it as a free parameter. The convergence as a function of this parameter is shown in Figure 4.
4.2 Conservation
The previous test does not demonstrate conservation because of flow through the domain boundaries. To eliminate this effect, we perform an evolution of the Burgers equation on a periodic domain. We use the same domain decomposition as for the previous example, but identify the endpoints at and . We initialize the field at to
| (31) |
The exact evolution of these initial conditions forms a shock at
| (32) |
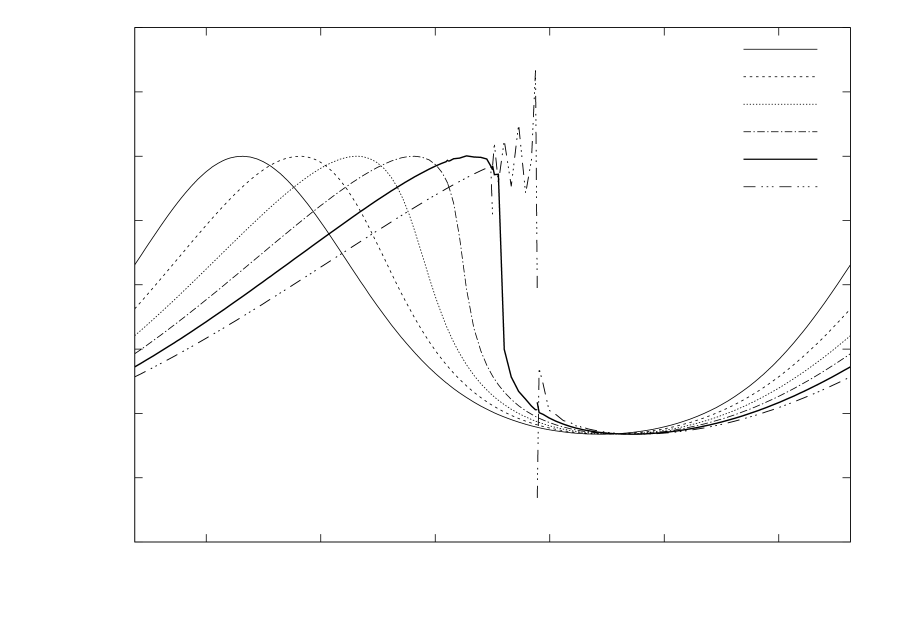
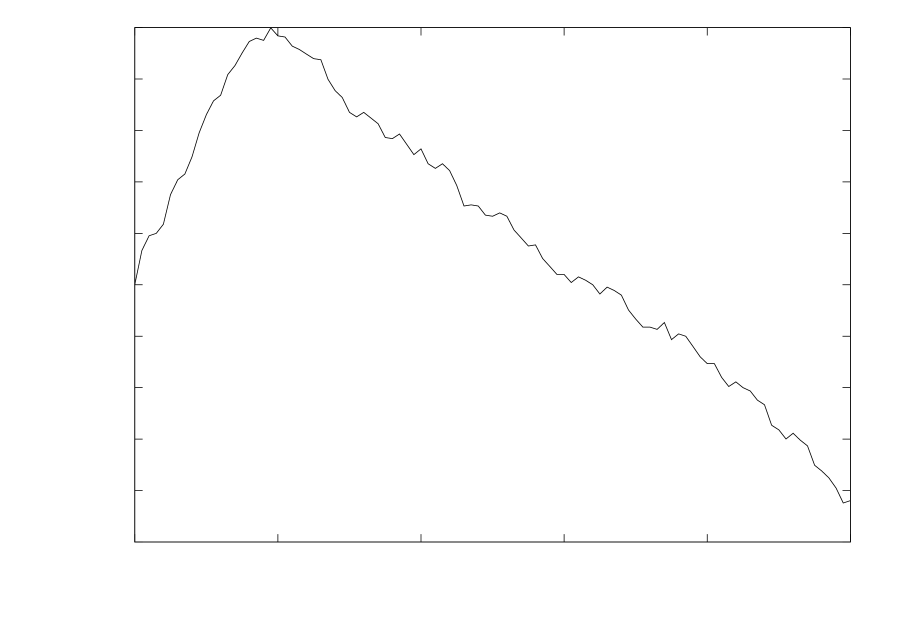
and the numerical evolution becomes poorly behaved at approximately that time as shown in Figure 5. This results in the fluctuating time steps visible in Figure 6. Despite the large departure from the correct solution, we find that the integral of is conserved to within a few orders of magnitude of machine epsilon, as shown in Figure 7.
4.3 Speed
To measure the speed improvement achieved by using the LTS method, we examined a system of more practical interest than the Burgers equation: the generalized harmonic formulation of the Einstein field equations [22] with elements coupled by the upwind flux given by (6.3) of [24]. We evolve the gauge wave solution given in Section 4.2 of [1], deriving the evolved quantities from the metric
| (33) | |||
| (34) |
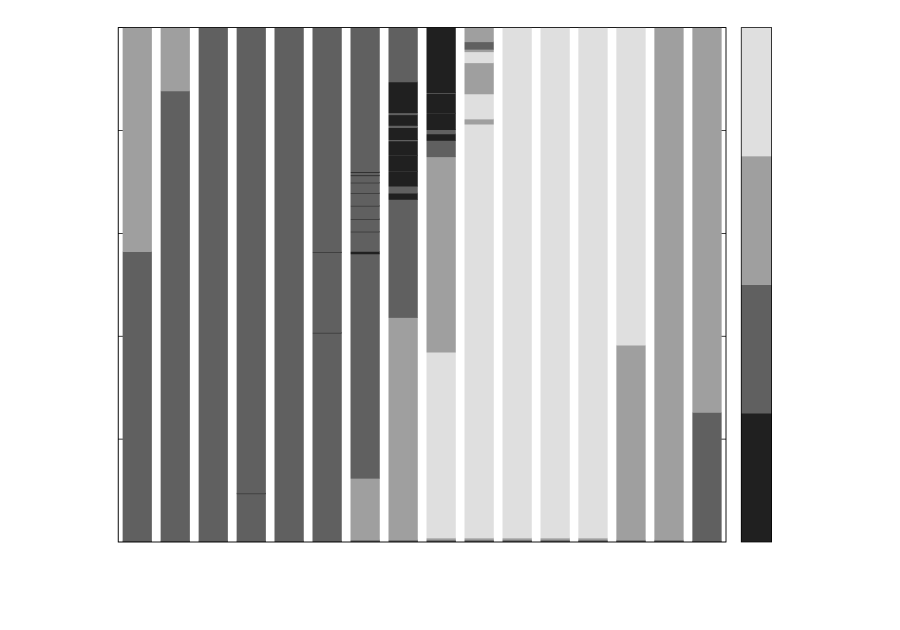
with amplitude and wavelength . The evolution domain consisted of a periodic unit cube divided into equal-sized blocks. The central block was refined into equal-sized elements, and nearby blocks were refined uniformly as needed to keep the lengths of adjacent elements within a factor of two of each other, as shown in Figure 8.
The CFL step size bound on the largest elements is 16 times the bound on the smallest elements, so if the cost of the simulation is dominated by the large elements, the LTS algorithm could achieve a theoretical speedup of 16. For the domain size chosen, however, there are sufficiently many small elements that cannot be improved by the LTS algorithm that the theoretical speedup is reduced to approximately .
These evolutions were performed on a cluster of 126 Lenovo Nextscale NX360 M5 compute nodes, each with 24 cores and 64 GB of RAM. The nodes communicated using Mellanox Infiniband.
We evolved the wave using integrators with orders from 1 to 8. For orders 1–4, evolution was performed on 8 nodes. For orders 5–8, the simulation was run on 12 nodes because of the higher memory requirements. The first order integrator was run to time 0.28, resulting in a total run time for the GTS evolution of approximately 10 hours. The final times for the higher-order evolutions were adjusted to keep the run times of the GTS evolutions similar by taking into account the Adams-Bashforth stability factors (Table 3) and the number of nodes used.
We found that the LTS evolutions of the wave ran 6–9 times faster than the corresponding GTS runs. These results were not strongly dependent on the order of the method.
4.4 Stability
| Order | ||||||||
|---|---|---|---|---|---|---|---|---|
For common GTS integrators, integration of a PDE will be stable if the step size taken is bounded by
| (35) |
where is the minimum spacing in the spatial discretization, is the largest characteristic speed of the PDE, and is a constant that depends on the system being integrated and the choice of integrator. For the standard Adams-Bashforth integrators, the values of for solving advection problems with finite-difference methods are given in Table 3. The values of for other systems are usually somewhat smaller, so we define
| (36) |
We measured the stability of our integrators when evolving the one-dimensional generalized harmonic equations using the gauge wave solution (33) with the transverse dimensions suppressed. We chose a wavelength of and an amplitude of . A small amplitude was chosen so the wave would have a negligible effect on the characteristic speeds of the system while still ensuring any unstable modes were excited.
We evolved the wave on a periodic domain of length . This was divided into two equal segments, one of which was refined into equal elements, and the other of which was refined into with . The solution on each element was described by 3 Legendre-Gauss-Lobatto points.
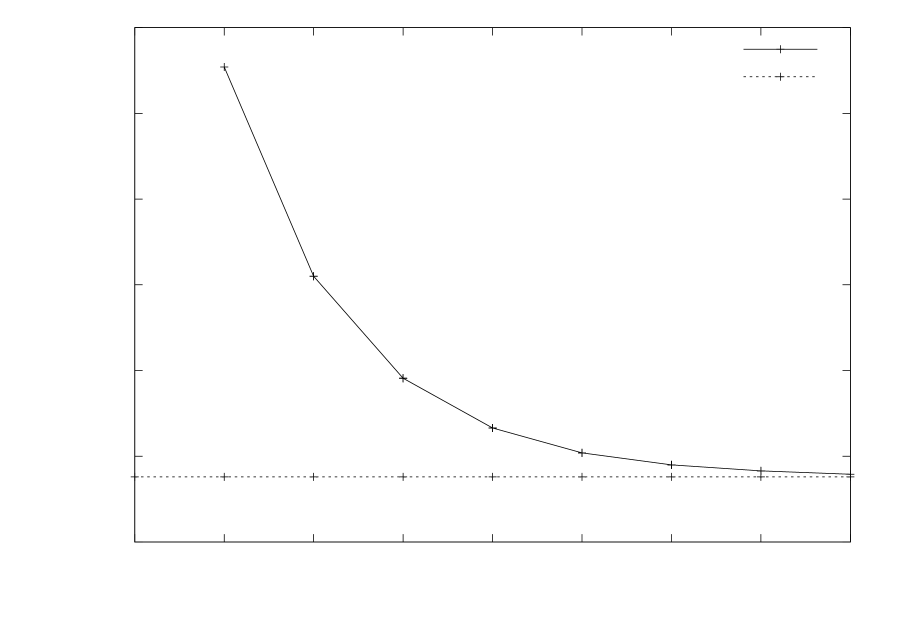
We found the first-order time stepper to be very unstable () for both global and local time-stepping. For steppers of order 2 and above, we found the values of to be independent of time-stepper order to within our measurement error of approximately . When run with global time-stepping (), we measured , independent of the refinement level. With non-uniform refinement () the LTS integrator was found to be more stable than the GTS integrator, with approaching the GTS value as the number of elements was increased, as shown in Figure 9. For element size ratios from to , we found that, to within our measurement error, was independent of the size of the large elements.
4.5 Convergence at constant CFL factor
Section 4.1 considered the convergence of the method with a particular discretization of the computational domain. When solving PDEs, another relevant test is the convergence as the domain is spatially refined and the time step is adjusted as necessary to maintain stability. We measured this rate using the one-dimensional gauge wave problem described in the previous section with a ratio of element sizes (). The time steps were restricted to be powers of 2 and their values were chosen using the CFL bound with . We found that, in most cases, the dominant source of error was the spatial discretization, and we were only able to make accurate measurements of the error caused by the time stepper for low-order integrators on comparatively high-order elements.
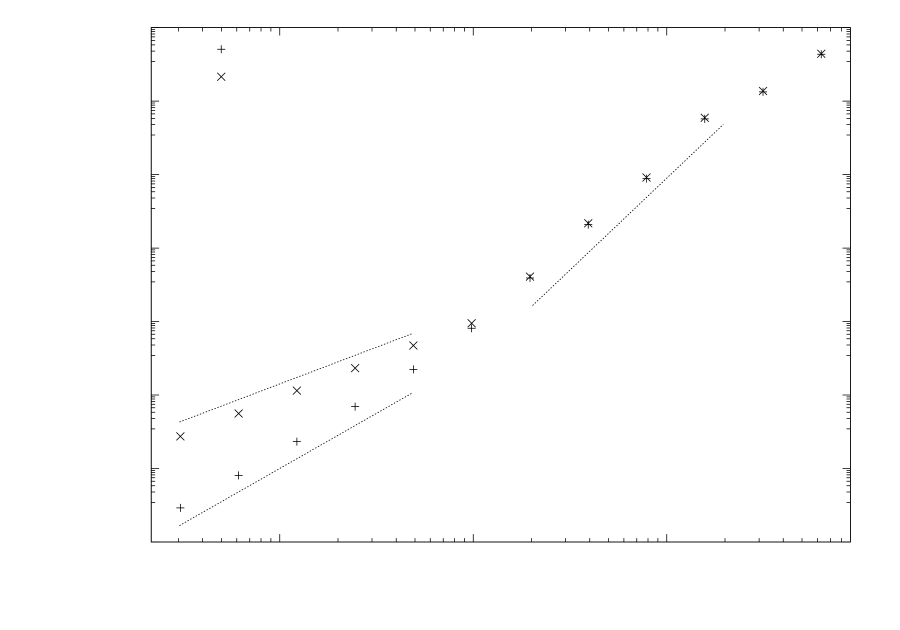
The largest characteristic speed of the gauge wave solution (33) is . For small amplitude waves, this speed will be nearly constant, but for larger amplitudes there can be significant variation as the wave propagates through the domain. At some threshold amplitude, this will start to cause time-dependent variation in the step size by causing the limit from (35) to cross one of the permitted power-of-two step sizes. We found that, when the amplitude was small enough that the step pattern was static, the convergence rate was unaffected by the step size variation across the domain. When the amplitude was large enough to cause a time-varying step pattern, however, the convergence order was reduced by one. The convergence for the third-order integrator is shown in Figure 10.
5 Conclusions
When integrating systems of coupled ODEs, particularly those arising from discretizations of PDE systems, it is often the case that time-step-related restrictions arise primarily in a small subset of the variables being integrated. Using standard evolution schemes, this forces all degrees of freedom to be evolved with the most restrictive stable time step, potentially causing significant waste of computational resources. A local time-stepping integrator removes this requirement, allowing different degrees of freedom to be updated at different frequencies.
This paper has presented a local time-stepping scheme based on the Adams-Bashforth family of multistep integrators. This method allows arbitrary step choices, with a completely independent choice of time step for each variable. Unlike some previous schemes, it retains the full convergence order of the Adams-Bashforth integrator it is based on. This method is also conservative in that all linear conserved quantities of the system are constant to numerical roundoff under evolution. The method will be efficient for DG methods or other algorithms with only local spatial couplings.
The use of this method was demonstrated on several systems evolved using the DG framework. The roundoff-level conservation of a conserved quantity was observed, and the expected convergence rate as the time step was decreased was observed for multiple integrator orders. The method was observed to converge one order more slowly when applied to a system with decreasing mesh spacing and dynamically updated time step sizes. For the evolution of a gauge wave using the generalized harmonic equations, we observed an evolution speed improvement by up to a factor of 6–9 from switching from the global to the local scheme.
This method will be used for DG evolutions of general relativity and magnetohydrodynamics in upcoming work using the SpECTRE code [20].
Appendix A Consistency and order of convergence
We will demonstrate here that the method given by (18) and (19) is consistent at the same order () as its base method. If we assume that all past values have been determined accurately, with error at most , then we can write
| (37) |
If we define a function
| (38) |
then, assuming is sufficiently smooth (), we can expand for steps near time as
| (39) | ||||
| (40) |
where is the value of differentiated times with respect to its first argument, times with respect to its second, etc., and evaluated at .
If we now substitute (19) and (40) into (18), we find that the entire expression factors into separate parts for each set of degrees of freedom:
| (41) |
The bracketed expression can be interpreted as an order- Lagrange interpolation from the times to of the polynomial . As , this interpolation is exact and we can simplify the above expression to
| (42) |
The sum over the can now again be interpreted as a Taylor series for , but evaluated this time with all arguments :
| (43) |
where the second equality follows from the definition of . This is now the expression for a single step of an Adams-Bashforth integral. The step has error , so it is equal to its analytic value to the accuracy of this expression. We can therefore perform the integral to find
| (44) |
Appendix B Error term
By repeating the calculation of consistency above keeping an additional term (and assuming now that has one more continuous derivative) we can obtain an estimate of the error of the method. If we take the old values to be accurate to order (which, for an order- method, we can assume them to be) then the calculations in the previous section are nearly unchanged until we reach (41), which now reads
| (45) |
As before, the bracketed quantity is an order- polynomial interpolation, but now the interpolations with are not exact. Evaluating the interpolations (and noting that for some set implies that for all the others) results in
| (46) |
The first term in the braces is the Taylor expansion of expanded in terms of . Using the sum over , we can integrate it to get and a correction term because the Adams-Bashforth integration does not integrate the order- term exactly. In the second term, the sum over can be used to integrate the Lagrange polynomial exactly. These manipulations produce
| (47) |
where we have defined the quantities
| (48) |
which are the Adams-Bashforth coefficients for integrating from to using known derivatives at the evaluation times on set .
We see now that there are two contributions to the error. The first has no dependence on the split of the solution into sets of degrees of freedom, and is therefore the error for the GTS Adams-Bashforth method. The second term is specific to the LTS method and occurs because of the difference in the error from using values from the different step patterns.
Appendix C Element splitting for general methods
When comparing integrators, one may wish to use a GTS integrator that is not usually expressed in terms of volume terms and boundary couplings (for example, a Runge-Kutta method) in a framework designed for an LTS integrator that is so expressed. This is easiest if the GTS integrator can be cast into the element splitting form (Section 3.1).
All common explicit GTS integrators (both multistep and substep) can be written in the form
| (49) |
Adams-Bashforth integrators are usually written in this form with the . Runge-Kutta methods take some manipulation. For example, the second-order midpoint method
| (50) |
can be written as
| (51) | ||||
| (52) |
where we have renumbered the steps so that the even numbered ones are the results of complete RK steps and .
For local time-stepping, the derivative values can depend on an additional set of values (which have their own, similar, update equation), but where we still expect the update rule to have the form of a linear combination:
| (53) |
We now perform an element splitting as in Section 3.1 by writing . Substituting this in gives
| (54) |
Since a general method must be independent of the details of the and functions, the bracketed terms in (54) must be the standard GTS method operating with only the “volume” portion of the equations, and the last term is a coupling correction. Notably, the coupling term does not require the function values directly, but only the value of the coupling evaluated at those values.
When using a GTS method in an LTS framework, the and will be evaluated at the same sequence of times and the coefficients will be diagonal in . Comparing (49) to the bracketed term in (54), we see that , so for a GTS method . Combining all this, we find that
| (55) |
that is, when using an arbitrary GTS integrator in a framework designed for LTS, one can evaluate the volume term using the standard GTS rule and the coupling contribution by using the usual update formula but with all the non-derivative terms set to zero. For the midpoint Runge-Kutta scheme above, this gives the split rule
| (56) | ||||
| (57) |
Appendix D Tables of coefficients for LTS rules
Below are tables of coefficients in (20) for order 2, 3, and 4 LTS rules with stepping, as well as the coefficients for transitioning between LTS and GTS stepping in these cases. The step patterns corresponding to these tables are shown in Figure 11. Additional values can be obtained using (19) and (21).
For the transition rules, the number of steps requiring special coefficients depends on the order of the integrator. Only tables for steps affected by the transition are shown below, after which either the rule or the GTS rule should be used, as appropriate.
D.1 Order 2
| LTS rule | |||||||||||
| (a) | (b) | (c) | |||||||||
| Transition to LTS by decreasing a step size | |||||||||||
| (d0) | (e0) | (f0) | |||||||||
| Transition to LTS by increasing a step size | |||||||||||
| (g0) | (h0) | (i0) | |||||||||
| Transitioning to GTS | |||||||||||
| (j0) | (k0) | ||||||||||
D.2 Order 3
| LTS rule | ||||||||||
| (a) | (b) | |||||||||
| (c) | ||||||||||
| Transition to LTS by decreasing a step size | ||||||||||
| (d0) | (e0) | |||||||||
| (f0) | ||||||||||
| Transition to LTS by increasing a step size | ||||||||||
| (g0) | (h0) | |||||||||
| (i0) | (g1) | |||||||||
| (h1) | (i1) | |||||||||
| Transitioning to GTS by decreasing a step size | ||||||||||
| (j0) | (j1) | |||||||||
| Transitioning to GTS by increasing a step size | ||||||||||
| (k0) | (k1) | |||||||||
D.3 Order 4
| LTS rule | ||||||||||||
| (a) | (b) | |||||||||||
| (c) | ||||||||||||
| Transition to LTS by decreasing a step size | ||||||||||||
| (d0) | (e0) | |||||||||||
| (f0) | (d1) | |||||||||||
| (e1) | (f1) | |||||||||||
| Transition to LTS by increasing a step size | ||||||||||||
| (g0) | (h0) | |||||||||||
| (i0) | (g1) | |||||||||||
| (h1) | (i1) | |||||||||||
| (g2) | (h2) | |||||||||||
| (i2) | ||||||||||||
| Transitioning to GTS by decreasing a step size | ||||||||||||
| (j0) | (j1) | |||||||||||
| (j2) | ||||||||||||
| Transitioning to GTS by increasing a step size | ||||||||||||
| (k0) | (k1) | |||||||||||
| (k2) | ||||||||||||
References
- [1] M. Alcubierre, G. Allen, C. Bona, D. Fiske, T. Goodale, F. S. Guzmán, I. Hawke, S. H. Hawley, S. Husa, M. Koppitz, C. Lechner, D. Pollney, D. Rideout, M. Salgado, E. Schnetter, E. Seidel, H. aki Shinkai, D. Shoemaker, B. Szilágyi, R. Takahashi, and J. Winicour, Towards standard testbeds for numerical relativity, Classical and Quantum Gravity, 21 (2003), pp. 589–613, https://doi.org/10.1088/0264-9381/21/2/019.
- [2] M. Almquist and M. Mehlin, Multilevel local time-stepping methods of Runge-Kutta-type for wave equations, SIAM J Sci Comput, 39 (2017), pp. A2020–A2048, https://doi.org/10.1137/16M1084407.
- [3] M. Berger, On conservation at grid interfaces, SIAM J Numer Anal, 24 (1987), pp. 967–984, https://doi.org/10.1137/0724063.
- [4] M. J. Berger and J. Oliger, Adaptive mesh refinement for hyperbolic partial differential equations, J Comp Phys, 53 (1984), pp. 484–512, https://doi.org/10.1016/0021-9991(84)90073-1, http://www.sciencedirect.com/science/article/pii/0021999184900731.
- [5] J. R. Cavalcanti, M. Dumbser, D. da Motta-Marques, and C. R. F. Junior, A conservative finite volume scheme with time-accurate local time stepping for scalar transport on unstructured grids, Advances in Water Resources, 86 (2015), pp. 217–230, https://doi.org/10.1016/j.advwatres.2015.10.002, http://www.sciencedirect.com/science/article/pii/S0309170815002390.
- [6] B. Chabaud and Q. Du, A hybrid implicit-explicit adaptive multirate numerical scheme for time-dependent equations, J Sci Comput, 51 (2012), pp. 135–157.
- [7] P. Chebyshev, Sur l’interpolation, in Oeuvres de P. L. Tchebychef, A. Markoff and N. Sonin, eds., vol. 1, l’Académie Impériale des Sciences, St. Petersburg, April 1899, pp. 541–560.
- [8] E. M. Constantinescu and A. Sandu, Extrapolated multirate methods for differential equations with multiple time scales, J Sci Comput, 56 (2013), pp. 28–44.
- [9] A. Demirel, J. Niegemann, K. Busch, and M. Hochbruck, Efficient multiple time-stepping algorithms of higher order, J Comp Phys, 285 (2015), pp. 133–148, https://doi.org/10.1016/j.jcp.2015.01.018, http://www.sciencedirect.com/science/article/pii/S0021999115000224.
- [10] P.-W. Fok, A linearly fourth order multirate Runge-Kutta method with error control, J Sci Comput, 66 (2016), pp. 177–195.
- [11] G. J. Gassner, F. Hindenlang, and C.-D. Munz, A Runge-Kutta based discontinuous Galerkin method with time accurate local time stepping, in Adaptive High-Order Methods in Computational Fluid Dynamics, World Scientific, 2011, pp. 95–118, https://doi.org/10.1142/9789814313193_0004, https://www.worldscientific.com/doi/abs/10.1142/9789814313193_0004.
- [12] C. W. Gear and D. R. Wells, Multirate linear multistep methods, BIT Numerical Mathematics, 24 (1984), pp. 484–502, https://doi.org/10.1007/BF01934907.
- [13] N. Y. Gnedin, V. A. Semenov, and A. V. Kravtsov, Enforcing the Courant-Friedrichs-Lewy condition in explicitly conservative local time stepping schemes, J Comp Phys, 359 (2018), pp. 93–105, https://doi.org/10.1016/j.jcp.2018.01.008, http://www.sciencedirect.com/science/article/pii/S0021999118300184.
- [14] M. Grote, M. Mehlin, and T. Mitkova, Runge-Kutta-based explicit local time-stepping methods for wave propagation, SIAM J Sci Comput, 37 (2015), pp. A747–A775, https://doi.org/10.1137/140958293.
- [15] M. Grote, M. Mehlin, and S. Sauter, Convergence analysis of energy conserving explicit local time-stepping methods for the wave equation, SIAM J Numer Anal, 56 (2018), pp. 994–1021, https://doi.org/10.1137/17M1121925.
- [16] M. J. Grote and T. Mitkova, High-order explicit local time-stepping methods for damped wave equations, Journal of Computational and Applied Mathematics, 239 (2013), pp. 270–289, https://doi.org/10.1016/j.cam.2012.09.046.
- [17] M. Günther and A. Sandu, Multirate generalized additive Runge Kutta methods, Numerische Mathematik, 133 (2016), pp. 497–524.
- [18] E. Hairer, S. P. Nørsett, and G. Wanner, Solving Ordinary Differential Equations I, Springer, second ed., 1993.
- [19] A. Harten, P. Lax, and B. van Leer, On upstream differencing and Godunov-type schemes for hyperbolic conservation laws, SIAM Review, 25 (1983), pp. 35–61, https://doi.org/10.1137/1025002.
- [20] L. E. Kidder, S. E. Field, F. Foucart, E. Schnetter, S. A. Teukolsky, A. Bohn, N. Deppe, P. Diener, F. cois Hébert, J. Lippuner, J. Miller, C. D. Ott, M. A. Scheel, and T. Vincent, SpECTRE: a task-based discontinuous Galerkin code for relativistic astrophysics, J Comp Phys, 335 (2017), pp. 84–114, https://doi.org/10.1016/j.jcp.2016.12.059, http://www.sciencedirect.com/science/article/pii/S0021999117300098.
- [21] L. Krivodonova, An efficient local time-stepping scheme for solution of nonlinear conservation laws, J Comp Phys, 229 (2010), pp. 8537–8551, https://doi.org/10.1016/j.jcp.2010.07.037.
- [22] L. Lindblom, M. A. Scheel, L. E. Kidder, R. Owen, and O. Rinne, A new generalized harmonic evolution system, Classical and Quantum Gravity, 23 (2006), pp. S447–S462, https://doi.org/10.1088/0264-9381/23/16/s09.
- [23] W. A. Mersman, Self-starting multistep methods for the numerical integration of ordinary differential equations, tech. report, National Aeronautics and Space Administration, July 1965.
- [24] O. Porth, H. Olivares, Y. Mizuno, Z. Younsi, L. Rezzolla, M. Moscibrodzka, H. Falcke, and M. Kramer, The black hole accretion code, Computational Astrophysics and Cosmology, 4 (2017), p. 1, https://doi.org/10.1186/s40668-017-0020-2.
- [25] A. Sandu and E. M. Constantinescu, Multirate explicit Adams methods for time integration of conservation laws, J Sci Comput, 38 (2009), pp. 229–249, https://doi.org/10.1007/s10915-008-9235-3.
- [26] A. Sandu and M. Günther, A generalized-structure approach to additive Runge-Kutta methods, SIAM J Numer Anal, 53 (2015), pp. 17–42, https://doi.org/10.1137/130943224.
- [27] S. Schoeder, M. Kronbichler, and W. A. Wall, Arbitrary high-order explicit hybridizable discontinuous Galerkin methods for the acoustic wave equation, J Sci Comput, 76 (2018), pp. 969–1006.
- [28] L. F. Shampine, Conservation laws and the numerical solution of ODEs, Computers & Mathematics with Applications, 12 (1986), pp. 1287–1296, https://doi.org/10.1016/0898-1221(86)90253-1, http://www.sciencedirect.com/science/article/pii/0898122186902531.
- [29] A. R. Winters and D. A. Kopriva, High-order local time stepping on moving DG spectral element meshes, J Sci Comput, 58 (2014), pp. 176–202, https://doi.org/10.1007/s10915-013-9730-z.