A holistic approach to computing first-arrival traveltimes using neural networks

The eikonal equation is a non-linear first-order PDE that is, for an isotropic medium, given as:

$$\left(\frac{\partial T}{\partial x}\right)^{2}+\left(\frac{\partial T}{\partial z}\right)^{2}=\frac{1}{v(x,z)^{2}},$$

(1)

subject to a point-source boundary condition as:

$$T(x_{s},z_{s})=0,$$

(2)

where $T(x,z)$ is the traveltime from the source point $(x_{s},z_{s})$ to a point $(x,z)$ in the computational domain, and $v(x,z)$ is the phase velocity of the isotropic medium. Since the curvature of the wavefront near the point-source is extremely large, previous studies [31, 49] have shown that it is better to solve the factored eikonal equation instead of equation (1). The idea is to factor the unknown traveltime into two multiplicative factors, where one of the factors is specified analytically to capture the source-singularity such that the other factor is gently varying in the source neighborhood. Therefore, we factor $T(x,z)$ into two multiplicative functions:

$$T(x,z)=T_{0}(x,z)\cdot\tau(x,z),$$

(3)

where $T_{0}(x,z)$ is the known function and $\tau(x,z)$ is the unknown function. Plugging this into equation (1), we get the factored eikonal equation for an isotropic model as:

$$\left(T_{0}\frac{\partial\tau}{\partial x}+\tau\frac{\partial T_{0}}{\partial x}\right)^{2}+\left(T_{0}\frac{\partial\tau}{\partial z}+\tau\frac{\partial T_{0}}{\partial z}\right)^{2}=\frac{1}{v^{2}},$$

(4)

subject to the updated point-source condition:

$$\tau(x_{s},z_{s})=1.$$

(5)

The known factor $T_{0}$ is the traveltime solution in a homogeneous isotropic model given as:

$$T_{0}(x,z)=\frac{\sqrt{(x-x_{s})^{2}+(z-z_{s})^{2}}}{v_{s}},$$

(6)

where $v_{s}$ is taken to be the velocity at the point-source location.

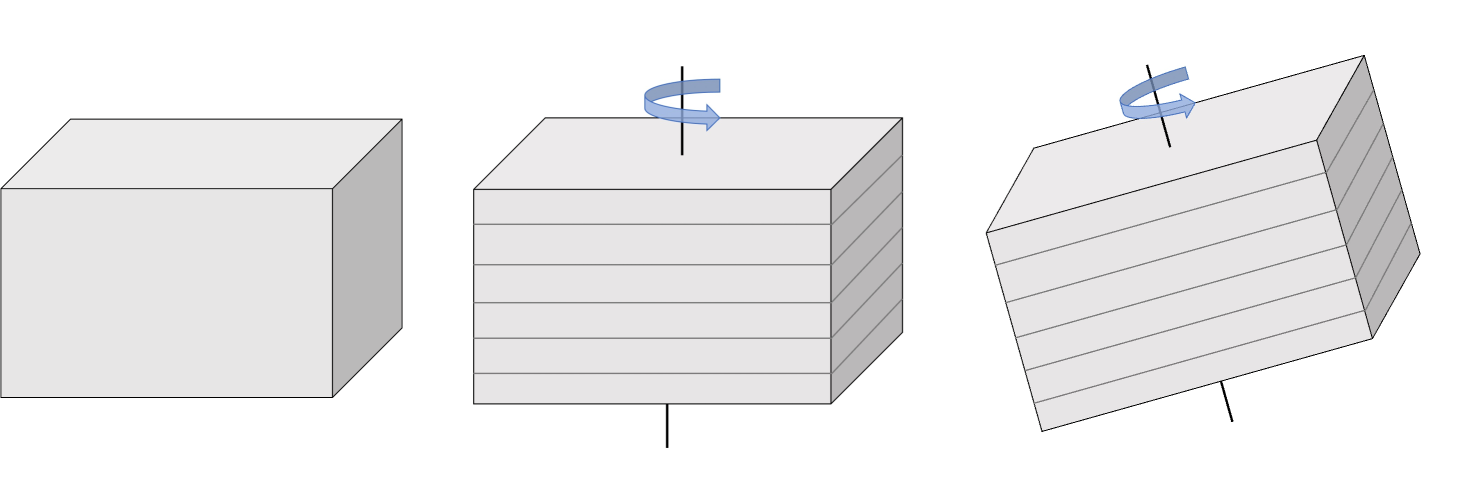
Equation (4) is the factored eikonal equation for an isotropic medium; however, sedimentary rocks exhibit at least some degree of anisotropy due to a number of factors including thin layering and preferential alignment of grains cracks  [50]. This results in the velocity being a function of the wave propagation direction, making the isotropic approximation of the Earth invalid. Therefore, traveltime computation algorithms must honor the anisotropic nature of the Earth for accurate subsurface imaging and other applications. Thus, we consider a realistic approximation of the subsurface anisotropy known as the tilted transverse isotropy (TTI) case. The factored eikonal equation for a TTI medium is considerably more complex than the isotropic case and is given, under the acoustic assumption, as [49]:

$\begin{aligned} &(1+2\epsilon)\left(\cos\theta\left(T_{0}\frac{\partial\tau}{\partial x}+\tau\frac{\partial T_{0}}{\partial x}\right)+\sin\theta\left(T_{0}\frac{\partial\tau}{\partial z}+\tau\frac{\partial T_{0}}{\partial z}\right)\right)^{2}\\ +&\left(\cos\theta\left(T_{0}\frac{\partial\tau}{\partial z}+\tau\frac{\partial T_{0}}{\partial z}\right)-\sin\theta\left(T_{0}\frac{\partial\tau}{\partial x}+\tau\frac{\partial T_{0}}{\partial x}\right)\right)^{2}\\ \times&\left(1-\frac{2\eta v_{t}^{2}(1+2\epsilon)}{1+2\eta}\left(\cos\theta\left(T_{0}\frac{\partial\tau}{\partial x}+\tau\frac{\partial T_{0}}{\partial x}\right)+\sin\theta\left(T_{0}\frac{\partial\tau}{\partial z}+\tau\frac{\partial T_{0}}{\partial z}\right)\right)^{2}\right)=\frac{1}{v_{t}^{2}},\end{aligned}$

(7)

where $v_{t}(x,z)$ is the velocity along the symmetry axis, $\epsilon(x,z)$ and $\eta(x,z)$ are the anisotropy parameters, and $\theta(x,z)$ is the tilt angle that the symmetry axis makes with the vertical. The point-source condition is the same as the one given in equation (5). Again $\tau(x,z)$ is the unknown function we solve equation (7) for, whereas $T_{0}(x,z)$ is the known function which may be taken as the solution of a homogeneous, tilted elliptically isotropic medium, given as [32]:

$$T_{0}(x,z)=\sqrt{\frac{b_{s}(x-x_{s})^{2}+2c_{s}(x-x_{s})(z-z_{s})+a_{s}(z-z_{s})^{2}}{a_{s}b_{s}-c_{s}^{2}}},$$

(8)

with

	$\displaystyle a_{s}$	$\displaystyle=v_{ts}^{2}(1+2\epsilon_{s})\cos\theta_{s}^{2}+v_{ts}^{2}\sin\theta_{s}^{2},$		(9)
	$\displaystyle b_{s}$	$\displaystyle=v_{ts}^{2}\cos\theta_{s}^{2}+v_{ts}^{2}(1+2\epsilon_{s})\sin\theta_{s}^{2},$
	$\displaystyle c_{s}$	$\displaystyle=\left(v_{ts}^{2}-v_{ts}^{2}(1+2\epsilon_{s})\right)\cos\theta_{s}\sin\theta_{s}.$

In the above expressions, $v_{ts}$ and $\epsilon_{s}$ are the velocity along the symmetry axis and the anisotropy parameter, respectively, at the point-source location. Similarly, $\theta_{s}$ is the tilt angle taken at the source-point.

It is worth highlighting that the isotropic and TTI cases represent mathematical approximations of the subsurface. An isotropic model considers the velocity to be invariant with respect to the direction of propagation, which is a crude representation of the Earth’s crust. The simplest practical anisotropic symmetry system is axisymmetric anisotropy, commonly known as transverse isotropy (TI). A TI medium with a vertical axis of symmetry (VTI) is a good approximation for horizontally layering shale formation or thin-layering sediments. The factored eikonal equation for VTI media can be obtained by setting $\theta=0$ in equation (7). For more complex geology, such as sediments near the flanks of salt domes and fold-and-thrust belts like the Canadian foothills, a TTI model represents the best approximation. Figure 1 illustrates these approximations graphically.

The reason for considering eikonal equations corresponding to different media is to highlight, in comparison with the conventional methods, how easy it is to adapt the proposed method to solve a relatively more complex eikonal equation (more on this in Section 2.4).

A feed-forward neural network, also known as a multi-layer perceptron, is a set of neurons organized in layers in which evaluations are performed sequentially through the layers. It can be seen as a computational graph with an input layer, an output layer, and an arbitrary number of hidden layers. In a fully connected neural network, neurons in adjacent layers are connected with each other, but neurons within a single layer share no connections. It is called a feed-forward neural network because information flows from the input through each successive layer to the output. Moreover, there are no feedback or recursive loops in a feed-forward neural network.

Neural networks are well-known for their strong representational power. A neural network with $n$ neurons in the input layer and $m$ neurons in the output layer can be used to represent a function $u:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$. In fact, it has been shown that a neural network with a finite number of neurons in the hidden layer can be used to represent any bounded continuous function to the desired accuracy. This is also known as the universal approximation theorem [51, 52]. In addition, it was later shown that by using a deep network with multiple hidden layers and a nonlinear activation function, the total number of neurons needed to represent a given function could be significantly reduced [53]. Therefore, our goal here is to train a DNN that could represent the mapping between the spatial coordinates $(x,z)$, as inputs to the network, and the unknown traveltime function $\tau(x,z)$ representing the output of the DNN. Figure 2 illustrates this idea pictorially showing a neural network with input neurons for the spatial coordinates $(x,z)$ that are passed through the hidden layers to the output layer for predicting the traveltime factor at the inputted spatial location.

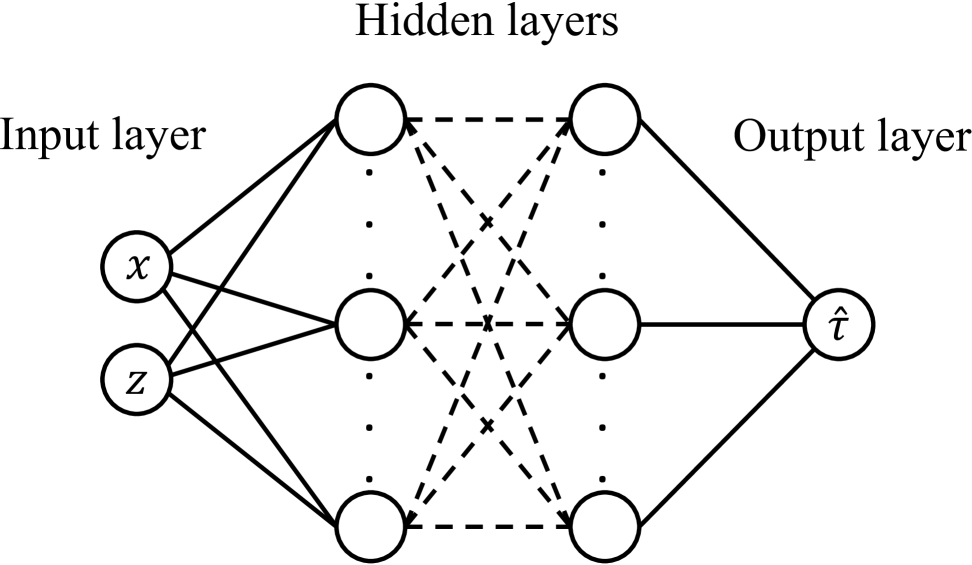
We formulate here considering a 2D case for simplicity of illustration. In a 3D model, one would need a neural network with three input neurons, one for each spatial dimension. It must also be noted that while DNNs are, in theory, capable of representing very complex functions, finding the actual parameters (weights and biases) needed to solve a given PDE can be very challenging.

Solving a PDE using neural networks requires a mechanism to accurately compute derivatives of the network’s output(s) with respect to the input(s). There are multiple ways to compute derivatives including hand-coded analytical derivatives, symbolic differentiation, numerical approximation, and automatic differentiation (AD) [54]. While manually working out the derivatives is exact, it is often time consuming to code and it is error-prone. Symbolic differentiation, while also exact, may result in exponentially large expressions and, therefore, can be prohibitively slow and memory intensive. Numerical differentiation, on the other hand, is easy to implement but can be highly inaccurate due to round-off errors. Contrary to these approaches, AD uses exact expressions with floating-point values instead of symbolic strings and it involves no approximation errors. This results in an accurate evaluation of derivatives at machine precision. Therefore, we evaluate the partial derivatives of the unknown traveltime factor $\tau$ with respect to the inputs $(x,z)$ using AD.

However, it must be noted that an efficient implementation of the AD algorithm can be non-trivial. Fortunately, many existing computational frameworks such as Tensorflow [55] and PyTorch [56] have made available efficiently implemented AD libraries.

We begin by considering how the different pieces of the puzzle outlined in the previous subsections can be combined to solve eikonal equations. First, we illustrate this using the factored isotropic eikonal equation (4) and then demonstrate how simple it is under the proposed framework to solve a more complex eikonal equation, such as the factored TTI eikonal equation (7).

To solve equation (4), we leverage the capabilities of neural networks as function approximators and define a loss function that minimizes the residual of the underlying PDE for a chosen set of training (collocation) points. This is achieved using the following components:

• i.

  a DNN approximation of the unknown traveltime field variable $\tau(x,z)$,

• ii.

  a differentiation algorithm, i.e., AD in this case, to evaluate partial derivatives of $\tau(x,z)$ with respect to the spatial coordinates $(x,z)$,

• iii.

  a loss function incorporating the underlying eikonal equation, sampled on a collocation grid, and

• iv.

  an optimizer to minimize the loss function by updating the neural network parameters.

To illustrate the idea, let us consider a two-dimensional domain $\Omega\in\mathbb{R}^{2}$. A point-source is located at coordinates $(x_{s},z_{s})$, where $\tau(x_{s},z_{s})=1$. The unknown traveltime factor $\tau(x,z)$ is approximated using a DNN, $\mathcal{N}_{\tau}$, such that:

$$\tau(x,z)\approx\hat{\tau}(x,z)=\mathcal{N}_{\tau}(x,z;\bm{\theta}),$$

(10)

where $x,z$ are network inputs, $\hat{\tau}$ is the network output, and $\bm{\theta}\in\mathbb{R}^{D}$ represents the set of all trainable parameters of the network with $D$ as the total number of parameters.

The loss function is given by the mean-squared error norm as

$$\mathfrak{J}=\frac{1}{N_{I}}\sum_{(x^{*},z^{*})\in I}\left\lVert\mathcal{L}\right\rVert^{2}+\frac{1}{N_{I}}\sum_{(x^{*},z^{*})\in I}\left\lVert\mathcal{H}(-\hat{\tau})|\hat{\tau}|\right\rVert^{2}\\ +\left\lVert\hat{\tau}(x_{s},z_{s})-1\right\rVert^{2},$$

(11)

where $\mathcal{L}$ represents the residual of the factored isotropic eikonal equation (4), given by

$\displaystyle\mathcal{L}=\left(T_{0}\frac{\partial\hat{\tau}}{\partial x}+\hat{\tau}\frac{\partial T_{0}}{\partial x}\right)^{2}+\left(T_{0}\frac{\partial\hat{\tau}}{\partial z}+\hat{\tau}\frac{\partial T_{0}}{\partial z}\right)^{2}-\frac{1}{v^{2}}.$

(12)

The first term on the right side of equation (11) imposes validity of the factored eikonal equation (4) on a given set of training points $(x^{*},z^{*})\leavevmode\nobreak\ \in\leavevmode\nobreak\ I$, where $N_{I}$ is the number of training samples. The second term forces the solution $\hat{\tau}$ to be positive by penalizing negative solutions using the Heaviside function $\mathcal{H}()$. The last term enforces the boundary condition by imposing the solution $\hat{\tau}$ to be unity at the source point $(x_{s},z_{s})$. The set of network parameters $\bm{\theta}^{*}$ that minimizes the loss function (11) on this set of training points, $(x^{*},z^{*})\leavevmode\nobreak\ \in\leavevmode\nobreak\ I$, is then identified by solving the optimization problem:

$$\bm{\theta}^{*}=\arg\min_{\bm{\theta}\in\mathbb{R}^{D}}\mathfrak{J}(x^{*},z^{*};\bm{\theta}).$$

(13)

Once the DNN is trained, we evaluate the network on a set of regular grid-points in the computational domain to obtain the unknown traveltime field. The final traveltime solution is obtained by multiplying it with the known traveltime part, i.e.,

$$\hat{T}(x,z)=T_{0}(x,z)\cdot\hat{\tau}(x,z).$$

(14)

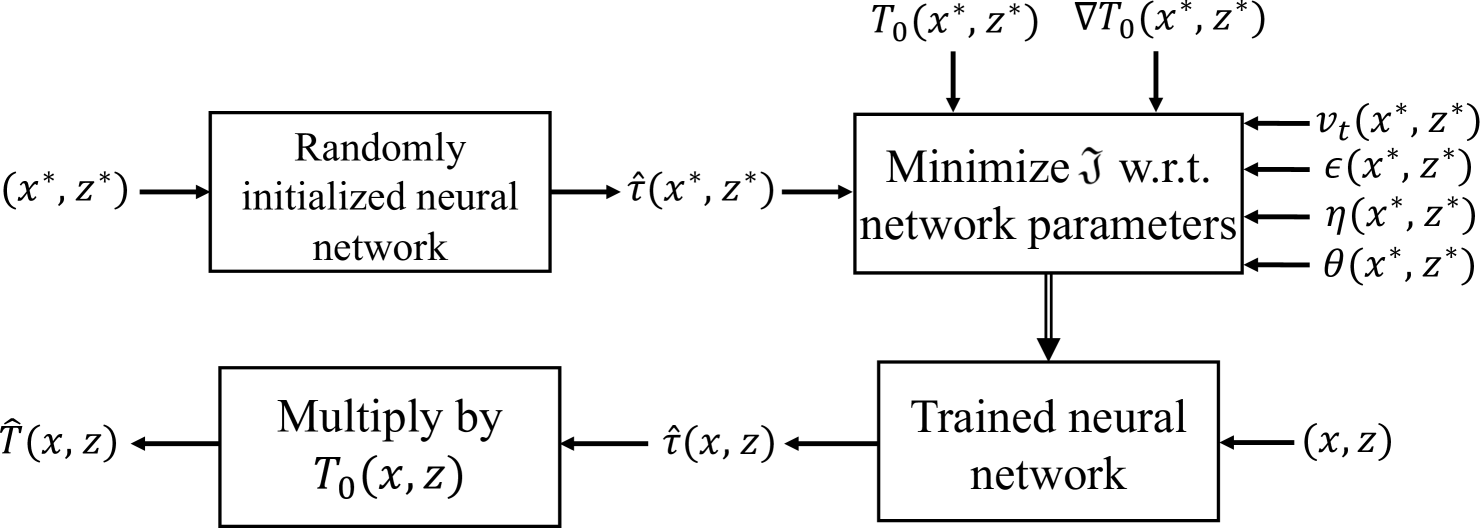
This yields traveltimes corresponding to an isotropic approximation of the Earth. However, it is well-known that the subsurface is anisotropic in nature. Therefore, a significant amount of research effort has been spent over the years on extending numerical eikonal solvers to anisotropic media. The complication in numerically solving the eikonal equation arises due to anellipticity of the wavefront [57] resulting in high-order nonlinear terms in the eikonal equation. These high-order terms dramatically increase the complexity in solving the anisotropic eikonal equation and, therefore, have been a topic of immense research interest. On the contrary, the proposed neural network formulation allows solving for the anisotropic eikonal equation by simply replacing the residual in equation (11) with the one corresponding to the anisotropic eikonal equation. Therefore, to solve the factored TTI eikonal equation (7), we would, instead of equation (12), use the following:

$\begin{aligned} \mathcal{L}=&\,(1+2\epsilon)\left(\cos\theta\left(T_{0}\frac{\partial\hat{\tau}}{\partial x}+\hat{\tau}\frac{\partial T_{0}}{\partial x}\right)+\sin\theta\left(T_{0}\frac{\partial\hat{\tau}}{\partial z}+\hat{\tau}\frac{\partial T_{0}}{\partial z}\right)\right)^{2}\\ +&\,v_{t}^{2}\left(\cos\theta\left(T_{0}\frac{\partial\hat{\tau}}{\partial z}+\hat{\tau}\frac{\partial T_{0}}{\partial z}\right)-\sin\theta\left(T_{0}\frac{\partial\hat{\tau}}{\partial x}+\hat{\tau}\frac{\partial T_{0}}{\partial x}\right)\right)^{2}\\ \times&\left(1-\frac{2\eta v_{t}^{2}(1+2\epsilon)}{1+2\eta}\left(\cos\theta\left(T_{0}\frac{\partial\hat{\tau}}{\partial x}+\hat{\tau}\frac{\partial T_{0}}{\partial x}\right)+\sin\theta\left(T_{0}\frac{\partial\hat{\tau}}{\partial z}+\hat{\tau}\frac{\partial T_{0}}{\partial z}\right)\right)^{2}\right)-\frac{1}{v_{t}^{2}}.\end{aligned}$

(15)

This is a highly desirable feature of this approach because eikonal equations corresponding to models with even lower symmetry than TTI can be easily solved by simply using a different residual term. By contrast, conventional algorithms such as fast marching or fast sweeping methods would require significant effort to incorporate such changes, thereby resulting in much slower scientific progress.

A workflow summarizing the proposed solver for the factored TTI eikonal equation is shown in Figure 3.

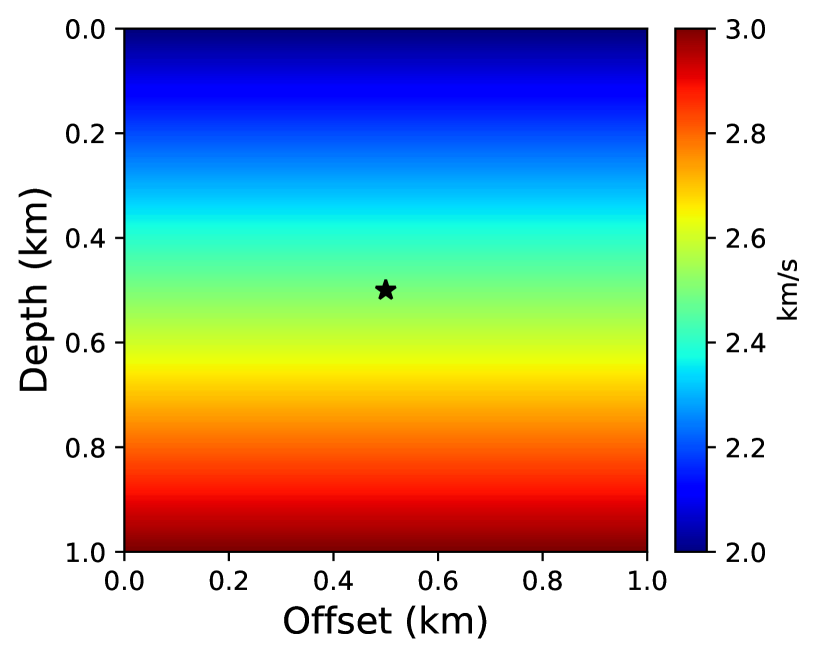
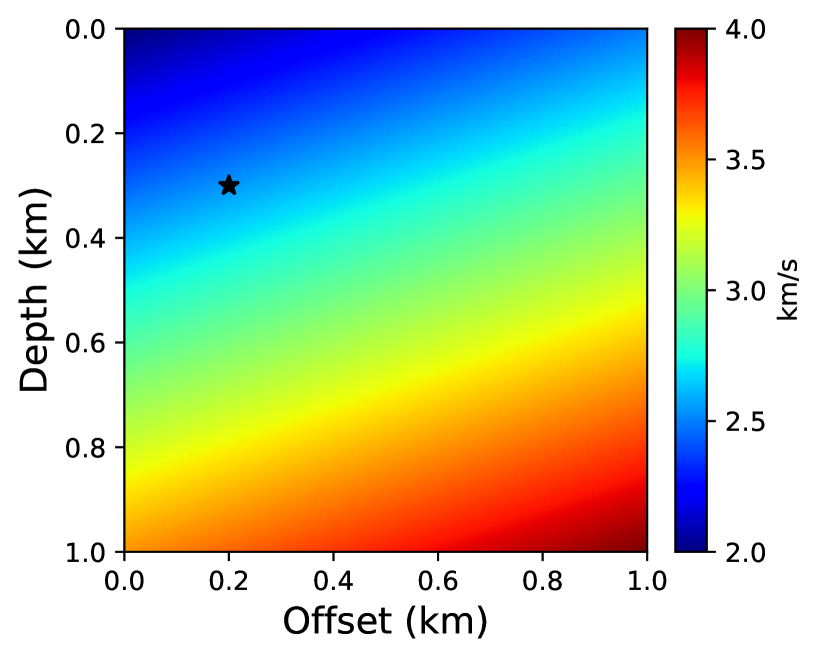
First, we consider a vertically varying $1\times 1$ km² isotropic model. The velocity at zero depth is 2 km/s and it increases linearly with a gradient of 1 s^-1 to 3 km/s at a depth of 1 km. We compute traveltime solutions using the neural network and first-order fast sweeping method by considering a point-source located at $(0.5\leavevmode\nobreak\ \text{km},0.5\leavevmode\nobreak\ \text{km})$. We compare their performance with a reference solution computed analytically [60]. The velocity model is shown in Figure 4 and is discretized on a 101$\times$101 grid with a 10 m grid interval along both axes.

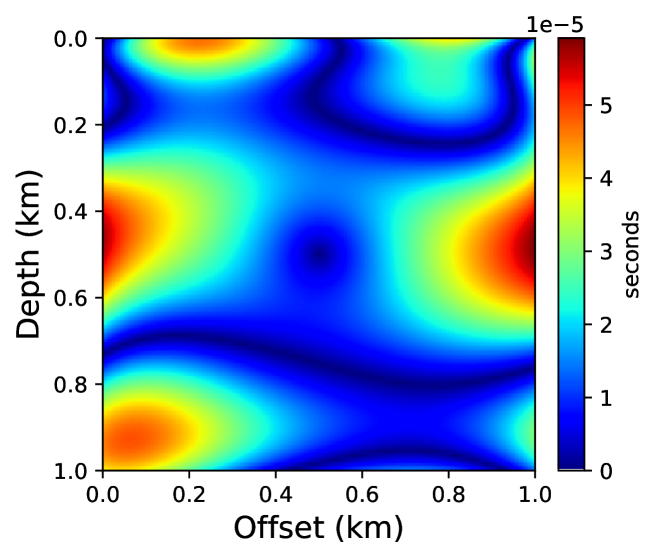
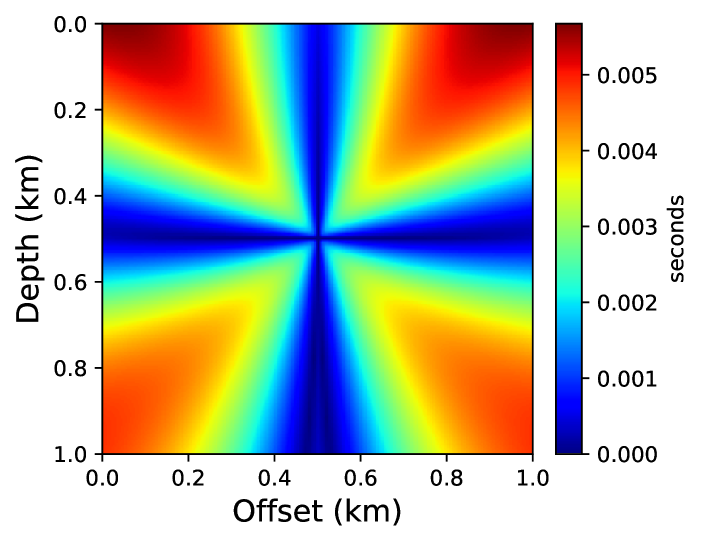
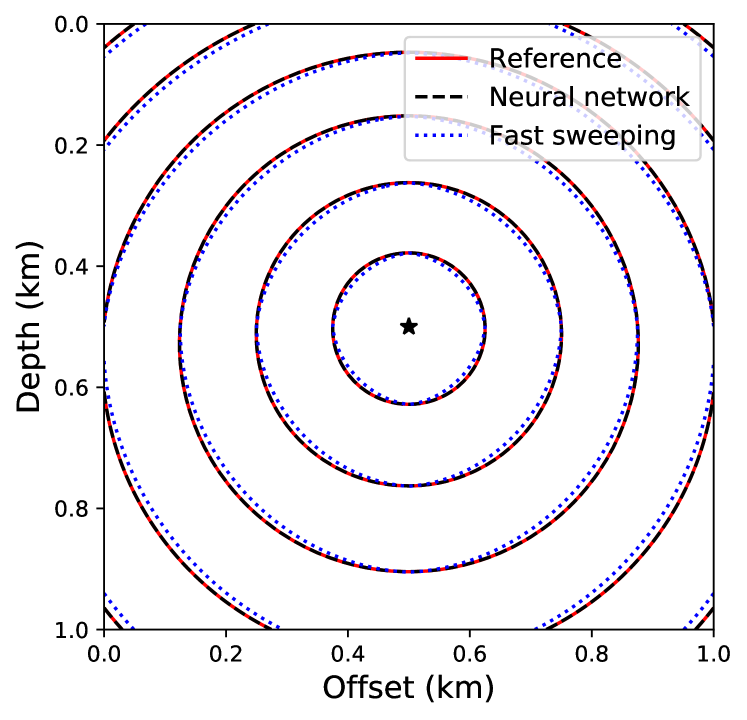
For training the neural network, we begin with randomly initialized parameters and train on 50% of the total grid points selected randomly and use the Adam optimizer [61] with 10,000 epochs. Once the network is trained, we evaluate the trained network on the regularly sampled (101$\times$101) grid to obtain the unknown traveltime field $\hat{\tau}$, which is then multiplied with the corresponding factored traveltime field $T_{0}$ to obtain the final traveltime solution. We compare the accuracy of the neural network solution and the first-order fast sweeping solution, computed on the same regular grid in Figure 5. We observe significantly better accuracy for the neural network based solution despite using only half of the total grid points for training. In Figure 6, we confirm this observation by plotting the corresponding traveltime contours.

Next, we train the neural network to solve the TTI eikonal equation. Compared to the fast sweeping method that requires significant modifications to the isotropic eikonal solver, the neural network based approach requires only an update to the loss function by incorporating the appropriate residual based on the TTI eikonal equation. For the velocity parameter $v_{t}$, we consider a linear velocity model with a vertical gradient of 1.5 $\text{s}^{-1}$ and a horizontal gradient of 0.5 $\text{s}^{-1}$ as shown in Figure 7. We use homogeneous models for the anisotropy parameters with $\epsilon$=0.2 and $\eta$ = 0.083. We also consider a homogeneous tilt angle of $\theta$ = 30^∘. These models are also discretized on a 101$\times$101 grid with 10 m grid interval along both axes.

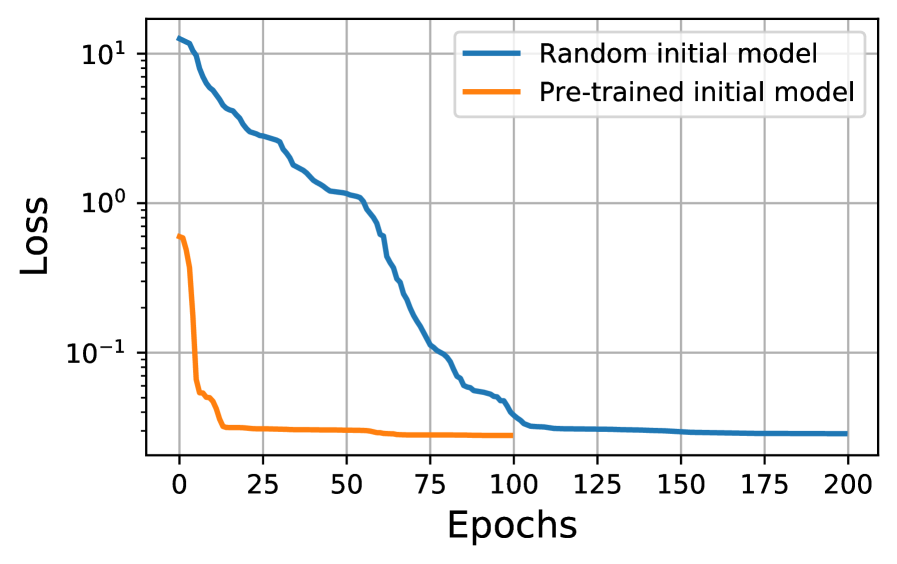
Instead of training the network from scratch, we use transfer learning, which is a machine learning technique that relies on storing knowledge gained while solving one problem and applying it to a different but related problem. Starting with a pre-trained network from example 1, we fine-tune the neural network parameters for the TTI model using 50% of the total grid points, selected randomly, using the L-BFGS-B solver [62] for 100 epochs. Starting with a pre-trained network allows us to use the L-BFGS-B method for faster convergence as opposed to starting with the Adam optimizer and then switching to L-BFGS-B as suggested by previous studies [43]. For comparison, we also train a neural network from scratch and the convergence history, shown in Figure 8, confirms that the solution converges much faster when using transfer learning.

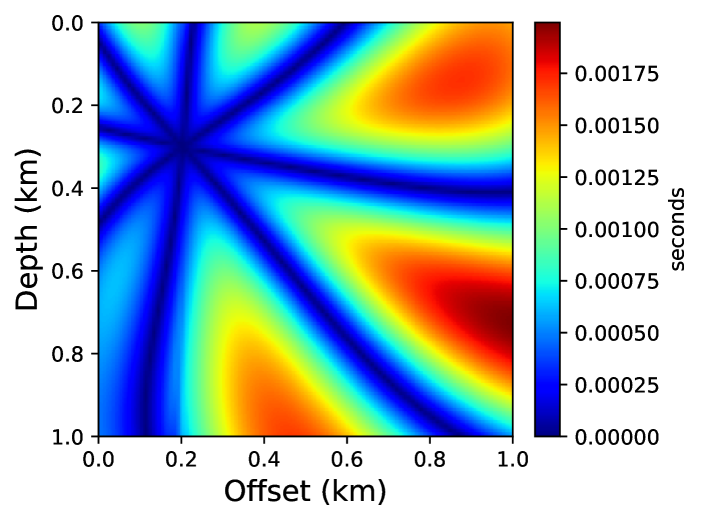
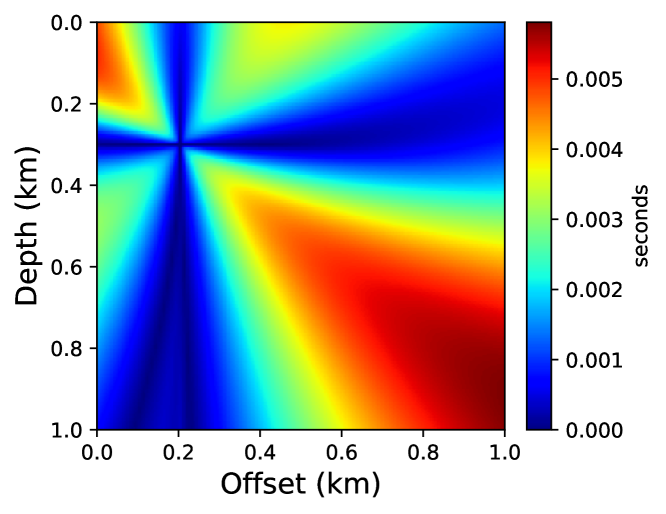
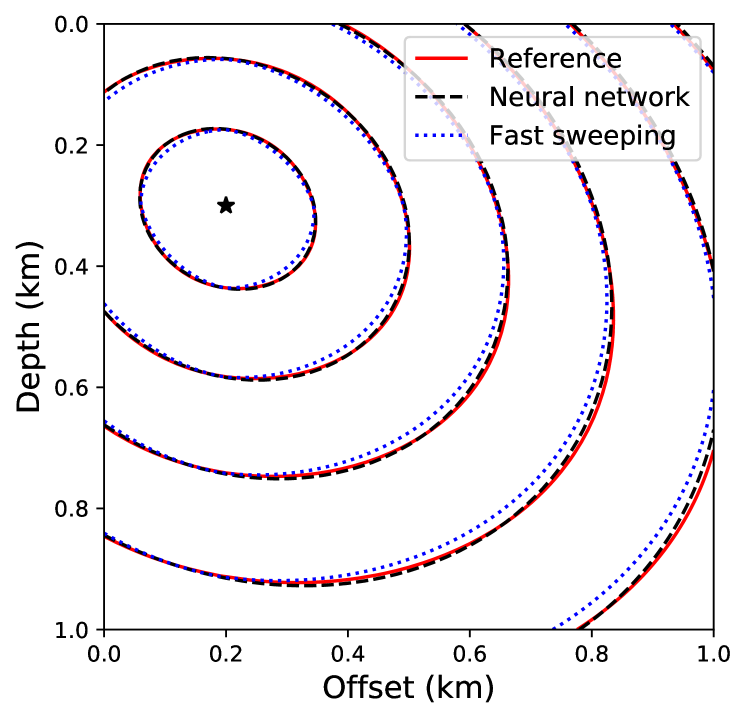
Figure 9 compares absolute traveltime errors computed using the neural network and the first-order fast sweeping method using the iterative solver of  Waheed et al. [33]. The reference solution is obtained using a high-order fast sweeping method on a finer grid. We observe that, despite using transfer learning, the accuracy of the neural network solution is considerably better than the fast sweeping method. We confirm this observation visually by comparing the corresponding traveltime contours in Figure 10. One can also observe the effect of the additional anisotropy parameters and the tilt angle on the traveltime contours here. By comparing the shapes of the contours in Figure 6 and 10, it is obvious that the wave propagation speed varies with the direction of propagation. A faster propagation is observed orthogonal to the symmetry direction, given by the tilt angle, compared to the propagation along the symmetry axis.

It is worth noting that while the complexity of the fast sweeping solvers and their computational cost increases dramatically when switching from an isotropic to a TTI model, for the neural network both cases require similar complexity and computational cost. Therefore, the proposed method is particularly suited to model complex physics involving media with anisotropy, attenuation, etc.

One of the main challenges in seismic imaging and inversion is the need for repeated traveltime computations for thousands of source locations and multiple updated velocity models. Unfortunately, conventional techniques do not allow the transfer of information from one solution to the next and, therefore, the same amount of computational effort is needed for even small perturbations in the source location and/or the velocity model. We noted above how transfer learning can be used to speed up convergence for a new velocity model and source position. This could be further extended by adding source location $(x_{s},z_{s})$ as input to the network and training a surrogate model.

To do so, we train a neural network on solutions computed for 16 sources located at regular intervals in the considered TTI model as shown in Figure 11. Through the training process, the network learns the mapping between a given source location and the corresponding traveltime field. Once the surrogate model is trained, traveltime fields for additional source locations can be computed instantly by using a single evaluation of the trained network. This is similar to obtaining an analytic solver as no further training is needed for computing traveltimes corresponding to new source locations. This feature is particularly advantageous for large 3D models that need thousands of such computations.

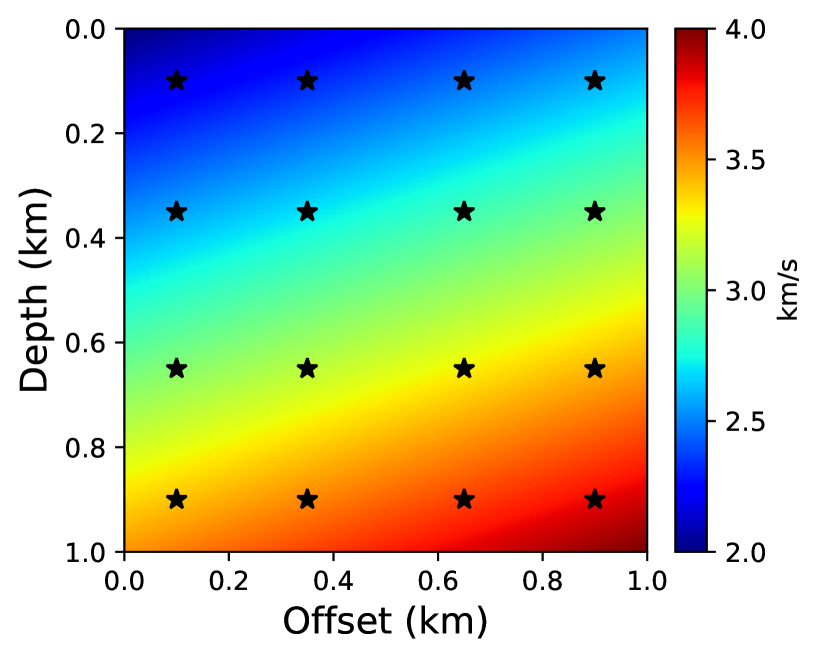
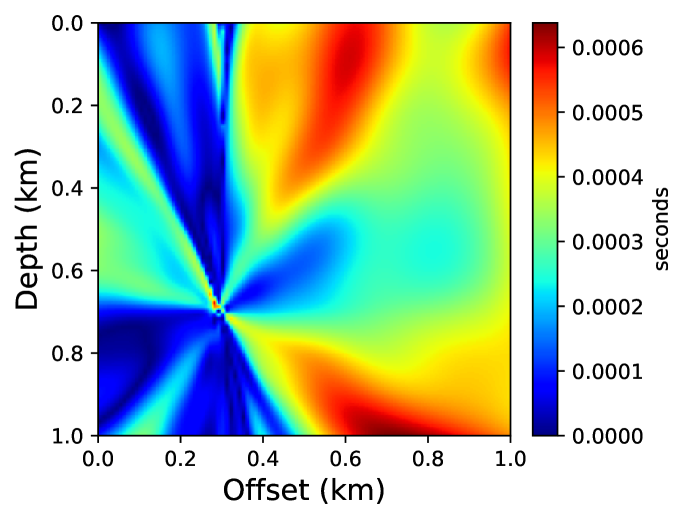
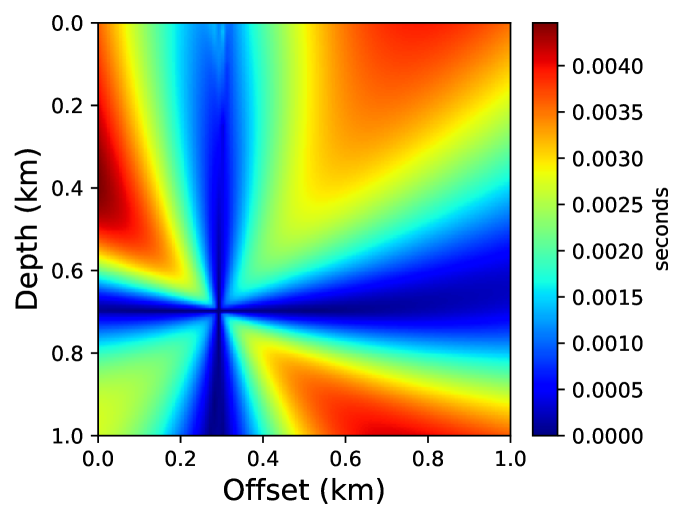
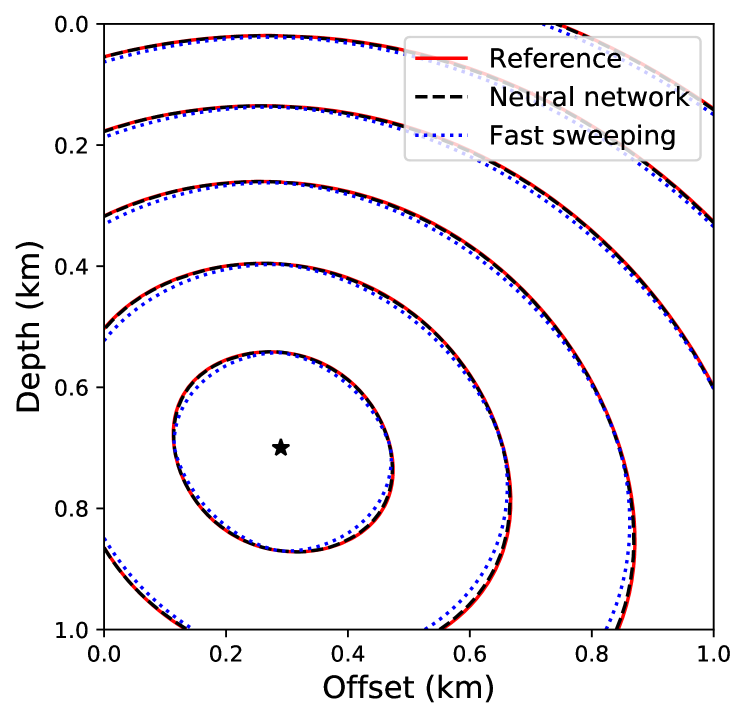
After training the surrogate model, we test its performance by computing the traveltime field corresponding to a randomly chosen source location. Figure 12 compares the absolute traveltime errors for the solution predicted by the surrogate model and the fast sweeping TTI solver. We observe that even without any additional training for this new source position, we obtain remarkably high accuracy compared to the fast sweeping method. This is also confirmed by visually comparing the corresponding traveltime contours in Figure 13.

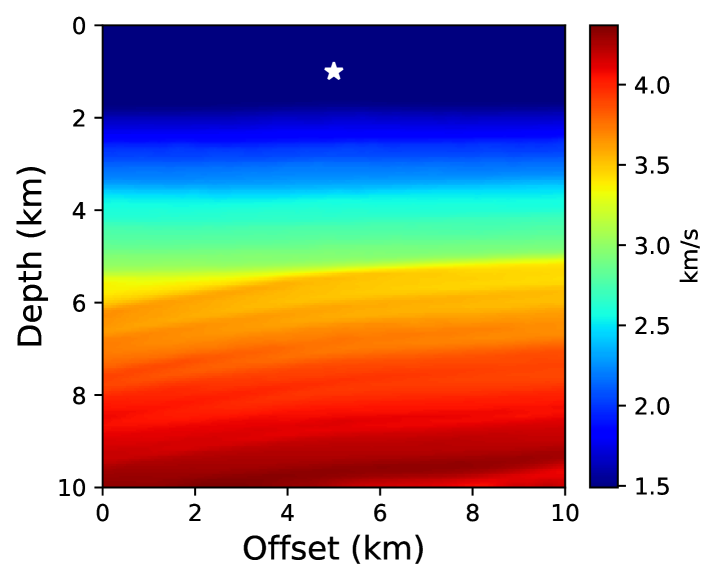
Next, we test the performance of the proposed method on a portion of the VTI SEAM model, shown in Figure 14. The model parameters are extracted from the 3D SEG Advanced Modeling (SEAM) Phase I subsalt earth model [63]. This is a particularly interesting example due to sharper variations in the velocity model and the anisotropy parameters. The model is discretized on a 101$\times$101 grid with a grid spacing of 100 m along both axes. Based on our recent efforts in using the neural network solver [47, 44], we observe that the convergence of the neural network approach slows down considerably in the presence of sharp variations in the velocity model. We have already seen above that using a pre-trained neural network yields faster convergence by allowing the use of the second-order optimization method (L-BFGS-B) directly. Therefore, in this example, we use the pre-trained network obtained from the TTI eikonal solver in example 2.

For further speedup, we propose a two-stage training scheme to obtain an accurate traveltime solution. In the first stage, when the neural network is learning a smooth representation of the underlying function, we use only a small percentage of grid points for training. In this case, we use only 1% of the total grid points chosen randomly for the first 200 epochs and then switch to using 50% of the total grid points in stage 2 for another 1000 epochs to update the learned function in better approximating sharp features in the resulting traveltime field. Again, since we start training with a pre-trained network, we use the L-BFGS-B optimizer for faster convergence.

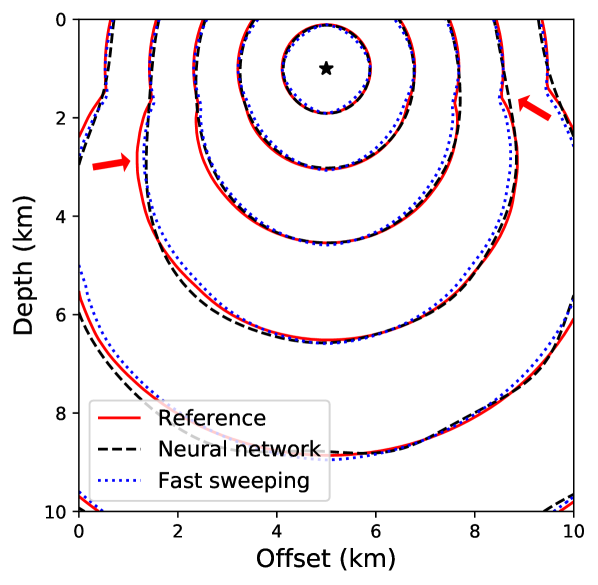
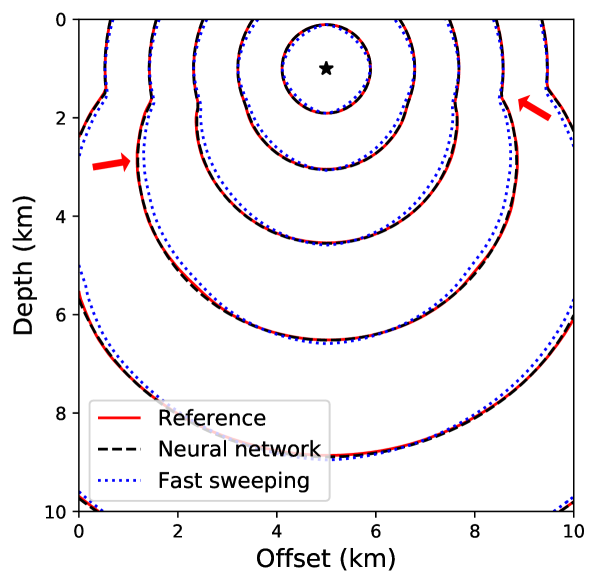
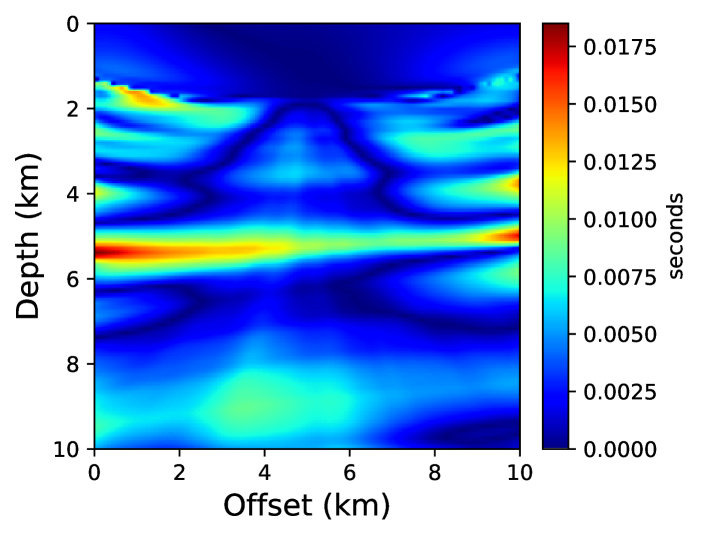
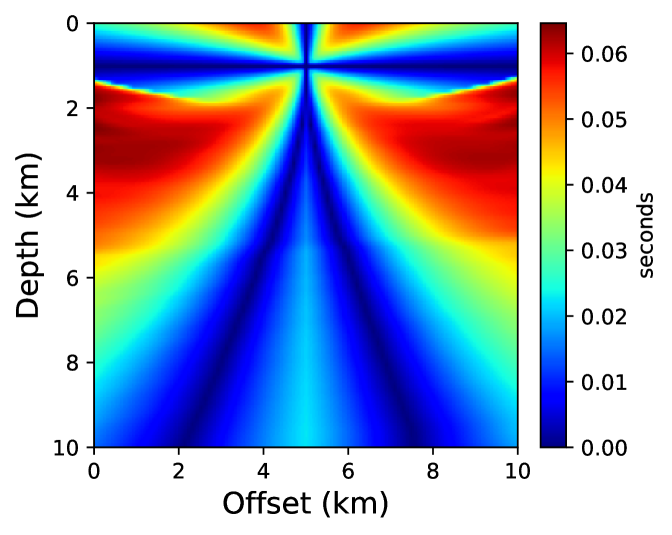
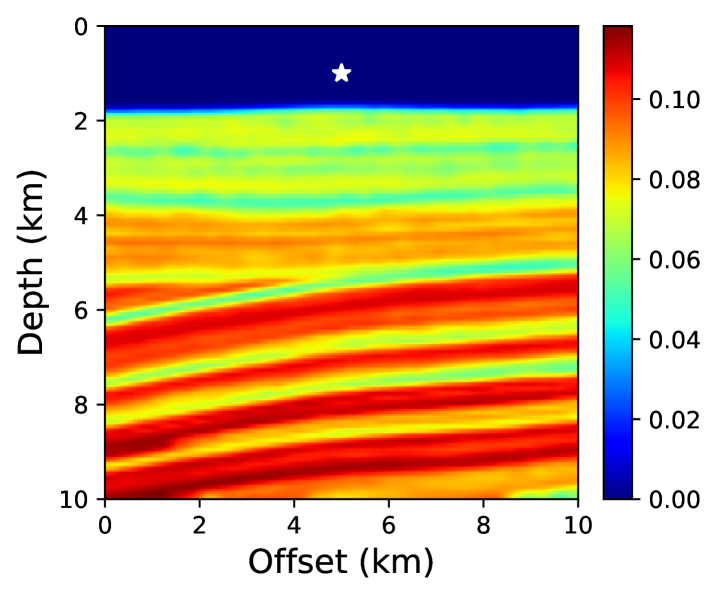
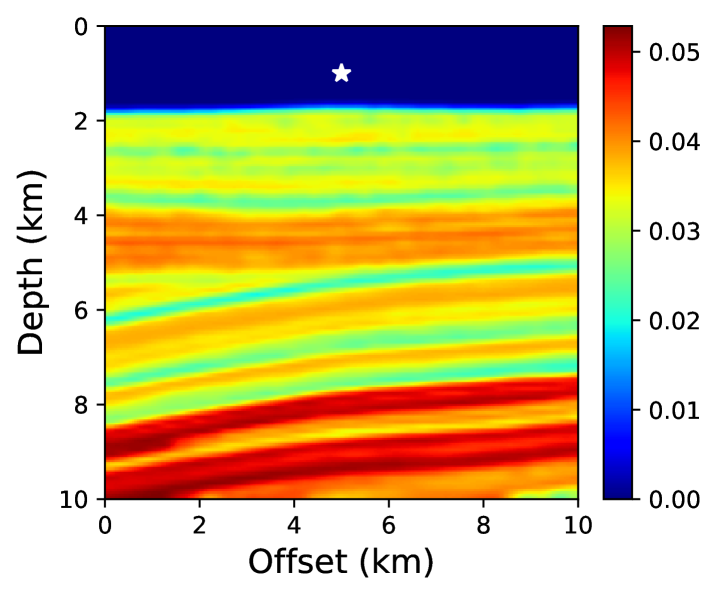
Figure 15 shows traveltime contours for a point-source located at (5 km, 1 km) for the reference solution, the neural network solution, and the first-order fast sweeping solution. In Figure 15, we show the neural network solution at the end of stage 1. It can be seen that the solution is quite smooth and misses sharp features visible in the reference solution. In Figure 15, we observe that the neural network solution captures these features as additional training points are added in the second stage of training. Therefore, using a small number of training points in stage 1 reduces the training cost without compromising on solution accuracy. By comparing the absolute traveltime errors in Figure 16, we observe that the neural network solution after stage 2 is considerably more accurate than the first-order fast sweeping method, even for a realistic VTI model.

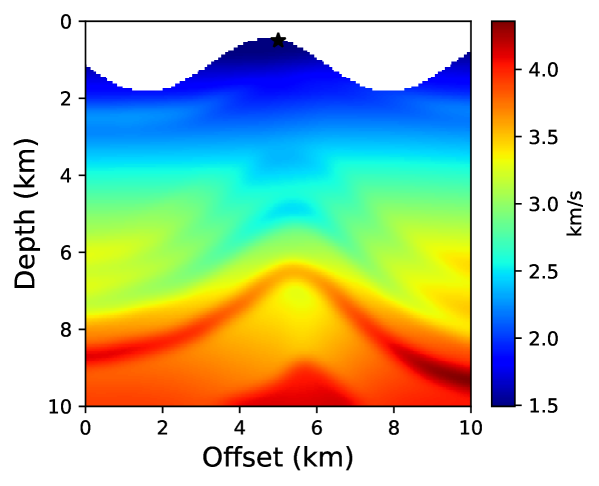
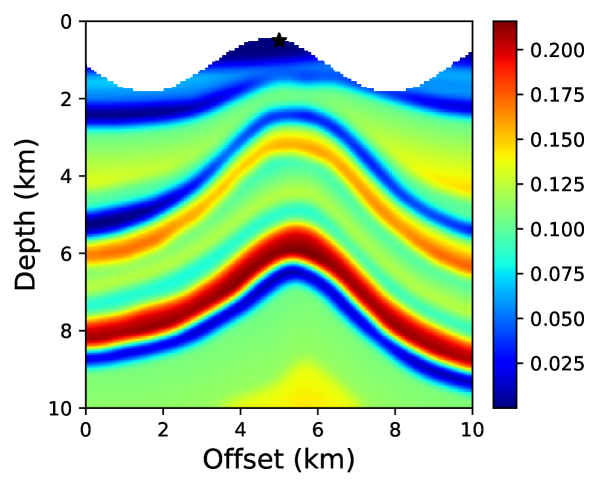
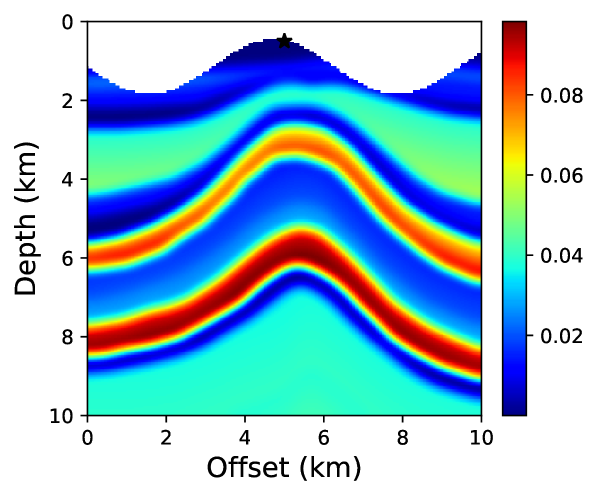
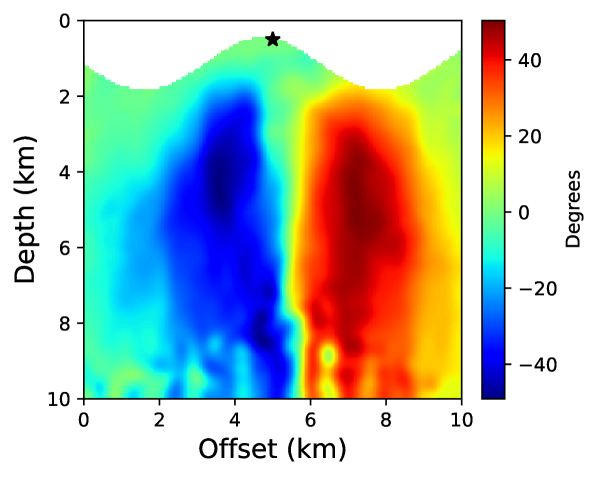
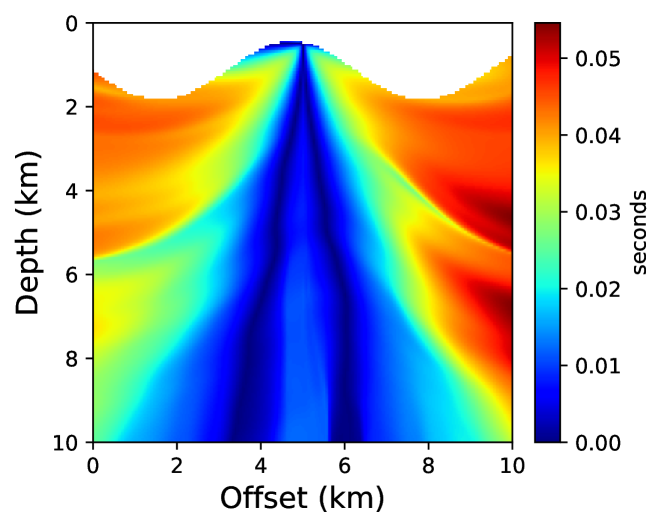
We have already seen how the neural network based approach is flexible in incorporating complex physics compared to conventional techniques. In this example, we will see how incorporating irregular topography is straightforward using the proposed approach. The free-surface encountered in land seismic surveys is often non-flat and requires taking this into account for accurate traveltime computation. One approach to tackle this is to transform from Cartesian to curvilinear coordinate system to mathematically flatten the free-surface and solve the resulting topography-dependent eikonal equation [37]. This adds additional computational cost and may result in instabilities when topography varies sharply. On the contrary, the neural network approach outlined here is mesh-free and doesn’t require any modification to the algorithm. We demonstrate this through a test on a portion of the BP TTI model, shown in Figure 17. The model was developed by Shah [64] and publicly provided courtesy of the BP Exploration Operating Company. The considered portion of the model is discretized on a 161$\times$161 grid using a grid spacing of 6.25 m along both axes. Points above the considered topography layer are then removed from the model.

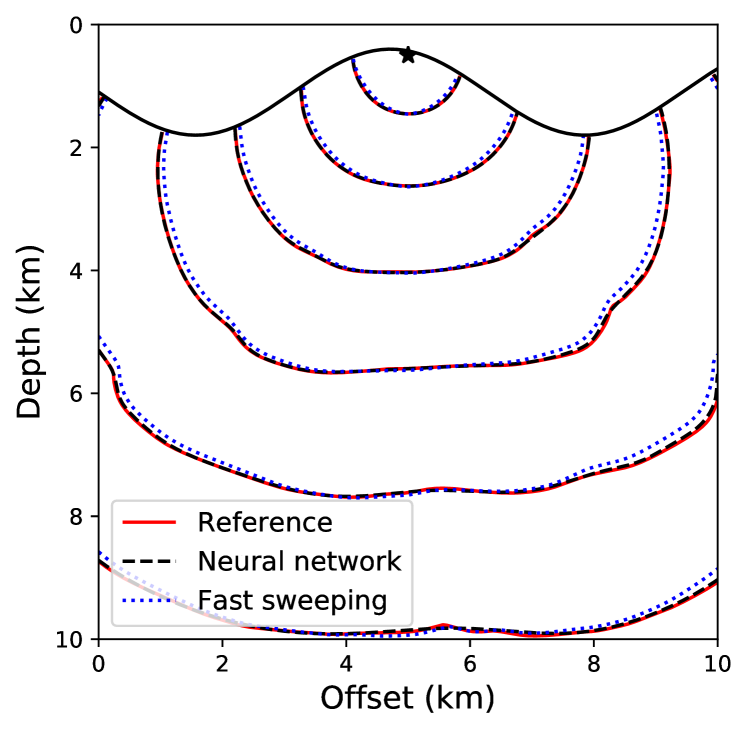
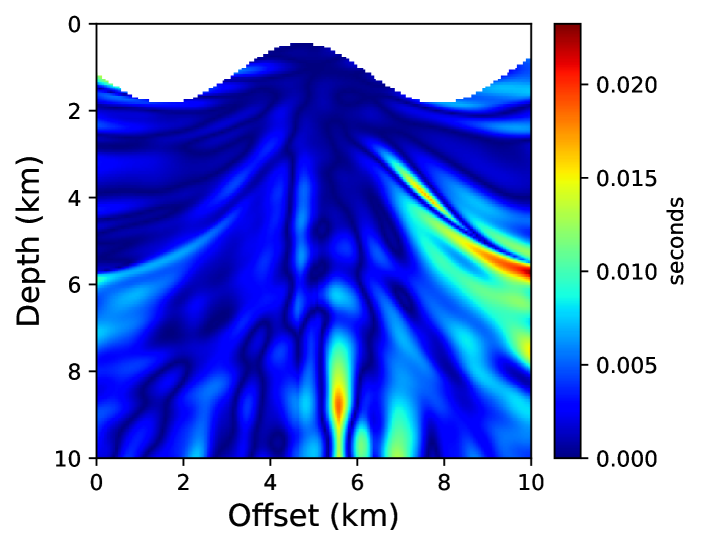
For a point-source located at (5 km, 0.5 km), we compare the neural network and fast sweeping traveltime solutions. For training the neural network, we take into account about 50% of the grid points below the topography and once the network is trained, we evaluate the solution on the regular grid points that fall below the topography. We start training using pre-trained parameters from example 2 and train for 10,000 epochs using an L-BFGS-B optimizer. Figure 18 shows absolute traveltime errors for the two cases, indicating that the neural network solution is again considerably more accurate than fast sweeping. We confirm this observation visually through traveltime contours plotted in Figure 19.

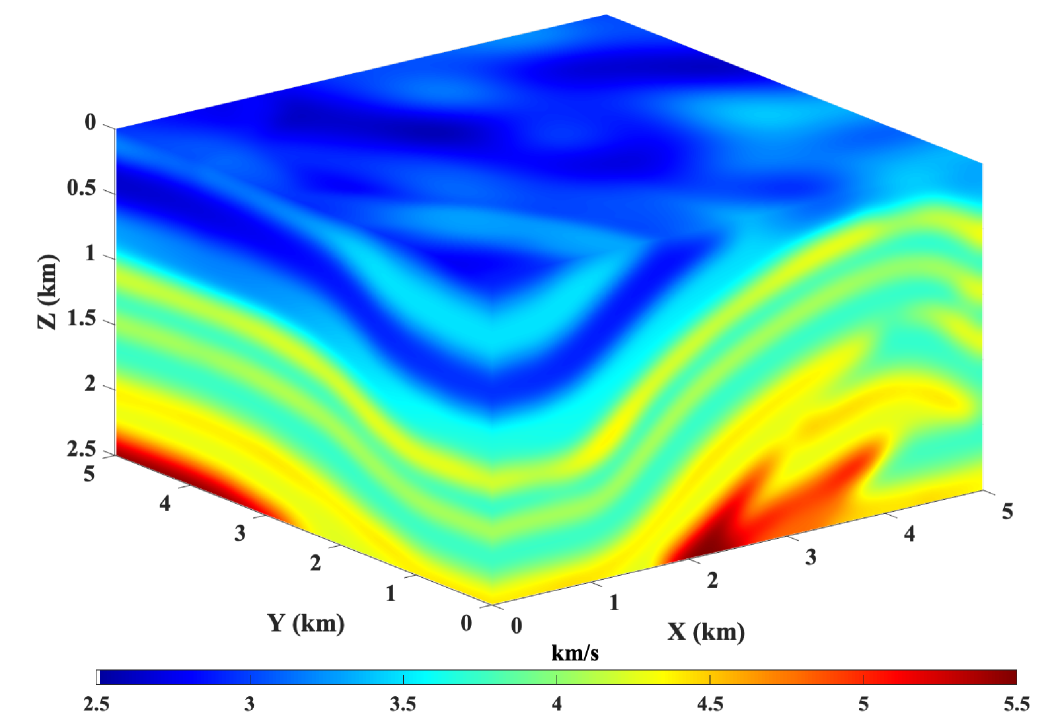
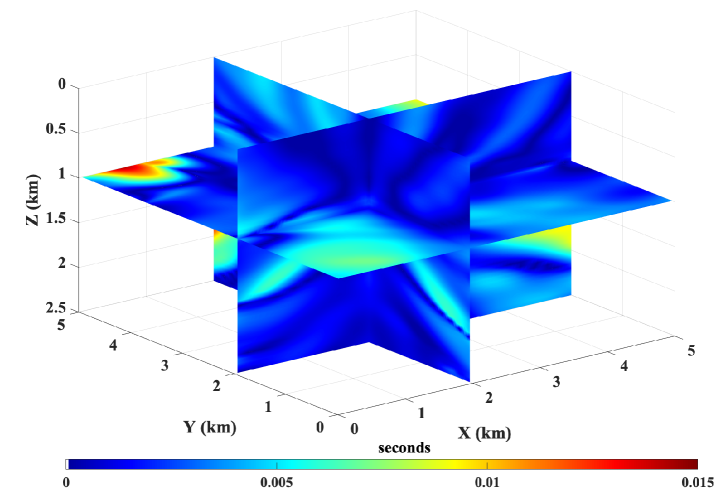
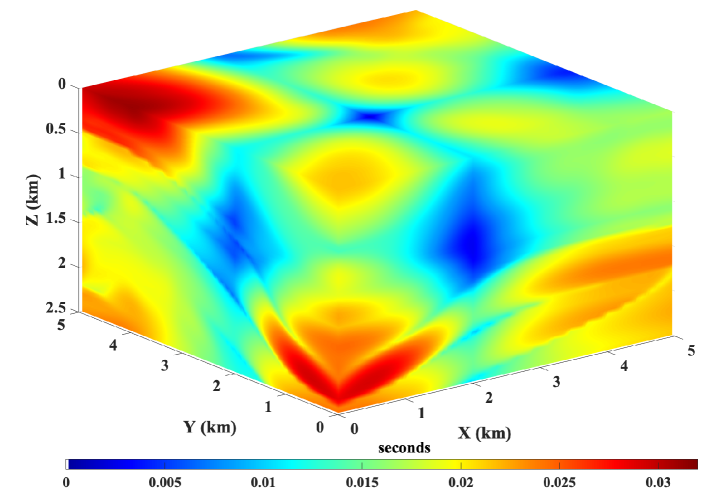
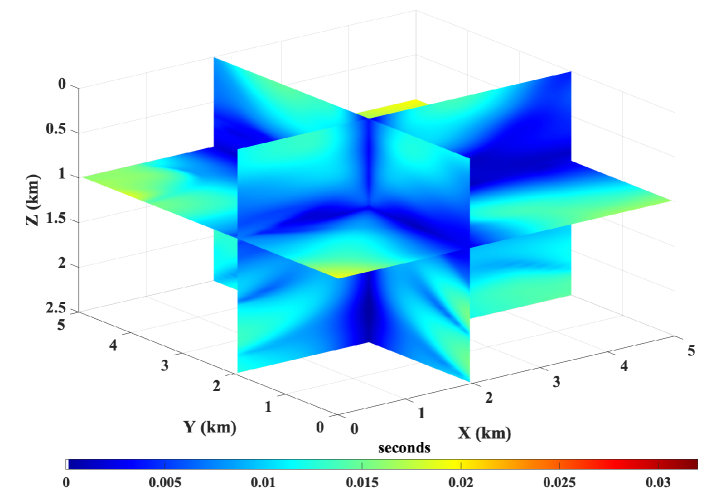
Finally, we show an example of extending the proposed method to a 3D TTI model. The model for the velocity parameter $v_{t}$ is shown in Figure 20. A homogeneous model is used for the anisotropy parameters with $\epsilon$=0.2 and $\eta$ = 0.1. We also consider a homogeneous tilt angle of 30^∘. The model is discretized on a 101$\times$101$\times$51 grid with a grid spacing of 50 m along each axis. The workflow for obtaining the neural network solution is essentially the same. In this case, the neural network takes three input parameters corresponding to the spatial axes $(x,y,z)$ and outputs the corresponding unknown traveltime field $\hat{\tau}(x,y,z)$. Similar to before, the neural network output is multiplied by the known traveltime factor $T_{0}(x,y,z)$ to obtain the final traveltime solution.

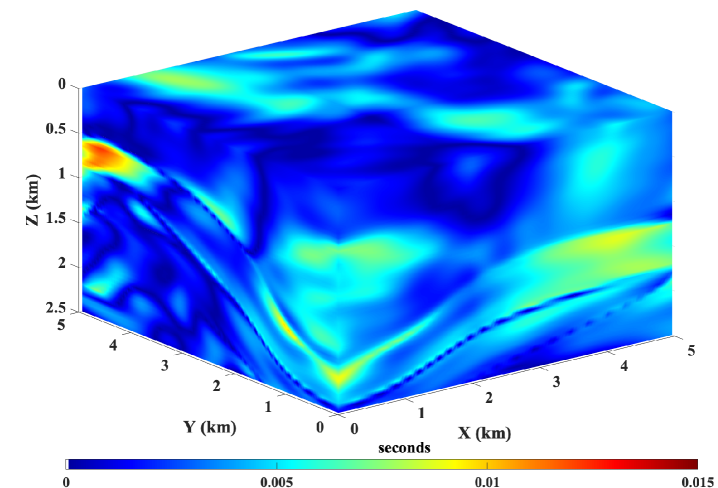
Starting with a pre-trained neural network on a smoothly varying TTI model, we train the network using 50% of the total grid points chosen randomly. We use 20,000 L-BFGS-B epochs during the training process. For a point-source located at $(x,y,z)$=(2 km, 2 km, 1 km), we compare the accuracy of the neural network solution and the first-order fast sweeping solution in Figure 21. We observe that the proposed method is capable of computing accurate traveltimes for 3D TTI models as well without requiring any major alteration to the underlying algorithm.