A hybrid green energy-based framework with a multi-objective optimization approach for optimal frost prevention in horticulture

Ercan Atam, Tamer F. Abdelmaguid, Muhammed Emre Keskin, Eric C. Kerrigan Ercan Atam and Eric C. Kerrigan are with Electrical and Electronic Engineering Department of Imperial College London, United Kingdom. Kerrigan is also with the Department of Aeronautics. Tamer F. Abdelmaguid is with Department of Mechanical Design & Production, Cairo University, Egypt. Muhammed Emre Keskin is with Department of Industrial Engineering, Ataturk University, Turkey. E-mails: e.atam@imperial.ac,uk, tabdelmaguid@eng.cu.edu.eg, emre.keskin@atauni.edu.tr, e.kerrigan@imperial.ac.uk.

Abstract

In this paper, first we propose a novel hybrid renewable energy-based solution for frost prevention in horticulture applications involving active heaters. Then, we develop a multi-objective robust optimization-based formulation to optimize the distribution of a given number of active heaters in a given large-scale orchard. The objectives are to optimally heat the orchard by the proposed frost prevention system and to minimize the total length of the energy distribution pipe network (which is directly related to the installation cost and the cost of energy losses during energy transfer). Next, the resulting optimization problem is approximated using a discretization scheme. A case study is provided to give an idea of the potential savings using the proposed optimization method compared to the result from a heuristic-based design, which showed a 24.13% reduction in the total pipe length and a 54.29% increase in frost prevention.

Index Terms:

Hybrid energy systems, active horticulture frost prevention systems, optimal design, multi-objective-optimization, k-MST, robust optimization.

I Introduction

Fruit constitutes an indispensable component of our daily nourishment and a significant fraction of export income for many countries (for example, $\approx$ €15-20 billion for EU member states [1]). However, during budding and/or flowering periods, buds or flowers of many fruits are vulnerable to low temperature levels, especially to temperatures below $0^{\circ}$ C, and hence for them frost occurrence can cause a significant yield loss. As an example, the frost occurrence on March 31, 2014 in Malatya, Turkey (which is the world capital for dry apricot production) caused around 95% of yield loss whose economic value was $1.2 billion US [2].

Active heaters which blow hot air on trees (to be called hot air blowing active heaters (HABAHs) in the rest of the paper) during frost periods can be a good choice for frost prevention in large-scale orchards [3, 4]. However, a significant barrier for widespread use of such systems is the installation and operation costs. Adoption of renewable or hybrid energy solutions (combination of renewable and non-renewable energies) to create hot air can reduce these costs up to some level. However, independent of the used energy source, two important design problems for active heater-based frost prevention systems are (i) the optimal distribution of a given number of active heaters inside a large-scale orchard so that maximum protection against frost episodes will be achieved and (ii) if hot air is distributed to HABAHs through a piping network, then optimization of the distribution pipe network to reduce pipeline cost and thermal energy losses.

A simplified schematic of the proposed hybrid energy-based frost prevention system where HABAHs are used is given in Figure 1. This system is called a hybrid energy system because a combination of renewable and non-renewable energy sources is used. The working principle of the system is as follows. Solar energy through solar collectors will be used to heat water and store it inside an insulated pool. The stored hot water will be used to heat air via a water-air heat exchanger and the hot air will be distributed through a pipe network to a number of blowers inside the orchard which will blow hot air on trees during frost periods. When necessary, additional energy from the grid will also be used to heat water in the pool (option 1), or to directly heat air via an array of electrical air heaters (option 2).

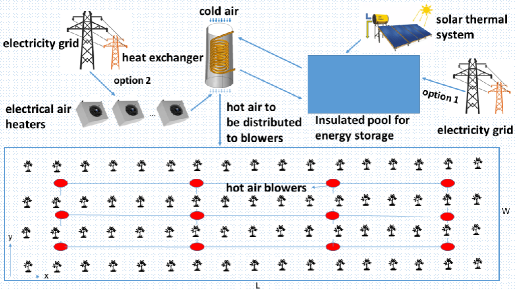
Refer to caption — Figure 1: Schematic of a hybrid energy-based frost prevention system integrating HABAHs for large-scale fruit orchards.

The use of a solar thermal system can provide significant advantages for regions with rich solar radiation, and for such regions, the extra energy that may be needed from the electricity grid to further heat the water or air will be a small fraction of the total energy used for frost prevention. As a result, the proposed hybrid solution will be an economically feasible and cost-effective solution. The economic feasibility analysis of the proposed hybrid frost prevention system (such as calculation of investment/operational costs and payback time) is not in the scope of the current paper and this will be studied in a future paper.

Note that the use of solar thermal collectors and the different insulation designs have already been considered for heating swimming pools with promising results [5, 6]. In the proposed hybrid energy solution, the purpose of the pool is to store solar thermal energy for a different application and pool will be completely covered from all sides with the most effective insulation material to minimize energy losses. As a result, the insulation and hence the storage efficiency requirements of the solar thermal-driven pool system of this study are more demanding.

Next, we developed a multi-objective robust optimization-based approach for optimal placement of a number of HABAHs inside a given large-scale orchard for effective frost prevention and optimal design of the energy distribution network of the proposed framework. The basic building blocks for the developed optimization scheme consists of (i) assuming a physically-reasonable function for spatial variation of the heating effect of a heater, (ii) modeling the optimal heating of the orchard against frost as an optimization constraint, (iii) constructing a k-node minimum spanning tree (k-MST) from a large undirected graph with unknown edge weights for optimal design of the layout of the energy distribution pipe network to reduce installation and energy loss costs. The resulting problem is a large-scale multi-objective robust mixed-integer nonlinear programming problem where we use a discretization scheme to approximate the problem with a mixed-integer linear programming (MILP) problem. Moreover, we developed a MILP-based k-MST formulation which is very useful for multi-objective optimization problems for which k-MST is a part. The k-MST is known to be NP-complete [7]. Furthermore, suboptimal k-MST heuristics developed in the literature, such as [9, 11, 8, 10], are not found suitable for the considered application since multiple objective functions are studied simultaneously, in addition to other non-traditional constraints that should be satisfied.

This paper is the first attempt in the open literature to propose a novel hybrid energy-based solution to the frost prevention problem in large-scale fruit orchards. This is also a pioneering work in proposing a multi-objective robust optimization-based approach, including a novel MILP-based k-MST formulation to tackle the challenging, but important inherent optimal design problems in applications based on a k-MST.

The rest of the paper is organized as follows. In Section II, an empirical, but physically reasonable model for the spatial variation of the heating effect of a HABAH is given. The development of the multi-objective robust optimization formulation for the considered application is described in detail in Section III, which includes the proposed discretization scheme for optimization approximation, the k-MST and robust counterpart formulations, each of which is a part of the overall optimization problem. A case study is given in Section IV to demonstrate the optimal savings using the optimization-based design compared to a heuristic-based design. Finally, the main findings of this study along with some future research directions are given in Section V.

II Spatial heater power effect variation modeling

The heating effect of any hot air blower-type active heater decreases with distance and this effect depends on a number of factors such as the installation configuration of the air blower, the mass flow rate of blown air and its temperature. In this paper, we assume the following representative empirical function for the spatial variation of the heating effect of a given HABAH:

	$\displaystyle P_{x_{i},y_{i}}(x,y)=$	$\displaystyle P_{0}k_{i}^{u}\underbrace{e^{-k_{tun}\sqrt{(x-x_{i})^{2}+(y-y_{i})^{2}}}}_{\triangleq f(x,y;x_{i},y_{i})}$
	$\displaystyle=$	$\displaystyle P_{0}k_{i}^{u}f(x,y;x_{i},y_{i})$		(1)

where $f(x,y;x_{i},y_{i})$ is the “effective heating power" of the $i$ -th active heater, which is centered at $(x_{i},y_{i})$ , at the point $(x,y)$ . Basically, $f(x,y;x_{i},y_{i})$ reflects the fraction of the maximum heating power $P_{0}$ transferred to the point $(x,y)$ in the orchard. The parameter $k_{tun}$ is a tuning parameter to vary the heating effect and the parameter $k_{i}^{u}$ is an uncertain parameter, lying in the interval $[\underline{k_{i}^{u}},\,\overline{k_{i}^{u}}]$ , to account for uncertainty in $P_{x_{i},y_{i}}(x,y)$ . For a specific type of hot air blowing heater, a function similar to $P_{x_{i},y_{i}}(x,y)$ can be used, and hence the developed general optimization framework in the next section can be used for any hot air blower.

III Energy distribution network optimization formulation

III-A The optimization problem

The motivation behind the use of optimization for the presented application is as follows. (i) For a given orchard, we want to locate $k$ HABAHs inside the orchard in order to heat the given orchard optimally in a balanced way. (ii) The heaters are connected through a pipe network in such a way that the length of the energy distribution pipeline network is minimized. Minimization of this length has a twofold benefit: first, the installation cost is minimized and, second the energy losses from the pipe network during energy circulation is minimized (the shorter the total pipe length, the smaller is the thermal energy loss because heat loss increases linearly with total pipe length).

As constraints of the optimization problem, the following conditions should be satisfied:

	$\displaystyle\underline{f}-\mu_{s}^{l}\leq\displaystyle\sum_{i=1}^{k}k_{i}^{u}f(x_{s}^{cp},y_{s}^{cp};x_{i},y_{i})\leq\overline{f}+\mu_{s}^{u},\,s=1,\cdots,n_{cp}$		(2)
	$\displaystyle(x_{i}-x_{j}^{t})^{2}+(y_{i}-y_{j}^{t})^{2}\geq d_{ht}^{2},\quad i=1,\cdots,k,\,j=1,\cdots,n_{t}$		(3)

Here, (2) is used to enforce the condition that at each selected discrete check point $(x_{s}^{cp},y_{s}^{cp})$ in the orchard (“cp" meaning check point) the sum of power fractions from all heaters should be in the range $[\underline{f},\overline{f}]$ whenever possible (if not possible, then minimum violations $\mu_{s}^{l},\mu_{s}^{u}$ are allowed); (3) is used to ensure that the distance between a heater and the root of a tree is a minimum of $d_{ht}$ meters because heaters should not be installed in areas occupied by tree stems and branches (assuming that the area occupied by a tree is approximately a circular area with center $(x_{j}^{t},y_{j}^{t})$ and radius $d_{ht}$ ). Note that the constraints in (2) are uncertain constraints since $k_{i}^{u}$ s are uncertain parameters, lying in the interval $[\underline{k_{i}^{u}},\,\overline{k_{i}^{u}}]$ .

The cost function to be minimized is

\displaystyle\sum_{(i,j)\in V\times V,\,j>i}q_{ij}\sqrt{(x_{i}-x_{j})^{2}+(y_{i}-y_{j})^{2}}+\alpha\sum_{s=1}^{n_{cp}}(\mu_{s}^{l}+\mu_{s}^{u})

(4)

where $V=\{1,2,\cdots,k\}$ , $q_{ij}$ is a binary variable indicating whether the energy pipe network contains a “direct" pipe branch ( $q_{ij}=1$ ) or not ( $q_{ij}=0$ ) from heater $i$ to heater $j$ . The objective function consists of the sum of two terms where the first one (the summation term) denotes the length of the minimum spanning tree consisting of k nodes (k-MST) and the second term is used to penalize power range violations at check points.

Note that the above optimization problem consisting of the cost function (4), constraints (2)-(3) and k-MST constraints (which we did not write at this point since they will be developed later in detail) is a multi-objective robust nonlinear programming problem.

III-B Discretization of orchard domain

In this section, we propose a discretization-based approach to be used in solving approximately the multi-objective robust nonlinear programming problem given in the previous section. In this approach we create a set of uniform discrete points inside the orchard satisfying the constraints in (3) as candidate heater location points (ch-lps) to place the heaters and we denote this set by $\mathcal{V}$ with $|\mathcal{V}|=n_{ch-lps}\gg k$ . Next, we construct an undirected weighted graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ where $\mathcal{E}$ is the set of weighted edges between each candidate heater location point and the edge weights $d_{e}^{ch-lps}$ , $e\in\mathcal{E}$ , are the distance between the candidate heater location points. The advantage of using this discretization technique is that the nonlinear constraints in (3) will be eliminated from the optimization problem, and we will be able to replace the nonlinear terms in (2) and (4) with linear terms as shown later.

Since k-MST is a part of the considered multi-objective robust optimization problem, next we develop a mixed-integer linear programming formulation for the k-MST problem.

III-C MILP-based formulation of k-MST problem

In this section, we extend the original Miller-Tucker-Zemlin (MTZ) MILP model developed for the travelling salesman problem [12] to the k-MST problem.

III-C1 Model structure and main variables

Consider a generic undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ where $\mathcal{V}$ is the node set and $\mathcal{E}$ is the set of weighted undirected edges. For every edge $e=\{i,j\}\in\mathcal{E}$ , where $i,j\in\mathcal{V}$ , a binary decision variable $z_{e}$ is defined which represents the edge’s inclusion (value of 1)/exclusion (value of 0) in the k-MST. Furthermore, for every node $i$ , we define a binary variable $\ell_{i}$ that equals 1 if node $i$ is included in the k-MST and zero otherwise. It is required to construct a tree with exactly $k$ nodes to achieve the stated objectives. Next, we develop the necessary constraints of the model.

III-C2 Constraints

The MTZ formulation is based on defining a pair of binary variables for each edge that suit the directed traveling salesman tour, denoted as $w_{(i,j)}$ and $w_{(j,i)}$ . The following set of constraints represent their relationships with $z_{e}=z_{\{i,j\}}$ :

z_{e}=w_{(i,j)}+w_{(j,i)}\;\;\;\;\forall e=\{i,j\}\in\mathcal{E}

(5)

The relationships provided in (5) enable smooth translations between the decisions of including/excluding the hypothetical directed arcs $(i,j)$ and $(j,i)$ and the inclusion/exclusion of the undirected edge $\{i,j\}$ .

In similar minimum spanning tree formulations, a node in $\mathcal{V}$ is arbitrarily selected and labeled as the terminal node. All resultant directed paths using the hypothetical directed arcs should end at that terminal node as part of the restrictions that lead to the formation of a tree [13]. In the case of k-MST, since not all the nodes will be included in the tree, that terminal node cannot be chosen from the nodes in $\mathcal{V}$ . Therefore, we add a dummy node $\tau$ to represent the terminal node in the current formulation. We also define a set of dummy edges $D=\{\{i,\tau\}:i\in\mathcal{V}\}$ . The lengths of the edges in $D$ do not affect the objective functions, and therefore, their values are not of concern. For every dummy edge $e\in D$ , a binary decision variable $z_{e}$ is augmented to the model, as well as pairs of $w_{(i,j)}$ and $w_{(j,i)}$ binary variables associated with its corresponding hypothetical directed arcs. Accordingly, similar to constraints (5), the following constraints are added to the model.

z_{e}=w_{(i,\tau)}+w_{(\tau,i)}\;\;\;\;\forall e=\{i,\tau\}\in D

(6)

In the MTZ formulation, there should be exactly one arc directed out of node $i$ , as well as exactly one arc directed into it in order to complete the travelling salesman tour. This restriction is not suitable for trees, since a node in a tree can have more than two edges connecting it to more than two nodes. As demonstrated in [13], this can be circumvented in the minimum spanning tree formulation by allowing only one restriction. That is, having exactly one arc directed out of a node, except the terminal node $\tau$ . In the k-MST formulation, this has to be governed by the condition of whether this node is included in the tree or not. The following constraints, represent these conditions:

	$\displaystyle\sum\limits_{j\in\mathcal{V}\cup\{\tau\},j\neq i}{w_{(i,j)}}=\ell_{i}$	$\displaystyle\forall i\in\mathcal{V}$		(7)
	$\displaystyle\sum\limits_{j\in\mathcal{V},j\neq i}{w_{(j,i)}}\leq(k-1)\ell_{i}$	$\displaystyle\forall i\in\mathcal{V}$		(8)

Here, the constraints in (7) restrict the number of selected outgoing arcs starting at node $i$ to be exactly 1 if it is included in the k-MST, and to be zero otherwise, for all nodes $i\in\mathcal{V}$ . Meanwhile, the constraints in (8) make sure that node $i$ will be connected by incoming arc(s) only when it is selected to be included in the k-MST.

Constraints (7) and (8) will result in a set of paths that start at a subset of nodes and can intersect at intermediate nodes. In the current model, all such paths should end at the dummy terminal node ( $\tau$ ). To achieve that, the following two constraints are added:

\sum\limits_{j\in\mathcal{V}}{w_{(\tau,j)}}=0

(9)

\sum\limits_{i\in\mathcal{V}}{w_{(i,\tau)}}=1

(10)

Constraints (9) and (10) make sure that only one edge connecting node $\tau$ will appear in the final solution. This restriction is necessary to make sure that all resultant $k$ nodes will be connected. The only edge that connects node $\tau$ to one of the other $k$ nodes can then be excluded when the final MILP solution is interpreted.

Subtours in the MTZ formulation are eliminated by introducing continuous variables $u_{i}$ for each node $i\in V\cup\{\tau\}$ . The elimination is done by allowing a directed arc $(i,j)$ to appear in the solution only when $u_{i}>u_{j}$ . The following constraints maintain this logic:

u_{i}\geq u_{j}+w_{(i,j)}-k(1-w_{(i,j)})\;\;\;\forall i\in\mathcal{V}-\{j\}\;\;\forall j\in\mathcal{V}\cup\{\tau\}

(11)

The range of values that can be assigned to the $u_{i}$ variables are defined by the following constraints:

$\displaystyle u_{\tau}=0$		(12)
$\displaystyle u_{i}\leq(k-1)\ell_{i}$	$\displaystyle\forall i\in\mathcal{V}$	(13)
$\displaystyle u_{i}\geq\ell_{i}$	$\displaystyle\forall i\in\mathcal{V}$	(14)

Finally, the constraint that specifies the number of selected nodes to be exactly $k$ and the domain constraints are defined as

$\displaystyle\sum\limits_{i\in V}{\ell_{i}}=k$		(15)
$\displaystyle\ell_{i}\in\{0,1\}$	$\displaystyle\forall i\in\mathcal{V}$	(16)
$\displaystyle w_{(i,j)},z_{\{i,j\}}\in\{0,1\}$	$\displaystyle\forall i,j\in\mathcal{V}\cup\{\tau\}$	(17)

III-D Robust counterpart formulation for uncertain constraints

As mentioned before, the constraints in (2) are uncertain constraints since the $k_{i}^{u}$ are uncertain parameters lying in the interval $[\underline{k_{i}^{u}},\,\overline{k_{i}^{u}}]$ . To develop a deterministic MILP problem corresponding to the robust MILP, which is called the “robust counterpart" in the robust optimization literature [14, 15], we need to express the uncertain constraints (2) in a deterministic form such that they are satisfied for all realizations of the uncertain parameters $k_{i}^{u},\,i=1,\cdots,k$ in their range $\underline{k_{i}^{u}}\leq k_{i}^{u}\leq\overline{k_{i}^{u}}$ . This happens if in (2) we replace $k_{i}^{u}$ s with their lower bounds $\underline{k_{i}^{u}}$ and upper bounds $\overline{k_{i}^{u}}$ for " $\leq$ " and " $\geq$ ", respectively. Using this replacement combined with the discretization scheme, we obtain the “robust counterpart constraints" as


$\displaystyle\underline{f}-\mu_{s}^{l}\leq\displaystyle\sum_{i=1}^{n_{ch-lps}}\ell_{i}\underline{k_{i}^{u}}h_{is}$	$\displaystyle s=1,\cdots,n_{cp}$	(18a)
$\displaystyle\displaystyle\sum_{i=1}^{n_{ch-lps}}\ell_{i}\overline{k_{i}^{u}}h_{is}\leq\bar{f}+\mu_{s}^{u}$	$\displaystyle s=1,\cdots,n_{cp}$	(18b)

where $h_{is}\triangleq f(x_{s}^{cp},y_{s}^{cp};x_{i}^{ch-lp},y_{i}^{ch-lp})$ denotes heat influence of a heater located at the $i$ -th candidate heater location point with coordinates $(x_{i}^{ch-lp},y_{i}^{ch-lp})$ at the $s$ -th check point with coordinates $(x_{s}^{cp},y_{s}^{cp})$ .

III-E The overall approximated optimization problem

Collecting all the previous developments, we can express the overall multi-objective robust optimization problem as in (19). The parameters $\beta_{1}^{nor},\beta_{2}^{nor}$ are used to normalized each part of the cost function to lie in the interval [0,1]. For a given large-scale orchard, it is important that a proper number of candidate heater location points and check points are created so that a good trade off is achieved between the optimality of the resulting approximated MILP problem and the number of resulting associated binary variables, which affect the solvability and the time required for the solution of the approximate MILP.

Approximate MILP:


$\displaystyle\displaystyle\min_{z_{\{i,j\}},w_{(i,j)},w_{(j,i)},w_{(i,\tau)},w_{(\tau,i)},\ell_{i},u_{i},\mu_{s}^{l},\mu_{s}^{u}}\left\{\frac{1}{\beta_{1}^{nor}}\sum_{\{i,j\}\in\mathcal{E}}z_{\{i,j\}}d_{i,j}^{ch-lp}+\frac{\alpha}{\beta_{2}^{nor}}\sum_{s=1}^{n_{cp}}(\mu_{s}^{l}+\mu_{s}^{u})\right\}$		(19a)
$\displaystyle\eqref{KMST_1}-\eqref{KMST_13}$	$\displaystyle(\text{k-MST constraints})$	(19b)
$\displaystyle\underline{f}-\mu_{s}^{l}\leq\displaystyle\sum_{i=1}^{n_{ch-lps}}\ell_{i}\underline{k_{i}^{u}}h_{is}$	$\displaystyle s=1,\cdots,n_{cp}$	(19c)
$\displaystyle\displaystyle\sum_{i=1}^{n_{ch-lps}}\ell_{i}\overline{k_{i}^{u}}h_{is}\leq\bar{f}+\mu_{s}^{u}$	$\displaystyle s=1,\cdots,n_{cp}$	(19d)
$\displaystyle\mu_{s}^{l},\mu_{s}^{u}\geq 0$	$\displaystyle s=1,\cdots,n_{cp}$	(19e)

IV A case study

In this section we will consider a case study and compare the results from a heuristic-based design with the multi-objective robust optimization results. The considered large-scale orchard together with candidate heater location points and check points are given in Figure 2 and its parameters are given in Table I. The heuristic-based design consists of two stages. In the first stage, we divide the orchard into $k$ parts having the same area and put a heater at the center of each part. If a heater is put too close to a tree (within $d_{ht}$ meters), it is pushed from the tree in the same direction so that the distance between the tree and the heater is $d_{ht}$ m. By doing so, we ensure that no heater is located too close to the trees. In the second stage, we find pairwise distances between the centers to construct an undirected graph and then a MST from the resulting graph using Kruskal’s algorithm. The heater locations and pipe network using this heuristic are given in Figure 3.

TABLE I: Orchard and optimization parameters

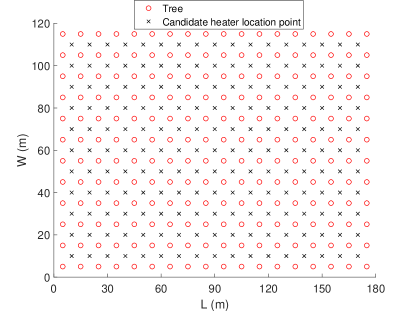
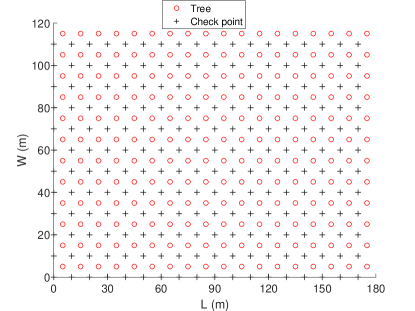
parameter	description	value
$L$	orchard length (m)	180
$W$	orchard width (m)	120
$n_{t}$	number of trees	216
$k$	number of heaters	21
$n_{ch-lps}$	number of candidate heater location points	187
$n_{cp}$	number of check points	216
$d_{ht}$	distance between the root of a tree and center of a heater (m)	3
$\underline{f}$	minimum total power fraction at check points	0.5
$\bar{f}$	maximum total power fraction at check points	1
$k_{i}^{u}$	parameter to represent the uncertainty in the heating effect of a heater at a point	$[0.8,\,1]$
$\underline{k_{i}^{u}}$	lower bound of $k_{i}^{u}$	0.8
$\overline{k_{i}^{u}}$	upper bound of $k_{i}^{u}$	1
$k_{tun}$	tuning variable for spatial variation of the heating effect of heaters	0.01
$\Delta_{t}$	horizontal and vertical distance between the roots of adjacent trees in the orchard (m)	10
$\Delta_{ch-lps}$	horizontal and vertical distance between adjacent candidate heater locations in the orchard (m)	10
$\Delta_{cp}$	horizontal and vertical distance between adjacent check points in the orchard (m)	10
$\beta_{1}^{nor}$	normalization parameter for the length of k-MST	600
$\beta_{2}^{nor}$	normalization parameter for the sum of power range violations	240

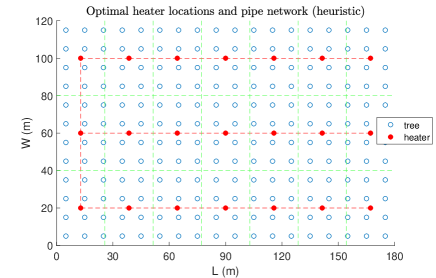
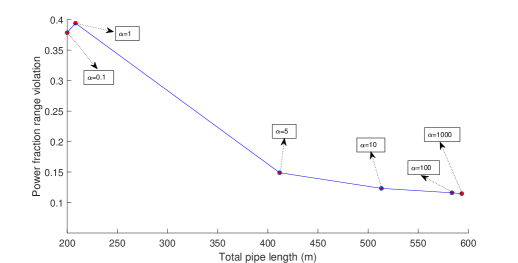
The multi-objective robust optimization results were obtained using Gurobi[16] as a solver on a laptop with the following hardware specifications: 8GB RAM, Intel(R) Core(TM) i7-8550U CPU @ 1.80GHz 1.99 GHz. Solver time was set to 3 hours to find a solution close to optimal. The optimization results are given in Table II where the first column includes a series of values for the multi-objective optimization parameter $\alpha$ , the second column gives the optimality gaps, and the last two columns denote

	$\displaystyle\text{obj}_{\text{part1}}\triangleq\sum_{e=\{i,j\}\in\mathcal{E}}z_{\{i,j\}}d_{i,j}^{ch-lp}$
	$\displaystyle\text{obj}_{\text{part2}}\triangleq\frac{1}{n_{cp}}\sum_{s=1}^{n_{cp}}(\mu_{s}^{l}+\mu_{s}^{u})$

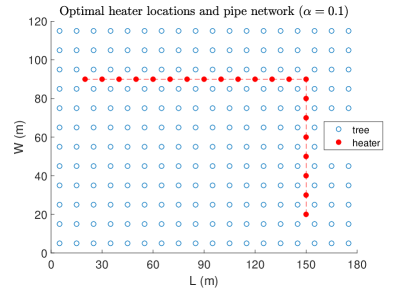
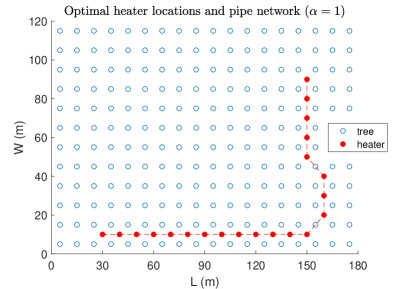
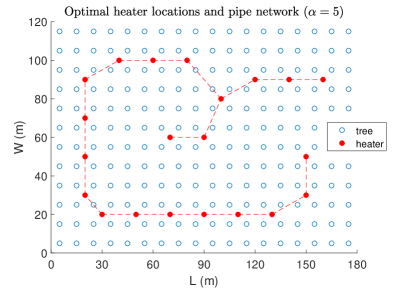
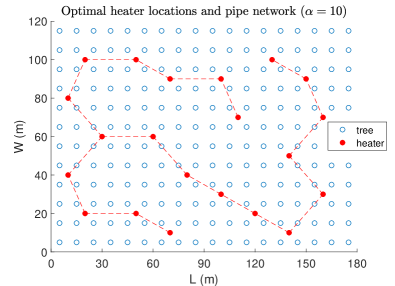
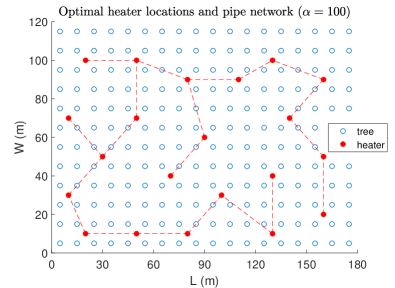
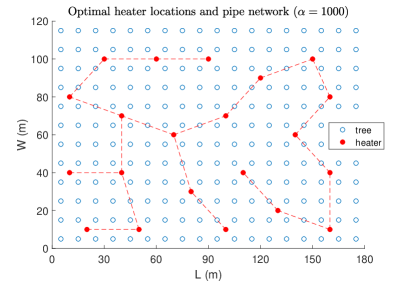
which are the total pipe length and average power fraction range violation, respectively. The Pareto curve of the multi-objective robust optimization and the corresponding optimal heater locations and pipe network for each case of the considered $\alpha$ value are given in Figure 4 and Figure 5, respectively, from which we conclude that among the considered $\alpha$ values $\alpha=5$ seems a good choice with $\text{obj}_{\text{part1}}=411.87$ (m) and $\text{obj}_{\text{part2}}=0.149$ . In the Pareto curve we notice that the point corresponding to $\alpha=1$ is higher than the point corresponding to $\alpha=0.1$ . Normally, the opposite should be the case. The cause for this abnormality is the fact that the optimality gap corresponding to $\alpha=1$ ( $35.9\%$ ) is considerably higher than the optimality gap corresponding to $\alpha=0.1$ ( $6.23\%$ ) obtained after 3 hours run of the optimization algorithm (see, Table II).

TABLE II: Multi-objective optimization and heuristic-based results

$\alpha$	$\text{optimality gap}(\%)$	$\text{obj}_{\text{part1}}$ (m)	$\text{obj}_{\text{part2}}(-)$
$0.1$	6.23	200	0.379
$1$	35.9	208,28	0.394
$\bf{5}$	31.94	411.87	0.149
$10$	24.56	513.31	0.123
$100$	25.40	583.64	0.116
$1000$	30.50	593.43	0.114
Heuristic-based	—-	542.85	0.326

Table II also shows the heuristic-based design results. When calculating the power fraction range violations in the heuristic case, $k_{i}^{u}$ value for each heater was created as a random number in the range [0.8, 1]. When the multi-objective robust optimization results corresponding to the best case $\alpha=5$ are compared to the heuristic-based results, we have a 24.13% reduction in the total pipe length and a 54.29% reduction in power fraction range violations, which clearly show the savings provided by the developed multi-objective robust optimization approach.

V Conclusions

Cost-effective frost prevention in large-scale orchards is a challenging problem, and development of any cheap and widespread usable technology for it will have a huge societal impact. Being aware of the importance of this problem, in this paper, first we presented a renewable energy-integrated (solar thermal) solution for frost prevention in horticulture, thus providing an important potential application where renewable energy can be used for. Second, we developed a multi-objective robust MILP formulation (i) to determine optimally the location of hot air blowers to heat the orchard in a balanced way to achieve maximum frost protection, (ii) to optimize the layout of hot air distribution pipe network to minimize the investment cost and energy losses. The proposed optimization method involved, as part of it, the development of a MILP-based k-MST formulation suitable for multi-objective optimization problems.

The proposed optimization method was tested on a case study with the dimensions $L\times W=180\text{m}\times 120\text{m}$ . The optimization results corresponding to the the optimal value of $\alpha$ obtained from the Pareto plot and a 3 hours run of the algorithm were compared with those of a heuristic-based design to show the degree of savings, which are a 24.13% reduction in the total pipe length and a 54.29% reduction in power fraction range violations. These savings clearly illustrate the importance of the use of a numerical optimization framework in optimal design of the suggested hybrid energy frost prevention system. Although here we focused on frost prevention for horticulture, the proposed framework can be used with minor modifications for other agricultural applications as well.

Examples of future works are economic feasibility analysis of the proposed hybrid energy solution, determination of the minimal number of heaters to be used for a given large-scale orchard and integration of a decomposition scheme for very large-scale optimization problems corresponding to very large-scale orchards.

References

[1] The fruit and vegetable sector in the EU - a statistical overview, http://ec.europa.eu/eurostat, last access August, 2020.
[2] Malatya Il Gida Tarim ve Hayvancilik Mudurlugu, Technical report (in Turkish), 2016.
[3] E. Atam and A. Arteconi, “Green energy-assisted frost prevention: a conceptual framework", Energy Procedia, vol. 141, pp. 155-159, 2017.
[4] E. Atam, S. W. Hong and A. Arteconi, “Thermofluid Modelling of Large-Scale Orchards for Optimal Design and Control of Active Frost Prevention Systems", Energies, vol. 13, no. 2, pp. 1-17, 2020.
[5] J. L. A. Francey, P. Golding and R. Clarke, “Low-cost solar heating of community pools using pool covers", Solar Energy, vol. 25, pp. 407-416, 1980.
[6] M. Dongellini, S. Falcioni, A. Martelli and G. L. Morini, “Dynamic simulation of outdoor swimming pool solar heating", Energy Procedia, vol. 81, pp. 1-10, 2015.
[7] M. Fischetti, H.W. Hamacher, K. Jørnsten and F. Maffioli, “Weighted k-cardinality trees: Complexity and polyhedral structure", Networks, vol. 24, no. 1, pp. 11-21, 1994.
[8] N. Garg, “A 3-approximation for the minimum tree spanning k vertices”, Proceedings of the 37th IEEE Symposium on Foundations of Computer Science, October 14-16, Vermont, USA pp. 302-309, 1996.
[9] S. Arya and H. Ramesh, “A 2.5 factor approximation algorithm for the k-MST problem”, Information Processing Letters, vol.65, pp. 117-118, 1998.
[10] N. Garg, “Saving an epsilon: A 2-approximation for the k-MST problem in graphs”, Proceedings of the 36th ACM Symposium on Theory of Computing, May 22-24, Baltimore, USA, pp. 396-402, 2005.
[11] S. Arora and G. Karakostas, “A 2 + $\epsilon$ approximation algorithm for the k-MST problem”, Mathematical Programming, vol.107. pp. 491-504, 2006.
[12] C. E. Miller, A. W. Tucker and R. A. Zemlin, “Integer Programming Formulation of Traveling Salesman Problems", Journal of the ACM, vol. 7, no. 4, pp. 326-329, 1960.
[13] T. F. Abdelmaguid, “An Efficient Mixed Integer Linear Programming Model for the Minimum Spanning Tree Problem", Mathematics, vol. 6, pp. 183, 2018.
[14] D. Bertsimas and M. Sim, “The price of robustness," Operations Research, vol. 52, no. 1, pp. 35-53, 2004.
[15] Z. Li, R. Ding and C. A. Floudas, “A comparative theoretical and computational study on robust counterpart optimization: I. Robust linear optimization and robust mixed integer linear optimization,", Industrial & Engineering Chemistry Research, vol.50, pp. 10567-10603, 2011.
[16] Gurobi Optimization Inc. Gurobi Optimizer, Software, https://www.gurobi.com, last access January, 2021.

Ercan Atam received his PhD from Boğaziçi University, Istanbul, Turkey, in 2010. He was a Postdoctoral Researcher with LIMSI-CNRS, France, from 2010 to 2012 working on fluid flow control. From 2012 to 2015, he was a Postdoctoral Researcher with KU Leuven, Belgium, working on control and optimization for smart buildings. Currently, he is an honorary research fellow at Imperial College London, UK. His research interests include optimization, predictive control, machine learning, renewable energy-integrated co-design applications and smart horticulture.

Tamer F. Abdelmaguid received his Ph.D. in Industrial and Systems Engineering at the University of Southern California in 2004. Currently, he is a professor of industrial engineering at Cairo University, Egypt. He has served as a visiting assistant professor at King Saud University from 2008 to 2010, and as a visiting associate professor at the American University in Cairo from 2017 to 2019. His research interests are related to mathematical modeling and optimization of manufacturing processes and production planning and scheduling.

Muhammed Emre Keskin received his B.S. degree from Industrial Engineering department of Bilkent University, Turkey, in 2004 and his M.S. and Ph.D. degrees from Industrial Engineering department of Boğaziçi University respectively in 2007 and 2014. He is currently working as an associate professor at Atatürk University. His research interests are mobile wireless sensor networks, mixed integer linear programming and decomposition of integer programs.

Eric C. Kerrigan (S’94-M’02-SM’16) received a BSc(Eng) from the University of Cape Town and a PhD from the University of Cambridge. His research is in the design of efficient numerical methods and computing architectures for solving optimal control problems in real-time, with applications in the design of aerospace, renewable energy and information systems. He is the chair of the IFAC Technical Committee on Optimal Control, a Senior Editor of IEEE Transactions on Control Systems Technology and an Associate Editor of IEEE Transactions on Automatic Control and the European Journal of Control.