A local theory for Mott-Anderson localization
Abstract
The paramagnetic metallic phase of the Anderson-Hubbard model (AHM) is investigated using a non-perturbative local moment approach within the framework of dynamical mean field theory with a typical medium. Our focus is on the breakdown of the metallic phase near the metal-insulators transition as seen in the single-particle spectra, scattering rates and the associated distribution of Kondo scales. We demonstrate the emergence of a universal, underlying low energy scale, . This lies close to the peak of the distribution of Kondo scales obtained within the metallic phase of the paramagnetic AHM. Spectral dynamics for energies, display Fermi liquid universality crossing over to an incoherent universal dynamics for in the scaling regime. Such universal dynamics indicate that within a local theory the low to moderately low energy physics is governed by an effective, disorder renormalised Kondo screening.
1 Introduction
Disorder is ubiquitous in real materials, strongly influencing their properties mirlin_review_2008 ; mackinnon_1993 ; fifty_years . Another aspect of several condensed matter systems like the heavy fermions or transition metal oxides is the presence of strong electron-electron interactions Phys_today_DMFT ; DMFT_RMP . In particular, Coulomb correlations and disorder may individually drive a system towards a metal-insulator transition. While the Anderson metal-insulator transition Anderson is caused by quenched disorder, the Mott-Hubbard metal-insulator transition emerges from strong Coulomb repulsion DMFT_RMP . The simultaneous presence of disorder () and interaction () effects is known to influence material properties in subtle ways. Over the last few decades, several experimental works on a range of systems mirlin_review_2008 ; kravchenko_review_2004 ; Miranda1997_review ; perovskite_maiti ; perovskite_kim ; perovskite_athena ; cold_atom1 ; cold_atom2 ; cold_atom3 have highlighted the importance of the interplay of disorder and interactions. The early theoretical studies of such systems TVR_Lee_RMP mainly focused on the weak disorder limit, perturbing around Fermi liquid theory. It is now known that the subtle interplay of disorder and interactions may lead to non-Fermi liquid like responses in the thermodynamic quantities, as observed in several experiments Miranda1997_review ; therefore, one requires a non-perturbative framework that can deal with interactions and disorder on an equal footing.
One of the most intriguing aspects of strongly correlated electron systems is the appearance of low-energy scales Raja_dyn_sca_pam ; Si_Steglich_QCP_review ; Bulla2001 . For metals with strong electronic correlations a frequently observed scenario is the presence of long-lived quasi-particles representing a coherent Fermi liquid picture at the lowest temperatures () and energy scales. A universal low energy scale, , lies at the heart of all strongly correlated electron systems that manifests in the universal transport properties of these materials Bulla2001 . Over the past few decades, the dynamical mean field theory (DMFT) has stood out as a very successful theoretical framework for understanding several aspects of the low energy physics of strongly correlated electron systems DMFT_RMP . Since, in DMFT, any lattice-fermion model reduces to a local quantum impurity model, the involvement of Kondo physics is inevitable. Thus, universal behavior due to the emergence of a universal low energy scale is generally attributed to the underlying Kondo effect. For example in the DMFT picture of the metallic phase of the Hubbard model DMFT_RMP ; Logan_mott_ins , the Kondo effect leads to full quenching of the electron spin degrees of freedom resulting in a non-degenerate Fermi liquid ground state characterized by a low energy Fermi liquid scale. In the vicinity of the Mott transition, the strongly correlated metal is therefore characterized by a low-energy scale corresponding to the coherence temperature of a Fermi liquid DMFT_RMP ; Logan_mott_ins .
The emergence of a single low energy/temperature scale may not be restricted to clean strongly-correlated electron systems, but has also been predicted in the context of diluted two-dimensional electron gases (2DEGs) 2DEGs_vlad . Phenomenological theories, based on experimental observations in 2DEGs kravchenko_review_2004 ; Kravchenko2 ; Kravchenko3 , established a similarity between the metal-insulator transitions in such disordered systems and the conventional Mott-Hubbard metal-insulator transition. Studies in these directions are important for understanding the true driving force behind metal-insulator transitions observed in disordered interacting systems. A finite temperature study of the effects of disorder on the non-zero temperature Mott transition disorder_Tneq0 also revealed the prevalence of a single parameter scaling of the distribution of quasi-particle weights in the vicinity of a disordered Mott transition.
A natural question that follows from these studies is whether such scaling with respect to a single low energy scale also manifests in the dynamics of the microscopic quantities like the single particle spectra or the disorder averaged scattering rate in a disordered interacting system at zero temperature. And if such universal dynamics exists, then how general is this observation across the phase diagram? The origin and evolution of such low energy scales with respect to and/or would then reflect upon the driving force behind the localization of the electrons.
The understanding of the behavior of the low energy scales in a strongly correlated system thus stand out as a key prerequisite irrespective of the presence or absence of disorder. Several theoretical frameworks have attempted to understand the interplay of disorder and strong correlations AA ; Punnoose2005 ; finkelstein . However, the study of emergent low energy scales in the simultaneous presence of disorder and electron-electron interactions require non-perturbative frameworks. Studies using the framework of the DMFT have provided several insights in these directions. A computationally inexpensive approach involves the framework of DMFT and utilization of the ‘typical’ density of states (TDoS, ) vlad_nikolic ; schubert for self-consistently obtaining the effectively local hybridizing medium, Byczuk2005 ; Aguiar_2006 ; Aguiar2009 ; 50_years_vollhardt ; aguiar_2013 , in which the single impurities are embedded. This construction of the DMFT bath utilizing the is known as the TMT-DMFT framework 50_years_vollhardt . The TDoS is most appropriately approximated as the geometric average of the local density of states (LDoS), with being the local density of states. Another way of representing this is , where represents the bare random potential and , the probability distribution followed by these bare site energies. While, is critical at the Anderson transition Vollhardt_review ; first_TMT_Vlad2003 , the average density of states (ADoS) given by is not critical. The TDoS behaves like an order parameter for the metal-insulator transition originating in the metallic phase; in the insulating phase it is trivially zero at all frequencies. Thus, in principle the TMT framework is designed to capture the physics of the metal-insulator transition approaching from the metallic phase.
The TMT-DMFT method was first applied to the Anderson-Hubbard model by Byczuk et al. Byczuk2005 who explored the paramagnetic phase diagram using numerical renormalization group (NRG) as the impurity solver. Three distinct phases were identified namely, a correlated metallic phase, a Mott insulating phase and an Anderson insulating phase. Additionally, a coexistent regime of the metal-Mott insulating phase was reported. The Mott and Anderson insulator phases were found to be continuously connected. The characterization of these phases were based on the behavior of the band center of the TDoS () and the ADoS (). The metallic phase featured a non-zero and . For weak to moderate , a sharp transition from the metallic to a gapped insulating phase was observed where both and . This metal-insulator transition was similar in characteristics with the conventional single band Hubbard model and hence this insulating phase was termed as the Mott insulator. Moreover, the density of states in this phase featured prominent Hubbard subbands. Additionally a metal-Mott insulator coexistence regime similar to the p-h symmetric single-band Hubbard model was identified in the - plane that terminated at a single . The Anderson insulator was characterized as a phase that featured and . Additionally, the Hubbard bands were broad and diffused.
Although, the NRG is highly efficient in capturing the Kondo effect, the distribution of Kondo scales, a natural occurrence in interacting disordered systems, was not explored in Ref. Byczuk2005, . Thus the role of the local Kondo scales could not be deduced from the above calculation. Such a direction was however explored using slave-boson mean-field theory calculations Aguiar2009 , highlighting the role of the local quasi-particle weights, , that may also serve as an order parameter for the localization physics in the Anderson-Hubbard model. Close to the disorder driven metal-insulator transition at a two fluid picture was proposed. Through TMT-DMFT calculations they proposed a spatially inhomogeneous picture where in certain regions there existed Mott fluid droplets with and at other regions representing Anderson localized particles. Irrespective of the spatially inhomogeneous picture, one would expect a metal-insulator transition to occur at a critical disorder strength, , when the is fixed, and this would coincide with the vanishing of the impurity hybridization obtained from the TDoS. A conventional Mott-like picture was proposed to prevail for the driven metal-insulator transition at sufficiently small disorder strengths. A similar line of reasoning based on the behavior of the impurity hybridization would lead us to expect that the Mott upper critical interaction, , would coincide with the vanishing of the impurity hybridization obtained from the TDoS.
However, it is also well known that slave-boson based solvers fail to account for inelastic scattering and thus fail to predict the correct lineshape of spectral functions and scattering rates senechal2006theoretical ; SB_artefact1 . Moreover, the physics at low energies, may be highly affected by the physics at higher energy scales. Thus, in order to have a precise understanding of the spectral/dynamical properties in a correlated system, we require all energy scales and interaction strengths, from weak to strong coupling, to be handled within a unified theoretical framework. In this work we revisit the metallic phase of the Anderson-Hubbard model using the local moment approach (LMA) Eastwood1998 as an impurity solver within the TMT-DMFT. The LMA has been successfully applied for several impurity Eastwood1998 ; LMA_pseudogap_AIM1 ; LMA_NRG_soft_gap_AIM and lattice models Eastwood1997 ; LMA_KIs ; Raja_dyn_sca_pam (within DMFT). The LMA is known to capture the Kondo effect correctly while also capturing the correct lineshape of the spectral functions. With this set up we look into the evolution of the distribution of Kondo scales as a function of and . Additionally, we explore the scattering dynamics within the current non-perturbative local framework, and identify universal dynamics and scaling similar to the clean interacting scenario. It should be noted that all the calculations presented in this work pertain to the metallic phase and an exploration of the insulating phases is beyond the scope of the current work. These results are therefore relevant in the context of the breakdown of the metallic phase towards Mott or Anderson localization.
2 Model
The Anderson-Hubbard model is considered as a paradigmatic model for looking into the interplay of strong electron interactions and disorder. It is given by,
| (1) |
where, () is the fermionic creation (annihilation) operator for an electron with spin at site , and , is the nearest neighbour site to site hopping amplitude considered to be constant in this work, is the onsite Coulomb interaction energy. The lattice is represented by a three-dimensional cubic DoS with full bandwidth, . The random local potential follows a ”box” distribution such that , where is the Heaviside step function. A global particle-hole symmetry is imposed by . At , this model reduces to the particle-hole (p-h) symmetric single-band Hubbard model, which displays a first order Mott transition at zero temperature, , as a function of . On approaching this transition from the Fermi liquid (FL) side, the Kondo scale, vanishes at a critical point, , marking the transition to the Mott insulating state. On approaching from the Mott insulating side, the Mott gap vanishes at a critical point, , where, . This scenario in the case motivates us to look at the regimes, and distinctly. For a three-dimensional simple cubic DoS, within the LMA, we have found out that the Mott MIT occurs at which corresponds to , the bandwidth () being equal to 3. This result compares well with the value predicted by NRG calculations () bonvca2009van .
For treating non-zero disorder in the presence of interactions (Eq. (1)) we employ the TMT-DMFT framework where we map the disordered lattice model on to an ensemble of single impurity Anderson models, each embedded in a self-consistently determined effective medium, , which is obtained from , as described in Appendix B. The reader is also referred to several previous works Byczuk2005 ; Aguiar_2006 ; Aguiar2009 ; aguiar_2013 ; Vollhardt_review for the details of the formalism. In Appendix A and B we also describe the implementation of the LMA within the TMT-DMFT framework. We typically solve for disorder realizations each of which involves the calculation of the local interaction self-energy, .
3 Results and discussions
In the absence of interactions, Eq. (1) reduces to the Anderson model of non-interacting electrons Anderson . Here, the metal to insulator transition is not characterized by the vanishing of the DoS. Instead, the hybridization paths get canceled accompanied by weak localization of the wave functions due to coherent backscattering from impurities or exponential localization of the wave functions in deep-trapped states Bulka1985 ; Bulla2001 ; mackinnon_1993 . As a result, the electrons occupying such exponentially localized states are confined to limited regions in the space and cannot contribute to the transport. As the disorder potential, , is increased, more and more regions in space become exponentially localized and the system undergoes a metal-insulator transition as a function of . At the Anderson localization transition the average DoS given by, , with being the LDoS, is not critical. However, the geometrical mean of the LDoS, , better approximates the critical nature of the Anderson localization transition. The local TMT framework adopted here reproduces some of the expected features of the Anderson localization transition, but underestimates the critical disorder strength, first_TMT_Vlad2003 . Although by construction the local TMT framework is able to describe qualitatively the effects of strong localization due to disorder, all non-local coherent backscattering effects are lost. The localization mechanism explicitly contained within the TMT is essentially the physics due to deep-trapped states where the states initially above and below the bare band-edge become localized in deeply trapped states mackinnon_1993 ; Bulka1985 ; Bulka1987 . This effect is subsequently fed back into the hybridizing medium so that the band center also localizes. Within TMT, the band edge of then monotonically moves towards the band center such that at the critical disorder strength even states at the band center are exponentially localized.
Perturbative studies on the weakly interacting disordered electron gas dates back to the seminal work of Altshuler and Aronov AA . Later extensions include the two-loop large- reormalization group analysis of Punnoose and Finkelstein Punnoose2005 , that could describe a metal-insulator transition in a two-dimensional electron gas. However, in disordered interacting systems there also exists a number of relevant phenomena that are beyond the reach of perturbative methods. For example, the work by Milanović, Sachdev and Bhatt Milov1989 and later by Bhatt and Fisher Bhatt1992 showed the importance of disorder in describing the instability of a disordered, interacting Fermi liquid towards the formation of local moments. The treatment of interactions within the non-pertubative framework of DMFT DMFT_RMP can naturally incorporate the tendency towards the formation of local moments Aguiar2009 .
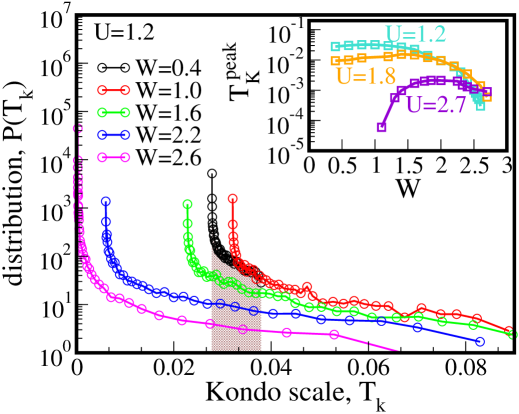
In this work, we revisit the paramagnetic phase of the AHM and try to elucidate the mechanism that could lead to the formation of such local moments in a disordered, interacting system. In particular, we look into the single particle quantities across a broad range of and parameters, putting particular emphasis on the scattering rate and the evolution of the distribution of Kondo scales with respect to and .
3.1 Distribution of Kondo scales:
It is well known that the metallic DoS of the particle-hole symmetric single-band Hubbard model exhibits a three peak structure, with a well defined Abrikosov-Suhl resonance centered around the Fermi energy, that signifies the low-energy quasiparticle coherence present in the system, symptomatic of an underlying coherence scale, DMFT_RMP . The full width at half maximum of this resonance is one measure of the low energy Kondo coherence scale, , present in the Fermi liquid. The local quasi-particle weight, provides another measurement of this energy scale. Above this coherence scale, physical properties are dominated by incoherent electron-electron scattering effects and Fermi liquid theory loses its validity although, recent state-of-art DMFT calculations indicate a resilient quasi-particle regime before the system crosses over to a bad metal regime deng2013bad . In the presence of disorder the translational invariance is broken, so the screening of the local moments by mobile electrons should be spatially non-uniform. While some sites may be strongly hybridized with the local medium, others may be weakly hybridized. For sites that are weakly hybridized with the local surroundings charge fluctuations are suppressed, thus representing a reduced screening in comparison to the sites that strongly hybridize with the surrounding medium. Therefore, in a strongly correlated disordered system, the coherence scale should in principle be viewed as a random position dependent quantity with an associated distribution.
Within the TMT-DMFT implementation we solve an ensemble of impurity problems embedded in an effective disorder averaged medium. We use the LMA as our impurity solver. The LMA is designed to capture the dynamical spin flip scattering processes encountered by an spin occupied impurity. These processes lie at the heart of the physics associated with the Kondo effect LMA_SIAM1 , and their energy scale is on the order of the Kondo scale. The LMA can capture such extremely low energy scales efficiently. Within the LMA, a measure of the Kondo scale is provided by the position of the resonance in the transverse spin polarization propagator LMA_SIAM1 . We therefore end up with a self-consistently determined distribution of such spin-flip scattering energy scales that represent the energies associated with the Kondo screening of the impurities by the disorder averaged effective non-interacting host.
In Fig. 1 we show the distributions of Kondo scales, , for various disorder strengths, , at a fixed . The local nature of the framework renders the distributions to be peaked and bounded from below (also observed in earlier works at non-zero temperature disorder_Tneq0 and square lattice Vlad_griffiths_phase ). This peak, , is associated with the particle-hole (p-h) symmetric limit of the effective impurity problem embedded in the disorder averaged medium that is also p-h symmetric and is identical for all such single-impurity sites. Due to the local nature of the solution, the effective Kondo screening experienced by any impurity moment could thus be only dependent on the of the respective impurity. Therefore sites which are at or close to the p-h symmetric limit will experience the least Kondo screening and hence will have the lowest . The shaded region in Fig. 1 demonstrates the narrow area under the curves corresponding to the low disorder limit of for , in contrast to the long tails in the distributions corresponding to the higher values of .
The initial effect of increasing is to screen the effects of even at the lowest energy scales, such that is pushed to higher values; subsequently, with increasing , decreases monotonically, signifying the onset of disorder induced scattering cooperating with interaction driven scattering in the low frequency region, and tending to localize the system.
In the inset of Fig.1 we plot as a function of for different interaction strengths, . When , the systems with and are Fermi liquids with Kondo scales and , respectively. For , the system is a Mott insulator with .
As shown in the inset of Fig.1, for , the evolves from being zero at low , and then at a non-zero emerges that subsequently increases with increasing disorder signifying a regime where disorder screens the effects of strong interactions. This initial screening of electron-electron interactions due to disorder is true even for smaller or () as discussed earlier. Subsequently, as is increased, an observation that holds true for both and .
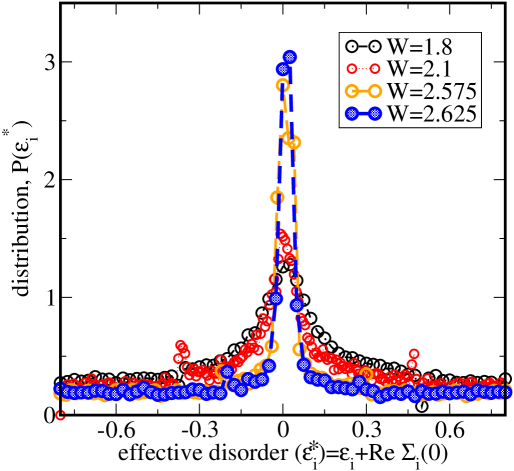
Particular insight about the respective behavior of may be obtained by looking at the evolution of the effective site potential energy () as a function of increasing . In Fig. 2 we show the distribution of the disorder renormalised site energy, , for at , with . The distribution is marked by a peak around , indicating that a majority of sites tend to attain a disorder renormalized site potential energy close to the p-h symmetric limit. This explains why the is determined by the Kondo scales corresponding to the sites that are at or close to half-filling. This peak is initially broad for a relatively low () and becomes sharper as the is increased. This shows that as the disorder is increased more number of sites experience a reduced Kondo screening. In other words, for stronger ’s, the distribution of Kondo scales become more and more skewed such that even sites that are quite far away from half filling may experience a reduced Kondo screening resulting in a Kondo energy scale close to that corresponding to the p-h symmetric limit.
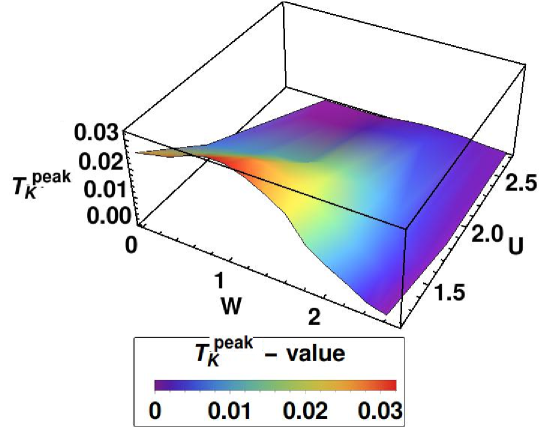
It is to be noted that such a behavior of has been shown to exist close to an interaction driven transition at a fixed aguiar_2003 ; Andrade20093167 , where such a behavior of has been dubbed as perfect disorder screening. In other words similar observations were shown to be prevalent close to the metal-Mott insulator phase boundary of the symmetric, paramagnetic AHM aguiar_2003 ; Andrade20093167 . In this work, we show that this behavior of and is generic to a broader parameter regime. These observations are not just restricted to driven metal-insulator transition at low , but applies to driven transitions also even if the bare interaction strength is small. The physical picture underlying the above observation is the following: for strong disorder potential, as we approach a disorder driven metal-insulator transition, the between any site and its host becomes sufficiently small such that the ratio, , and these sites with experience stronger interaction effects, pushing towards zero, even though the bare interaction strength is small. In Fig. 3 we summarize the above analysis by representing the surface of scales as a function of both and . Since represents the most probable value of the underlying Kondo scale, we now ask the question whether this can be related to the scattering dynamics of the system close to the metal-insulator transitions observed in the AHM. In the following section we therefore explore the imaginary part of the disorder averaged self-energy, -Im.
3.2 Scattering dynamics
In a strongly correlated system the imaginary part of the interaction self-energy, -Im, relates to the scattering rate. Thus the -Im is a mirror of the underlying scattering dynamics present. In a disordered interacting system we need to look at the average self-energy, -Im, obtained from the arithmetically averaged Green’s function, , where denotes arithmetic averaging with respect to . It is this average quantity that represents the physical Green’s function of the system. The quantity, may be obtained from the Hilbert transform of , given by, . Accordingly, the average self-energy, that represents the scattering dynamics, is obtained from the Dyson’s equation given by . The host Green’s function embodies the typical nature of the disorder-averaged medium.
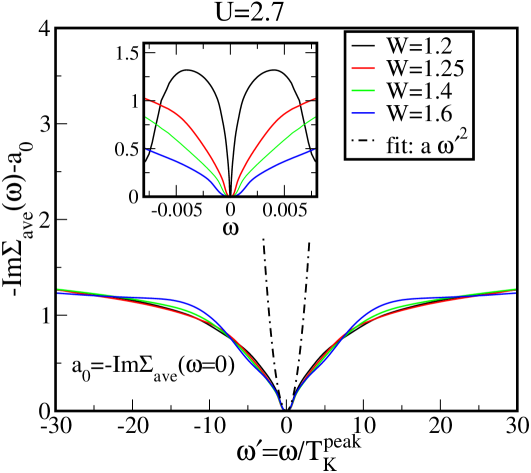
, in the scaling regime.
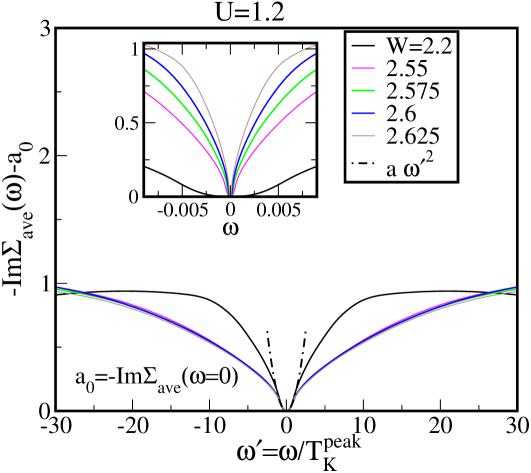
In a clean Fermi liquid, the for (where is the lattice-coherence scale or the Kondo scale in a clean lattice). With this background we look at the low frequency region of -Im. In Fig. 4, we subtract the static contribution of the impurity scattering, and plot the quantity, -Im for various disorder strengths at fixed interaction strengths, (left panel) (right panel). The parameters presented are close to the disorder driven metal-insulator transition boundary. In the main panels we plot this quantity on a frequency rescaled, axis, relating to the inverse scattering rate of the particles. The insets to these figures show the low frequency part of the self-energy spectrum, -Im, on an absolute scale, i.e. vs. . In either case ( or ) of Fig. 4 the self-energy spectrum for various ’s look quite distinct on the bare energy scale being dependent on the disorder strength, . These plots also reflect upon the diminution of the effective Kondo scale as is increased, thus relating to Fig. 1. In contrast to the insets of Fig. 4, the main panels of Fig. 4 illustrate the self-energy spectrum on a rescaled axis, with the rescaled frequency, . It is also observed that the low energy spectral dynamics of -Im for . At higher energy scales, a clear departure from is evident as anticipated. A universal scaling collapse of the single-particle self-energy, with respect to is observed reminiscent of the conventional correlated lattice scenario Logan_mott_ins ; Zitko_Shastry . The clear collapse due to this rescaling suggests that, within a local theory, even in presence of a random potential, an energy scale serves as a Fermi liquid scale, just as in the clean case. Moreover, as seen from the main panel of Fig. 4, although the coherent Fermi liquid scattering regime is restricted for , a universal scattering dynamics is significantly observed until much higher energy scales. In other words, this signifies that within a local theory for interacting disordered systems, the quasi-particle excitations are in fact determined by a disorder renormalized single impurity Kondo scale, . Let us now comment on the parameter regime where this collapse is most significantly observed. The scaling collapse for holds true for higher disorders and very close to the transition where the itself is exponentially small. Note that the values of in Fig. 4 correspond to very small scales in Fig. 1. So, in Fig. 4(left panel) representing , the ’s represent values close to the metal to a disorder driven Mott-Anderson insulator transition. A similar scenario is observed for , as shown in the left panel of Fig. 4. If we now locate in Fig. 1 (violet curve), these values would approximately correspond to respectively, and would thus represent ’s close to a metal-insulator transition resembling a clean Mott transition. Note that according to Ref. Byczuk2005, , at the critical disorder strength where this metal-insulator transition would occur the , would vanish simultaneously, ‘on the spot’. In Ref. Byczuk2005, , the insulating phase resulting from this transition was termed as the disordered Mott insulator phase. In accordance with the observations of Ref. Aguiar2009, , we also speculate that the would continuously vanish to zero at the critical . So, as observed in Fig. 4, universal scaling, until is observed from and , representing parameters very close to the disordered Mott transition. Note that since we could not reach such low energy scales for the metal to Mott-Anderson insulator transition at higher for , demonstrating such a scenario in this regime was beyond the scope of the current work.
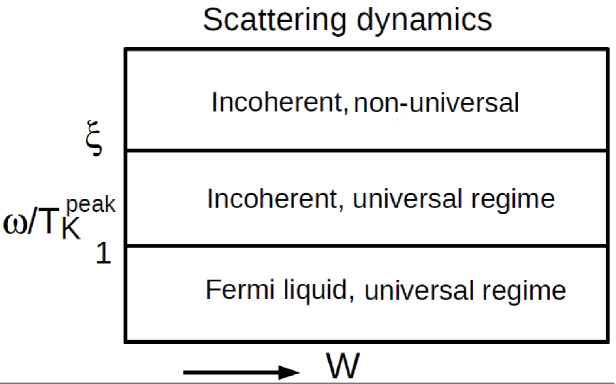
We note in passing, that such a universal scaling collapse scenario could already be anticipated from Fig. 2 where we demonstrated the evolution of the distribution of the renormalised site energies, as a function of increasing disorder. As is increased in presence of a fixed , the pronounced tendency of an appreciable number of sites to acquire a renormalised site potential, , already reflect upon the possible emergence of a universal low energy scale close to the disorder driven metal-insulator transition. This in turn manifests as a universal scaling collapse in the spectral dynamics of -Im. This renormalized single-particle dynamics is summarized in Fig. 5 as a schematic. Such universal physics determined by a single energy scale, even in the presence of strong disorder, suggests that the local effect of disorder is to only renormalize the onsite interaction between the electrons, such that the underlying low energy quasiparticle excitations are still determined by Fermi liquid dynamics, similar to a conventional Mott transition scenario. This is possibly a consequence of the underlying scattering mechanism due to deep-trapped states prevalent within a local theory and its resulting feedback to the low energy sector of the (local) hybridizing medium. It is worth mentioning that a similar universal scaling scenario of the single particle density of states was hinted at in an earlier study by Aguiar et al. in Ref. Aguiar_2006, . They considered an ensemble of single impurity Anderson models embedded in a model bath. The model bath was manually chosen, and the typical nature of the hybridization function was parametrized in order to mimic a disorder driven metal-insulator transition. In this work we elucidate and demonstrate a universal scaling picture of scattering dynamics within a self-consistent scheme, where the typical medium is determined self-consistently and depends on the amount of disorder present.
3.3 Density of states
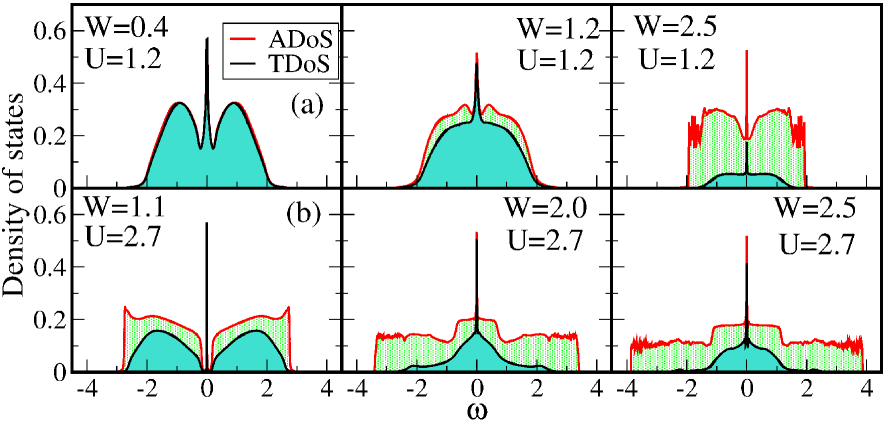
The arithmetically averaged DoS (ADoS) is defined as, , where, is the local DoS (LDoS). The typical DoS is obtained via geometric averaging of the LDoS and is defined as, . As mentioned earlier, represents the distribution followed by the random site potential energies, that in this paper is chosen to be a box distribution. In Fig. 6(a), we plot the arithmetically averaged DoS (ADoS) and the typical DoS (TDoS) for various at a fixed interaction strength . In agreement with the scenario, when the disorder, , is small, both the ADoS and the TDoS produce almost the same density of states. With increasing disorder, the TDoS gets suppressed over all energy scales (note that this is not spectral weight transfer, as the TDoS is not normalized). As seen from Fig. 6(a) there exists remnants of the limit Kondo resonance centered around . With increasing disorder, this resonance initially broadens but then progressively narrows down. In Fig. 6(b), we plot the same as above but for that represents a Mott insulator in the limit of the p-h symmetric AHM. The introduction of randomness allows for local charge fluctuations that in turn leads to delocalization of the otherwise localized moments, beyond a certain critical disorder strength, . This picture is in agreement with the NRG calculations of Ref. Byczuk2005, . This naturally manifests as the emergence of a finite density of states at the Fermi level (). In other words, a sharp Kondo resonance reappears in the middle of a prominent gap, with the inclusion of a finite amount of disorder, ; this gap reminds us of the Mott insulating gap in the limit. Based on the spectral fingerprints, we may speculate the following: if we start from at and decrease we should expect a metal-insulator transition at . This transition is similar to the Mott metal-insulator transition obtained in the conventional single band Hubbard model. This should be reflected as the narrowing of (not shown here for ) and an associated decrease in as is pushed towards . The latter is illustrated in the inset of Fig. 1. For both Fig. 6(a) and Fig. 6(b), the high energy Hubbard bands broaden and acquire reduced spectral intensities. This broadening that is also manifested in the self-consistently determined hybridization function (not shown here) highlight the fact that presence of disorder introduces additional scattering pathways. In the context of DMFT, this increases the rate at which these high energy electrons hop off from the impurity site into the embedding host, thus reducing its lifetime and hence broadening the spectra at such energy scales.
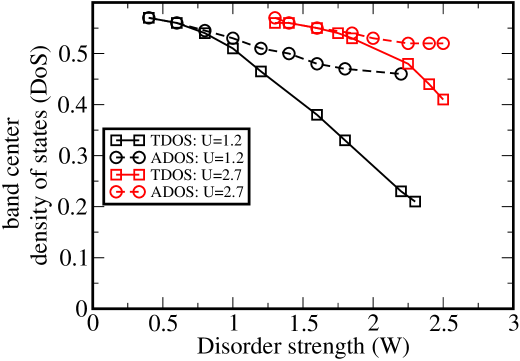
To conclude this section, we compare the decay of the and the for the two regimes of interaction discussed above, namely, and . From Fig.7, appears to be monotonically vanishing as is increased while appears to saturate. If the metal-insulator transition encountered at large is continuous, as expected for small values of , then these results suggest that the remains finite even in the insulating phase such that the Anderson-Mott insulator phase is gapless Byczuk2005 . A true characterization of the phases would require numerical simulations very close to the metal-insulator transitions. The numerical calculations become very unstable as one approaches this limit and hence is beyond the scope of the current work.
4 Conclusions
We employed the dynamical mean field theory framework with a typical medium, to look into the interplay of disorder and strong correlations in the paramagnetic metallic phase of the particle-hole symmetric Anderson-Hubbard model using the local moment approach. Particularly, we explored the single particle dynamics by analyzing the disorder averaged self-energy and identified the existence of a universal ‘Kondo’ scale within such a local theoretical framework that considers the strong correlation physics in presence of disorder scattering only due to deep trapped states. Additionally, we showed that this scale could be represented by the peak () in the distribution function of the Kondo scales. Moreover, the universal regime is shown to exist up to significantly high energies, although a strict Fermi liquid scattering dynamics holds true for . While such universal dynamics similar to that observed in the strong coupling limit of the conventional single-band Hubbard model Logan_mott_ins ; Zitko_Shastry is anticipated in the low disorder regime disorder_Tneq0 , the same is surprising in the proximity of a Anderson-Mott transition, where the disorder is much stronger in comparison to the interaction. But then, such an observation highlights the incipient disorder renormalised Kondo screening of the local moments to be the dominant mechanism determining the low energy physics of the system.
As mentioned before, within the local framework of the dynamical mean field theory in combination within the typical medium theory, the Anderson-Hubbard model is mapped onto an ensemble of impurity problems, where the host for the impurities is determined by the typical density of states. The tendency of an impurity site to form a local moment is governed by the impurity-host hybridization function that is determined by the typical impurity density of states. Thus the low energy physics will be determined by the peak of the distribution of the density of states and reinforced by this self consistency since all the sites see the same hybridization function. In this case, these sites are the ones with the lowest Kondo scale, which are at the peak of the distribution. They are the ones closest to Mott character. The inhibition of the low energy hybridization function would be felt by all the impurities leading to a pronounced tendency towards forming local moments.
Since the disorder, especially near an Anderson localization transition, strongly suppresses the hybridization to the impurity, our observations highlight that in a disordered interacting system, Anderson and Mott mechanism of localization may not be disentangled. It is worth noting that the behavior of the local Kondo scales and the density of states are in agreement with the previous works as in Refs. Byczuk2005, ; Aguiar2009, . In our work we perform a detailed investigation of the spectra, and find that the broad distribution of Kondo scales and the underlying universal scattering dynamics corroborate the physical picture of the emergence of the formation of local moments in the presence of metallic droplets, as proposed in Refs. Paalanen1988, ; Aguiar2009, . While the emergent local moments would tend towards a common Kondo scale, we speculate that the Kondo scales and hence the low energy physics associated with the metallic droplets could be inhomogeneous. These observations are particularly relevant for understanding the underlying mechanisms that lead to the breakdown of the metallic phase towards a Mott or Mott-Anderson localization transition. However, in order to assert the true nature of this spatial inhomogeneity we require to go beyond the local framework and incorporate non-local dynamical fluctuations.
The local moment approach is an inherently non-perturbative impurity solver neither confined to low energies like the slave-boson approach nor to weak coupling like the iterated perturbation theory or modified perturbation theory approaches. While for non-disordered correlated systems this has clearly been demonstrated LMA_SIAM1 ; LMA_NRG_benchmark1 , our present calculations show that it does capture the strong correlation physics in accordance with the numerically exact NRG calculations for disordered correlated systems Byczuk2005 . With this set up established, one then asks the question as to what happens if we include short-range dynamical fluctuations due to disorder. Such directions within the framework of the typical medium dynamical cluster approximation Chinedu_TMDCA2014 are currently under our consideration.
Acknowledgments
We would like to acknowledge fruitful discussions with Pinaki Majumdar and Subroto Mukerjee. S.S. acknowledges the financial support from CSIR, India and JNCASR, India. This material is based upon work supported by the National Science Foundation award DMR-1237565 and by the EPSCoR Cooperative Agreement EPS-1003897 with additional support from the Louisiana Board of Regents. Supercomputer support is provided by the Louisiana Optical Network Initiative (LONI) and HPC@LSU.
Appendix A Local moment approach (LMA)
1.1 Starting point: unrestricted Hartree Fock
In the following we will discuss some of the basic concepts of the zero temperature LMA formalism. A key physical aspect of this method is the inclusion of low energy spin-flip excitations in the single-particle dynamics. This is facilitated at the inception by starting from the unrestricted Hartree Fock (UHF) state: local moments, , are introduced from the outset, to get a direct handle on the low energy spin-flip processes. The solutions are built around simple symmetry broken static mean-field, UHF, states, containing two degenerate states , where, , the average being over the UHF ground state. We label and for solutions or respectively LMA_SIAM1 . For an understanding of the formal details the reader is referred to LMA_SIAM1 ; LMA_asymm_SIAM ; LMA_KIs ; Raja_dyn_sca_pam ; Eastwood1998 ; Dickens2001 . Here, we briefly recap the main equations. The single particle UHF Green’s functions for the paramagnetic case, are given by,
| (2) | |||
| (3) |
where, is the hybridization function for the impurity-host coupling, that, for the paramagnetic case, is spin independent; and , where is the mean-field charge as described in the following. The density of the single-particle excitations is given by, , where, . The local moment, in general, would be given by, , and has to be obtained self-consistently. When we are away from particle-hole symmetry then we also need the impurity occupancy to be given by, . For the pure mean-field UHF solution, we have,
| (4) | |||
| (5) |
to be solved self-consistently. So, if we now fix and (note that they are not the bare parameters of the Hamiltonian), then Eqs. (4) and (5) would provide the solution at one shot and accordingly, the bare parameters may be inferred as and . However, if and are fixed then this has to be obtained by iterative cycling. The UHF solution is severely deficient (see LMA_SIAM1 ; glossop2002single ; LMA_asymm_SIAM ; LMA_gapless_fermi ; LMA_KIs ), for not capturing the Fermi liquid picture. In any case, being a static approximation, one has to go beyond it to incorporate dynamics.
1.2 Inclusion of spin-flip scattering dynamics
Within the LMA in practice, we approximate the dynamical part of the self-energy by the (nonperturbative) class of spin-flip diagrams shown in Fig. 8. Here, the bare propagators are that of UHF and therefore the inclusion of all these diagrams constitute the UHF+random phase approximation (RPA) scheme. We thus build a two self-energy description, as represented in Fig. 8 and mathematically represented as,
| (6) |
is the transverse-spin polarization propagator (with ), which in the current RPA scheme employed is expressed as, . The bare polarization propagator, is expressed in terms of broken symmetry mean-field propagators as, .
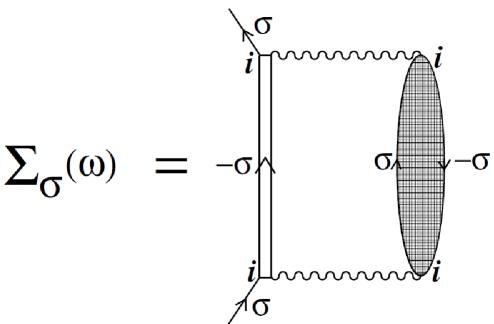
The UHF propagators should result in a self-energy that satisfies the basic criteria for a Fermi liquid. After some detailed algebra LMA_SIAM1 , we can then arrive at self-consistency equation for determining the exact local moment that satisfies such constraints, so that the two self-energy description may be written as,
| (7) |
The above equation is known as the symmetry-restoration condition. Finally, the single self-energy may be obtained as,
| (8) |
where,
| (9) |
with and the impurity Green’s function, , with and . Additionally, for p-h asymmetric situations glossop2002single one also needs to satisfy the Luttinger’s theorem given by,
| (10) |
The self-consistent imposition of Eq. (7) amounts to a self-consistency condition for the local moment that enters Eqs. (2), (3). A low energy spin-flip scale, is generated; this scale that manifests as a strong resonance in the imaginary part of the transverse spin polarization propagator, Im, is proportional to the Kondo scale LMA_SIAM1 ; glossop2002single . If the symmetry-restoration condition Eq (7) is not satisfied then a spin-flip scale occurs at signaling the breakdown of a Fermi liquid.
A practical implementation of the LMA involves fixing and LMA_SIAM1 ; LMA_asymm_SIAM ; LMA_KIs ; Raja_dyn_sca_pam ; Raja2_2005 . The current nature of the problem, however, requires us to fix the bare parameters of the single impurity Anderson model, namely, and . However, we should also note that if is fixed instead of then, Eq. (7) and Eq. (10) would have to be solved self-consistently requiring several symmetry-restoration steps increasing the computation time enormously. Instead, if we fix and and tune we can drastically reduce this requirement again ending up in solving 5-6 symmetry-restoration iterations, as in the fixed , fixed algorithm. The scheme is described as following:
-
1.
We start with an initial guess local moment, with which we calculate and subsequently, from UHF spectral functions.
-
2.
The calculation of and , and, follows.
-
3.
Eq. (7) is checked and steps (1), (2), (3) are repeated until a convergence of or lower is achieved. With this step it can be realized that the entire process involves calculations of coupled equations for finding the root of Eq. (7), for which one therefore has to provide a judicious guess to reach the solution correctly and efficiently.
-
4.
Finally, with proper guesses for the underlying self-consistency equations a converged is obtained. With this self-energy, we can now satisfy Eq. (10) by tuning .
In particular to the problem treated in this paper, we also had to take care of the computation time required to be able to sample sufficient number of disorder realizations. We achieved this by bringing in some additional schemes which would be discussed in detail in the following section.
Appendix B Numerical implementation of TMT-DMFT
In this section we provide technical details of our implementation of the LMA within the TMT-DMFT framework. For the sake of completeness we also outline the steps involved in the TMT-DMFT implementation. As outlined in the previous section, employing the LMA with the bare parameters and , would require a lot of computational time. This results from the fact that, away from p-h symmetry the impurity parameter that acts like a pseudo chemical potential and explicitly enters the UHF Green’s functions via Eqs. (2), (3), would have to be tuned so that the symmetry-restoration (Eq. (7)) and the Luttinger’s theorem (Eq. (10)) are self-consistently satisfied. Recall that this would result in repeating the symmetry restoration (Eq. (7)) step described in several times. Instead, the impurity self-energy may be obtained at a much cheaper effort if the bare parameters and the impurity parameter is fixed. In that case, once the symmetry restored impurity self-energy and Green’s functions are obtained, one can tune the such that the the Luttinger’s theorem (Eq. (10)) is satisfied. This can be done without having to repeat the impurity self-energy calculation. However, in the current problem, the is a random quantity following a particular distribution. So, in order to resort to the fixed , fixed scheme discussed in the earlier section we have to first build a database for the respective pair with the given hybridization. In other words, before going to the actual calculation we do the following:
Step 1:
-
1.
Given a hybridization function, we start from the particle-hole symmetric limit with and , for which the Luttinger’s theorem (Eq. (10)) is naturally satisfied. Note that in the main text, , has been denoted as . So, in this step the LMA solver is provided with (a) , (b) , (c) .
-
2.
We now increment the by a small step, say 0.02111This is optimized by experience to minimize the number of steps or pairs required to obtain a good database.. So, in this step the LMA solver is provided with (a) , (b) , (c) . Accordingly, the is derived by satisfying the Luttinger’s theorem (Eq. (10)) and an pair for the given is generated.
-
3.
The above step (2) is continued until the obtained overshoots the limit set by the disorder strength, . Note that, , where is a random number between .
-
4.
For the actual random configuration, , and therefore, the , we now interpolate the corresponding from the database and compute the local self-energy, . Finally, we construct the local Green’s function, , using the equation, , where, . This would now be used to construct .
Step 2:
The output of the Step 1 comprises local impurity self-energies, that gives us local impurity Green’s function, . With the local spectral functions, , we construct the disorder averaged DoS, using geometric averaging:
| (11) |
Using Eq. (11) we can now construct the typical Green’s function, , from the Hilbert transform of :
| (12) |
Step 3: We define the coarse-grained lattice Green’s function as , given by,
| (13) |
where refers to the bare density of states, that in the current problem is that of the 3-dimensional cubic lattice.
Step 4: The new hybridization may be obtained as,
| (14) |
where, is a mixing parameter typically set to a value of 0.5. With we can go back to Step 1 and continue until -Im converges within some tolerance, which in our implementation is chosen to be .
Note that in order to look into the scattering dynamics, we calculate the arithmetic average of the local density of states, . As described in the main text, this is given by, and it represents the average density of states (ADoS) of the lattice. From the ADoS, we can then calculate the arithmetic average of the local Green’s function, , using the, Hilbert transform relation, . The disorder-averaged self-energy, , that represents the scattering dynamics is then calculated as, .
References
References
- (1) F. Evers and A. D. Mirlin, Rev. Mod. Phys. 80, 1355 (Oct 2008)
- (2) B. Kramer and A. MacKinnon, Rev. Prog. Phys. 56, 1469 (June 1993)
- (3) E. Abrahams, Fifty Years of Anderson Localization (Singapore: World Scientific, 2010)
- (4) G. Kotliar and D. Vollhardt, Physics Today 57, 53 (March 2004)
- (5) A. Georges, G. Kotliar, W. Krauth, and M. J. Rozenberg, Rev. Mod. Phys. 68, 13 (Jan 1996)
- (6) P. W. Anderson, Phys. Rev. 109, 1492 (Mar 1958)
- (7) S. V. Kravchenko and M. P. Sarachik, Reports on Progress in Physics 67, 1 (2004)
- (8) E. Miranda and V. Dobrosavljević, Reports on Progress in Physics 68, 2337 (2005)
- (9) K. Maiti, R. S. Singh, and V. R. R. Medicherla, Phys. Rev. B 76, 165128 (Oct 2007)
- (10) K. W. Kim, J. S. Lee, T. W. Noh, S. R. Lee, and K. Char, Phys. Rev. B 71, 125104 (Mar 2005)
- (11) A. S. Sefat, J. E. Greedan, G. M. Luke, M. Niéwczas, J. D. Garrett, H. Dabkowska, and A. Dabkowski, Phys. Rev. B 74, 104419 (Sep 2006)
- (12) L. Sanchez-Palencia and M. Lewenstein, Nature Physics 6, 87 (2010)
- (13) M. White, M. Pasienski, D. McKay, S. Q. Zhou, D. Ceperley, and B. DeMarco, Phys. Rev. Lett. 102, 055301 (Feb 2009)
- (14) S. S. Kondov, W. R. McGehee, W. Xu, and B. DeMarco, Phys. Rev. Lett. 114, 083002 (Feb 2015)
- (15) P. A. Lee and T. V. Ramakrishnan, Rev. Mod. Phys. 57, 287 (Apr 1985)
- (16) N. S. Vidhyadhiraja and D. E. Logan, European Physical Journal B 39, 313 (2004)
- (17) Q. Si and F. Steglich, Science 329, 1161 (2010)
- (18) R. Bulla and T. Pruschke, “Strong electronic correlations and low energy scales,” in Open Problems in Strongly Correlated Electron Systems, edited by J. Bonča, P. Prelovšek, A. Ramšak, and S. Sarkar (Springer Netherlands, Dordrecht, 2001) pp. 381–386
- (19) D. E. Logan and M. R. Galpin, Journal of Physics: Condensed Matter 28, 025601 (2016)
- (20) M. M. Radonjić, D. Tanasković, V. Dobrosavljević, K. Haule, and G. Kotliar, Phys. Rev. B 85, 085133 (Feb 2012)
- (21) S. V. Kravchenko and M. P. Sarachik, Reports on Progress in Physics 67, 1 (2004)
- (22) B. Spivak, S. V. Kravchenko, S. A. Kivelson, and X. P. A. Gao, Rev. Mod. Phys. 82, 1743 (May 2010)
- (23) M. C. O. Aguiar, V. Dobrosavljević, E. Abrahams, and G. Kotliar, Phys. Rev. B 71, 205115 (May 2005)
- (24) B. Altshuler and A. Aronov, in Electron-electron interactions in disordered systems, edited by A.L. Efros and M. Pollak (North-Holland, Amsterdam, 1985)
- (25) A. Punnoose and A. M. Finkel’stein, Science 310, 289 (2005)
- (26) A. Finkelstein, in Soviet Science Reviews, Vol. 9 (edited by I. M. Khalatnikov (Harwood Academic, London, 1990), 1990) p. 3
- (27) V. Dobrosavljević, A. A. Pastor, and B. K. Nikolić, Europhysics Letters 62, 76 (2003)
- (28) G. Schubert, J. Schleede, K. Byczuk, H. Fehske, and D. Vollhardt, Phys. Rev. B 81, 155106 (Apr 2010)
- (29) K. Byczuk, W. Hofstetter, and D. Vollhardt, Phys. Rev. Lett. 94, 056404 (Feb 2005)
- (30) M. C. O. Aguiar, V. Dobrosavljević, E. Abrahams, and G. Kotliar, Phys. Rev. B 73, 115117 (Mar 2006)
- (31) M. C. O. Aguiar, V. Dobrosavljević, E. Abrahams, and G. Kotliar, Phys. Rev. Lett. 102, 156402 (Apr 2009)
- (32) K. Byczuk, W. Hofstetter, and D. Vollhardt, in 50 years of Anderson localization, edited by E. Abrahams (World Scientific, 2010) p. 473
- (33) M. C. O. Aguiar and V. Dobrosavljević, Phys. Rev. Lett. 110, 066401 (Feb 2013)
- (34) K. Byczuk, W. Hofstetter, U. Yu, and D. Vollhardt, The European Physical Journal Special Topics 180, 135 (2009), ISSN 1951-6355
- (35) V. Dobrosavljević, A. A. Pastor, and B. K. Nikolić, Europhysics Letters 62, 76 (2003)
- (36) D. Sénéchal, A.-M. Tremblay, and C. Bourbonnais, Theoretical methods for strongly correlated electrons (Springer Science & Business Media, 2006)
- (37) A. Benlagra, T. Pruschke, and M. Vojta, Phys. Rev. B 84, 195141 (Nov 2011)
- (38) D. E. Logan, M. P. Eastwood, and M. A. Tusch, Journal of Physics Condensed Matter 10, 2673 (MAR 30 1998)
- (39) M. T. Glossop and D. E. Logan, Journal of Physics: Condensed Matter 15, 7519 (2003)
- (40) R. Bulla, M. T. Glossop, D. E. Logan, and T. Pruschke, Journal of Physics: Condensed Matter 12, 4899 (2000)
- (41) D. E. Logan, M. P. Eastwood, and M. A. Tusch, Journal of Physics Condensed Matter 9, 4211 (MAY 19 1997)
- (42) V. Smith, D. Logan, and H. Krishnamurthy, The European Physical Journal B 32, 49 (2003)
- (43) J. Bonča, T. Pruschke, et al., Phys. Rev. B 80, 245112 (2009)
- (44) B. R. Bulka, B. Kramer, and A. MacKinnon, Zeitschrift für Physik B Condensed Matter 60, 13 (1985), ISSN 1431-584X
- (45) B. Bulka, M. Schreiber, and B. Kramer, Zeitschrift für Physik B Condensed Matter 66, 21 (1987)
- (46) M. Milovanović, S. Sachdev, and R. N. Bhatt, Phys. Rev. Lett. 63, 82 (Jul 1989)
- (47) R. N. Bhatt and D. S. Fisher, Phys. Rev. Lett. 68, 3072 (May 1992)
- (48) X. Deng, J. Mravlje, M. Ferrero, G. Kotliar, A. Georges, et al., Phys.Rev.Lett 110, 086401 (2013)
- (49) D. E. Logan, M. P. Eastwood, and M. A. Tusch, Journal of Physics: Condensed Matter 10, 2673 (1998)
- (50) E. C. Andrade, E. Miranda, and V. Dobrosavljević, Phys. Rev. Lett. 102, 206403 (May 2009)
- (51) D. Tanasković, V. Dobrosavljević, E. Abrahams, and G. Kotliar, Phys. Rev. Lett. 91, 066603 (Aug 2003)
- (52) E. Andrade, E. Miranda, and V. Dobrosavljević, Physica B: Condensed Matter 404, 3167 (2009), ISSN 0921-4526, proceedings of the International Conference on Strongly Correlated Electron Systems
- (53) R. Žitko, D. Hansen, E. Perepelitsky, J. Mravlje, A. Georges, and B. S. Shastry, Phys. Rev. B 88, 235132 (Dec 2013)
- (54) M. A. Paalanen, J. E. Graebner, R. N. Bhatt, and S. Sachdev, Phys. Rev. Lett. 61, 597 (Aug 1988)
- (55) M. R. Galpin and D. E. Logan, Journal of Physics: Condensed Matter 17, 6959 (2005)
- (56) C. E. Ekuma, H. Terletska, K.-M. Tam, Z.-Y. Meng, J. Moreno, and M. Jarrell, Phys. Rev. B 89, 081107 (Feb 2014)
- (57) M. T. Glossop and D. E. Logan, Journal of Physics: Condensed Matter 14, 6737 (2002)
- (58) N. L. Dickens and D. E. Logan, Journal of Physics Condensed Matter 13, 4505 (MAY 21 2001)
- (59) M. T. Glossop and D. E. Logan, Journal of Physics: Condensed Matter 14, 6737 (2002)
- (60) D. E. Logan and M. T. Glossop, Journal of Physics: Condensed Matter 12, 985 (2000)
- (61) N. S. Vidhyadhiraja and D. E. Logan, Journal of Physics: Condensed Matter 17, 2959 (2005)
- (62) This is optimized by experience to minimize the number of steps or pairs required to obtain a good database.