A new proof of the Gasca - Maeztu conjecture for n = 5

Gagik Vardanyan

(July 2021)

Abstract

An $n$ -correct node set $\mathcal{X}$ is called $GC_{n}$ set if the fundamental polynomial of each node is a product of $n$ linear factors. In 1982 Gasca and Maeztu conjectured that for every $GC_{n}$ set there is a line passing through $n+1$ of its nodes.So far, this conjecture has been confirmed only for $n\leq 5.$ The case $n=4,$ was first proved by J. R. Bush in 1990 . Several other proofs have been published since then. For the case $n=5$ there is only one proof: by H. Hakopian, K. Jetter and G. Zimmermann (Numer Math $127,685--713,2014$ ). Here we present a second, much shorter and easier proof.

Keywords: Polynomal interpolation; the Gasca-Maeztu conjecture; $n$ -correct set; $GC_{n}$ set; maximal line.

Mathematics Subject Classification (2000) 41A05; 41A63.

1 Introduction

Denote by $\Pi_{n}$ the space of bivariate polynomials of total degree at most $n:$

\Pi_{n}=\left\{\sum_{i+j\leq{n}}a_{ij}x^{i}y^{j}\right\},\quad N:=\dim\Pi_{n}=\binom{n+2}{2}.

Consider a set of distinct nodes $\mathcal{X}_{s}=\{(x_{1},y_{1}),(x_{2},y_{2}),\dots,(x_{s},y_{s})\}.$

The problem of finding a polynomial $p\in\Pi_{n}$ which satisfies the conditions

p(x_{i},y_{i})=c_{i},\ \ \quad i=1,2,\dots s,

(1.1)

is called interpolation problem.

Definition 1.1.

The interpolation problem with the set of nodes $\mathcal{X}_{s}$ is called $n$ -poised if for any data $\{c_{1},\dots,c_{s}\}$ there exists a unique polynomial $p\in\Pi_{n}$ , satisfying the conditions (1.1).

A necessary condition of $n$ -poisedness is: $\#\mathcal{X}_{s}=s=N.$ If this latter equality takes place then the following holds:

Proposition 1.2.

A set of nodes $\mathcal{X}_{N}$ is $n$ -poised if and only if

p\in\Pi_{n},\ p(x_{i},y_{i})=0\quad i=1,\dots,N\implies p=0.

A polynomial $p\in\Pi_{n}$ is called an $n$ -fundamental polynomial for a node $A=(x_{k},y_{k})\in\mathcal{X}_{s}$ if

p(x_{i},y_{i})=\delta_{ik},\ i=1,\dots,s,

where $\delta$ is the Kronecker symbol. We denote the $n$ -fundamental polynomial of $A\in\mathcal{X}_{s}$ by $p_{A}^{\star}=p_{A,\mathcal{X}}^{\star}.$

Definition 1.3.

A set of nodes $\mathcal{X}_{s}$ is called $n$ -independent if all its nodes have $n$ -fundamental polynomials. Otherwise, $\mathcal{X}_{s}$ is called $n$ -dependent. A set of nodes $\mathcal{X}_{s}$ is called essentially $n$ -dependent if none of its nodes has $n$ -fundamental polynomial.

Fundamental polynomials are linearly independent. Therefore a necessary condition of $n$ -indepen-dence is $\#\mathcal{X}_{s}=s\leq N.$

One can readily verify that a node set $\mathcal{X}_{s}$ is $n$ -independent if and only if the interpolation problem (1.1) is solvable, meaning that for any data $\{c_{1},\dots,c_{s}\}$ there exists a (not necessarily unique) polynomial $p\in\Pi_{n}$ satisfying the conditions (1.1).

A plane algebraic curve is the zero set of some bivariate polynomial of degree $\geq 1.$ To simplify notation, we shall use the same letter, say $p$ , to denote the polynomial $p$ of degree $\geq 1$ and the curve given by the equation $p(x,y)=0$ . In particular, by $\ell,$ we denote a linear polynomial $\ell\in\Pi_{1}$ and the line defined by the equation $\ell(x,y)=0.$

Definition 1.4.

Let $\mathcal{X}$ be an $n$ -poised set. We say, that a node $A\in\mathcal{X}$ uses a line $\ell$ , if $\ell$ is a factor of the fundamental polynomial $p_{A}^{\star},$ i.e., $p_{A}^{\star}=\ell q,$ where $q\in\Pi_{n-1}.$

Since the fundamental polynomial of a node in an $n$ -poised set is unique we get

Lemma 1.5 ([9], Lemma 2.5).

Suppose $\mathcal{X}$ is a poised set and a node $A\in\mathcal{X}$ uses a line $\ell.$ Then $\ell$ passes through at least two nodes from $\mathcal{X}$ , at which $q$ does not vanish.

Definition 1.6.

Let $\mathcal{X}$ be a set of nodes. We say, that a line $\ell$ is a $k$ -node line if it passes through exactly $k$ nodes of $\mathcal{X}:\ \ell\cap\mathcal{X}=k.$

The following proposition is well-known (see e.g. [8] Proposition 1.3):

Proposition 1.7.

Suppose that a polynomial $p\in\Pi_{n}$ vanishes at $n+1$ points of a line $\ell.$ Then we have that $p=\ell r,\ \text{where}\ r\in\Pi_{n-1}.$

From here we readily get that at most $n+1$ nodes of an $n$ -poised set $\mathcal{X}_{N}$ can be collinear. In view of this an $(n+1)$ -node line $\ell$ is called a maximal line [2].

Next, let us bring the Cayley-Bacharach theorem (see e.g. [6], Th. CB4; [8], Prop. 4.1).

Theorem 1.8.

Assume that two algebraic curves of degree $m$ and $n$ , respectively, intersect at $mn$ distinct points. Then the set $\mathcal{X}$ of these intersection points is essentially $(m{+}n{-}3)$ -dependent.

We are going to consider a special type of $n$ -poised sets defined by Chung and Yao:

Definition 1.9 ([5]).

An n-poised set $\mathcal{X}$ is called $GC_{n}$ set, if the $n$ -fundamental polynomial of each node $A\in\mathcal{X}$ is a product of $n$ linear factors.

Now we are in a position to present the Gasca-Maeztu conjecture.

Conjecture 1.10 ([7]).

For any $GC_{n}$ set $\mathcal{X}$ there is a maximal line, i.e., a line passing through its $n+1$ nodes.

Since now the Gasca-Maeztu conjecture was proved to be true only for $n\leq 5$ . The case $n=2$ is trivial, and the case $n=3$ is easy to verify. The case $n=4$ first was proved by J. R. Bush [3]. Several other proofs have been published since then (see e.g. [4], [9], [1]). For the case $n=5$ there is only one proof by H. Hakopian, K. Jetter and G. Zimmermann [10].

1.1 The m-distribution sequence of a node

In this section we bring a number of concepts, properties and results from [10].

Suppose that $\mathcal{X}$ is a $GC_{n}$ set. Consider a node $A\in\mathcal{X}$ together with the set of $n$ used lines $\mathcal{L}_{A}.$ The $N-1$ nodes of $\mathcal{X}\setminus\{A\}$ are somehow distributed in the lines of $\mathcal{L}_{A}.$

Let us order the lines of $\mathcal{L}_{A}$ in the following way:

The line $\ell_{1}$ is a line in $\mathcal{L}_{A}$ that passes through maximal number of nodes of $\mathcal{X},$ denoted by $k_{1}:$ $\mathcal{X}\cap\ell_{1}=k_{1}.$

The line $\ell_{2}$ is a line in $\mathcal{L}_{A}\setminus\{\ell_{1}\}$ that passes through maximal number of nodes of $\mathcal{X}\setminus\ell_{1},$ denoted by $k_{2}:$ $(\mathcal{X}\setminus\ell_{1})\cap\ell_{2}=k_{2}.$

In the general case the line $\ell_{s},\ s=1,\ldots,n,$ is a line in $\mathcal{L}_{A}\setminus\{\ell_{1},\ldots,\ell_{s-1}\}$ that passes through maximal number of nodes of the set $\mathcal{X}\setminus\cup_{i=1}^{s-1}\ell_{i},$ denoted by $k_{s}:$ $(\mathcal{X}\setminus\cup_{i=1}^{s-1}\ell_{i})\cap\ell_{s}=k_{s}.$

A correspondingly ordered line sequence

\mathcal{S}=(\ell_{1},\ldots,\ell_{n})

is called a maximal line sequence or briefly an m-line sequence. The sequence $(k_{1},\ldots,k_{n})$ is called a maximal distribution sequence. Briefly we call it m-distribution sequence or m-d sequence.

Evidently, for the m-d sequence we have that

k_{1}\geq k_{2}\geq\cdots\geq k_{n}\ \hbox{and}\ k_{1}+\cdots+k_{n}=N-1.

(1.2)

As it is shown in [10] the m-distribution sequence for a node $A$ is unique, while it may correspond to several m-line sequences.

Note that, an intersection point of several lines of $\mathcal{L}_{A}$ is counted for the line containing it which appears in $\mathcal{S}$ first. Each node in $\mathcal{X}$ is called a primary node for the line it is counted for, and a secondary node for the other lines containing it.

According to Lemma 1.5, every used line has to contain at least two primary nodes, i.e.,

k_{i}\geq 2\quad\text{for }i=1,\ldots,n\,.

(1.3)

Let $\mathcal{S}=(\ell_{1},\ldots,\ell_{n})$ be an m-line sequence with the associated m-d sequence $(k_{1},\ldots,k_{n})$ .

Lemma 1.11 ([10], Lemma 2.5).

Assume that $k_{i}=k_{i+1}=:k$ for some $i$ . If the intersection point of lines $\ell_{i}$ and $\ell_{i+1}$ belongs to $\mathcal{X}$ , then it is a secondary node for both $\ell_{i}$ and $\ell_{i+1}$ . Moreover, interchanging $\ell_{i}$ and $\ell_{i+1}$ in $\mathcal{S}$ still yields an m-line sequence.

We say that a polynomial has $(s_{i},\ldots,s_{j})$ primary zeroes in the lines $(\ell_{i},\ldots,\ell_{j})$ if the zeroes are primary nodes in the respective lines. From Proposition 1.7 we get

Corollary 1.12.

If a polynomial $p\in\Pi_{m-1}$ has $(m,m-1,\ldots,m-k)$ primary zeroes in the lines $(\ell_{m-k},\ell_{m-k+1}\ldots,\ell_{m})$ then we have that $p=\ell_{m}\ell_{m-1}\cdots\ell_{m-k}r,\ \text{where}\ r\in\Pi_{m-k}.$

In some cases we shall fix a particular line ${\widetilde{\ell}}$ used by a node and then study the properties of the other factors of the fundamental polynomial. In particular, this will be the case for a line ${\widetilde{\ell}}$ that is shared by several nodes.

In this case in the corresponding m-line sequence, called ${\widetilde{\ell}}$ -m-line sequence, we take as the first line $\ell_{1}$ the line ${\widetilde{\ell}},$ no matter through how many nodes it passes. Then the second and subsequent lines are chosen, as in the case of the m-line sequence.

Thus the line $\ell_{2}$ is a line in $\mathcal{L}_{A}\setminus\{{\widetilde{\ell}}_{1}\}$ that passes through maximal number of nodes of $\mathcal{X}\setminus{\widetilde{\ell}}_{1},$ and so on.

Correspondingly we define ${\widetilde{\ell}}$ -m-distribution sequence.

2 The Gasca-Maeztu conjecture for $n=5$

Let us formulate the Gasca-Maeztu conjecture for $n=5$ as:

Theorem 2.1.

For any $GC_{5}$ set $\mathcal{X}$ of $21$ nodes there is a maximal line, i.e., a $6$ -node line.

To prove the theorem assume by way of contradiction the following.

Assumption 2.2.

The set $\mathcal{X}$ is a $GC_{5}$ set with no maximal line.

In view of (1.2) and (1.3) the only possible m-d sequences for any node $A\in\mathcal{X}$ are

(5,5,5,3,2);\quad(5,5,4,4,2);\quad(5,5,4,3,3);\quad(5,4,4,4,3);\quad(4,4,4,4,4).

(2.1)

The results from [10] below show how many times a line can be used, depending the number of nodes it passes through. In each statement it is assumed that $\mathcal{X}$ is a $GC_{5}$ set with no maximal line.

Proposition 2.3 ([10], Prop. 2.11).

Suppose that ${\widetilde{\ell}}$ is a $2$ -node line. Then ${\widetilde{\ell}}$ can be used by at most one node of $\mathcal{X}$ .

Proposition 2.4 ([10], Prop. 2.12).

Suppose that ${\widetilde{\ell}}$ is a $3$ -node line and is used by two nodes $A$ , $B\in\mathcal{X}$ . Then there exists a third node $C$ using ${\widetilde{\ell}}$ . Furthermore, $A$ , $B$ , and $C$ share three other lines, each passing through five primary nodes. For each of the three nodes, the m-d sequence is $(5,5,5,3,2)$ , and the other two nodes are the primary nodes in the respective fifth line. In particular, ${\widetilde{\ell}}$ is used exactly three times.

Proposition 2.5 ([10], Prop. 2.13).

Suppose that a line ${\widetilde{\ell}}$ is used by three nodes $A$ , $B$ , $C\in\mathcal{X}$ . Then ${\widetilde{\ell}}$ passes through at least three nodes of $\mathcal{X}$ .

If ${\widetilde{\ell}}$ is a $4$ -node line, then $A$ , $B$ , and $C$ share ${\widetilde{\ell}}$ and three other lines, $\ell_{2}$ and $\ell_{3}$ passing through five and $\ell_{4}$ through four primary nodes. For each of the three nodes, the $\widetilde{\ell}$ -m-distribution sequence with respect to ${\widetilde{\ell}}$ is $(4,5,5,4,2)$ . ${\widetilde{\ell}}$ can only be used by $A$ , $B$ , and $C$ , i.e., it is used exactly three times.

Corollary 2.6 ([10], Cor. 2.14).

Suppose that a line ${\widetilde{\ell}}$ is used by four nodes in $\mathcal{X}$ . Then ${\widetilde{\ell}}$ is a $5$ -node line.

Proposition 2.7 ([10], Prop. 2.15).

Suppose that a line ${\widetilde{\ell}}$ is used by five nodes in $\mathcal{X}$ . Then ${\widetilde{\ell}}$ is a $5$ -node line, and it is actually used by exactly six nodes in $\mathcal{X}$ . These six nodes form a $GC_{2}$ set and share two more lines with five primary nodes each, i.e., each of these six nodes has the m-d sequence $(5,5,5,3,2)$ .

At the end we bring a (part of a) table from [10] which follows from Propositions 2.3, 2.4, 2.5, Corollary 2.6, and Proposition 2.7. It shows under which conditions a $k$ -node line ${\widetilde{\ell}},\ 2\leq k\leq 5,$ can be used at most how often, provided that the considered $GC_{5}$ set has no maximal line.

\begin{array}[]{c|c|c|}&\lx@intercol\hfil\text{maximal \#\ of nodes using ${\widetilde{\ell}}$}\hfil\lx@intercol\vrule\lx@intercol\\ \hline\cr\text{total \#}&\text{in general}&\text{no node uses}\\ \text{of nodes}&&(5,5,5,3,2)\\ \text{in ${\widetilde{\ell}}$}&\text{\phantom{no node uses}}&\text{m-d sequence}\\ &&\\ \hline\cr 5&6&4\\ \hline\cr 4&3&3\\ \hline\cr 3&3&1\\ \hline\cr 2&1&1\\ \hline\cr\end{array}

(2.2)

2.1 The case $(5\,{,}\,5\,{,}\,5\,{,}\,3\,{,}\,2)$

In this and the following sections, we will prove the following

Proposition 2.8.

Assume that $\mathcal{X}$ is a $GC_{5}$ set with no maximal line. Then for no node in $\mathcal{X}$ the m-d sequence is $(5,5,5,3,2)$ .

Assume by way of contradiction the following.

Assumption 2.9.

$\mathcal{X}$ contains a node for which an m-line sequence $(\ell_{1},\ell_{2},\ell_{3},\ell_{4},\ell_{5})$ implies the m-d sequence $(5,5,5,3,2)$ .

Set $\mathcal{X}=\mathcal{A}\cup\mathcal{B}$ (see Fig. 2.1), with

\mathcal{A}=\mathcal{X}\cap\{\ell_{1}\cup\ell_{2}\cup\ell_{3}\},\quad\#\mathcal{A}=15,\quad\text{and}\quad\mathcal{B}=\mathcal{X}\setminus\mathcal{A},\quad\#\mathcal{B}=6.

Denote $\mathcal{L}_{3}:=\{\ell_{1},\ell_{2},\ell_{3}\}.$ Note that no intersection point of the three lines of $\mathcal{L}_{3}$ belongs to $\mathcal{X}$ .

Below we bring a simple proof for

Lemma 2.10 ([10], Lemma 3.2).

(i)

The set $\mathcal{B}$ is a $GC_{2}$ set, and each node $B\in\mathcal{B}$ uses the three lines of $\mathcal{L}_{3}$ and the two lines it uses within $\mathcal{B}$ , i.e.,

$p_{B,\mathcal{X}}^{\star}=\ell_{1}\,\ell_{2}\,\ell_{3}\,p_{B,\mathcal{B}}^{\star}\,.$ (2.3)
(ii)

No node in $\mathcal{A}$ uses any of the lines of $\mathcal{L}_{3}.$

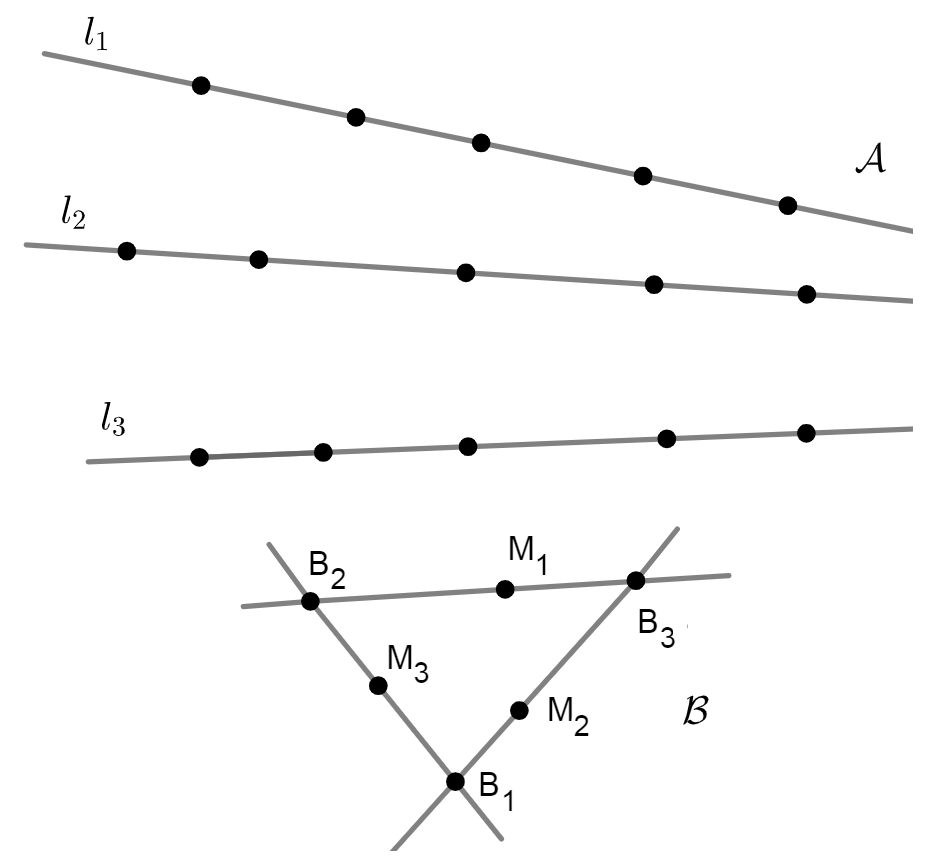
Refer to caption — Figure 2.1: The case $(5,5,5,3,2)$ with $\mathcal{X}=\mathcal{A}\cup\mathcal{B}.$

Proof.

(i) Suppose by way of contradiction that the set $\mathcal{B}$ is not $2$ -poised, i.e., it is a subset of a conic $\mathcal{C}.$ Then $\mathcal{X}$ is a subset of the zero set of the polynomial $\ell_{1}\,\ell_{2}\,\ell_{3}\,\mathcal{C},$ which contradicts Proposition 1.2. Then we readily obtain the formula (2.3).

(ii) Without loss of generality assume that $A\in\ell_{1}$ uses the line $\ell_{2}.$ Then $p_{A}^{\star}=\ell_{2}\,q,$ where $q\in\Pi_{4}.$ It is easily seen that $q$ has (5,4) primary zeros in the lines $(\ell_{3},\ell_{1}).$ Therefore, in view of Corollary 1.12, we obtain that $p_{A}^{\star}=\ell_{2}\,\ell_{3}\,\ell_{1}\,r,$ which is a contradiction.

∎

Evidently, any node in a $GC_{2}$ set uses a maximal line, i.e., $3$ -node line. Hence we conclude readily that any $GC_{2}$ set, including also $\mathcal{B},$ possesses at least three maximal lines (see Figure 2.1).

A node $A\in\mathcal{X}$ is called a $2_{m}$ -node if it is the intersection point of two maximal lines. Note that the nodes $B_{i},\ i=1,2,3,$ in Fig. 2.1, are $2_{m}$ -nodes for $\mathcal{B}.$

Definition 2.11.

We say, that a line $\ell$ is a $k_{\mathcal{A}}$ -node line if it passes through exactly $k$ nodes of $\mathcal{A}.$

Lemma 2.12.

(i) Assume that a line ${\widetilde{\ell}}\notin\mathcal{L}_{3}$ does not intersect a line $\ell\in\mathcal{L}_{3}$ at a node in $\mathcal{X}.$ Then the line ${\widetilde{\ell}}$ can be used at most by one node from $\mathcal{A}.$ Moreover, this latter node belongs to $\ell\cap\mathcal{A}.$

(ii) If a line $\ell$ is $0_{\mathcal{A}}$ or $1_{\mathcal{A}}$ -node line then no node from $\mathcal{A}$ uses the line $\ell.$

(iii) If a line $\ell$ is $2_{\mathcal{A}}$ -node line then $\ell$ can be used by at most one node from $\mathcal{A}.$

(iv) Suppose $\ell$ is a maximal line in $\mathcal{B}.$ Then $\ell$ can be used by at most one node from $\mathcal{A}.$

Proof.

(i) Without loss of generality assume that $\ell=\ell_{1}$ and $A\in\ell_{2}$ uses ${\widetilde{\ell}}:$

p_{A}^{\star}={\widetilde{\ell}}\,q,\ q\in\Pi_{4}.

It is easily seen that $q$ has $(5,4,3)$ primary zeros in the lines $(\ell_{1},\ell_{3},\ell_{2}).$ Therefore, in view of Corollary 1.12, we conclude that $p_{A}^{\star}={\widetilde{\ell}}\,\ell_{1}\,\ell_{2}\,\ell_{3}\,r,\ r\in\Pi_{1},$ which is a contradiction.

Now assume conversely that $A,B\in\ell_{1}\cap\mathcal{X}$ use the line ${\widetilde{\ell}}.$ Choose a point $C\in\ell_{2}\setminus({\widetilde{\ell}}\cup\mathcal{X}).$ Then choose numbers $\alpha$ and $\beta,$ with $|\alpha|+|\beta|\neq 0,$ such that $p(C)=0,$ where $p:=\alpha p_{A}^{\star}+\beta p_{B}^{\star}.$ It is easily seen that $p={\widetilde{\ell}}\,q,\ q\in\Pi_{4}$ and the polynomial $q$ has $(5,4,3)$ primary zeros in the lines $(\ell_{2},\ell_{3},\ell_{1}).$ Therefore $p={\widetilde{\ell}}\ell_{1}\,\ell_{2}\,\ell_{3}\,q,$ where $q\in\Pi_{1}.$ Thus $p(A)=p(B)=0,$ implying that $\alpha=\beta=0$ , which is a contradiction.

The items (ii) and (iii) readily follow from (i). The item (iv) readily follows from (iii). ∎

Denote by $\ell_{AB}$ the line passing through the points $A$ and $B.$

Proposition 2.13.

Let $\ell_{B_{1}M_{1}}$ be 5-node line, which is used by all the six nodes of a subset $\mathcal{A}_{6}\subset\mathcal{A}.$ Suppose also that $\ell$ is a 4-node line passing through $B_{1}$ . If the line $\ell$ is used by three nodes from $\mathcal{A}$ then all these three nodes belong to $\mathcal{A}_{6}.$

Proof.

The six nodes of $\mathcal{A}_{6}$ use the $5$ -node line $\ell_{B_{1}M_{1}}.$ Therefore, in view of Proposition 2.7, these six nodes share also two more lines passing through five primary nodes. It is easily seen that these latter two lines are the lines $\ell_{B_{2}M_{2}}$ and $\ell_{B_{3}M_{3}}.$ Assume by way of contradiction that the nodes $D_{1},D_{2},D_{3}\in\mathcal{A}$ are using the line $\ell$ and $D_{1}\notin\mathcal{A}_{6}.$ According to Proposition 2.5 these three nodes share also two lines passing through five primary nodes. In view of Lemma 2.12, (iv), these latter two lines cannot be maximal lines in $\mathcal{B}.$ Therefore they belong to the set $\{\ell_{B_{2}M_{2}},\ell_{B_{3}M_{3}},\ell_{M_{1}M_{2}},\ell_{M_{2}M_{3}},\ell_{M_{1}M_{3}}\}$ . One of them should be $\ell_{B_{2}M_{2}}$ or $\ell_{B_{3}M_{3}}$ , since any two lines from $\{\ell_{M_{1}M_{2}},\ell_{M_{2}M_{3}},\ell_{M_{1}M_{3}}\}$ share a node. Therefore one of them will be used by seven nodes, namely by $D_{1}$ and the nodes of $\mathcal{A}_{6}.$ This contradicts Proposition 2.7. ∎

2.2 The proof of Proposition 2.8

Consider all the lines passing through $B:=B_{1}$ and at least one more node of ${\mathcal{X}}$ . Denote the set of these lines by $\mathcal{L}(B).$ Let $m_{k}(B),\ k=1,2,3,$ be the number of $k_{\mathcal{A}}$ -node lines from $\mathcal{L}(B).$

We have that

1m_{1}(B)+2m_{2}(B)+3m_{3}(B)=\#\mathcal{A}=15.

(2.4)

Lemma 2.14.

Suppose that a line $\ell,$ passing through $B$ and different from the line $\ell_{BM_{1}},$ is a $3_{\mathcal{A}}$ -node line. Then $\ell$ can be used by at most three nodes from $\mathcal{A}.$

Proof.

Note that $\ell$ is not a maximal line for $\mathcal{B},$ since otherwise $\ell$ will be a maximal line for $\mathcal{X}.$ Therefore $\ell$ is a $4$ -node line and Proposition 2.5 completes the proof. ∎

Lemma 2.15.

We have that $m_{3}(B)\leq 4.$

Proof.

The equality (2.4) implies that $m_{3}(B)\leq 5.$ Assume by way of contradiction that five lines pass through $B$ and three nodes in $\mathcal{A}.$ Therefore these five lines intersect the three lines $\ell_{1},\ell_{2},\ell_{3},$ at the $15$ nodes of $\mathcal{A}.$ Then, by Theorem 1.8, these $15$ nodes are $5+3-3=5$ -dependent, which is a contradiction. ∎

Now we are in a position to start

Proof of Proposition 2.8.

In view of Proposition 2.7 we divide the proof into the following three cases. Case 1. Suppose that $\ell_{BM_{1}}$ is 5-node line used by six nodes from $\mathcal{A}.$

Denote the set of these six nodes by $\mathcal{A}_{6}\subset\mathcal{A}.$

We have that any node from $\mathcal{A}$ uses at least one line from $\mathcal{L}(B).$ Proposition 2.13 implies that all $3_{\mathcal{A}}$ -node lines from $\mathcal{L}(B),$ except $\ell_{BM_{1}},$ can be used by at most two nodes from $\mathcal{A}\setminus\mathcal{A}_{6}.$

From Lemma 2.12, we have that

15-6\leq 0m_{1}(B)+1m_{2}(B)+2(m_{3}(B)-1).

(2.5)

In view of (2.4) we get

m_{1}(B)+2m_{2}(B)+3m_{3}(B)-6\leq 1m_{2}(B)+2m_{3}(B)-2.

(2.6)

Therefore we conclude that $m_{1}(B)+m_{2}(B)+m_{3}(B)\leq 4,$ or, in other words, $3m_{1}(B)+3m_{2}(B)+3m_{3}(B)\leq 12,$ which contradicts equality 2.4.

Case 2. Suppose that $\ell_{BM_{1}}$ is not $5$ -node line.

Then, in view of the table (2.2), it can be used by at most three nodes of $\mathcal{A}.$ From Lemmas 2.12 and 2.14, (ii),(iii), we have that

15\leq 1m_{2}(B)+3m_{3}(B).

(2.7)

In view of (2.4) we get

m_{1}(B)+2m_{2}(B)+3m_{3}(B)\leq m_{2}(B)+3m_{3}(B).

(2.8)

Hence $m_{1}(B)=m_{2}(B)=0$ and $m_{3}(B)\geq 5,$ which contradicts Lemma 2.15.

Case 3. Suppose that $\ell_{BM_{1}}$ is 5-node line used by at most four nodes of $\mathcal{A}.$

In this case we have that

15\leq 1m_{2}(B)+3(m_{3}(B)-1)+4.

In view of (2.4) we get

m_{1}(B)+2m_{2}(B)+3m_{3}(B)\leq 1m_{2}(B)+3m_{3}(B)+1.

(2.9)

Hence $2m_{1}(B)+2m_{2}(B)\leq 2.$ In view of (2.4) we have that

3m_{3}(B_{1})\geq 13,

(2.10)

which contradicts Lemma 2.15. ∎

2.3 The cases $(5\,{,}\,5\,{,}\,4\,{,}\,4\,{,}\,2)$ , $(5\,{,}\,5\,{,}\,4\,{,}\,3\,{,}\,3)$ and $(5\,{,}\,4\,{,}\,4\,{,}\,4\,{,}\,3)$

Let us fix a node $A\in\mathcal{X}$ and consider the set of lines $\mathcal{L}(A).$ Let $n_{k}(A)$ be the number of $(k+1)$ -node lines from $\mathcal{L}_{A}.$ In view of Assumption 2.2 we have that

1n_{1}(A)+2n_{2}(A)+3n_{3}(A)+4n_{4}(A)=\#\bigl{(}{\mathcal{X}}\setminus\{A\}\bigr{)}=20.

(2.11)

Next we bring a result from [10]. We present also the proof for the convenience.

Lemma 2.16 ([10], Lemma 3.13).

Assume that $\mathcal{X}$ is a $GC_{5}$ set with no maximal line. By Proposition 2.8, for no node of $\mathcal{X}$ the m-d sequence is $(5,5,5,3,2)$ . Then the following hold.

(i)

There is no $3$ -node line and $m$ -node line is used exactly $m-1$ times, where $m=2,4,5.$
(ii)

No two lines used by the same node intersect at a node in $\mathcal{X}.$

Proof.

(i) Consider all the lines in $\mathcal{L}(A)$ . From the third column of the table in (2.2), it follows that for the total number $M(A)$ of uses of these lines, we have that

M(A)\leq 1\,n_{1}(A)+1\,n_{2}(A)+3\,n_{3}(A)+4\,n_{4}(A)\,.

(2.12)

Since each node in $\mathcal{X}\setminus\{A\}$ uses at least one line through $A$ , we must have $M(A)\geq 20$ . In view of the equality (2.11) we conclude that $M(A)=20$ and $n_{3}(A)=0$ .

Moreover, we deduce that any line containing $m$ nodes including $A$ has to be used exactly $m{-}1$ times, where $m=2,4,5$ . Since the node $A$ is arbitrary, this is true for all lines containing at least two nodes of $\mathcal{X}$ .

(ii) Assume conversely that two lines $\ell_{1},\ell_{2},$ used by a node $A\in\mathcal{X}$ intersect at a node $B\in\mathcal{X}$ . Then each of the nodes in $\mathcal{X}\setminus\{A,B\}$ uses at least one line through $B$ , while the node $A$ uses at least two lines. Thus we have $M(A)\geq 21,$ which is a contradiction. ∎

Corollary 2.17.

For no node in $\mathcal{X}$ the m-d sequence is $(5,5,4,3,3)$ or $(5,4,4,4,3)$ .

Proof.

Suppose, that for a node $A\in\mathcal{X},$ the m-d sequence is $(5,5,4,3,3)$ or $(5,4,4,4,3)$ . In view of Lemma 2.16, (ii), there are no secondary nodes in the used lines. Thus the presence of $3$ the m-d sequence implies presence of a $3$ -node line in an $m$ -line sequence, which contradicts Lemma 2.16, (i). ∎

Proposition 2.18.

For no node in $\mathcal{X}$ the m-d sequence is $(5,5,4,4,2)$ .

Proof.

Assume that for a node $A\in\mathcal{X}$ some m-line sequence $(\ell_{1},\ell_{2},\ell_{3},\ell_{4},\ell_{5})$ implies the m-d sequence $(5,5,4,4,2)$ . In view of Lemma 2.16, (ii), the lines $\ell_{1},...,\ell_{5},$ contain exactly ${5,5,4,4,2,}$ nodes, respectively. Denote by $B$ and $C$ the two nodes in the line $\ell_{5}.$ Then we have

p_{B}^{\star}=\ell_{1}\,\ell_{2}\,\ell_{3}\,\ell_{4}\,\ell_{AC}\quad\text{and}\quad p_{C}^{\star}=\ell_{1}\,\ell_{2}\,\ell_{3}\,\ell_{4}\,\ell_{AB}).

In view of Lemma 2.16 the line $\ell_{1}$ is used by exactly four nodes of $\mathcal{X}$ . Therefore, there exists a node $D\in\mathcal{X}\setminus\{A,B,C\},$ which is using the line $\ell_{1}.$

In view of (2.1), Proposition 2.8, and Corollary 2.17, for the node $D\in\mathcal{X}$ some m-line sequence $(\ell_{1},\ell_{2}^{\prime},\ell_{3}^{\prime},\ell_{4}^{\prime},\ell_{5}^{\prime})$ yields the m-d sequence $(5,5,4,4,2)$ .

Now, as above, we have that the two nodes in the line $\ell_{5}^{\prime}$ use the line $\ell_{1}.$ In view of Proposition 2.3, the line $\ell_{5}^{\prime},$ used by the node $D,$ cannot coincide with the lines $\ell_{AB},\ell_{AC}$ or $\ell_{BC}$ . Therefore $\ell_{5}^{\prime}$ contains a node different from $A,B,C,D.$ Hence, the line $\ell_{1}$ is used at least five times, which is a contradiction. ∎

2.4 Proof of theorem 2.1

What is left to complete the proof of Theorem 2.1 is the following

Proposition 2.19.

For no node in $\mathcal{X}$ the m-d sequence is $(4,4,4,4,4)$ .

Proof.

Let us fix a node $A\in\mathcal{X}$ . In view of (2.1), Propositions 2.8, 2.18 and Corollary 2.17, for the node $A$ , m-d sequence is $(4,4,4,4,4)$ . Thus, in view of Lemma 2.16, (ii), all used lines are $4$ -node lines. Therefore, in view of Lemma 2.16, (i), we conclude that $n_{1}(A)=n_{2}(A)=n_{3}(A)=n_{4}(A)=0.$ Now, the equality (2.11) implies that $3n_{3}(A)=20$ , which is not possible. ∎

References

[1] V. Bayramyan, H. Hakopian, and S. Toroyan, A simple proof of the Gasca-Maeztu conjecture for $n=4,$ Jaen J. Approx. 7 (1) (2015), 137–147.
[2] C. de Boor, Multivariate polynomial interpolation: conjectures concerning GC sets, Numer. Algorithms 45 (2007) 113–125.
[3] J. R. Busch, A note on Lagrange interpolation in $\mathbb{R}^{2}$ , Rev. Un. Mat. Argentina 36 (1990) 33–38.
[4] J. M. Carnicer and M. Gasca, A conjecture on multivariate polynomial interpolation, Rev. R. Acad. Cienc. Exactas Fís. Nat. (Esp.), Ser. A Mat. 95 (2001) 145–153.
[5] K. C. Chung and T. H. Yao, On lattices admitting unique Lagrange interpolations, SIAM J. Numer. Anal. 14 (1977) 735–743.
[6] D. Eisenbud, M. Green, and J. Harris Cayley-Bacharach theorems and conjectures, Bull. Amer. Math. Soc. (N.S.), 33 (3), (1996) 295–324.
[7] M. Gasca and J. I. Maeztu, On Lagrange and Hermite interpolation in $\mathbb{R}^{k}$ , Numer. Math. 39 (1982) 1–14.
[8] H. Hakopian, K. Jetter, and G. Zimmermann, Vandermonde matrices for intersection points of curves, Jaén J. Approx. 1 (2009) 67–81.
[9] H. Hakopian, K. Jetter, and G. Zimmermann, A new proof of the Gasca-Maeztu conjecture for $n=4$ , J. Approx. Theory 159 (2009) 224–242.
[10] H. Hakopian, K. Jetter, and G. Zimmermann, The Gasca-Maeztu conjecture for $n=5$ , Numer. Math., 127 (2014) 685–713.

A new proof of the Gasca - Maeztu conjecture for n = 5

Abstract

1 Introduction

Definition 1.1.

Proposition 1.2.

Definition 1.3.

Definition 1.4.

Lemma 1.5 ([9], Lemma 2.5).

Definition 1.6.

Proposition 1.7.

Theorem 1.8.

Definition 1.9 ([5]).

Conjecture 1.10 ([7]).

1.1 The m-distribution sequence of a node

Lemma 1.11 ([10], Lemma 2.5).

Corollary 1.12.

2 The Gasca-Maeztu conjecture for n=5n=5

Theorem 2.1.

Assumption 2.2.

Proposition 2.3 ([10], Prop. 2.11).

Proposition 2.4 ([10], Prop. 2.12).

Proposition 2.5 ([10], Prop. 2.13).

Corollary 2.6 ([10], Cor. 2.14).

Proposition 2.7 ([10], Prop. 2.15).

2.1 The case (5, 5, 5, 3, 2)(5\,{,}\,5\,{,}\,5\,{,}\,3\,{,}\,2)

Proposition 2.8.

Assumption 2.9.

Lemma 2.10 ([10], Lemma 3.2).

Proof.

Definition 2.11.

Lemma 2.12.

Proof.

Proposition 2.13.

Proof.

2.2 The proof of Proposition 2.8

Lemma 2.14.

Proof.

Lemma 2.15.

Proof.

Proof of Proposition 2.8.

2.3 The cases (5, 5, 4, 4, 2)(5\,{,}\,5\,{,}\,4\,{,}\,4\,{,}\,2) , (5, 5, 4, 3, 3)(5\,{,}\,5\,{,}\,4\,{,}\,3\,{,}\,3) and (5, 4, 4, 4, 3)(5\,{,}\,4\,{,}\,4\,{,}\,4\,{,}\,3)

Lemma 2.16 ([10], Lemma 3.13).

Proof.

Corollary 2.17.

Proof.

Proposition 2.18.

Proof.

2.4 Proof of theorem 2.1

Proposition 2.19.

Proof.

References

2 The Gasca-Maeztu conjecture for $n=5$

2.1 The case $(5\,{,}\,5\,{,}\,5\,{,}\,3\,{,}\,2)$

2.3 The cases $(5\,{,}\,5\,{,}\,4\,{,}\,4\,{,}\,2)$ , $(5\,{,}\,5\,{,}\,4\,{,}\,3\,{,}\,3)$ and $(5\,{,}\,4\,{,}\,4\,{,}\,4\,{,}\,3)$