A note on affinely regular polygons

Chrestenson [6] has shown that any (planar) regular polygon whose vertices are contained in $\mathbbm{Z}^{d}$ for some $d\geq 2$ must have $3,4$ or $6$ vertices. More generally, Gardner and Gritzmann [9] have characterized the numbers of vertices of affinely regular lattice polygons, i.e., images of non-degenerate regular polygons under a non-singular affine transformation of the plane whose vertices are contained in the square lattice $\mathbbm{Z}^{2}$ or, equivalently, in some arbitrary planar lattice $L$. It turned out that the affinely regular lattice polygons are precisely the affinely regular triangles, parallelograms and hexagons. As a first step beyond the case of planar lattices, this short text provides a generalization of this result to planar sets $\varLambda$ that are non-degenerate in some sense and satisfy a certain affinity condition on finite scales (Theorem 3.3). The obtained characterization can be expressed in terms of a simple inclusion of real field extensions of $\mathbbm{Q}$ and particularly applies to algebraic Delone sets, thus including cyclotomic model sets. These cyclotomic model sets range from periodic examples, given by the vertex sets of the square tiling and the triangular tiling, to aperiodic examples like the vertices of the Ammann-Beenker tiling, of the Tübingen triangle tiling and of the shield tiling, respectively. I turns out that, for cyclotomic model sets $\varLambda$, the numbers of vertices of affinely regular polygons in $\varLambda$ can be characterized by a simple divisibility condition (Corollary 4.1). In particular, the result on affinely regular lattice polygons is contained as a special case (Corollary 4.2(a)). Additionally, it is shown that the obtained divisibility condition implies a weak estimate in the discrete tomography of cyclotomic model sets (Corollary 5.5).

Natural numbers are always assumed to be positive, i.e., $\mathbbm{N}\,=\,\{1,2,3,\dots\}$ and we denote by $\mathcal{P}$ the set of rational primes. If $k,l\in\mathbbm{N}$, then $\operatorname{gcd}(k,l)$ and $\operatorname{lcm}(k,l)$ denote their greatest common divisor and least common multiple, respectively. The group of units of a given ring $R$ is denoted by $R^{\times}$. As usual, for a complex number $z\in\mathbbm{C}$, $|z|$ denotes the complex absolute value, i.e., $|z|=\sqrt{z\bar{z}}$, where $\bar{.}$ denotes the complex conjugation. The unit circle in $\mathbbm{R}^{2}$ is denoted by $\mathbb{S}^{1}$, i.e., $\mathbb{S}^{1}=\{x\in\mathbbm{R}^{2}\,|\,|x|=1\}$. Moreover, the elements of $\mathbb{S}^{1}$ are also called directions. For $r>0$ and $x\in\mathbbm{R}^{2}$, $B_{r}(x)$ denotes the open ball of radius $r$ about $x$. A subset $\varLambda$ of the plane is called uniformly discrete if there is a radius $r>0$ such that every ball $B_{r}(x)$ with $x\in\mathbbm{R}^{2}$ contains at most one point of $\varLambda$. Further, $\varLambda$ is called relatively dense if there is a radius $R>0$ such that every ball $B_{R}(x)$ with $x\in\mathbbm{R}^{2}$ contains at least one point of $\varLambda$. $\varLambda$ is called a Delone set (or Delaunay set) if it is both uniformly discrete and relatively dense. For a subset $S$ of the plane, we denote by $\operatorname{card}(S)$, $\mathcal{F}(S)$, $\operatorname{conv}(S)$ and $\mathbbm{1}_{S}$ the cardinality, set of finite subsets, convex hull and characteristic function of $S$, respectively. A direction $u\in\mathbb{S}^{1}$ is called an $S$-direction if it is parallel to a non-zero element of the difference set $S-S:=\{s-s^{\prime}\,|\,s,s^{\prime}\in S\}$ of $S$. Further, a finite subset $C$ of $S$ is called a convex subset of $S$ if its convex hull contains no new points of $S$, i.e., if $C=\operatorname{conv}(C)\cap S$ holds. Moreover, the set of all convex subsets of $S$ is denoted by $\mathcal{C}(S)$. Recall that a linear transformation (resp., affine transformation) $\Psi\!:\,\mathbbm{R}^{2}\rightarrow\mathbbm{R}^{2}$ of the Euclidean plane is given by $z\mapsto Az$ (resp., $z\mapsto Az+t$), where $A$ is a real $2\times 2$ matrix and $t\in\mathbbm{R}^{2}$. In both cases, $\Psi$ is called singular when $\operatorname{det}(A)=0$; otherwise, it is non-singular. A homothety $h\!:\,\mathbbm{R}^{2}\rightarrow\mathbbm{R}^{2}$ is given by $z\mapsto\lambda z+t$, where $\lambda\in\mathbbm{R}$ is positive and $t\in\mathbbm{R}^{2}$. A convex polygon is the convex hull of a finite set of points in $\mathbbm{R}^{2}$. For a subset $S\subset\mathbbm{R}^{2}$, a polygon in $S$ is a convex polygon with all vertices in $S$. A regular polygon is always assumed to be planar, non-degenerate and convex. An affinely regular polygon is a non-singular affine image of a regular polygon. In particular, it must have at least $3$ vertices. Let $U\subset\mathbb{S}^{1}$ be a finite set of directions. A non-degenerate convex polygon $P$ is called a $U$-polygon if it has the property that whenever $v$ is a vertex of $P$ and $u\in U$, the line $\ell_{u}^{v}$ in the plane in direction $u$ which passes through $v$ also meets another vertex $v^{\prime}$ of $P$. For a subset $\varLambda\subset\mathbbm{C}$, we denote by $\mathbbm{K}_{\varLambda}$ the intermediate field of $\mathbbm{C}/\mathbbm{Q}$ that is given by

where $\varLambda-\varLambda$ denotes the difference set of $\varLambda$. Further, we set $\mathbbm{k}_{\varLambda}:=\mathbbm{K}_{\varLambda}\cap\mathbbm{R}$, the maximal real subfield of $\mathbbm{K}_{\varLambda}$.

For $n\in\mathbbm{N}$, we always let $\zeta_{n}:=e^{2\pi i/n}$, as a specific choice for a primitive $n$th root of unity in $\mathbbm{C}$. Let $\mathbbm{Q}(\zeta_{n})$ be the corresponding cyclotomic field. It is well known that $\mathbbm{Q}(\zeta_{n}+\bar{\zeta}_{n})$ is the maximal real subfield of $\mathbbm{Q}(\zeta_{n})$; see [17]. Throughout this text, we shall use the notation

Except for the one-dimensional cases $\mathbbm{K}_{1}=\mathbbm{K}_{2}=\mathbbm{Q}$, $\mathbbm{K}_{n}$ is an imaginary extension of $\mathbbm{Q}$. Further, $\phi$ will always denote Euler’s phi-function, i.e.,

Occasionally, we identify $\mathbbm{C}$ with $\mathbbm{R}^{2}$. Primes $p\in\mathcal{P}$ for which the number $2p+1$ is prime as well are called Sophie Germain prime numbers. We denote by $\mathcal{P}_{\rm SG}$ the set of Sophie Germain prime numbers. They are the primes $p$ such that the equation $\phi(n)=2p$ has solutions. It is not known whether there are infinitely many Sophie Germain primes. The first few are

see entry A005384 of [16] for further details. We need the following facts from the theory of cyclotomic fields.

Since $\mathbbm{k}_{n}$ is the maximal real subfield of the $n$th cyclotomic field $\mathbbm{K}_{n}$, Fact 2.2 immediately gives the following result.

Consider an algebraic number field $\mathbbm{K}$, i.e., a finite extension of $\mathbbm{Q}$. A full $\mathbbm{Z}$-module $\mathcal{O}$ in $\mathbbm{K}$ (i.e., a free $\mathbbm{Z}$-module of rank $[\mathbbm{K}:\mathbbm{Q}]$) which contains the number $1$ and is a ring is called an order of $\mathbbm{K}$. Note that every $\mathbbm{Z}$-basis of $\mathcal{O}$ is simultaneously a $\mathbbm{Q}$-basis of $\mathbbm{K}$, whence $\mathbbm{Q}\mathcal{O}=\mathbbm{K}$ in particular. It turns out that among the various orders of $\mathbbm{K}$ there is one maximal order which contains all the other orders, namely the ring of integers $\mathcal{O}_{\mathbbm{K}}$ in $\mathbbm{K}$; see [5, Chapter 2, Section 2]. For cyclotomic fields, one has the following well-known result.

The following notions will be of crucial importance.

Before we turn to examples of planar sets $\varLambda$ having properties (Alg) and (Aff), let us prove the central result of this text, where we use arguments similar to the ones used by Gardner and Gritzmann in the proof of [9, Theorem 4.1].

Let $\mathbbm{L}$ be an imaginary algebraic number field with $\overline{\mathbbm{L}}=\mathbbm{L}$ and let $\mathcal{O}_{\mathbbm{L}}$ be the ring of integers in $\mathbbm{L}$. Then, every translate $\varLambda$ of $\mathbbm{L}$ or $\mathcal{O}_{\mathbbm{L}}$ is non-degenerate and satisfies the properties (Alg) and (Aff). To this end, we first show that in both cases one has $\mathbbm{K}_{\varLambda}=\mathbbm{L}$. If $\varLambda$ is a translate of $\mathbbm{L}$, this follows immediately from the calculation

If $\varLambda$ is a translate of $\mathcal{O}_{\mathbbm{L}}$, one has to observe that

since $\overline{\mathbbm{L}}=\mathbbm{L}$ implies $\overline{\mathcal{O}_{\mathbbm{L}}}=\mathcal{O}_{\mathbbm{L}}$. In the first case, property (Aff) is evident, whereas, if $\varLambda$ is a translate of $\mathcal{O}_{\mathbbm{L}}$, property (Aff) follows from the fact that there is always a $\mathbbm{Z}$-basis of $\mathcal{O}_{\mathbbm{L}}$ that is simultaneously a $\mathbbm{Q}$-basis of $\mathbbm{L}$. Thus, if $F\subset\mathbbm{L}$ is a finite set, then a suitable translate of $aF$ is contained in $\varLambda$, where $a$ is defined as the least common multiple of the denominators of the $\mathbbm{Q}$-coordinates of the elements of $F$ with respect to a $\mathbbm{Q}$-basis of $\mathbbm{L}$ that is simultaneously a $\mathbbm{Z}$-basis of $\mathcal{O}_{\mathbbm{L}}$. Hence, for these two examples, property (Aff) may be replaced by the stronger property

• (Hom)

  For all $F\in\mathcal{F}(\mathbbm{K}_{\varLambda})$, there is a homothety $h\!:\,\mathbbm{R}^{2}\rightarrow\mathbbm{R}^{2}$ such that $h(F)\subset\varLambda$ .

Thus, we have obtained the following consequence of Theorem 3.3.

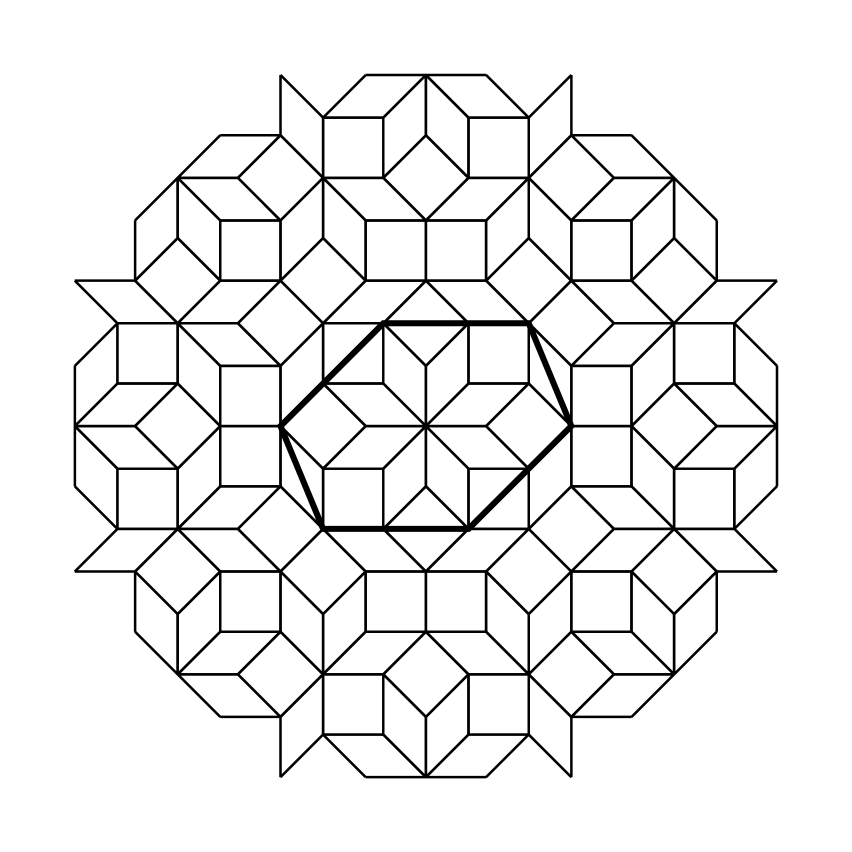
Remarkably, there are Delone subsets of the plane satisfying properties (Alg) and (Hom). These sets were introduced as algebraic Delone sets in [13, Definition 4.2]. Note that algebraic Delone sets are always non-degenerate, since this is true for all relatively dense subsets of the plane. It was shown in [13, Proposition 4.15] that the so-called cyclotomic model sets $\varLambda$ are examples of algebraic Delone sets; cf. Section 4 of [13] and [13, Definition 4.6] in particular for the definition of cyclotomic model sets. Any cyclotomic model set $\varLambda$ is contained in a translate of $\mathcal{O}_{n}$, where $n\geq 3$, in which case the $\mathbbm{Z}$-module $\mathcal{O}_{n}$ is called the underlying $\mathbbm{Z}$-module of $\varLambda$. With the exception of the crystallographic cases of translates of the square lattice $\mathcal{O}_{4}$ and translates of the triangular lattice $\mathcal{O}_{3}$, cyclotomic model sets are aperiodic (i.e., they have no translational symmetries) and have long-range order; cf. [13, Remarks 4.9 and 4.10]. Well-known examples of cyclotomic model sets with underlying $\mathbbm{Z}$-module $\mathcal{O}_{n}$ are the vertex sets of aperiodic tilings of the plane like the Ammann-Beenker tiling [1, 2, 11] ($n=8$), the Tübingen triangle tiling [3, 4] ($n=5$) and the shield tiling [11] ($n=12$); cf. [13, Example 4.11] for a definition of the vertex set of the Ammann-Beenker tiling and see Figure 1 and [13, Figure 1] for illustrations. For further details and illustrations of the examples of cyclotomic model sets mentioned above, we refer the reader to [14, Section 1.2.3.2]. Clearly, any cyclotomic model set $\varLambda$ with underlying $\mathbbm{Z}$-module $\mathcal{O}_{n}$ satisfies

whence $\mathbbm{k}_{\varLambda}\subset\mathbbm{k}_{n}$. It was shown in  [13, Lemma 4.14] that cyclotomic model sets $\varLambda$ with underlying $\mathbbm{Z}$-module $\mathcal{O}_{n}$ even satisfy the following stronger version of property (Hom) above:

• (Hom)

  For all $F\in\mathcal{F}(\mathbbm{K}_{n})$, there is a homothety $h\!:\,\mathbbm{R}^{2}\rightarrow\mathbbm{R}^{2}$ such that $h(F)\subset\varLambda$ .

This property enables us to prove the following characterization.

Although the equivalence (i) $\Leftrightarrow$ (iv) in Corollary 4.1 is fully satisfactory, the following consequence deals with the two cases where condition (ii) can be used more effectively.

For further illustrations and explanations of the above results, we refer the reader to [14, Section 2.3.4.1] or [12, Section 5]. This references also provide a detailed description of the construction of affinely regular $m$-gons in cyclotomic model sets, given that they exist.

Discrete tomography is concerned with the inverse problem of retrieving information about some finite object from information about its slices; cf. [8, 9, 12, 13, 14] and also see the refences therein. A typical example is the reconstruction of a finite point set from its (discrete parallel) $X$-rays in a small number of directions. In the following, we restrict ourselves to the planar case.

In [13], we studied the problem of determining convex subsets of algebraic Delone sets $\varLambda$ by $X$-rays. Solving this problem amounts to find small sets $U$ of suitably prescribed $\varLambda$-directions with the property that different convex subsets of $\varLambda$ cannot have the same $X$-rays in the directions of $U$. More generally, one defines as follows.

Let $\varLambda\subset\mathbbm{R}^{2}$ be a Delone set and let $U\subset\mathbb{S}^{1}$ be a set of two or more pairwise non-parallel $\varLambda$-directions. Suppose the existence of a $U$-polygon $P$ in $\varLambda$. Partition the vertices of $P$ into two disjoint sets $V,V^{\prime}$, where the elements of these sets alternate round the boundary of $P$. Since $P$ is a $U$-polygon, each line in the plane parallel to some $u\in U$ that contains a point in $V$ also contains a point in $V^{\prime}$. In particular, one sees that $\operatorname{card}(V)=\operatorname{card}(V^{\prime})$. Set

and, further, $F:=C\cup V$ and $F^{\prime}:=C\cup V^{\prime}$. Then, $F$ and $F^{\prime}$ are different convex subsets of $\varLambda$ with the same $X$-rays in the directions of $U$. We have just proven direction (i) $\Rightarrow$ (ii) of the following equivalence, which particularly applies to cyclotomic model sets, since any cyclotomic model set is an algebraic Delone set by [13, Proposition 4.15].

By combining Corollary 4.1, direction (i) $\Rightarrow$ (ii) of Theorem 5.3 and Remark 5.4, one immediately obtains the following consequence.

Let us finally note the following relation between $U$-polygons and affinely regular polygons. The proof uses a beautiful theorem of Darboux [7] on second midpoint polygons; cf. [10] or [8, Ch. 1].

I am indebted to Michael Baake, Richard J. Gardner, Uwe Grimm and Peter A. B. Pleasants for their cooperation and for useful hints on the manuscript. Interesting discussions with Peter Gritzmann and Barbara Langfeld are gratefully acknowledged.