A note on the Independent domination polynomial of zero divisor graph of rings
Abstract
In this note we consider the independent domination polynomial problem along with their unimodal and log-concave properties which were earlier studied by Gürsoy, Ülker and Gürsoy (Soft Comp. 2022). We show that the independent domination polynomial of zero divisor graphs of for where are primes with are not unimodal thereby contradicting the main result of Gürsoy, Ülker and Gürsoy [13]. Besides the authors show that the zero of the independent domination polynomial of these graphs have only real zero and used concept of Newton’s inequalities to establish the log-concave property for the afore said polynomials. We show that these polynomials have complex zeros and the technique of Newton’s inequalities are not applicable. Finally, by definition of log-concave, we prove that these polynomials are log-concave and fix the flaws in Theorem 10 of Gürsoy, Ülker and Gürsoy [13].
Keywords: Zero divisor graphs, commutative ring, independent domination polynomial; unimodal; log-concave; Computing
AMS subject classification: 05C25, 05C31, 05C69, 05C90.
1 Introduction
All graphs considered in this note are finite, simple and undirected graphs. A graph is usually symbolized by with its vertex set and edge set . The numbers is order and size of An edge among vertices and is denoted by . The degree of a vertex is the number of vertices incident on it. The union of two graphs and , denoted by , defined as a graph with vertex set and edge set The join of and , denoted by , is a graph with vertex set and edge set
A set is called a dominating set if each vertex in is adjacent to at least one vertex in The minimum order (cardinality) among all such dominating sets of is called the domination number of The theory of domination of graphs is well studied, see textbook [14]. A set in a graph is called an independent set if vertices of are pairwise non-adjacent. The cardinality of the maximum independent set is called the independence number of A subset of is independent dominating set of which is both dominating and independent in . The independent domination number is the minimum size of all independent dominating sets of The invariants and of is related by (see, [14]). The independent set problem in a graph is strongly NP-hard problem while the dominating set problem of a graph is NP-complete problem. These problems are well studied both in theoretical computer science and mathematics.
A polynomial is called unimodal if coefficients ’s form a unimodal sequence, that is, there exists a positive integer known as the mode, such that . Equivalently the coefficients of increase to some stage and then decrease from thereafter. The polynomial is log-concave (logarithmically concave) if
| (1.1) |
If ’s are non negative and all the zeros of are real. Then the basic approach for unimodal and log-concave is the Newton’s inequalities [15] stated as:
| (1.2) |
The condition for log-concave given in (1.2) is stronger than the one given in (1.1), see [21]. Also log-concave sequence of positive terms is unimodal [21]. However, if implies that either or (no internal zeros), then a non-negative log-concave sequence is unimodal [21]. Log-concavity of sequences is related to the surface embedding of graphs in topological graph theory, like the log-concavity of genus polynomials of graphs [12].
Clearly, the polynomial is unimodal whereas is not unimodal, since the coefficients decrease, then increase and then decrease. An effective information about the increase or decrease of coefficients can measure the unimodal property. As it is clear that unimodal sequence either increases or decreases, or increase and then decrease. The number of changes of directions (increasing or decreasing) of is defined as the of oscillations of . Obviously, for the unimodal polynomial the oscillations of must be at most one. For polynomial , then , since change of decreasing directions are two. Sometimes it is equally good to identify the oscillations for non unimodal polynomials.
Identifying unimodal or log-concave property (or both) of a given polynomial is a very well studied non-trivial problem. Several open problems and conjectures exist in literature related to these entities for different types of polynomials. These properties of polynomials are mostly studied for graph polynomial, like independent polynomial, dominating polynomial, matching polynomial, clique polynomial and several other polynomials.
Let be the number of independent dominating sets of order in . The independent domination polynomial of is defined as
A root of the equation is called as the independent domination root of
The independent domination polynomial is a generating function of number of the independent dominating sets of certain cardinalities of . The independent domination polynomials and their roots, unimodal and log-concave property have attracted many researchers, see [5, 19, 10, 11]. Jahari and Alikhani [16] obtained the independent domination polynomials of generalized compound graphs and constructed graphs whose independent domination polynomials have real zeros. More about independent domination polynomials and other polynomials can be seen in [2, 1, 3, 17, 18, 4]. Recently, Gürsoy, Ülker and Gürsoy [13] presented the results related to the independent domination polynomial of zero-divisors graphs associated to commutative rings. In particular, they showed that the independent domination polynomial of zero divisor graph of is unimodal and log-concave. We will consider this study in the present note and modify the existing results of Gürsoy, Ülker and Gürsoy [13] and fix the errors in the published article.
In Section 2, we give basic of zero divisor graphs of and recall the results of Gürsoy, Ülker and Gürsoy [13] along with the properties of log-concave and unimodal. We give several examples having complex independent domination zeros countering a result of [13]. We discuss the unimodal and log-concave property of for where are primes in Propositions 2.2, 2.3 and 2.4. Theorems 2.6 gives the independent domination polynomial in simplified form and Theorem 2.7 established the non unimodal and log-concave property of where is prime and is a positive integer.
2 Independent domination polynomial of zero divisor graphs of commutative rings
For a given commutative ring with non-zero identity, is a zero divisor of if there is such that Beck in 1988 [8] put forward the concept of zero divisor graphs to study the colouring of rings. He included identity in the vertex set of zero divisor graphs and defined edges among zero divisor if and if their product is zero, thereby we see that is adjacent to all vertices of such a graphs. Anderson and Livingston in 1999 [7] modified the definition Beck’s zero divisor graphs and excluding of ring in zero divisor graph and defined edges between two non-zero zero divisors if and only if their product is zero. Several interesting results related to these graphs and their underlying rings were published in the past years, mostly recent notably works are: Chattopadhyay Panigrahi [9] obtained the graphical structure of and showed that it is join of certain complete and null graphs (non empty graphs without any edges). Anderson and Weber [6] determine all zero-divisor graphs with at most vertices. First spectral analysis of zero divisor graphs were carried in [22]. Complete spectral and structural analysis were given in [20]. Gürsoy, Ülker and Gürsoy [13] introduced the concept of independent domination polynomials for zero divisor graphs for for certain values of We will carry the work Gürsoy, Ülker and Gürsoy [13] forward in this note. First we understand the structure of .
Consider the sets as given below:
where is a divisor of and denotes the greatest common divisor of and It is clear that , for . Thus, it implies that are pairwise disjoint and partitions the vertex set of as
and vertices of are adjacent to vertices of in if and only if where is scaler (see [9]). Also, , for (see [22]). Besides the induced subgraphs of is either either clique or its complement. More precisely is is divides otherwise it is (see [9]). Next, we state a results related to the unimodal and log-concave property of the independent domination polynomial of for several values of proved as a main and interesting result in Gürsoy, Ülker and Gürsoy [13]. We restate it and avoid the ambiguity in the stated version of [13].
Theorem 2.1 ([13], Theorem 10).
The independent domination polynomials of zero divisor graphs of rings and is unimodal and log-concave for prime numbers with . The independent domination polynomial of zero divisor graph of is log-concave and unimodal for prime , where is a positive integer.
The proof of Theorem 10 from Gürsoy, Ülker and Gürsoy [13] reads the following:
The independent domination polynomials of and are unimodal since the sequence of its coefficients are a sequence of non-negative numbers, and these polynomials have only real zeros. Then, we have
from Newton’s inequalities. Therefore, the sequence is log-concave and unimodal.
Note 1.
We note two important points from the above result and its proof.
-
1.
The zero of the independent domination polynomials of the zero divisor graphs of and are not always real and they have complex zeros as well, where are primes with and is a positive integer. We will show it in next couple of examples along with their graphical representation on complex plane.
-
2.
Since the zeros of the independent domination polynomials of the zero divisor graphs of and are not always real, so Newton’s inequalities are not applicable and log-concave cannot be established with this procedure used in the proof pf Theorem 10 of [13].
Next, we give a sequence of examples of the independent domination polynomials of the zero divisor graphs of the families of the commutative rings mentioned in Theorem 2.1 having complex zeros as well and are not unimodal. We consider the some examples from [13]. Their graphs are given in [13] and graphs of other examples can be drawn in a similar fashion.
-
1.
For with and the independent domination polynomial is (see Theorem 4, [13]) and its zeros are and . The graphical representation of the zeros of is easy to visualise.
-
2.
For with and the independent domination polynomial is (see Example 1, [13]) and its set of zeros are
The graphical representation of the zeros of is shown in Figure 1, where green dots represent the zeros.
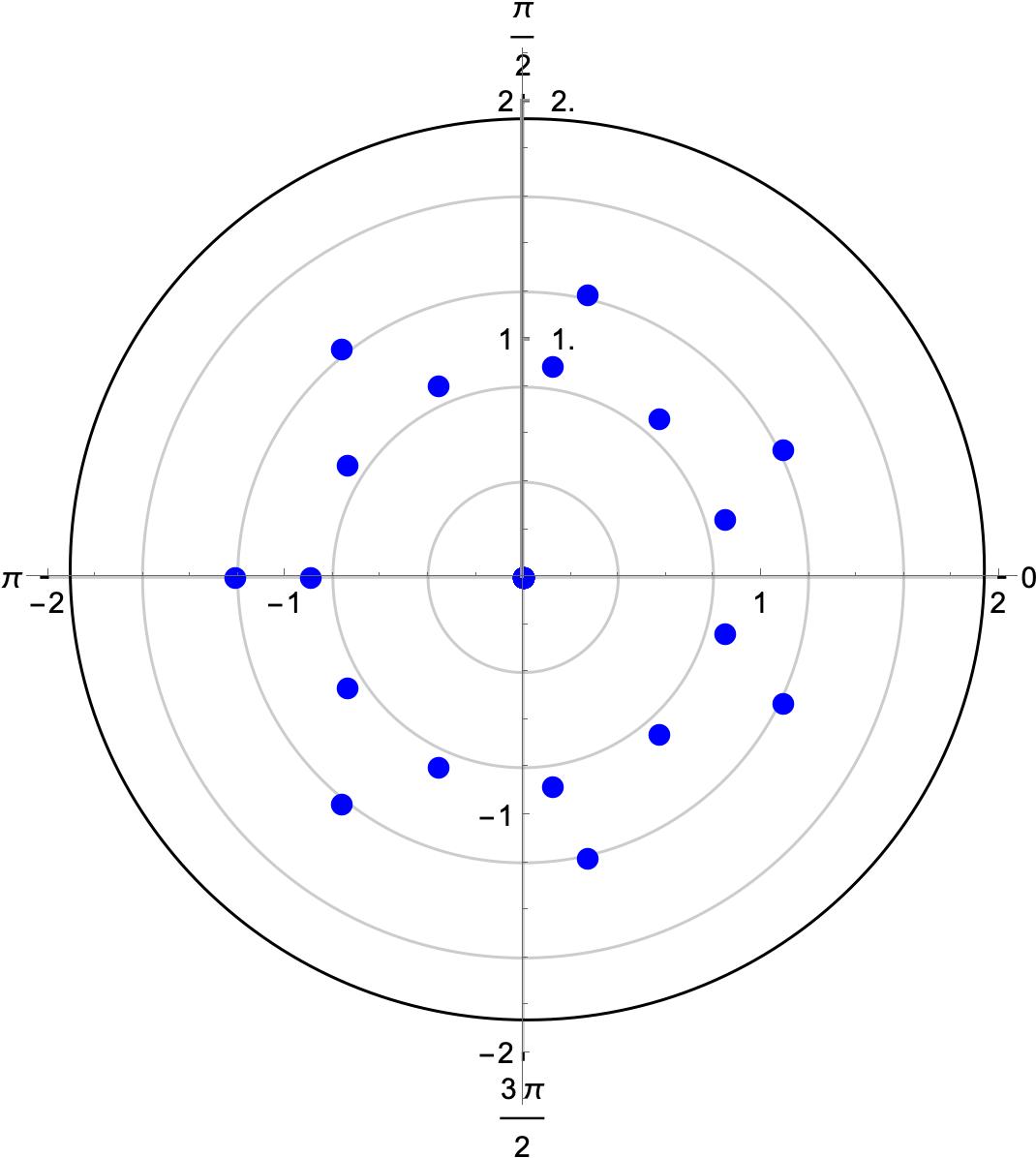
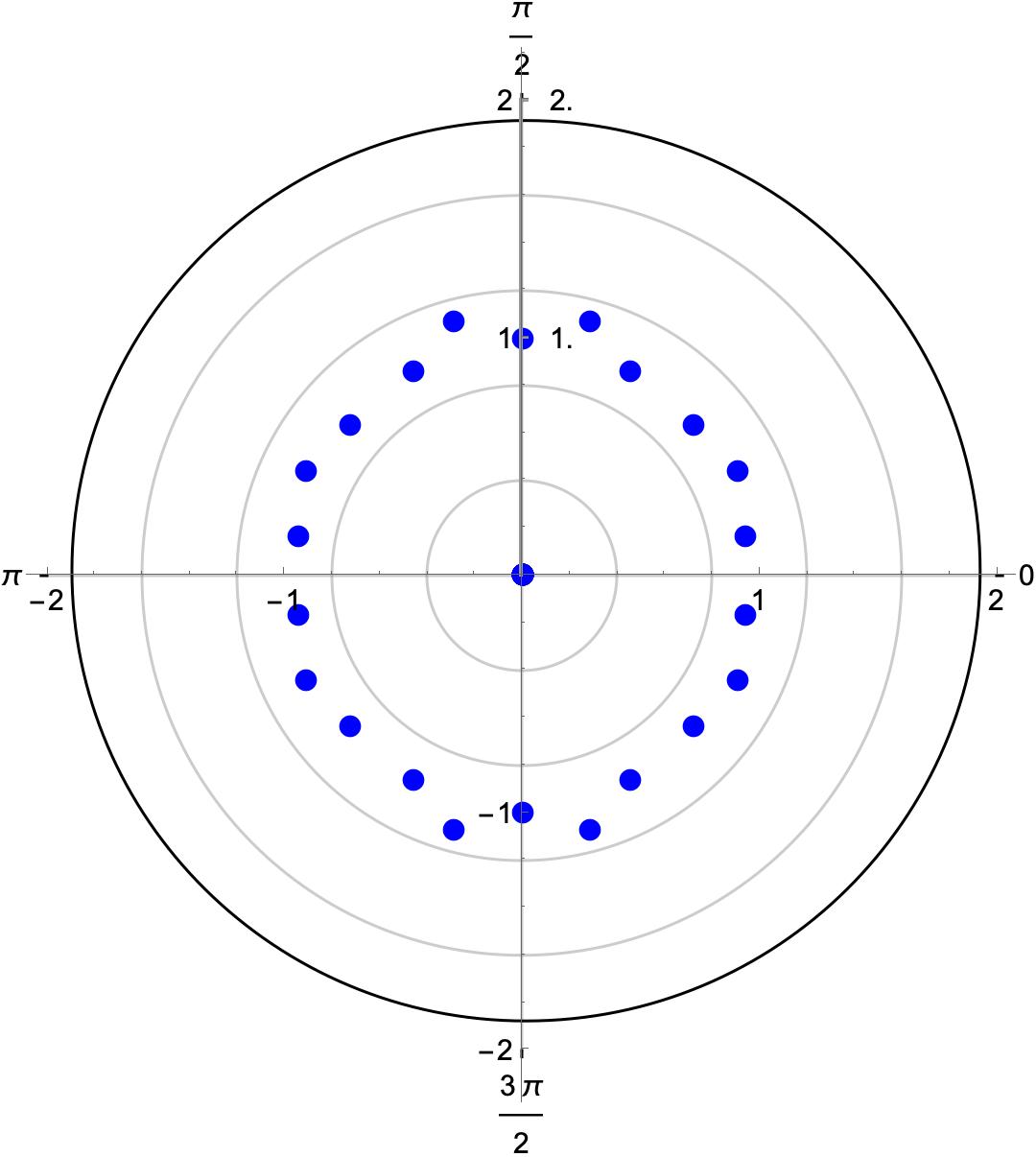
Zeros of Zeros of
Figure 1: Pictorial representation of the zeros of on a plane. - 3.
-
4.
For with and the independent domination polynomial is (see Example 3, [13]) and the set of zeros of this polynomial is very long. So, we represent it by the graphical picture as shown in Figure 2
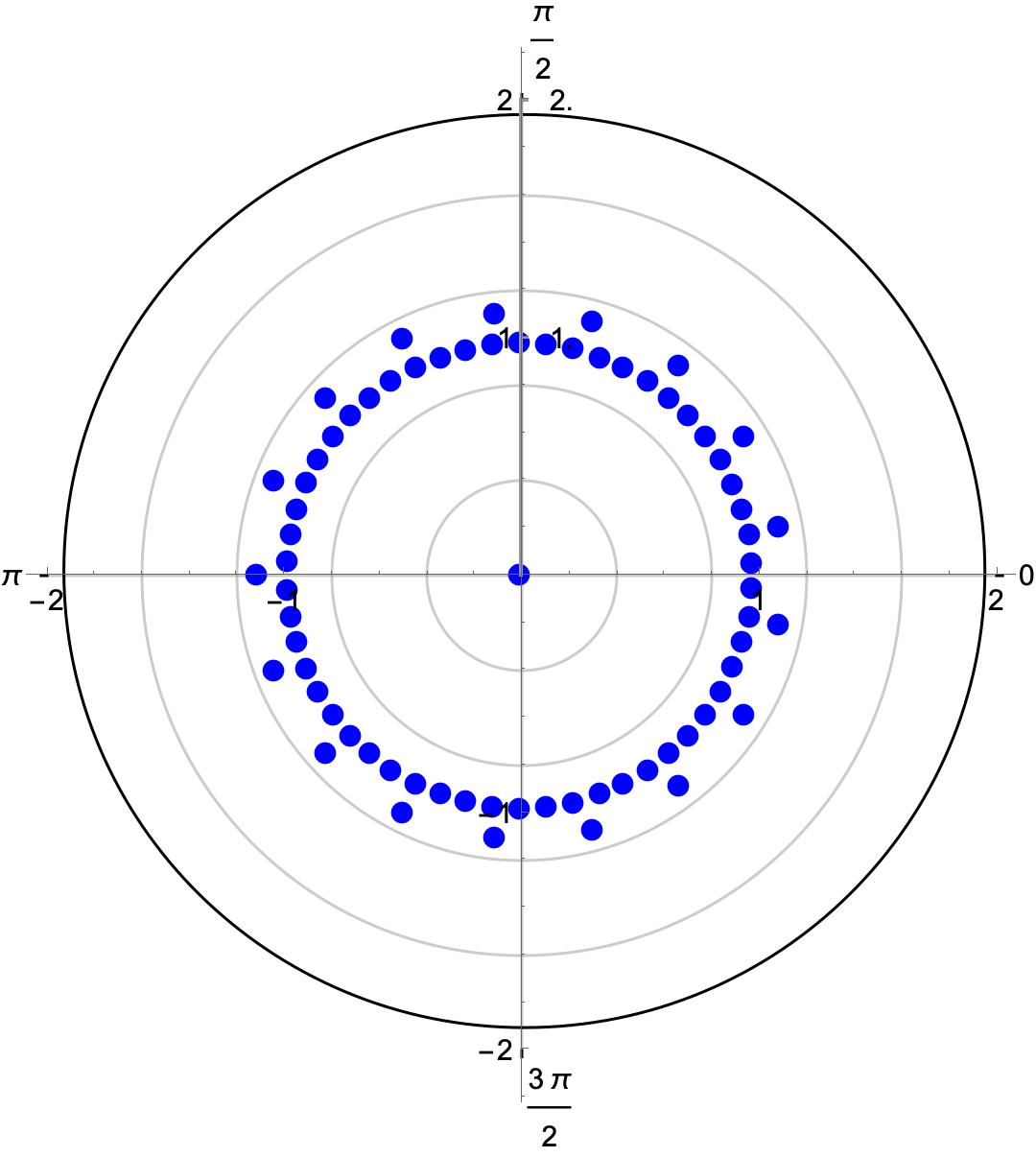
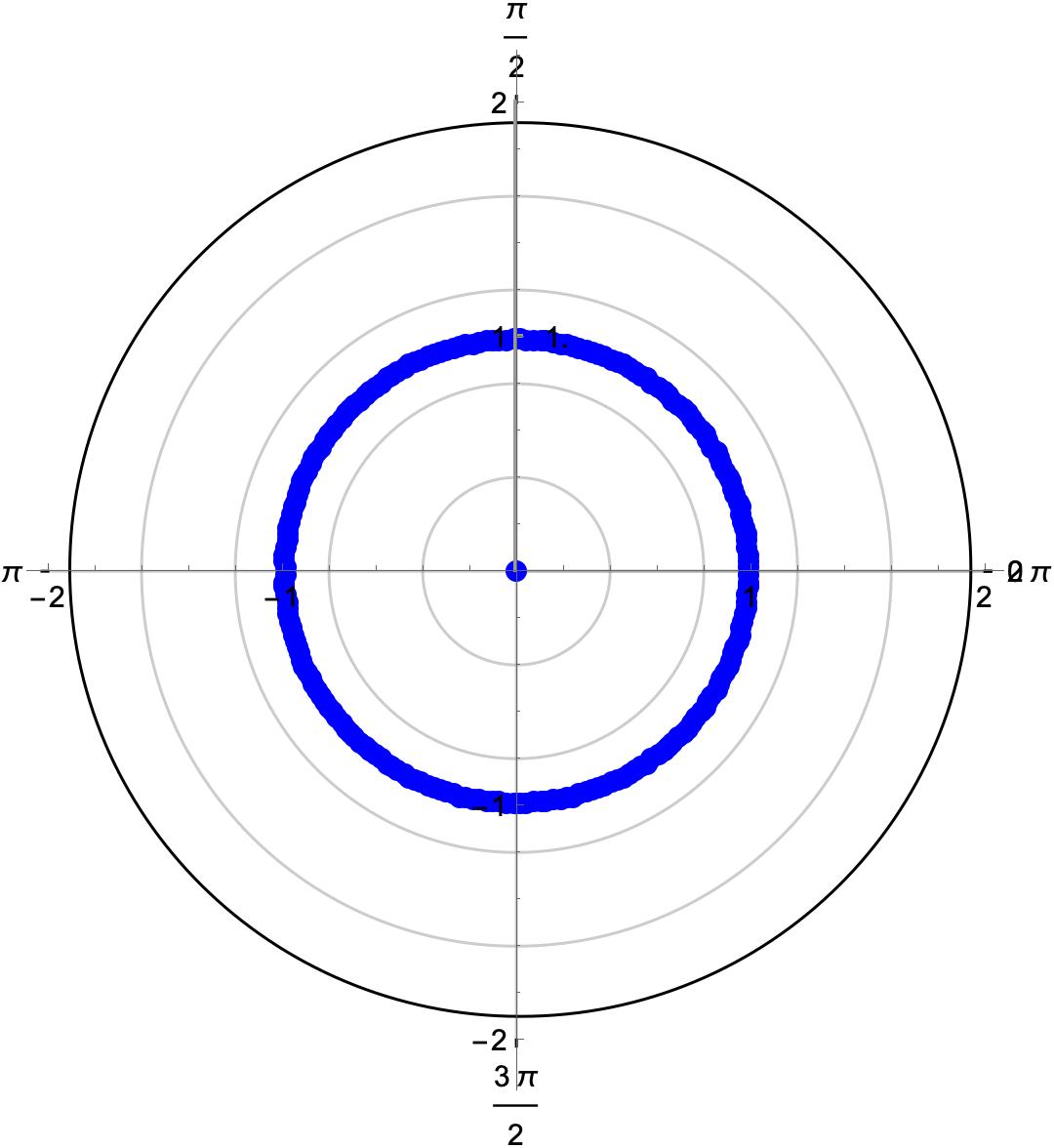
Zeros of Zeros of
Figure 2: Pictorial representation of the zeros of on a plane. -
5.
For with and the independent domination polynomial is and the list of zeros of this polynomial is very long. So, we avoid listing them and present its graphical representation in Figure 2 (right).
Next, we will check the unimodal property of the independent domination polynomial of the zero divisor graphs for and
We recall that the independent domination polynomial of is which is clearly unimodal as sequence of its coefficients form an increasing sequence of non-negative integers. From now onwards, whenever we consider , we assume to avoid case. Next for to be unimodal, we have which must be less than or equal to coefficient of , which can happen if and only if as its coefficient is already one. Otherwise if then some coefficients between the linear term and -th must be zero. Which will imply that thereby contradicting the requirement for unimodal property. Also, by definition the log-concave property is satisfied trivially for . However, for we see that and for , we get , which are always true, and it follows that is log-concave. We make these observation precise in the following result.
Proposition 2.2.
Let be a prime. Then the following hold.
-
(i)
For prime , the independent domination polynomial of is unimodal and log-concave.
-
(ii)
For prime , the independent domination polynomial of is always log-concave and is unimodal if and only if
With a similar argument as in (ii) of Proposition 2.2, we have the following result.
Proposition 2.3.
The independent domination polynomial of with primes is log-concave but it is unimodal if and only if and
Proposition 2.4.
The independent domination polynomial of with primes is log-concave but not unimodal.
Proof. From Theorem 5 [13], without evaluating Euler functions, the independent domination polynomial of is
For and the above polynomial becomes
and it is clear that , since the change of decreasing (increasing) directions of coefficients is two. So, it is not unimodal. Now, for other values of and , if , then we obtain and from it, we get , which is true. Also, . Thus, the coefficients of increase, then decrease and then again increase, then decrease. Thus, it implies that and is not unimodal. It is easy to see that the coefficients of satisfies the conditions for and it implies the log-concave property of ∎
We note that the number of oscillation in the independent domination polynomial of the above results is presciently three, since
The following result gives the unimodal and log-concave property for the zero divisor graphs when is product of three primes and the result corrects Theorem 10 of [13] for .
Proposition 2.5.
The independent domination polynomial of with primes is never unimodal and it is log-concave if and only if
Proof. Let be the zero divisor graph of , where we assume that without any loss of generality. The independent domination polynomial of is (see Theorem 6, [13])
| (2.3) |
If then all the exponents of the polynomial given in (2.3) are Euler function, which are even and so is their sum. Thus, as coefficients increase four times and decrease three times. So, is not unimodal. If , then exponent in (2.3) is odd and other coefficients are even. In this case is at least three and it implies that is not unimodal. However depending on , it is clear that either or is the largest exponent. Also, if with , then and . It implies that there is difference of more two between and Thus, in this case we obtain and polynomial is not unimodal. Next, we turn our attention toward the log-concave property of . It is clear that the minimum value of is , so and . It implies that the difference between and is more than two. Likewise, same is true for and However, depending on the values of , sometimes is larger and sometimes is larger. Therefore, or satisfies the property of log-concave. We are concerned with coefficients between and If and differ by two, then
where or
where So, with the above observation, the polynomial given in (2.3) is log-concave if and only if the difference between and is away from two. ∎
As classified by the above result, we mention some of the classes of the independent domination polynomials of zero divisor graphs of which are not log-concave.
-
1.
The independent domination polynomial of is which is not log-concave, since
-
2.
The independent domination polynomial of is which is not log-concave, since
-
3.
The independent domination polynomial of is which is not log-concave, since
-
4.
The independent domination polynomial of is which is not log-concave, since
For the above classes of polynomials, we see that is bigger or sometimes is bigger, oscillation is exactly four, and they are not unimodal.
Next, we discuss the independent domination polynomial of when is a prime power. We will state the result without proof, since it is similar to Theorem 7 given in [13]. We recall number theoretic facts: , where is prime and is a positive integer and for relatively primes and , we have .
Theorem 2.6.
Let be a zero divisor graph of . Then the following hold.
-
(i)
If where is prime and is a positive integer, then the independent domination polynomial of is given by
-
(ii)
If where is prime and is a positive integer, then the independent domination polynomial of is given by
The following results gives the non unimodal and log-concave property of when is prime power.
Theorem 2.7.
If is the prime power, then the independent domination polynomial of is log-concave but not unimodal.
Proof. Let , where is prime and is a positive integer. Then the independent domination polynomial of is
All the exponents of the above polynomial are odd except last exponent which is even. So, and it follows that is not unimodal. In fact as all the coefficients of are strictly increasing, for and is strictly greater than , for So the coefficients of increase precisely times.
For the independent domination polynomial of in standard form is
As in odd case, the exponents of the above expression are odd except and coefficients increase precisely times. From the representation of coefficients and exponents of , it is easy to see that and have large gaps for respective values of Thus by definition, the log-concave property holds trivially. ∎
3 Conclusion
This note gives the unimodal and log concave property of the independent domination polynomial of for and thereby corrects the results in [13] and flaws in their proof. The challenging task about the independent domination polynomial of is the location of zeros in the complex plane or possibly in some smaller annular region. The other graph polynomial like independent and the domination polynomials is another idea for carrying this work forward for the zero divisor graphs of commutative rings.
Data Availability:
There is no data associated with this article.
Conflict of interest
The authors declare that they have no competing interests.
Funding Statement
There is no funding for this article.
Ethical Statement
Not Applicable
References
- [1] S. Alikhani, The domination polynomial of a graph at , Graphs Combin. 29 (2013) 1175–1181.
- [2] S. Alikhani, J. Brown and S. Jahari, On the Domination Polynomials of Friendship Graphs, Filomat 30(1) (2016) 169–178.
- [3] S. Alikhani, Y. H. Peng, Introduction to domination polynomial of a graph, Ars Combin. 114 (2014) 257–266.
- [4] B. M. Anthony and M. E. Picollelli, Complete r-partite graphs determined by their domination polynomial, Graphs Combin. 31 (2015) 1993–2002.
- [5] A. Alwardi, P.M. Shivaswamy and N.D. Soner, Independent dominating polynomial in graphs, Int. J. Sci. Inn. Math. Research, 2 (2014) 757-763.
- [6] D. F. Anderson and D. Weber, The zero-divisor graph of a commutative ring without identity, Int. Elect. J. Algebra 223 (2018) 176–202.
- [7] D. F. Anderson and P.S. Livingston, The zero divisor graph of a commutative ring, J. Algebra 217 (1999) 434–447.
- [8] I. Beck, Coloring of a commutative rings, J. Algebra 116 (1988) 208–226.
- [9] S. Chattopadhyay, K. L. Patra, B. K. Sahoo, Laplacian eigenvalues of the zero divisor graph of the ring , Linear Algebra Appl. 584 (2020) 267–286.
- [10] M. Dod, The independent domination polynomial, (2016) https://arxiv.org/abs/1602.08250.
- [11] W. Goddard and M. A. Henning, independent domination in graphs: a survey and recent results, Discrete Math. 313 (2013) 839–854.
- [12] J. L. Gross,T. Mansour,T. W. Tucker and D. G. L. Wang, Log-concavity of combinations of sequences and applications to genus distributions, SIAM J. Discrete Math. 29(2) (2015) 1002–1029.
- [13] N. K. Gürsoy, A. Ülker and A. Gürsoy, Independent domination polynomial of zero-divisor graphs of commutative rings, Soft Comp. 26 6989–6997.
- [14] T. W. Haynes, S. T. Hedetniemi and P. J. Slater, Fundamentals of Domination in Graphs, Marcel Dekker, New York, 1998.
- [15] G. H. Hardy, J. E. Littlewood and G. Pólya, Inequalities, Cambridge University Press, Cambridge, 1952.
- [16] S. Jahari and S. Alikhani, On the independent domination polynomial of a graph, Discrete Appl. Math. 289 (2021) 416–426.
- [17] V. E. Levit and E. Mandrescu, On the independence polynomial of the corona of graphs, Discrete Appl. Math. 203 (2016) 85–93.
- [18] V. E. Levit and E. Mandrescu, The independence polynomial of a graph-a survey, in: Proc. Int. Con. Algeb. Inf. Aristotle Univ. Thessaloniki, Greece (2005) 233-254.
- [19] G. P. Lonzaga, Independent dominating polynomial of corona of some special graphs, Int. J. Sci. and Eng. Research 9(5) (2018) 262–267.
- [20] Bilal A. Rather, S. Pirzada, T. A. Naikoo, Y. Shang, On Laplacian eigenvalues of the zero-divisor graph associated to the ring of integers modulo , Math. 9(5) (2021) 482.
- [21] R. P. Stanley, Log-concave and unimodal sequences in algebra, combinatorics and geometry, Graph Theory and Its Applications East and West: Proceedings of the First China‐USA International Graph Theory Conference, Annals New York Academy Sci. 567(1) (1989) 500–535.
- [22] M. Young, Adjacency matrices of zero divisor graphs of integer modulo , Involve 8 (2015) 753–761.