A physics lab inside your head:
Quantum thought experiments as an educational tool
^††thanks: I thank the Heilbronn Institute for Mathematical Research and IBM Quantum for their generous support.

Schrödinger’s cat is a well-known thought experiment proposed by Erwin Schrödinger in 1935 [1]. It begins with a cat, a vial of poison, a radioactive atom, and a hammer, all inside a box (depicted in Figure 1). If the atom decays, the hammer is activated to break the vial, killing the cat. If the atom does not decay, the cat survives. The atom enters a superposition of decaying and not decaying. According to quantum theory, when it interacts with the hammer, poison and cat, they all become entangled. They enter a joint superposition, with one term where the atom has decayed and the cat is dead, and another where the atom has not decayed and the cat is alive.

The so-called collapse postulate of quantum mechanics says that quantum systems in superposition collapse to a single state when observed. Hence, an outside observer looking into the box forces the cat to be either dead or alive. An alternative theory is that quantum mechanics can be consistently applied to the observer, and in fact any observer or detector. Another way of phrasing this viewpoint is that quantum theory is a universal theory, so it can be applied to all parts of the universe, including observers, detectors and the environment. In this case, an observer measuring a quantum system also becomes entangled with the system, again resulting in a joint superposition of states.

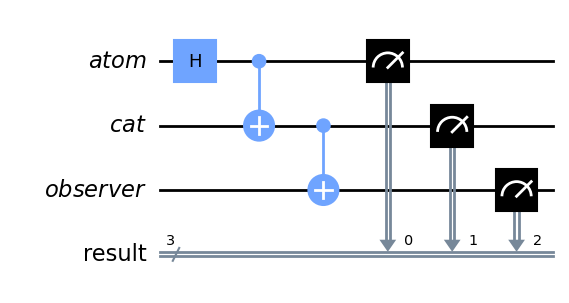
To model this experiment as a quantum circuit, I will represent the radioactive atom by a qubit. It is prepared in a $\ket{+}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})$ state by a Hadamard gate, indicating a superposition of non-decayed ($\ket{0}$) and decayed ($\ket{1}$) states. I use a second qubit to represent the cat being living ($\ket{0}$) or dead ($\ket{1}$). To model the interaction of the cat and the atom, I will introduce a CNOT gate, controlled on the atom qubit and targeted on the cat qubit. Then the cat qubit’s state changes only if the atom qubit is in the decayed state ($\ket{1}$), representing the cat’s death. This assumes that the cat’s observation of the atom does not irreversibly collapse the system, but instead that it becomes entangled with the atom, resulting in a joint superposition state of $\ket{00}+\ket{11}$ (from this point forwards I will neglect the normalisation factor of the global state, for simplicity).

Treating the observer as a quantum system, they become entangled with the cat upon looking inside the box. I use a third qubit to denote the observer’s memory, with another CNOT gate copying the cat’s state to the observer’s memory. Hence, the atom, cat, and observer’s memory evolve into a large entangled superposition: $\ket{000}+\ket{111}$. The corresponding quantum circuit is depicted in Figure 2, created using Qiskit [11], which was used for all the circuit diagrams in this paper. The Qiskit code to create the circuit is:

Overall, the atom-cat-observer statevector evolves as follows:

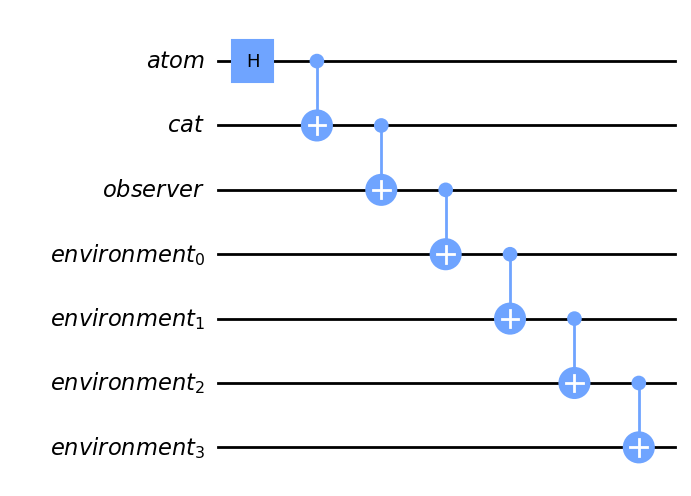
The joint state contains a term where the observer saw the cat alive, and a term where the observer saw the cat dead. Then, why does the observer perceive only a single outcome? This can be attributed to decoherence [13] – as the observer interacts with the rest of the environment, more and more of the environment joins in the entangled superposition. The environment can be modelled as an array of qubits, with a series of CNOT gates transmitting information from the observer to each environment qubit. After decoherence, the atom, cat, observer and environment are in a joint state $\ket{00...0}+\ket{11...1}$. The quantum circuit that includes decoherence from the environment is depicted in Figure 3.

Note that whether or not macroscopic superpositions can be realized remains an active topic of research amongst the quantum community, with recent experiments putting increasingly macroscopic systems into superposition (e.g. [14]). What the quantum circuit representation of Schrödinger’s cat helps to demonstrate is that there is no internal contradiction in the existence of macroscopic superpositions.

The Wigner’s friend thought experiment explores the nature of measurement in quantum mechanics [2]. In this scenario, Wigner’s friend observes a quantum system in a superposition, which I will represent as a qubit. The friend perceives a definite state, either $\ket{0}$ or $\ket{1}$, which suggests a projection of the qubit to a single state upon measurement.

However, Wigner begins isolated from his friend and the qubit, such that from Wigner’s perspective, his friend and the qubit just became entangled. This entanglement resulted in a joint superposition of his friend observing $\ket{0}$ and the qubit being $\ket{0}$, and the converse state. The setup is depicted in Figure 4.

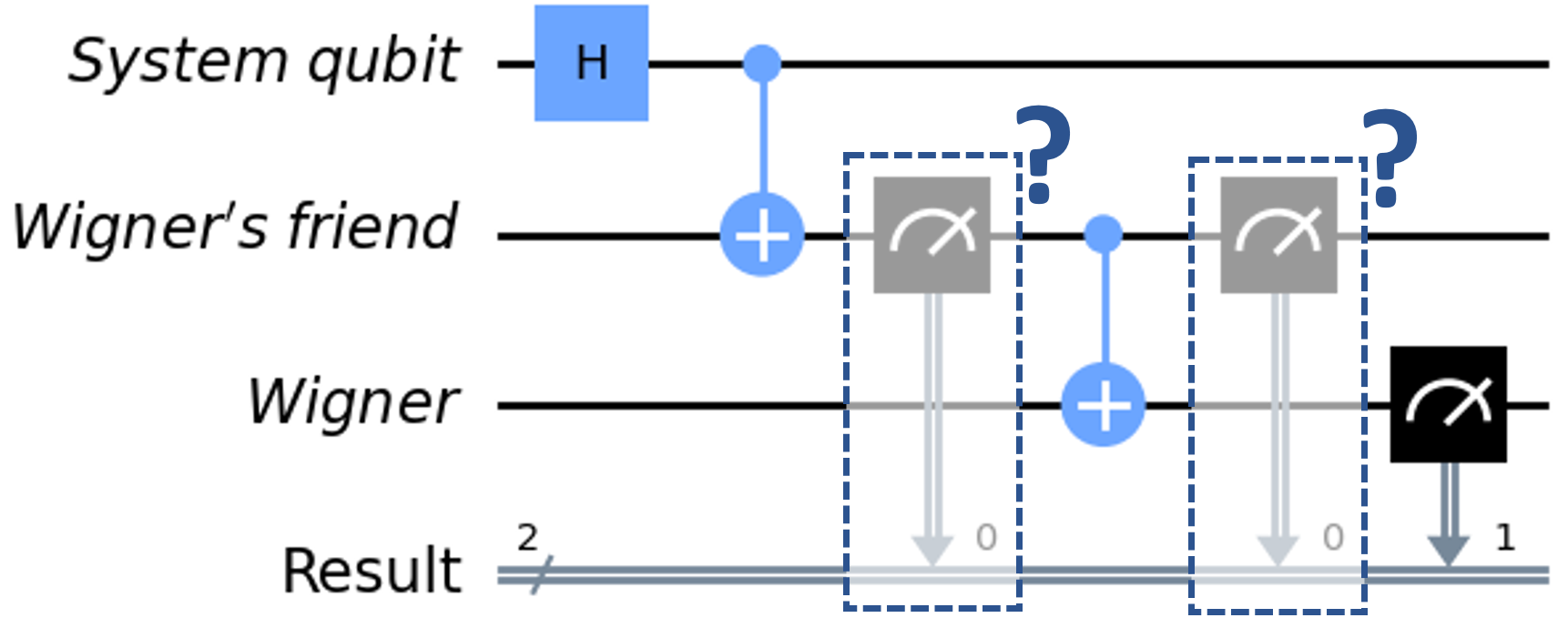
To visualize this in a quantum circuit, I will model the friend’s memory as a qubit. I first apply a Hadamard gate to the qubit that will be measured, preparing it in a superposition of $\ket{0}$ and $\ket{1}$. Then I represent the friend’s measurement of the qubit as a CNOT gate, which copies the qubit’s state to the friend’s memory, leading to a maximally entangled Bell state.

When Wigner asks his friend for the measurement result, his friend communicates either 0 or 1. According to Wigner, this instant triggers the projection of the qubit and friend into a single state. This step is illustrated by another CNOT gate, this time between the friend’s memory and Wigner’s memory. The resulting quantum circuit is demonstrated in Figure 5, with only the measurement in the dashed box on the right included.

The crucial question then is, when did the actual projection occur? Here there is a paradox, if observation induces an irreversible collapse. In that case, the friend insists the collapse happened when the qubit was measured, whereas Wigner insists it happened when he learnt the qubit’s state from his friend. Specifically, Wigner’s friend would say the true quantum circuit includes the measurement before the final CNOT in Figure 5. This discrepancy is known as the measurement problem.

The prevalent “Copenhagen interpretation” suggests that a quantum system collapses into a single state upon observation. Since this explanation lacks a clear mechanism describing the measurement process, it fails to resolve the Wigner’s friend paradox. This makes the Copenhagen interpretation self-contradictory, unless it is augmented with a modified explanation for measurement.

A plausible resolution to the paradox is treating all observers, including Wigner and his friend, as quantum systems, taking seriously the depiction of their memory states as qubits in our quantum circuit. This perspective reveals that both observers encountering a distinct measurement outcome is self-consistent, since they each join an entangled superposition upon interacting with the system or each other. Therefore, considering Wigner and his friend as quantum systems resolves the paradox.

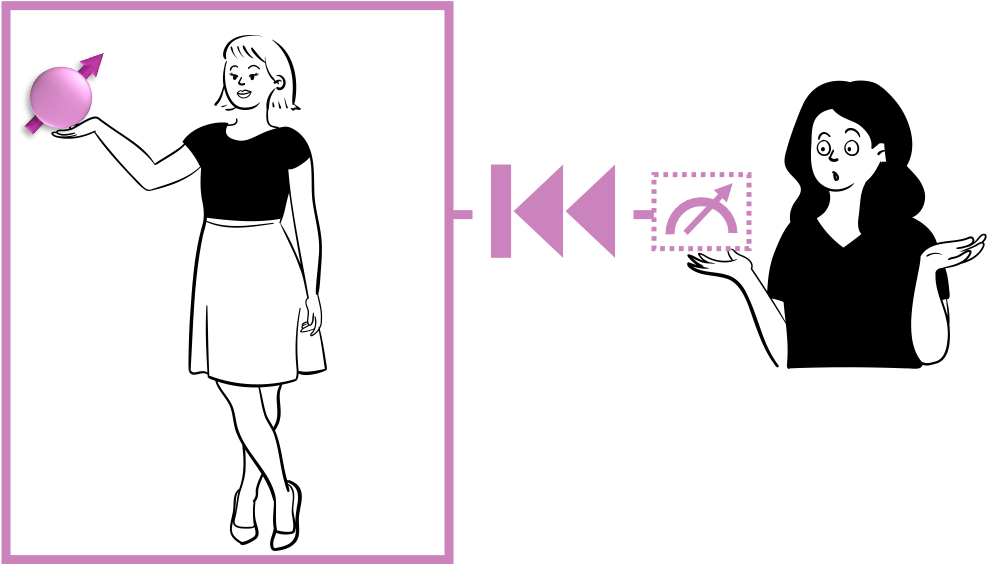
In 1985, David Deutsch devised a thought experiment to test whether quantum measurements are reversible, thereby avoiding collapse, or irreversible, inducing collapse [3]. Motivated as a test for the many-worlds theory of quantum mechanics against the Copenhagen interpretation, the thought experiment also included the first description of a quantum-coherent universal quantum computer.

The thought experiment involves simulating an observer measuring a quantum system in superposition, then attempting to reverse the measurement to ascertain if the quantum system reverts to its initial superposition (depicted in Figure 6). Modelling the system as a qubit: if the observation caused an irreversible collapse to either $\ket{0}$ or $\ket{1}$, the measurement cannot be reversed. Conversely, if the observation is a quantum interaction resulting in entanglement, the measurement can be reversed, and the qubit returns to the original superposition of $\ket{0}$ and $\ket{1}$.

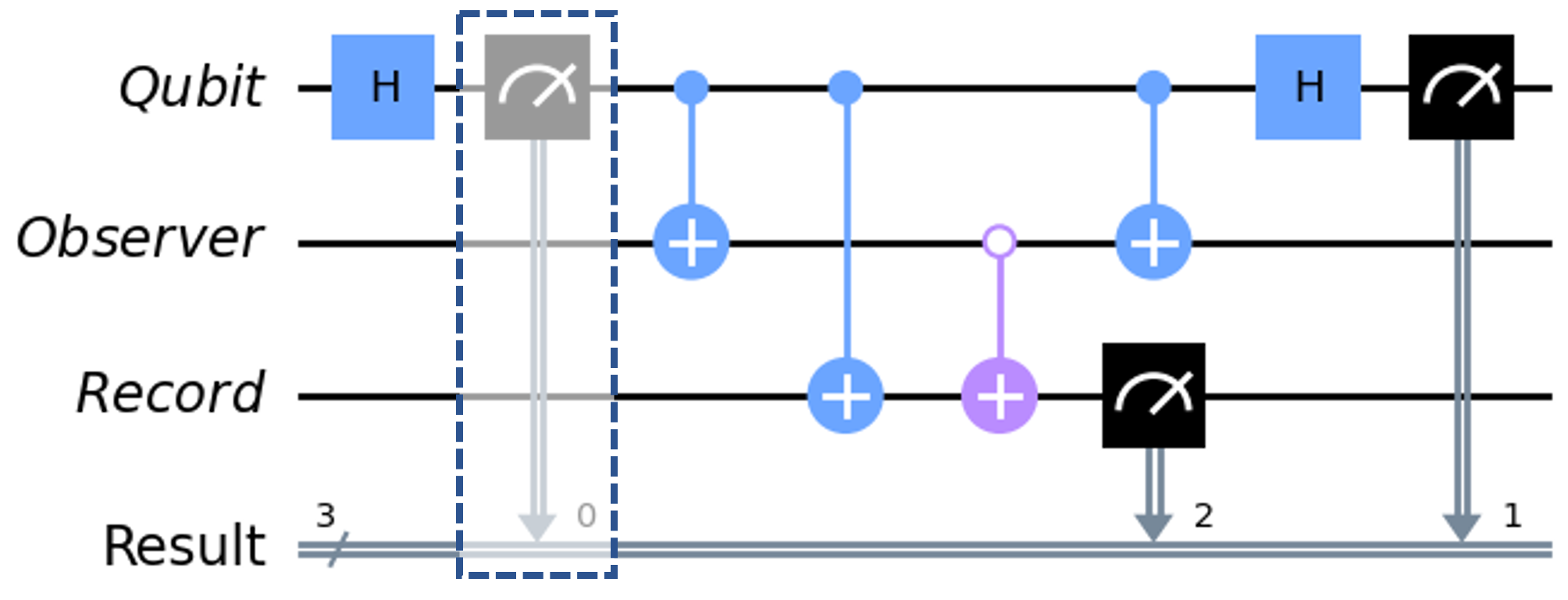
My quantum circuit representation of this thought experiment uses three qubits: one is the quantum system to be measured, beginning in the $\ket{+}$ state; the second represents the observer’s memory; and a third provides a permanent record of the fact the observer made the measurement. I apply a Hadamard gate to the first qubit to prepare it in the $\ket{+}$ state, before it is measured by the observer.

For the no-collapse scenario, the observer, considered a quantum system, becomes entangled with the qubit upon measurement. This interaction is modeled by a CNOT gate, which copies the qubit’s state onto the observer’s memory.

Next is arguably the ingenious part of this thought experiment. A “record” qubit is introduced to maintain evidence that the observer indeed made a measurement, but crucially, this can be done without revealing the observer’s measurement outcome. This is what will enable us to later reverse the observer’s measurement, while maintaining our record of the measurement taking place. (If the record qubit stored any information about the observer’s measurement outcome, then the measurement would be impossible to reverse by manipulating the observer and their qubit alone - they will have decohered due to their environment having a record of the result.)

To store this record of the fact a measurement took place, without revealing the actual information, we can implement a parity check between the system qubit and observer, targeted on the record qubit. This checks whether the measurement was done successfully by indicating whether or not the system qubit and observer are in the same state. It can be implemented using a CNOT gate and anti-CNOT gate: if the states of the observer and qubit are correlated, then the measurement was done successfully, and the Record qubit flips to $\ket{1}$; if not, it remains at $\ket{0}$.

Now to reverse the observer’s measurement, we need to reverse the entanglement of the observer and the qubit. This process would require extraordinary coherent control over a living system. A more feasible but still demanding approach would be to simulate an observer on a computer, under quantum coherent control. This was the insight that led to Deutsch’s description of this many-worlds vs Copenhagen thought experiment becoming the first proposal for a quantum-coherent universal quantum computer.

To reverse the entanglement of the observer and qubit in the quantum circuit, I apply a CNOT gate between the system qubit and observer. Then a final Hadamard gate on the qubit transforms its state deterministically to 0.

If successful, the circuit simulation should yield a deterministic outcome of 0 for the qubit and 1 for the Record, indicating that a measurement did indeed take place, yet the measurement was reversed, requiring a no-collapse explanation. The overall quantum circuit is depicted in Figure 7, when the mid-circuit measurement in the dashed box is not included.

To represent collapse, an irreversible mid-circuit measurement is introduced before the measurement CNOT gate, causing the qubit to collapse into a single state and lose its coherence. In this case, the final gates cannot reverse the measurement and return the qubit to the $\ket{0}$ state. The final CNOT still erases the observer’s memory of their observed outcome, but the system qubit remains in a fixed state of $\ket{0}$ or $\ket{1}$, not a superposition. Hence, the final Hadamard gate places the qubit in a superposition state of $\ket{+}$ or $\ket{-}$, resulting in a 50-50 chance of measuring $\ket{0}$ or $\ket{1}$ over multiple runs. This scenario’s quantum circuit is displayed in Figure 7 with the inclusion of the mid-circuit measurement in the dashed box.

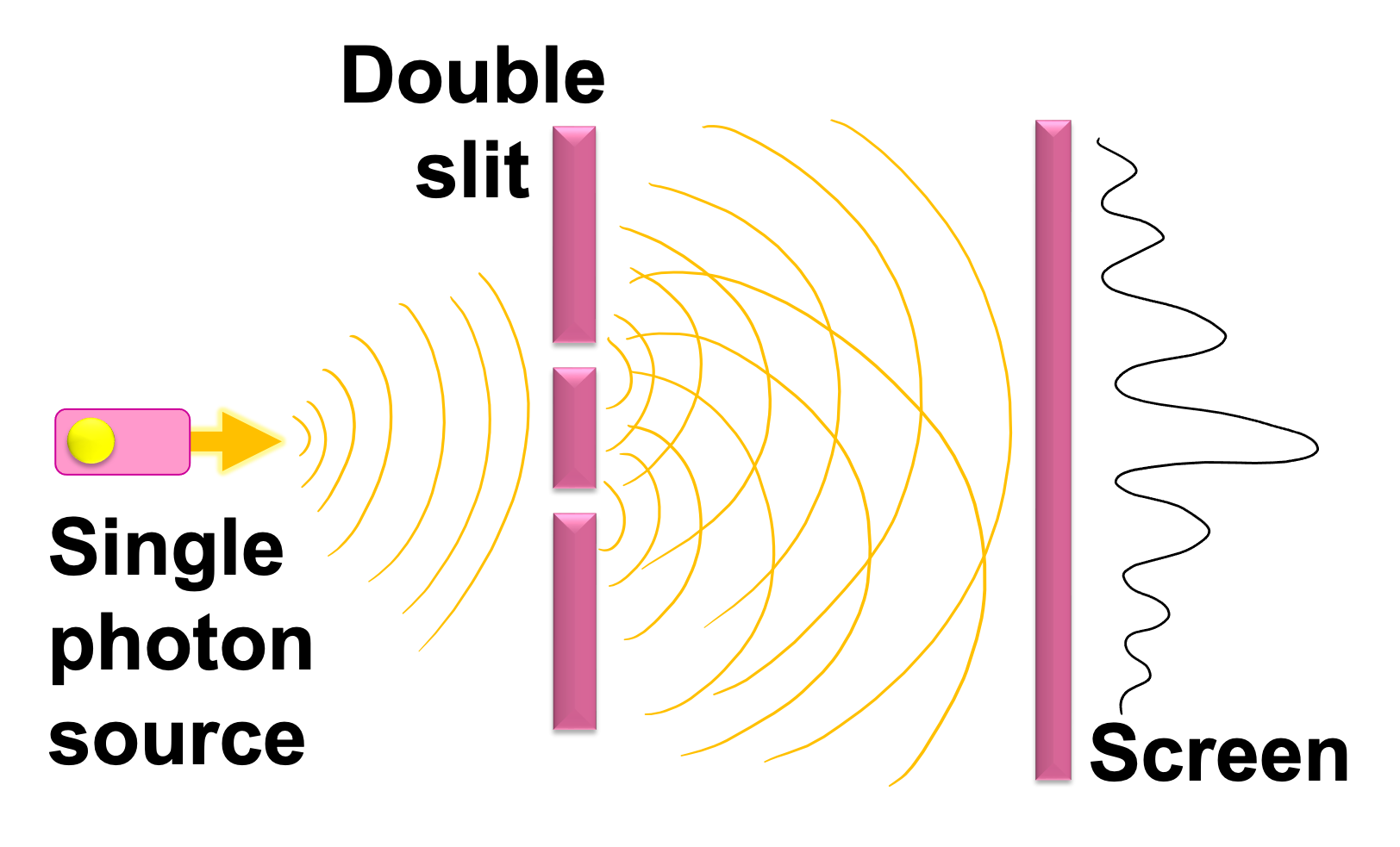
The double-slit thought experiment is the standard example of so-called wave-particle duality in quantum physics [4]. Here, single quantum systems, such as individual photons or electrons, demonstrate wave-like interference. However, the interference effect disappears if we observe the particle’s path. This property is often used as the first illustration of the peculiarities of quantum mechanics; in the UK, wave-particle duality forms part of some secondary school physics syllabuses.

The conventional explanation presents this thought experiment as somewhat inexplicable: somehow quantum systems can behave both as particles and waves, making them exotic and perhaps even indescribable. By extracting the key features of the double slit thought experiment and translating it to quantum circuits, I will provide an intuitive and non-contradictory explanation for the wave- and particle-like behaviour of quantum systems, including the subtle effect of observation.

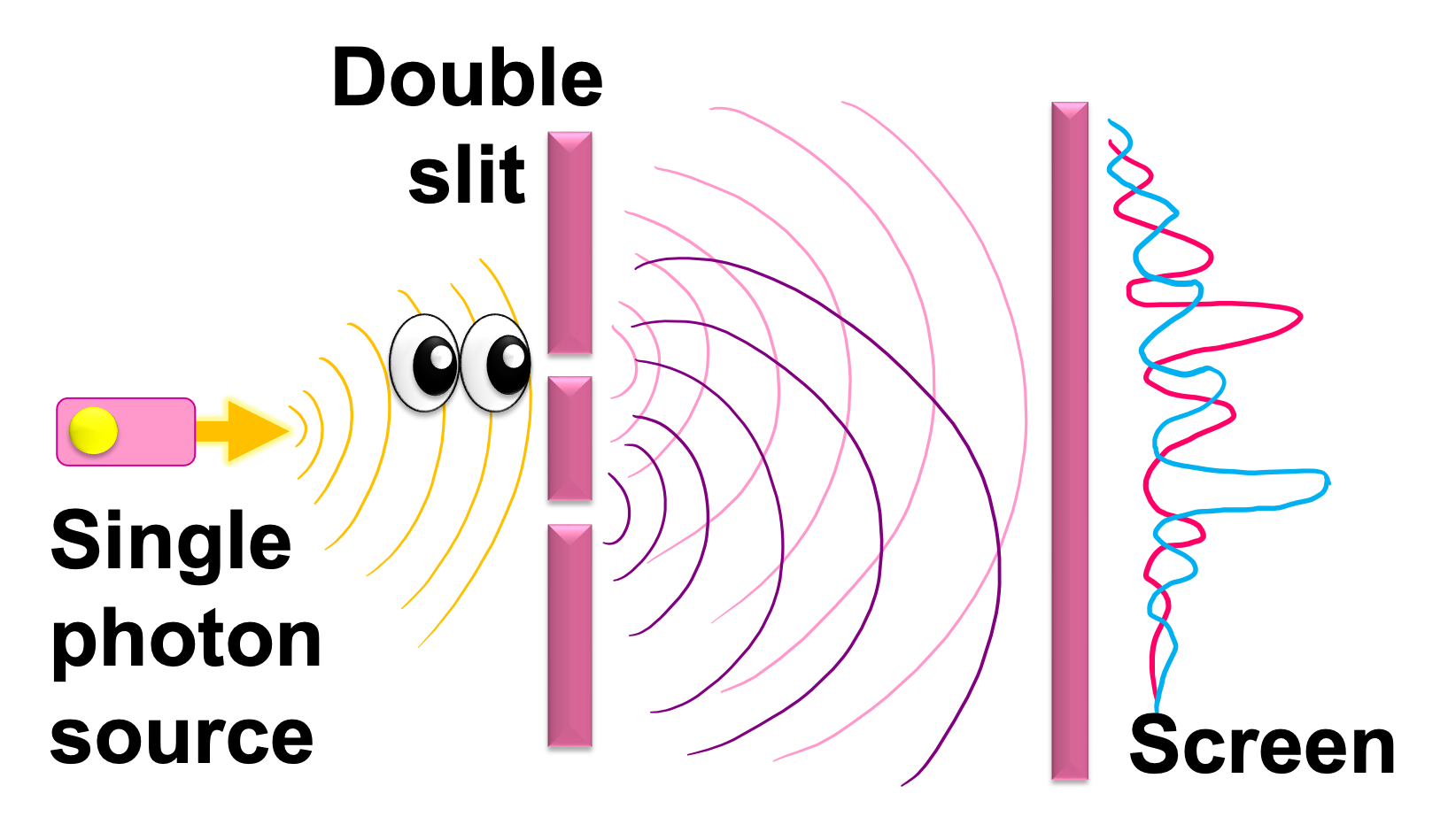
The typical setup of a double-slit thought experiment involves directing individual photons towards a barrier with two slits. Beyond the barrier, there is a screen detecting the photons. If the photons behaved like classical particles, we would expect two bright bands on the screen, one corresponding to each slit. However, the actual result is an interference pattern of light and dark bands, like for a wave passing through the two slits, depicted in Figure 8.

This interference pattern implies that each photon is somehow passing through both slits simultaneously and interfering with itself. If we add a detector at the slits to determine which slit the photon took, the interference pattern disappears, leaving only two bright regions corresponding to each slit, demonstrating the particle-like behavior of photons.

To visualize this better, we can use the Mach-Zehnder interferometer, an analogous experiment with a simple quantum circuit representation. This setup splits a single photon into a superposition of two paths, mirrored in a quantum circuit by a qubit, where the state $\ket{0}$ corresponds to the bottom path, and the state $\ket{1}$ corresponds to the top path. The beam-splitter creating this superposition is represented by a Hadamard gate.

Case 1: Without a detector

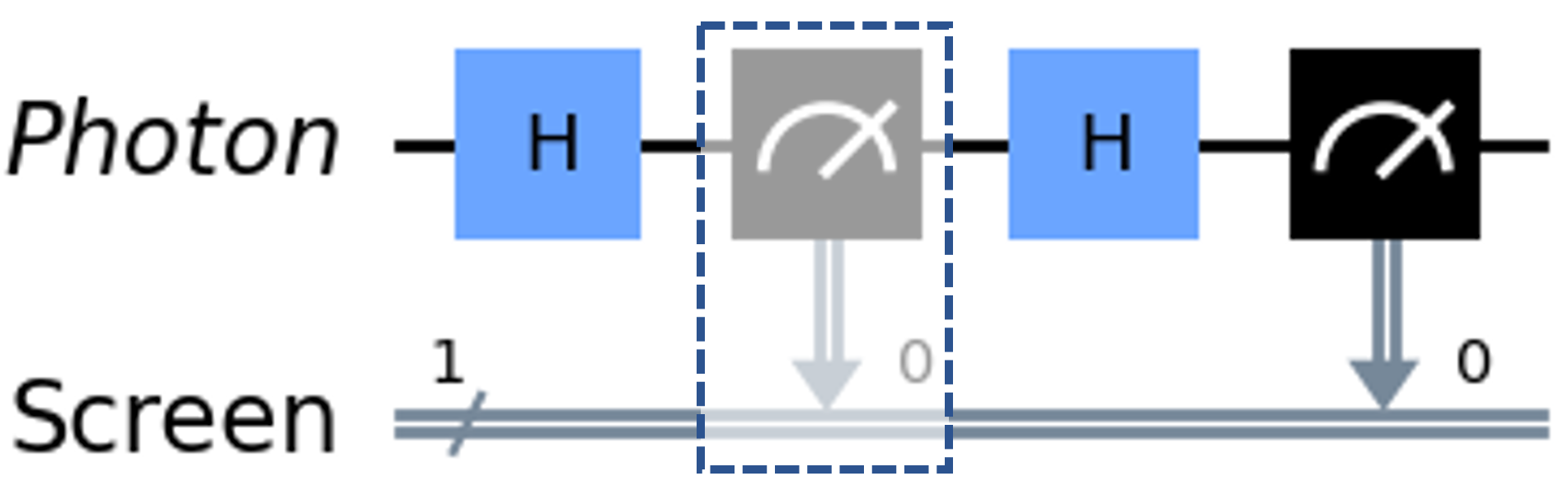
The photon encounters another beam-splitter after following both paths, where it constructively interferes with itself, merging the two parts of the superposition back into a single transmitted photon. In the quantum circuit representation, the second beam-splitter is another Hadamard gate, taking the qubit from the $\ket{+}$ state to the state $\ket{0}$. This interference can be observed by a measurement on the photon qubit, which always returns $\ket{0}$ (corresponding to a transmitted photon detected after the second beam-splitter). The quantum circuit for this wave-like behaviour is shown in Figure 9, when the measurement in the dashed box is omitted.

Case 2: With a path detector

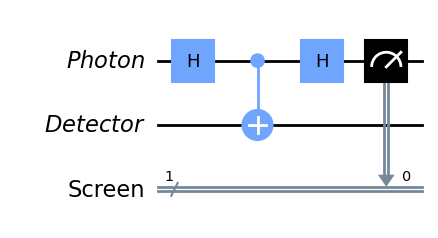
If we add a detector in one of the photon’s paths, it projects the photon into a definite path, preventing it from interfering with itself. At the second beam-splitter, the photon then splits into an equal superposition, with each detector having a 50$\%$ chance of activation. This is modeled in the quantum circuit by adding a measurement operation after the first Hadamard gate, yielding a 50/50 chance of ending in the state $\ket{0}$ or $\ket{1}$. The quantum circuit for this particle-like behaviour is shown in Figure 9, when the measurement in the dashed box is included.

Case 3: Using a detector qubit

One way to demystify the detector’s impact on the photon’s behavior is by modeling the detector as a quantum system. In the quantum circuit, we represent the detector as another qubit, and the detection process as a CNOT gate between the photon and detector. This entangles the photon qubit with the detector qubit. Consequently, the photon cannot interfere with itself anymore. The quantum circuit for the experiment with a detector qubit is depicted in Figure 10, reconciling the wave-like and particle-like quantum circuits by demonstrating that the key difference is the introduction of the CNOT gate from the photon qubit to another system.

Even without “classically” observing the detector qubit’s state, just entangling it with the photon is sufficient to disrupt the interference. This demonstrates that any interaction which copies the photon’s path information into the environment is enough to alter its behavior. This is the mechanism behind decoherence - it arises due to unwanted interactions between quantum systems. There is no need for any notion of a classical or irreversible measurement to explain decoherence.

To summarize, the double-slit experiment is the standard example of how quantum systems display both wave-like and particle-like behaviors, depending on whether their path information is accessible. Understanding how the particle-like behaviour can arise from entanglement with a single detector qubit unifies these two behaviours of quantum systems, and demonstrates the mechanism behind decoherence.

The delayed-choice quantum-eraser experiment is a sophisticated adaptation of Wheeler’s delayed-choice experiment, which itself extends the classic double-slit experiment [5, 6]. It seems to hint that present-time measurements of a quantum system could retroactively determine its past behavior – specifically, whether it acted as a wave or a particle.

Consider the setup of the double-slit thought experiment. As in the previous section, instead of employing a classical detector to discern the slit a photon passed through, we use a small, controlled quantum system, or a “detector qubit”, that interacts with the photon at the slits.

The key insight for this thought experiment is that the detector qubit can be measured in a way that reveals which slit the photon went through, or it can be measured such that this information is lost (i.e. erased). This measurement choice can be made at any time after the detection of the photon on the screen, even years later.

The key question is then, what kind of pattern should we anticipate on the screen of the double-slit experiment? I explained using the double-slit experiment quantum circuit, that mere interaction of the detector qubit with the photon prevents the typical interference pattern from emerging. This makes intuitive sense, since when which-path information can be extracted, interference should not be possible, even if we do not yet copy this information into our macroscopic measurement instruments.

The more subtle part arises when the detector qubit is measured in a way that erases the information about the photon’s path. Using the results of this measurement, it is possible to discern an interference pattern from the screen data. Suppose our detector qubit yields two outcomes, $\ket{0}$ or $\ket{1}$. If we separate the photon impacts on the screen corresponding to a $\ket{0}$ from those corresponding to a $\ket{1}$, interference patterns emerge in the two distinct sets of patterns on the screen.

Therefore, if we choose to measure our detector in a way that erases the photon’s path information, we can extract interference patterns. Naively, this seems to suggest that individual photons interfered with themselves and passed through both slits, leading to a perplexing paradox. It appears as if we can retroactively dictate the photon’s behavior (whether it behaved as a particle through one slit, or as a wave through both slits) by choosing how to measure our detector qubit after the photons hit the screen. This implies a bizarre ability to influence a photon’s past based on current actions.

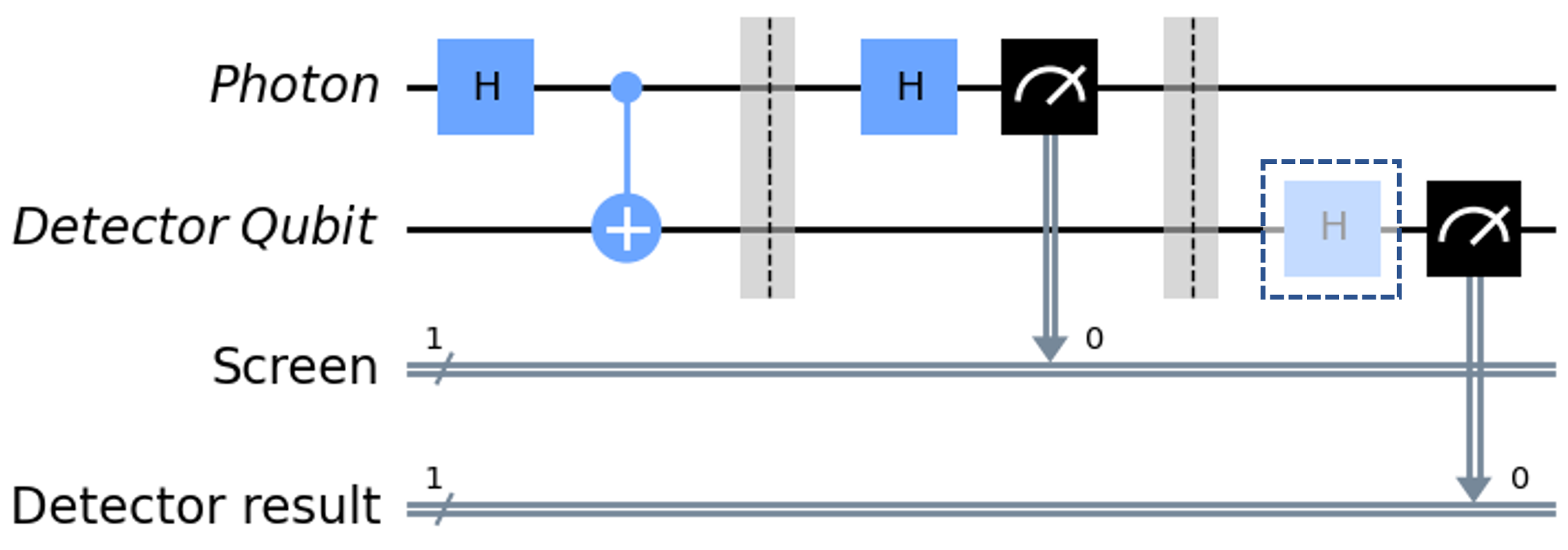
To resolve this paradox, we can again represent it as a quantum circuit, as a variation of the final quantum circuit in the double-slit discussion in Figure 10. We have two options: the first is to apply a standard Z-measurement to the detector qubit, resulting in a random mix of outcomes revealing which path the photon took, shown in Figure 12 when omitting the Hadamard in the dashed box. The second is to make an X-measurement (by applying a Hadamard gate and then a Z-measurement), which retrieves no path information, shown in Figure 12 with the Hadamard in the dashed box included.

Let’s see how to extract the apparent interference pattern from the X-measurement results to resolve the paradox. We find that the X-measurement outcomes on the detector qubit are exactly correlated with the measurement outcomes of the photon. We can see from the quantum circuit that this is exactly as expected: we prepared a Bell state between the photon qubit and detector qubit, making them maximally entangled, then measured them both in the X basis, hence their outcomes will be precisely correlated.

In terms of the Mach-Zehnder interferometer, this means that one set of qubit detector outcomes is always correlated with one of the final photon detector outcomes - i.e. each individual run of one set of the qubit detector outcomes gives the same behaviour at the interferometer as single-photon intereference does, namely a consistent detection at just one of the detectors after the second beam-splitter. Translating this back to the double-slit context: when we isolate one set of detector outcomes and look at the screen outcomes correlated with those, we see the same behaviour as the single-photon interference setup, with bright and dark fringes. With our quantum circuit representation, we can see that this behaviour is in fact a signature of quantum entanglement between the photon and detector qubit, and it does not come from the photon interfering with itself. This insight resolves the apparent paradox: the interference pattern we are able to extract with the pathway-erasing measurements on the detector is not a signature of single-photon interference, but a signature of entanglement.

In summary: the photon’s behavior does not change based on how we measure the detector qubit. The detector qubit causes decoherence and destroys the single-photon interference pattern. Measuring the detector qubit in the X basis does not alter the photon’s past behavior, but demonstrates the entanglement between the detector and photon qubits. Extracting the photon outcomes correlated with one set of detector outcomes gives the illusion of retroactively extracting a single-photon interference pattern.

Imagine you are given a box and you cannot see what is inside. All you know is that it is either empty – or it contains a highly sensitive bomb. If this bomb is hit by even a single photon, it will explode. Your challenge is to work out whether or not there is a bomb in the box, without exploding it.

Classically, there is no way to check if there is a bomb in the box without exploding it. As soon as we open the box to take a look, if the bomb is there it will be hit by a particle and explode.

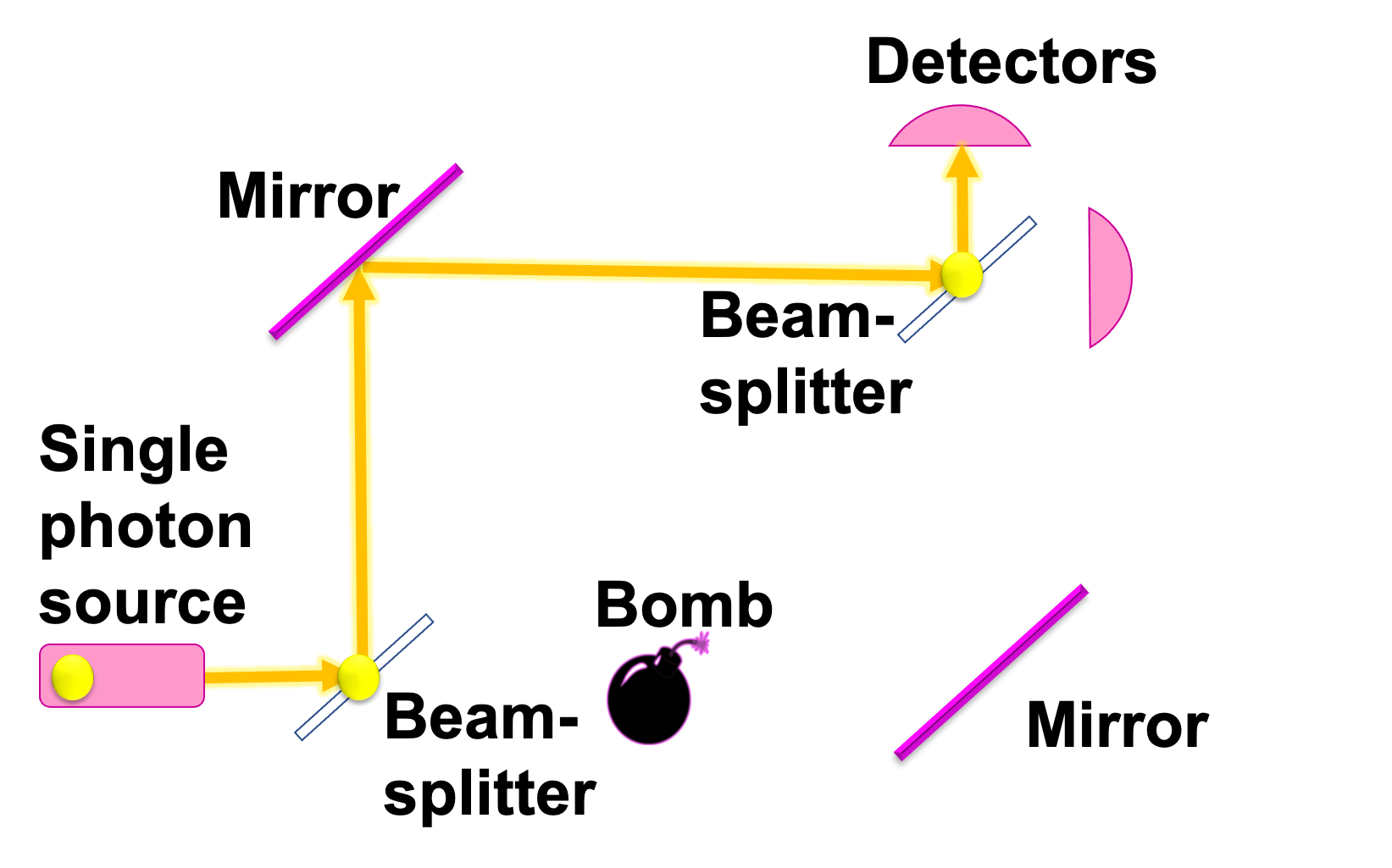
Avshalom Elitzur and Lev Vaidman came up with a “quantum bomb tester”, which uses the quantum properties of photons to work out if a bomb is there without exploding it [12]. They suggested putting the box into one path of the Mach-Zehnder interferometer, let’s say it is the bottom path. If there is no bomb, then after passing through the empty box, the photon will then interfere with the top path and end up going straight through the second beam-splitter, as with the standard Mach-Zehnder interferometer setup. But if the bomb is there, the photon will be projected from the superposition to either the top or bottom path. If it is projected into the path with the bomb, then the bomb will explode. But if it is projected into the top path, it will then reach the second beam-splitter, and split into a superposition of being reflected and going straight through. So if we place detectors around the second beam-splitter, and detect the photon was reflected, we know for sure that the bomb is there, without setting it off! Now in this setup, there is only a 25$\%$ chance that we detect the bomb is there without setting it off. But other bomb testers were later proposed that allow us to detect the bomb with 100$\%$ probability [15].

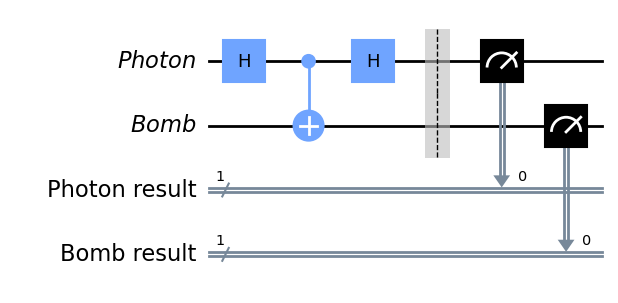
To translate this setup to a quantum circuit, I use a qubit to represent the photon and a qubit to represent the bomb. As before, each beam-splitter is a Hadamard gate.

After the first beam-splitter we may or many not have a bomb present, which effectively measures which path the photon has taken, causing the projection of the photon into one of the two paths. I will represent this bomb by a CNOT gate between the photon qubit and bomb qubit. If the CNOT gate is present (i.e. the bomb is in the path of the photon), then: If the photon qubit is in the 0 state, nothing happens to the bomb qubit (it stays ”unexploded” in the $\ket{0}$ state). If the photon qubit is in the 1 state, then the bomb qubit is flipped to a $\ket{1}$, the exploded state.

Finally we pass the photon through another beam-splitter, which is another Hadamard gate on the photon qubit. Then we measure the photon’s state: if it is a $\ket{0}$, then the CNOT may or may not have been there, so we do not know whether there was a bomb. If it is a $\ket{1}$, then we know for sure that the CNOT was there, so there was a bomb. We also need to measure our bomb qubit to check if it has exploded or not exploded (given by a $\ket{1}$ or a $\ket{0}$ respectively). If we manage to get the photon being a $\ket{1}$ and the bomb a $\ket{0}$ then we have success – we have measured the bomb was there without exploding it. The full quantum circuit is shown in Figure 14.

1. 1.

   Setting the Stage: Begin by explaining the quantum bomb tester problem. Emphasize the impossibility of detecting the bomb classically without it exploding, whereas quantum mechanics provides a resolution.

2. 2.

   Introduction to Mach-Zehnder Interferometer: Explain the operation of the Mach-Zehnder interferometer without the presence of a bomb. Discuss how a beam-splitter induces a superposition of two paths for a photon and how the photon paths interfere constructively at the second beam-splitter to produce a single photon.

3. 3.

   The Effect of a Bomb: Discuss the alteration in the interferometer’s operation when a bomb is placed in one of its paths. Highlight the projection of the photon into either the path containing the bomb (resulting in detonation) or the path without the bomb. Explain how the different outcomes at the second beam-splitter, due to the absence of interference, can be used to successfully detect the bomb without exploding it!

4. 4.

   Mapping to Quantum Circuits: Translate the interferometer setup to the setting of quantum bits (qubits) and quantum gates. Introduce the notion of qubits, the Hadamard gate, and the CNOT gate. Explain how the photon and bomb can be modeled as qubits and the interaction between them can be represented with quantum gates.

5. 5.

   Running the Quantum Circuit: Guide the participants to code the quantum circuits themselves and run them on a quantum simulator. Discuss the different outcomes for scenarios with and without the bomb.

6. 6.

   Interactive Game - Quantum Minesweeper: Engage participants in a game of ”Quantum Minesweeper” based on the more effective bomb tester. This could involve participants competing to get the highest score, by having the best success rate at determining the presence of a bomb without detonating it.

7. 7.

   The Philosophy and the Technology: Depending on the interests of the participants, you can discuss the philosophical implications of the quantum bomb tester (e.g. how Vaidman proposed it as evidence for the many-worlds theory of quantum mechanics) and the technological applications (e.g. interaction-free measurement being applied to imaging delicate objects, and counterfactual quantum communication and quantum computing protocols).

8. 8.

   Extension - 100% Effective Bomb Tester: For participants with more experience, extend the workshop to explain the 100% effective bomb tester. This forms the mechanism behind the Quantum Minesweeper game. The concept can first be explained using interferometers, and then participants can either be shown how to code it or be challenged to find a way to code it themselves.