A Physiological-Model-Based Neural Network Framework for Blood Pressure Estimation from Photoplethysmography Signals
Abstract
Continuous blood pressure (BP) estimation via photoplethysmography (PPG) remains a significant challenge, particularly in providing comprehensive cardiovascular insights for hypertensive complications. This study presents a novel physiological model-based neural network (PMB-NN) framework for BP estimation from PPG signals, incorporating the identification of total peripheral resistance (TPR) and arterial compliance (AC) to enhance physiological interpretability. Preliminary experimental results, obtained from a single healthy participant under varying activity intensities, demonstrated promising accuracy, with a median root mean square error of 6.69 mmHg for systolic BP and 3.26 mmHg for diastolic BP. The median (min, max) difference between estimated and measured TPR was 0.043 (0.024, 0.061) mmHg·s/cm³. As expected, estimated TPR decreased with increasing activity intensity, while AC increased within a physiologically plausible range (0.5–2.5 cm³/mmHg).
I Introduction
Hypertension affects over 1.28 billion adults globally, yet only 21% received adequate control. Effective and continuous blood pressure (BP) monitoring and management in daily life activities are crucial for high-risk populations with hypertension-related complications. Traditional cuff-based BP measurements were intermittent and unsuitable for continuous, real-time monitoring due to the discomfort caused by repeated cuff inflation and deflation. Recently, photoplethysmography (PPG) sensors had emerged as a non-invasive and continuous alternative tool for measuring microvascular blood volume changes, presenting promising potential for BP estimation in daily life scenarios.
Based on PPG signals, the pulse wave velocity (PWV)-based method gained prominence and popularity for BP estimation [1]. Although PWV has proven to be a reliable method for BP estimation, it requires two sensors placed at different locations, limiting its applicability in mobile health settings. To address this limitation, single PPG-sensor-based methods emerged, reducing hardware complexity and enhancing usability. These PPG-based methods include parametric models, which applies predefined physiological modeling equations and specific features (e.g., heart rate, systolic/diastolic intervals), and non-parametric models, which relies solely on features derived from PPG signals [2]. While parametric models provide insights into physiology, they often required high-quality PPG signals and individual calibration for personalized estimations. This was impractical in dynamic daily life conditions [2][3]. Non-parametric models, such as neural networks [4][5] and regression models [6][7][8], provide higher accuracy in real-life environments, though they are still affected by signal degradation from motion and lighting variations. The parametric model provide physiological insights, while the non-parametric model offer high accuracy, making them complementary for BP estimation. This combination enable more reliable and accurate BP estimation across diverse real-world conditions, particularly in aging populations with complex hypertension profiles.
Hypertension is a key risk factor for coronary artery disease (CAD) due to its role in accelerating atherosclerosis. Increased total peripheral resistance (TPR) and reduced arterial compliance (AC), both associated with vessel stiffening, elevate cardiovascular stress and pulse pressure, particularly in elderly hypertensive patients [9]. While invasive catheterization had been the gold standard for assessing AC and TPR, non-invasive options, such as oscillometry combined with impedance cardiography [10], provide a feasible clinical alternative, though they are impractical for daily monitoring. Estimating TPR and AC concurrently with BP during daily life could have enhanced cardiovascular risk assessment and offered insights into therapeutic efficacy, paving the way for personalized hypertension management. In this study, we proposed a novel physiological model-based neural network (PMB-NN) to estimate BP from finger PPG, while simultaneously identifying TPR and AC across different activity intensities, and its performance was evaluated.
II Methods
II-A Data collection
A flow diagram of the procedure, starting from data collection, is shown in Figure 1. The study was approved by the Ethics Committee Computer and Information Science (EC-CIS) of the University of Twente (No. 240831) and conducted in Roessingh Research and Development (RRD). 10 healthy participants aged between 20 and 29 were enrolled in the study. Informed consent was received from all the participants and the study was performed in accordance with the declaration of Helsinki.
Participants were asked to perform three exercise activities in 35 minutes. They started with sitting 5 minutes on a chair and standing 5 minutes. Then they were asked to cycle on an Bremshey® exercise bike at a fixed speed of 45 rpm, power of 50(10) watts for 10 minutes. After 1 minute’s resting, they started cycling again on the same bike at a fixed speed of 45 rpm, power of 100(10) watts for 10 minutes. Exercise intensities were set to assure patients trained within the aerobic threshold, and 10 minutes period length was chosen to guarantee the blood pressure, total peripheral resistance, and arterial compliance reached a steady-state, free from transient fluctuations at the start of exercise. During the whole study, subjects kept their left hand in a sling to prevent hydrostatic pressure artifacts. PPG signal was collected on the left index finger (Shimmer 3 GSR+ Unit, Shimmer Wearable Sensory Technology) and BP was measured continuously using volume-clamp PPG on the left middle finger (Finometer® Model-2, Finapres Medical Systems, Enschede, the Netherlands). During the whole study, the left hand was placed in a sling suspended around the neck where the left hand’s index and middle fingers were kept at heart level to prevent hydrostatic pressure artifacts for blood pressure and PPG’s reliable measurement. Each participant has conducted the whole experiment twice on different days.
II-B Data Preprocessing
Beat-to-beat systolic and diastolic blood pressure (SBP, DBP) signals, cardiac output (CO)(in mL/min) and total peripheral resistance (TPR)(mmHg·s/cm³) were exported from BeatScope® Easy software with Modelflow algorithm embeded, along with the estimated stroke volume (SV) on the beat to beat arterial waveform analysis. A second order Savitzky-Golay filter with the window size of 5 cycles was applied to smoothen the irregular turbulence of the above variables (SBP, DBP, CO, TPR).
The finger PPG signal from Shimmer GSR+ unit was exported from Consensys® software with a sampling rate of 64Hz. The preprocessing pipeline for PPG signals consisted of four key steps to enhance data quality and minimize artifacts. First, baseline drift was removed using a linear detrending method, ensuring the signal remained centered around its baseline. Second, motion artifacts were mitigated through the application of a median filter with a window size of 0.5 seconds, to reduce transient spikes caused by sudden movements. Third, a fourth-order Butterworth bandpass filter with cutoff frequencies of 0.5 Hz and 5.0 Hz was applied to isolate the physiological frequency range of PPG signals while suppressing noise outside this range. The cutoff frequencies were selected based on the Nyquist frequency, computed based on the sampling rate. Lastly, the denoised signal underwent a moving average filter with a 0.1-second window to further smoothen residual noise.
II-C PMB-NN Inputs and Outputs
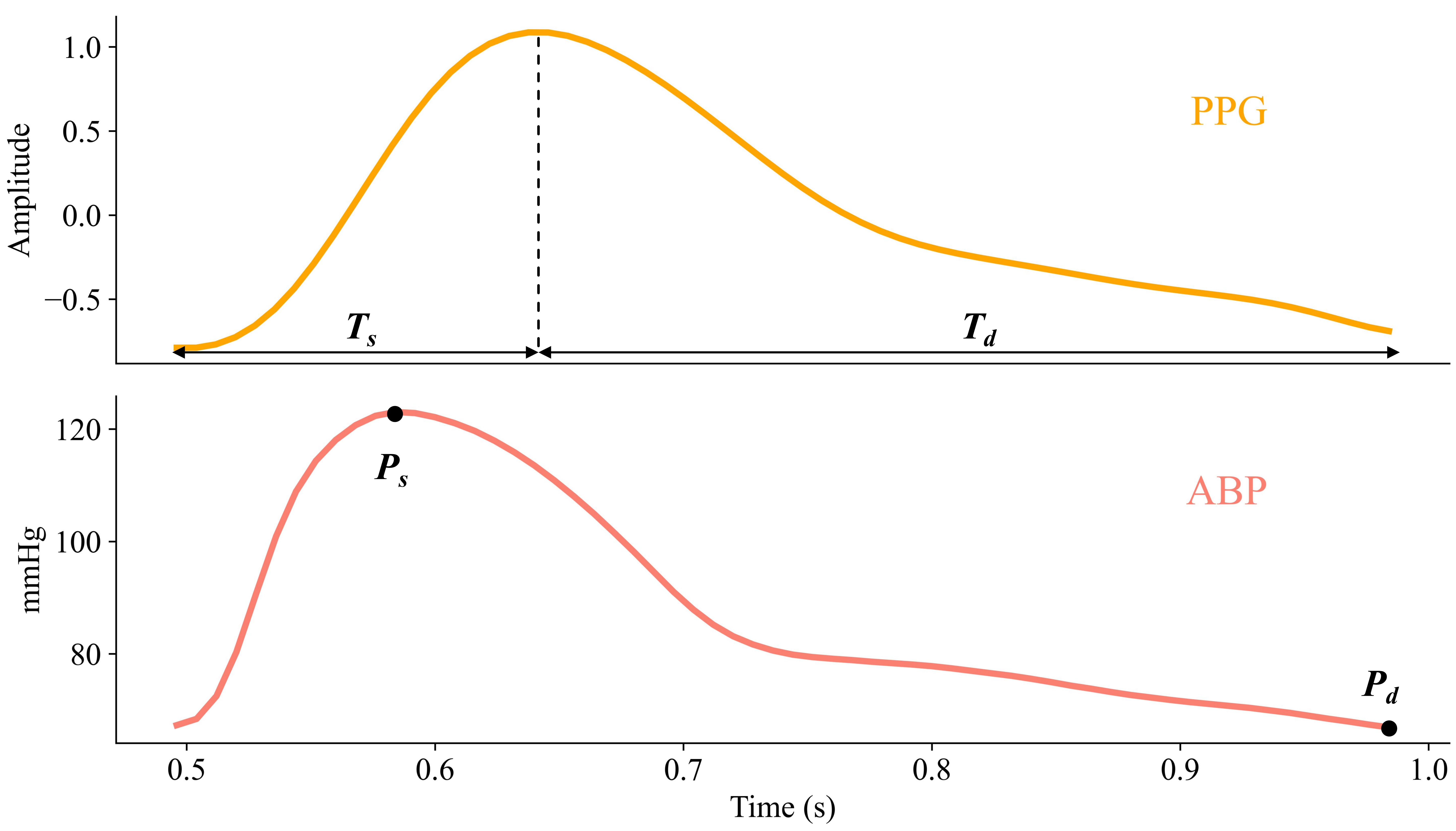
The systolic upstroke time () and diastolic time () from PPG were set as model inputs, while systolic pressure () and diastolic pressure () were set as outputs. Figure 2 illustrated these variables in one cycle’s PPG and BP signal. For signal synchronization, both BP and PPG preprocessed signals were aligned according to the time stamps of each activity and each device’s system time. Since PPG and BP were collected at the middle knuckle of index and middle finger on left hand, respectively, the physiological blood-flow time difference measured by the two signals was assumed as negligible.
II-D Physiological Model
The physiological model was defined by a set of validated equations (Eq.1 and Eq.2) [11] based on the two-element Windkessel model proposed by Otto Frank [12], that describes the mechanical properties of the arterial vessels in terms of total peripheral resistance and arterial compliance.
| (1) |
| (2) |
where the units for and are in seconds and for and are in mmHg. and are the initial values of and , respectively. Every cardiac cycle is assumed to start with a systolic period, and is set to an initial value as the condition of first cardiac cycle. and , in all the following text, refer to TPR and AC in units of mmHg·s/cm³ and cm³/mmHg, respectively. The blood flows from the ventricle to the aorta was assumed as a sine wave where is the peak amplitude, calculated as Eq.3.
| (3) |
where is cardiac output (in mL/min) and (= + ) is the duration of one heart cycle.
II-E Physiological Model-based Neural Network Structure
Figure 3 reveals the structure of our PMB-NN model. It consists of two parts, neural network and composed loss. We constructed a fully connected neural network (FCNN) with single input T and single output P, and 1 input layer, 3 hidden layers, and1 output layer (1-128-128-128-1) with ReLU activation functions mapping the input (which comprises and ) to the output . The input vector is merged of the two feature arrays ( and ) alternatively and the target vector is merged in the same way, either.
The composed loss, consists of one data fitting term and two physiological constraint terms derived from Eq.1 and Eq.2, was used to optimize the hyperparameters (weights and biases) in the FCNN training. The data fitting term, is calculated as a loss function in Eq.4.
| (4) |
where is the length of . and are the FCNN output and ground truth of blood pressure, respectively. The physiological constraint terms, and , are defined as another two loss functions in Eq.5 and 6 according to the parametric model in Eq.1 and 2. Initial values for and were both set as 1.
| (5) |
| (6) |
where equals to , is the length of /. and are the functions at the right side of Eq.4 and 5. and represent the predicted systolic and diastolic pressure in the cycle. and are real diastolic pressure in the cycle and systolic pressure in the cycle.
The optimization adjusts the model’s parameters, including neural network weights, biases, and physiological parameters and , to minimize the total loss, . The Adam optimizer, combined with a learning rate scheduler with initial rate as 0.01, was used to iteratively refine these parameters and ensure stable convergence. The model was iteratively trained until drops below a predefined threshold of 10 mmHg² within 1000 iterations, ensuring the model achieves a balance between accuracy and physical plausibility.
II-F Model Evaluation
Training and testing data sets were the same length (10 minutes each activity for different types) collected on the same participant on different dates, respectively. We tested the performance of PMB-NN by comparing and estimated and measured pressure values counted on systolic pressure and diastolic pressure, separately. Both performances were revealed in terms of root mean squared error (RMSE) (in mmHg) and mean absolute percentage error (MAPE) (in %). The estimated was compared with the golden standard which was calculated by the Beatscope software, while we only reported the estimated given the lack of measured using Finometer Model-2 devices.
III Results
We presented the preliminary result of only one participant’s data. Table I listed the error of PMB-NN estimation on systolic pressure and diastolic pressure, respectively. The estimation error for both and is the lowest in activity of resting among the three activities.
| Estimated Pressure | ||||
|---|---|---|---|---|
| Activity | ||||
| RMSE | MAPE | RMSE | MAPE | |
| Resting | 3.89 | 3.30 | 4.85 | 6.46 |
| Cycling 50 watts | 8.69 | 5.68 | 3.29 | 3.89 |
| Cycling 100 watts | 7.28 | 4.25 | 2.67 | 2.96 |
| Median | 6.69 | 4.78 | 3.26 | 3.93 |
The estimated , from PMB-NN and the measured , corresponding to various activity types are listed in Table II. It showed that the difference between the estimated and measured resistance is relatively small (median (min, max) as 0.043 (0.024, 0.061)) mmHg·s/cm³. We also observed that the estimated decreased and increased from 1.109 to 1.562 cm³/mmHg (within a plausible range of 0.34 to 2.8 cm³/mmHg [13]) from resting to increasing cycling workload.
| Activity | Measured | Estimated | Estimated |
|---|---|---|---|
| (mmHg·s/cm³) | (mmHg·s/cm³) | (cm³/mmHg) | |
| Resting | 0.845 | 0.869 | 1.109 |
| Cycling 50 watts | 0.567 | 0.610 | 1.429 |
| Cycling 100 watts | 0.434 | 0.495 | 1.562 |
IV Discussion
Experimental results demonstrated that the PMB-NN model achieved systolic blood pressure (SBP) estimation accuracy during rest and diastolic blood pressure (DBP) estimation accuracy across varying activity intensities, both meeting the Association for the Advancement of Medical Instrumentation (AAMI) standard with a root mean square error (RMSE) below 5 mmHg. Compared to the benchmark Bidirectional LSTM method [14], which yielded a median RMSE of 5.73 mmHg for SBP and 2.94 mmHg for DBP on our dataset, the PMB-NN model demonstrated comparable performance. Furthermore, the estimated vascular resistance (R) and compliance (C) exhibited physiologically consistent trends, with R decreasing and C increasing as activity intensity increased, aligning with established cardiovascular responses to exercise. These findings validate the model’s capability to capture dynamic hemodynamic adaptations.
The above findings proved that the PMB-NN framework holds potential for mobile health applications, particularly in high-risk populations requiring continuous BP monitoring. Its capability to estimate R and C alongside BP provides additional metrics for cardiovascular risk assessment, enabling a more comprehensive understanding of patient health. Furthermore, this approach could facilitate the early detection of hypertension-related complications and improve the personalization of treatment strategies by providing accurate BP, R, and C estimates.
Despite the promising results, it was notable that systolic pressure estimation was affected by higher errors compared to diastolic pressure. This discrepancy may stem from the inherent complexity and variability of systolic pressure due to transient cardiovascular dynamics during activity. Meanwhile, the estimated systolic and diastolic pressure values tended to converge toward the median, likely due to limited input variability, which failed to capture subtle blood pressure fluctuations. On the other hand, if the initial values for resistance and compliance are set orders of magnitude away from the true values, the model may struggle to converge quickly. Additionally, the unverified identification of the compliance parameter value (C) further limited the model’s reliability. To address these limitations, future efforts should focus on incorporating additional signal features, such as waveform morphology, which may enhance the model’s sensitivity to systolic fluctuations. We also plan to expand the dataset by incorporating data from 10 participants, which will further validate the PMB-NN framework and pave the way for its potential application in mobile health monitoring systems.
V Conclusion
This study introduced a novel PMB-NN framework for blood pressure estimation using PPG signals. By combining physiological model and deep learning approaches, the PMB-NN achieved promising performance under human movement conditions while providing physiological insights through TPR and AC estimation. The PMB-NN framework represented its potential toward daily BP monitoring. Its ability to deliver accurate BP estimates and additional cardiovascular metrics highlights its utility in mobile health applications like personalized hypertension management.
References
- [1] Q. Hu, D. Wang, and C. Yang, “Ppg-based blood pressure estimation can benefit from scalable multi-scale fusion neural networks and multi-task learning,” Biomedical Signal Processing and Control, vol. 78, p. 103891, 9 2022.
- [2] G. Wang, M. Atef, and Y. Lian, “Towards a continuous non-invasive cuffless blood pressure monitoring system using ppg: Systems and circuits review,” IEEE Circuits and Systems Magazine, vol. 18, pp. 6–26, 2018.
- [3] C. El-Hajj and P. A. Kyriacou, “A review of machine learning techniques in photoplethysmography for the non-invasive cuff-less measurement of blood pressure,” Biomedical Signal Processing and Control, vol. 58, p. 101870, 4 2020.
- [4] B. C. Casadei, A. Gumiero, G. Tantillo, L. D. Torre, and G. Olmo, “Systolic blood pressure estimation from ppg signal using ann,” Electronics, vol. 11, p. 2909, 9 2022.
- [5] C. Sideris, H. Kalantarian, E. Nemati, and M. Sarrafzadeh, “Building continuous arterial blood pressure prediction models using recurrent networks.” IEEE, 5 2016, pp. 1–5.
- [6] X. Teng and Y. Zhang, “Continuous and noninvasive estimation of arterial blood pressure using a photoplethysmographic approach.” IEEE, pp. 3153–3156.
- [7] K. Duan, Z. Qian, M. Atef, and G. Wang, “A feature exploration methodology for learning based cuffless blood pressure measurement using photoplethysmography.” IEEE, 8 2016, pp. 6385–6388.
- [8] J. Dey, A. Gaurav, and V. N. Tiwari, “Instabp: Cuff-less blood pressure monitoring on smartphone using single ppg sensor.” IEEE, 7 2018, pp. 5002–5005.
- [9] J. Steppan, V. Barodka, D. E. Berkowitz, and D. Nyhan, “Vascular stiffness and increased pulse pressure in the aging cardiovascular system.” Cardiology research and practice, vol. 2011, p. 263585, 2011.
- [10] R. D. Olano, W. G. Espeche, M. R. Salazar, P. Forcada, J. A. Chirinos, A. de Iraola, C. E. L. Sisnieguez, B. C. L. Sisnieguez, E. Balbín, and H. A. Carbajal, “Evaluation of ventricular-arterial coupling by impedance cardiography in healthy volunteers,” Physiological Measurement, vol. 40, p. 115002, 12 2019.
- [11] V. V. M. C. Mridu Sinha, “Model of aortic blood flow using the windkessel effect,” 10 2012.
- [12] K. Sagawa, “Translation of otto frank’s paper “die grundform des arteriellen pulses” zeitschrift für biologie 37: 483–526 (1899),” Journal of Molecular and Cellular Cardiology, vol. 22, pp. 253–254, 3 1990.
- [13] D. Chemla, J.-L. Hébert, C. Coirault, K. Zamani, I. Suard, P. Colin, and Y. Lecarpentier, “Total arterial compliance estimated by stroke volume-to-aortic pulse pressure ratio in humans,” American Journal of Physiology-Heart and Circulatory Physiology, vol. 274, pp. H500–H505, 2 1998.
- [14] S. Maqsood, S. Xu, M. Springer, and R. Mohawesh, “A benchmark study of machine learning for analysis of signal feature extraction techniques for blood pressure estimation using photoplethysmography (ppg),” IEEE Access, vol. 9, pp. 138 817–138 833, 2021.