A radial limit on polar circumbinary orbits from general relativity
Abstract
A particle orbiting a misaligned eccentric orbit binary undergoes nodal precession either around the binary angular momentum vector (a circulating orbit) or around a stationary inclination (a librating orbit). In the absence of general relativity, the stationary inclination is inclined by to the binary angular momentum vector (aligned with the binary eccentricity vector) and does not depend on the particle semi-major axis. General relativity causes apsidal precession of the binary orbit. Close to the binary, the behaviour of the particle is not significantly affected, a librating particle precesses with the binary. However, we find that the stationary inclination and the minimum inclination required for libration both increase with the particle semi-major axis. There is a critical radius beyond which there are no librating orbits, only circulating orbits, and therefore there is a maximum orbital radius for a stationary polar orbiting body. The critical radius is within planet forming regions around binaries with semi-major axis . This has implications for the search for misaligned circumbinary planets and the radial extent of polar circumbinary disks.
1 Introduction
Many planets have been detected orbiting around binary star systems (e.g. Doyle et al., 2011; Orosz et al., 2012). All of the currently observed systems are in orbits that are close to coplanar to their host binary orbit. This may be representative of nature (Li et al., 2016; Martin et al., 2019) but it may be a result of selection effects since the Kepler binaries are all around very short orbital period binaries. Transits for even slightly misaligned circumbinary planets are less frequent than for circumstellar planets because of their nodal precession, however, the probability of a transit at some point is higher (Martin & Triaud, 2015; Martin, 2017). Eclipse timing variations may provide a way to detect highly misaligned planets in the future (Zhang & Fabrycky, 2019).
We expect that planets may form in misaligned orbits around wider binaries (with semi-major axis ) since protoplanetary gas disks around these binaries may be more highly misaligned (Czekala et al., 2019). Observations show that misaligned circumbinary gas disks are common (e.g. Chiang & Murray-Clay, 2004; Capelo et al., 2012; Brinch et al., 2016). HD 98800 was the first circumbinary gas disk to be found in a polar configuration (Kennedy et al., 2019). In a polar alignment, a low mass disk (or planet) is misaligned by close to to the central binary orbit with its angular momentum aligned to the eccentricity vector of the binary. This is a stable configuration (Aly et al., 2015; Martin & Lubow, 2017; Lubow & Martin, 2018; Zanazzi & Lai, 2018; Cuello & Giuppone, 2019).
The dynamics of misaligned circumbinary planet orbits have been studied in depth both analytically and numerically (Verrier & Evans, 2009; Farago & Laskar, 2010; Doolin & Blundell, 2011; Zanardi et al., 2017; Chen et al., 2019). Around a circular orbit binary, the nodal precession is always around the binary angular momentum vector, we call these circulating orbits. However, around an eccentric binary, a sufficiently misaligned orbit can precess instead about the stationary inclination that is aligned with the binary eccentricity vector, we call these librating orbits. Most previous work has ignored the effects of general relativity that causes an additional apsidal precession of the binary orbit in the same direction as orbital motion (Naoz et al., 2017). Zanardi et al. (2018) examined the effects of GR on the orbit of an asteroid around a star with an inner eccentric orbit planet. Childs & Martin (2021) found that general relativity (GR) does not affect the dynamics of very close in (orbital radius ) terrestrial planets around a semi-major axis binary since the planet orbits precess with the binary and remain polar aligned.
In this work, for the first time, we consider how the additional precession due to GR affects the dynamics of circumbinary planet orbits in wide orbits around close binaries. Without GR, circumbinary orbital dynamics do not change much with the planet semi-major axis (e.g. Doolin & Blundell, 2011). However, in Section 2 we use -body simulations to show that GR significantly alters the orbits of wider orbit planets relative to the binary orbit. We find that there is a critical radius outside of which the orbits are circulating for all initial inclinations. In Section 3 we show how this critical radius depends upon the the properties of the binary. In Section 4 we discuss the implications of our results for both the dynamics of circumbinary planets and the evolution of circumbinary disks.
2 Circumbinary planet orbital dynamics with GR

The calculations for this paper were made using the REBOUND -body code (Rein & Liu, 2012) and the REBOUNDx package extension to include GR effects using the gr_full package (Tamayo et al., 2020; Newhall et al., 1983). All simulations used the WHFAST integrator, a symplectic Wisdom-Holman integrator (Rein & Tamayo, 2015; Wisdom & Holman, 1991), but the critical points were checked with the IAS15, a 15th order Gauss-Radau integrator (Rein & Spiegel, 2015) and the SimulationArchive format was used to have a fully stored state of the system for analysis (Rein & Tamayo, 2017).
We analyse the particle orbits in the frame of the binary. The inclination is the angle between the direction of the angular momentum vector of the test particles orbit and the direction of the angular momentum vector of the binary given by
| (1) |
where is a unit vector in the direction of the binary’s angular momentum and a unit vector in the direction the test particles angular momentum would be if it were not zero mass. The nodal phase angle measured relative to the eccentricity vector of the binary is given by
| (2) |
(Chen et al., 2019, 2020) where is the eccentricity vector of the binary.
2.1 Comparison to previous work without General Relativistic Effects
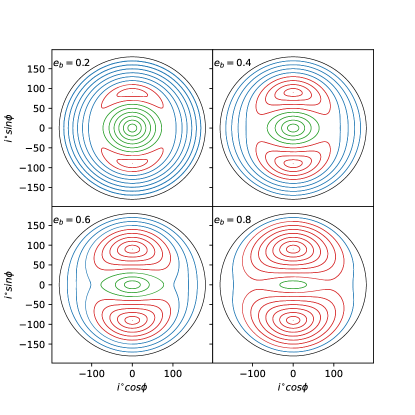
We first ran some simulations without GR with a binary consisting of two stars with masses with a semi-major axis of au and eccentricities of , 0.4, 0.6 and . The test particles began in a circular orbit with a semi-major axis of au. The orbits have an initial inclination, , between 10 and 170∘ with an interval of and initial longitude of ascending node .
Fig. 1 shows the phase plane for these orbits. In this diagram, an orbit with the angular momentum vector aligned, or anti-aligned, with the eccentricity vector of the binary is a point at (0,90), or at (0,-90) respectively. A coplanar orbit is a point at (0,0) and a retrograde coplanar orbit is a circle of radius centered around (0,0). In the case of the retrograde coplanar orbit, the phase angle is not defined and so these orbits are represented on the figures in black for reference purposes as they represent the edge of the phase space. The stationary inclination is the inclination about which the (red) librating orbits precess. For these orbits without GR it is always .
As the eccentricity of the binary increases we see the librating regions expand and the circulating regions shrink. The librating orbits are symmetric about and so librating orbits with the initial inclinations of the same offset from in this plot trace over each other (e.g. traces over and so on). The minimum initial inclination for librating orbits, , decreases with the binary eccentricity. These plots are in good agreement with the test particle simulations in Doolin & Blundell (2011) as well as the low planet mass simulations of Chen et al. (2019).
We also ran these cases without GR for particle semi-major axes of , , and au and found that these are nearly identical to the au orbits. Note that while the track on the surface is independent of the particle semi-major axis, the timescale for one complete precession around the stationary inclination is not. Also, at small radii the orbits can become unstable due to interactions with the binary (e.g. Hong et al., 2019; Chen et al., 2020).
2.2 With General Relativistic Effects at large radii
Next, we consider the effects of GR on circumbinary particle orbits. The simulations are run with the same initial conditions as described in the previous section but we fix and consider varying particle semi-major axes. The results are shown in Figs. 2 and 3. Comparing the upper left panel of Fig. 2 to the lower left panel of Fig. 1, we see that the orbits at are nearly identical to those without GR.
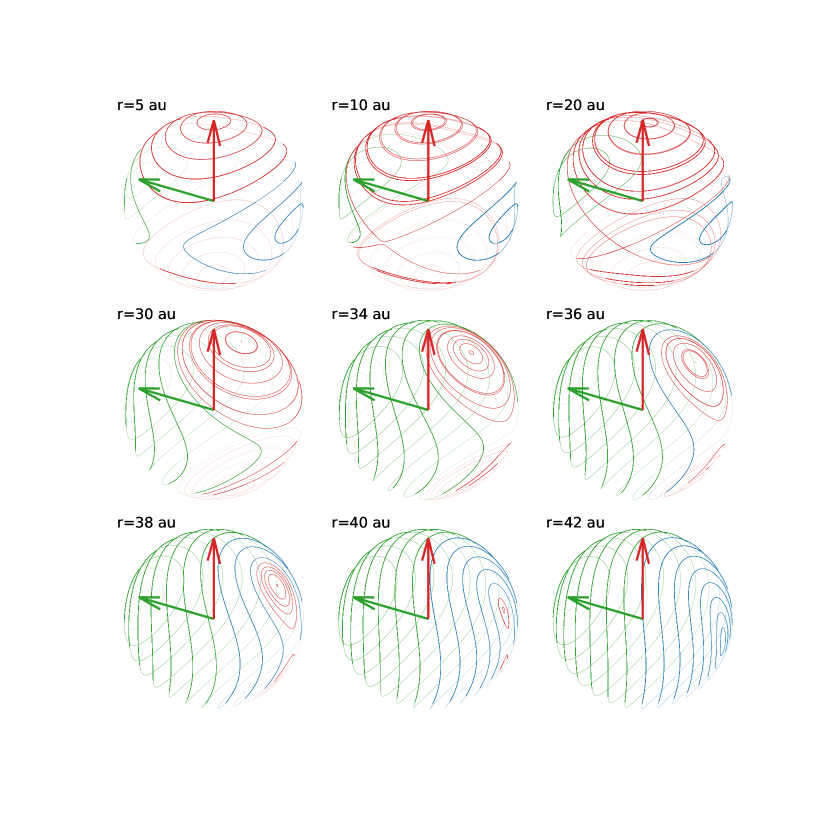
As the particle semi-major axis increases, the stationary inclination at the center of the librating region moves to higher (retrograde) inclinations. The circulating region expands and the retrograde circulating region shrinks. One effect of the moving stationary inclination is that the librating orbits appear to have thicker lines in the case compared with the case. This is because the stationary inclination has moved slightly away from . The initial inclinations relative to the stationary inclination are no longer symmetric about the stationary inclination. Therefore orbits beginning at say and no longer lie on top of each other. Also note that the orbit has become librating in the panel as the stationary inclination moved to higher inclinations. As we move to even larger radii, eventually the librating region disappears completely as the stationary inclination moves beyond . For particle semi-major axis greater than about , there are only circulating orbits, as can be seen in the panel. The effects of GR have removed the possibility for librating orbits at large orbital radius.
Fig. 3 shows another view of the same results shown in Fig 2 except here the inclination and phase angle are plotted on the surface of a sphere. The eccentricity unit vector and angular momentum unit vector are also plotted. The angular momentum unit vector points at the prograde circulating region, which in this view is on the back left of sphere and the eccentricity unit vector points, in the r=5 au plot, at the librating region on top of the sphere. At greater radius, , both the librating regions move toward and merge.
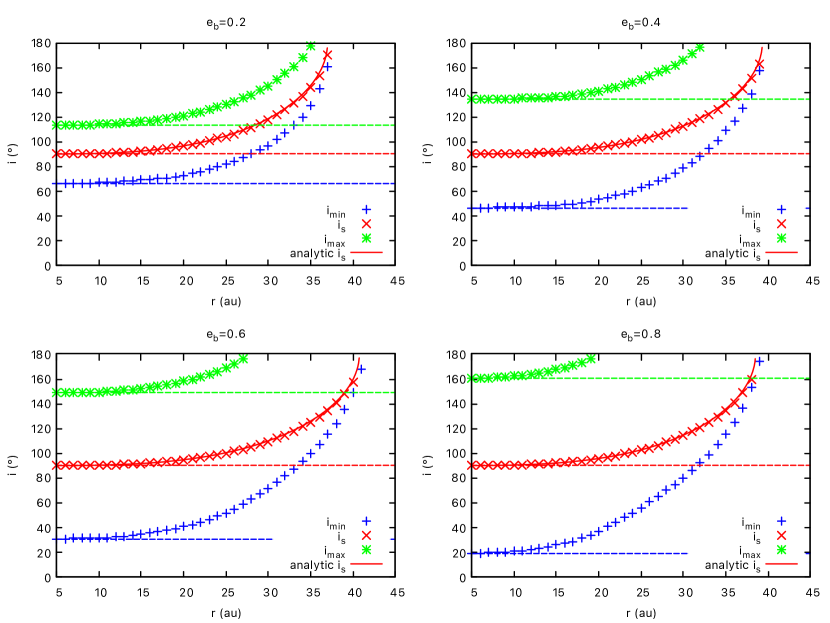
Next we explore the librating region further by plotting in Fig. 4 the stationary inclination, the lowest librating initial inclination, , and the highest librating initial inclination, , as a function of particle radius for the binary eccentricities of , , and . The librating region is found by changing the inclination by one degree and finding the first inclination that librates and the last inclination that librates. The stationary inclination is found by searching which initial inclination is stationary on the surface. This is done by starting with inclinations on each side of the stationary inclination and integrating for two test particle orbital periods. The projection of the orbits on the surface move in opposite directions. On the y-axis an initial inclination less than the stationary inclination will initially move to smaller angles for , while an initial inclination larger than the stationary inclination will initially move to larger angles. If we bracket the stationary inclination a binary search root finder can be used to find the stationary inclination.
As with the surface panels, the panels in Fig. 4 map out the librating region. At au the librating region extends over the same range as was found in the without GR calculations. The case has the smallest librating region and the case has the largest. As the particle semi-major axis increases, the stationary inclination and the librating region tend toward . First to reach is the maximum inclination of the librating region. At this point there is no longer a retrograde circulating region. Another interesting point is where the lower edge of the librating region passes , at this point the librating region lies entirely in the retrograde region. For the case this happens before the higher edge reaches and so for some radii the librating region is bracketed by prograde and retrograde circulation. Eventually the stationary inclination reaches and no more librating orbits are possible.
The orbit of a test particle around an inner binary including GR effects was explored by Naoz et al. (2017) and Zanardi et al. (2018). They used a quadrupole approximation and explored the effect general relativity has on a test particle orbit. General relativity causes the inner binary to precess on a timescale of
| (3) |
where is the speed of light and is the gravitational constant. This means that the frame of the binary is a rotating frame. They solve for the orbits within this rotating frame and find how the ascending node of the outer planet changes with time. Zanardi et al. (2018) take this result and find the stationary inclination, , where the ascending node relative to the binary does not change to be
| (4) |
(this is their equation (7) with the eccentricity of the test particle set to zero and the ascending node of the test particle to ), where is a constant given by
| (5) |
This is plotted in Fig 4 as the solid red lines and is seen to be in good agreement with our numerical results.
Another way to look at the stationary inclination, is to consider the calculation without GR as was shown in Fig. 1. Here we can see that the orbits in the surface are such that when they cross the y-axis there is always an extemum of inclination. So the inclination is initially constant as the orbit moves off the y-axis and all the change comes from a change in . This change in is toward smaller for inclinations less than and toward larger for inclinations greater than . The inclination doesn’t change at a uniform rate, but if one takes the average over a full test particle orbit then one can get an average rate of change for a particular radius and initial inclination. The precession of the binary due to GR is such that it causes a change in toward smaller values. Thus, there is some inclination greater than where on the y-axis in the surface the precession from GR exactly cancels the motion in from the initial motion of the orbit caused by the interaction of the binary and the test particle orbit. We have written an addition program, which for each radius of test particle orbit in a non-GR calculation, it searches for an inclination in which the initial motion of averaged over two test particle orbits is equal to the precession which would be caused by GR and this reproduces our stationary inclination calculated with GR.
3 Critical radius for librating orbits
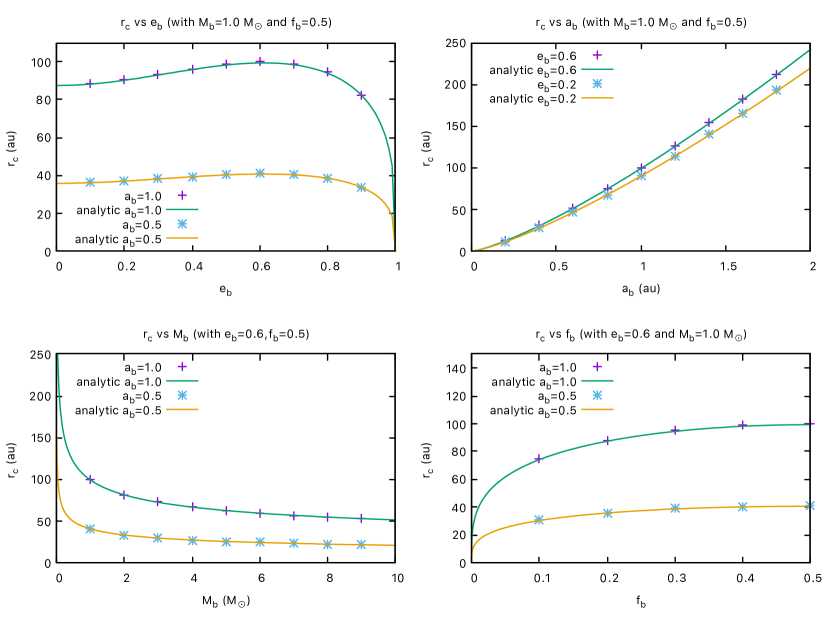
Without GR, the stationary inclination is at to the binary orbit and is independent of the particle semi-major axis (see Section 2.1). With GR, there is a critical semi-major axis, , where the stationary inclination reaches and beyond this there are no librating orbits (see section 2.2). We found this radius numerically in Fig. 5 for varying binary eccentricity, semi-major axis, total binary mass, and binary mass fraction .
We can also solve for the critical radius, , by setting the stationary inclination to in Equation 4 and solving for the critical semi-major axis to get
| (6) |
For some typical parameters we can write this as
| (7) |
where and are functions with a maximum value of one characterizing the effects of the mass fraction and eccentricity on the critical semi-major axis. They are given by
| (8) |
and
| (9) |
where the maximum value for these functions occur at and , respectively. These analytic results are plotted also in Fig 5 along with the numerical simulations discussed above and they match very well.
The critical radius goes to infinity, matching the non-GR case as goes to infinity and as goes to zero. This can be explained as in both these limits, the binary precession rate goes to zero which matches the lack of precession in the non-GR case. As the goes to zero or the goes to infinity the precession rate goes to infinity and the critical semi-major axis goes to zero. The critical semi-major axis is not a strong function of either binary eccentricity or mass fraction. However, the critical semi-major axis goes to zero as the binary eccentricity goes to 1, where the precession rate also goes toward infinity, In the case of the mass fraction, the critical radius goes to zero as the mass fraction goes to zero, but this is because the binary is no longer a binary in this limit.
Finally, we examine the radius at which the stationary inclination reaches a particular angle. The stationary inclination varies from the non-GR case of to the limit of which it reaches at . The radius or semi-major axis where it passes through a particular angle is a fixed fraction of the critical semi-major axis. This fraction is given by
| (10) |
So for example the stationary inclination will be at at a radius of of the critical radius and the stationary inclination will be at when the radius is at of .
4 Conclusions
Circumbinary orbits around an eccentric binary undergo nodal precession. The precession may be centered on the binary angular momentum vector (circulating orbits) or the stationary inclination (librating orbits). In the absence of general relativity, the stationary inclination is always at for a test particle and aligned with the binary eccentricity vector. We have shown that the effects of general relativity increase the stationary inclination. For particles that are close to the binary, the stationary inclination remains close to , however it increases with the particle semi-major axis. There is a critical radius outside of which there are no polar librating orbits, only circulating orbits. The critical radius is not very sensitive to the binary eccentricity but increases with the binary semi-major axis. The critical radius is in planet forming regions around close binaries with separation .
We have not included the effect of the mass of the particle in our calculations. A massive third body causes a retrograde apsidal precession of the binary. If the particle is massive enough, it may effectively cancel out the prograde precession caused by general relativity. However, the work presented here does not change significantly if the outer test particle is replaced by a Jupiter mass planet (see also Chen et al., 2019; Martin & Lubow, 2019) and does not affect the orbit of the binary (Martin & Triaud, 2016). However, the effect of the mass may become important when considering a massive or radially extended circumbinary disk (see also Migaszewski & Goździewski, 2011).
The particle simulations are run with point masses and are valid for that limit. At small separations, but before the orbits are circularised, tidal forces and the spin of the stars cause precessions which may compete with the GR precession. The precession due to these other processes can be quite complicated and depends on the exact composition and structure of the two stars (Sterne, 1939; Sirotkin & Kim, 2009) or compact objects (Hamilton & Rafikov, 2021). A faster prograde precession would lead to a smaller critical radius for polar orbits to exist.
The dynamics of a circumbinary gas disk are qualitatively similar to those of test particles. Each ring of the disk wants to behave in the same way as a particle, however, communication between the rings leads to differing behaviour. For protoplanetary discs, the communication typically occurs in the bending waves regime (Papaloizou & Pringle, 1983). The disk remains in a coherent structure if the communication timescale (that is about half the sound speed) is shorter than the precession timescale (Papaloizou & Terquem, 1995; Larwood et al., 1996; Papaloizou et al., 1998). In this case, a given radius of the disc may display dynamically different behaviour to a particle at the same radius. However, circumbinary disks can be sufficiently radially extended that they are not in good communication and can undergo disk breaking (Nixon et al., 2013).
Another difference with the disk compared to the particles is that there is viscous dissipation. A misaligned circumbinary gas disc moves towards either coplanar or polar alignment (Papaloizou & Terquem, 1995; Nixon et al., 2013; Martin & Lubow, 2017, 2018). For a binary with a critical radius, , that is within a circumbinary disk, the evolution may depend on the radial extent of the disk and disk properties such as the sound speed and the viscosity. If the disc extends beyond , disc breaking may lead to an inner polar disc and an outer disc that is circulating and moving towards coplanar. It is interesting to note that the observed polar gas disc HD 98800 has a exterior companion that could truncate the circumbinary disc and prevent it from spreading to the critical radius that we have found (Martin et al., 2022). The semi-major axis of HD98800 is about (Kennedy et al., 2019) and this corresponds to a critical radius of about , much larger than the size of the observed disc.
These results have important implications for observations of misaligned circumbinary planets. Stationary polar planets and polar librating planets, can only be inside of the critical radius. Similarly, debris discs, that may typically extend to tens or hundreds of au, must be close to the binary to be polar-aligned. Note that the polar debris disc around 99 Herculis would not be affected by GR since the separation of the binary is about (Kennedy et al., 2012; Smallwood et al., 2020), much larger than those considered in this work. This suggests that we would not expect a solar system analogue with a polar close central binary. The inner planets in the solar system could be polar, but the outer planets and the Kuiper belt or debris disc are more likely to be coplanar if they are the remnants of a circumbinary gas disc.
References
- Aly et al. (2015) Aly, H., Dehnen, W., Nixon, C., & King, A. 2015, MNRAS, 449, 65
- Brinch et al. (2016) Brinch, C., Jørgensen, J. K., Hogerheijde, M. R., Nelson, R. P., & Gressel, O. 2016, ApJ, 830, L16
- Capelo et al. (2012) Capelo, H. L., Herbst, W., Leggett, S. K., Hamilton, C. M., & Johnson, J. A. 2012, ApJ, 757, L18
- Chen et al. (2019) Chen, C., Franchini, A., Lubow, S. H., & Martin, R. G. 2019, MNRAS, 490, 5634
- Chen et al. (2020) —. 2020, MNRAS, 495, 141
- Chen et al. (2020) Chen, C., Lubow, S. H., & Martin, R. G. 2020, Monthly Notices of the Royal Astronomical Society, 494, 4645
- Chiang & Murray-Clay (2004) Chiang, E. I., & Murray-Clay, R. A. 2004, ApJ, 607, 913
- Childs & Martin (2021) Childs, A. C., & Martin, R. G. 2021, ApJ, 920, L8
- Cuello & Giuppone (2019) Cuello, N., & Giuppone, C. A. 2019, A&A, 628, A119
- Czekala et al. (2019) Czekala, I., Chiang, E., Andrews, S. M., et al. 2019, ApJ, 883, 22
- Doolin & Blundell (2011) Doolin, S., & Blundell, K. M. 2011, MNRAS, 418, 2656
- Doyle et al. (2011) Doyle, L. R., Carter, J. A., Fabrycky, D. C., et al. 2011, Science, 333, 1602
- Farago & Laskar (2010) Farago, F., & Laskar, J. 2010, MNRAS, 401, 1189
- Hamilton & Rafikov (2021) Hamilton, C., & Rafikov, R. R. 2021, MNRAS, 505, 4151
- Hong et al. (2019) Hong, Z., Quarles, B., Li, G., & Orosz, J. A. 2019, AJ, 158, 8
- Kennedy et al. (2012) Kennedy, G. M., Wyatt, M. C., Sibthorpe, B., et al. 2012, MNRAS, 421, 2264
- Kennedy et al. (2019) Kennedy, G. M., Matrà, L., Facchini, S., et al. 2019, Nature Astronomy, 3, 230
- Larwood et al. (1996) Larwood, J. D., Nelson, R. P., Papaloizou, J. C. B., & Terquem, C. 1996, MNRAS, 282, 597
- Li et al. (2016) Li, G., Holman, M. J., & Tao, M. 2016, ApJ, 831, 96
- Lubow & Martin (2018) Lubow, S. H., & Martin, R. G. 2018, MNRAS, 473, 3733
- Martin (2017) Martin, D. V. 2017, MNRAS, 465, 3235
- Martin & Triaud (2015) Martin, D. V., & Triaud, A. H. M. J. 2015, MNRAS, 449, 781
- Martin & Triaud (2016) —. 2016, MNRAS, 455, L46
- Martin et al. (2019) Martin, D. V., Triaud, A. H. M. J., Udry, S., et al. 2019, A&A, 624, A68
- Martin et al. (2022) Martin, R. G., Lepp, S., Lubow, S. H., et al. 2022, arXiv e-prints, arXiv:2202.06878
- Martin & Lubow (2017) Martin, R. G., & Lubow, S. H. 2017, ApJ, 835, L28
- Martin & Lubow (2018) —. 2018, MNRAS, 479, 1297
- Martin & Lubow (2019) —. 2019, MNRAS, 490, 1332
- Migaszewski & Goździewski (2011) Migaszewski, C., & Goździewski, K. 2011, MNRAS, 411, 565
- Naoz et al. (2017) Naoz, S., Li, G., Zanardi, M., de Elía, G. C., & Di Sisto, R. P. 2017, AJ, 154, 18
- Newhall et al. (1983) Newhall, X. X., Standish, E. M., & Williams, J. G. 1983, A&A, 125, 150
- Nixon et al. (2013) Nixon, C., King, A., & Price, D. 2013, MNRAS, 434, 1946
- Orosz et al. (2012) Orosz, J. A., Welsh, W. F., Carter, J. A., et al. 2012, ApJ, 758, 87
- Papaloizou & Pringle (1983) Papaloizou, J. C. B., & Pringle, J. E. 1983, MNRAS, 202, 1181
- Papaloizou & Terquem (1995) Papaloizou, J. C. B., & Terquem, C. 1995, MNRAS, 274, 987
- Papaloizou et al. (1998) Papaloizou, J. C. B., Terquem, C., & Lin, D. N. C. 1998, ApJ, 497, 212
- Rein & Liu (2012) Rein, H., & Liu, S. F. 2012, A&A, 537, A128
- Rein & Spiegel (2015) Rein, H., & Spiegel, D. S. 2015, MNRAS, 446, 1424
- Rein & Tamayo (2015) Rein, H., & Tamayo, D. 2015, MNRAS, 452, 376
- Rein & Tamayo (2017) —. 2017, MNRAS, 467, 2377
- Sirotkin & Kim (2009) Sirotkin, F. V., & Kim, W.-T. 2009, ApJ, 698, 715
- Smallwood et al. (2020) Smallwood, J. L., Franchini, A., Chen, C., et al. 2020, MNRAS, 494, 487
- Sterne (1939) Sterne, T. E. 1939, MNRAS, 99, 451
- Tamayo et al. (2020) Tamayo, D., Rein, H., Shi, P., & Hernandez, D. M. 2020, MNRAS, 491, 2885
- Verrier & Evans (2009) Verrier, P. E., & Evans, N. W. 2009, MNRAS, 394, 1721
- Wisdom & Holman (1991) Wisdom, J., & Holman, M. 1991, j, 102, 1528
- Zanardi et al. (2018) Zanardi, M., de Elía, G. C., Di Sisto, R. P., & Naoz, S. 2018, A&A, 615, A21
- Zanardi et al. (2017) Zanardi, M., de Elía, G. C., Di Sisto, R. P., et al. 2017, A&A, 605, A64
- Zanazzi & Lai (2018) Zanazzi, J. J., & Lai, D. 2018, MNRAS, 473, 603
- Zhang & Fabrycky (2019) Zhang, Z., & Fabrycky, D. C. 2019, ApJ, 879, 92