A Simple and Efficient Estimation of the Average Treatment Effect in the Presence of Unmeasured Confounders
Abstract
Wang and Tchetgen Tchetgen (2017) studied identification and estimation of the average treatment effect when some confounders are unmeasured. Under their identification condition, they showed that the semiparametric efficient influence function depends on five unknown functionals. They proposed to parameterize all functionals and estimate the average treatment effect from the efficient influence function by replacing the unknown functionals with estimated functionals. They established that their estimator is consistent when certain functionals are correctly specified and attains the semiparametric efficiency bound when all functionals are correctly specified. In applications, it is likely that those functionals could all be misspecified. Consequently their estimator could be inconsistent or consistent but not efficient. This paper presents an alternative estimator that does not require parameterization of any of the functionals. We establish that the proposed estimator is always consistent and always attains the semiparametric efficiency bound. A simple and intuitive estimator of the asymptotic variance is presented, and a small scale simulation study reveals that the proposed estimation outperforms the existing alternatives in finite samples.
Keywords: Average treatment effect; Unmeasured confounders; Semiparametric efficiency; Endogeneity.
1 Introduction
A common approach to account for individual heterogeneity in the treatment
effect literature on observational data is to assume that there exist
confounders, and conditional on these confounders, there is no systematic
selection into the treatment (i.e., the so-called Unconfounded
Treatment Assignment condition suggested in Rosenbaum and Rubin (1983, 1984)). Under this assumption, several procedures for
estimating the average treament effect (hereafter ATE) have been proposed,
including the weighting procedure (Rosenbaum (1987), Hirano, Imbens, and Ridder (2003), Tan (2010), Imai and Ratkovic (2014), Chan, Yam, and Zhang (2016), Yiu and Su (2018)); the matching procedure (Rosenbaum (2002), Rosenbaum et al. (2002), Dehejia and Wahba (1999)); and the regression procedure (Heckman, Ichimura, and Todd (1997), Heckman, Ichimura, and Todd (1998), Imbens, Newey, and Ridder (2006),
Chen, Hong, and Tarozzi (2008)). For example survey, see Imbens and Wooldridge (2009) and Imbens and Rubin (2015). A critical requirement in
this literature is that all confounders are observed and available to
researchers. In applications, however, it is often the case that some
confounders are either not observed or not availale. In this case, the
average treatment effect is only partially identified even with the aid of
some insrumental variables (see Imbens and Angrist (1994), Angrist, Imbens, and Rubin (1996), Abadie (2003), Abadie, Angrist, and Imbens (2002), Tan (2006), Cheng, Small, Tan, and Have (2009), Ogburn, Rotnitzky, and Robins (2015)
for examples).
Recently Wang and Tchetgen Tchetgen (2017) suggested a noval identification condition
of ATE when some confounders are not available. Under their condition, they
showed that the semiparametric efficient influence function of ATE depends
on five unknown functionals. They proposed to parameterize all five
functionals, estimate those functionals with appropriate parametric
approaches, plug the estimated functionals into the influence function, and
then estimate the ATE from the estimated influence function. They
established that their estimator is consistent if certain functionals are
correctly parameterized and attains the semiparametric efficiency bound if
all functionals are correctly specified. In applications, it is quite
possible that some or all of the five functionals are misspecified and
consequently their estimator could be inefficient or worse, inconsistent.
This paper proposes an alternative, intuitive and easy to compute estimation
that does not require parameterization of any of the five unknown
functionals. We estbalish that under some sufficient conditions the proposed
estimator is consistent, asymptotically normally distributed and attains the
semiparametric efficiency bound. Moreover, the proposed procedure provides a
natural and convenient estimate of the asymptotic variance.
The paper is organized as follows. Section 2 describes the basic framework. Section 3 describes the proposed estimation and derives the large sample properties of the proposed estimator. Section 4 presents a consistent variance estimator. Since the proposed procedure depends on smoothing parameters, Section 5 presents a data driven method for selecting the smoothing paprameters. Section 6 reports a small scale simulation study to evaluate the finite sample performance of the proposed estimator. Some concluding remarks are in Section 7. All technical proofs are relegated to the Appendix and the supplementary material.
2 Basic Framework
Let denote the binary treatment indicator, and let and denote the potential outcomes when an individual is assigned to the treatment and control group respectively. The parameter of interest is the population average treatment effect . Estimation of is complicated by the presence of confounders and the fact that and cannot be observed simultaneously. To distinguish observed confounders from unobserved confounders, we shall use to denote the observed confounders and use to denote the unmeasured confounders. It is well established in the literature that, when all confounders are observed, the following Unconfounded Treatment Assignment condition is sufficient to identify :
Assumption 2.1.
.
When is unmeasured, we have the classical omitted variable problem, causing the treament indicator to be endogenous. To tackle the endogeneity problem, instrumental variable is often the preferred choice. Let denote the variable satisfying the following classical instrumental variable conditions:
Assumption 2.2 (Exclusion restriction).
, , where is the response that would be observed if a unit were exposed to and the instrument had taken value to be well defined.
Assumption 2.3 (Independence).
.
Assumption 2.4 (IV relavance).
.
Wang and Tchetgen Tchetgen (2017) showed that Asssumptions 2.1- 2.4 alone do not identify , but if in addition one of the following conditions holds:
-
1.
there is no additive - interaction in :
-
2.
there is no additive - interaction in :
then ATE is identified and can be expressed as
| (2.1) |
where
Furthermore, Wang and Tchetgen Tchetgen (2017) derived the efficient influence function for :
where is the conditional probability mass function of given . Clearly, the efficient influence function depends on five unknown functionals: , , , and . They proposed to parameterize all five functionals, estimate the functionals with appropriate parametric approaches, and plug the estimated functionals into the efficient influence function to estimate . They established that their estimator of is consistent and asymptotically normally distributed if
-
•
either , , and are correctly specified
-
•
or and are correctly specified
-
•
or and are correctly specified,
and their estimator attains the semiparametric efficiency bound only when all five functionals are correctly specified. The main goal of this paper is to present an alternative, intuitive and easy approach to compute estimator that does not require parameterization of any of the functionals and is always consistent and asymptotically normal and attains the semiparametric efficiency bound.
3 Point Estimation
To motivate our estimation procedure, we rewrite the treatment effect coefficient. Applying the tower law of conditional expectation, we obtain:
| (3.1) |
The above expression suggests a natural and intuitive plugin estimation, with and replaced by some consistent estimates. There are many approaches to estimate these functionals including parametric and nonparametric approaches, but as noted by Hirano, Imbens, and Ridder (2003), not all estimates can lead to efficient estimation of . In this paper, we present an intuitive and easy way to compute estimates of functionals that ensure efficiency of the plugin estimation of . To illustrate our procedure, we notice that the following conditions hold for any integrable functions and :
| (3.2) | |||
| (3.3) |
and (3.2) and (3.3) uniquely determine and . These conditions impose restrictions on the unknown functionals and they must be taken into account when estimating those functionals. One difficulty with these conditions is that they must be imposed in an infinite dimmensional functional space. To overcome this difficulty, we propose to impose the conditions on a smaller sieve space. Specifically, let denote a known basis functions that can approximate any suitable function arbitrarily well (see Chen (2007) or Appendix A.1 for further dicussion). Conditions (3.2) and (3.3) imply for any integers and :
| (3.4) |
and
| (3.5) |
We shall construct estimates of the functionals by imposing the above conditions. To ensure consistency, we shall allow and to increase with sample size at appropriate rates.
3.1 Estimation of
Consider estimation of . An obvious approach is to solve from the sample analogue of (3.4):
| (3.6) | |||||
| (3.7) |
But there are many solutions and all solutions are consistent estimates of . The question is which solution is the best estimate of in the sense of ensuring efficient estimation of . Let denote a strictly increasing and concave function and let denote its first derivative. Denote
with maximizing the following objective function
| (3.8) |
It is easy to show that satisfies (3.6). Moreover, can be interpreted as a generalized empirical likelihood
estimator of (see Appendix A.2) and hence is the best
estimate. The fact that is globally concave implies that
its maximand is easy to compute.
Applying the same idea to (3.7), we have
with maximizing the following globally concave objective function
| (3.9) |
Again, satisfies (3.7) and can be interpreted as a
generalized empirical likelihood estimatior of .
The function can be any increasing and strictly concave function. Some examples include for the exponential tilting (Kitamura and Stutzer, 1997, Imbens, Spady, and Johnson, 1998), for the empirical likelihood (Owen, 1988, Qin and Lawless, 1994), for the continuous updating of the generalized method of moments (Hansen, 1982, Hansen, Heaton, and Yaron, 1996) and for the inverse logistic.
3.2 Estimation of and
Having estimated , we now apply the same principle to estimate . But there is one difference. Here and the function is not suitable. We shall use the following strictly convex function
whose derivative is the tanh function with range . We estimate by
with maximizing the following globally concave function
Again, can be interpreted as a generalized empirial
likelihood estimator and hence is the best estimate.
Finally, the plugin estimator of is given by
3.3 Large Sample Properties
To establish the large sample properties of , we shall impose the following assumptions:
Assumption 3.1.
and .
Assumption 3.2.
The support of -dimensional covariate is a Cartesian product of compact intervals.
Assumption 3.3.
We assume that there exist three positive constants such that
Assumption 3.4.
There are , , , , , and in and such that
as , where for .
Assumption 3.5.
, and , where and is the usual Frobenius norm defined by for any matrix .
Assumption 3.6.
is a strictly concave function defined on , i.e. , and the range of contains .
Assumption 3.1 ensures the asymptotic variance to be bounded.
Assumption 3.2 restricts the covariates to be bounded. This
condition, though restrictive, is commonly imposed in the nonparametric
regression literature. Assumption 3.3 requires the probability
function to be bounded away from 0 and 1. Condition of this sort is familiar
in the literature. Assumption 3.4
is needed to control for the approximation bias, and they
are commonly imposed in the nonparametric literature. Assumption 3.5
imposes restrictions on the smoothing parameter so that the proposed
estimator of ATE is root-N consistent. This condition, however, is
practically unhelpful. We shall present a data driven approach to determine and . Assumption 3.6 is a mild restriction on
and is satisfied by all important special cases considered in the
literature.
Under the above assumptions, the following theorem establishes the consistency, asymptotic normality and the semiparmetric efficiency of .
Theorem 3.7.
Sketched proof can be found in Appendix A.4 and detailed proofs are provided in the supplementary material.
4 Variance Estimation
To conduct the statistical inference on , we need a consistent estimator of the asymptotic variance of . Note that the asymptotic varance of ,
depends on five unknown functionals. Direct estimation of the variance
requires replacing the five unknown functionals with consistent estimates.
In this section, we present an alternative estimation that does not require
estimation of those functionals.
To illustrate the idea, we denote:
and
with . Let and . Then is the moment estimator solving the following moment condition:
| (4.1) |
Applying Mean Value Theorem, we obtain
| (4.2) |
where lies on the line joining and . We show in the supplemental material that
| (4.3) |
Note that
| (4.4) |
where is a -dimensional
column vector whose last element is and other components are all of ’s.
5 Selection of Tuning Parameters
The large sample properties of the proposed estimator permit a wide range of values of and . This presents a dilemma for applied researchers who have only one finite sample and would like to have some guidance on the selection of smoothing parameters. In this section, we present a data-driven approach to select and . Notice that , and satisfy the following regression equations:
Since , and are consistent estimators of , and respectively, the mean-squared-error (MSE) of the nuisance parameters and are defined by
The smoothing parameters and shall be chosen to minimize and . Specifically, denote the upper bounds of and by and (e.g. in our simulation studies). The data-driven and are given by
6 Simulation Studies
In this section, we conduct a small scale simulation
study to evaluate the finite sample performance of the proposed estimator.
To evaluate the performance of our estimator against the existing
alternatives, particularly the estimators proposed by Wang and Tchetgen Tchetgen (2017), we adopt the exact same design (i.e., the same data generating processes
(DGP)). In each Monte Carlo run, we generate sample of data from DGP for two
sizes: and respectively, and from each sample we compute
our estimator and other existing estimators. We then repeat the Monte Carlo
runs for times.
The observed baseline covariates are , where include an
intercept term and a continuous random variable uniformly
distributed on the interval . The unmeasured
confounder is a Bernoulli random variable with mean 0.5. The
instrumental variable , treatment variable and outcomes variable are generated according to the simulation design of Wang and Tchetgen Tchetgen (2017). The true value of the average treatment effect is .
We compute the proposed estimator (cbe), the naive estimator, the multiply robust estimator (mr) and the bounded multiply robust estimator (b-mr) proposed by Wang and Tchetgen Tchetgen (2017). Details of calculations are given below.
-
1.
the proposed estimator (cbe) is computed with ;
-
2.
the naive estimator is computed by the difference of group means between treatment and control groups;
-
3.
the multiply robust estimator (mr) and the bounded multiply robust estimator (b-mr) are computed by the procedures proposed by Wang and Tchetgen Tchetgen (2017).
The multiply robust estimator (mr) and the bounded multiply robust estimator
(b-mr) proposed by Wang and Tchetgen Tchetgen (2017) depend on parameterization of five
unknown functionals. In their paper they considered several models, denoted
by , and (see Wang and Tchetgen Tchetgen (2017) for a detailed discussion of the model specification).
Following Wang and Tchetgen Tchetgen (2017), we consider scenarios where some or all
functionals are misspecified.
| Estimators | Bias | Stdev | RMSE |
|---|---|---|---|
| Naive | -0.057 | 0.045 | 0.073 |
| mr(All) | 0.003 | 0.139 | 0.139 |
| mr() | 0.004 | 0.139 | 0.139 |
| mr() | -0.004 | 0.163 | 0.163 |
| mr() | -30.973 | 883.036 | 884.579 |
| mr(None) | -13.887 | 419.412 | 419.648 |
| b-mr(All) | 0.006 | 0.145 | 0.145 |
| b-mr() | -0.015 | 0.163 | 0.164 |
| b-mr() | -0.010 | 0.207 | 0.207 |
| b-mr() | 0.008 | 0.142 | 0.143 |
| mr(None) | -0.137 | 0.648 | 0.663 |
| cbe | 0.003 | 0.152 | 0.152 |
| Estimators | Bias | Stdev | RMSE |
| Naive | -0.056 | 0.031 | 0.064 |
| mr(All) | -0.002 | 0.102 | 0.102 |
| mr() | -0.0005 | 0.102 | 0.102 |
| mr() | -0.011 | 0.121 | 0.121 |
| mr() | -94.930 | 1737.95 | 1740.541 |
| mr(None) | 9.708 | 240.259 | 240.455 |
| b-mr(All) | 0.003 | 0.104 | 0.104 |
| b-mr() | -0.021 | 0.134 | 0.136 |
| b-mr() | -0.008 | 0.141 | 0.141 |
| b-mr() | 0.002 | 0.103 | 0.103 |
| b-mr(None) | 0.224 | 0.638 | 0.676 |
| cbe | 0.004 | 0.110 | 0.110 |
The true value for of the average tratment effects is 0.087. Bias, standard deviation (Stdev), root mean squared error (RMSE) of each estimator after Monte Carlo trials are reported. All: all of the three models are correctly specified; : only the model is correctly specified; : only the model is correctly specified; : only the model is correctly specified; None: all of the models are misspecified.
| Methods | Situation | Deviation Estimate |
| All | 3.04 | |
| 3.19 | ||
| mr | 3.22 | |
| 2260.0 | ||
| None | 3596.7 | |
| All | 3.04 | |
| 3.19 | ||
| b-mr | 3.22 | |
| 2078.0 | ||
| None | 3572.2 | |
| cbe | —- | 3.41 |
| Methods | Situation | Deviation Estimate |
| All | 3.04 | |
| 3.20 | ||
| mr | 3.22 | |
| 2291.9 | ||
| None | 1363.0 | |
| All | 3.04 | |
| 3.20 | ||
| b-mr | 3.23 | |
| 1491.8 | ||
| None | 1341.8 | |
| cbe | —- | 3.36 |
The true value of efficient deviation is 3.04. All: all of the three models are correctly specified; : only the model is correctly specified; : only the model is correctly specified; : only the model is correctly specified; None: all of the models are misspecified.
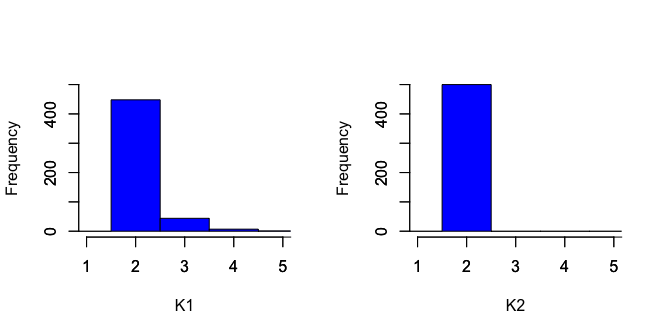
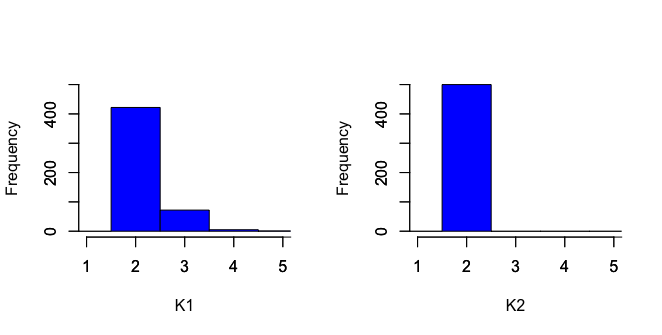
Table 1 reports the bias, standard deviation (Stdev), and the root mean
square error (RMSE) of from the 500 Monte Carlo runs. In
each Monte Carlo run, we use the data driven approach to select and and their histograms are depicted in Figure 1. The estimated
asymptotic variances are reported in Table 2.
Glancing at these tables, we have the following observations:
-
1.
The naive estimator has large bias. This is not surprising since it ignores the confounding effect.
-
2.
The multiple robust estimators (mr) of Wang and Tchetgen Tchetgen (2017) has huge bias when some functionals are misspecified.
-
3.
The bounded multiple robust estimator (b-mr) of Wang and Tchetgen Tchetgen (2017) is more robust than mr-estimator, but it still has a significant bias if some functionals are misspecified. And the bias does not valish as the sample size increases. Moreover, if all functionals are misspecified, the bias of b-mr estimator is substantially large.
-
4.
The proposed estimator (cbe) is unbiased for both and . Its performance (Bias, Stdev, RMSE) is comparable to Wang and Tchetgen Tchetgen (2017) ’s estimator when all functionals are correctly parameterized.
-
5.
In variance estimation, both the multiple robust estimator (mr) and the bounded multiple robust estimator (b-mr) have large biases when some functionals are misspecified. In contrast, the proposed variance estimator is consistent.
-
6.
The histograms in Figure 1 reveal that for both and , and are most preferred, suggesting that the growing rate of and is slow, an observation consistent with Assumption 3.5.
Overall, the simulation results show that the proposed estimator out-performs the existing estimators.
7 Concluding Remarks
Most of the existing treatment effect literature on
observational data assume that all confounders are observed and available to
researchers. In applications, it is often the case that some confounders are
not observed or not available. Wang and Tchetgen Tchetgen (2017) studied identification
and estimation of the average treament effect when some confounders are not
observed. They propose to parameterize five unknown functionals and show
that their estimation is consistent when certain functionals are correctly
specified and is efficient when all functionals are correctly specified.
This paper proposes an alternative estimation. Unlike Wang and Tchetgen Tchetgen (2017), the proposed estimation does not parameterize any of the functionals and
is always consistent. Moreover, the proposed estimator attains the
semiparametric efficiency bound. A simple asymptotic variance estimator is
presented, and a small scale simulation study suggests the practicality of
the proposed procedure.
Our procedure only applies to the binary treatment with unmeasured confounders. However, other forms of treatment, such as multiple valued or continuous treatment, may arise in applications. Extension of the proposed methodology to those forms of treatment with unmeasured confounders is certainly of great interest. This extension shall be pursued in a future project.
References
- (1)
- Abadie (2003) Abadie, A. (2003): “Semiparametric instrumental variable estimation of treatment response models,” Journal of Econometrics, 113(2), 231–263.
- Abadie, Angrist, and Imbens (2002) Abadie, A., J. Angrist, and G. Imbens (2002): “Instrumental Variables Estimates of the Effect of Subsidized Training on the Quantiles of Trainee Earnings,” Econometrica, 70(1), 91–117.
- Angrist, Imbens, and Rubin (1996) Angrist, J. D., G. W. Imbens, and D. B. Rubin (1996): “Identification of Causal Effects Using Instrumental Variables (Disc: P456-472),” Publications of the American Statistical Association, 91(434), 444–455.
- Chan, Yam, and Zhang (2016) Chan, K. C. G., S. C. P. Yam, and Z. Zhang (2016): “Globally efficient non-parametric inference of average treatment effects by empirical balancing calibration weighting,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 78(3), 673–700.
- Chen (2007) Chen, X. (2007): “Large sample sieve estimation of semi-nonparametric models,” Handbook of econometrics, 6, 5549–5632.
- Chen, Hong, and Tarozzi (2008) Chen, X., H. Hong, and A. Tarozzi (2008): “Semiparametric efficiency in GMM models with auxiliary data,” Ann. Statist., 36(2), 808–843.
- Cheng, Small, Tan, and Have (2009) Cheng, J., D. S. Small, Z. Tan, and T. R. T. Have (2009): “Efficient nonparametric estimation of causal effects in randomized trials with noncompliance,” Biometrika, 96(1), 19–36.
- Dehejia and Wahba (1999) Dehejia, R. H., and S. Wahba (1999): “Causal effects in nonexperimental studies: Reevaluating the evaluation of training programs,” Journal of the American statistical Association, 94(448), 1053–1062.
- Hansen (1982) Hansen, L. (1982): “Large sample properties of generalized method of moments estimators,” Econometrica, 50, 1029–1054.
- Hansen, Heaton, and Yaron (1996) Hansen, L., J. Heaton, and A. Yaron (1996): “Finite-sample properties of some alternative GMM estimators,” Journal of Business & Economic Statistics, 14(3), 262–280.
- Heckman, Ichimura, and Todd (1998) Heckman, J. J., H. Ichimura, and P. Todd (1998): “Matching as an econometric evaluation estimator,” The review of economic studies, 65(2), 261–294.
- Heckman, Ichimura, and Todd (1997) Heckman, J. J., H. Ichimura, and P. E. Todd (1997): “Matching as an econometric evaluation estimator: Evidence from evaluating a job training programme,” The review of economic studies, 64(4), 605–654.
- Hirano, Imbens, and Ridder (2003) Hirano, K., G. Imbens, and G. Ridder (2003): “Efficient Estimation of Average Treatment Effects Using the Estimated Propensity Score,” Econometrica, 71(4), 1161–1189.
- Imai and Ratkovic (2014) Imai, K., and M. Ratkovic (2014): “Covariate balancing propensity score,” J. R. Statist. Soc. B (Statistical Methodology), 76(1), 243–263.
- Imbens, Newey, and Ridder (2006) Imbens, G., W. Newey, and G. Ridder (2006): “Mean-Squared-Error Calculations for Average Treatment Effects,” Unpublished manuscript, University of California Berkeley.
- Imbens, Spady, and Johnson (1998) Imbens, G., R. Spady, and P. Johnson (1998): “Information Theoretic Approaches to Inference in Moment Condition Models,” Econometrica, 66(2), 333–357.
- Imbens and Angrist (1994) Imbens, G. W., and J. D. Angrist (1994): “Identification and Estimation of Local Average Treatment Effects,” Econometrica, 62(2), 467–475.
- Imbens and Rubin (2015) Imbens, G. W., and D. B. Rubin (2015): Causal inference in statistics, social, and biomedical sciences. Cambridge University Press.
- Imbens and Wooldridge (2009) Imbens, G. W., and J. M. Wooldridge (2009): “Recent developments in the econometrics of program evaluation,” Journal of economic literature, 47(1), 5–86.
- Kitamura and Stutzer (1997) Kitamura, Y., and M. Stutzer (1997): “An information-theoretic alternative to generalized method of moments estimation,” Econometrica, 65(4), 861–874.
- Newey (1994) Newey, W. K. (1994): “The Asymptotic Variance of Semiparametric Estimators,” Econometrica, 62(6), 1349–1382.
- Newey (1997) (1997): “Convergence Rates and Asymptotic Normality for Series Estimators,” Journal of Econometrics, 79, 147–168.
- Ogburn, Rotnitzky, and Robins (2015) Ogburn, E. L., A. Rotnitzky, and J. M. Robins (2015): “Doubly robust estimation of the local average treatment effect curve,” J R Stat Soc, 77(2), 373–396.
- Owen (1988) Owen, A. (1988): “Empirical likelihood ratio confidence intervals for a single functional,” Biometrika, 75(2), 237–249.
- Qin and Lawless (1994) Qin, J., and J. Lawless (1994): “Empirical likelihood and general estimating equations,” Ann. Statist., 22, 300–325.
- Rosenbaum (1987) Rosenbaum, P. R. (1987): “Model-based direct adjustment,” J. Am. Statist. Ass., 82(398), 387–394.
- Rosenbaum (2002) (2002): “Observational studies,” in Observational studies, pp. 1–17. Springer.
- Rosenbaum et al. (2002) Rosenbaum, P. R., et al. (2002): “Covariance adjustment in randomized experiments and observational studies,” Statistical Science, 17(3), 286–327.
- Rosenbaum and Rubin (1983) Rosenbaum, P. R., and D. B. Rubin (1983): “The central role of the propensity score in observational studies for causal effects,” Biometrika, 70(1), 41–55.
- Rosenbaum and Rubin (1984) (1984): “Reducing bias in observational studies using subclassification on the propensity score,” J. Am. Statist. Ass., 79(387), 516–524.
- Tan (2006) Tan, Z. (2006): “Regression and Weighting Methods for Causal Inference Using Instrumental Variables,” Publications of the American Statistical Association, 101(476), 1607–1618.
- Tan (2010) Tan, Z. (2010): “Bounded, efficient and doubly robust estimation with inverse weighting,” Biometrika, 97(3), 661–682.
- Tseng and Bertsekas (1987) Tseng, P., and D. P. Bertsekas (1987): “Relaxation methods for problems with strictly convex separable costs and linear constraints,” Mathematical Programming, 38(3), 303–321.
- Wang and Tchetgen Tchetgen (2017) Wang, L., and E. Tchetgen Tchetgen (2017): “Bounded, efficient and multiply robust estimation of average treatment effects using instrumental variables,” Journal of the Royal Statistical Society: Series B (Statistical Methodology).
- Yiu and Su (2018) Yiu, S., and L. Su (2018): “Covariate association eliminating weights: a unified weighting framework for causal effect estimation,” Biometrika.
Appendix A Appendix
A.1 Discussion on
To construct our estimator, we need to specify the sieve basis . Although the approximation theory is derived for general sequences of sieve basis, the most common class of functions are power series and splines. In particular, we can approximate any function by , where is a prespecified sieve basis. Because , we can also use as the new basis for approximation. By choosing appropriately we obtain a system of orthonormal basis (with respect to some weights). In particular, we choose so that
| (A.1) |
We define the usual Frobenius norm for any matrix . Define
| (A.2) |
In general, this bound depends on the array of basis that is used. Newey (1994, 1997) showed that
-
1.
for power series: there exists a universal constant such that ;
-
2.
for regression splines: there exists a universal constant such that .
A.2 Duality of Constrained Optimization
Let be a distance measure that is continuously differentiable in , non-negative, strictly convex in and . The general idea of calibration is to minimize the aggregate distance between the final weights to a given vector of design weights subject to moment constraints. Being motivated by (3.4), we consider to construct the calibration weights by solving the following constrained optimization problem:
| (A.5) |
where as the sample size , yet with . The constrained optimization problem stated above is equivalent to two separate constrained optimization problems.
| (A.6) | |||
| (A.7) |
Because the primal problems (A.6) and (A.7) are convex separable programs with linear
constraints, Tseng and Bertsekas (1987) showed that the dual problems
are unconstrained convex maximization problems that can be solved by
numerical efficient and stable algorithms.
We show the dual of (A.6) is the unconstrained optimization (3.8) by using the methodology introduced in Tseng and Bertsekas (1987). Let , , , , and , then we can rewrite the problem (A.6) as
For every , we define the conjugate convex function (Tseng and Bertsekas, 1987) of to be
where the third equality follows by , and satisfies the first order condition:
then we can have
where
By Tseng and Bertsekas (1987), the dual problem of (A.6) is
where is the -th column of , i,e., , which is our formulation (3.8).
Since is strictly convex, i.e., , and , then is also strictly convex and is strictly increasing. Note that
Differentiating on both sides in above equation yields:
Since , we can have
then we differentiate on both sides to get , which implies
Therefore, the convexity of is equivalent to the concavity of .
A.3 Convergence Rates of Estimated Weights
The following result ensures the consistency of , and as well as their convergence rates. The proof is presented in Section 2 of the supplemental material.
A.4 Sketched Proof of Theorem 3.7
The detailed proof of Theorem 3.7 is given in the supplementary material. Here we present the outline of whole the proof. By Assumption 3.5, , without loss of generality, we assume that . We introduce the following notation: let , and be the theoretical counterparts of , and defined by
We also introduce the following notation:
where lies on the line joining and . Note that is the weighted projection of on the space linearly spanned by . Note that
We first derive the influence function of , and similarly obtain that of . We can decompose as follows:
| (A.8) | ||||
| (A.9) | ||||
| (A.10) | ||||
| (A.11) | ||||
| (A.12) | ||||
| (A.13) | ||||
| (A.14) | ||||
| (A.15) | ||||
| (A.16) |
The following lemmas are proved in the supplemental material.