A Simple Information-Based Approach to Unsupervised Domain-Adaptive Aspect-Based Sentiment Analysis
Abstract
Aspect-based sentiment analysis (ABSA) is a fine-grained sentiment analysis task which aims to extract the aspects from sentences and identify their corresponding sentiments. Aspect term extraction (ATE) is the crucial step for ABSA. Due to the expensive annotation for aspect terms, we often lack labeled target domain data for fine-tuning. To address this problem, many approaches have been proposed recently to transfer common knowledge in an unsupervised way, but such methods have too many modules and require expensive multi-stage preprocessing. In this paper, we propose a simple but effective technique based on mutual information maximization, which can serve as an additional component to enhance any kind of model for cross-domain ABSA and ATE. Furthermore, we provide some analysis of this approach. Experiment results111The code is available at https://github.com/CasparSwift/DA_MIM show that our proposed method outperforms the state-of-the-art methods for cross-domain ABSA by 4.32% Micro-F1 on average over 10 different domain pairs. Apart from that, our method can be extended to other sequence labeling tasks, such as named entity recognition (NER).
1 Introduction
Aspect-Based Sentiment Analysis (ABSA) Liu (2012); Pontiki et al. (2015) task can be split into two sub-tasks: Aspect Term Extraction (ATE) and Aspect Sentiment Classification (ASC). The former extracts the aspect terms from sentences while the latter aims to predict the sentiment polarity of every aspect term. ATE is considered to be a crucial step for ABSA because the errors of ATE may be propagated to the ASC task in the following stage. However, due to the expensive fine-grained token-level annotation for aspect terms, we often lack labeled training data for various domains, which becomes the major obstacle for ATE.
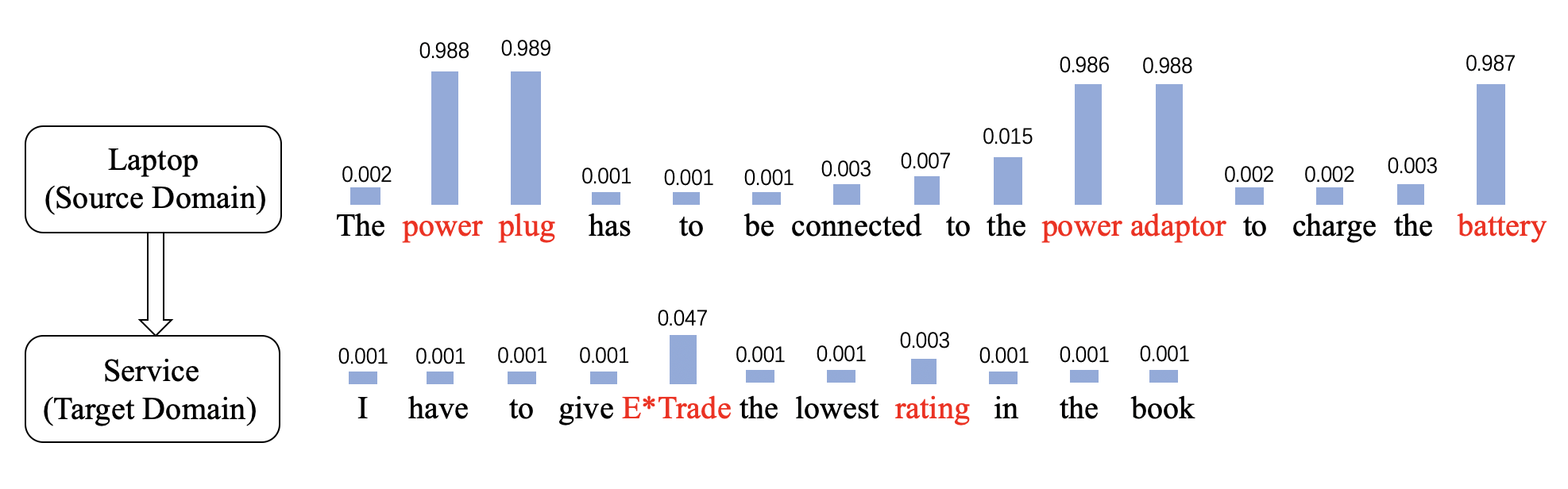
To address such issue, previous studies follow the Unsupervised Domain Adaptation (UDA) Ramponi and Plank (2020) scenario, which aims to transfer common knowledge from the source domain to the target domain. In UDA settings, we only have labeled source domain data and unlabeled target domain data. However, most aspect terms are strongly related to specific domains. The distribution of aspect terms may be significantly different across the domains, which causes performance degradation when transferring the domain knowledge. As shown in Figure 1, the model trained on the source domain (laptop) does not generalize well in the target domain (service). The model can easily extract the aspects related to laptop, such as "power plug", "power adaptor" and "battery", but it fails to extract the aspect terms "E*Trade" and "rating" that rarely appear in the laptop domain. Therefore, how to accurately discover the aspect terms from the unlabeled target domain data (raw texts) becomes the key challenge for cross-domain ABSA or ATE.
Previous studies propose several approaches to tackle this problem. However, these methods still have some shortcomings in practical applications: (1) Model Complexity. Many existing approaches have multiple components, including domain classifier Li et al. (2019b); Gong et al. (2020); Chen and Qian (2021), auto-encoder Wang and Pan (2018), syntactically-aware self-attention Pereg et al. (2020). Some studies introduce auxiliary tasks such as opinion co-extraction Ding et al. (2017); Wang and Pan (2018, 2019); Li et al. (2019b); Pereg et al. (2020) and part-of-speech/dependency prediction Wang and Pan (2018); Gong et al. (2020). Adding too many training objectives to the model may make it hard to optimize. Although these approaches are fancy and novel, we still need to seek for a simple but effective method according to the principle of Ockham’s Razor. (2) Multi-Stage Preprocessing. Many previous methods require carefully designed multi-stage preprocessing, including non-lexical features extraction Jakob and Gurevych (2010); Li et al. (2012); Ding et al. (2017); Wang and Pan (2018); Pereg et al. (2020); Gong et al. (2020); Chen and Qian (2021) and target domain review generation Yu et al. (2021). However, these preprocessing approaches are expensive when applied to real-world large scale datasets. Therefore, a single-stage method in an end-to-end manner is preferred. (3) Extensibility. All the above-mentioned methods are specifically designed for ABSA or ATE. However, essentially both ABSA and ATE can be formulated as sequence tagging tasks Mitchell et al. (2013); Zhang et al. (2015). It’s necessary to further investigate a unified technical scheme which can solve some other cross-domain extractive tagging tasks (e.g. named entity recognition (NER)).
In this paper, we get back to analyzing the intrinsic reason for the performance degradation when transferring aspect terms. From Figure 1, we have two important observations: (1) Class Collapse. The predictions tend to collapse into one single class (not an aspect term). (2) Unconfident Predictions. The predicted probabilities of ground truth aspects, namely "E*Trade" (0.047) and "rating" (0.003), are both slightly higher than other words. It seems that the model has the potential to identify correct aspects, but the prediction is not so confident.
Based on these two observations, in this paper, we propose a variant of the standard mutual information maximization technique Shi and Sha (2012); Li et al. (2020, 2021) named "FMIM" (means Fine-grained Mutual Information Maximization). The core idea is to maximize the token-level mutual information , where denotes input tokens and denotes their predicted labels. We maximize to prevent the model from collapsing into one class, and minimize to enhance the confidence of model’s predictions. Since it’s difficult to precisely compute because the joint distribution of is intractable, FMIM uses a simple reduce mean approach to approximate it. FMIM is a general technique and can be added on top of any kinds of backbones or methods for cross-domain ABSA and ATE. Without adding any other modules or auxiliary tasks as the previous work did, all we do is to simply introduce an additional mutual information loss term, which achieves the model simplification and does not require any preprocessing.
We find that FMIM is particularly effective for cross-domain ABSA and ATE. The experiment results show that our method substantially exceeds the state-of-the-art Yu et al. (2021) by 4.32% Micro-F1 (on average) over 10 domain pairs on ABSA task. Moreover, our method can be extended to other extractive tasks like cross-domain NER. We explore the effectiveness of our approach on cross-domain NER dataset and observe a considerable improvement over the state-of-the-art.
2 Related Work
Domain Adaptation
For sentiment analysis, existing domain adaptation methods mainly focus on coarse-grained sentiment classification: (1) Pivot-based methods Blitzer et al. (2006); Pan et al. (2010); Bollegala et al. (2012); Yu and Jiang (2016); Ziser and Reichart (2017, 2018, 2019) designed an auxiliary task of predicting pivots to transfer domain-invariant knowledge. (2) Adversarial methods Alam et al. (2018); Du et al. (2020) adopted Domain Adversarial Neural Network (DANN) Ganin et al. (2016), which introduces a domain classifier to classify the domains of the instances. This method commonly serves as an important component of many state-of-the-art DA methods Du et al. (2020); Chen and Qian (2021). (3) Feature-based methods Fang and Xie (2020); Giorgi et al. (2021); Li et al. (2021) introduced contrastive learning to learn domain-invariant features. For the sequence labeling task, we need token-level fine-grained features for the sentences.
Cross-Domain ABSA
Due to the accumulated errors between the two sub-tasks of ABSA (namely ATE and ASC), ABSA is typically combined together as a sequence labeling task Mitchell et al. (2013); Zhang et al. (2015); Li et al. (2019a). Thus we need fine-grained domain adaptation for ABSA, which is more difficult than the coarse-grained one. Jakob and Gurevych (2010) studied the cross-domain aspect extraction based on CRF. Another line of work Li et al. (2012); Ding et al. (2017); Wang and Pan (2018); Pereg et al. (2020); Gong et al. (2020); Chen and Qian (2021) utilized general syntactic or semantic relations to bridge the domain gaps, but they still relied on extra linguistic resources (e.g. POS tagger or dependency parser). Li et al. (2019b) proposed a selective adversarial training method with a dual memory to align the words. However, adversarial training has been proven to be unstable Fedus et al. (2018). FMIM considers cross-domain ABSA task from a brand-new perspective. We proved that only adding a mutual information maximization loss can substantially outperform all the above-mentioned methods with less complexity.
Mutual Information Maximization
Mutual Information (MI) is a measure of the mutual dependency of two random variables in information theory Shannon (1948). Mutual Information Maximization (MIM) serves as a powerful technique for self-supervised learning Oord et al. (2018); Hjelm et al. (2018); Tschannen et al. (2019) as well as semi-supervised learning Grandvalet et al. (2005). Therefore, MIM can help to learn domain-invariant features for domain adaptation approaches. Shi and Sha (2012) first proposed to maximize the MI between the target domain data and their estimated labels to learn discriminative clustering. Different from this approach, FMIM jointly optimizes the MI on both the source and target domains, which serves as an implicit alignment between the two domains. Moreover, most of the existing methods Shi and Sha (2012); Khan and Heisterkamp (2016); Li et al. (2020, 2021) only adopt MIM technique to deal with cross-domain image or sentiment classification tasks. To the best of our knowledge, this is the first work that illustrates the effectiveness of MIM for cross-domain sequence labeling tasks.
3 Methodology
In this section, we first formulate our domain adaptation problem and introduce some notations. Then we present the proposed mutual information loss term and provide some analysis on it from both theoretical and empirical perspectives.
3.1 Fine-Grained Mutual Information Maximization (FMIM)
Let and denote the source domain training data and the target domain unlabeled data, respectively. For each sentence , where denote the tokens, we have the predicted labels . Each is the label predicted by a model and , where is the tag set and . Specifically, for ABSA, the tag set is O, POS, NEU, NEG222Different from the previous work Li et al. (2019b); Gong et al. (2020), we adopt a different unified tagging scheme for ABSA instead of using B, I, O to mark the aspect boundary. We extract the consecutive POS/NEU/NEG phrases as our final predictions. The experiment results show that the tagging scheme doesn’t influence the performance., while for NER, the tag set is O, PER, ORG, LOC, MISC. Theoretically, the mutual information between a token and predicted label can be formulated as follows (, are random variables here):
| (1) | ||||
However, Eq 1 is too complex to be precisely computed. We can use a mini-batch of data to approximate it. At each iteration of the training period, we randomly sample a mini-batch of data from , and sample a mini-batch of data from . Then, we collect and concatenate the model’s outputs (the probability distributions over the tag set after softmax activation) of all samples from and . After concatenation, we obtain an tensor , where equals to the sum of the token numbers of all samples. For illustration, we denote as the concatenation of tokens of all samples. Then, the -entry of the tensor indicates the conditional probability of the predicted label being tag given -th token in , denoted as .
For the first term of Eq 1 (information entropy of ), we first calculate the distribution of the tags within the mini-batch and . We define a tag probability by the reduce-mean of the model outputs:
| (2) |
Therefore, the first term can be approximated as:
| (3) |
For the second term (negative conditional entropy), we can approximate it by the model’s output probabilities as well:
| (4) |
Then we define our mutual information loss which is equivalent to the negative approximated mutual information. In practice, we do not expect to be as large as possible. Thus, as suggested by Li et al. (2020, 2021), we only maximize when it is smaller than a pre-defined threshold :
| (5) |
The overall training objective is simply to jointly optimize the proposed MI loss and the original cross entropy loss for sequence labeling. We use a hyperparameter to balance these two loss terms:
| (6) |
3.2 Analysis
We can understand FMIM from the following three perspectives:
Firstly, by minimizing (i.e. maximizing if ), we keep larger than a certain value . We push the distribution of the predicted label (in mini-batches from both source and target) away from the 0-1 distribution where . Consequently, we prevent the model from collapsing to a particular class and increase the diversity of the outputs Cui et al. (2020). The model can extract more aspects in target domain, which can enhance the recall without reducing precision. Thus we solve the problem of the class collapse in section 1.
Secondly, by minimizing (i.e. maximizing , namely, minimizing the conditional entropy). We encourage the model to make more confident predictions. Thus we solve the problem of unconfident predictions in section 1. Moreover, minimizing the conditional entropy intuitively enlarges the margin between different classes, which makes the decision boundary learned on source domain data easier to fall into the margin Grandvalet et al. (2005); Li et al. (2020, 2021). This is beneficial to the domain transferring.
Thirdly, MIM is a commonly used technique in unsupervised learning or self-supervised learning (SSL) Hjelm et al. (2018); Tschannen et al. (2019). According to the results given by Oord et al. (2018), mutual information is an upper bound of negative InfoNCE which is a loss function widely used in contrastive learning He et al. (2020); Chen et al. (2020a, b, c):
| (7) |
where is a constant. Therefore minimizing the InfoNCE is equivalent to maximizing mutual information. In other words, introducing can be viewed as an implicit way of contrastive learning.
4 Experiments
To evaluate the effectiveness of FMIM technique introduced in Section 3, we apply our method to cross-domain ABSA, ATE and NER datasets.
4.1 Experiment Setup
Datasets
Our experiment is conducted on four benchmarks with different domains: Laptop (), Restaurant (), Device (), and Service (). and are from SemEval ABSA challenge Pontiki et al. (2014, 2015, 2016). is provided by Hu and Liu (2004) and contains digital product reviews. is provided by Toprak et al. (2010) and contains reviews from web services.
It’s worth noting that there are two different dataset settings in previous studies, so we evaluate our method on both of them. For ABSA task, previous work Li et al. (2019a, b); Gong et al. (2020); Yu et al. (2021) conducted experiments for 10 domain pairs on the above-mentioned four domains. For ATE task only, previous work Wang and Pan (2018, 2019); Pereg et al. (2020); Chen and Qian (2021) conducted experiments for 6 domain pairs on , and . They use three different data splits with a fixed train-test ratio 3:1. Apart from that, the amount of sentences of some domains are different. Detailed statistics are shown in Table 1 and 2.
| Domain | Sentences | Train | Test |
|---|---|---|---|
| Laptop () | 3845 | 3045 | 800 |
| Restaurant () | 6035 | 3877 | 2158 |
| Device () | 3836 | 2557 | 1279 |
| Service () | 2239 | 1492 | 747 |
| Domain | Sentences | Train | Test |
|---|---|---|---|
| Laptop () | 3845 | 2884 | 961 |
| Restaurant () | 5841 | 4381 | 1460 |
| Device () | 3836 | 2877 | 959 |
| Domain | CoNLL2003 | CBS News |
|---|---|---|
| Train (labeled) | 15.0K | - |
| Train (unlabeled) | - | 398,990 |
| Dev | 3.5K | - |
| Test | 3.7K | 2.0K |
For cross-domain NER, following the same dataset setting of Jia et al. (2019); Jia and Zhang (2020), we take CoNLL2003 English dataset Sang and De Meulder (2003) and CBS SciTech News dataset collected by Jia et al. (2019) as the source and target domain data, respectively. Detailed statistics of the datasets are shown in Table 3.
Evaluation
For ABSA, all the experiments are repeated 5 times with 5 different random seeds and we report the Micro-F1 over 5 runs, which is the same as the previous work. Only correct aspect terms with correct sentiment predictions can be considered to be true positive instances. For ATE, following Chen and Qian (2021), we report the mean F1-scores of aspect terms over three splits with three random seeds (9 runs for each domain pair). For NER, we report the F1-score of named entities.
Implementation Details
For all the tasks, we use the pre-trained BERT-base-uncased Devlin et al. (2019) model provided by HuggingFace Wolf et al. (2019) as our feature extractor. The maximum input length of BERT is 128. Our sentiment classifier is a MLP with two hidden layers with hidden size 384. We take ReLU as the activation function. For the optimization of model parameters, we use the AdamW Loshchilov and Hutter (2018) as the optimizer with a fixed learning rate of or . We train the model for 20 epochs for ABSA and 3 epochs for NER.
For ABSA, we set for , for , for , for and for the rest of domain pairs. We set for cross-domain NER333Our results can be improved by tuning the hyperparameters carefully, but this is not what we mainly focus on..
For ATE, the hyperparameter settings are presented in Table 4.
| Hyperparameter | RL | LR | RD | DR | LD | DL |
|---|---|---|---|---|---|---|
| 0.015 | 0.01 | 0.015 | 0.01 | 0.015 | 0.01 | |
| 0.7 | 0.5 | 0.2 | 0.5 | 0.2 | 0.5 | |
| weight decay | 0.1 | 0.1 | 1 | 0.1 | 1 | 0.1 |
| batch size | 16 | 16 | 16 | 16 | 16 | 16 |
| Methods | SR | LR | DR | RS | LS | DS | RL | SL | RD | SD | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Hier-Joint Ding et al. (2017) | 31.10 | 33.54 | 32.87 | 15.56 | 13.90 | 19.04 | 20.72 | 22.65 | 24.53 | 23.24 | 23.71 |
| RNSCN Wang and Pan (2018) | 33.21 | 35.65 | 34.60 | 20.04 | 16.59 | 20.03 | 26.63 | 18.87 | 33.26 | 22.00 | 26.09 |
| AD-SAL Li et al. (2019b) | 41.03 | 43.04 | 41.01 | 28.01 | 27.20 | 26.62 | 34.13 | 27.04 | 35.44 | 33.56 | 33.71 |
| BERT-Base∗ Devlin et al. (2019) | 44.76 | 26.88 | 36.08 | 19.41 | 27.27 | 27.62 | 28.95 | 29.20 | 29.47 | 33.96 | 30.36 |
| BERT-Base Gong et al. (2020) | 44.66 | 40.38 | 40.32 | 19.48 | 25.78 | 30.31 | 31.44 | 30.47 | 27.55 | 33.96 | 32.43 |
| BERT-DANN Gong et al. (2020) | 45.84 | 41.73 | 34.68 | 21.60 | 25.10 | 18.62 | 30.41 | 31.92 | 34.41 | 23.97 | 30.83 |
| BERT-UDA Gong et al. (2020) | 47.09 | 45.46 | 42.68 | 33.12 | 27.89 | 28.03 | 33.68 | 34.77 | 34.93 | 32.10 | 35.98 |
| CDRG (Indep) Yu et al. (2021) | 44.46 | 44.96 | 39.42 | 34.10 | 33.97 | 31.08 | 33.59 | 26.81 | 25.25 | 29.06 | 34.27 |
| CDRG (Merge) Yu et al. (2021) | 47.92 | 49.79 | 47.64 | 35.14 | 38.14 | 37.22 | 38.68 | 33.69 | 27.46 | 34.08 | 38.98 |
| BERT-Base + FMIM (ours) | 50.20 | 53.24 | 54.98 | 42.78 | 43.20 | 46.69 | 38.20 | 32.49 | 35.87 | 35.38 | 43.30† |
| Methods | SR | LR | DR | RS | LS | DS | RL | SL | RD | SD | AVG |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Hier-Joint Ding et al. (2017) | 46.39 | 48.61 | 42.96 | 27.18 | 25.22 | 29.28 | 34.11 | 33.02 | 34.81 | 35.00 | 35.66 |
| RNSCN Wang and Pan (2018) | 48.89 | 52.19 | 50.39 | 30.41 | 31.21 | 35.50 | 47.23 | 34.03 | 46.16 | 32.41 | 40.84 |
| AD-SAL Li et al. (2019b) | 52.05 | 56.12 | 51.55 | 39.02 | 38.26 | 36.11 | 45.01 | 35.99 | 43.76 | 41.21 | 43.91 |
| BERT-Base∗ Devlin et al. (2019) | 54.93 | 30.98 | 40.15 | 22.92 | 31.63 | 31.27 | 35.07 | 36.96 | 32.08 | 38.17 | 35.42 |
| BERT-Base Gong et al. (2020) | 54.29 | 46.74 | 44.63 | 22.31 | 30.66 | 33.33 | 37.02 | 36.88 | 32.03 | 38.06 | 37.59 |
| BERT-DANN Gong et al. (2020) | 54.32 | 48.34 | 44.63 | 25.45 | 29.83 | 26.53 | 36.79 | 39.89 | 33.88 | 38.06 | 37.77 |
| BERT-UDA Gong et al. (2020) | 56.08 | 51.91 | 50.54 | 34.62 | 32.49 | 34.52 | 46.87 | 43.98 | 40.34 | 38.36 | 42.97 |
| CDRG (Indep) Yu et al. (2021) | 53.79 | 55.13 | 50.07 | 41.74 | 44.14 | 37.10 | 40.18 | 33.22 | 30.78 | 34.97 | 42.11 |
| CDRG (Merge) Yu et al. (2021) | 56.26 | 60.03 | 52.71 | 42.36 | 47.08 | 41.85 | 46.65 | 39.51 | 32.60 | 36.97 | 45.60 |
| BERT-Base + FMIM (ours) | 59.24 | 63.41 | 57.29 | 51.35 | 54.92 | 52.85 | 49.42 | 42.44 | 39.72 | 37.62 | 50.83† |
4.2 Baselines & Compared Methods
Cross-Domain ABSA
Hier-Joint Ding et al. (2017) use manually designed syntactic rule-based auxiliary tasks. RNSCN Wang and Pan (2018) is based on a novel recursive neural structural correspondence network. And an auxiliary task is designed to predict the dependency relation between any two adjacent words. AD-SAL Li et al. (2019b) dynamically learn an alignment between words by adversarial training. BERT-UDA Gong et al. (2020) incorporates masked POS prediction, dependency relation prediction and instance reweighting. BERT-Base Devlin et al. (2019) indicates directly fine-tuning BERT-base-uncased model on the source training data. BERT-DANN Gong et al. (2020) performs adversarial training on each word in the same way as Ganin et al. (2016). CDRG Yu et al. (2021) generates the target domain reviews with independent and merge training strategies.
Cross-Domain ATE
BERT-UDA can be modified for ATE by remapping the B/I/O labels. SA-EXAL Pereg et al. (2020) incorporates syntactic information with attention mechanism. BERT-Cross Xu et al. (2019) conducts BERT post-training on a combination of Yelp and Amazon corpus. BaseTagger Chen and Qian (2021) is a strong baseline which takes CNN as its backbone. SemBridge Chen and Qian (2021) uses semantic relations to bridge the domain gap.
Cross-Domain NER
Cross-Domain LM Jia et al. (2019) designs parameter generation network and performs cross-domain language modeling. Multi-Cell LSTM Jia and Zhang (2020) designs a multi-cell LSTM structure to model each entity type using a separate cell state.
| Methods | Embedding | RL | LR | RD | DR | LD | DL | Avg. |
|---|---|---|---|---|---|---|---|---|
| BERT-UDA Gong et al. (2020) | BERTB | 44.24 | 50.52 | 40.04 | 53.39 | 41.48 | 52.33 | 47.00 |
| SA-EXAL Pereg et al. (2020) | BERTB | 47.59 | 54.67 | 40.50 | 54.54 | 42.19 | 47.72 | 47.87 |
| BERT-Cross Xu et al. (2019) | BERTE | 46.30 | 51.60 | 43.68 | 53.15 | 44.22 | 50.04 | 48.17 |
| BaseTagger Chen and Qian (2021) | Word2vec | 48.86 | 61.42 | 40.56 | 57.67 | 43.75 | 51.95 | 50.70 |
| BaseTagger + FMIM | Word2vec | 49.74 | 65.60 | 40.64 | 59.38 | 44.22 | 51.87 | 51.91 |
| SemBridge Chen and Qian (2021) | Word2vec | 51.53 | 65.96 | 43.03 | 60.61 | 45.37 | 53.77 | 53.38 |
| SemBridge + FMIM | Word2vec | 49.00 | 67.41 | 43.10 | 63.30 | 45.68 | 53.00 | 53.58 |
| BERT-Base Devlin et al. (2019) | BERTB | 33.89 | 42.74 | 35.30 | 36.86 | 43.54 | 46.06 | 39.73 |
| BERT-Base + FMIM | BERTB | 52.00 | 71.63 | 38.73 | 65.18 | 44.62 | 49.46 | 53.58 |
| Methods | Micro-F1 | Raw Texts of Target Domain |
|---|---|---|
| Cross-Domain LM Jia et al. (2019) | 73.59 | 18,474K |
| Multi-Cell LSTM Jia and Zhang (2020) | 72.81 | 1.931K |
| Multi-Cell LSTM (All) Jia and Zhang (2020) | 73.56 | 8,664K |
| BERT-Base Devlin et al. (2019) | 74.23 | - |
| BERT-Base + FMIM (ours) | 75.32 | 45K |
4.3 Results for Cross-Domain ABSA
The overall results for cross-domain ABSA are shown in Table 5. As the previous work did, we conduct our experiments on 10 different domain pairs. We observe that BERT-Base+FMIM outperforms the state-of-the-art method CDRG Yu et al. (2021) in most of domain pairs except when is the target domain. Our approach achieve 1.3%9.47% absolute improvement of Micro-F1 compared to CDRG (Merge). When taking as the target domain, we can obtain 7.64%, 5.06% and 9.47% improvement respectively.
Following Gong et al. (2020); Yu et al. (2021), we also provide the results for the ATE sub-task in Table 6. We can observe that FMIM can consistently improve the performance of ATE on most of the domain pairs and achieves an average improvement of 5.23% Micro-F1 compared to CDRG.
(1) The vanilla BERT-base model Devlin et al. (2019) can beat the previous models based on RNN or LSTM (Hier-Joint Ding et al. (2017), RNSCN Wang and Pan (2018)) and it has a competitive performance with AD-SAL Li et al. (2019b), which shows that the language model pre-trained on large-scale corpora has the generalization ability across domains to some extent. But this result still can be improved by some specific domain adaptation techniques.
(2) The improvement of BERT-DANN is quite marginal and inconsistent across 10 domain pairs compared to the vanilla BERT-base model. This is reasonable because BERT-DANN discriminates the domains in word level, which cannot capture the semantic relations between words. Moreover, many common words may appear in both source and target domain, and classifying the domains of these words will unavoidably introduce noise to the model and result in unstable training.
(3) FMIM substantially outperforms CDRG Yu et al. (2021), the state-of-the-art method for cross-domain ABSA. We think the reason for this improvement is that simply generating target domain review data may not directly address the class collapse and unconfident predictions problems. However, FMIM is entirely orthogonal with CDRG, so adding it on the top of CDRG can possibly achieve better performance.
4.4 Results for Cross-Domain ATE
Table 7 shows the results for cross-domain ATE. In this section, we illustrate the effectiveness of adding FMIM to other methods. All the methods with FMIM outperforms the BERT-UDA, SA-EXAL and BERT-Cross baselines. When adding on top of BaseTagger, we can observe an absolute improvement of 1.21%. For the state-of-the-art SemBridge method, we improve the F1-score by 1.45%, 2.69%, 0.31% on , , . When taking the vanilla BERT-base as our backbone, FMIM can achieve an improvement of 13.85%. This results illustrates that FMIM can serve as an effective technique to enhance common cross-domain ATE models.
4.5 Results for Cross-Domain NER
The experiment results on unsupervised domain adaptation of NER are presented in Table 8. Due to the similarity of NER task and aspect term extraction task, FMIM based on BERT-Base Devlin et al. (2019) can still outperform the state-of-the-art cross-domain NER model Multi-Cell LSTM Jia and Zhang (2020) by 1.76% F1-scores. FMIM also exceeds the baseline of directly using BERT-Base by 1.09% F1-scores. It’s worth noting that the amount the raw texts of target domain we used is 192 times less than that of Jia and Zhang (2020), which shows the great data efficiency of FMIM.
| Method | Predictions | |||
| Sentence: Trading through e*trade is fairly easy. | ||||
| BERT-Base | 0.54 | 0.33 | 0.21 | None× |
| BERT-Base + FMIM (ours) | 0.88 | 0.04 | 0.84 | Trading (POS)✓, e*trade (POS)✓ |
| Sentence: The few problems that I have had with Etrade are mainly concerning delayed trade confirmations. | ||||
| BERT-Base | 0.22 | 0.13 | 0.09 | None× |
| BERT-Base + FMIM (ours) | 0.74 | 0.06 | 0.68 | Etrade (NEG)✓, trade confirmations (NEG)✓ |
| E1: facilities including a comprehensive [glossary]× of [terms]× , [FAQs]✓ , and a [forum]✓. |
| E2: The [faculty in]× OH was great and so was the administration . |
| E3: [ETrade]✓ gives you a $75 bonus upon establishing an account . |
5 Analysis
Ablation Study
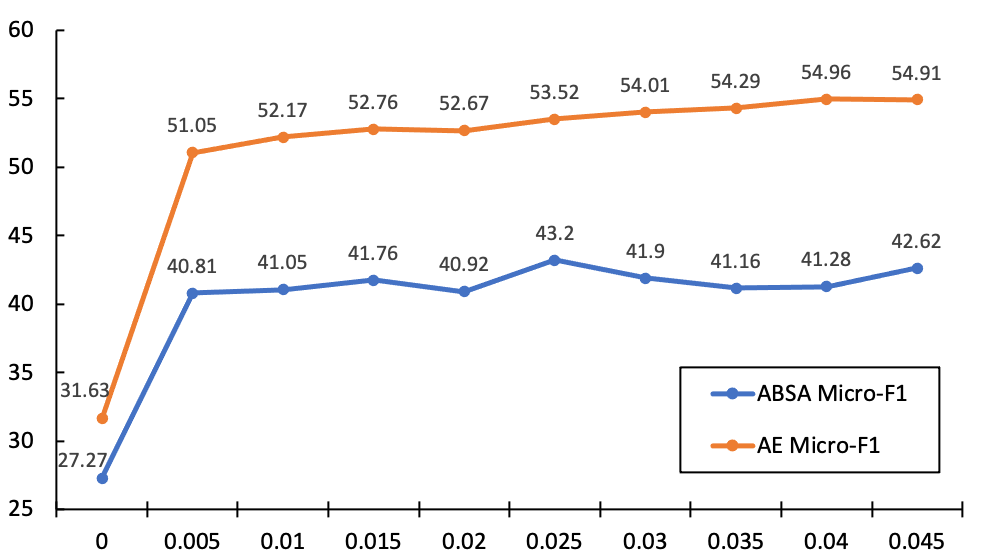
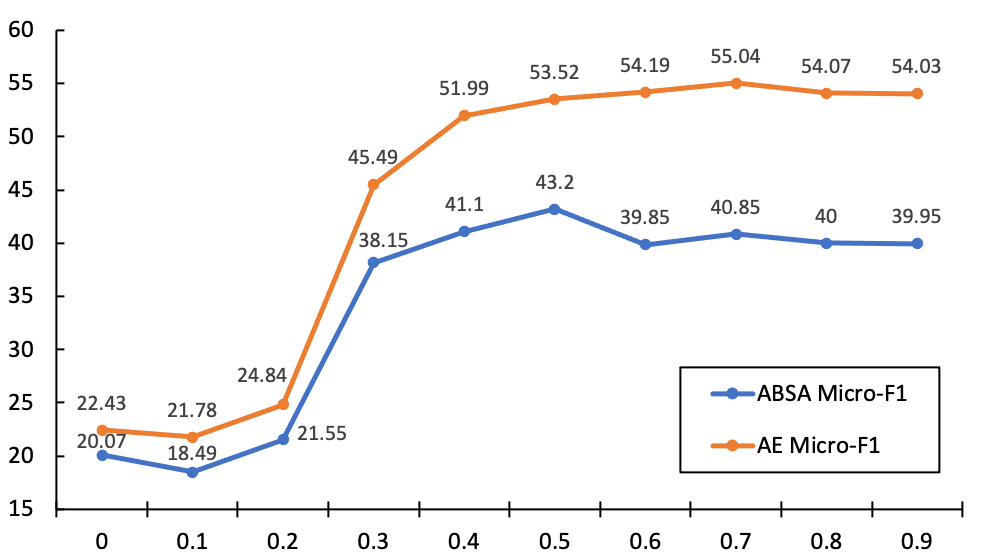
Since FMIM has only one single component, we can still investigate the effect of the hyperparameters. There are two crucial hyperparameters in our MI loss (see Eq 5 and Eq 6): the loss balancing factor and the entropy threshold . We test the performance of the model with different values of and on setting.
On one hand, we keep and alter the value of in the range from 0 to 0.045. As illustrated in Figure 2, our method degenerates into BERT-Base baseline when setting , which results in worse performance. For ABSA, the Micro-F1 reaches the peak (43.20) when setting . Moreover, we find FMIM’s robustness to the change of . The performance keeps in a relatively stable range of 40.8143.20 when varying from 0.005 to 0.045. For ATE sub-task, we can observe that the performance maintains an upward trend with the increasing of . This demonstrates that FMIM’s effectiveness in ATE task. However, since ATE is a sub-task, improving ATE does not necessarily improve ABSA. One can try to find a trade-off between them by tuning carefully.
On the other hand, we keep and change the value of from 0 to 0.9. As illustrated in Figure 3, FMIM achieves the best performance when setting . Similar to the phenomenon shown in Figure 2, the performance of our model maintains stable when . FMIM collapses when , because setting an extremely small is equivalent to only optimizing the conditional entropy without optimizing , which may make the wrong predictions more confident. In practice, simply setting can observe a fairly competitive performance.
Case Study
In this section, we further study some cases to sufficiently illustrate our model’s effectiveness qualitatively. With comparison to BERT-Base baseline, we calculate the two terms of mutual information (i.e. entropy of predicted labels and conditional entropy ) to demonstrate the necessity of maximizing it.
Table 9 shows two sentences extracted from the service domain test data in setting. For BERT-Base method, the model fails to give any predictions with a lower , a higher and a lower mutual information. While our FMIM method substantially increases the mutual information of the two sentences by 0.63 and 0.59, which lowers and increases . This leads to the correct final predictions.
Error Analysis
We further study the errors that our approach still makes to provide some suggestions for future research. As shown in Table 10, there are three main error types. (1) discontinuous extraction, which may predict "glossary" and "terms" as aspects but omit "of" in the middle. (2) over-extraction, which may view the following "in" as part of the aspects. (3) under-recall, which may omit some aspects that require complex semantic relations. The inconsistent annotation of the dataset may also be a reason for this phenomenon.
6 Conclusion
In this paper, we propose using the fine-grained mutual information maximization (FMIM) technique to improve unsupervised domain adaptation for ABSA, ATE and NER. Our method is simple but has incredibly significant improvements over the strong baselines.
The question of how to efficiently transfer domain knowledge remains unanswered. In the future, we plan to evaluate our method on more different tasks. Moreover, our proposed FMIM technique only introduces an additional loss term, which is orthogonal to all the previous domain adaptation methods for ABSA and NER. The effect of jointly using them still needs to be further explored.
Acknowledgments
This work was supported by National Natural Science Foundation of China (61772036), Beijing Academy of Artificial Intelligence (BAAI) and Key Laboratory of Science, Technology and Standard in Press Industry (Key Laboratory of Intelligent Press Media Technology). Xiaojun Wan is the corresponding author. Thank the anonymous reviewers for the constructive suggestions. Thank Xinyu for useful discussions. Thank Yifan for paper revision.
References
- Alam et al. (2018) Firoj Alam, Shafiq Joty, and Muhammad Imran. 2018. Domain adaptation with adversarial training and graph embeddings. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers).
- Blitzer et al. (2006) John Blitzer, Ryan McDonald, and Fernando Pereira. 2006. Domain adaptation with structural correspondence learning. In Proceedings of the 2006 conference on empirical methods in natural language processing, pages 120–128.
- Bollegala et al. (2012) Danushka Bollegala, David Weir, and John Carroll. 2012. Cross-domain sentiment classification using a sentiment sensitive thesaurus. IEEE transactions on knowledge and data engineering, 25(8):1719–1731.
- Chen et al. (2020a) Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. 2020a. A simple framework for contrastive learning of visual representations. In International conference on machine learning, pages 1597–1607. PMLR.
- Chen et al. (2020b) Ting Chen, Simon Kornblith, Kevin Swersky, Mohammad Norouzi, and Geoffrey Hinton. 2020b. Big self-supervised models are strong semi-supervised learners. arXiv preprint arXiv:2006.10029.
- Chen et al. (2020c) Xinlei Chen, Haoqi Fan, Ross Girshick, and Kaiming He. 2020c. Improved baselines with momentum contrastive learning. arXiv preprint arXiv:2003.04297.
- Chen and Qian (2021) Zhuang Chen and Tieyun Qian. 2021. Bridge-based active domain adaptation for aspect term extraction. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pages 317–327.
- Cui et al. (2020) Shuhao Cui, Shuhui Wang, Junbao Zhuo, Liang Li, Qingming Huang, and Qi Tian. 2020. Towards discriminability and diversity: Batch nuclear-norm maximization under label insufficient situations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 3941–3950.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 4171–4186.
- Ding et al. (2017) Ying Ding, Jianfei Yu, and Jing Jiang. 2017. Recurrent neural networks with auxiliary labels for cross-domain opinion target extraction. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 31.
- Du et al. (2020) Chunning Du, Haifeng Sun, Jingyu Wang, Qi Qi, and Jianxin Liao. 2020. Adversarial and domain-aware bert for cross-domain sentiment analysis. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 4019–4028.
- Fang and Xie (2020) Hongchao Fang and Pengtao Xie. 2020. Cert: Contrastive self-supervised learning for language understanding. arXiv preprint arXiv:2005.12766.
- Fedus et al. (2018) William Fedus, Mihaela Rosca, Balaji Lakshminarayanan, Andrew M Dai, Shakir Mohamed, and Ian Goodfellow. 2018. Many paths to equilibrium: Gans do not need to decrease a divergence at every step. In International Conference on Learning Representations.
- Ganin et al. (2016) Yaroslav Ganin, Evgeniya Ustinova, Hana Ajakan, Pascal Germain, Hugo Larochelle, François Laviolette, Mario Marchand, and Victor Lempitsky. 2016. Domain-adversarial training of neural networks. The Journal of Machine Learning Research, 17(1):2096–2030.
- Giorgi et al. (2021) John Giorgi, Osvald Nitski, Bo Wang, and Gary Bader. 2021. DeCLUTR: Deep contrastive learning for unsupervised textual representations. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pages 879–895. Association for Computational Linguistics.
- Gong et al. (2020) Chenggong Gong, Jianfei Yu, and Rui Xia. 2020. Unified feature and instance based domain adaptation for end-to-end aspect-based sentiment analysis. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 7035–7045.
- Grandvalet et al. (2005) Yves Grandvalet, Yoshua Bengio, et al. 2005. Semi-supervised learning by entropy minimization. In CAP, pages 281–296.
- He et al. (2020) Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick. 2020. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 9729–9738.
- Hjelm et al. (2018) R Devon Hjelm, Alex Fedorov, Samuel Lavoie-Marchildon, Karan Grewal, Phil Bachman, Adam Trischler, and Yoshua Bengio. 2018. Learning deep representations by mutual information estimation and maximization. In International Conference on Learning Representations.
- Hu and Liu (2004) Minqing Hu and Bing Liu. 2004. Mining and summarizing customer reviews. In Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining, pages 168–177.
- Jakob and Gurevych (2010) Niklas Jakob and Iryna Gurevych. 2010. Extracting opinion targets in a single and cross-domain setting with conditional random fields. In Proceedings of the 2010 conference on empirical methods in natural language processing, pages 1035–1045.
- Jia et al. (2019) Chen Jia, Xiaobo Liang, and Yue Zhang. 2019. Cross-domain ner using cross-domain language modeling. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 2464–2474.
- Jia and Zhang (2020) Chen Jia and Yue Zhang. 2020. Multi-cell compositional lstm for ner domain adaptation. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 5906–5917.
- Khan and Heisterkamp (2016) Mohammad Nazmul Alam Khan and Douglas R Heisterkamp. 2016. Adapting instance weights for unsupervised domain adaptation using quadratic mutual information and subspace learning. In 2016 23rd international conference on pattern recognition (ICPR), pages 1560–1565. IEEE.
- Li et al. (2020) Bo Li, Yezhen Wang, Tong Che, Shanghang Zhang, Sicheng Zhao, Pengfei Xu, Wei Zhou, Yoshua Bengio, and Kurt Keutzer. 2020. Rethinking distributional matching based domain adaptation. arXiv preprint arXiv:2006.13352.
- Li et al. (2012) Fangtao Li, Sinno Jialin Pan, Ou Jin, Qiang Yang, and Xiaoyan Zhu. 2012. Cross-domain co-extraction of sentiment and topic lexicons. In Proceedings of the 50th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 410–419.
- Li et al. (2021) Tian Li, Xiang Chen, Shanghang Zhang, Zhen Dong, and Kurt Keutzer. 2021. Cross-domain sentiment classification with contrastive learning and mutual information maximization. In ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pages 8203–8207. IEEE.
- Li et al. (2019a) Xin Li, Lidong Bing, Piji Li, and Wai Lam. 2019a. A unified model for opinion target extraction and target sentiment prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 6714–6721.
- Li et al. (2019b) Zheng Li, Xin Li, Ying Wei, Lidong Bing, Yu Zhang, and Qiang Yang. 2019b. Transferable end-to-end aspect-based sentiment analysis with selective adversarial learning. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 4590–4600.
- Liu (2012) Bing Liu. 2012. Sentiment analysis and opinion mining. Synthesis lectures on human language technologies, 5(1):1–167.
- Loshchilov and Hutter (2018) Ilya Loshchilov and Frank Hutter. 2018. Fixing weight decay regularization in adam.
- Mitchell et al. (2013) Margaret Mitchell, Jacqui Aguilar, Theresa Wilson, and Benjamin Van Durme. 2013. Open domain targeted sentiment. In Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing, pages 1643–1654.
- Oord et al. (2018) Aaron van den Oord, Yazhe Li, and Oriol Vinyals. 2018. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748.
- Pan et al. (2010) Sinno Jialin Pan, Xiaochuan Ni, Jian-Tao Sun, Qiang Yang, and Zheng Chen. 2010. Cross-domain sentiment classification via spectral feature alignment. In Proceedings of the 19th international conference on World wide web, pages 751–760.
- Pereg et al. (2020) Oren Pereg, Daniel Korat, and Moshe Wasserblat. 2020. Syntactically aware cross-domain aspect and opinion terms extraction. In Proceedings of the 28th International Conference on Computational Linguistics, pages 1772–1777.
- Pontiki et al. (2016) Maria Pontiki, Dimitrios Galanis, Haris Papageorgiou, Ion Androutsopoulos, Suresh Manandhar, Mohammad Al-Smadi, Mahmoud Al-Ayyoub, Yanyan Zhao, Bing Qin, Orphée De Clercq, et al. 2016. Semeval-2016 task 5: Aspect based sentiment analysis. In International workshop on semantic evaluation, pages 19–30.
- Pontiki et al. (2015) Maria Pontiki, Dimitrios Galanis, Harris Papageorgiou, Suresh Manandhar, and Ion Androutsopoulos. 2015. Semeval-2015 task 12: Aspect based sentiment analysis. In Proceedings of the 9th international workshop on semantic evaluation (SemEval 2015), pages 486–495.
- Pontiki et al. (2014) Maria Pontiki, Dimitris Galanis, John Pavlopoulos, Harris Papageorgiou, Ion Androutsopoulos, and Suresh Manandhar. 2014. SemEval-2014 task 4: Aspect based sentiment analysis. In Proceedings of the 8th International Workshop on Semantic Evaluation (SemEval 2014), pages 27–35, Dublin, Ireland. Association for Computational Linguistics.
- Ramponi and Plank (2020) Alan Ramponi and Barbara Plank. 2020. Neural unsupervised domain adaptation in nlp—a survey. In Proceedings of the 28th International Conference on Computational Linguistics, pages 6838–6855.
- Sang and De Meulder (2003) Erik F Sang and Fien De Meulder. 2003. Introduction to the conll-2003 shared task: Language-independent named entity recognition. arXiv preprint cs/0306050.
- Shannon (1948) Claude E Shannon. 1948. A mathematical theory of communication. The Bell system technical journal, 27(3):379–423.
- Shi and Sha (2012) Yuan Shi and Fei Sha. 2012. Information-theoretical learning of discriminative clusters for unsupervised domain adaptation. In Proceedings of the 29th International Coference on International Conference on Machine Learning, pages 1275–1282.
- Toprak et al. (2010) Cigdem Toprak, Niklas Jakob, and Iryna Gurevych. 2010. Sentence and expression level annotation of opinions in user-generated discourse. In Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics, pages 575–584.
- Tschannen et al. (2019) Michael Tschannen, Josip Djolonga, Paul K Rubenstein, Sylvain Gelly, and Mario Lucic. 2019. On mutual information maximization for representation learning. In International Conference on Learning Representations.
- Wang and Pan (2018) Wenya Wang and Sinno Jialin Pan. 2018. Recursive neural structural correspondence network for cross-domain aspect and opinion co-extraction. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 2171–2181.
- Wang and Pan (2019) Wenya Wang and Sinno Jialin Pan. 2019. Transferable interactive memory network for domain adaptation in fine-grained opinion extraction. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 7192–7199.
- Wolf et al. (2019) Thomas Wolf, Lysandre Debut, Victor Sanh, Julien Chaumond, Clement Delangue, Anthony Moi, Pierric Cistac, Tim Rault, Rémi Louf, Morgan Funtowicz, et al. 2019. Huggingface’s transformers: State-of-the-art natural language processing. ArXiv, pages arXiv–1910.
- Xu et al. (2019) Hu Xu, Bing Liu, Lei Shu, and Philip Yu. 2019. BERT post-training for review reading comprehension and aspect-based sentiment analysis. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 2324–2335, Minneapolis, Minnesota. Association for Computational Linguistics.
- Yu et al. (2021) Jianfei Yu, Chenggong Gong, and Rui Xia. 2021. Cross-domain review generation for aspect-based sentiment analysis. In Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021, pages 4767–4777.
- Yu and Jiang (2016) Jianfei Yu and Jing Jiang. 2016. Learning sentence embeddings with auxiliary tasks for cross-domain sentiment classification. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing.
- Zhang et al. (2015) Meishan Zhang, Yue Zhang, and Duy-Tin Vo. 2015. Neural networks for open domain targeted sentiment. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pages 612–621.
- Ziser and Reichart (2017) Yftah Ziser and Roi Reichart. 2017. Neural structural correspondence learning for domain adaptation. In Proceedings of the 21st Conference on Computational Natural Language Learning (CoNLL 2017), pages 400–410.
- Ziser and Reichart (2018) Yftah Ziser and Roi Reichart. 2018. Pivot based language modeling for improved neural domain adaptation. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics.
- Ziser and Reichart (2019) Yftah Ziser and Roi Reichart. 2019. Task refinement learning for improved accuracy and stability of unsupervised domain adaptation. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 5895–5906.