A size-consistent Grüneisen-quasiharmonic approach for lattice thermal conductivity
Abstract
We propose a size-consistent Grüneisen-quasiharmonic approach (GQA) to calculate the lattice thermal conductivity where the Grüneisen parameters that measure the degree of phonon anharmonicity are calculated directly using first-principles calculations. This is achieved by identifying and modifying two existing equations related to the Slack formulae for that suffer from the size-inconsistency problem when dealing with non-monoatomic primitive cells (where the number of atoms in the primitive cell is greater than one). In conjunction with other thermal parameters such as the acoustic Debye temperature that can also be obtained within the GQA, we predict for a range of materials taken from the diamond, zincblende, rocksalt, and wurtzite compounds. The results are compared with that from the experiment and the quasiharmonic Debye model (QDM). We find that in general the prediction of is rather consistent among the GQA, experiment, and QDM. However, while the QDM somewhat overestimates the Grüneisen parameters and hence underestimates for most materials, the GQA predicts the experimental trends of Grüneisen parameters and more closely. We expect the GQA with the modified Slack formulae could be used as an effective and practical predictor for , especially for crystals with large .
I Introduction
Thermal conductivity of a material is of fundamental interest and crucial for the performance of thermal management, heat dissipation, thermoelectrics, and thermal barrier coatings[1, 2, 3, 4, 5, 6, 7, 8, 9]. Determining lattice thermal conductivity from a truly first-principles approach requires handling of phonon-phonon interactions[10, 11] that is extremely compute intensive and therefore cannot be done in a routine manner. To treat many systems in a reliable and computationally efficient manner a few feasible methods have been proposed. These include the quasiharmonic Debye model (QDM)[12], the relaxation-time approximation (RTA) method[13], and a modified Debye-Callaway model[14]. Among these the QDM is interesting due to its high computing efficiency. The workhorse of the QDM for calculating is the Slack formulae[15] that require two key input parameters, i.e., the acoustic Debye temperature and the Grüneisen parameters. These two quantities could be deduced approximately by an equation-of-state analysis[16] which requires the total energy as a function of volume that may be easily obtained from only first-principles total energy calculations, thereby avoiding the moderately expensive phonon calculations. Even though the QDM somewhat consistently underestimates due to overestimations of Grüneisen parameters, it can still reliably predict the ordinal ranking of for several classes of semiconductor materials. It was shown[12] that the QDM is able to deliver high Pearson correlation between the predicted and experimental . In view of the advantages of the QDM, it is interesting to ask if the prediction of could be further improved when and the Grüneisen parameters are obtained from the standard first-principles phonon calculations. One may argue that phonon calculations may be still be expensive for a routine calculation, but they are considered to be very inexpensive compared to a full density-functional theory (DFT) anharmonic treatment[17] that accounts for multiple-phonon scatterings. Indeed, phonon databases[18, 19, 20] have been established that show the feasibility of standard phonon calculation route with today’s computing resources. We note that systematic Grüneisen parameter determinations have also been feasibly carried out for the evaluation of the thermal expansion coefficients within the Grüneisen formalism.[21, 22, 23, 24, 25, 26, 27, 28, 29]
The outline of this paper is as follows. In Section II we review the existing Slack formulae in estimating . The size consistency issue of the original Slack formulae is then diagnosed and discussed. Subsequently we propose the necessary modifications, using the specific heat argument, to the existing Slack formulae to preserve size consistency. In Section III we present the results obtained using the proposed GQA. Section IV contains conclusions and a summary.
II Methodology
The lattice thermal conductivity at temperature according to the Slack formula [15] is given by
| (1) |
Here is the acoustic Debye temperature[15] that can be deduced from the Debye temperature and the number of atoms in a primitive cell according to
| (2) |
We note there are different phononic properties, one related to the heating and another to heat conduction, that are appropriately described by, respectively, the Debye temperature , and the acoustic Debye temperature where the optical modes contribute little to the heat conduction. At , is given by[30, 31, 32, 15]
| (3) |
where is the macroscopic Grüneisen parameter evaluated at (we shall use Eq. 8 to evaluate ). The primitive cell has a mass and a volume . and are the Planck and Boltzmann constants, respectively.
In this work, we obtain by finding the Debye cutoff frequency that gives the best match[25] between the constant-volume heat capacity from the Debye model and the constant-volume heat capacity from the DFT. This is achieved through minimizing the absolute error
| (4) |
According to the Debye model[33], the Debye phonon density of states for where to ensure normalization, and vanishes outside the range. This allows the calculation of
| (5) |
Here the heat capacity contributed by a phonon mode of frequency is , . From the DFT calculations, we obtain
| (6) |
The summation is over all phonon mode indices and wavevector in the Brillouin zone (BZ). We note that may also be determined using the DFT phonon density of states information where
| (7) |
where is the maximum frequency in the phonon spectrum.
The mode Grüneisen parameter is defined as . With , the macroscopic Grüneisen parameter[25, 34] as a function of is
| (8) |
Now we discuss the size-consistency issue. Eq. 3 was originally derived for the monoatomic case, where . While the efficacy of the Slack formulae (Eqs. 1, 2, and 3) have been well established[15] when , we note that Eq. 2 may not be appropriate for cells with large since depends on the atomic mass and bond strength but is independent[15] of . In fact we expect the expression for is to be independent of if we assume there are two crystals that are similar physically but differing only in . Take the rocksalt NaCl crystal as an example. We could choose a primitive cell with two atoms () to do a first calculation. However, we could also use the conventional cubic cell with eight atoms () to do a second calculation and we expect to be the same as that from the first calculation. In Section III we will show the heat capacities at deduced from Eq. 2 for some wurtzite compounds with is indeed smaller compared with that of the zincblende and rocksalt compounds with . Next, because of Eqs. 2 and 3, is seen to scale as , which is undesirable since we would expect to be also independent of . To overcome this size-consistency issue while retaining the good efficacy[15] of the method when , we propose to define
| (9) |
with . This choice of is made so that we can retain the same numerical results as that obtained with the original Slack formulae in order to make a direct comparison between the GQA (that uses the DFT input parameters) and QDM for the case of . The optimal choice of may be further investigated in a future study. To be consistent with Eq. 9 we restore the size-consistency of Eq. 3 by using the following modified equation
| (10) |
where . Notice that the exponent of in the above equation has been changed from in Eq. 3 to to achieve size consistency. The size consistency of Eq. 10 is seen by observing that both and scale linearly with , therefore the appearance of in the numerator cancels out the effect of in the denominator. With this modification, we obtain a modified equation for the lattice thermal conductivity where
| (11) |
In this work, since the calculations for each compound involve many steps, it is important to design a workflow that will automatically generate the structures required for atomic relaxations and phonon calculations. It also needs to handle automatic job submissions and post-processing of DFT results such as scanning of Debye cutoff frequencies to find the Debye temperature.
III Results
We use the optimized structures from a phonon database [19] as a starting point to perform the necessary atomic and cell relaxations. Density-functional theory (DFT) calculations are carried out as implemented in the Vienna Ab initio Simulation Package (VASP)[35] with projected augmented-wave pseudopotentials and a PBEsol[36] functional. A relatively high cutoff energy of eV is used throughout. Atomic relaxation is stopped when the maximum force on all atoms is less than eV/Å. Phonon calculations are performed with a small-displacement method[37, 38]. We have used a supercell of for the cubic based compounds (i.e., diamond, zincblende, and rocksalt) and for the wurtzite compounds.
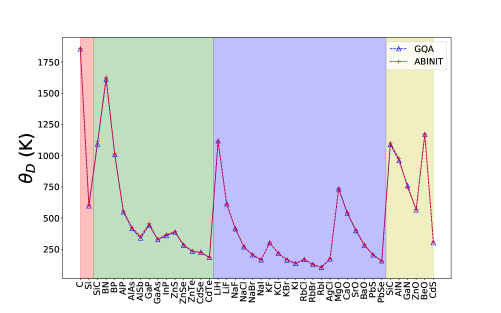
From the phonon density of states obtained from the DFT calculations we carry out the error minimization as outlined in Section II to find the Debye frequency and then determine the Debye temperature . Note that most numerical values related to the GQA have been tabulated in the Supplementary Material. Fig. 1, shows the Debye temperatures obtained from the VASP and the ABINIT codes that are very similar even though one is based on the small-displacement method (VASP) and the other on the density-functional perturbation theory (ABINIT)[19]. As expected, the compounds with large tend to consist of only very light elements.
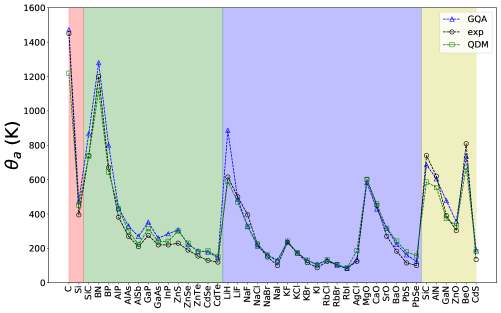
Fig. 2 shows the results of from the GQA and QDM[12] (that are deduced from Eq 2), as well as that from the experiment. We note that the estimation of from the QDM is rather impressive even though it uses only the energy vs. volume information (i.e., without any direct phonon information). We find that the GQA delivers that is somewhat larger than that from experiment for the zincblende compounds. However, the agreement is better for the rocksalt compounds. The agreement between from the GQA and experiment is poor for compounds involving very light elements (such as LiH), presumably due to the presence of very high-frequency phonons. We note that better estimates of may be achieved by a proper modification of Eq 2 for each crystal class. However, since we aim to report the results obtained from the original Slack formulae, we leave the improvement of estimation in a future study.
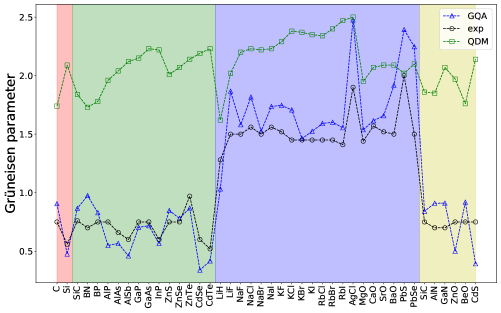
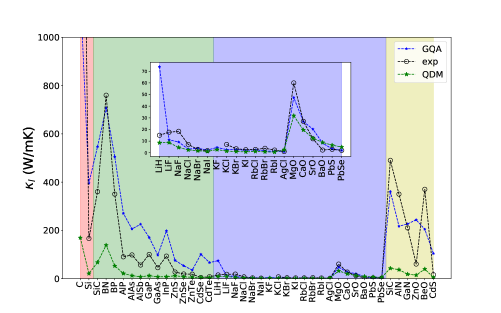
The Grüneisen parameters are calculated using a finite central-difference scheme with strains of and a phonon-band connectivity technique.[39]. Fig. 3 shows the results of the macroscopic Grüneisen parameters from the GQA, QDM, and experiment. Here we see that the GQA gives a consistent trend as the experiment where diamond, zincblende, and wurtzite compounds have mostly ranges between and . For the rocksalt compounds, is larger than . It is noticed that the QDM consistently overestimates the Grüneisen parameters, especially for the diamond and zincblende compounds, and this leads to low that is seen in Fig. 4. For the diamond and zincblende compounds, the GQA somewhat overestimates which is attributed the fact that are generally overestimated as shown in Fig. 2. In contrast to these compounds, the rocksalt compounds show better agreement between the GQA and experiment, where are generally smaller than the diamond and zincblende compounds due to larger phonon anharmonicities as reflected in larger Grüneisen parameters for the rocksalt compounds (see Fig. 3).
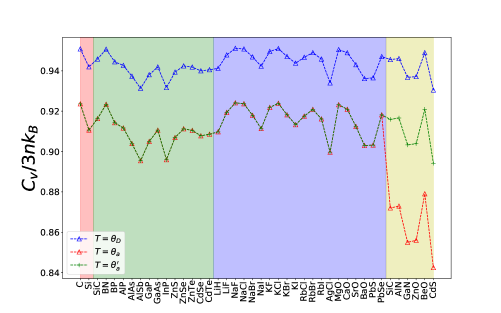
In Section II we have discussed the possible improper estimations of that is based on Eq. 2, especially when the number of atoms in the primitive cell is large. In our study all diamond, zincblende, and rocksalt compounds have , while all six wurtzite compounds SiC, AlN, GaN, ZnO, BeO, and CdS have . Fig. 5 shows the normalized heat capacity evaluated at fluctuates around a mean of . However, it is seen that evaluated at fluctuates around and exhibits the same variation as that of at except for the wurtzite compounds where there is a sudden drop to lower values of . However, restores its expected variation when it is evaluated using Eq. 9. This shows that may be more appropriately estimated by the same consistent fractional change of the as suggested by Eq. 9. We adopt a simple modification that results in Eq. 9 because the original Slack formulae made very good predictions[15] of for compounds with .
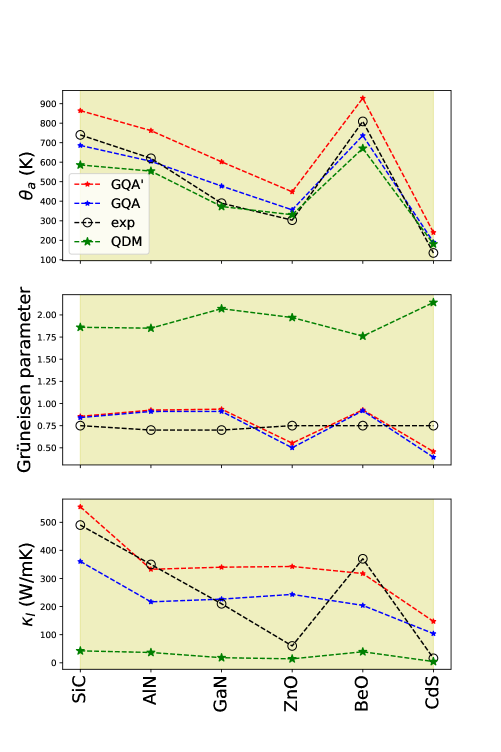
For the wurtzite compounds, Fig. 6 shows the results of the acoustic Debye temperatures , (top panel), the macroscopic Grüneisen parameters and (middle panel), the lattice thermal conductivities and obtained from the original and modified Slack formulae (bottom panel) at K. For each of these compounds, it is not surprising that calculated based on the modified Slack formulae (Eq. 9) is predicted to be larger than that based on the original Slack formulae (Eq. 2). However, these values of and make almost the same prediction of the macroscopic Grüneisen parameters. Finally, we find that obtained with the modified equation has a closer agreement with the experimental values for SiC, AlN, and BeO. These results show that the prediction of is rather sensitive on the way in which is estimated, which is already noticeable even with a relatively small value of . Future studies may include conducting comparative studies with and without the modified Slack formulae in studying compounds with large such as the special quasirandom structures[40] or half-Heusler crystals[41].
IV Summary
In this paper we have calculated the lattice thermal conductivity that is based on the original Slack formulae[15] where various equation inputs such as the Debye temperature , the acoustic Debye temperature , the Grüneisen parameters are determined from the density-functional theory (DFT) phonon calculations. This approach, called the Grüneisen-quasiharmonic approach (GQA), is able to give , Grüneisen parameters, and that follow the experimental trends well, despite the empirical nature of the Slack formulae. We have identified a possible size consistency problem of the original Slack formulae that involves the number of atoms in the primitive cell . We then proposed a simple way to rectify it. The modified Slack formulae preserved the high efficacy of prediction when , while it was shown that the effect of size consistency is noticeable even for as small as when we considered the wurtzite structures. It is expected the GQA with the modified Slack formulae could be used as an effective and practical predictor of for a large range of materials.
V Acknowledgment
We acknowledge fruitful discussions with D. Ding. We thank the National Supercomputing Center, Singapore (NSCC) and A*STAR Computational Resource Center, Singapore (ACRC) for computing resources. This work is supported by RIE2020 Advanced Manufacturing and Engineering (AME) Programmatic Grant No A1898b0043.
References
- Yan and Kanatzidis [2022] Q. Yan and M. G. Kanatzidis, High-performance thermoelectrics and challenges for practical devices, Nature Mater. 21, 503 (2022).
- Kundu et al. [2021] A. Kundu, X. Yang, J. Ma, T. Feng, J. Carrete, X. Ruan, G. K. H. Madsen, and W. Li, Ultrahigh thermal conductivity of -phase tantalum nitride, Phys. Rev. Lett. 126, 115901 (2021).
- Chen et al. [2019] L. Chen, H. Tran, R. Batra, C. Kim, and R. Ramprasad, Machine learning models for the lattice thermal conductivity prediction of inorganic materials, Comput. Mater. Sci. 170, 109155 (2019).
- Miller et al. [2017] S. A. Miller, P. Gorai, B. R. Ortiz, A. Goyal, D. Gao, S. A. Barnett, T. O. Mason, G. J. S. Q. Lv, V. Stevanovic, and E. S. Toberer, Capturing anharmonicity in a lattice thermal conductivity model for high-throughput predictions, Chem. Mater. 29, 2494 (2017).
- Yu et al. [2016] H. Yu, S. Dai, and Y. Chen, Enhanced power factor via the control of structural phase transition in SnSe, Sci. Rep. 6, 1 (2016).
- Waldrop [2016] M. M. Waldrop, More than Moore, Nature 530, 145 (2016).
- Nath et al. [2017] P. Nath, J. J. Plata, D. Usanmaz, C. Toher, M. Fornari, M. B. Nardelli, and S. Curtarolo, High throughput combinatorial method for fast and robust prediction of lattice thermal conductivity, Scr. Mater. 129, 88 (2017).
- Tadano and Tsuneyuki [2018] T. Tadano and S. Tsuneyuki, Quartic anharnonicity of rattlers and its effect on lattice thermal conductivity of clathrates from first principles, Phys. Rev. Lett. 120, 105901 (2018).
- Seko et al. [2015] A. Seko, A. Togo, H. Hayashi, K. Tsuda, L. Chaput, and I. Tanaka, Prediction of low thermal conductivity compounds with first-principles anharmonic lattice-dynamics calculations and bayesian optimization, Phys. Rev. Lett. 2, 17053 (2015).
- Lindsay [2016] L. Lindsay, First principles Peierls-Boltzmann phonon thermal transport: A topical review, Nano. Micro. Thermophy. Eng. 20, 67 (2016).
- Ward et al. [2009] A. Ward, D. A. Broido, D. A. Stewart, and G. Deinzer, Ab initio theory of the lattice thermal conductivity in diamond, Phys. Rev. B 80, 125203 (2009).
- Toher et al. [2014] C. Toher, J. J. Plata, O. Levy, M. de Jong, M. Asta, M. BuongiornoNardelli, and S. Curtarolo, High-throughput computational screening of thermal conductivity, Debye temperature, and Grüneisen parameter using a quasiharmonic Debye model, Phys. Rev. B 90, 174107 (2014).
- Bjerg et al. [2014] L. Bjerg, B. B. Iversen, and G. K. H. Madsen, Modeling the thermal conductivities of the zinc antimonides ZnSb and Zn4Sb3, Phys. Rev. B 89, 024304 (2014).
- Gorai et al. [2017] P. Gorai, V. Stevanović, and E. Toberer, Computationally guided discovery of thermoelectric materials, Nature Rev. Mat. 2, 17053 (2017).
- Morelli and Slack [2006] D. T. Morelli and G. A. Slack, High lattice thermal conductivity solids, in High Thermal Conductivity Materials, edited by S. L. Shindé and J. S. Goela (Springer, New York, 2006) p. 37.
- Blanco et al. [2004] M. A. Blanco, E. Francisco, and V. Luaña, Gibbs: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic debye model, Comput. Phys. Commun. 158, 57 (2004).
- Garg et al. [2011] J. Garg, N. Bonin, B. Kozinsky, and N. Marzari, Role of disorder and anharmonicity in the thermal conductivity of silicon-germanium alloys: A first-principles study, Phys. Rev. Lett. 106, 045901 (2011).
- Mat [2022] The Materials Project, https://materialsproject.org (2022).
- Petretto et al. [2018] G. Petretto, S. Dwaraknath, H. P. Miranda, D. Winston, M. Giantomassi, M. J. van Setten, X. Gonze, K. A. Persson, G. Hautier, and G.-M. Rignanese, Data descriptor: High-throughput density-functional perturbation theory phonons for inorganic materials, Sci. Data 5, 180065 (2018).
- Togo [2020] A. Togo, Phonon database at Kyoto University, http://phonondb.mtl.kyoto-u.ac.jp (2020).
- Schelling and Keblinski [2003] P. K. Schelling and P. Keblinski, Thermal expansion of carbon structures, Phys. Rev. B 68, 035425 (2003).
- Ding and Xiao [2015] Y. Ding and B. Xiao, Thermal expansion tensors, Grüneisen parameters and phonon velocities of bulk MT2 (M=W and Mo; T=S and Se) from first principles calculations, RSC Adv. 5, 18391 (2015).
- Gan et al. [2015] C. K. Gan, J. R. Soh, and Y. Liu, Large anharmonic effect and thermal expansion anisotropy of metal chalcogenides: The case of antimony sulfide, Phys. Rev. B 92, 235202 (2015).
- Liu et al. [2017] G. Liu, H. M. Liu, J. Zhou, and X. G. Wan, Temperature effect on lattice and electronic structures of WTe2 from first-principles study, J. Appl. Phys. 121, 045104 (2017).
- Gan and Lee [2018] C. K. Gan and C. H. Lee, Anharmonic phonon effects on linear thermal expansion of trigonal bismuth selenide and antimony telluride crystals, Comput. Mater. Sci. 151, 49 (2018).
- Liu and Allen [2018] J. Liu and P. B. Allen, Internal and external expansions of wurtzite ZnO from first principles, Comput. Mater. Sci. 154, 251 (2018).
- Gan and Chua [2019] C. K. Gan and K. T. E. Chua, Large thermal anisotropy in monoclinic niobium trisulfide: A thermal expansion tensor study, J. Phys.: Condens. Matter 31, 265401 (2019).
- Liu et al. [2019] G. Liu, Z. Gao, and J. Ren, Anisotropic thermal expansion and thermodynamic properties of monolayer beta-Te, Phys. Rev. B 99, 195436 (2019).
- Gan et al. [2022] C. K. Gan, A. I. Al-Sharif, A. Al-Shorman, and A. Qteish, A first-principles investigation of the linear thermal expansion coefficients of BeF2: Giant thermal expansion, RSC Adv. 12, 26588 (2022).
- Leibfried and Schlömann [1954] G. Leibfried and E. Schlömann, Nachr. Akad. Wiss. Göttinger II a(4), 71 (1954).
- Julian [1965] C. L. Julian, Theory of heat conduction in rare-gas crystals, Phys. Rev. 137, A128 (1965).
- Slack [1979] G. A. Slack, in Solid State Physics, Vol. 34, edited by H. Ehrenreich, F. Seitz, and D. Turnbull (Academic, New York, 1979) p. 1.
- McQuarrie [2000] D. A. McQuarrie, Statistical Mechanics (University Science Books, Sausalito, 2000).
- Ashcroft and Mermin [1976] N. W. Ashcroft and N. D. Mermin, Solid State Physics (Saunders College Publishing, New York, 1976).
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci. 6, 15 (1996).
- Perdew et al. [2008] J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou, and K. Burke, Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett. 100, 136406 (2008).
- Kresse et al. [1995] G. Kresse, J. Furthmüller, and J. Hafner, Ab initio force constant approach to phonon dispersion relations of diamond and graphite, Europhys. Lett. 32, 729 (1995).
- Gan et al. [2021] C. K. Gan, Y. Liu, T. C. Sum, and K. Hippalgaonkar, Efficacious symmetry-adapted atomic displacement method for lattice dynamical studies, Comput. Phys. Commun. 259, 107635 (2021).
- Gan and Ong [2021] C. K. Gan and Z.-Y. Ong, Complementary local-global approach for phonon mode connectivities, J. Phys. Commun. 5, 015010 (2021).
- Gan et al. [2010] C. K. Gan, X. F. Fan, and J.-L. Kuo, Composition-temperature phase diagram of BexZn1-xO from first principles, Comput. Mater. Sci. 49, S29 (2010).
- Shiomi et al. [2011] J. Shiomi, K. Esfarjani, and G. Chen, Thermal conductivity of half-Heusler compounds from first-principles calculations, Phys. Rev. B 84, 104302 (2011).