A Soft SIMD Based Energy Efficient
Computing Microarchitecture

Single Instruction Multiple Data is a well-known approach to enhance parallelism, hence performance, when executing regular computation patterns. Indeed, mainstream Instruction Set Architectures (ISAs) do define SIMD extensions, e.g., in the form of ARM Neon [11], or x86 AVX [12] instructions. Their hardware implementation entails using wide registers hosting a fixed number of sub-words (of fixed bitwidth) and the corresponding parallel functional units performing vector operations among registers.

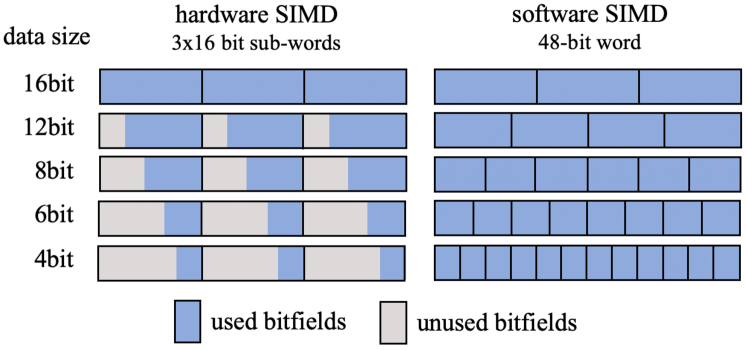
Soft SIMD, proposed in [4][5], challenges this paradigm, allowing arbitrary partitioning of vector registers in sub-words, as illustrated in Figure 1. Soft SIMD formats can then be configured in software at run-time (hence the name), ensuring that operations on a sub-word would not cause side effects on other sub-words, even in the case of positive/negative overflows. Soft SIMD is particularly appealing when a fine-grained control of bitwidths is beneficial, employed bitwidths are small, and/or the desired data representation changes in different computation phases. These features truly characterize ML applications, as discussed in Section I.

Soft SIMD can be embodied along two alternative approaches: reserving bit locations in-between sub-words (guardbits) or adopting configurable carry generation at sub-word boundaries in arithmetic units with low additional hardware cost and timing path increase [4][5][13]. In the implementation presented in this work, we employ a configurable carry generation, but our strategy is also compatible with the approaches using guardbits.

Our proposed pipeline performs parallel multiplications as a sequence of arithmetic shifts and additions between multiplicands and accumulators, processing one bit of a multiplier operand each time. As detailed in Section III-B, only the shift operation is performed when the multiplier bit is ‘0’. Therefore, multiple shifts can be coalesced in the same clock cycle when processing bit patterns with trailing zeros such as “10”, “100”, etc. To maximize the ensuing performance benefit, we herein adopt a Canonical Signed Digit (CSD) representation for multiplier values [6][7]. Such encoding employs three symbols for each digit: ‘1’, ‘0’, and ‘-’, where the latter indicates that the number should be interpreted as negative. As an example, the number “0-01” in CSD notations equals to $(-4)+1=-3$. In CSD numbers, $\sim{}(\tfrac{2}{3})$ of the digits are zeroes, increasing opportunities for coalescing multiple shifts.

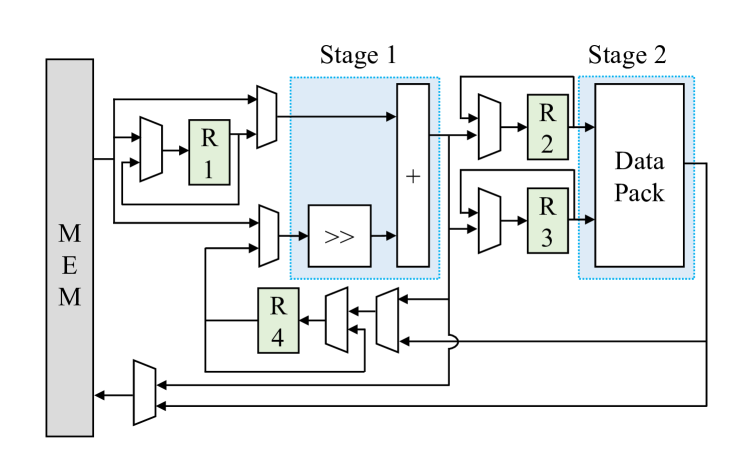
A block scheme of the hardware design is illustrated in Figure 2. It is composed of two pipeline stages. The first one is dedicated to parallel shift-add operations, hence sequentially performing multiplications. As we will show in Section IV, such an approach leads to higher efficiency (especially for small-bitwidth operands) with respect to using combinatorial multipliers because it requires simpler (leaner, faster) logic. The second pipeline stage is instead devoted to data packing, namely, to the translation of values between bitwidths across computation phases adopting different SIMD formats. This second stage can be bypassed if no data conversion is required. Details on datapath stages are provided in the following sub-sections.

The first pipeline stage allows the multiplication of values represented in fixed-point $Q1.X$ notation, i.e., with one leading bit for the integer parts and the rest devoted to the fractional part. Operations are performed parallel among a multiplier, encoded in CSD notation, and several multiplicands are represented in 2’s complement notation.

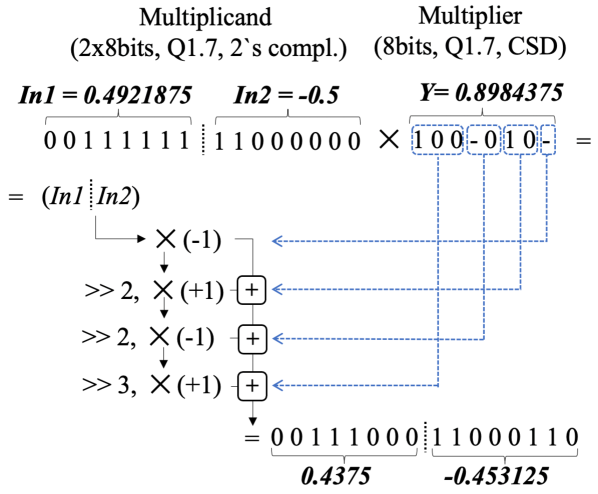
The employed algorithm is shown in Figure 3 using an example of a $Q1.7$ multiplier and two 8-bit multiplicands stored as Soft SIMD sub-words, themselves represented as $Q1.7$ values. Notice that since the bitwidth of results and that of the multiplicands are the same, truncation errors can and do occur. Nonetheless, these are negligible even for very constrained bitwidths, e.g., approximately $1\%$ in the shown 8-bit example.

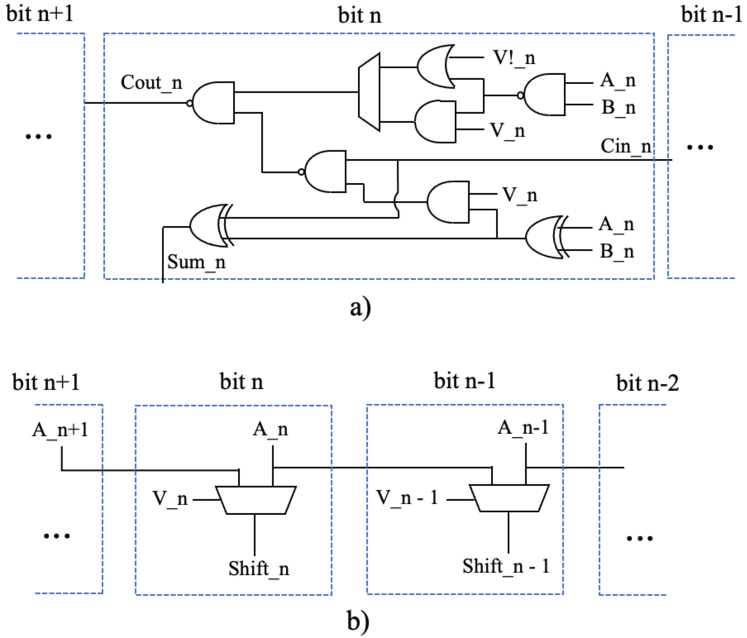
Figure 3 showcases that right shifts, complements (multiplications by $-1$), and additions are required to implement multiplication. Such operations must not result in interference from one sub-word to the next. To this end, sub-word boundaries prevent overflow from passing in additions and provide +1 for the next sub-word in subtractions in our design by expandable control signals. The employed circuit is shown in Figure 4-a. Since the carry logic operation of the multi-bit adder is performed simultaneously, the increase in the time path is very small. As the shift operation, the Most Significant Bit (MSB) of sub-words propagates the corresponding bit position of the input, hence implementing sign extension (Figure 4-b). It has to be noted that muxes can be employed selectively, depending on the supported bitwidths. Indeed, no mux is required if a bit position is never the MSB of a sub-word for all supported Soft SIMD formats. Such a strategy can scale to support multiple shifts by employing further combinatorial stages of 1-bit muxes. In this way, multi-bit patterns with trailing zeros can be processed in a single clock cycle, as shown in Figure 3. In our design, we support up to 3-bit patterns, as more extensive sequences of consecutive zeros are rare and do not justify the additional logic.

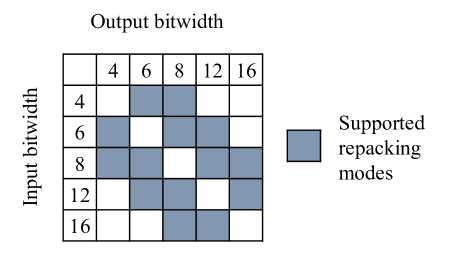
The role of the data packing unit is to bridge across SIMD formats. To this end, a crossbar [14] is employed to connect bits in different bit ranges of the Stage2 inputs (registers R2, R3 in Figure 2) to the Stage2 output (registers R4 or write back to memory). The hardware resources required by the crossbar depend on the width of the datapath and the set of employed Soft SIMD formats. In the design investigated in Section IV, we considered a 48-bits datapath and sub-words of 4, 6, 8, 12, and 16 bits. We support many conversions between modes, as indicated in Figure 5. Finally, the entire stage can be bypassed if no change in sub-word format is required.

Across experiments, we target a 48-bit pipeline. To investigate its performance, we compare its efficiency with that of Hard SIMD solutions employing combinatorial multipliers. The first baseline Hard SIMD architecture supports sub-word configurations 4, 6, 8, 12, and 16 bits, while the other only supports 8 and 16 bits. In all cases, timing, area, and energy characterizations are performed on post-synthesis data based on a 28nm technology library under varying timing constraints.

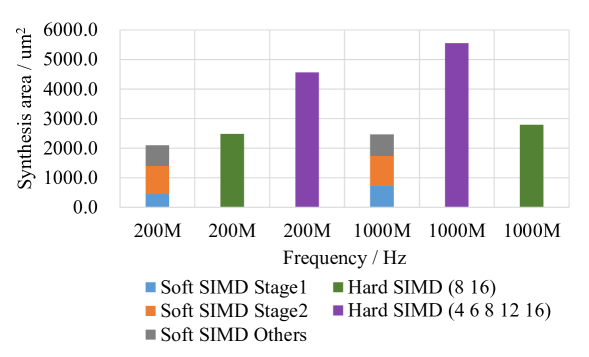
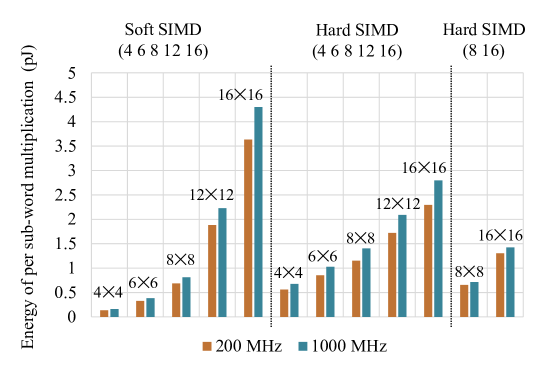
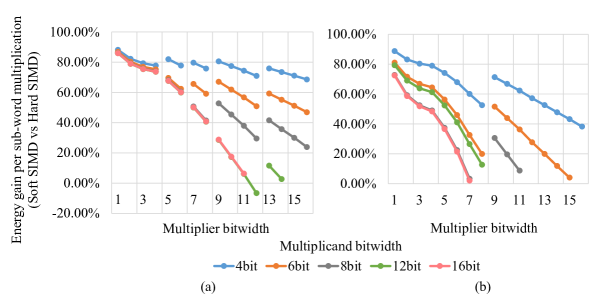
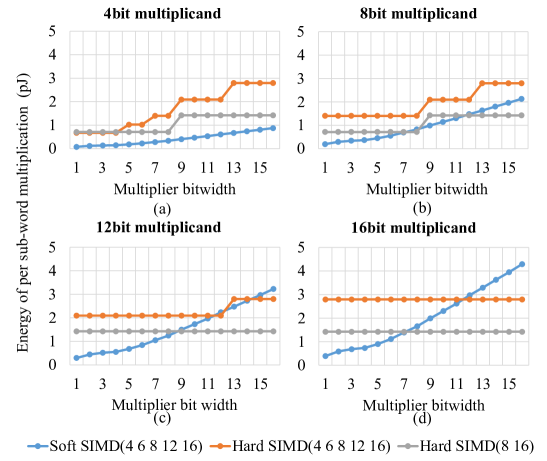
Figure 6 compares the area of Hard SIMD and Soft SIMD solutions. As expected, as Soft SIMD does not require a resource-hungry combinatorial multiplier, its area requirements are markedly lower with respect to Hard SIMD for the same supported bitwidths (less than half across different timing constraints). Moreover, the area efficiency of Soft SIMD is not matched by Hard SIMD even when only 8- and 16-bit sub-words are supported in the latter, which still remains more than 10% larger in all cases. In addition, stage 2 of Soft SIMD remains basically constant at different frequencies while stage 1 and other parts (registers, etc.) grow with frequency. The design layout is presented in Figure 7.

We evaluated the efficiency of the proposed pipeline in terms of the energy (pico-Joules) required to perform a multiplication among multiplicands and multipliers of varying bitwidths. In all cases, the bitwidth of the result matches that of the multiplicand. Absolute energy results for selected configurations are shown in Figure 8, highlighting that Soft SIMD achieves better energy efficiency for widths smaller than 8 bits. Moreover, Soft SIMD can seamlessly support a large number of data widths, while in the Hard SIMD case, flexibility comes at a hefty cost in terms of efficiency, as the comparison between the two Hard SIMD solutions in the $8\times{}8$ and $16\times{}16$ configurations highlights.

A comprehensive view of the efficiency of our proposed pipeline and that of the compared baseline designs is presented in Figure 9. This figure plots the energy gain of Soft SIMD with respect to the two Hard SIMD implementations when executing multiplications of different multiplicands and multipliers widths. These results show that import gains are obtained, especially for small bitwidths. Moreover, in these comparisons, the plotted series present discontinuities when the multiplicand width exceeds the size of the Hard SIMD sub-words, i.e., between 8 and 9 bits in Figure 9, on the left side.

Finally, as Figure 10 shows, the benefits of Soft SIMD derive from its graceful scaling to different bitwidths in terms of energy requirements. Conversely, even though Hard SIMD often enables the support of many SIMD formats, this flexibility does not lead to efficiency increases. In fact, the Hard SIMD (4 6 8 12 16) solution consistently underperformed the simpler Hard SIMD (8 16) option in our experiments.

In summary, Soft SIMD achieves significant energy gains (up to 88.8%) for multiplications with small bit-width operands compared to traditional Hard SIMD alternatives. Such characteristics are of great interest for algorithms amenable to aggressive quantization, such the machine learning ones.

This paper presents a novel computing pipeline, leveraging the Soft SIMD paradigm and CSD encoding to achieve ultra-high energy efficiency when performing arithmetic operations among aggressively quantized values. The pipeline features the skipping of trailing ’0’ digits in multiplier operands, seamless support of a wide range of quantization levels, and a repacking unit to bridge across SIMD formats.

Experiments showcase that our Soft SIMD design greatly outperforms Hard SIMD alternatives when executing multiplications among small-bitwidth operands, highlighting energy gains of up to 88.8% in energy, while requiring fewer hardware resources.