A tight upper bound on the (2,1)-total labeling number of outerplanar graphs
Abstract
A -total labeling of a graph is an assignment from the vertex set and the edge set to the set of nonnegative integers such that if is a vertex and is an edge incident to , and if and are a pair of adjacent vertices or a pair of adjacent edges, for all and in . The -total labeling number of a graph is defined as the minimum among all possible assignments. In [4], Chen and Wang conjectured that all outerplanar graphs satisfy , where is the maximum degree of , while they also showed that it is true for with . In this paper, we solve their conjecture completely, by proving that even in the case of .
1 Introduction
In the channel/frequency assignment problems, we need to assign different frequencies to ‘close’ transmitters so that they can avoid interference. The -labelings of a graph have been widely studied as one of important graph theoretical models of this problem. An -labeling of a graph is an assignment from the vertex set to the set of nonnegative integers such that if and are adjacent and if and are at distance 2, for all and in . We call this invariant (i.e., the minimum value ) the -labeling number and denote it by . Notice that we can use different labels when since we can use 0 as a label for conventional reasons. We can find many results on -labelings in comprehensive surveys by Calamoneri [3] and by Yeh [16].
In [15], Whittlesey et al. studied the -labeling number of incidence graphs, where the incidence graph of a graph is the graph obtained from by replacing each edge with two edges and introducing one new vertex . Observe that an -labeling of the incidence graph of a given graph can be regarded as an assignment from to the set of nonnegative integers such that if is a vertex and is an edge incident to , and if and are a pair of adjacent vertices or a pair of adjacent edges, for all and in . Such a labeling of is called a -total labeling of , introduced by Havet and Yu [7, 8]. The -total labeling number is defined as the minimum value , and denoted by .
Notice that a -total labeling of is equivalent to a total coloring of . Generalizing the Total Coloring Conjecture [2, 13], Havet and Yu [7, 8] conjectured that
| (1) |
holds for any graph , where denotes the maximum degree of a vertex in . They also showed that (i) for any graph where and denote the chromatic number and the chromatic index of , respectively, (ii) if and , (iii) if and is an odd , and (iv) if is the complete graph where ; the conjecture (1) is true if (a) , (b) and , or (c) is the complete graph. By (i), it follows that for any bipartite graph [1, 7, 8] (by and [9]). Also, Bazzaro et al. [1] investigated that for any -degenerated graph (by and [12]), where an -degenerated graph is a graph which can be reduced to a trivial graph by successive removal of vertices with degree at most , and that for any planar graph (by the Four-Color Theorem). They also showed sufficient conditions about and girth for which the conjecture (1) holds. In [11], Montassier and Raspaud proved that when and and the maximum average of degree satisfy some conditions. In [10], Lih et al. showed that for any graph . They also investigated of the complete bipartite graphs .
Let be an outerplanar graph. In [1], Bazzaro et al. pointed out that for any outerplanar graph other than an odd cycle, since any outerplaner graph is 2-degenerated, and any outerplaner graph other than an odd cycle satisfies [5]. In particular, Chen and Wang [4] conjectured that in the case of , , which is a better bound than the conjecture (1). They also proved that this conjecture is true if (i) , (ii) and is 2-connected, or (iii) and every two faces consisting of three vertices have no vertex in common. In the case of (i.e., is a path or a cycle), we can easily see that , since the incidence graph of a path (resp., a cycle) is also a path (resp., a cycle), and the -labeling number for a cycle with vertices is at most 4 [6]. The cases of are clear. However, the general cases of were left open. In this paper, we solve Cheng and Wang’s conjecture completely, by showing the remaining cases of . On the other hand, the bound is tight, since there exist infinitely many outerplanar graphs such that if , as investigated in [4].
2 Preliminaries
A graph is an ordered set of its vertex set and edge set and is denoted by . We assume throughout this paper that a graph is undirected, simple and connected, unless otherwise stated. Therefore, an edge is an unordered pair of vertices and , which are end vertices of , and we often denote it by . For two graphs and , we denote by . For a vertex set , let be the subgraph of induced by . For an edge set , let (resp., ) be the graph (resp., where is the set of end vertices of edges in ). Two vertices and are adjacent if . Let denote the set of neighbors of a vertex in ; . The degree of a vertex is , and is denoted by . A vertex with is called a -vertex. We use (resp., ) to denote the maximum (resp., minimum) degree of a graph . A path in is a sequence of vertices such that for ; we may denote as and let and . We often drop in these notations if there are no confusions.
The vertex-connectivity of a graph , denoted by , is defined as the minimum cardinality of a vertex set such that is disconnected or trivial. A vertex is called a cut vertex of if is disconnected. Notice that a graph has no cut vertex if and only if . Two vertices and are called 2-connected if they belong to the same connected component in for any cut vertex of with . A subgraph of is called a 2-connected component if every two vertices in are 2-connected and is maximal to this property. It is not difficult to see that if , then there exists a 2-connected component which contains exactly one cut vertex of .
A graph is called planar if it can be drawn in the plane without generating a crossing by two edges. For such a drawing of in the plane, after omitting the line segments, the plane is divided into regions; such a region is called a face. A face whose vertex set is with , (where ) is denoted by . We call a face consisting of vertices a -face.
A planar graph is called outerplanar if it can be drawn in the plane so that all vertices lie on the boundary of some face. Such a drawing is referred to as an outerplane graph. The face whose boundary contains all vertices of is called the outer face and all other faces are called inner faces. We call an edge belonging to the boundary of the outer face an outer edge and all other edges inner edges. An inner face is called an endface if its boundary contains exactly one inner edge (note that there exist at least two endfaces if contains an inner edge).
Let and be a (2,1)-total labeling of . For an edge , we may denote by . Let denote the labeling such that for each . Notice that is also a (2,1)-total labeling of .
3 Case
Let be an outerplane graph with . Chen and Wang [4] showed that if , then . First review their constructive proof of the case of . Assume that on the boundary of its outerface, each 3-vertex (i.e., each vertex which some inner edge is incident to) is numbered in clockwise order. Also assume that for , each 2-vertex on the path connecting and (on the boundary of its outerface) is numbered in clockwise order, where . A (2,1)-total labeling can be obtained by the following algorithm, which slightly generalizes Chen and Wang’s method.
Algorithm LABEL-K2
Input: An outerplane graph with .
Output: A total (2,1)-labeling of .
1. Assign labels 0 and 1 alternately to a sequence of 3-vertices.
2. For each , label 2-vertices as follows. Without loss of generality, let and .2.1. If is even, then assign labels 1 and 0 alternately to a sequence of 2-vertices.
2.2. If is odd, then assign label 2 to for some , and labels 1 and 0 alternately to a sequence of 2-vertices other than .
3. Assign label 3 to each inner edge.
4. Label outer edges as follows.
4.1. If is even, then assign labels 4 and 5 alternately in clockwise order.
4.2. If is odd, then pick up an arbitrary endface . Without loss of generality, let and .
4.2.1. If is an even or an odd with , then assign label 3 to and labels 4 and 5 alternately to all remaining outer edges. Then if or , then reassign labels for , , and as , , and .
4.2.2. If , then assign labels 5, 2, and 3 to , , and , respectively, and labels 4 and 5 alternately to all remaining outer edges. Then if the label for two outer edges incident to and other than and is 4 (resp., 5), reassign a label for as (resp., 4).
Observe that for each inner edge , we have , since otherwise the subgraph of induced by would have odd 3-vertices, a contradiction, where denotes the path . Notice that the reassignment in Step 4.2.1 is necessary because otherwise or would hold. Also notice that in Step 4.2.2, holds for two outer edges (resp., ) incident to (resp., ) other than (resp., ), since is odd and . Thus, a labeling obtained from the above procedure is a (2,1)-total labeling of . Here, we have the following easy observation:
Observation 1. In Step 4.2, we can start with assigning an arbitrary label in to an arbitrary outer edge for the label assignment of outer edges except (resp., and ) in Step 4.2.1 (resp., Step 4.2.2).
Moreover, we can see the following property.
Lemma 1
Let be an outerplane graph with , be a 2-connected component in , and be an inner edge in . Assume that contains a connected component with no cut vertex in and . Let (resp., be the neighbor of (resp., ) in (note that by , such and are uniquely determined and that by , we have ). If has a 2,1-total labeling such that
then there exists a 2,1-total labeling .
Proof
By symmetry of labelings, we only consider the case where , , and . Without loss of generality, let and . There are the two possible cases (Case-1) and (Case-2) .
(Case-1) Let be the graph obtained from by adding two new vertices and and three new edges , and . Notice that is an outerplane graph with . There are the following two possible cases: (1.1) both of and are 2-vertices or 3-vertices, (1.2) otherwise.
(1.1) If and are both 2-vertices, then add an inner edge to and redefine by the resulting graph. By applying Algorithm LABEL-K2 to as , we can obtain a 2,1-total labeling such that and . Moreover, by choosing an endface not containing in Step 4.2 of Algorithm LABEL-K2, we can obtain such a labeling that (note that by Observation 1, we can start with assigning label to for the label assignment of outer edges). Observe that the labeling such that for each and for each is a 2,1-total labeling of .
(1.2) Assume that is a 3-vertex and is a 2-vertex (the other case can be treated similarly). Let be a 2,1-total labeling obtained by applying Algorithm LABEL-K2 to as ; . Moreover, as observed in (Case-1.1), we can obtain such a that . Also, if is not adjacent to a 3-vertex, we can obtain such a that by avoiding assigning label 2 to any vertex in in Step 2.2. Observe that if , then a 2,1-total labeling of can be constructed by combining and similarly to (Case-1.1). Hence, we consider the case where the vertex adjacent to in is a 3-vertex; . Then we can reassign labels for , and as any one of two possible labelings (a) , and and (b) , and without violating the feasibility. Observe that the labeling such that for each , for each , and is a 2,1-total labeling of .
(Case-2) Let be the graph obtained from by adding a new vertex and two new edges and . Notice that is an outerplane graph with . There are the following two possible cases: (2.1) both of and are 2-vertices or 3-vertices, (2.2) otherwise.
(2.1) If and are both 2-vertices, then add an inner edge to and redefine by the resulting graph. By applying Algorithm LABEL-K2 to as , we can obtain a 2,1-total labeling such that and . Moreover, by choosing an endface not containing in Step 4.2 of Algorithm LABEL-K2, we can obtain such a labeling that and . Observe that the labeling such that for each and for each is a 2,1-total labeling of .
(2.2) Assume that is a 3-vertex and is a 2-vertex (the other case can be treated similarly). Let be a 2,1-total labeling obtained by applying Algorithm LABEL-K2 to as ; . Moreover, as observed in (Case-2.1), we can obtain such a that and . Also, in the case where Step 2.2 is applied to the sequence of 2-vertices containing and , we can assign label 1 to by assigning label 2 to (notice that in this case, is not adjacent to any 3-vertex because the sequence of 2-vertices containing consists of odd vertices). Observe that if , then a 2,1-total labeling of can be constructed by combining and similarly to (Case-2.1). Hence, we consider the case where Step 2.1 is applied to the sequence of 2-vertices containing and ; . Then we can reassign label 2 to without violating the feasibility. We can see that the labeling such that for each , for each , and is a 2,1-total labeling of . ∎
By using this lemma, we can prove that Chen and Wang’s conjecture is true in the case of .
Theorem 3.1
If is an outerplane graph with , then .
Proof
We prove this by induction on . The theorem clearly holds if . Consider the case of and assume that for each , this theorem holds. We also assume that is connected, since otherwise we can treat each component separately. Thus, .
Consider the case where . Let be a vertex with . By the induction hypothesis, has a (2,1)-total labeling . Let be the neighbor of in and be vertices adjacent to in where may occur (note that ). Hence we can extend to the edge and the vertex as follows: assign a label to , and then a label in to .
Consider the case of . In [4], Chen and Wang showed that if , then . Hence, we here only consider the case of . Let be a 2-connected component in which has exactly one cut vertex of . By , we have and hence . By and , it follows that holds and and are connected by a bridge incident to , where a bridge is an edge whose deletion makes the graph disconnected; denote this bridge by where . By the induction hypothesis, has a (2,1)-total labeling . By symmetry, it suffices to consider the following three possible cases: (Case-1) , (Case-2) , and (Case-3) . In each case, we will extend to a (2,1)-total labeling of . Let for every .
First consider the case where has no inner edge. Assume that on the boundary of its outerface in , each vertex is numbered in clockwise order. Then, in each case of (Case-1)–(Case-3), we can obtain a (2,1)-total labeling of in the following manner:
1. If , , and , then let , , , , , and . If , , and , then let , , , , , and .
2. Unless and , then assign labels for vertices or edges in as follows.
2.1. Assign a label in (say, 0) to .
2.2. Assign labels 1 and 0 alternately to . Then, if is odd, then reassign label 2 to .
2.3. If (resp., ), then assign label 5 (resp., 4) to , and labels 4 and 5 (resp., 5 and 4) alternately to the sequence of outer edges in counter-clockwise order. Then if , then reassign label 3 to , and if and is odd, then reassign label 3 to and label 4 to .
Next consider the case where has an inner edge. Assume that on the boundary of its outerface in , each 3-vertex is numbered in clockwise order. Also assume that for , each 2-vertex on the path connecting and (on the boundary of its outerface) is numbered in clockwise order, where . Also, if , then let . Let denote the path . Without loss of generality, assume that is a 2-vertex between and in ; for some . Let be a (2,1)-total labeling obtained by applying Algorithm LABEL-K2 to , while (A) choosing as a vertex other than in Step 2.2 if , and (B) choosing as a vertex not in in Step 2.2 if (i) or (ii) and , and (C) choosing an endface not containing in Step 4.2.
Consider the case where is adjacent to a 2-vertex in ; . Without loss of generality, assume that is a 2-vertex. Then by and the choice of in Step 2.2 of Algorithm LABEL-K2, we can see that ; . Moreover, we can assume that since otherwise we recompute a (2,1)-total labeling of by starting with instead of in Step 1 of Algorithm LABEL-K2 and redefine by . Also, we can assume that in the case of (resp., 5), if or , then (resp., 5) and if and , then (resp., 5) for with (note that this is possible by Observation 1 and that in the case of and , exactly one of and has label 2 in ). Let for each . Observe that if , then is a (2,1)-total labeling of . In the case of , if or (resp., and ), reassign a label for (resp., ) as (resp., ). Then, we can see that the resulting is a (2,1)-total labeling of since if or , then by the choice of in Step 2.2 and otherwise then .
Finally, consider the case where ; . Let be a 3-vertex such that is an inner edge of . Let be the subgraph of induced by . Let (resp., ) be the neighbor of (resp., ). Notice that the component in containing has no cut vertex in . Below, we will show that if , then there exists a (2,1)-total labeling of satisfying the conditions of Lemma 1. Note that in this case, Lemma 1 ensures the existence of a (2,1)-total labeling of . Also, in the case of , we will show directly the existence of a (2,1)-total labeling of .
(Case-1) .
(1.1) Assume that .
Let for each . Then, is a (2,1)-total labeling of (note that ).
(1.2) Assume that .
If and , then let , , , , , , , , and . Observe that the resulting labeling is a (2,1)-total labeling of .
If and , then let , , , , , , , , , and . Observe that the resulting labeling is feasible for and satisfies the conditions of Lemma 1.
Assume that . Then we can obtain a (2,1)-total labeling of in the following manner, where “assigning a label to ” means that .
1. Assign label 3 to each inner edge in .
2. Let . Assign labels 1 and 0 alternately to 3-vertices (note that as a result, ). Assign labels to 2-vertices () according to Step 2 of algorithm LABEL-K2.
3. Trace outer edges from to on in clockwise order and assign labels 4 and 5 alternately.
3.1. If , then assign labels to the remaining vertices or edges as follows. Let , , , , and . Assign labels 0 and 1 alternately to outer edges . Moreover, if is even (resp., odd), then assign labels 4 and 5 (resp., 5 and 4) alternately to 2-vertices . If , then let and . If , then let , , and , and extend to a (2,1)-total labeling of according to Lemma 1.
3.2. If and , then let , , , , and , and extend to a (2,1)-total labeling of according to Lemma 1.
3.3. If , and , then let , , , , , , and , and .
3.4. If , and , then let , , , , , , and , and .
(Case-2) .
(2.1) Assume that .
If and , then let , , , , , , , , and .
If and , then let , , , , , , , . Observe that the resulting labeling is feasible for and satisfies the conditions of Lemma 1.
The case of can be treated similarly to (Case-1.2), by starting with assigning to label 5 instead of label 4.
(2.2) Assume that .
If and , then let , , , , , , , , and .
If and , then , , , , , , , , , and . Observe that the resulting labeling is feasible for and satisfies the conditions of Lemma 1.
Assume that . Then we can obtain a (2,1)-total labeling of in the following manner.
1. Assign label 3 to each inner edge in .
2. Trace outer edges from to on in clockwise order and assign labels 5 and 4 alternately.
2.1. If and , then assign labels for the remaining vertices and edges as follows. Let . Assign labels 1 and 0 alternately to 3-vertices (notice that ). Assign labels to 2-vertices () according to Step 2 of algorithm LABEL-K2. Let , , , , , , , and . Assign labels 1 and 0 alternately to 2-vertices . Then, extend to a (2,1)-total labeling of according to Lemma 1.
2.2. If and , then assign labels for the remaining vertices and edges as follows. Let . Assign labels 0 and 1 alternately to 3-vertices (notice that ). Assign labels to 2-vertices () according to Step 2 of algorithm LABEL-K2. Let , , , , , , , and . Assign labels 0 and 1 alternately to 2-vertices . Then, extend to a (2,1)-total labeling of according to Lemma 1.
2.3. If and , then assign labels for the remaining vertices and edges as follows. Let . Assign labels 1 and 0 alternately to 3-vertices (notice that ). Assign labels to 2-vertices () according to Step 2 of algorithm LABEL-K2. Let , , , , , , and . Assign labels 1 and 0 alternately to 2-vertices .
2.4. If and , then assign labels for the remaining vertices and edges as follows. Let . Assign labels 0 and 1 alternately to 3-vertices (notice that ). Assign labels to 2-vertices () according to Step 2 of algorithm LABEL-K2. Let , , , , , , and . Assign labels 0 and 1 alternately to 2-vertices .
(Case-3) .
First consider the case where and . If , then let , , , , , , , , and . If , then let , , , , , , , , and .
Next consider the case where and . If , then let , , , , , , , , , and . If , then let , , , , , , , , , and . Observe that in both cases, the resulting labeling is feasible for and satisfies the conditions of Lemma 1.
Finally consider the case where . We divide this case into the following two subcases: (3.1) and (3.2) .
(3.1) Assume that .
We can obtain a (2,1)-total labeling of in the following manner.
1. Assign label 3 to each inner edge in .
2. Let . Assign labels 1 and 0 alternately to 3-vertices (note that as a result, ). Assign labels to 2-vertices () according to Step 2 of algorithm LABEL-K2. Assign labels 1 and 0 alternately to 2-vertices .
3. Trace outer edges from to on in clockwise order and assign labels 4 and 5 (resp., 5 and 4) alternately if the number of outer edges in is even (resp., odd). Notice that as a result, the edge has label 5.
3.1. If , then let , , , , , , , and . Then, extend to a (2,1)-total labeling of according to Lemma 1.
3.2. If , then let , , , , , , and .
(3.2) Assume that .
We can obtain a (2,1)-total labeling of in the following manner.
1. Assign label 2 to each inner edge in .
2. Let . Assign labels 4 and 5 alternately to 3-vertices (note that as a result, ). Assign labels to 2-vertices () according to Step 2 of Algorithm LABEL-K2’, where Algorithm LABEL-K2’ denotes the algorithm obtained from Algorithm LABEL-K2 by replacing each label to be assigned with . Assign labels 4 and 5 alternately to 2-vertices .
3. Trace outer edges from to on in clockwise order and assign labels 1 and 0 (resp., 0 and 1) alternately if the number of outer edges in is even (resp., odd). Notice that as a result, the edge has label 0.
3.1. If , then let , , , , , , , and . Then, extend to a (2,1)-total labeling of according to Lemma 1.
3.2. If , then let , , , , , , and .
∎
4 Case
Let be an outerplane graph. The following structural properties of outerplane graphs are known.
Theorem 4.1
[14]
Every outerplane graph with contains one of the
following
configurations:
(C1) two adjacent 2-vertices and .
(C2) a 3-face with and .
(C3) two 3-faces and such that
and .
In [4], Chen and Wang proved that if does not contain (C3) and holds, then . Their proof utilizes the property that if contains (C1) or (C2), then a (2,1)-total labeling of can be extended from a (2,1)-total labeling of some proper subgraph of . Here, we investigate the case where contains neither (C1) nor (C2), and derive a new structural property, i.e, if contains neither (C1) nor (C2) and holds, then contains a new configuration as shown in Lemma 2 below, which includes (C3) as a subconfiguration.
Assume that . Define a chain of 3-faces as a sequence
of 3-faces such that and are on the outer face of and is an inner edge for each (see Fig. 1).
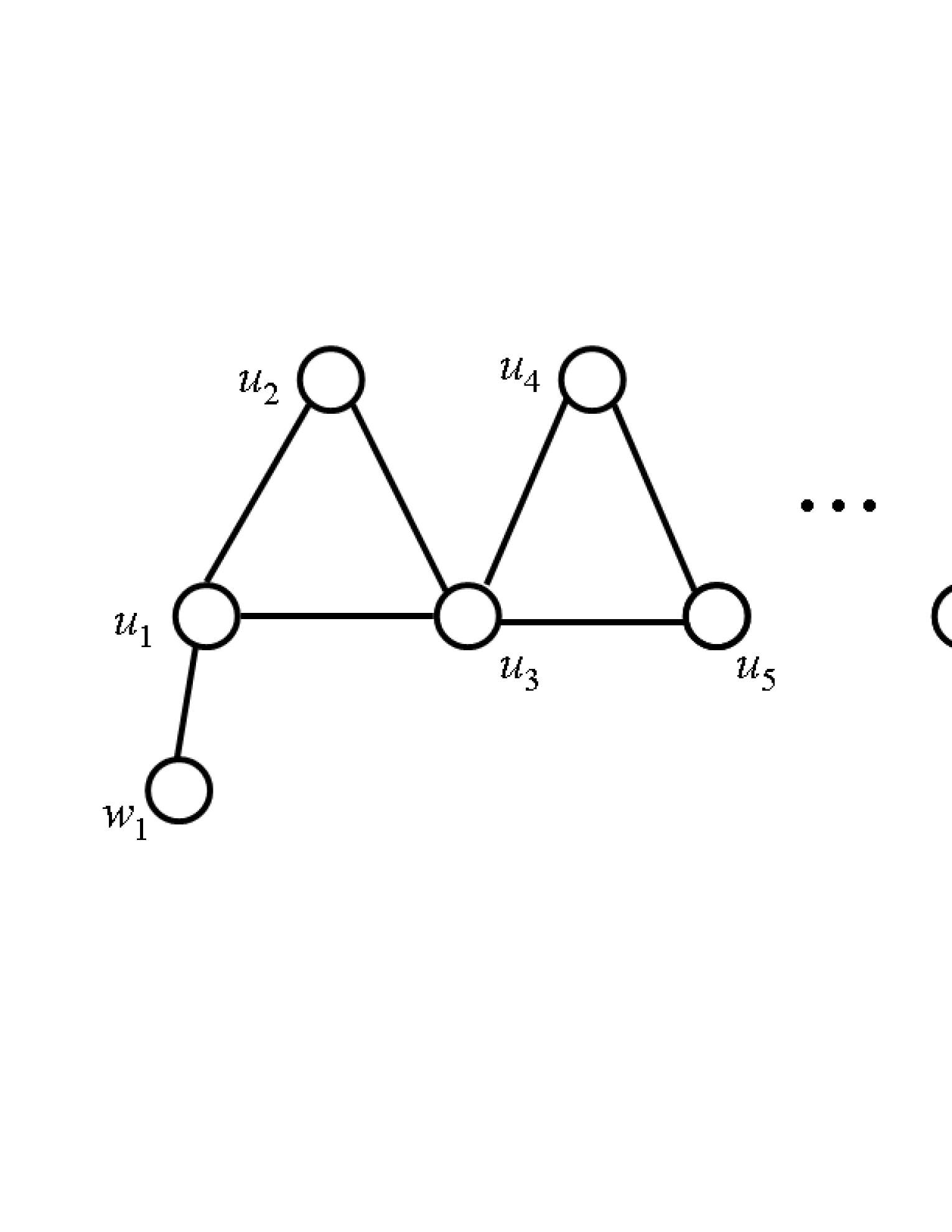
Notice that holds for each and that holds for each by ; no vertex other than , and is adjacent to .
Lemma 2
If is an outerphane graph with and which contains neither (C1) nor (C2), then has a chain of 3-faces such that is an inner edge.
Proof
Let be an outerphane graph with which contains neither (C1) nor (C2). Let be a 2-connected component of which contains exactly one cut vertex of if is not 2-connected, otherwise. Notice that by . Then has an inner edge since otherwise contains (C1). There are the following two possible cases: (Case-I) every inner edge in belongs to some endface, (Case-II) otherwise. Assume that each vertex on the boundary of the outerface of is numbered in clockwise order. Notice that each endface not containing as a 2-vertex in is a 3-face since otherwise it would contain (C1).
(Case-I) Notice that there are at least two end faces in . Without loss of generality, let be an endface of with ; . Then an inner edge other than is incident to , since otherwise holds and the 3-face would satisfy the conditions of (C2). By the assumption of Case-I, the inner edge belongs to some endface, and hence we can see that another 3-face exists; is a chain. Moreover, observe that if also holds, then is a 3-face and is a chain. By repeating similar observations, it follows that there exists a chain . Then notice that (resp., 2) if is odd (resp., even); by , if exists, then is some vertex with . Hence, we can see that if exists, then contains a chain with an inner edge , and that otherwise is a chain with an inner edge as required.
(Case-II) For an inner edge , let denote the subgraph of induced by . Without loss of generality, let be an inner edge in which does not belong to any endface such that does not contain . Moreover, we can choose such an edge that any inner edge in belongs to some endface of . Note that if contains an inner edge not in any endface, then the number of inner edges not in any endface in is less than that in and this observation indicates that this choice of is possible. Then by applying the similar arguments in Case-I to endfaces in (also in ), we can observe that there exists a chain , which is a required chain. ∎
By utilizing this lemma, we show that holds even if .
Theorem 4.2
If is an outerplane graph with , then .
Proof
We prove this by induction on . The theorem clearly holds if . Consider the case of and assume that for each , this theorem holds. We also assume that is connected, since otherwise we can treat each component separately. Thus, .
In the case of , similarly to the proof of Theorem 3.1, we can observe that has a (2,1)-total labeling .
Consider the case where . By Theorem 4.1, contains at least one of the configurations (C1)–(C3). In [4, Theorem 13], Chen and Wang showed that if contains (C1) or (C2), then a (2,1)-total labeling of can be obtained from a feaible labeling of some subgraph of . Here we only consider the case where contains neither (C1) nor (C2). By Lemma 2, contains a chain of 3-faces such that is an inner edge. Let (resp., ) denote the vertex not in which is adjacent to (resp., ) (note that by , no edge other than and connects and the remaining part of ). By the induction hypothesis, has a (2,1)-total labeling . Then by , we can assign any label in (resp., ) to (resp., ) without violating the feasibility. Let and denote the sets of such possible labels with respect to for and , respectively; and . Notice that and .
Claim
contains one of , and .
Proof
Assume for contradiction that this claim does not hold. First consider the case of . By assumption, . This inidcates that (a1) and or (a2) and . In the case of (a1), we have (i.e., and in the case of (a2), we have (i.e., ), a contradiction.
Next consider the case of and . By assumption, . This indicates that (b1) and , (b2) and , (b3) and , (b4) and , or (b5) and . In the case of (b1) (resp., (b2), (b3), (b4), (b5)), we have (resp., , , , ). By assumption that does not satisfy this claim, it follows that in the case of (b1) (resp., (b2), (b3), (b4), (b5)), (resp., , , ). All of these cases contraict .
By symmetry of labelings, the case of and can be treated similarly to the previous case. Finally, consider the case of . Assume that , since any other case can be treated similarly by exchanging parts of and . Then we can observe that , , , and . It follows that or are contained in , a contradiction. ∎
By symmetry, it suffices to consider the following four cases: (Case-1) and , (Case-2) and , (Case-3) and , and (Case-4) and . In each case, we will extend to a (2,1)-total labeling of . Let for every .
(Case-1) Let and .
(1.1) Assume that is even; .
(1.1.1) Assume that and .
Let , , , , , , , , and . For , let , , , , , , , , , and . Denote this labeling by (see Fig. 2).
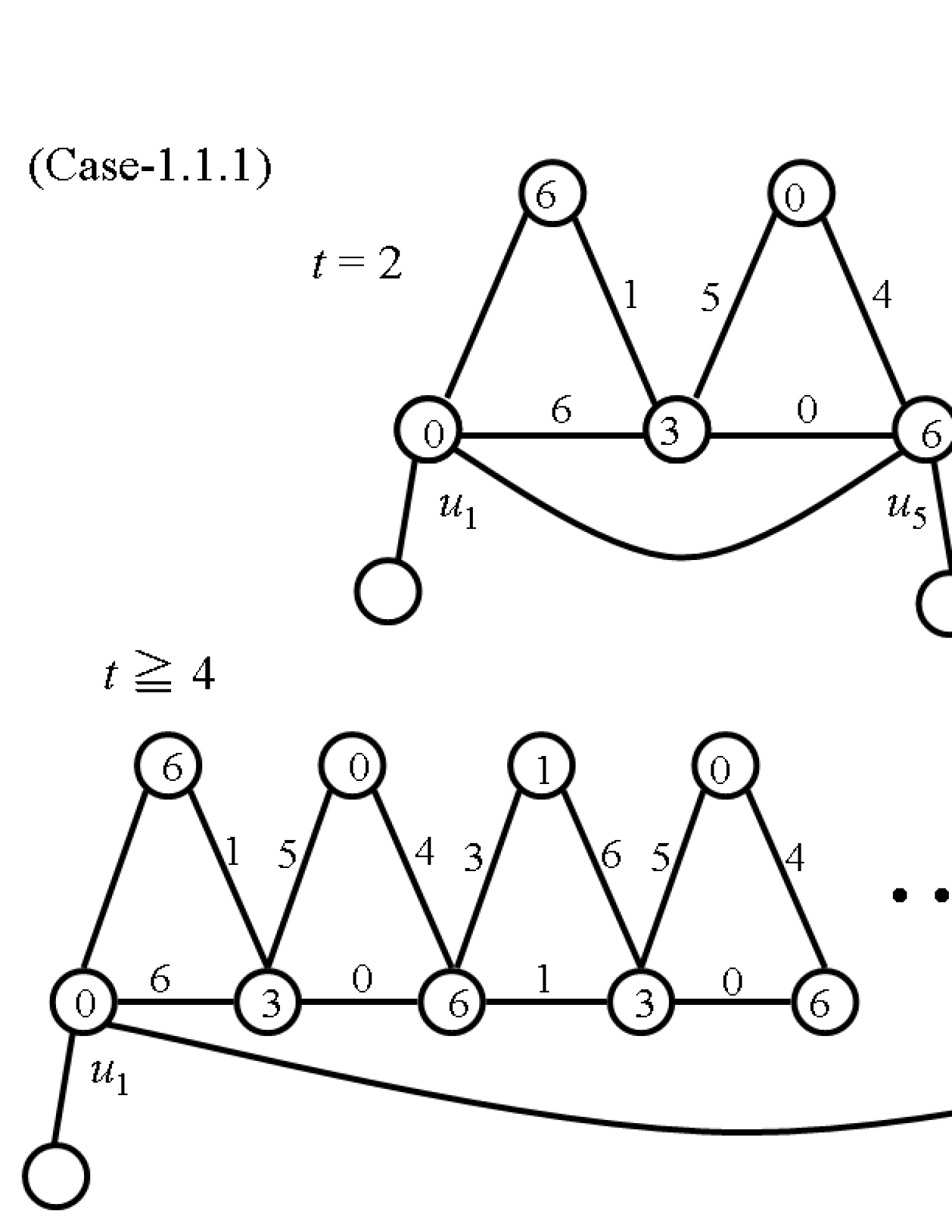
We next assign a label to , and a label in to . Reassign a label in to . Then the resulting labeling is a a (2,1)-total labeling of .
(1.1.2) Assume that and .
Let . We reassign labels for some vertices and edges as follows. Let , , , and . Next we assign a label in to and reassign a label in to . Then the resulting labeling is a a (2,1)-total labeling of .
(1.1.3) Assume that and .
Let . We reassign labels for some vertices and edges as follows. Let , , , , and . Next we assign a label in to and a label in to . Then the resulting labeling is a (2,1)-total labeling of .
(1.1.4) Assume that and .
We can obtain a (2,1)-total labeling of as follows. If , then let , , , , , , , , , and .
Assume that . Let . We reassign labels for some vertices and edges similarly to (1.1.2) and (1.1.3). Namely, let , , , , , , , , , , and .
(1.2) Assume that is odd; .
(1.2.1) Assume that and .
Let , , , , , , , , , , , , , and . For , let , , , , , , , , , and . Denote this labeling by (see Fig. 3).
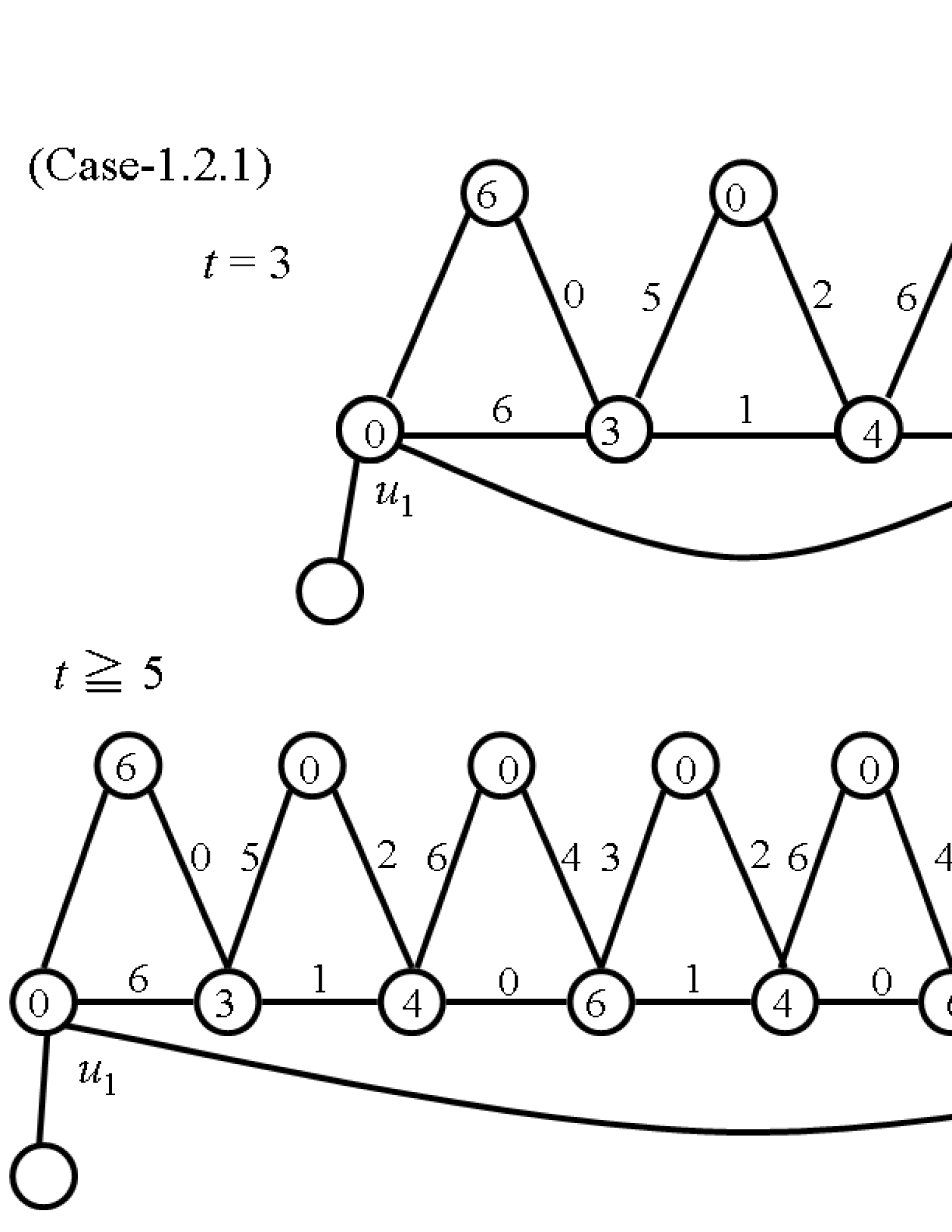
We next assign a label to and assign a label in to . Reassign a label in to .
(1.2.2) Assume that and .
Let . We reassign labels for some vertices and edges as follows. Let , , , , and . Next we assign a label in to . Reassign a label in to .
(1.2.3) Assume that and .
Let . We reassign labels for some vertices and edges as follows. Let , , , , and . Next we assign a label in to and a label in to .
(1.2.4) Assume that and .
Let . We reassign labels for some vertices and edges similarly to (1.2.2) and (1.2.3). Namely, let , , , , , , , , , , and .
(Case-2) Let and .
(2.1) Assume that is even; .
(2.1.1) Assume that and .
Let , , , , , , , , and . For , let , , , , , , , , , and . Denote this labeling by (see Fig. 4).
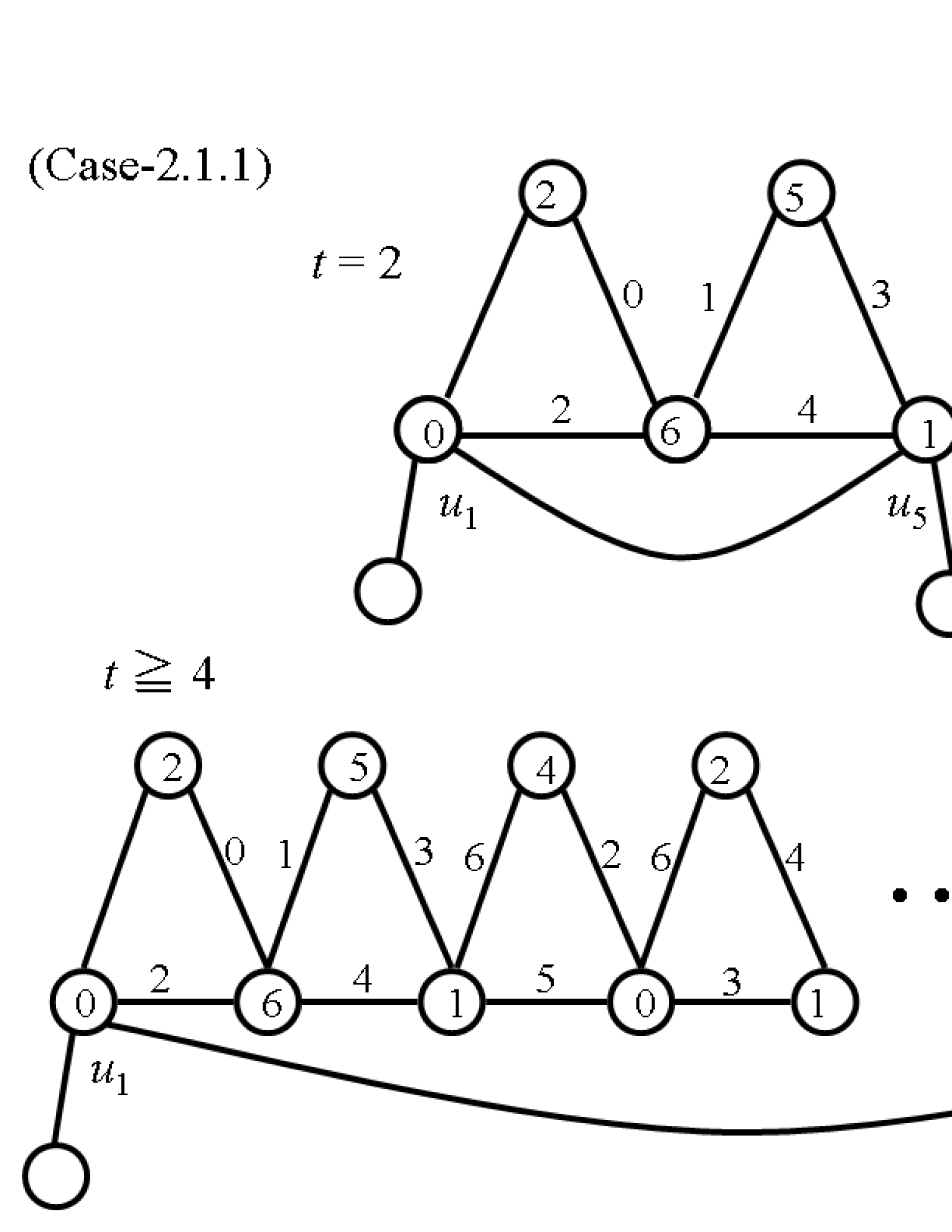
Consider the case of . We assign a label to and a label in to . Reassign a label in to . Then if , then reassign a label for as .
Consider the case of . Assign a label to and a label in to . Reassign a label in to . Then if , then reassign a label for as .
(2.1.2) Assume that and .
Let . We reassign a label for to 3.
Consider the case of . Assign a label in to and a label in to . Reassign a label in to . Then if , then let .
Consider the case of . Assign a label in to and a label in to . Reassign a label in to . Then, if , then let .
(2.1.3) Assume that and .
If , then we can obtain a feasible labeling similarly to (2.1.1). Consider the case of . Let . Reassign a label for as . Next we assign a label in to and a label in to . Reassign a label in to . Then if , then let and , and if , then let .
(2.1.4) Assume that and .
If , then we can obtain a feasible labeling similarly to (2.1.1). Consider the case of . Let . We reassign labels for and as and . Next we assign a label in to and a label in to . Reassign a label in to .
(2.1.5) Assume that and .
If , then we can obtain a feasible labeling similarly to (2.1.2). Consider the case of . Let . We reassign labels for some vertices and edges similarly to (2.1.2) and (2.1.3). Namely, let , , , , , , and .
(2.1.6) Assume that and .
If , then we can obtain a feasible labeling similarly to (2.1.2). If , let , , , , , , , , , and .
(2.2) Assume that is odd; .
(2.2.1) Assume that and .
Let , , , , , , , , , , , , , and . For , let , , , , , , , , , and . Denote this labeling by (see Fig. 5).
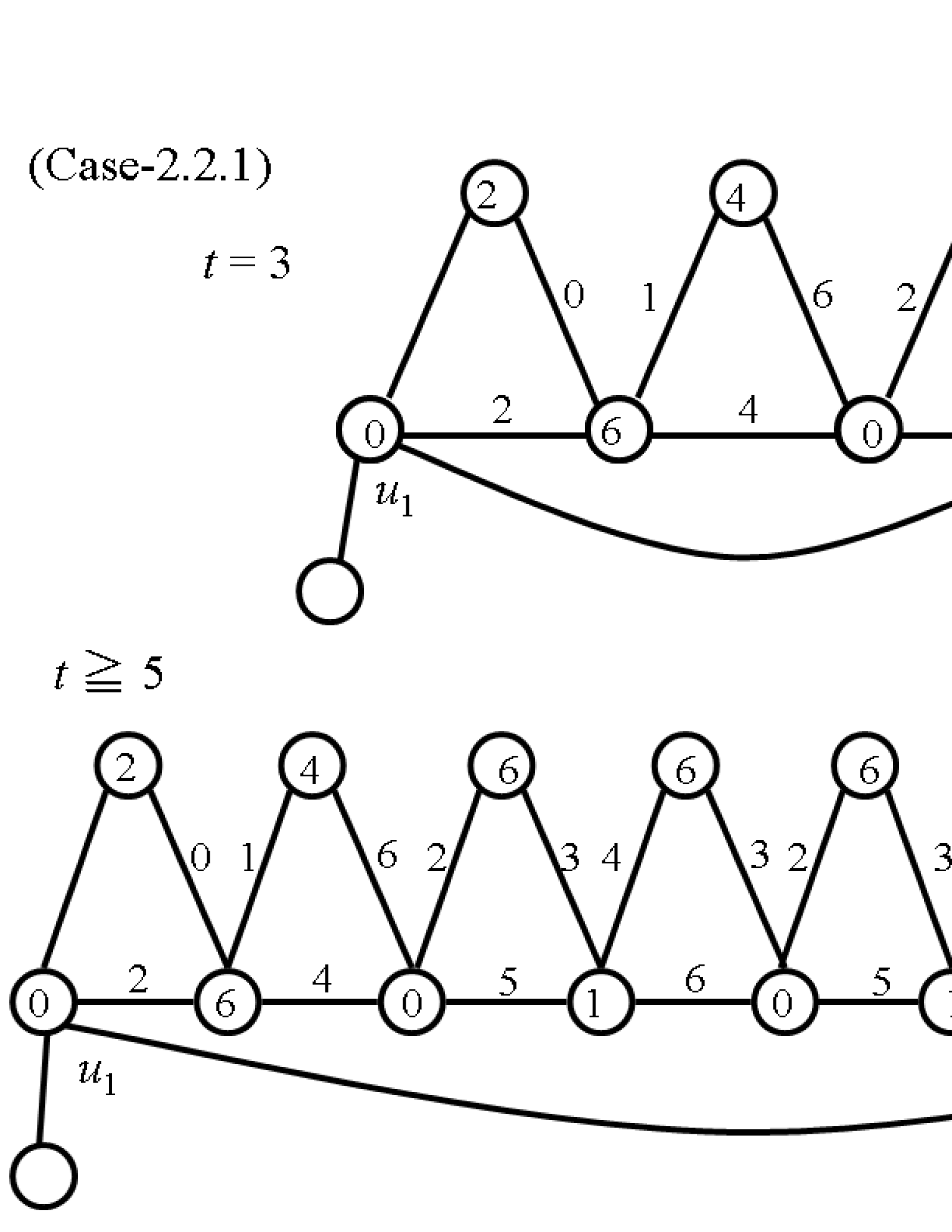
We next assign a label to . and a label in to . Reassign a label in to . Then if , then let .
(2.2.2) Assume that and .
Let . We reassign labels for some vertices and edges as follows. Let and . Next we assign a label in to . Reassign a label in to . Then if , then let .
(2.2.3) Assume that and .
Let .
First consider the case of . Let , , and . Next we assign a label in to and a label in to . Reassign a label in to .
Next consider the case of . Let . Next we assign a label in to and a label in to . Reassign a label in to . Then if , then .
(2.2.4) Assume that and .
Let . We reassign labels for some vertices and edges similarly to (2.2.2) and (2.2.3). Namely, if , let , , , , , , and . If , then let , , , and .
(Case-3) Let and .
(3.1) Assume that is even; .
(3.1.1) Assume that and .
Let , , , , , , , , and . For , let , , , , , , , , , and . Denote this labeling by (see Fig. 6).
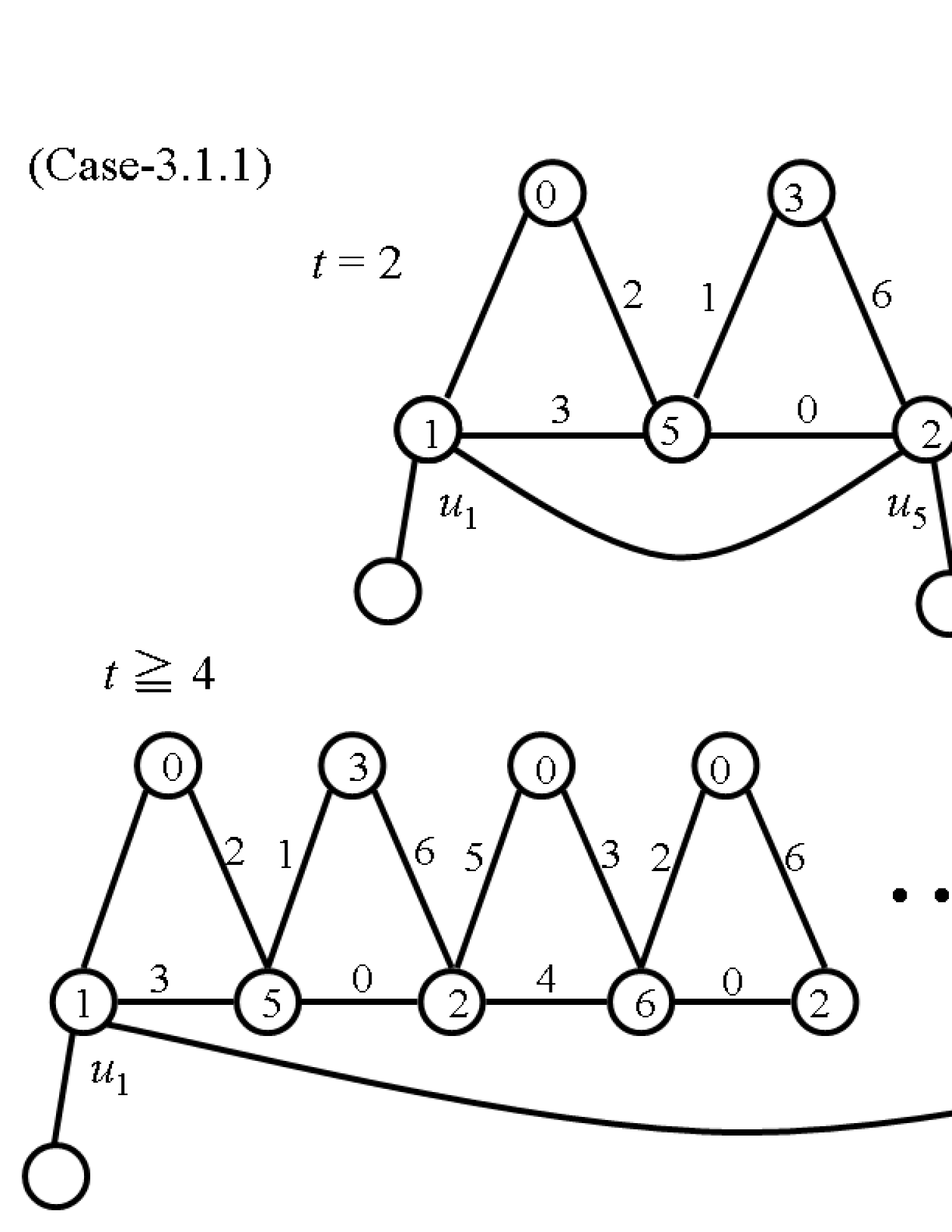
Assign a label to and a label in to . Reassign a label in to . Then if , then let .
(3.1.2) Assume that and .
Let . We reassign labels for some vertices and edges as follows. Let , , and . Assign a label in to and a label in to . Reassign a label in to . Then if , then let and .
(3.1.3) Assume that and .
Let .
Consider the case of . Let and . Next we assign a label in to and a label in to . Reassign a label in to .
Consider the case of . Let , , and . Next we assign a label in to and a label in to . Reassign a label in to . Then if , then let , and if , then let .
(3.1.4) Assume that and .
If , let , , , , , , , , , and .
Consider the case of . Let . We reassign labels for some vertices and edges similarly to (3.1.2) and (3.1.3). Namely, let , , , , , , , , and .
(3.2) Assume that is odd; .
(3.2.1) Assume that and .
Let , , , , , , , , , , , , , and . For , let , , , , , , , , , and . Denote this labeling by (see Fig. 7).
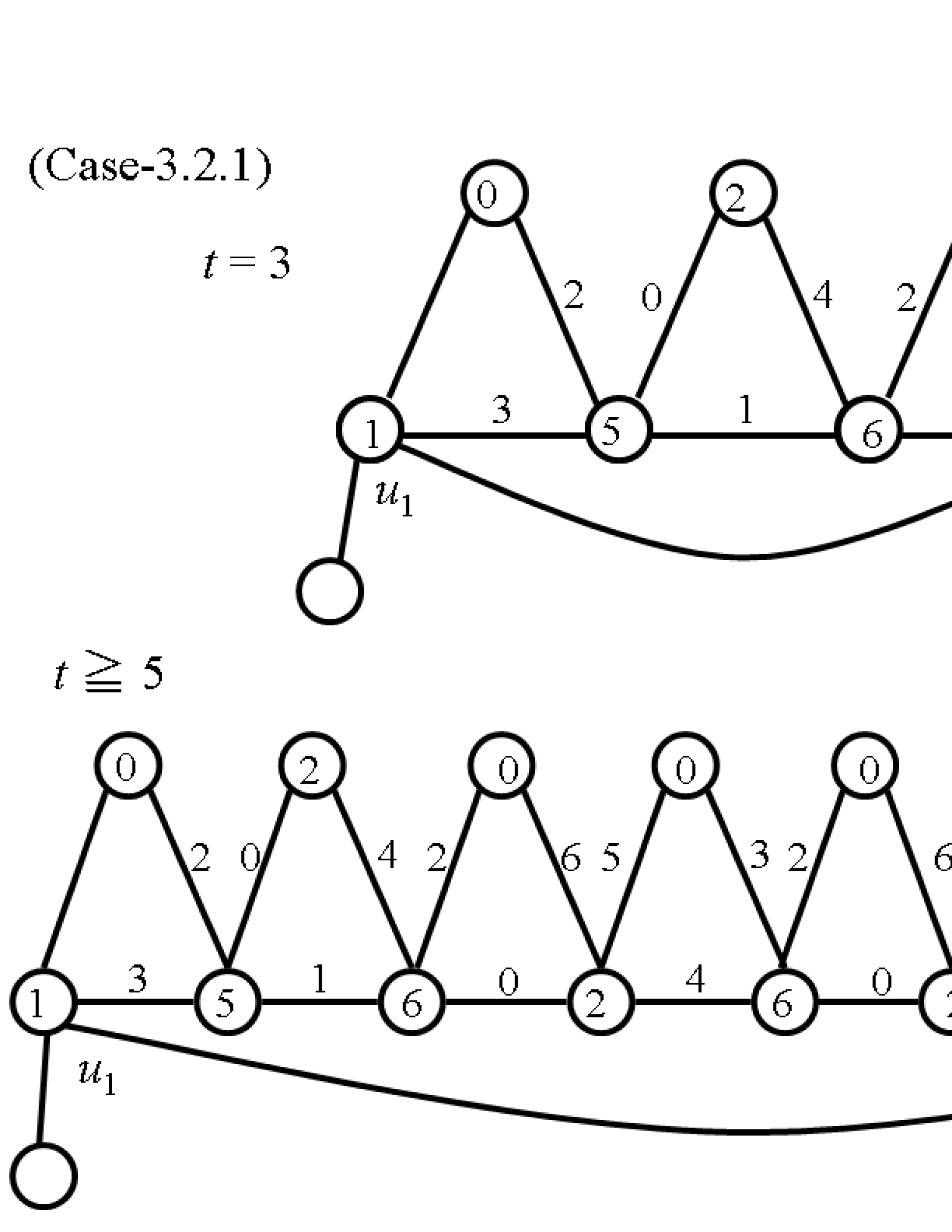
We next assign a label to and a label in to . Reassign a label in to .
(3.2.2) Assume that and .
Let . We reassign labels for some vertices and edges as follows. Let and . Next we assign a label in to and a label in to . Reassign a label in to .
(3.2.3) Assume that and .
Let .
First consider the case of . Let , , , and . Next we assign a label in to and a label in to . Reassign a label in to .
Next consider the case of . Let , , , , and . Next we assign a label in to and a label in to . Reassign a label in to . Then if (resp., 5), then let (resp., 1) and (resp., 4).
(3.2.4) Assume that and .
Let . We reassign labels for some vertices and edges similarly to (3.2.2) and (3.2.3). Namely, if , let , , , , , , , , , , and . If , then let , , , , , , , , , , , and .
(Case-4) Let and .
(4.1) Assume that is even; .
(4.1.1) Assume that and .
Let , , , , , , , , and . For , let , , , , , , , , , and . Denote this labeling by (see Fig. 8).
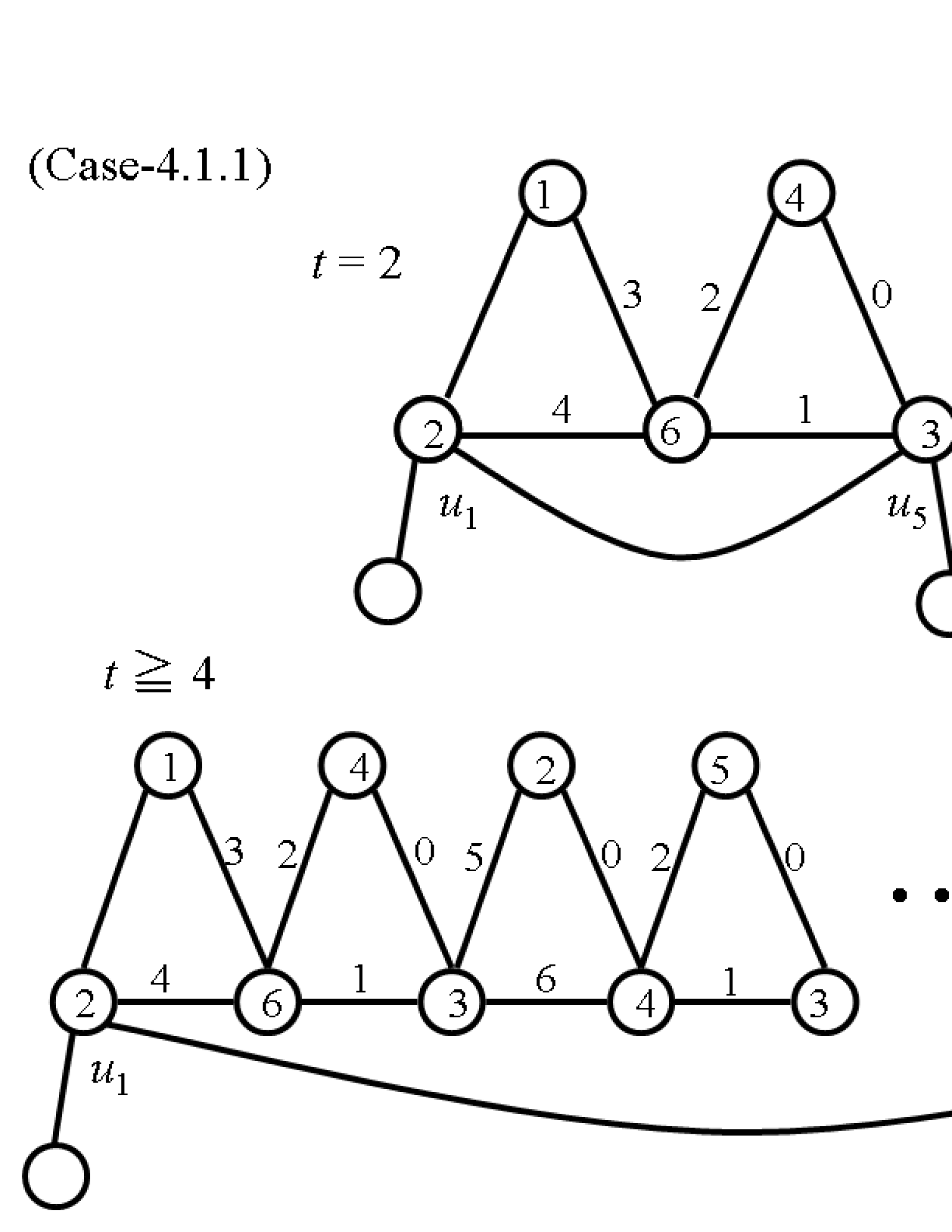
Assign a label to and a label in to . Reassign a label in to . Then if , then let , and if , then let .
(4.1.2) Assume that and .
Let . We reassign a label for as . Assign a label in to and a label in to . Reassign a label in to . Then if , then let .
(4.1.3) Assume that and .
Let .
Consider the case of . Let and . Next we assign a label in to and a label in to . Reassign a label in to . Then if , then let .
Consider the case of . Let , , , , and . Next we assign a label in to and a label in to . Reassign a label in to . Then if , then let .
(4.1.4) Assume that and .
If , let , , , , , , , , , and .
Consider the case of . Let . We reassign labels for some vertices and edges similarly to (4.1.2) and (4.1.3). Namely, let , , , , , , , and .
(4.2) Assume that is odd; .
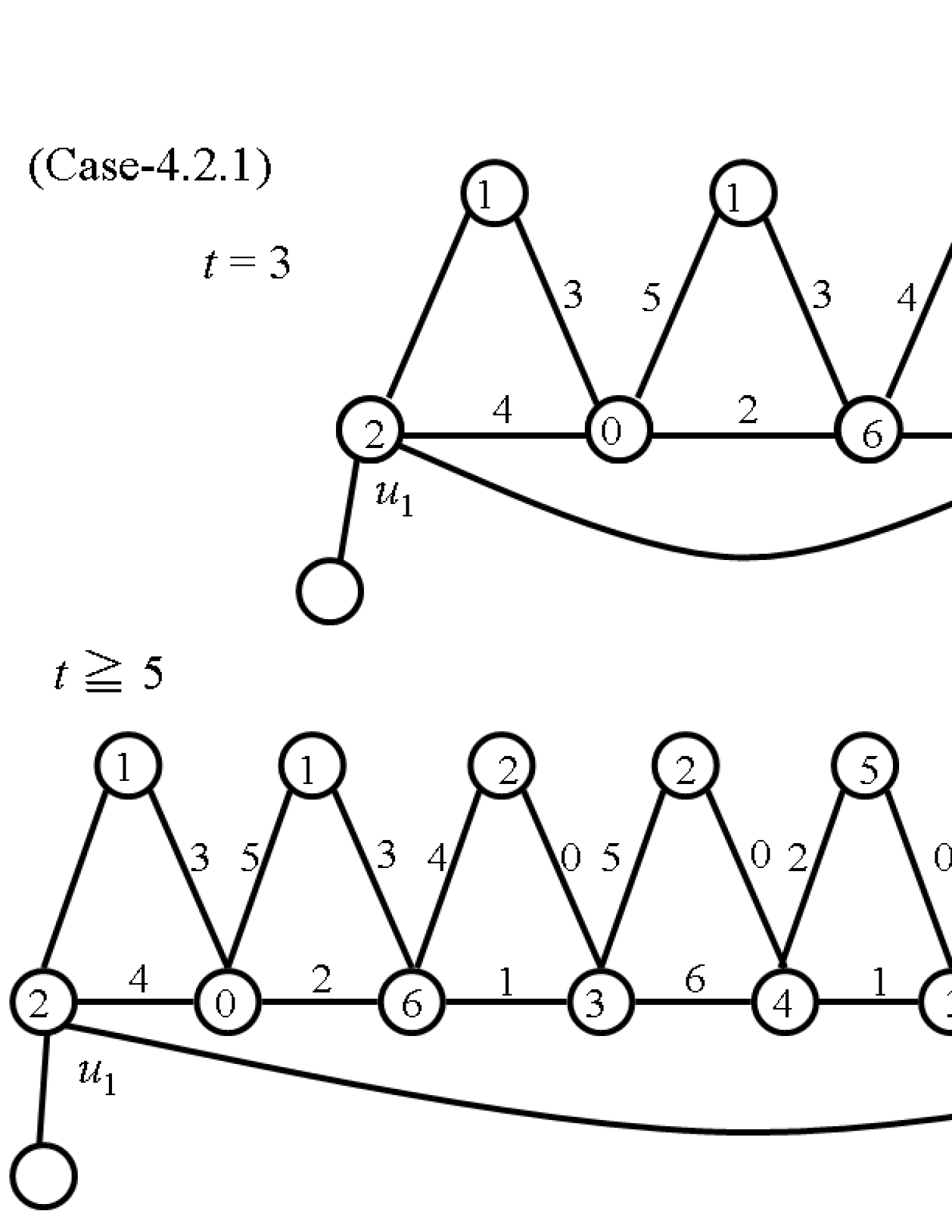
(4.2.1) Assume that and .
Let , , , , , , , , , , , , , and . For , let , , , , , , , , , and . Denote this labeling by (see Fig. 9). We next assign a label to and a label in to . Reassign a label in to . Then if , then let , and if , then let .
(4.2.2) Assume that and .
Let . We reassign a label for as . Next we assign a label in to and a label in to . Reassign a label in to . Then if , then let , and if , then let .
(4.2.3) Assume that and .
Let .
First consider the case of . Let . Next we assign a label in to and a label in to . Reassign a label in to . Then if , then let .
Next consider the case of . Let , , , , and . Next we assign a label in to and a label in to . Reassign a label in to . Then if , then let , and if , then let .
(4.2.4) Assume that and .
Let . We reassign labels for some vertices and edges similarly to (4.2.2) and (4.2.3). Namely, if , let , , , , , and . If , then let , , , , , , , , , and . ∎
References
- [1] F. Bazzaro, M. Montassier, and A. Raspaud. (,1)-total labelling of planar graphs with large girth and high maximum degree. Discr. Math. 307, 2141–2151 (2007).
- [2] M. Behzad. Graphs and their chromatic numbers. Ph.D. Thesis, Michigan State University, 1965.
- [3] T. Calamoneri. The -labelling problem: A survey and annotated bibliography. The Computer Journal 49, 585–608 (2006). (The -Labelling Problem: A Survey and Annotated Bibliography, http://www.dsi.uniroma1.it/~calamo/PDF-FILES/survey.pdf, ver. Jan. 13, 2009.)
- [4] D. Chen and W. Wang. (2,1)-Total labelling of outerplanar graphs. Discr. Appl. Math. 155, 2585–2593 (2007).
- [5] S. Fiorini. On the chromatic index of outerplanar graphs. J. Combin. Theory Ser. B 18, 35–38 (1975).
- [6] J. R. Griggs and R. K. Yeh. Labelling graphs with a condition at distance 2. SIAM J. Disc. Math. 5, 586–595 (1992).
- [7] F. Havet and M. -L. Yu. (,1)-Total labelling of graphs. Technical Report 4650, INRIA, 2002.
- [8] F. Havet and M. -L. Yu. (,1)-Total labelling of graphs. Discr. Math. 308, 496–513 (2008).
- [9] D. König. Über graphen und ihre anwendug auf determinantentheorie und mengenlehre. Math. Ann. 77, 453–465 (1916).
- [10] K.-W. Lih, D. D.-F. Liu and W. Wang. On -total numbers of graphs. Discr. Math. 309, 3767–3773 (2009).
- [11] M. Montassier and A. Raspaud. (,1)-total labeling of graphs with a given maximum average degree. J. Graph Theory 51, 93–109 (2006).
- [12] V. G. Vizing. On the estimate of the chromatic class of a -graphs. Diskret. Analiz. 3, 25–30, (1964) (in Russian).
- [13] V. G. Vizing. Some unsolved problems in graph theory. Russian Mathematical Surveys 23, 125–141, (1968).
- [14] W. Wang and K. Zhang. -Matchings and edge-face chromatic numbers. Acta. Math. Appl. Sinica 22, 236–242 (1999).
- [15] M. A. Whittlesey, J. P. Georges, and D. W. Mauro. On the -number of and related graphs. SIAM J. Discr. Math. 8, 499–506 (1995).
- [16] R. K. Yeh. A survey on labeling graphs with a condition at distance two. Discr. Math. 306, 1217–1231 (2006).