Ab initio framework for nuclear scattering and reactions induced by light projectiles
Abstract
A quantitative and predictive microscopic theoretical framework that can describe reactions induced by particles (4He nuclei) and heavier projectiles is currently lacking. Such a framework would contribute to reducing uncertainty in the modeling of stellar evolution and nucleosynthesis and provide the basis for achieving a comprehensive understanding of the phenomenon of nuclear clustering (the organization of protons and neutrons into distinct substructures within a nucleus). We have developed an efficient and general configuration-interaction framework for the description of low-energy reactions and clustering in light nuclei. The new formalism takes full advantage of powerful second-quantization techniques, enabling the description of - scattering and an exploration of clustering in the exotic 12Be nucleus. We find that the 4HeHe differential cross section computed with non-locally regulated chiral interactions is in good agreement with experimental data. Our results for 12Be indicate the presence of strongly mixed helium-cluster states consistent with a molecular-like picture surviving far above the 6He+6He threshold, and reveal the strong influence of neutron decay in both the 12Be spectrum and in the 6He(6He,)8He cross section. We expect that this approach will enable the description of helium burning cross sections and provide insight on how three-nucleon forces influence the emergence of clustering in nuclei.
The low-energy interactions of particles among themselves and with other nuclei play a prominent role in the helium-burning and later stages of stellar evolution, and are critical to the formation of the chemical elements. Most emblematic is the triple- process Burbidge et al. (1957); the fusion of two 4He nuclei into the transient 8Be resonance, immediately followed by the capture of a third particle. The triple- process provides one of the main mechanisms for bridging the instability of the mass elements and hence a path for the production of carbon, oxygen and all heavier species. The description of -induced processes is closely intertwined with the description of nuclear clustering, where particles and their dynamical interactions are also the main building blocks, due to their large binding energies. More broadly, elastic scattering and transfer reactions induced by light (-shell) nuclei are often used as indirect means to determine capture reaction rates at stellar temperatures, as well as for probing the cluster structure of exotic nuclear states such as molecular resonances in beryllium isotopes.
There is a long history of studying -induced reactions and clustering with microscopic approaches using phenomenological potentials Matsuse et al. (1975); Wada and Horiuchi (1988); Baye et al. (2000); Kanada-En’yo and Horiuchi (2003); Betan and Nazarewicz (2012); Funaki et al. (2015); Lyu et al. (2019); Dreyfuss et al. (2020). Ab initio approaches have only recently begun making first steps, describing - scattering phase shifts Elhatisari et al. (2015), as well as clustering in carbon and other light isotopic chains Epelbaum et al. (2012); Elhatisari et al. (2017), starting from nucleon-nucleon (NN) and three-nucleon (3N) forces up to next-to-next-to-leading order of chiral effective field theory (EFT) Machleidt and Sammarruca (2016). Ref. Freer et al. (2018) presents a thorough review of microscopic approaches to nuclear clustering.
In this letter we introduce an efficient and general configuration-interaction implementation of the ab initio no-core shell model (NCSM) combined with the resonating group method (or NCSM/RGM approach) Quaglioni and Navrátil (2008); Navrátil et al. (2016) that enables the calculation of reactions induced by any light projectile, including particles and -shell nuclei. We present an ab initio calculation of - scattering with chiral NN+3N forces and further demonstrate the versatility of our approach by studying the 6He(6He,)8He transfer reaction and the cluster structure of the 12Be system, which has been under thorough experimental Korsheninnikov et al. (1995); Freer et al. (1999, 2001); Saito et al. (2004); Charity et al. (2007); Yang et al. (2014); Smith et al. (2014); Freer et al. (2017) and theoretical Kanada-En’yo and Horiuchi (2001, 2003); Descouvemont and Baye (2001); Ito (2012); Lyu et al. (2019) investigation.
In the NCSM/RGM approach Quaglioni and Navrátil (2009), the continuous amplitudes describing the partial wave of relative motion (with spin-parity and isospin ) of two nuclei in the reaction channel (specified by the quantum numbers of target and projectile, channel spin and relative angular momentum ) is found by solving the coupled-channel equations
| (1) |
where is a non-local, translationally invariant integration kernel containing all the information about the structure and interactions of the many-body system. We compute the localized (short- and medium-range) components of by means of the expansion
| (2) |
where is the radial part of a harmonic oscillator (HO) wave functions , is the linear transformation defined in Eq. (32) of Ref. Quaglioni and Navrátil (2009) relating relative-coordinate and Slater-Determinant (SD) channel states (with ), and are matrix elements of the microscopic many-body Hamiltonian minus the total energy over the reaction channels
| (3) |
Here, the state is the SD wave function of the target obtained within the -body HO expansions of the NCSM Navrátil et al. (2000); Barrett et al. (2013), depending trivially on its c.m. coordinate . Similarly,
| (4) |
is the eigenstate of the projectile nucleus, obtained once again in the NCSM SD basis, with its c.m. wave function subsequently excited in the oscillator state. The formalism and operators for implementing the latter boost of the c.m. quanta are described in Refs. Kravvaris and Volya (2017, 2019). Being products of SD wave functions, the basis states of Eq. (3) can be written as linear combinations of -body SD wave functions, where is a second-quantization operator that creates a particle in a state defined by the set of quantum numbers denoted by , and a coefficient determining the weight of the -th SD state in the reaction channel vector, with occupied orbitals . In practice, the total number of Slater determinants for each channel is truncated to make calculations tractable. See Supplemental Material for how this truncation affects observables.
The present formalism takes full advantage of powerful second-quantization techniques for constructing the reaction channels and evaluating their full matrix elements, unlike our previous approach Quaglioni and Navrátil (2009); Hupin et al. (2013), where only the wave function of the target nucleus and its transition densities were computed starting from Slater determinants. Furthermore, compared to Ref. Quaglioni and Navrátil (2009)–where the explicit antisymmetrization of the matrix elements enabled us to distinguish the contributions to the integration kernel coming from the inter-cluster and clusters’ Hamiltonians–the present formalism loses track of the identity of particles belonging to the projectile and target nuclei. The full matrix elements of the many-body Hamiltonian are computed at once. The two methodologies eventually become equivalent at convergence in the HO expansion. For smaller model spaces minor differences arise in the computed internal energies of the reacting nuclei, which in the approach of Ref. Quaglioni and Navrátil (2009) are included as the eigenenergies at the given NCSM model space size, . See Supplemental Material for a comparison between the two methods. The exact treatment of all other (non-localized) terms of the kernel and the solution of Eq. (1) are achieved following the methodology outlined in Ref. Quaglioni and Navrátil (2009).
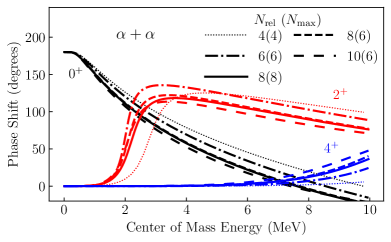
As a first demonstration, we investigate the scattering of two particles and how the 3N force shapes the resulting differential cross section. The adopted Hamiltonian includes NN and 3N interaction terms: the N3LO NN interaction introduced in Ref. Entem and Machleidt (2003) with a regulator cutoff of =500 MeV, denoted simply as NN; and the leading-order 3N force van Kolck (1994) in the local form of Ref. Navrátil (2007) with cutoff MeV of Ref. Gazit et al. (2019), denoted as , as well as with mixed local and non local regulators of Ref. Somà et al. (2020), denoted as . In all cases the interactions are softened via a similarity renormalization group (SRG) transformation in three-body space Jurgenson et al. (2009) with a momentum resolution scale of fm-1. The 3N force matrix elements are included up to a total number of single-particle quanta for the three-body basis of =16.
The calculations are carried out with an HO frequency of = 24 MeV and model space size of =8. Starting at 6, where the wave function is close to convergence (Table 1), the model-space dependence of the - phase shifts is mainly driven by the convergence of the inter-cluster interaction, that is by the maximum number of quanta in the relative motion . A complete =10 calculation would require 3N force matrix elements beyond the current truncation of =16. The convergence error at =8 can be estimated (while still capturing nearly all of the contribution of the 3N force) by increasing and keeping the overall maximum number of HO shells equal or below 16. To this aim, we performed additional calculations with =6 particles and =8 and . The close agreement between the =8(6) and 10(6) phase shifts suggests that convergence is reached around =8. Unless otherwise specified, in the reminder we set .
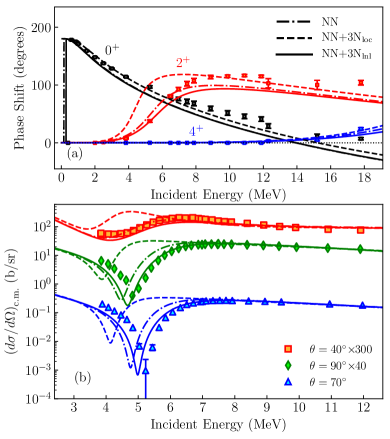
The choice of 3N-force regulator plays a major role in determining the behavior of the + system. Compared to the results obtained with the NN interaction, where the 8Be ground state (g.s.) is found as a resonance at 78 keV above threshold, the inclusion of the 3Nloc interaction produces additional attraction. Specifically, the g.s. becomes bound by 0.6 MeV and the resonance is shifted to an energy lower than what the phase shifts extracted from experiment Afzal et al. (1969) suggest (Fig. 2a). The lower-energy position of the dip of the differential cross section is another sensitive indicator of this overbinding. Conversely, the 3Nlnl force has a repulsive effect. The centroid of the g.s. resonance is found at 136 keV above threshold and the dip of the differential cross section moves closer to the experimental data (Fig. 2b), yielding the overall most accurate description of the + system.
To further demonstrate the general applicability of the approach we now consider the 12Be nucleus. Its low-energy continuum is characterized by multiple binary particle decay thresholds. Correspondingly, multiple modes of clusterization need to be included to describe this system. We carried out calculations including three of such modes, namely 11Be+, He, and 6He+6He. The three-body + channel is beyond the scope of this demonstration and is not considered here, though its inclusion can be achieved in the future by combining the present approach with the ab initio frameworks for three-cluster dynamics of Refs. Quaglioni et al. (2013, 2016, 2018).
As a first application of the approach to reactions with -shell projectiles, we limit ourselves to a soft NN Hamiltonian obtained from the SRG evolution in two-body space of the N3LO NN interaction of Ref. Entem and Machleidt (2003) with fm-1, denoted here as NN-only. The 11Be and 4,6,8He wave functions are obtained within a MeV, HO model space. The parity-inverted ground state of 11Be results from a subtle interplay of 3N-force and 10Be+ continuum effects Calci et al. (2016), neither of which is included in the present calculations. Regardless, we selected the first state from the NCSM calculation of 11Be, despite it not being the theoretically predicted ground state. All helium isotopes are considered to be in their ground states. The computed energies for all clusters are summarized in Table 1.
| Nucleus | Interaction | Eg.s. (MeV) | (MeV) | |
|---|---|---|---|---|
| 4He | NN | -25.3 | 8 | 24.0 |
| 4He | NN+3Nloc | -27.7 | 4 | 24.0 |
| 4He | NN+3Nloc | -28.3 | 6 | 24.0 |
| 4He | NN+3Nloc | -28.4 | 8 | 24.0 |
| 4He | NN+3Nlnl | -28.3 | 8 | 24.0 |
| 4He | NN-only | -28.4 | 6 | 20.0 |
| 6He | NN-only | -27.8 | 6 | 20.0 |
| 8He | NN-only | -28.6 | 6 | 20.0 |
| 11Be | NN-only | -65.9 | 6 | 20.0 |
In the limit of no mixing between the 4He+8He and 6He+6He cluster modes, the NCSM/RGM Hamiltonian would be block-diagonal, and the spectrum of energy levels would be the sum of the spectra computed with individual partitions (first and second column of Fig. 3). The shift of the energy levels (e.g., MeV for the ground state) in the coupled calculation (third column of Fig. 3) suggests otherwise. This is consistent with a picture of molecular orbits with four valence neutrons covalently shared by two centers Kanada-En’yo and Horiuchi (2003). A similar result was found in Ref. Descouvemont and Baye (2001). We note that all negative parity states for the 6He+6He system are Pauli blocked, and only natural parity states can exist in both modes.
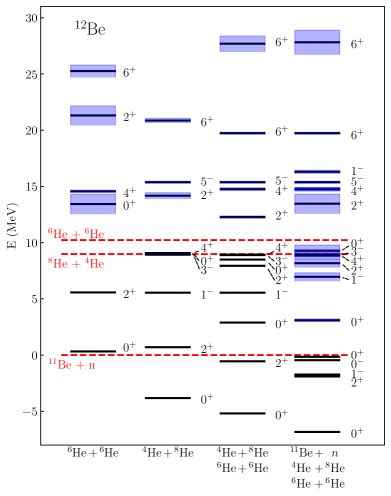
The most dramatic change in the spectrum of 12Be comes from he inclusion of the 11Be+ channel (fourth column of Fig 3). States that were previously bound are now found above the neutron decay threshold. In the absence of 3N-forces (both chiral and SRG-induced), the calculated g.s. energy with respect to the 11Be+ decay threshold (-6.84 MeV) is overbound compared with experiment (-3.17 MeV). The state appearing just below the decay threshold has not been observed in experiment; it may in fact be the tentative state observed in Ref. Smith et al. (2014), though calculations including the 10Be+ and 11Be+ mass partitions would be needed to confirm this assessment. The now unbound 0+ state observed around 4 MeV remains essentially constant and does not have an appreciable neutron decay width, suggesting that it maintains its helium-cluster characteristics. Proximity to a decay threshold, suggested as the underlying mechanism for the emergence of clustering in Ref. Okołowicz et al. (2012), does not play a role in this case.
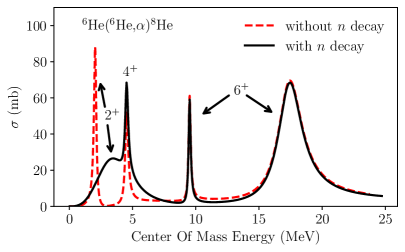
In the region above 10 MeV, where states are unbound with respect to the 6He+6He threshold, we observe little change with the inclusion of the 11Be+ channel. That is, nearly all resonances maintain strong helium-cluster characteristics. The sole exception is the 2+ resonance, which acquires a significant decay width. This broadening of the 2+ resonance is clearly visible in the 6He(6He,)8He reaction cross section (Fig. 4). This demonstrates that the interaction through the continuum of neutron decay channels allows for further coupling between the two decay modes, leading to a reorganization of the many-body wave function. Finally, it should be noted that the first 6+ state remains extremely narrow despite lying 10 MeV from the nearest decay threshold. It can be identified as a helium-clustered state, as it exists in the calculation including both helium mass partitions and remains unchanged with the inclusion of the 11Be + channel. Such survival of rotational bands well into the continuum is an effect of the large angular momentum barrier, which suppresses the decay rate Garrido et al. (2013); Fossez et al. (2016).
By exploiting c.m. quanta boosting techniques in the construction of the microscopic reaction channels used to compute the underlying integration kernel, we have developed an efficient and general configuration-interaction implementation of the ab initio NCSM/RGM approach. The new implementation enables a major leap forward in the unified ab initio description of nuclear clustering and low-energy reactions induced by any light projectile, including particles and p-shell nuclei. First applications of the approach reveal the sensitivity of - scattering observables to the choice of chiral 3N-force regulator, and explain the role of helium clusters and neutron decay in shaping the spectrum of 12Be and the 6He(6He,)8He cross section. Additionally, the new formalism allows for a controlled lowering of the fidelity of the calculation by truncating the wave functions of the reaction channels at the many-body level. The resulting reduced-fidelity calculations will be a key component of future efforts in quantifying chiral EFT uncertainties for scattering and reaction observables Kravvaris et al. (2020). The implementation of the present formalism within the generalized microscopic-cluster expansions of the no-core shell model with continuum Baroni et al. (2013a, b)–currently under way–will soon enable the ab initio description of helium burning cross sections and help explaining how 3N forces influence the emergence of clustering in nuclei.
Acknowledgements.
Computing support for this work came from the LLNL institutional Computing Grand Challenge program. Prepared in part by LLNL under Contract DE-AC52-07NA27344. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under Work Proposal No. SCW0498, and by Grant No. SAPIN-2016-00033. TRIUMF receives federal funding via a contribution agreement with the National Research Council of Canada.References
- Burbidge et al. (1957) E. M. Burbidge, G. R. Burbidge, W. A. Fowler, and F. Hoyle, Rev. Mod. Phys. 29, 547 (1957).
- Matsuse et al. (1975) T. Matsuse, M. Kamimura, and Y. Fukushima, Progress of Theoretical Physics 53, 706 (1975).
- Wada and Horiuchi (1988) T. Wada and H. Horiuchi, Phys. Rev. C 38, 2063 (1988).
- Baye et al. (2000) D. Baye, P. Descouvemont, and R. Kamouni, Few-Body Systems 29, 131 (2000).
- Kanada-En’yo and Horiuchi (2003) Y. Kanada-En’yo and H. Horiuchi, Phys. Rev. C 68, 014319 (2003).
- Betan and Nazarewicz (2012) R. I. Betan and W. Nazarewicz, Phys. Rev. C 86, 034338 (2012).
- Funaki et al. (2015) Y. Funaki, H. Horiuchi, and A. Tohsaki, Progress in Particle and Nuclear Physics 82, 78 (2015).
- Lyu et al. (2019) M. Lyu, K. Yoshida, Y. Kanada-En’yo, and K. Ogata, Phys. Rev. C 99, 064610 (2019).
- Dreyfuss et al. (2020) A. C. Dreyfuss, K. D. Launey, J. E. Escher, G. H. Sargsyan, R. B. Baker, T. Dytrych, and J. P. Draayer, Phys. Rev. C 102, 044608 (2020).
- Elhatisari et al. (2015) S. Elhatisari, D. Lee, G. Rupak, E. Epelbaum, H. Krebs, T. A. Lahde, T. Luu, and U.-G. Meißner, Nature 528, 111 (2015).
- Epelbaum et al. (2012) E. Epelbaum, H. Krebs, T. A. Lähde, D. Lee, and U.-G. Meißner, Phys. Rev. Lett. 109, 252501 (2012).
- Elhatisari et al. (2017) S. Elhatisari, E. Epelbaum, H. Krebs, T. A. Lähde, D. Lee, N. Li, B.-n. Lu, U.-G. Meißner, and G. Rupak, Phys. Rev. Lett. 119, 222505 (2017).
- Machleidt and Sammarruca (2016) R. Machleidt and F. Sammarruca, Physica Scripta 91, 083007 (2016).
- Freer et al. (2018) M. Freer, H. Horiuchi, Y. Kanada-En’yo, D. Lee, and U.-G. Meißner, Rev. Mod. Phys. 90, 035004 (2018).
- Quaglioni and Navrátil (2008) S. Quaglioni and P. Navrátil, Phys. Rev. Lett. 101, 092501 (2008).
- Navrátil et al. (2016) P. Navrátil, S. Quaglioni, G. Hupin, C. Romero-Redondo, and A. Calci, Physica Scripta 91, 053002 (2016).
- Korsheninnikov et al. (1995) A. Korsheninnikov, E. Nikolskii, T. Kobayashi, D. Aleksandrov, M. Fujimaki, H. Kumagai, A. Ogloblin, A. Ozawa, I. Tanihata, Y. Watanabe, and K. Yoshida, Physics Letters B 343, 53 (1995).
- Freer et al. (1999) M. Freer, J. C. Angélique, L. Axelsson, B. Benoit, U. Bergmann, W. N. Catford, S. P. G. Chappell, N. M. Clarke, N. Curtis, A. D’Arrigo, E. de Goes Brennard, O. Dorvaux, B. R. Fulton, G. Giardina, C. Gregori, S. Grévy, F. Hanappe, G. Kelly, M. Labiche, C. Le Brun, S. Leenhardt, M. Lewitowicz, K. Markenroth, F. M. Marqués, M. Motta, J. T. Murgatroyd, T. Nilsson, A. Ninane, N. A. Orr, I. Piqueras, M. G. Saint Laurent, S. M. Singer, O. Sorlin, L. Stuttgé, and D. L. Watson, Phys. Rev. Lett. 82, 1383 (1999).
- Freer et al. (2001) M. Freer, J. C. Angélique, L. Axelsson, B. Benoit, U. Bergmann, W. N. Catford, S. P. G. Chappell, N. M. Clarke, N. Curtis, A. D’Arrigo, E. de Góes Brennard, O. Dorvaux, B. R. Fulton, G. Giardina, C. Gregori, S. Grévy, F. Hanappe, G. Kelly, M. Labiche, C. Le Brun, S. Leenhardt, M. Lewitowicz, K. Markenroth, F. M. Marqués, J. T. Murgatroyd, T. Nilsson, A. Ninane, N. A. Orr, I. Piqueras, M. G. Saint Laurent, S. M. Singer, O. Sorlin, L. Stuttgé, and D. L. Watson, Phys. Rev. C 63, 034301 (2001).
- Saito et al. (2004) A. Saito, S. Shimoura, S. Takeuchi, T. Motobayashi, T. Minemura, Y. Matsuyama, H. Baba, H. Akiyoshi, Y. Ando, N. Aoi, Z. Fülöp, T. Gomi, Y. Higurashi, M. Hirai, K. Ieki, N. Imai, N. Iwasa, H. Iwasaki, Y. Iwata, S. Kanno, H. Kobayashi, S. Kubono, M. Kunibu, M. Kurokawa, Z. Liu, S. Michimasa, T. Nakamura, S. Ozawa, H. Sakurai, M. Serata, E. Takeshita, T. Teranishi, K. Ue, K. Yamada, Y. Yanagisawa, and M. Ishihara, Nuclear Physics A 738, 337 (2004), proceedings of the 8th International Conference on Clustering Aspects of Nuclear Structure and Dynamics.
- Charity et al. (2007) R. J. Charity, S. A. Komarov, L. G. Sobotka, J. Clifford, D. Bazin, A. Gade, L. Jenny, S. M. Lukyanov, W. G. Lynch, M. Mocko, S. P. Lobastov, A. M. Rogers, A. Sanetullaev, M. B. Tsang, M. S. Wallace, S. Hudan, C. Metelko, M. A. Famiano, A. H. Wuosmaa, and M. J. vanGoethem, Phys. Rev. C 76, 064313 (2007).
- Yang et al. (2014) Z. H. Yang, Y. L. Ye, Z. H. Li, J. L. Lou, J. S. Wang, D. X. Jiang, Y. C. Ge, Q. T. Li, H. Hua, X. Q. Li, F. R. Xu, J. C. Pei, R. Qiao, H. B. You, H. Wang, Z. Y. Tian, K. A. Li, Y. L. Sun, H. N. Liu, J. Chen, J. Wu, J. Li, W. Jiang, C. Wen, B. Yang, Y. Y. Yang, P. Ma, J. B. Ma, S. L. Jin, J. L. Han, and J. Lee, Phys. Rev. Lett. 112, 162501 (2014).
- Smith et al. (2014) J. K. Smith, T. Baumann, D. Bazin, J. Brown, S. Casarotto, P. A. DeYoung, N. Frank, J. Hinnefeld, M. Hoffman, M. D. Jones, Z. Kohley, B. Luther, B. Marks, N. Smith, J. Snyder, A. Spyrou, S. L. Stephenson, M. Thoennessen, N. Viscariello, and S. J. Williams, Phys. Rev. C 90, 024309 (2014).
- Freer et al. (2017) M. Freer, N. Ashwood, N. Achouri, W. Catford, N. Curtis, F. Delaunay, H. Al Falou, F. Marqués, T. Munoz-Britton, N. Orr, R. Raabe, N. Soić, J. Thomas, C. Wheldon, and V. Ziman, Physics Letters B 775, 58 (2017).
- Kanada-En’yo and Horiuchi (2001) Y. Kanada-En’yo and H. Horiuchi, Progress of Theoretical Physics Supplement 142, 205 (2001).
- Descouvemont and Baye (2001) P. Descouvemont and D. Baye, Physics Letters B 505, 71 (2001).
- Ito (2012) M. Ito, Phys. Rev. C 85, 044308 (2012).
- Quaglioni and Navrátil (2009) S. Quaglioni and P. Navrátil, Phys. Rev. C 79, 044606 (2009).
- Navrátil et al. (2000) P. Navrátil, J. P. Vary, and B. R. Barrett, Phys. Rev. C 62, 054311 (2000).
- Barrett et al. (2013) B. R. Barrett, P. Navrátil, and J. P. Vary, Prog. Part. Nucl. Phys. 69, 131 (2013).
- Kravvaris and Volya (2017) K. Kravvaris and A. Volya, Phys. Rev. Lett. 119, 062501 (2017).
- Kravvaris and Volya (2019) K. Kravvaris and A. Volya, Phys. Rev. C 100, 034321 (2019).
- Hupin et al. (2013) G. Hupin, J. Langhammer, P. Navrátil, S. Quaglioni, A. Calci, and R. Roth, Phys. Rev. C 88, 054622 (2013).
- Entem and Machleidt (2003) D. R. Entem and R. Machleidt, Phys. Rev. C 68, 041001(R) (2003).
- van Kolck (1994) U. van Kolck, Phys. Rev. C 49, 2932 (1994).
- Navrátil (2007) P. Navrátil, Few-Body Syst. 41, 117 (2007).
- Gazit et al. (2019) D. Gazit, S. Quaglioni, and P. Navrátil, Phys. Rev. Lett. 122, 029901(E) (2019).
- Somà et al. (2020) V. Somà, P. Navrátil, F. Raimondi, C. Barbieri, and T. Duguet, Phys. Rev. C 101, 014318 (2020).
- Jurgenson et al. (2009) E. D. Jurgenson, P. Navrátil, and R. J. Furnstahl, Phys. Rev. Lett. 103, 082501 (2009).
- Afzal et al. (1969) S. A. Afzal, A. A. Z. Ahmad, and S. Ali, Rev. Mod. Phys. 41, 247 (1969).
- Tombrello and Senhouse (1963) T. A. Tombrello and L. S. Senhouse, Phys. Rev. 129, 2252 (1963).
- Quaglioni et al. (2013) S. Quaglioni, C. Romero-Redondo, and P. Navrátil, Phys. Rev. C 88, 034320 (2013).
- Quaglioni et al. (2016) S. Quaglioni, C. Romero-Redondo, and P. Navrátil, Phys. Rev. C 94, 019902(E) (2016).
- Quaglioni et al. (2018) S. Quaglioni, C. Romero-Redondo, P. Navrátil, and G. Hupin, Phys. Rev. C 97, 034332 (2018).
- Calci et al. (2016) A. Calci, P. Navrátil, R. Roth, J. Dohet-Eraly, S. Quaglioni, and G. Hupin, Phys. Rev. Lett. 117, 242501 (2016).
- Okołowicz et al. (2012) J. Okołowicz, M. Płoszajczak, and W. Nazarewicz, Progress of Theoretical Physics Supplement 196, 230 (2012).
- Garrido et al. (2013) E. Garrido, A. S. Jensen, and D. V. Fedorov, Phys. Rev. C 88, 024001 (2013).
- Fossez et al. (2016) K. Fossez, W. Nazarewicz, Y. Jaganathen, N. Michel, and M. Płoszajczak, Phys. Rev. C 93, 011305(R) (2016).
- Kravvaris et al. (2020) K. Kravvaris, K. R. Quinlan, S. Quaglioni, K. A. Wendt, and P. Navrátil, Phys. Rev. C 102, 024616 (2020).
- Baroni et al. (2013a) S. Baroni, P. Navrátil, and S. Quaglioni, Phys. Rev. Lett. 110, 022505 (2013a).
- Baroni et al. (2013b) S. Baroni, P. Navrátil, and S. Quaglioni, Phys. Rev. C 87, 034326 (2013b).