Ab initio prediction of an order-disorder transition in Mg₂GeO₄: implication for the nature of super-Earth’s mantles

Ab initio quasiharmonic (QHA) calculations of polymorphic phase transitions at extreme pressure and temperature conditions have proven to be highly predictive for nearly two decades RIMG2010 . Combined with materials discovery methods (e.g., Refs. Glass2006 ; Lonie2011 ; Pickard2011 ; Wang2012 ; Wu2014 ; Curtis2018 ), these simulation tools offer a powerful approach to investigating phase transition phenomena at challenging experimental conditions typical of planetary interiors. Mineral physics and geophysics have benefitted immensely from these developments in materials simulations in the past two decades. For example, in 2004, ab initio predictions played a crucial role in discovering and elucidating the major post-perovskite (PPv) transition in MgSiO₃ bridgmanite at deep Earth interior conditions, e.g., 2,500K at 125 GPa Murakami2004 ; Oganov2004 ; Tsuchiya2004 . More recently, ab initio QHA calculations have explored pressure and temperature conditions expected in interior of super-Earths, terrestrial-type exoplanets more massive than Earth. The interest in these planets stems from their similarities and differences with Earth and their potential habitability. Besides, ab initio methods are highly predictive when addressing planet-forming silicates and oxides, motivating experiments. These phases are oxides involving Mg, Si, ferrous and ferric Fe, Al, and Ca, primarily. In deep interiors of large super-Earths with up to $\sim$13 Earth mass ($M_{\oplus}$), the range of pressures and temperatures can reach tens of tera-Pascals (TPa) (hundreds of Mbar) and $10^{4}$–$10^{5}$ K Hakim2018 ; vandenBerg2019 . Despite remarkable developments in experimental techniques Smith2014 ; Dubrovinsky2012 ; Dubrovinskaia2016 ; Dewaele2018 ; Sakai2018 , these pressure-temperature conditions are still very challenging to experiments making ab initio predictions of phase transition phenomena in planet-forming phases critical to advancing planetary modeling. This progress has been registered in a series of ab initio discoveries concerning the nature of super-Earth’s mantle-forming phases in the important MgO-SiO₂ system Wu2014 ; Umemoto2006a ; UmemotoWentzcovitch2011 ; Niu2015 ; Umemoto2017 . They have culminated in partial experimental confirmations in a low-pressure analog system, NaF-MgF₂ Dutta2018 , and detailed modeling of these planets’ internal structure and dynamics Hakim2018 ; vandenBerg2019 . In particular, a sequence of “post-post-perovksite” (post-PPv) transitions in the MgO-SiO₂ system Wu2014 ; Umemoto2006a ; UmemotoWentzcovitch2011 ; Niu2015 ; Umemoto2017 was predicted to occur up to $\sim$3 TPa and 10,000 K, starting from MgSiO₃ PPv and ending in its dissociation into the elementary oxides MgO and SiO₂. This dissociation process was predicted to occur in three stages: 1) a dissociation reaction, MgSiO₃ PPv $\to$ $I\bar{4}2d$-type Mg₂SiO₄ + $P2_{1}/c$-type MgSi₂O₅; 2) further dissociation of $P2_{1}/c$-type MgSi₂O₅ $\to$ $I\bar{4}2d$-type Mg₂SiO₄ + Fe₂P-type SiO₂; 3) final dissociation of $I\bar{4}2d$-type Mg₂SiO₄ $\to$ CsCl-type MgO + Fe₂P-type SiO₂. If MgSiO₃ coexists with MgO or SiO₂, other intermediate recombination reactions producing Mg₂SiO₄ or MgSi₂O₅ can intervene in the three-stage dissociation process. These post-PPv transitions were shown to have profound effects on super-Earths’ mantle dynamics Hakim2018 ; vandenBerg2019 . However, the exceedingly high predicted transition pressures ($>\sim 500$ GPa) make their experimental confirmation quite challenging.

Two potential low-pressure analog systems, i.e., MgO-GeO₂ and NaF-MgF₂, were proposed as viable experimental alternates UmemotoWentzcovitch2015 ; UmemotoWentzcovitch2019 . Both displayed some of these novel high-pressure phases found in the MgO-SiO₂ system. NaMgF₃ PPv was predicted to exhibit the novel $P2_{1}/c$-type structure of MgSi₂O₅ under pressure before its full dissociation into NaF and MgF₂. The predicted phases and transformations were experimentally confirmed Dutta2018 . In contrast, MgGeO₃ PPv under pressure was expected to produce the novel $I\bar{4}2d$-type Mg₂SiO₄ structure. The predicted reactions in the MgO-GeO₂ system have not been experimentally confirmed yet since they happen at higher pressures. Also, both systems were expected to display the respective analog recombination reactions. This state of affairs brings us to our present study.

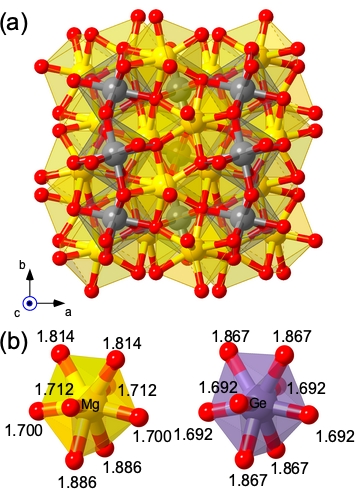
Using ab initio techniques, we predict another type of phase transition in the MgO-GeO₂ system, a temperature-induced change from $I\bar{4}2d$-type to Th₃P₄-type structure in Mg₂GeO₄. This is not a regular polymorphic phase transition but an order-disorder transition (ODT) in the cation sublattices. The crystal structure of $I\bar{4}2d$-type Mg₂GeO₄ is shown in Fig. 1. In this phase, Mg and Ge cations are regularly ordered. Disorder in the cation sublattices makes the cation sites indistinguishable and results in the Th₃P₄-type structure. Details of both crystal structures are given in Supplementary Information. The result predicted here is unexpected since disorder occurs between two sublattices containing cations with nominally different valences. Specifically, Mg and Ge are known to form stoichiometric end-member phases (MgO and GeO₂), preserving their nominal valence at comparable pressures. This type of prediction is also uncommon since it requires reliable methods to compute free energy in disordered solid-solutions, which is computationally much more costly than regular polymorphic transition. The predicted pressure and temperature transition conditions for this ODT are more easily achievable in laboratory experiments than the analog one in Mg₂SiO₄. Still, a similar ODT is also expected to occur in $I\bar{4}2d$-type Mg₂SiO₄ and should be crucial for modeling interiors of super-Earths.

The ODT critical temperature, $T_{c}$, was calculated using the same approach previously used to compute the ice-VII to -VIII ODT boundary Umemoto2010 . The method consists in sampling, if not all, the most significant symmetrically distinct (irreducible) atomic configurations of a chosen supercell. To represent the disordered Th₃P₄-type phase we chose a 56-atom supercell (8 Mg₂GeO₄, $\sqrt{2}\times\sqrt{2}\times 1$ supercell of the conventional unit cell) and generated an ensemble of 125 irreducible configurations using the scheme described below. We then computed the static partition function for this ensemble of 125 configurations:

$$Z_{static}(V,T)=\sum^{125}_{i=1}w_{i}\exp\left(-\frac{E_{i}(V)}{k_{B}T}\right),$$

(1)

where $E_{i}(V)$ and $w_{i}$ are the total energy and multiplicity of the $i$th irreducible configuration ($\sum_{i=1}^{125}w_{i}=3489$), and $k_{B}$ is the Boltzmann’s constant. The static partition function is then extended to include zero-point motion (ZPM) and phonon thermal excitation energies within the QHA Umemoto2010 ; Qin2019 . From $Z(V,T)$, all thermodynamic potentials and functions can be calculated: Helmholtz free energy $F(V,T)=-k_{B}\ln Z$, pressure $P(V,T)=-(\partial F/\partial V)_{T}$, Gibbs free energy $G(V,T)=F+PV$ (converted to $G(P(V,T),T)$), entropy $S(V,T)=-(\partial F/\partial T)_{V}$, constant-volume heat capacity $C_{V}(V,T)=-T(\partial^{2}S/\partial T^{2})_{V}$, constant-pressure heat capacity $C_{P}(P,T)=-T(\partial^{2}S/\partial T^{2})_{P}$, and so forth. Finally the ODT is obtained by locating a peak in $C_{P}{(T)}$. The procedure used to generate the 125 cation configurations in Eq. 1 is schematically depicted in Fig. S1. We started with the ordered structure containing the 24 cations (16 Mg and 8 Si ions) in their respective Wyckoff sites of the $I\bar{4}2d$-type phase. This lowest enthalpy configuration is shown in Fig. 1(a) and corresponds to the leftmost configuration in Fig. S1. We refer to it as the “zero-interchange structure”. Then we sequentially interchanged Mg/Ge pairs once. These single interchanges produce 128 (16 $\times$ 8) configurations where only 4 are irreducible, each with its distinct multiplicity. We refer to this first generation of structure as “one-interchange” configurations. Starting from these 128 configurations, we repeat this process and produce 3360 configurations among which 120 are irreducible “two-interchange” configurations. With zero, one, and two cation interchanges, a total of $1+4+120=125$ configurations were generated and used to compute the partition function. Discussion of convergence issues related to supercell size and number of configurations is offered in the Supplementary Information section.

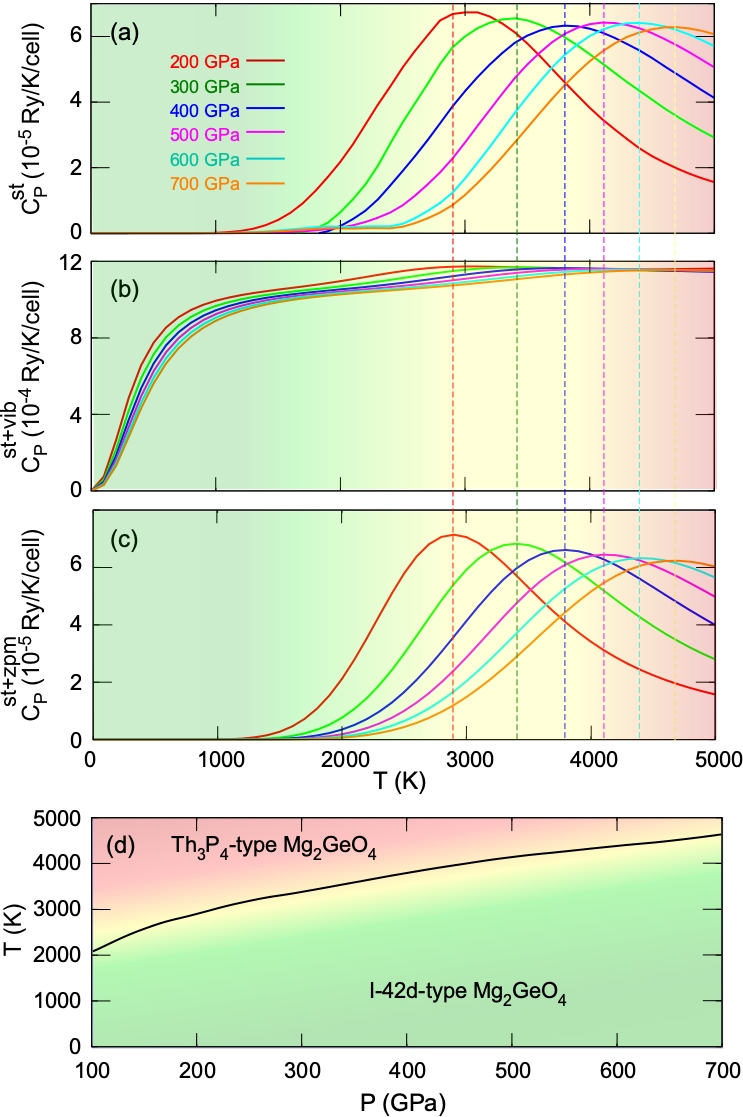
$C_{P}$ profiles at several pressures obtained using static free energy calculations ($C_{P}^{st}$) are shown in Fig. 2(a). The peak in $C_{P}^{st}$ can be easily identified. Including the vibrational free energy contribution to the total free energy, a Debye-like contribution is added to $C_{P}^{st}$ producing $C_{P}^{st+vib}$. The peak in $C_{P}^{st+vib}$ appears as a hump in the Dulong-Petit regime of $C_{P}^{st+vib}$ (Fig. 2(b)). The peak would have appeared very sharp if the calculation could have been carried out with an infinitely large supercell and number of configurations. By adding only the ZPM energy, $E_{ZPM}$, the heat capacity ($C_{P}^{st+zpm}$) still resembles $C_{P}^{st}$, except that $T_{c}$ lowers by $\sim$100 K at 200 GPa (Fig. 2(c)). This temperature shift is essentially a volume effect caused by the expansion of the equilibrium volume upon inclusion of $E_{ZPM}$.

With increasing pressure, $T_{c}$, i.e., the peak temperature in $C_{P}$, increases producing the phase boundary shown in Fig. 2(d). This happens because the enthalpy difference between all configurations and the ground state one, the ordered $I\bar{4}2d$-type phase, increases with pressure as shown in Fig. S3. Among the 125 configurations, the $I\bar{4}2d$-type phase has the lowest enthalpy at all pressures investigated here. The four irreducible configurations generated by one-interchange of cations are more similar to the ordered ground state structure and tend to have lower enthalpies than the 120 irreducible configurations produced by two-interchanges, with some exceptions. This behavior of $T_{c}$, i.e., the positive Clapeyron slope is opposite to that observed in the ice-VII to -VIII ODT. In the case of ice, all configuration enthalpies converge to a single value under pressure, that of ice X. This is because the ice ODT precedes and turns into a hydrogen-bond symmetrization transition under pressure Umemoto2010 . Besides, in the present ODT $T_{c}$ is only slightly altered by quantum effects, e.g, ZPM or thermal excitation effects. It takes place above the Debye temperature, $\theta_{\rm Debye}$, in the Dulong-Petit regime of $C_{V}$. Therefore, it has a classical origin and can be reasonably well addressed using the static partition function in Eq. 1.

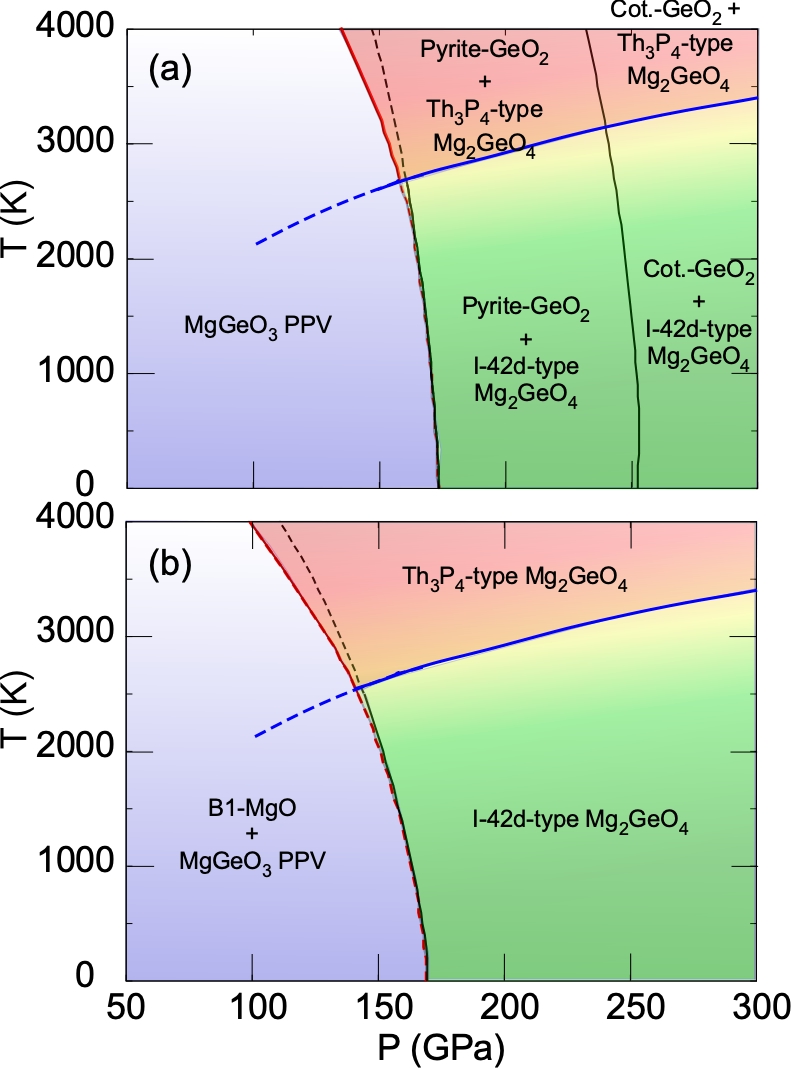
The following dissociation and recombination post-PPv transitions were predicted in the MgO-GeO₂ system  UmemotoWentzcovitch2019 :

Dissociation -

MgGeO₃ (PPv) $\to$ Mg₂GeO₄ ($I\bar{4}2d$-type) + GeO₂ (pyrite-type) at $\sim$ 175 GPa followed by the transition of GeO₂ from pyrite- to cotunnite-type, which is not affected by the order-disorder transition;

Recombination -

MgGeO₃ (PPv) + MgO (B1-type) $\to$ Mg₂GeO₄ ($I\bar{4}2d$-type) at $\sim$ 173 GPa.

These transitions remain valid at low temperatures, but above the ODT’s, $T_{c}$ one should replace the $I\bar{4}2d$-type phase by the Th₃P₄-type one. The newly computed phase boundaries for these transitions are shown in Fig. 3. Both reactions have negative Clapeyron slopes, a common behavior in pressure induced structural transitions involving an increase in cation coordination Navrotsky1980 . The ODT widens the stability fields of the dissociation products of MgGeO₃ PPv (GeO₂ and Mg₂GeO₄) and of the recombination product (Mg₂GeO₄) because the configuration entropy lowers the Gibbs free energy of Mg₂GeO₄ in the disordered Th₃P₄-type phase at higher temperatures. The configuration entropy also decreases in magnitude the negative Clapeyron slopes of dissociation and recombination transitions $(dT/dP=\Delta V/\Delta S)$ at high temperatures. As pointed out earlier UmemotoWentzcovitch2019 , hysteresis might prevent experimental observation of these dissociation and recombination transitions from MgGeO₃ PPv, in which case a polymorphic from PPv to a Gd₂S₃-type phase might intervene. A similar phenomenon was observed experimentally in the NaF-MgF₂ system in which NaMgF₃ PPv transformed to a U₂S₃-type post-PPv phase at low temperatures Dutta2018 .

We have predicted an order-disorder transition (ODT) in the cation sublattices of the $I\bar{4}2d$-type Mg₂GeO₄, a post-PPv phase in the Mg-Ge-O system. This type of prediction is uncommon and is not accomplished simply using modern materials discovery techniques (e.g., Refs. Glass2006 ; Lonie2011 ; Pickard2011 ; Wang2012 ; Wu2014 ; Curtis2018 ). In addition to structural prediction, the ODT prediction requires effective statistical sampling of atomic configurations Umemoto2010 . Besides, $T_{c}$ cannot be calculated by direct comparison of Gibbs free energy as in a regular first order transition. Instead, $T_{c}$ is obtained by calculating the position of a peak in $C_{P}(T)$ throughout this second order transition. In this study, this was accomplished using ab initio quasiharmonic (QHA) calculations on a 56-atom supercell. Although anharmonic effects may play a role in first order transitions at the high temperatures investigated here, harmonic or anharmonic vibrational effects play a secondary role in the present ODT.

The predicted $I\bar{4}2d$-type to Th₃P₄-type phase change expands toward lower pressures and temperatures the stability fields of the post-PPv dissociation/recombination products containing Mg₂GeO₄. The MgO-GeO₂ system is a partly low-pressure analog of the Earth/planet-forming MgO-SiO₂ system. Both $I\bar{4}2d$-type Mg₂GeO₄ and Mg₂SiO₄ were predicted to occur as post-PPv dissociation/recombination transition products. Therefore, the present study strongly suggests that a similar ODT should also occur in the Mg and Si cation sublattices of $I\bar{4}2d$-type Mg₂SiO₄ at the high temperatures typical of the deep interiors of super-Earths Hakim2018 ; vandenBerg2019 .

Finally, it should be noted that the Th₃P₄-type structure is a high temperature form of several rare-earth sesquisulfides, $RR^{\prime}$S₃ ($R$,$R$’=lanthanoid or actinoid), with vacancies at cation sites Zachariasen1949 ; Flahaut1979 . For example, Gd₂S₃ is stabilized in the orthorhombic $\alpha$ phase at low temperature and transforms to the Th₃P₄-type $\gamma$ phase with vacancies at high temperature. As pointed out earlier Umemoto2008 , the $RR^{\prime}$S₃ family of structures form an analog system to high-pressure phases of MgSiO₃ and Al₂O₃ (bridgmanite, PPv, and U₂S₃-type). Hence, the prediction of the Th₃P₄-type phase in this study strengthens further the structural relationship between Earth/planet-forming phases at ultrahigh pressures and rare-earth sesquisulfides.

Calculations for the 125 cation configurations were performed using the local-density approximation Perdew1981 to density-functional theory. For all atomic species, Vanderbilt-type pseudopotentials Vanderbilt1990 were generated. The valence electron configurations and cutoff radii for the pseudopotentials were $2s^{2}2p^{6}3s^{2}$ and 1.6 a.u. for Mg, $4s^{2}4p^{1}3d^{10}$ and 1.6 a.u. for Ge, and $2s^{2}2p^{4}$ and 1.4 a.u. for O, respectively. Cutoff energies for the plane-wave expansion are 70 Ry. The $2\times 2\times 2$ k-point mesh was used for the 56-atom supercell. For structural optimization under arbitrary pressures between 100 and 800 GPa, we used the variable-cell-shape damped molecular dynamics Wentzcovitch1991 ; Wentzcovitch1993 . Dynamical matrices were calculated on the $2\times 2\times 2$ q mesh using density-functional perturbation theory Giannozzi1991 ; Baroni2001 . The vibrational contribution to the partition function was taken into account within the quasi-harmonic approximation (QHA) Wallace1972 ; Umemoto2010 ; Qin2019 . The $8\times 8\times 8$ q-point mesh was used for the QHA summation. All calculations were performed using the Quantum-ESPRESSO Giannozzi2009 and the qha software Qin2019 .

K.U. acknowledges support of a JSPS Kakenhi Grant # 17K05627. R.M.W. acknowledges support of a US Department of Energy Grant DE-SC0019759. All calculations were performed at Global Scientific Information and Computing Center and in the ELSI supercomputing system at the Tokyo Institute of Technology, the HOKUSAI system of RIKEN, and the Supercomputer Center at the Institute for Solid State Physics, the University of Tokyo.