Acoustic anomaly Detection via Latent Regularized Gaussian Mixture Generative Adversarial Networks
Abstract
Acoustic anomaly detection aims at distinguishing abnormal acoustic signals from the normal ones. It suffers from the class imbalance issue and the lacking in the abnormal instances. In addition, collecting all kinds of abnormal or unknown samples for training purpose is impractical and time-consuming. In this paper, a novel Gaussian Mixture Generative Adversarial Network (GMGAN) is proposed under semi-supervised learning framework, in which the underlying structure of training data is not only captured in spectrogram reconstruction space, but also can be further restricted in the space of latent representation in a discriminant manner. Experiments show that our model has clear superiority over previous methods, and achieves the state-of-the-art results on DCASE dataset.
Index Terms— Acoustic anomaly detection, Semi-supervised learning, Generative Adversarial Networks, Gaussian Mixture Model, Energy estimation
1 Introduction
Acoustic anomaly detection task is to find the abnormal samples in audios. Since audio data has typical time series characteristics, it is commonly processed by using Recurrent Neural Network (RNN) techniques [1] [2]. However, RNN such as Long Short Term Memory networks (LSTM) [3] has some limitations in memory step size and parallel training, especially when the input data is a long sequence. To solve this problem, convolutional autoregressive architecture [4] was proposed. This series of models are highly parallelizable in the training phase, meaning that computation made more tractable due to effective resource utilization.
Several previous work formulate acoustic anomaly detection task as the acoustic event classification problem by using the Gaussian Mixture Model (GMM) and the Hidden Markov Model (HMM) [5] to detect various types of sounds. However, it is impractical to reconstruct all possible kinds of abnormal event audios. Some propose the methods rely on machine learning algorithms which are usually trained with abnormal samples directly and extract the abnormal features. Nevertheless, to take all types of abnormal samples into account is impossible. In this paper, on the contrary, only the normal data, which is so much easier to collect, will be used for training. One sample is regarded as abnormal if it does not satisfy normal features. Then the main challenge becomes extracting the characteristic of normal acoustic signals only and exploit them to detect signals that deviate from the normality. Several studies exploit the autoencoder based on Long Short-Term Memory units [6] trained on the normal samples only. During the testing period, it is expected to get higher image reconstruction error on abnormal spectrogram not existing in the training process. The autoencoder approaches [7] [8] [9] outperform GMM and HMM approaches. Actually, minimizing the image reconstruction error is not original intension of the task. Our aim is to exploit more separable latent representation features between the normalities and the anomalies.
Motivated by the above limitations in previous methods, we propose a novel semi-supervised learning framework for acoustic anomaly detection, consisting of the compression network and the estimation network. For compression network, compared with conventional GAN style architecture, the auxiliary encoder and the latent regularizer are adopted to minimize the distance between the bottleneck features of original input data and encoded latent feature of the generated data, resulting in a more concentrated distribution for target class. The main function of the estimation network is to execute density estimation. Given the low dimension representation of input data from compression network, instead of using decoupled two-stage training and the standard Expectation-Maximization (EM) algorithm [10], the estimation network estimates the parameters of GMM and evaluates the energy for samples. The estimation network helps the compression network escape from less attractive local optima and further reduce reconstruction errors.
2 Proposed Method
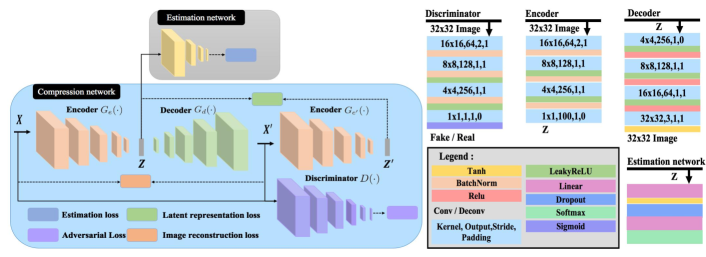
In this section, we present more details of the proposed framework, then describe each term in loss function.
2.1 Network Architecture
Inspired by the anomaly detection methods [11, 12, 13, 14], proposed architecture is shown in Fig. 1, consists of two subnetworks: compression network and estimation network.
2.1.1 Compression network
The compression network consists the discriminator and a generative sub-network with an auxiliary encoder. The generative sub-network, including an encoder () and a decoder (), attempts to reconstruct the original input sample to fool the discriminator, while the discriminator tries to distinguish original images from generated images. The model captures the real characteristic of normal samples by minimizing the distance between original input image () and generated image ().
The main function of the auxiliary encoder () is to minimize the distance between the bottleneck features () of original input image and encoded latent feature () of the generated image. The reason why we employ an auxiliary encoder in our framework can be concluded as follows: (1) The auxiliary encoder could obtain the high-quality reconstruction of latent feature only for the normal samples. (2) Since the latent regularizer might incur the distribution distortion in latent feature space, the feature representation can be regarded as the anchor to prevent from drifting.
Avoid being fooled by the generative sub-network, the discriminator learns the real concept in the target class. In addition, the discriminator also helps the generative sub-network to get more robust and stable parameters during the training period. This part of parameters could make normal and abnormal samples more separable.
2.1.2 Estimation network
In [15] and [16], Gaussian Mixture Model is greatly leveraged over the learned latent space to deal with density estimation tasks for input data with network structure. Instead of using decoupled two-stage training and the standard Expectation-Maximization (EM) algorithm [10], we employ the estimation network in our framework to execute density estimation. In the process of training, given the low dimension representation of input data from compression network, the estimation network estimates the parameters of GMM and evaluates the energy for samples. In order to achieve the above, a multi-layer neural network regarded as the estimation network predicts the mixture membership for each sample.
2.2 Overall Loss Function
We define a loss function in Eqn. (1) including four components, , the image reconstruction loss , the adversarial loss , the latent representation loss and the estimation loss
| (1) |
where , , , and are the weighting parameters balancing the impact of individual item to the overall object function.
Adversarial Loss: GAN was first used by Goodfellow [17], which consists of a generator and a discriminator having two competing objectives: the discriminator is learned to distinguish generated images from original input images, while the generator is trained to produce realistic images to fool . The training objective of GAN can be formulated as :
| (2) | |||
Image reconstruction loss: Image reconstruction loss measures the pixel-wise reconstruction error between original input image and generated image, which helps the generator to sufficiently capture the input sample distribution for normal samples. The training objective is shown below:
| (3) |
Latent representation loss: With the adversarial loss and image reconstruction loss defined above, the model can generate the realistic image. In additional to these objectives, the latent feature of generated image and that of the original input image are also expected to be consistent, which could help the generator to capture the latent feature for common examples. Hence, we consider to add a constraint by minimizing the distance between latent feature of input images from generator and encoded latent feature of generated image from auxiliary encoder as follows.
| (4) |
Estimation loss: Given the latent representation from compression network and an integer as the number of mixture components. The estimation network is a multi-layer network followed by a softmax layer, which makes mixture-component membership prediction as follows:
where is a -dimensional vector for the soft mixture-component membership prediction, which is the output of the estimation network parameterized by . denotes the probability of the input sample belongs to the distribution. Given a batch of N samples and their membership prediction, we can further estimate the parameters in GMM as follows:
| (5) | ||||
where , , are the component mixture weights, , the component mixture mean and the component mixture covariance. is the membership prediction of the input sample . n is the number of input samples. With the GMM parameters, the energy function of an input sample can be formulated as follows:
| (6) |
The objective function of estimation network is to minimize following equation,
| (7) |
where the first term is the sum of sample energy. The second term is the regularizer, which penalizes small values on the diagonal entries in covariance matrices . The purpose of this measure is to avoid the singularity problem in GMM. and are the meta parameters in estimation network.
3 Experiments
This section contains the description of datasets used for evaluation. Besides, some experiments present the effectiveness of the proposed method and the high performances that we obtained.
3.1 Experimental Setting

Datasets: We extract 15 datasets from the 2017 DCASE Challenge Task 2 dataset [18], as it is done in [19]. Three different abnormal event exists in this dataset (i.e., gunshot, babycry and glassbreak). All of these abnormal event audios are artificially mixed with background audios respectively which includes 15 different kinds of environmental settings (i.e.,home, bus, and train). Fig. 2 shows the office environment audio mixed with galss-break audio. All acoustic signals are converted to the spectrogram data, which is used as input data for proposed framework.
According to the work [14], CIFAR10 and MNIST dataset are used to construct a toy experiment to illustrate our superiority to other state-of-the-art abnormal detectors. One of classes would be regarded as an normal class, while the rest ones belong to the anomaly class. In total, we get ten sets for MNIST dataset and CIFAR10 dataset.
Evaluation Measures: In testing process, the latent representation loss of each given spectrogram is regarded as an abnormal score. We compute the Area Under the ROC Curve (AUC) to measure the performance of proposed method.
Implementation Details: We implement our approach in PyTorch by optimizing the weighted loss (defined in Eq. (1)) with the weight values , , , and , which are empirically chosen to yield optimum results.
3.2 Toy experiment
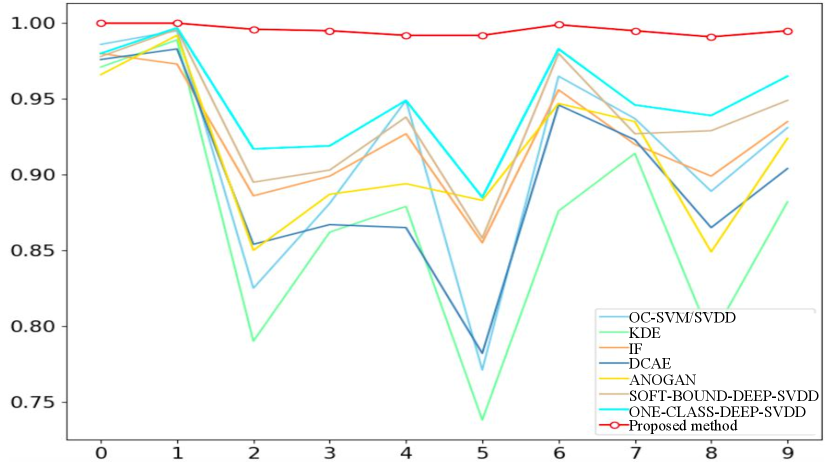
In this subsection, we observe the clear superiority of our approach over previous abnormal detection models (OC-SVM/SVDD [20], KDE [21], IF [22], DCAE[23], ANOGAN [12], DEEP-SVDD [24]), as it is shown in Fig. 3. For each digit chosen as normal class in MNIST dataset, the proposed method achieves the best performance in term of AUC value, which could be illustrated by using red curves. In the right of the Fig. 3, we also present the comparison result in CIFAR10 dataset.
3.3 Ablation Study
| Scenes [AUC] | |||||||
|---|---|---|---|---|---|---|---|
| Loss composition | forest | store | cafe |
|
train Í | ||
| + | 0.73 | 0.75 | 0.68 | 0.69 | 0.89 | ||
| ++ | 0.75 | 0.82 | 0.74 | 0.76 | 0.90 | ||
| +++ | 0.77 | 0.83 | 0.76 | 0.78 | 0.92 | ||
Since all loss functions are presented in subsection 2.2, giving the ablation study to the different combinations of loss functions is necessary. As illustrated in Tab. 1, five background-event experiments are done in the three kinds of loss combinations respectively. Each loss function we designed in the proposed framework can improve the performance.
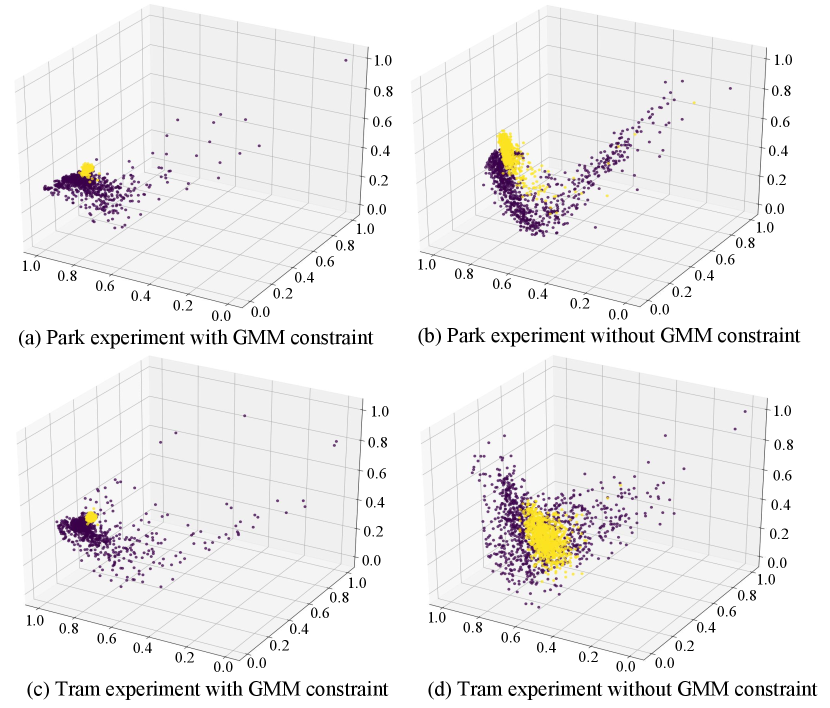
To further explain the necessity of estimation constraint, Fig. 4 presents the visualization of the latent feature, where the proposed method with and without estimation constraint are compared on park and tram experiment setting. To sum up, comparison result can indicate the following: (1) Compared with the model without estimation constraint, the normal samples (yellow dots) are more concentrated with estimation constraint. (2) The anomalous samples can be more separated from normal samples (yellow dots).
3.4 Comparison with State-of-the-art Methods
| Scene | CAE [9] | WaveNet [19] | Proposed method |
|---|---|---|---|
| beach | 0.69 | 0.72 | 0.80 |
| bus | 0.79 | 0.83 | 0.89 |
| cafe/restaurant | 0.69 | 0.76 | 0.76 |
| car | 0.79 | 0.82 | 0.93 |
| city center | 0.75 | 0.82 | 0.83 |
| forest path | 0.65 | 0.72 | 0.77 |
| grocery store | 0.71 | 0.77 | 0.83 |
| home | 0.69 | 0.69 | 0.69 |
| library | 0.59 | 0.67 | 0.85 |
| metro station | 0.74 | 0.79 | 0.81 |
| office | 0.78 | 0.78 | 0.80 |
| park | 0.70 | 0.80 | 0.89 |
| residential area | 0.73 | 0.78 | 0.78 |
| train | 0.82 | 0.84 | 0.92 |
| tram | 0.80 | 0.87 | 0.94 |
The performance of three models across the 15 datasets is shown in Table 2. We find that the proposed model consistently outperforms the other models in almost all datasets, with a tie in the home, cafe/restaurant and residential area scenarios.
4 Conclusion
To capture the real characteristic of normal samples and obtain more separable latent representation features between the normalies and the anomalies, this paper exploits the technique of acoustic anomaly detection to learn an regularized latent space by using adversarial training under semi-supervised learning framework. Extensive experiments have been conducted on several datasets, showing high performance of the proposed method and the benefit of using latent regularizer from estimation network.
References
- [1] Erik Marchi, Fabio Vesperini, Stefano Squartini, and Björn Schuller, “Deep recurrent neural network-based autoencoders for acoustic novelty detection,” Computational intelligence and neuroscience, vol. 2017, 2017.
- [2] Timothy J O’Shea, T Charles Clancy, and Robert W McGwier, “Recurrent neural radio anomaly detection,” arXiv preprint arXiv:1611.00301, 2016.
- [3] Sepp Hochreiter and Jürgen Schmidhuber, “Long short-term memory,” Neural computation, vol. 9, no. 8, pp. 1735–1780, 1997.
- [4] Aaron van den Oord, Sander Dieleman, Heiga Zen, Karen Simonyan, Oriol Vinyals, Alex Graves, Nal Kalchbrenner, Andrew Senior, and Koray Kavukcuoglu, “Wavenet: A generative model for raw audio,” arXiv preprint arXiv:1609.03499, 2016.
- [5] Stavros Ntalampiras, Ilyas Potamitis, and Nikos Fakotakis, “Probabilistic novelty detection for acoustic surveillance under real-world conditions,” IEEE Transactions on Multimedia, vol. 13, no. 4, pp. 713–719, 2011.
- [6] Wei Bao, Jun Yue, and Yulei Rao, “A deep learning framework for financial time series using stacked autoencoders and long-short term memory,” PloS one, vol. 12, no. 7, pp. e0180944, 2017.
- [7] Emanuele Principi, Fabio Vesperini, Stefano Squartini, and Francesco Piazza, “Acoustic novelty detection with adversarial autoencoders,” in 2017 International Joint Conference on Neural Networks (IJCNN). IEEE, 2017, pp. 3324–3330.
- [8] Weining Lu, Yu Cheng, Cao Xiao, Shiyu Chang, Shuai Huang, Bin Liang, and Thomas Huang, “Unsupervised sequential outlier detection with deep architectures,” IEEE transactions on image processing, vol. 26, no. 9, pp. 4321–4330, 2017.
- [9] Dong Oh and Il Yun, “Residual error based anomaly detection using auto-encoder in smd machine sound,” Sensors, vol. 18, no. 5, pp. 1308, 2018.
- [10] Peter J Huber, Robust statistics, Springer, 2011.
- [11] Houssam Zenati, Chuan Sheng Foo, Bruno Lecouat, Gaurav Manek, and Vijay Ramaseshan Chandrasekhar, “Efficient gan-based anomaly detection,” arXiv preprint arXiv:1802.06222, 2018.
- [12] Thomas Schlegl, Philipp Seeböck, Sebastian M Waldstein, Ursula Schmidt-Erfurth, and Georg Langs, “Unsupervised anomaly detection with generative adversarial networks to guide marker discovery,” in International conference on information processing in medical imaging. Springer, 2017, pp. 146–157.
- [13] Dan Li, Dacheng Chen, Jonathan Goh, and See-kiong Ng, “Anomaly detection with generative adversarial networks for multivariate time series,” arXiv preprint arXiv:1809.04758, 2018.
- [14] Samet Akcay, Amir Atapour-Abarghouei, and Toby P Breckon, “Ganomaly: Semi-supervised anomaly detection via adversarial training,” in Asian Conference on Computer Vision. Springer, 2018, pp. 622–637.
- [15] Bo Zong, Qi Song, Martin Renqiang Min, Wei Cheng, Cristian Lumezanu, Daeki Cho, and Haifeng Chen, “Deep autoencoding gaussian mixture model for unsupervised anomaly detection,” 2018.
- [16] Shuangfei Zhai, Yu Cheng, Weining Lu, and Zhongfei Zhang, “Deep structured energy based models for anomaly detection,” arXiv preprint arXiv:1605.07717, 2016.
- [17] Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio, “Generative adversarial nets,” in Advances in neural information processing systems, 2014, pp. 2672–2680.
- [18] Annamaria Mesaros, Toni Heittola, Aleksandr Diment, Benjamin Elizalde, Ankit Shah, Emmanuel Vincent, Bhiksha Raj, and Tuomas Virtanen, “Dcase 2017 challenge setup: Tasks, datasets and baseline system,” 2017.
- [19] Ellen Rushe and Brian Mac Namee, “Anomaly detection in raw audio using deep autoregressive networks,” in ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019, pp. 3597–3601.
- [20] Yunqiang Chen, Xiang Sean Zhou, and Thomas S Huang, “One-class svm for learning in image retrieval,” in Proceedings 2001 International Conference on Image Processing (Cat. No. 01CH37205). IEEE, 2001, vol. 1, pp. 34–37.
- [21] Emanuel Parzen, “On estimation of a probability density function and mode,” The annals of mathematical statistics, vol. 33, no. 3, pp. 1065–1076, 1962.
- [22] Fei Tony Liu, Kai Ming Ting, and Zhi-Hua Zhou, “Isolation forest,” in 2008 Eighth IEEE International Conference on Data Mining. IEEE, 2008, pp. 413–422.
- [23] Jonathan Masci, Ueli Meier, Dan Cireşan, and Jürgen Schmidhuber, “Stacked convolutional auto-encoders for hierarchical feature extraction,” in International conference on artificial neural networks. Springer, 2011, pp. 52–59.
- [24] Lukas Ruff, Robert Vandermeulen, Nico Goernitz, Lucas Deecke, Shoaib Ahmed Siddiqui, Alexander Binder, Emmanuel Müller, and Marius Kloft, “Deep one-class classification,” in International conference on machine learning, 2018, pp. 4393–4402.