Action-Constrained Reinforcement Learning for Frame-Level Bit Allocation in HEVC/H.265 through Frank-Wolfe Policy Optimization
Abstract
This paper presents a reinforcement learning (RL) framework that leverages Frank-Wolfe policy optimization to address frame-level bit allocation for HEVC/H.265. Most previous RL-based approaches adopt the single-critic design, which weights the rewards for distortion minimization and rate regularization by an empirically chosen hyper-parameter. More recently, the dual-critic design is proposed to update the actor network by alternating the rate and distortion critics. However, the convergence of training is not guaranteed. To address this issue, we introduce Neural Frank-Wolfe Policy Optimization (NFWPO) in formulating the frame-level bit allocation as an action-constrained RL problem. In this new framework, the rate critic serves to specify a feasible action set, and the distortion critic updates the actor network towards maximizing the reconstruction quality while conforming to the action constraint. Experimental results show that when trained to optimize the video multi-method assessment fusion (VMAF) metric, our NFWPO-based model outperforms both the single-critic and the dual-critic methods. It also demonstrates comparable rate-distortion performance to the 2-pass average bit rate control of x265.
Index Terms— Frame-level bit allocation, rate control, action-constrained reinforcement learning
1 Introduction
The task of frame-level bit allocation is to assign bits to every video frame in a group of pictures (GOP), aiming at minimizing the total distortion of a GOP subject to a rate constraint. In essence, it is a constrained optimization problem, with the inter-frame dependencies between the reference and non-reference frames incurring dependent decision-making.
Reinforcement learning (RL) is a promising technique for addressing dependent decision-making. Recently, some early attempts apply RL to the bit allocation problem for video coding. Chen et al. [1] and Zhou et al. [2] learn RL agents to determine quantization parameters (QP) for frame-level bit allocation. The former tackles the GOP coding with hierarchical bi-prediction, while the latter targets low-delay coding. Ren et al. [3] extend the idea to region-of-interest (ROI)-based coding for gaming content. Fu et al. [4] adopt a similar approach to streaming applications. In common, these prior works all train the RL agent with a single reward function that usually mixes the distortion and the rate rewards by a fixed hyper-parameter , e.g. . However, the choice of the hyper-parameter is a non-trivial task. It affects crucially how the agent weighs the distortion minimization against the rate regularization. Using a fixed hyper-parameter may lead to an RL agent that does not generalize well to varied video sequences.
Different from the single-critic approaches [1, 2, 3, 4], Ho et al.[5] learn two separate critics, one for estimating the distortion reward and the other for the rate reward. They introduce a dual-critic learning algorithm that trains the RL agent by alternating the rate critic with the distortion critic according to how the RL agent behaves in encoding a GOP. If the agent violates the rate constraint, the rate critic is chosen to update the actor; otherwise, the distortion critic is applied to train the agent towards minimizing the distortion. Although the dual-critic scheme is found to generalize better on different types of video, the training convergence is not guaranteed.
In this paper, we propose an action-constrained RL framework though Neural Frank-Wolfe Policy Optimization (NFWPO). Similar to the dual-critic idea [5], our scheme includes a rate critic and a distortion critic. However, unlike [5], the rate critic is utilized to specify a state-dependent feasible set, i.e. an action space that meets the rate constraint. Next, we apply NFWPO [6] together with the distortion critic to identify a feasible action that works toward minimizing the distortion. It then follows that the chosen action is used as a target to guide the actor network. In particular, we choose the video multi-method assessment fusion (VMAF) [7] as the distortion metric for two reasons. First, VMAF can better reflect subjective video quality than mean-squared error (MSE). Second, we show that our RL framework is generic in that it can accommodate an intractable quality metric such as VMAF.
Our main contributions are as follows: (1) this work presents a novel RL framework that incorporates the Frank-Wolfe policy optimization to address the frame-level bit allocation for HEVC/H.265; (2) it outperforms both the single-critic [1] and the dual-critic [5] methods, showing comparable rate-distortion (R-D) results to the 2-pass ABR of x265. It is to be noted that our scheme performs bit allocation in one pass at test time.
2 Neural Frank-Wolfe Policy Optimization
Neural Frank-Wolfe Policy Optimization (NFWPO) [6] is an action-constrained reinforcement learning (RL) technique. Unlike the vanilla RL setup, the action-constrained RL requires the agent to maximize the reward-to-go subject to the feasible action constraints :
| (1) |
where the reward-to-go is the expected cumulative future rewards under the policy (i.e. ). In this paper, the policy is implemented by a deterministic, continuous actor network, which takes the state as input and produces a continuous action as output.
Some prior works [8] deal with the action-constrained RL by adding a projection layer at the output of the actor network. The projection layer projects the action driven by the actor network onto the feasible set by
| (2) |
where is a pre-projection action and is the post-projection action. However, due to the projection layer, the zero-gradient issue may occur when updating the actor network by seeking the action which maximizes the reward-to-go through the gradient ascent. One example of the projection layer is the ReLU operation, which may be employed to constrain the action to be a non-negative value. Apparently, it causes a zero gradient during back-propagation.
To circumvent this issue, NFWPO updates the actor network in three sequential steps. First, it identifies a feasible update direction according to
| (3) |
where the operator takes the inner product of and . Second, it evaluates a reference action by
| (4) |
where is the learning rate of NFWPO. Lastly, it learns the actor network through gradient decent by minimizing the squared error between the reference action and :
| (5) |
It is worth noting that even though NFWPO still involves a projection layer, there is no zero-gradient issue during training because the projection layer does not participate in the back-propagation.
3 Proposed Method
3.1 Problem Formulation
The objective of the frame-level bit allocation is to minimize the distortion (i.e. maximize the VMAF score) of a GOP subject to a rate constraint. This is achieved by allocating available bits properly among video frames in a GOP through choosing their quantization parameters (QP). In symbols, we have
| (6) |
where indicates the QP for the i-th frame, denotes the GOP size, is the distortion (measured in VMAF) of frame encoded with , is the number of encoded bits of frame , and is the GOP-level rate constraint.
We address the problem in Eq. (6) by learning an RL agent that is able to determine in sequential steps the QP of every video frame in a GOP, so that the resulting number of encoding bits approximates while maximizing the cumulative VMAF score. To this end, we introduce the NFWPO-based RL framework.
We begin by drawing an analogy between the NFWPO-based RL setup and the problem in Eq. (6). Consider a video frame whose is to be determined. First, the minimization of the cumulative distortion over the entire GOP in Eq. (6) is regarded as the maximization of the reward-to-go in Eq. (1) in determining , where in our problem corresponds to the sum of VMAF scores from frame till the very last frame in the GOP. That is, the local QP decision for frame needs to ensure that the reward in the long run (respectively, the cumulative distortion till the very last frame) can be maximized (respectively, minimized). In addition, in determining , we wish to satisfy the rate constraint in Eq. (6). Obviously, not every possible can meet the constraint. Therefore, needs to be confined in a feasible set , which is a function of the current coding context represented by a state signal . How is specified is detailed in Section 3.6. With these in mind, we translate the problem in Eq. (6) into
| (7) |
which shares the same form as Eq. (1). We can thus learn an actor network for determining based on the action-constrained RL setup (Section 2).
3.2 System Overview
Fig. 1 presents an overview of our action-constrained RL setup. When encoding frame , (1) a state is first evaluated (Section 3.3). (2) It is then taken by the neural network-based RL agent to output as an action (Section 3.4). (3) With , frame is encoded and decoded by the specified codec (e.g. x265). Upon the completion of encoding frame , our proposed NFWPO-based RL algorithm evaluates a distortion reward and a rate reward (Section 3.5). These steps are repeated iteratively until all the video frames in a GOP are encoded.
At training time, the agent interacts with the codec intensively by encoding every GOP as an episodic task. To predict the distortion and rate rewards, we resort to two neural network-based critics, the distortion critic and the rate critic , both of which take the state signal and as inputs. As will be seen, the rate critic , which predicts the rate reward-to-go (or the rate deviation from the bit budget at the end of encoding a GOP), allows us to specify a feasible set of for the current coding frame. With , we apply NFWPO [6] to train the agent, in order to maximize the distortion reward-to-go , which gives an estimate of the cumulative VMAF score. That is, we substitute for in Eq. (7).
3.3 State Signals
The state signal provides informative information for the agent to make decisions. Inspired by [1], we form our state signal with the following hand-crafted features. (1) The intra-frame feature calculates the variance of pixel values for the current frame. Likewise, (2) the inter-frame feature evaluates the mean of pixel values for the frame differences based on uni- and bi-prediction, where we adopt zero motion compensation as a compromise between performance and complexity. (3) The average of the intra-frame features averages the intra-frame features over the remaining frames that are not encoded yet. (4) The average of the inter-frame features averages the inter-frame features over the remaining frames. Note that we refer to the original frames for computing frame differences whenever the coded reference frames are not available. (5) The number of remaining bits in percentage terms evaluates , where and are the GOP-level rate constraint and the number of bits encoded up to the current frame, respectively. (6) The number of remaining frames in the GOP counts the frames that have not been encoded yet. (7) The temporal identification signals the level of the frame prediction hierarchy to which the current frame belongs. (8) The rate constraint of the GOP indicates the target bit rate for the current GOP. (9) The base QP specifies the default QP values for I-, B-, and b-frames, which are determined a priori irrespective of the input video.
3.4 Actions
The action of our RL agent indicates the QP difference (known as the delta QP) from the base QP. That is, the final QP value (i.e. in Fig. 1) is the sum of the delta and the base QP’s. In our implementation, the delta QP ranges from -5 to 5 irrespective of the frame type (I-, B-, or b-frame). The fact that the agent learns to decide the delta QP helps reduce the search space. Note that different frame types have different base QPs (see Section 4.1).
3.5 Rewards
The ultimate goal of RL is to maximize the expected cumulative reward in the long run. In order for the agent to behave in a desired way, it is crucial to define proper rewards.
In this work, we specify two immediate rewards, the distortion reward and the rate reward . The former is defined as
| (8) |
where and are the VMAF [7] scores of frame when encoded with the QP values chosen by our learned agent and by the rate control algorithm of x265, respectively. In other words, characterizes the gain in VMAF achieved by our policy. This gain is intended to be maximized.
The immediate rate reward, denoted by , given to every video frame in a GOP is zero, except the last frame, the of which is given by
| (9) |
The sum represents the negative absolute deviation of the GOP bit rate from the target in percentage terms.
With these immediate rewards, the distortion reward-to-go and the rate reward-to-go in Section 3.2 are evaluated as
| (10) |
| (11) |
where is the discount factor. In particular, these reward-to-go functions are approximated by two separate networks, known as the distortion critic and the rate critic, respectively.
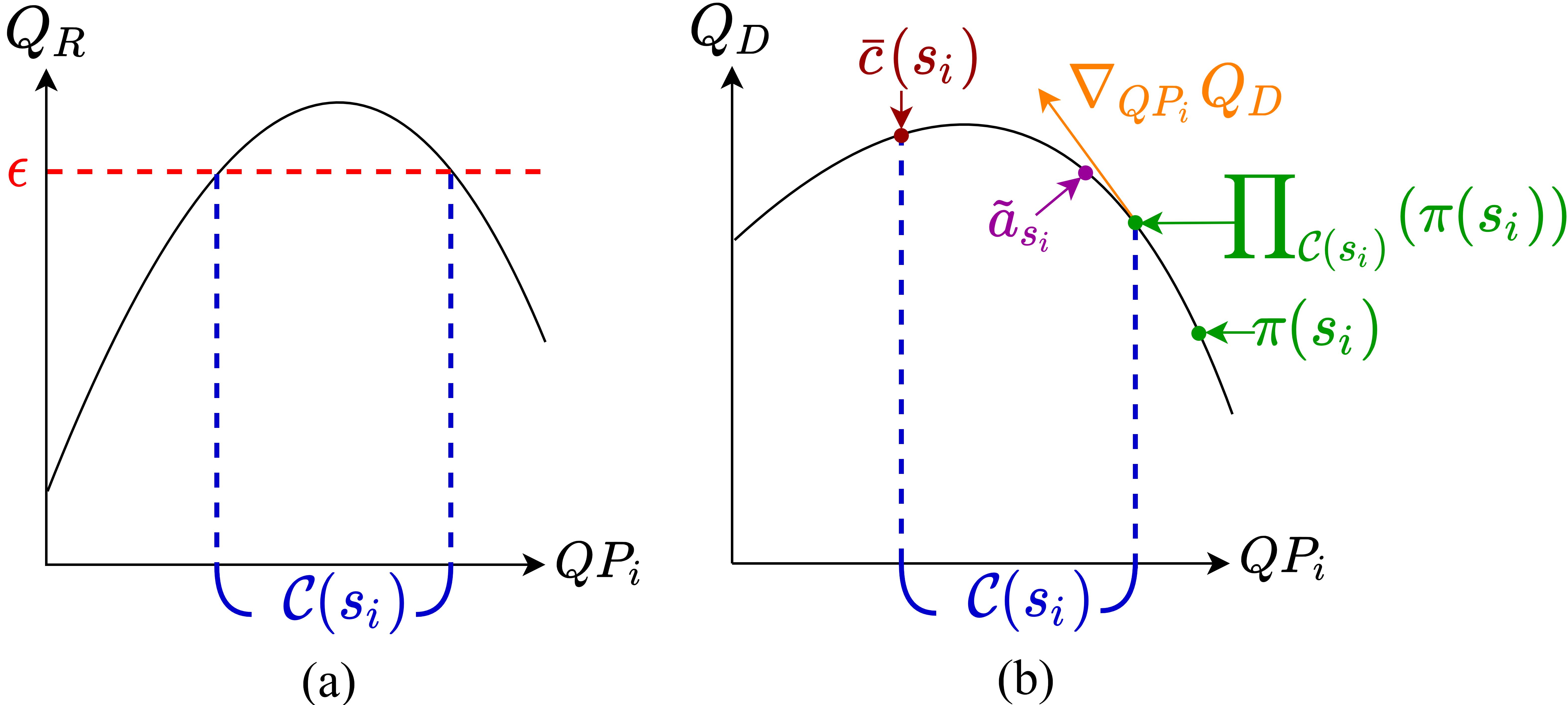
3.6 NFWPO-based RL for Frame-level Bit Allocation
This section presents how we make use of the two critic networks to implement NFWPO. We begin with defining the feasible set in coding a video frame . In order to meet the GOP-level rate constraint, the feasible set includes the QP values satisfying the requirement that the rate reward-to-go is greater than or equal to a threshold , given the current state (see Fig. 2 (a)):
| (12) |
According to Eqs. (9) and (11), this implies that includes QP values that ensure the absolute rate deviation is upper bounded by the discounted . In particular, we discretize these QP values by querying the rate critic in discrete steps of 0.1 within the delta QP range (i.e. }).
Given the feasible set , we follow the process in Section 2 to generate the reference action . Fig. 2 (b) illustrates the process, in which the actor output is assumed to be outside of the feasible set. As shown, will first be projected onto the feasible set to arrive at . We then evaluate according to Eq. (3), where we use for , and obtain based on Eq. (4). Finally, we update the actor network by Eq. (5).
Algorithm 1 details our proposed NFWPO-based RL algorithm. Similar to the DDPG algorithm, lines 5 to 12 roll out the learned policy with an exploration noise. The resulting transitions of states, actions, and rewards are stored in the replay buffer and are sampled to update the critics and in lines 15 and 17, respectively. Lines 19 to 22 correspond to NFWPO (Section 2).
Our actor and critic networks have similar network architectures to [5], but take different state signals as inputs.
4 Experimental Results
4.1 Settings and Training Details
We experiment with the proposed method on x265 using a hierarchical-B coding structure (GOP=16) as depicted in Fig. 3. To focus on the GOP-level bit allocation scheme, we follow the same GOP-level bit allocation as x265. To this end, we first encode every test sequence with fixed QP’s 22, 27, 32, and 37. This establishes four target bit rates at the sequence level. Next, we enable the 2-pass ABR rate control mode of x265 (–pass –bitrate –vbv-bufsize –vbv-maxrate ) in generating the anchor bitstreams, to meet these target bit rates. Finally, we observe the GOP-level bit rates of x265 and use them as our . Since we use VMAF as the quality metric, to obtain the best perceptual quality, we turn off the –tune option in accordance with the x265 manual. It is to be noted that all the RL-based schemes (i.e. the single-critic method, the dual-critic method, and ours) are one-pass schemes. They do not make use of any information in the first encoding pass for bit allocation.
For training our model, the training dataset includes video sequences in UVG, MCL-JCV, and JCT-VC Class A. To expedite the training, all these sequences are resized to . Likewise, the test videos, which are Class B and Class C sequences in JCT-VC dataset, are resized to the same spatial resolution. The single-critic and dual-critic methods use the same dataset for training.
We determine the hyper-parameters as follows. The base QP are selected as , , and for I-, B-, and b-frame, respectively, where are 22, 27, 32, and 37. The learning rate for NFWPO in Eq. (4) is set to , and the learning rate for the actor and critic networks is . We use a discount factor and the 3-step temporal difference learning to train our critics. The threshold of the feasible set is set to , allowing for a maximum rate deviation of . For a fair comparison, the same rate requirement applies to the single- and dual-critic methods.
4.2 R-D Performance and Bit Rate Deviations
We assess the competing methods in terms of their R-D performance (in VMAF) and rate control accuracy.
Table 1 presents BD-rate results, with the 2-pass ABR of x265 serving as anchor. From Table 1, our scheme outperforms the single-critic [1] and the dual-critic [5] methods, both of which exhibit rate inflation as compared to x265 (operated in ABR mode with two-pass encoding). Ours achieves comparable performance to x265, yet with one-pass encoding. One point to note here is that all three RL-based models, including ours, perform poorly on BQMall. When this out-liner is excluded, our scheme performs slightly better than x265, showing a 0.41% average bit rate saving.
To shed light on why our scheme does not work well on BQMall, we overfit our NFWPO-based model to the test sequences. In other words, the model is trained on the test sequences. The overfitting results presented in the right most column of Table 1 indicate that BQMall, on which our previous model performs poorly, benefit the most from overfitting. Moreover, the overfit model performs comparably to the non-overfit model on the other test sequences. This then implies that our NFWPO-based RL algorithm and the model capacity are less of a problem. The root cause of the poor performance on BQMall may be attributed to the less representative training data.
Table 2 further presents the average bit-rate deviations from the GOP target . The results are provided only for the highest and the lowest rate points due to the space limitation. In reporting the average rate deviation, any deviation from the within is regarded as to account for our tolerance margin. As seen from the table, our model shows fairly good rate control accuracy. The average rate deviations at high and low rates are around and , respectively. In contrast, the rate deviations of the dual-critic method average and at high and low rates, respectively. The single-critic method has relatively inconsistent results: at high rates, the average rate deviation is as low as , whereas at low rates, it is as high as . This inconsistency in rate control accuracy between the low and high rates is attributed to the use of a fixed for trading off the rate penalty against the distortion reward.
| Sequences | BD-rate (%) | |||
| Single | Dual | Ours | Ours* | |
| BasketballDrill | 3.14 | 7.88 | 0.09 | -0.03 |
| BasketballDrive | 1.58 | 4.41 | -0.01 | -0.45 |
| BQMall | 6.66 | 3.38 | 5.01 | -0.36 |
| BQTerrace | 8.07 | 0.20 | 0.98 | -2.57 |
| Cactus | 2.00 | 0.81 | -1.39 | -0.35 |
| Kimono | 0.92 | 2.80 | -1.64 | -0.49 |
| ParkScene | 4.70 | 3.32 | -1.79 | 0.23 |
| PartyScene | 5.19 | 4.29 | 1.43 | -1.61 |
| RaceHorses | 1.71 | 1.02 | -0.93 | 0.27 |
| Average (w/o BQMall) | 3.42 | 3.09 | -0.41 | -0.63 |
| Average | 3.78 | 3.12 | 0.20 | -0.60 |
| Sequences | Bit rate | Single | Dual | Ours | Bit rate | Single | Dual | Ours |
| Kbps | Err. (%) | Err. (%) | Err. (%) | Kbps | Err. (%) | Err. (%) | Err. (%) | |
| BasketballDrill | 992 | 0.0 | 2.3 | 0.5 | 168 | 4.4 | 1.2 | 4.1 |
| BasketballDrive | 1093 | 0.0 | 3.7 | 0.9 | 171 | 1.3 | 1.1 | 1.0 |
| BQMall | 819 | 0.0 | 4.7 | 3.0 | 132 | 4.8 | 5.9 | 3.6 |
| BQTerrace | 691 | 0.0 | 4.2 | 1.1 | 93 | 28.2 | 10.9 | 5.7 |
| Cactus | 1108 | 7.4 | 3.3 | 2.2 | 158 | 6.0 | 1.6 | 0.7 |
| Kimono | 1022 | 1.8 | 6.3 | 1.5 | 139 | 16.8 | 9.9 | 3.6 |
| ParkScene | 881 | 0.0 | 2.0 | 0.0 | 103 | 50.1 | 3.6 | 1.4 |
| PartyScene | 1487 | 0.4 | 8.5 | 4.1 | 202 | 4.4 | 8.7 | 1.9 |
| RaceHorses | 1777 | 1.3 | 7.2 | 5.7 | 231 | 8.6 | 1.0 | 0.3 |
| Average | 1097 | 1.2 | 4.7 | 2.1 | 155 | 13.9 | 4.9 | 2.5 |
4.3 Effectiveness of Our NFWPO-based Model
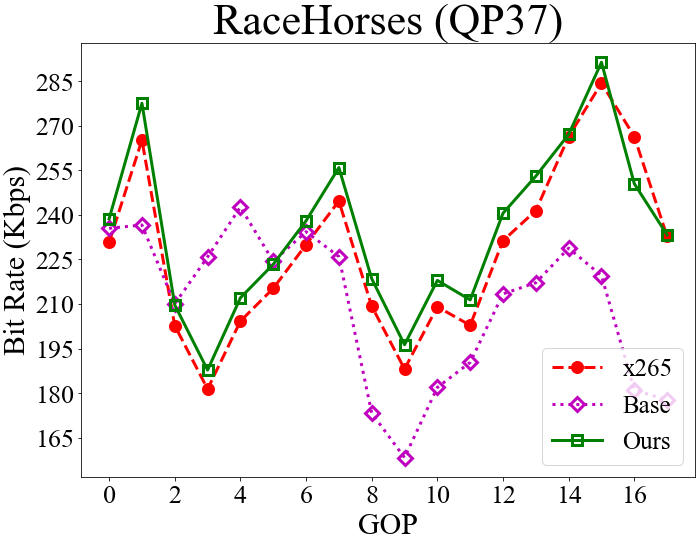
To understand the effectiveness of our rate control scheme, the top row of Fig. 4 visualizes the GOP-level bit rates for RaceHorses and BQMall while the bottom row presents the corresponding VMAF scores. The objective here is to achieve better VMAF results when encoding every GOP at the same bit rate as x265 (Section 4.1). As shown, applying the base QP alone, which corresponds to a fixed nested QP scheme, can hardly match the bit rates of x265. However, with our RL-based delta QP correction, the resulting bit rates match closely those of x265. Furthermore, our scheme shows similar or better VMAF scores than x265 in most GOPs, except for GOPs 12 to 24 in BQMall. This confirms the effectiveness of our RL training.
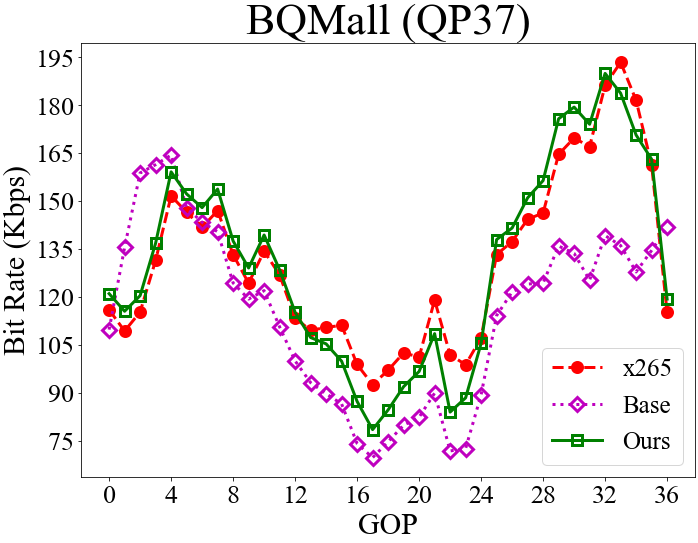
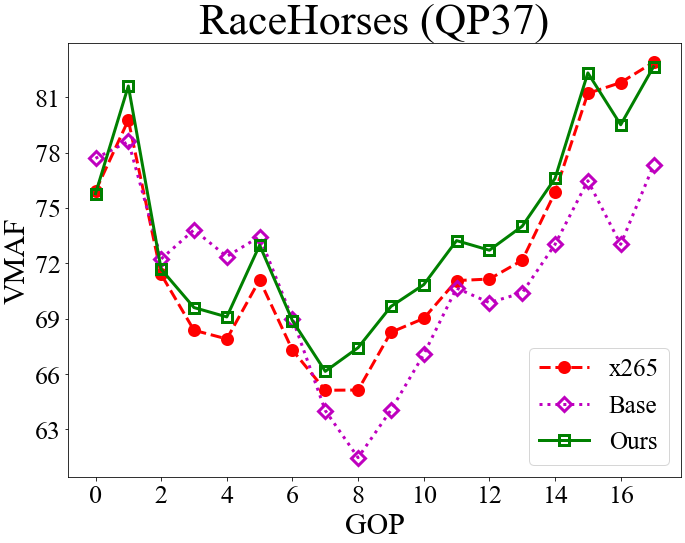
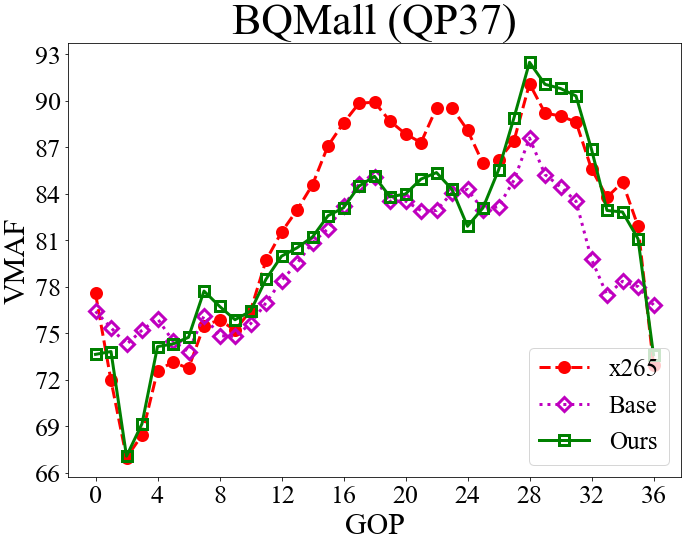
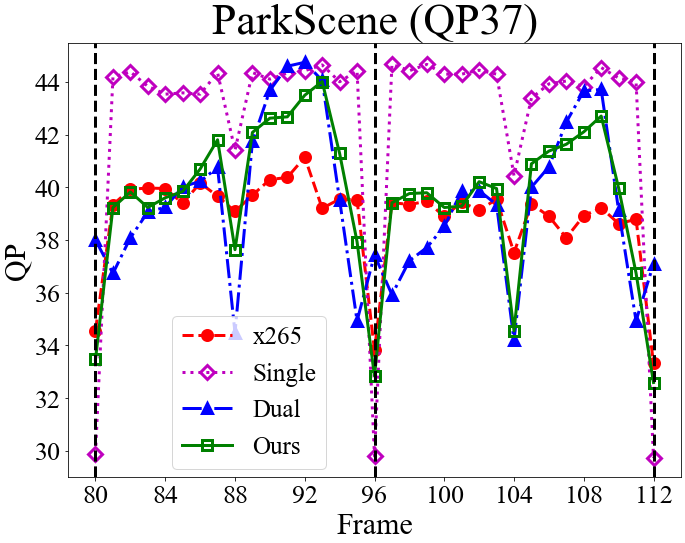
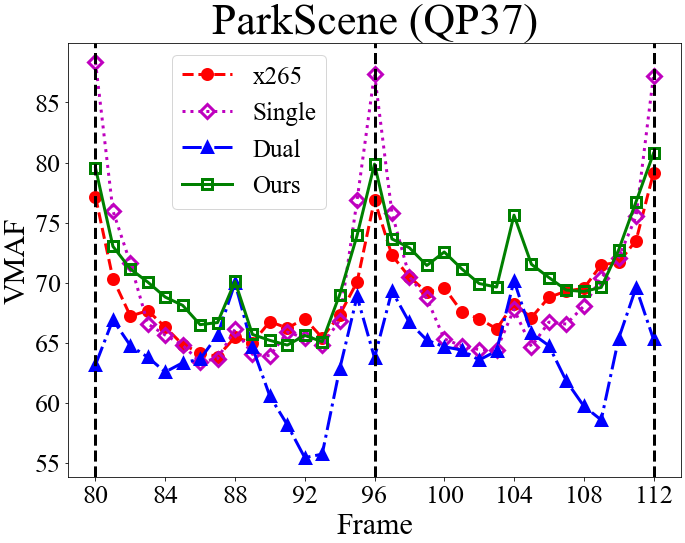
4.4 Rate Control Accuracy and QP Assignment
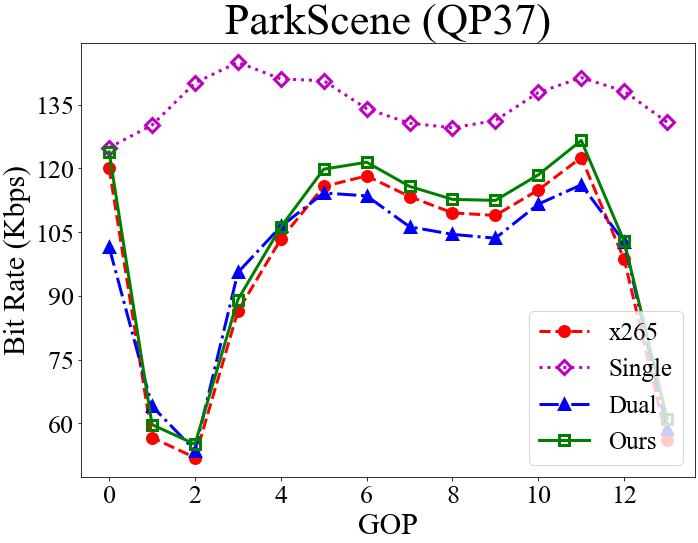
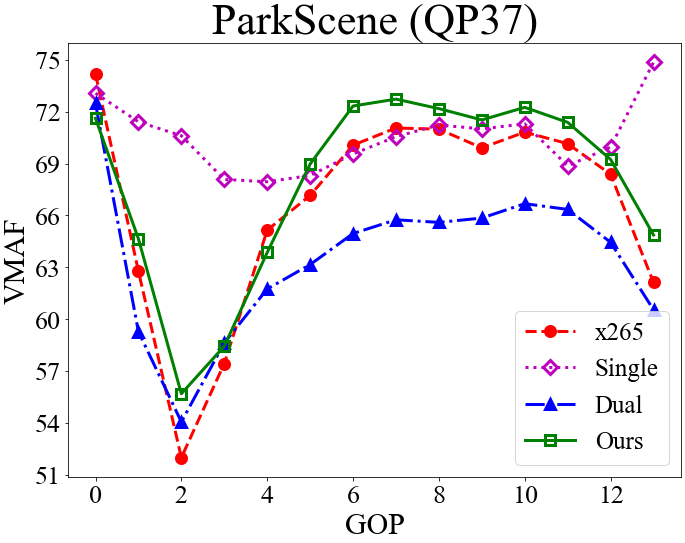
Fig. 5 presents the GOP-level bit rates, the frame-level QP assignment, and the corresponding VMAF scores for the competing methods. Again, the objective is to match the GOP-level bit rate of x265 while maximizing the VMAF scores (Section 4.1).
From the QP assignment, we see that the single-critic method tends to choose smaller QP values for I-frames, causing the resulting bit rate to exceed the target bit rate. The results presented correspond to the low-rate setting, where the single-critic method usually shows larger rate deviations (Section 4.2 & Table 2). We attribute the reason to the use of a fixed hyper-parameter in formulating a single reward function . The varying dynamics between and at different bit rates and on different sequences may render the rate reward/constraint less prominent in some cases. In contrast, the dual-critic method has fairly precise rate control accuracy. It, however, shows lower VMAF scores because of choosing higher QP values for I-frames. The general observation is that at low rates, the dual-critic method tends to disregard the distortion in order to meet the stricter rate constraint. Different from these two methods, our model chooses similar QP values to x265 for I-frames. An intriguing finding is that it tries to improve the VMAF score by choosing relatively smaller QP values for the B-frame and the first group of b-frames (frames 1-7 in Fig. 3) in a GOP. It then chooses larger QP values for the second group of b-frames (frames 9-15 in Fig. 3) to meet the rate constraint. Another observation is that our NFWPO-based model is relatively more robust to varied coding conditions, showing good rate control accuracy at both low and high rates.
4.5 Subjective Quality Comparison
Fig. 6 presents a subjective quality comparison. We see that our proposed method preserves more texture details and shows sharper image quality. More subjective quality comparisons are provided in the supplementary document.

5 Conclusion
This paper presents a NFWPO-based RL framework for frame-level bit allocation in HEVC/H.265. It overcomes the empirical choice of the hyper-parameter in the single-critic method and the convergence issue in the dual-critic method. It outperforms both of these existing RL frameworks and shows comparable R-D results to the 2-pass average bit rate control of x265.
References
- [1] Lian-Ching Chen, Jun-Hao Hu, and Wen-Hsiao Peng, “Reinforcement learning for HEVC/H.265 frame-level bit allocation,” in IEEE DSP, 2018.
- [2] Mingliang Zhou, Xuekai Wei, Sam Kwong, Weijia Jia, and Bin Fang, “Rate control method based on deep reinforcement learning for dynamic video sequences in HEVC,” IEEE Transactions on Multimedia, 2020.
- [3] Ren Guangjie, Liu Zizheng, Chen Zhenzhong, and Liu Shan, “Reinforcement learning based ROI bit allocation for gaming video coding in VVC,” in IEEE VCIP, 2021.
- [4] Fu Jun, Hou Chen, and Chen Zhibo, “360HRL: Hierarchical reinforcement learning based rate adaptation for 360-degree video streaming,” in IEEE VCIP, 2021.
- [5] Yung-Han Ho, Guo-Lun Jin, Yun Liang, Wen-Hsiao Peng, and Xiaobo Li, “A dual-critic reinforcement learning framework for frame-level bit allocation in HEVC/H.265,” in DCC, 2021.
- [6] Jyun-Li Lin, Wei Hung, Shang-Hsuan Yang, Ping-Chun Hsieh, and Xi Liu, “Escaping from zero gradient: Revisiting action-constrained reinforcement learning via Frank-Wolfe policy optimization,” UAI, 2021.
- [7] Zhi Li, Christos Bampis, Julie Novak, Anne Aaron, Kyle Swanson, Anush Moorthy, and JD Cock, “VMAF: The journey continues,” Netflix Technology Blog, 2018.
- [8] Gal Dalal, Krishnamurthy Dvijotham, Matej Vecerik, Todd Hester, Cosmin Paduraru, and Yuval Tassa, “Safe exploration in continuous action spaces,” arXiv preprint arXiv:1801.08757, 2018.