ifaamas \acmConference[AAMAS ’22]Proc.of the 21st International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2022)May 9–13, 2022 OnlineP. Faliszewski, V. Mascardi, C. Pelachaud, M.E. Taylor (eds.) \copyrightyear2022 \acmYear2022 \acmDOI \acmPrice \acmISBN \acmSubmissionID719 \affiliation \institutionTufts University \cityMedford \countryUSA \affiliation \institutionTufts University \cityMedford \countryUSA \affiliation \institutionTufts University \cityMedford \countryUSA \affiliation \institutionTufts University \cityMedford \countryUSA \affiliation \institutionTufts University \cityMedford \countryUSA
ACuTE: Automatic Curriculum Transfer from
Simple to Complex Environments
Abstract.
Despite recent advances in Reinforcement Learning (RL), many problems, especially real-world tasks, remain prohibitively expensive to learn. To address this issue, several lines of research have explored how tasks, or data samples themselves, can be sequenced into a curriculum to learn a problem that may otherwise be too difficult to learn from scratch. However, generating and optimizing a curriculum in a realistic scenario still requires extensive interactions with the environment. To address this challenge, we formulate the curriculum transfer problem, in which the schema of a curriculum optimized in a simpler, easy-to-solve environment (e.g., a grid world) is transferred to a complex, realistic scenario (e.g., a physics-based robotics simulation or the real world). We present “ACuTE”, Automatic Curriculum Transfer from Simple to Complex Environments, a novel framework to solve this problem, and evaluate our proposed method by comparing it to other baseline approaches (e.g., domain adaptation) designed to speed up learning. We observe that our approach produces improved jumpstart and time-to-threshold performance even when adding task elements that further increase the difficulty of the realistic scenario. Finally, we demonstrate that our approach is independent of the learning algorithm used for curriculum generation, and is Sim2Real transferable to a real world scenario using a physical robot.
Key words and phrases:
Curriculum Learning; Transfer Learning; Reinforcement Learning1. Introduction
Curriculum Learning (CL) attempts to optimize the order in which an agent accumulates experience, increasing performance while reducing training time for complex tasks Narvekar et al. (2020); Foglino et al. (2019); Narvekar et al. (2017). The core of CL is to generalize the experience and knowledge acquired in simple tasks and leverage it to learn complex tasks. Viable results are achieved in simulation, where the system dynamics can be easily modeled and the environment is predictable. One major limitation of many curriculum learning approaches is that the time to generate the curriculum is greater than the time to learn the target task from scratch, which prohibits the use of such methods in complex, real-world, high-fidelity domains Narvekar et al. (2020). The useful scenario of transfer to the real world remains challenging: System identification, domain adaptation, and domain randomization have performed Sim2Real transfer by attempting to match simulation with the physical environment (see 2), but these methods are elaborate and time-consuming if the simulation dynamics are expensive.
Since the dynamics of high-fidelity (HF) environments may not lend themselves to optimize a curriculum Zhang et al. (2020b, a), we propose learning the curriculum in a simplified version of the HF environment, which we call the low-fidelity (LF) environment. Parameters from each LF task can then be transferred, generating a corresponding task in the HF environment. This curriculum transfer problem is an open question (see Narvekar et al. (2020)), and to our knowledge, our novel approach is the first to address this problem. We refer to this as transferring the schema of the curriculum: only task parameters are transferred as to address situations where policies and value functions cannot be directly transferred due to differences in the observation and action spaces. High-level task descriptions can be used to model inter-task relationships, and tasks with similar task-descriptors are shown to aid positive transfer Rostami et al. (2020); Sinapov et al. (2015). We show that our curriculum transfer approach leads to a quicker convergence even in cases where the dynamics of the LF and HF environments are different enough such that traditional domain adaptation methods do not produce a sufficient boost in learning.
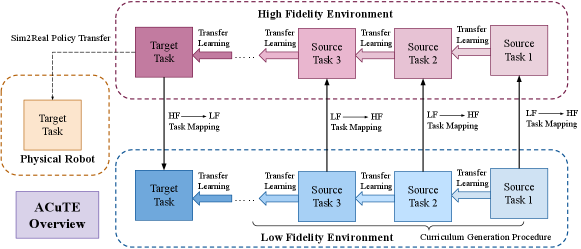
An overview of our approach is shown in Fig 1. We consider a complex task and call it the HF target task, and map it to its simplified LF representation. The simplified dynamics of the LF environment allows curricula generation and experimentation to avoid costly setup and expensive data collection associated with the HF environment. Once an optimized curriculum is generated in the LF environment, the task parameters are mapped to obtain their respective HF counterparts. We learn these source tasks iteratively, transferring skills, before learning the target task. Finally, we perform a demonstration with Sim2Real transfer from the HF environment to test our effectiveness on a physical TurtleBot.
In this work, we perform extensive experimental evaluation to demonstrate that curriculum transfer enables the agent to reduce the overall target task time compared to baselines. Through ACuTE, we propose an autonomous curriculum transfer method, which we refer to as “Automated Curriculum Transfer”, that parameterizes the target task to generate and optimize the sequence of source tasks. We notice quick and efficient learning compared to baseline approaches present in literature such as Domain Adaptation Carr et al. (2019), Self-Play Sukhbaatar et al. (2018) and Teacher-Student curriculum learning Matiisen et al. (2020). Additionally, we observe an improved jumpstart and time to threshold performance even when we add elements that make the HF target task too difficult to learn without a curriculum. We demonstrate that our approach is independent of the learning algorithm by showing improved performance in the HF environment when using a different learning algorithm from the one used when optimizing the curriculum, and also demonstrate positive transfer with imperfect mapping between the two environments. We observe that the Sim2Real transfer achieves successful task completion performance, equivalent to the HF agent’s performance, on a physical TurtleBot.
2. Related Work
Transfer Learning uses knowledge from learned tasks and transfers it to a complex target task Taylor and Stone (2009). Policy transfer is one such approach, in which the policy learned in a source task is used to initialize the policy for the next task in the curriculum Narayan et al. (2017); Da Silva and Costa (2019); Taylor and Stone (2009); Lazaric (2012). One popular transfer learning technique is to transfer the value function parameters learned in one task to initialize the value function of the next task in curriculum Liu and Stone (2006); Abel et al. (2018); Liu et al. (2019); Lazaric (2012).
Sim2Real Transfer allows a model to be trained in simulation before deploying onto hardware, reducing time, cost, and safety issues. However, it encounters what Tobin et. al. Tobin et al. (2017) describe as the “Reality Gap” where a model does not allow an agent to train on realistic details. The same authors introduce “domain randomization” as a solution, later expanded upon by Peng et. al. Peng et al. (2018). Continual learning on incremental simulations can help tackle the sample inefficiency problem of domain randomization Josifovski et al. (2020). In contrast, Operational Space Control Kaspar et al. (2020) avoids domain randomization while speeding up training with fewer hyperparameters. Carr et. al. Carr et al. (2019) proposed a domain adaptation strategy approach, where state knowledge is transferred across semantically related games. Unlike aforementioned works, in this paper, we transfer the curriculum and not the policy to handle situations where Sim2Real fails, e.g., when the observation and action spaces of the simulation and real environment are different.
Curriculum Learning was introduced in the early 1990’s, where it was used for grammar learning Elman (1993), control problems Sanger (1994) and in supervised classification tasks Bengio et al. (2009). CL has been extensively used for RL, with applications ranging from complex games Gao and Wu (2021); Wu et al. (2018), to robotics Karpathy and Van De Panne (2012), and self-driving cars Qiao et al. (2018). In Narvekar et al. (2020), the authors propose a framework for curriculum learning (CL) in RL, and use it to classify and survey existing CL algorithms. The three main elements of CL are task generation, task sequencing, and transfer learning. Task generation produces a set of source tasks that can be learned before learning the target task Silva and Costa (2018); Kurkcu et al. (2020). Task sequencing orders the generated tasks to facilitate efficient transfer from the source to the target task Narvekar et al. (2017); Sukhbaatar et al. (2018); Matiisen et al. (2020). Metaheuristic search methods are a popular tool to evaluate the performance of the task sequencing optimization framework Foglino et al. (2019). In our work, we propose a framework to generate the source tasks and optimize their sequence, while evaluating performance against three baseline approaches. In most existing methods, generating and optimizing the curricula to learn a complex task is still time-consuming and sometimes takes longer compared to learning from scratch. Our proposed framework addresses this concern by generating, optimizing, and then transferring the schema of the curriculum from a simple and easy-to-learn environment to a complex and realistic environment.
3. Theoretical Framework
3.1. Markov Decision Processes
An episodic Markov Decision Process (MDP) is defined as a tuple , where is the set of states, is the set of actions, is the transition function, is the reward function and is the discount factor. For each timestep , the agent observes a state and performs an action given by its policy function , with parameters . The agent’s goal is to learn an optimal policy , maximizing its discounted return until the end of the episode at timestep .
 |
 |
 |
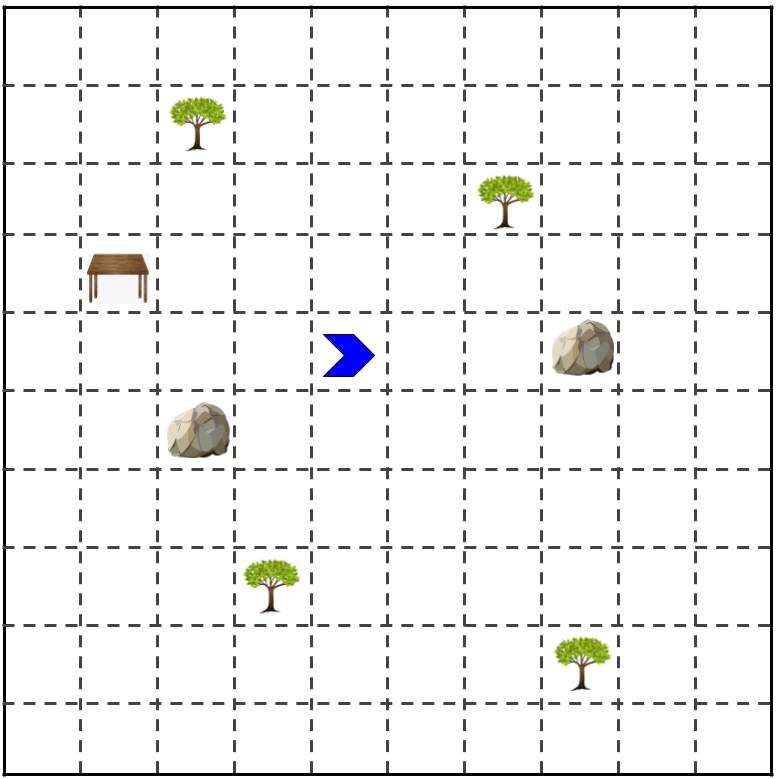
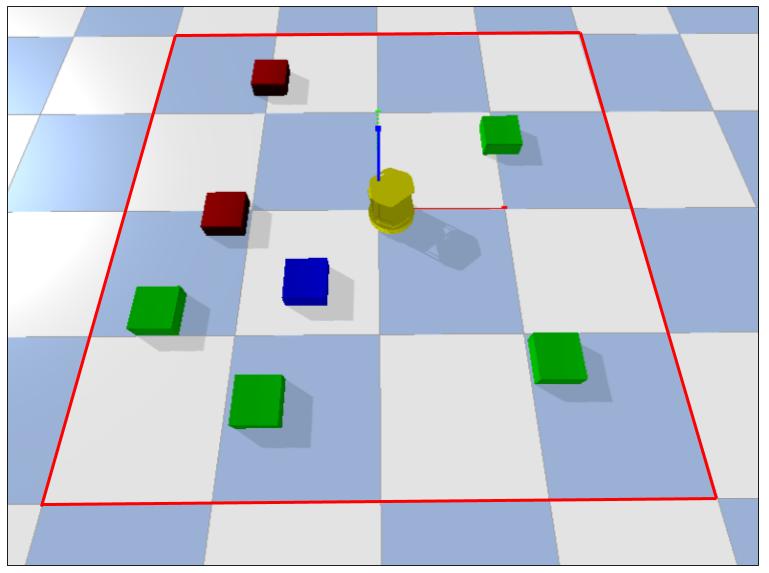
| (a) Target task in Low Fidelity Environment | (b) Target task in High Fidelity Environment | (c) Target task in Physical Environment, using a camera (blue) to interact with fiducials (red). LIDAR (green) is also visible. |
3.2. Curriculum Learning (CL)
We define a task-level curriculum as:
Let be a set of tasks, where is a task in . Let be the set of all possible transition samples from tasks in : . A curriculum is an ordered list of tasks, where is the task in the curriculum. The ordered list signifies that samples from must be used for training a policy before samples from are used. The sequence of tasks terminates on the target task .
3.3. Problem Formulation
The aim of CL is to generate a curriculum and train an agent on a sequence of tasks , such that the agent’s performance on the final target task improves relative to learning from scratch. The domains and of possible tasks are sets of MDPs in the high-fidelity (HF) and the low-fidelity (LF) environments, respectively. An individual task can be realized by varying a set of parametric variables and subjecting the task to a set of constraints. The parametric variables are a set of attribute-value pair features that parameterize the environment to produce a specific task. Each has a range of possible values that the feature can take while the of a domain are a set of tasks attained by determining the goal condition .
Let be the set of all curricula over tasks of length in the LF environment. Similarly, let be the set of all curricula over tasks of length in the HF environment. The goal is to find a curriculum in the LF environment that can be transferred through a set of mapping functions to attain the curriculum in the HF environment . A mapping function maps the parametric variables in the LF environment () to the parametric variables in the HF environment (). We characterize the mapping as an affine transformation given by:
where and denote linear mapping and translation vector and is the Hadamard product. Thus, a parameter mapping () is given by:
The source tasks of the curriculum in the HF environment are learned before final target task as described in Section 3.2.
3.4. Running Example
For the physical environment shown in Fig 2c, we generate Crafter-TurtleBot (Fig 2b), a realistic simulation of the physical environment. The aim is to learn a policy in this high-fidelity (HF) environment, through an automated curriculum transfer from the low-fidelity (LF) environment (Fig 2a), and perform Sim2Real Policy transfer from the HF environment to execute the task in the physical environment.
The agent’s goal is to break 2 trees to collect 2 pieces of wood, break a rock to collect a stone and craft a stone axe at the crafting table. The agent needs to navigate, face the object and perform the break action to collect it in inventory. The parametric variables for this task are the width and height of the navigable area, the number of trees , rocks , and crafting table present, the number of wood and stones present in the inventory of the agent when the episode starts, and the goal of the task. The goal is drawn from a discrete set, which can be navigating to an item, breaking a subset of the items present in the environment or crafting the stone axe.
As described in Fig 1, the HF target task is mapped to its LF equivalent. The simplified LF dynamics allow efficient curriculum optimization. Once the curriculum is generated, each task of the LF is mapped back to generate an equivalent HF task, which are learned through a curriculum to develop a successful task policy for the target HF task. This policy is then transferred to the Physical Robot through a Sim2Real Transfer.
3.5. Curriculum Transfer Approach
ACuTE consists of three parts: Generating a LF target task, Curriculum generation in LF, and Task sequencing and learning in HF. Algorithm 1 presents our approach. The first step entails generating the LF target task from the HF target task. To obtain the task parameters for the LF task, we pass the HF target task parameters () through the inverse of the affine mapping functions followed by Generate_Env (line 1), to obtain the parameters for the target task in the LF environment. The two requirements for obtaining a corresponding mapping are as follows:
-
•
Each task parameter in the HF environment () needs a corresponding task parameter in the LF environment (). s.t. . Varying these task parameters yields different tasks that are sequenced to form a curriculum.
-
•
The final task in the HF environment must be mapped to the final task in the LF environment. Thus, we can guarantee that each source task obtained through the curriculum in the LF can be mapped to a corresponding task for the HF environment.
The actions in the HF can be complex, but each action can be simplified to an LF action that need not be correspondingly equivalent. Our approach does not assume an equivalency between the state or the action spaces between the LF and the HF environments, but only on the two requirements listed above. To generate and sequence the source tasks in the LF environment, we compared two approaches. The first approach, called Handcrafted Curriculum Transfer (HC), involves a human expert deciding the parametric variables for the tasks for the curriculum (line 3). The second approach, Automated Curriculum Transfer (AC), automatically generates and optimizes a sequence of source tasks from the parametric variables for the agent to learn the final task with the fewest number of episodes (line 5).
3.6. Handcrafted and Automated Curriculum Transfer Generation
To optimize curricula through Handcrafted Curriculum Transfer (Generate_HC) (HC), a human expert determines the parametric variables and the task sequence for the source tasks in the curriculum. Whereas, for optimizing curriculum using the Automated (AC) procedure (Generate_AC), we use the approach given in Algorithm 2. We start from an empty sequence of source task parameters . The algorithm calls a parameterizing function (Init_Src) that assigns random values to the parametric variables for the first source task from the range of values can attain while simultaneously initializing an RL agent (Init_Agent). Based on , the algorithm generates the first task for the agent, , using the function (Generate_Env). The agent attempts learning this source task with the initial policy , until the stopping criterion is met. The stopping criterion determines if the agent’s goal rate () is in the last episodes (Algorithm 1 line 12). Failure to meet the stopping criterion implies that the agent has reached maximum permitted episodes (termed budget ()) signifying . The value for is set at for our experiments.
Output: HF target task policy:
Algorithm:
In AC, the first task of the curriculum is randomly initialized times and learned until stopping criterion is met. The algorithm then finds the most promising solutions (), based on fewest interactions to meet the stopping criterion. To optimize the sequence of the curriculum, we use beam search Lowerre (1976). Beam search is a greedy search algorithm that uses a breadth-first search approach to formulate a tree. At each level of the tree, the algorithm sorts all the () successors of the tree ( successor tasks for each task of ) at the current level in increasing order of number of episodes required to learn the task . Then, it selects number of best tasks at each level, given by fewest interactions to reach stopping criterion, and performs the same step until the tree reaches the desired number of levels .
Output: LF Curriculum Parameters:
Placeholder Initialization:
Timesteps:
LF task params for all tasks at each beam level
LF task params at each width and level
LF curriculum params
LF task policies for all tasks at each beam level:
LF task policies for each width and level:
Algorithm:
Now, using the parametric variables for each task in the beam (), the algorithm generates parametric variables () for the next task in the curriculum. This is done by choosing a goal not encountered by the agent until the current level in the beam , and randomly initializing parametric variables the minimum required to accomplish this goal. The agent then attempts learning with the final policy of the previous source task in the beam (). The task terminates when the agent meets the stopping criterion. The algorithm finds the most promising solutions, given by fewest interactions to reach stopping criterion () and carries out this procedure iteratively, until the final target task is learned. The parameters of the curriculum with the lowest number of episodes to reach the stopping criterion is selected as the most promising solution () for learning the target task. The curriculum generation procedure requires the length of the curriculum to be the number of goals attainable. This ensures all the goals available () are encountered by the agent in the curriculum.
3.6.1. Task Sequencing and Learning in HF
Once the LF curriculum parametric variables () are obtained, they are passed through the set of mapping functions () to attain the task parameters in HF, generating the curriculum source tasks from these parameters. The agent attempts learning the first source task with an initial policy . The task terminates when the agent meets the stopping criterion, generating the final policy . This learned policy is used as an initial policy for the next source task in the curriculum. This procedure is carried out iteratively, culminating at the HF target task, returning (Algorithm 1, line 8-15).
4. Experimental Results
 |
 |
 |
| (a) LF - gridworld | (b) HF - Crafter-Turtlebot | (c) Crafter-Turtlebot Baselines |
 |
 |
 |
| (d) LF w/ Fire - gridworld | (e) HF w/ Fire - Crafter-Turtlebot | (f) Crafter-Turtlebot w/ Fire - Baselines |
We aim to answer the following questions: (1) Does the automated curriculum transfer yield sample efficient learning? (2) Does it scale to environments that are too difficult to learn from scratch? (3) Is the curriculum transfer framework independent of the RL algorithm used to generate the curriculum? (4) Can we perform a Sim2Real transfer to a physical robot? (5) Can the curriculum transfer framework yield successful convergence with imperfect (e.g., noisy) mappings between the HF and LF environments? 111Code available at: https://github.com/tufts-ai-robotics-group/ACuTE
To answer the first question, we evaluate our curriculum transfer method on grid-world as low-fidelity (LF) and Crafter-TurtleBot as the high-fidelity (HF) environments. In the LF environment, the agent can move 1 cell forward if the cell ahead is clear or rotate clockwise or counter-clockwise. In the target task, the agent receives a reward of upon crafting a stone axe, and reward for all other steps. In the source tasks of the curriculum, the agent also receives reward for breaking an item that is needed for crafting. This reward shaping is absent in the final target task. The agent’s sensor emits a beam at incremental angles of to determine the closest object in the angle of the beam (i.e., the agents received a local-view of its environment). Two additional sensors provide information on the amount of wood and stones in the agent’s inventory (See Appendix Section A.1 for further details).
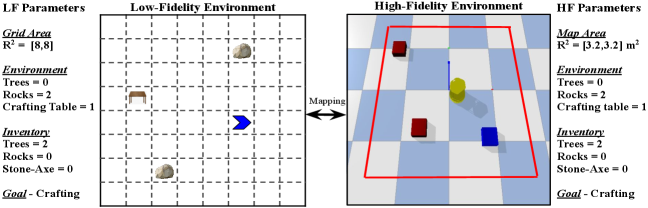
The HF environment, Crafter-TurtleBot, is structurally similar to the grid-world domain, but differs in that objects are placed in continuous locations to more closely model the real-world. The agent is a TurtleBot, rendered in PyBullet Coumans and Bai (2019). An example of the LF HF mapping between the tasks in LF and HF environments is shown in Fig 3. Here, the task mapping is demonstrated on an intermediate task of the curriculum, whose goal is to break a rock and craft a stone axe at the crafting table. The task mapping function ensures the LF and HF tasks have the same number and types of objects in the environments and the inventory. The mapping considers increased navigable area in the HF and does not assume the positions of the objects are preserved. In each episode, objects are positioned randomly within the boundaries of the environment. Refer to Appendix A.6 for details on mapping function set .
In the HF environment, the agent’s navigation actions are moving forward 0.25 units and rotating by radians. The break and craft actions and the reward shaping in source tasks is identical to the LF environment. The HF agent’s sensor is similar to the LF agent’s sensor; however, it emits beams at incremental angles of , accounting for the large state space of the location of objects.
To evaluate the performance of curriculum transfer, we used the jumpstart Lazaric (2012); Foglino et al. (2019) metric. Jumpstart evaluates the performance increase over episodes after transfer from a source task as compared to a baseline approach. Jumpstart is defined as:
where and are the returns obtained during episode in task (learning through automated curriculum transfer) and the baseline task respectively. Another metric we used is the time to threshold metric Taylor and Stone (2009); Narvekar et al. (2020), which computes how faster an agent can learn a policy that achieves expected return on the target task if it transfers knowledge, as opposed to learning from another approach, where is desired performance threshold.
4.1. Curriculum Generation in High Fidelity
We used the algorithm presented in Algorithm 1 to generate and sequence the source tasks using the handcrafted curriculum transfer (HC) and the automated curriculum transfer (AC) approach. The navigable area in target task in low-fidelity (LF) environment is a grid of , as seen in Fig 2a, and the high-fidelity (HF) target task area is a continuous space, as seen in Fig 2b. Both these environments contain 4 trees, 2 rocks and 1 crafting table, placed at random locations.
The RL algorithm was a Policy Gradient Williams (1992) network with -greedy action selection for learning the optimal policy. The episode terminates when the agent successfully crafts a stone axe or exceeds the total number of timesteps permitted, which is in the LF environment and in the HF environment. All experiments are averaged over 10 trials. (See Appendix Section A.2).
For generating the AC in the LF environment, we set the width of the beam search algorithm at , and the length of the beam at , the curriculum length was , and budget . We obtained the parameters after performing a heuristic grid search over the space of the search algorithm. We evaluated our curriculum transfer framework with four other baselines. Learning from scratch trains the final HF target task without any curriculum. We also adopted three approaches from the literature designed for speeding-up RL agents: Asymmetric Self-play Sukhbaatar et al. (2018), Teacher-Student Curriculum learning Matiisen et al. (2020) and Domain Adaptation for RL Carr et al. (2019). The first two baselines do not make use of the LF environment while the third uses the LF environment as the source domain. All baseline approaches involve reward shaping similar to the source task of the automated curriculum transfer approach.
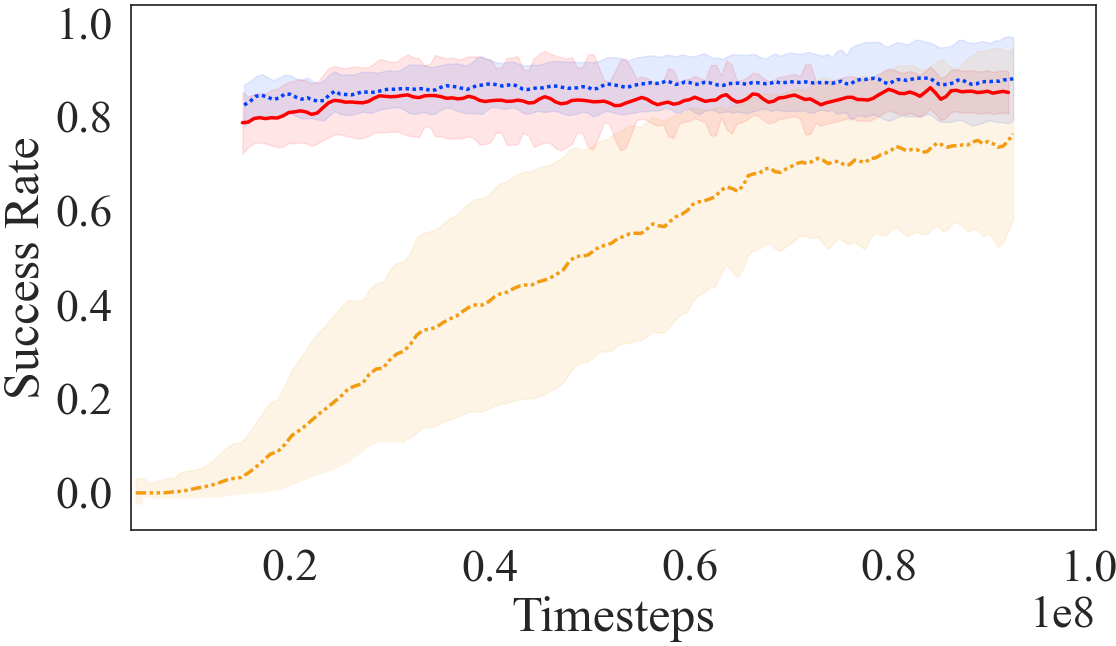
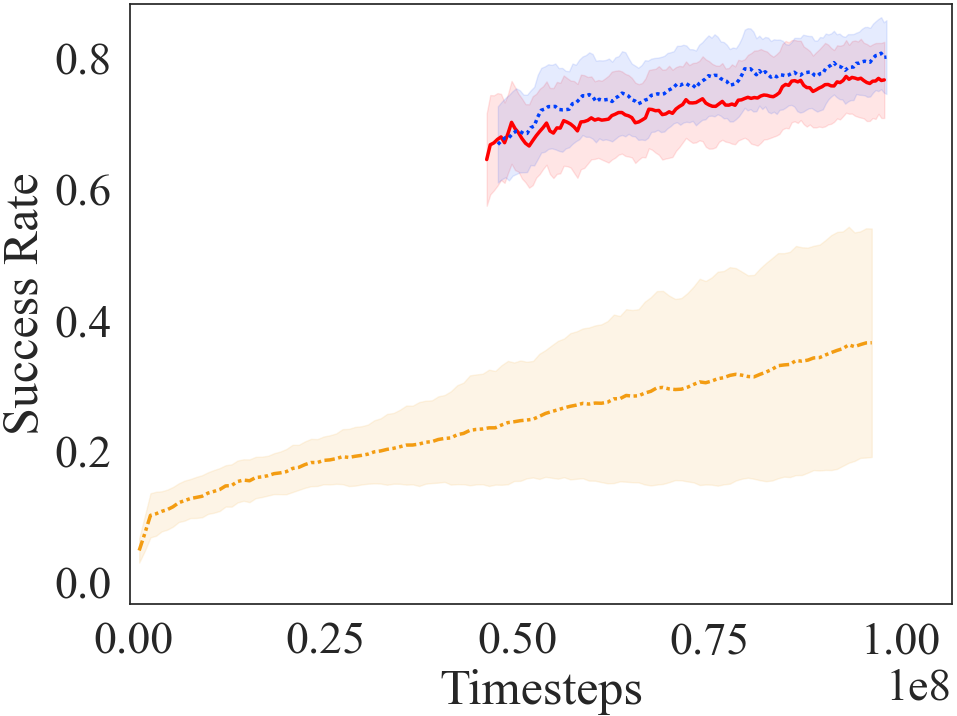
The results in Figs 4a and 4b show that the AC approach results in a substantial improvement in learning speed, and is comparable to the curriculum proposed by a human expert. Furthermore, as shown in Fig 4f, the curriculum transfer method outperforms the three baseline approaches222Refer Appendix Section A.5 for learning curves for reward in terms of learning speed. The learning curve for our curriculum transfer approaches has an offset on the x-axis to account for the time steps used to go through the curriculum before moving on to the target task, signifying strong transfer Taylor and Stone (2009). The other three baseline approaches perform better than learning from scratch, but do not outperform the curriculum transfer approach. Self-Play requires training a goal-proposing agent, which contributes to the sunk cost for learning. Whereas, Domain Adaptation relies on the similarity between the tasks. Teacher-Student curriculum learning requires defining the source tasks of the curriculum beforehand, and the teacher attempts to optimize the order of the tasks. All baselines involve interactions in the costly high-fidelity domain for generating/optimizing the curriculum, which proves to be costly. This sunk cost has been accounted in the learning curves by having an offset on the x-axis. See Appendix Section A.3 for details on our adaptation and tuning of these three baselines.
Table 1 compares the jumpstart values for AC with the baselines. The higher jumpstart, the better performance of the curriculum. AC achieves high positive jumpstart and time to threshold performance in comparison to baseline approaches, denoting improved performance and quicker learning (magnitude timesteps).
4.2. Results with Added Complexity
To answer the second question, we evaluated our framework in a situation where the target task in the HF environment is too difficult to learn from scratch. To do this, both the LF and HF environments were modified by adding a new type of object, “fire”, such that when the agent comes in contact with it, the episode terminates instantly with a reward of .
| Env | Methods | Jumpstart (Return) | Time-to-threshold |
|---|---|---|---|
| HF | AC Learning from scratch | 304 242 | 5.4 |
| AC Carr et. al. | 231160 | 3.5 | |
| AC Sukhbaatar et. al. | 85130 | 2.1 | |
| AC Matiisen et. al. | 568 205 | 6.3 | |
| HF w/ Fire | AC Learning from scratch | 628284 | 1.02 |
| AC Carr et. al. | 519126 | 8.4 | |
| AC Sukhbaatar et. al. | 28887 | 7.8 | |
| AC Matiisen et. al. | 346121 | 4.6 |
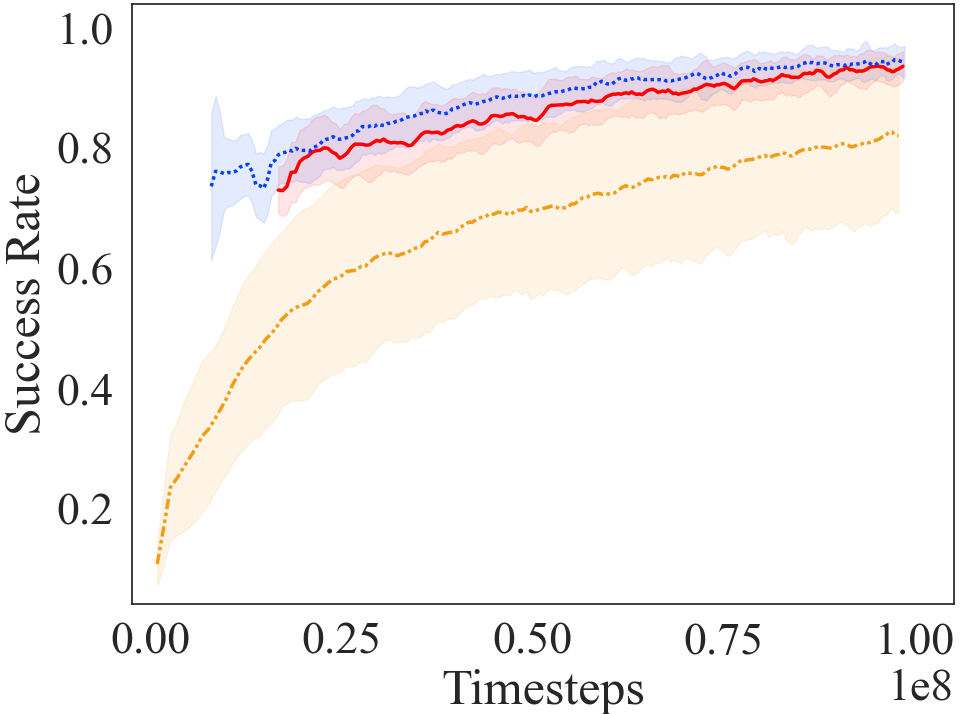
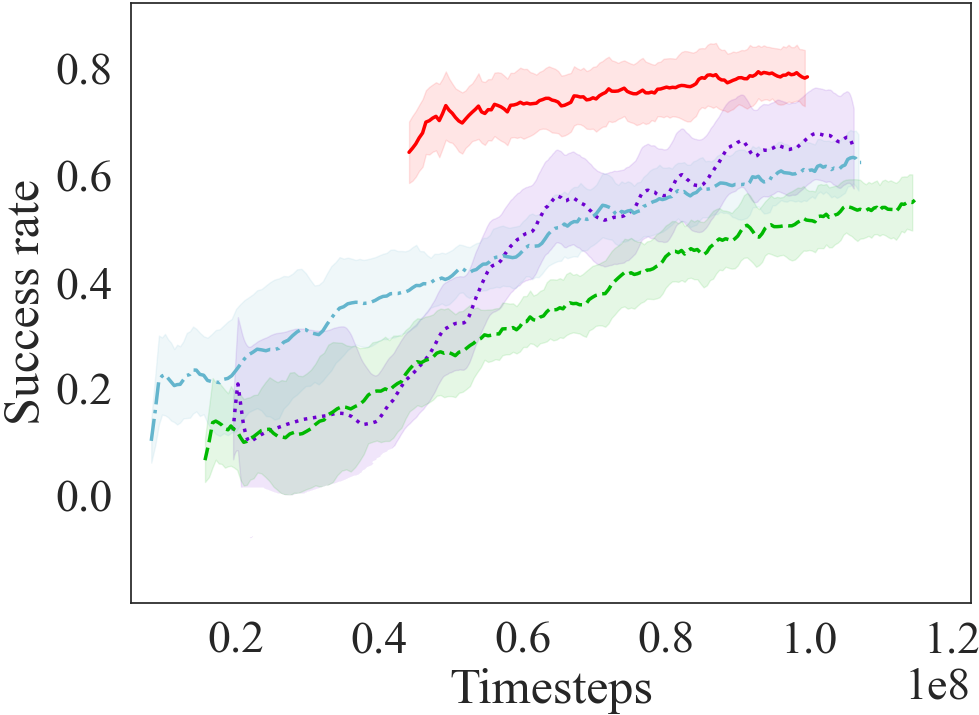
The parameters listed in Section 4.1 are used to optimize AC in the LF environment. From learning curves in Figs. 4d, 4e, 4f and Table 1, we observe our curriculum transfer approach, AC, consistently achieving higher average reward, better jumpstart and time to threshold performance compared to baselines. Learning from scratch fails to converge to a successful policy in interactions, while the other baseline achieves marginally better performance than learning from scratch. Table 1 summarizes the jumpstart and the time-to-threshold between the approaches. Our approach still achieves a high jumpstart, and converges much quicker than other approaches. Through this experiment, we see our AC approach extrapolates to challenging environments, producing quicker and efficient convergence. Refer Appendix section A.1.1 for trends observed in different runs in our AC approach.
4.3. Results with Different RL Algorithms
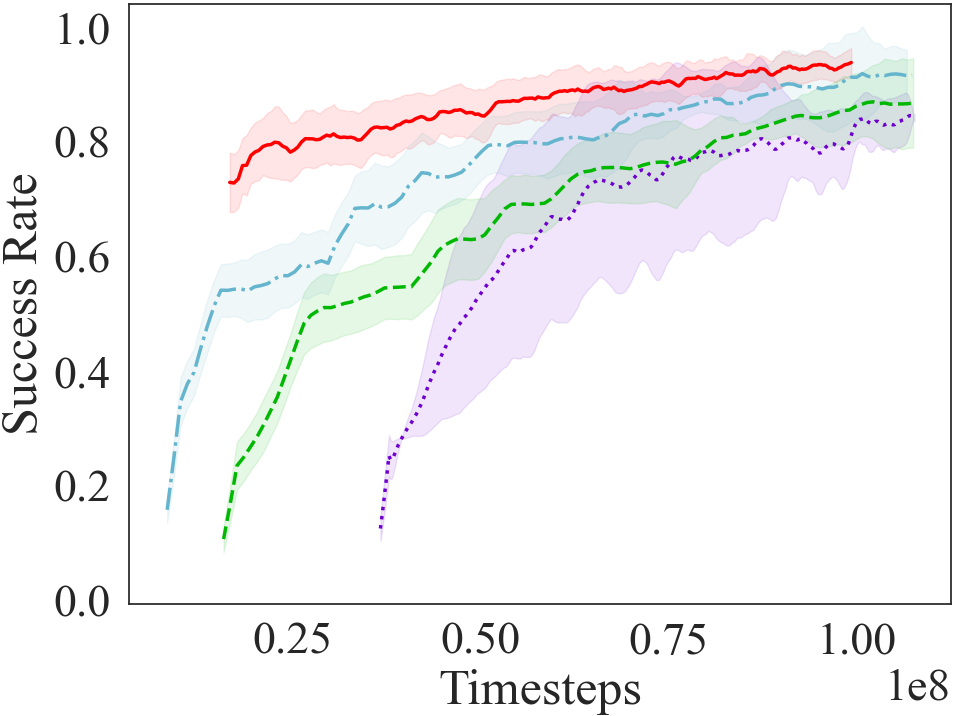
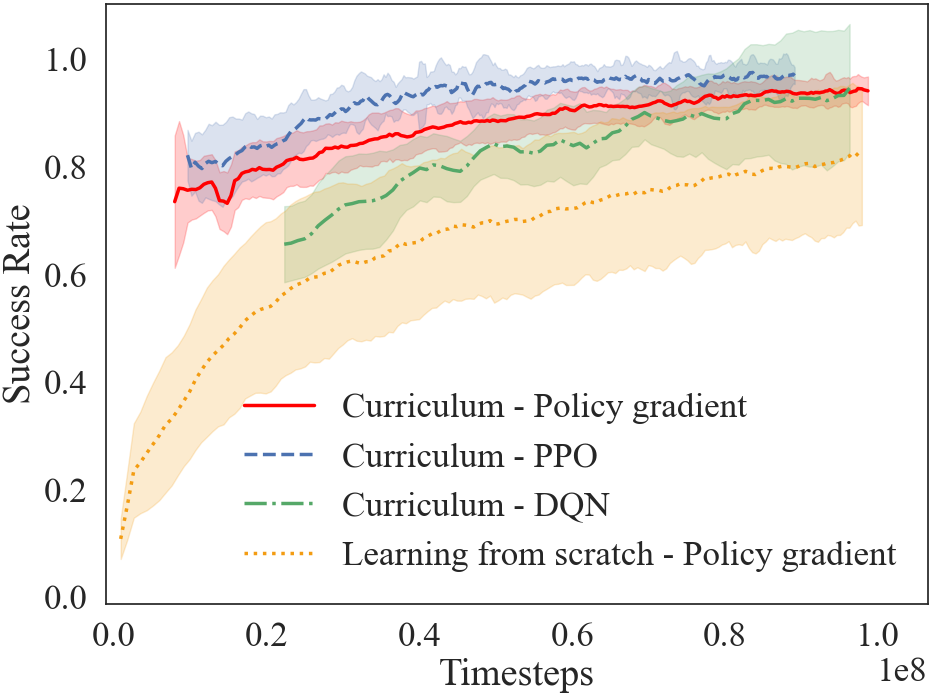
To answer the third question, we conducted experiments by making the HF learning algorithm different (PPO Schulman et al. (2017) and DQN Mnih et al. (2015)) from the RL algorithm used for generating the curriculum in the LF environment (Policy gradient). Fig 5 shows the result of this test (See Appendix A.4 for hyperparameters). In all the cases, learning through a curriculum is quicker and more efficient than learning from scratch. Here, we do not intend to find the best RL algorithm to solve the task, but demonstrate that actor-critic networks, policy gradients and value function based approaches learn the HF target task through curriculum, irrespective of the RL algorithm used to optimize the LF curriculum.
|
 |
 |
|---|---|---|
| (a) Noisy mappings - HF | (b) Noisy mappings - HF w/ Fire |
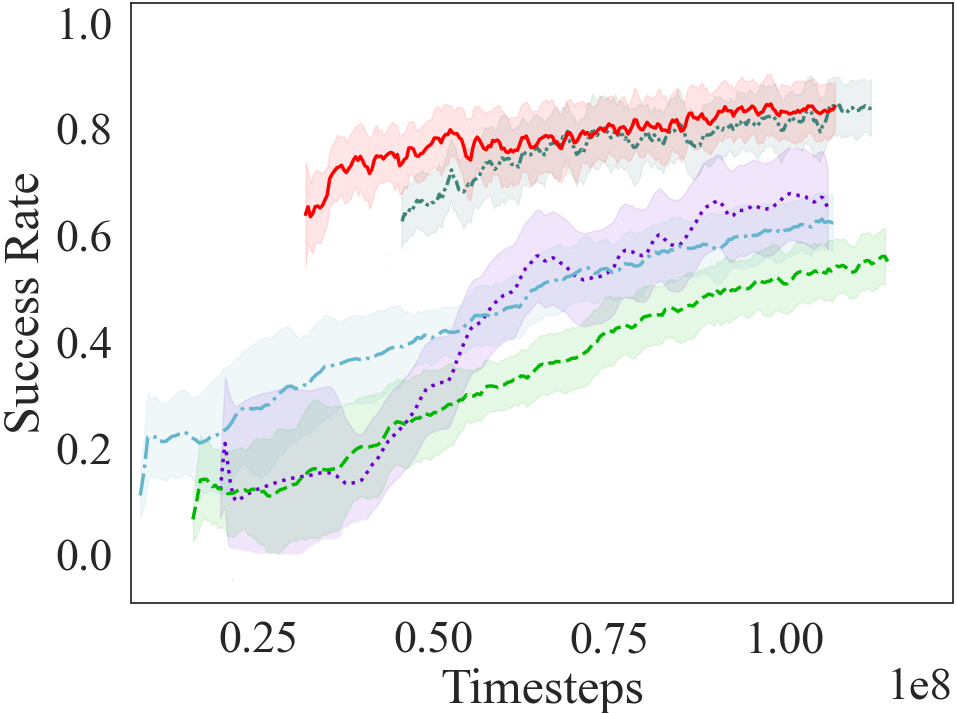
4.4. Noisy Mappings
In the above sections, we evaluated the curriculum transfer schema on accurate mappings between the two environments. In certain partially observable environments, it might not be possible to obtain such an accurate mapping between the two environments. To demonstrate the efficacy of our approach in imperfect mappings, we evaluate the experiments by incorporating noise in the mapping function. The noisy mapping function involves a multivariate noise over the range of the parametric variables. While obtaining the noisy parameters, we do not incorporate any noise in the parameter for the goal condition, as we can safely assume that the goals have been mapped accurately. The noisy mappings are given by:
where is the covariance matrix, which is symmetric and positive semi-definite, and , covers the entire range of the parametric variable in six standard deviations. We verify whether the noisy parameters meet the minimum requirements of reaching the goal for the sub-task. If the requirements are not met, we generate a new set of noisy parameters until the requirements are met.
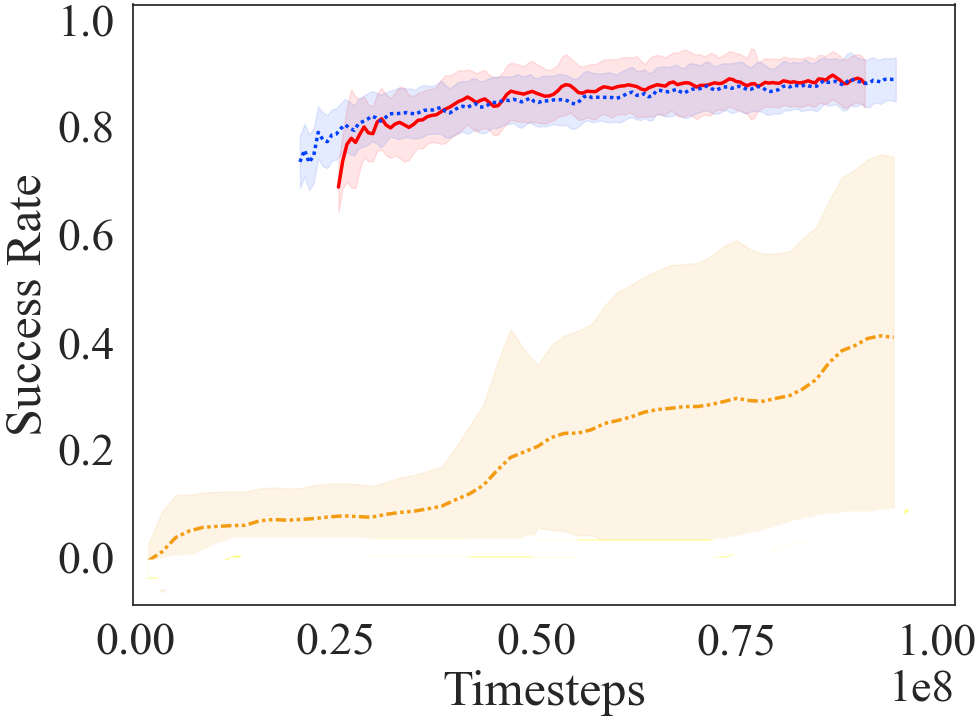
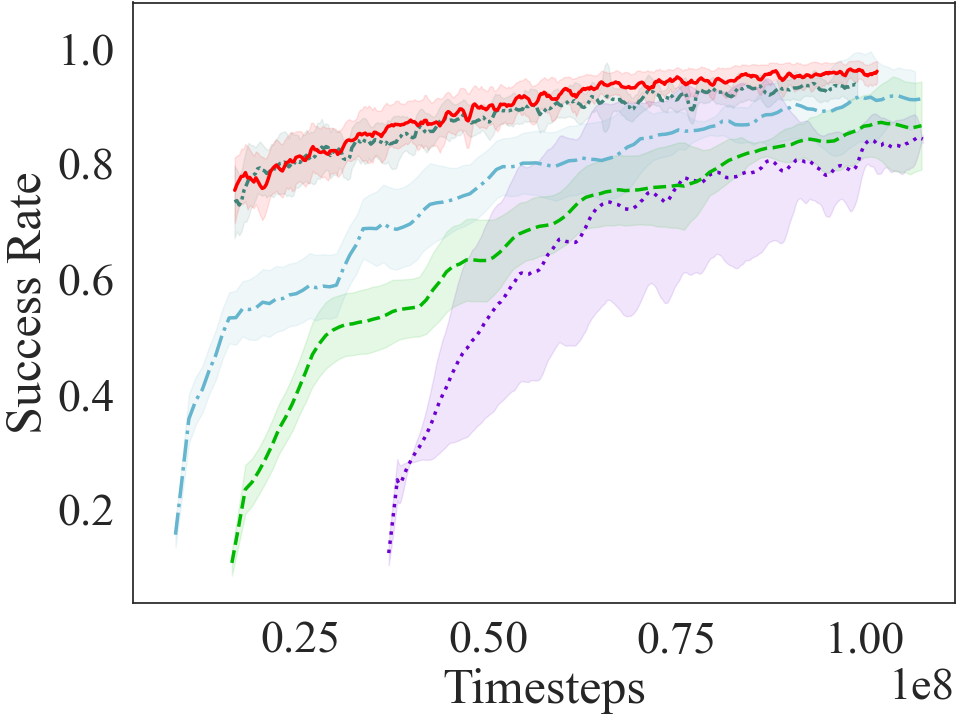
The learning curves for the automated curriculum transfer generated through noisy parameters are shown in Fig 6. We compare its performance with learning curves for automated curriculum transfer generated through exact mappings, and with other baseline approaches present in the literature. Even with noisy mappings, the automated curriculum transfer outperforms other curriculum approaches, and performs comparable to the automated curriculum transfer with exact mappings. On the complicated task (HF with Fire), the automated curriculum transfer with noisy mappings takes longer to converge on the source tasks of the curriculum, yet it achieves a significant performance advantage over other baselines.
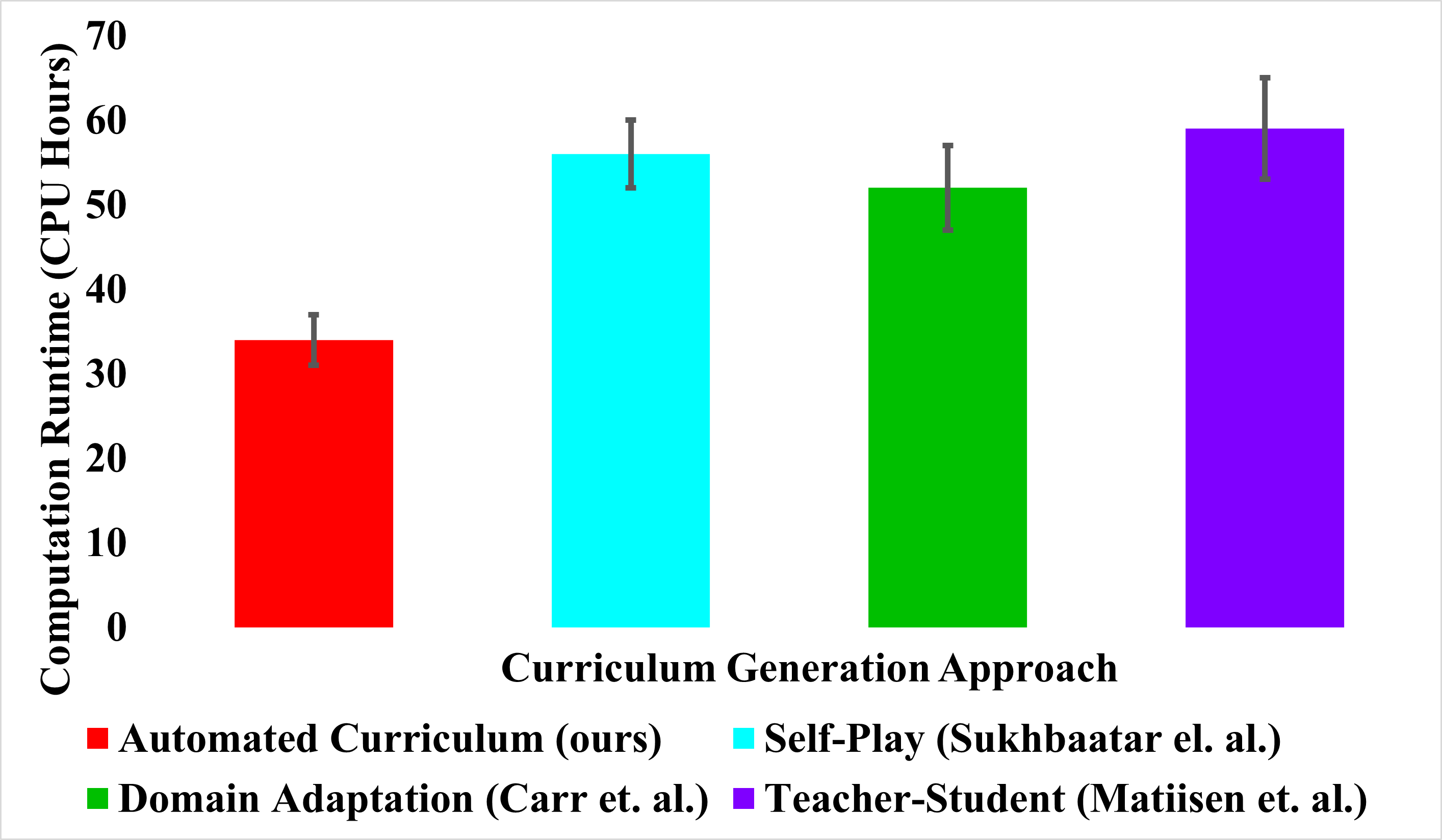
4.5. Runtime Comparison
Since our approach relies on the low-fidelity environment for curriculum generation, its sunk cost in computational runtime is significantly lesser than baseline approaches, in which curriculum generation requires extensive interactions in the costly high-fidelity environment. Fig 7 compares the computational runtime (in CPU Hours) required to run one trial (with each episode having a maximum of timesteps) of the high-fidelity task until the stopping criterion is met. The experiments were conducted using a 64-bit Linux Machine, having Intel(R) Core(TM) i9-9940X CPU @ 3.30GHz processor and 126GB RAM memory. The sunk cost of our automated curriculum transfer approach involves the interactions required to optimize the curriculum in the LF environment, and the interactions required to learn the source tasks in the HF environment.
5. Transfer to a Physical Robot
To answer the fourth question and demonstrate the efficacy of this approach in the real-world, we performed a Sim2Real transfer on a TurtleBot after the simulated robot had learned the target task through the curriculum. We demonstrate object breaking and item retrieval, followed by crafting, through a TurtleBot which reads fiducials scattered throughout the environment.
We made use of the TurtleBot 2, modified to have an on-board laptop (running Ubuntu 16.04 and ROS Kinetic) which interfaces with a camera (the Intel D435i) and a LIDAR unit (the Slamtec RPLIDAR-A2). These additional sensors were used to provide more stable odometry via the Canonical Scan Matcher Censi (2008), as the default odometry stack was found to have too much drift to be relied upon. The full platform is visible in Fig 2c. Making use of the modified odometry stack, movement was provided as actions that attempt movement in the approximate units expected by the high-fidelity environment.
In this setting, the target task policy learned through our automated curriculum transfer approach in the high-fidelity Crafter-TurtleBot environment is transferred to run in this physical setting. No learning is taking place on the agent as the physical experimentation continues. These fiducials are QR codes corresponding to the different possible objects in the known environment: trees, rocks, and the crafting table. When demonstrated, the agent controls the TurtleBot to navigate to the Tree locations before calling the break action, and is then visible navigating to the Rock locations before again calling the break action. The agent completes the sequence by navigating to the crafting table before calling the craft action. The policy is run without any modifications.
It is important to note that breaking and crafting actions are successful only in the event of reading the fiducial. In this way, we restrict the agent to being successful only in the cases where it has operated successfully in the physical environment, allowing the agent to proceed only in the event of a sensible Sim2Real transfer.
6. Conclusion and Future Work
We proposed a framework for automated curriculum transfer from an easy-to-solve environment to a real-world scenario. Our curriculum transfer approach generated results comparable to a curriculum generated by a human expert, exceeding the baseline performances. Our experimental evaluations show improved learning time and jumpstart performance on the final target task, even when additional challenging elements are introduced. We demonstrated ACuTE is independent of the RL algorithm used to generate the curriculum and is easily Sim2Real transferable to a physical robot setting and is also scalable to environments with inexact mappings.
An extension of our approach will be to scale the algorithm to multi-agent settings, with inter-agent curriculum transfer. A limitation of this work is that the task mapping is generated heuristically, a future work would involve automating the mapping generation. Future work can investigate how a LF version of the environment can be created autonomously, and providing a theoretical guarantee for the curriculum transfer approach. Second, while in this work we only transferred the schema of the curriculum, our baseline comparison with Domain Adaptation suggests that DA can be combined with curriculum transfer such that the agent can learn the tasks in the curriculum even faster. Finally, our algorithms for optimizing the curriculum in the LF environment did not make use of any data from the HF domain, and in future work, we plan to modify our framework to use interaction experience from both domains when constructing the curriculum.
The research presented in this paper was conducted with partial support from DARPA (contract W911NF-20-2-0006) and AFRL (contract FA8750-22-C-0501).
References
- (1)
- Abel et al. (2018) David Abel, Yuu Jinnai, Sophie Yue Guo, George Konidaris, and Michael Littman. 2018. Policy and value transfer in lifelong reinforcement learning. In International Conference on Machine Learning. PMLR, 20–29.
- Bengio et al. (2009) Yoshua Bengio, Jérôme Louradour, Ronan Collobert, and Jason Weston. 2009. Curriculum learning. In Proc.of the 26th annual Intl Conf. on machine learning. 41–48.
- Carr et al. (2019) Thomas Carr, Maria Chli, and George Vogiatzis. 2019. Domain Adaptation for Reinforcement Learning on the Atari. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems. 1859–1861.
- Censi (2008) Andrea Censi. 2008. An ICP variant using a point-to-line metric. In 2008 IEEE International Conference on Robotics and Automation. 19–25. https://doi.org/10.1109/ROBOT.2008.4543181
- Coumans and Bai (2019) Erwin Coumans and Yunfei Bai. 2016–2019. PyBullet, a Python module for physics simulation for games, robotics and machine learning. http://pybullet.org.
- Da Silva and Costa (2019) Felipe Leno Da Silva and Anna Helena Reali Costa. 2019. A survey on transfer learning for multiagent reinforcement learning systems. Journal of Artificial Intelligence Research 64 (2019), 645–703.
- Elman (1993) Jeffrey L Elman. 1993. Learning and development in neural networks: The importance of starting small. Cognition 48, 1 (1993), 71–99.
- Foglino et al. (2019) Francesco Foglino, Christiano Coletto Christakou, and Matteo Leonetti. 2019. An optimization framework for task sequencing in curriculum learning. In 2019 Joint IEEE 9th Intl Conf. on Development and Learning and Epigenetic Robotics (ICDL-EpiRob). IEEE, 207–214.
- Gao and Wu (2021) Yifan Gao and Lezhou Wu. 2021. Efficiently Mastering the Game of NoGo with Deep Reinforcement Learning Supported by Domain Knowledge. Electronics 10, 13 (2021), 1533.
- Josifovski et al. (2020) Josip Josifovski, Mohammadhossein Malmir, Noah Klarmann, and Alois and Knoll. 2020. Continual Learning on Incremental Simulations for Real-World Robotic Manipulation Tasks. In 2nd Workshop on Closing the Reality Gap in Sim2Real Transfer for Robotics at Robotics: Science and Systems (R:SS) 2020. Nicht veröffentlichter Vortrag. https://sim2real.github.io/assets/papers/2020/josifovski.pdf
- Karpathy and Van De Panne (2012) Andrej Karpathy and Michiel Van De Panne. 2012. Curriculum learning for motor skills. In Canadian Conference on Artificial Intelligence. Springer, 325–330.
- Kaspar et al. (2020) Manuel Kaspar, Juan David Munoz Osorio, and Jürgen Bock. 2020. Sim2Real Transfer for Reinforcement Learning without Dynamics Randomization. arXiv preprint arXiv:2002.11635 (2020).
- Kurkcu et al. (2020) Anil Kurkcu, Domenico Campolo, and Keng Peng Tee. 2020. Autonomous Curriculum Generation for Self-Learning Agents. In 2020 16th Intl Conf. on Control, Automation, Robotics and Vision (ICARCV). IEEE, 1104–1111.
- Lazaric (2012) Alessandro Lazaric. 2012. Transfer in reinforcement learning: a framework and a survey. In Reinforcement Learning. Springer, 143–173.
- Liu et al. (2019) Yong Liu, Yujing Hu, Yang Gao, Yingfeng Chen, and Changjie Fan. 2019. Value Function Transfer for Deep Multi-Agent Reinforcement Learning Based on N-Step Returns.. In IJCAI. 457–463.
- Liu and Stone (2006) Yaxin Liu and Peter Stone. 2006. Value-function-based transfer for reinforcement learning using structure mapping. In AAAI. 415–420.
- Lowerre (1976) Bruce T Lowerre. 1976. The HARPY speech recognition system. Technical Report. Carnegie Mellon University, PA, Department of Computer Science.
- Matiisen et al. (2020) Tambet Matiisen, Avital Oliver, Taco Cohen, and John Schulman. 2020. Teacher-Student Curriculum Learning. IEEE Trans. Neural Networks Learn. Syst. 31, 9 (2020), 3732–3740. https://doi.org/10.1109/TNNLS.2019.2934906
- Mnih et al. (2015) Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A. Rusu, Joel Veness, Marc G. Bellemare, Alex Graves, Martin Riedmiller, Andreas K. Fidjeland, Georg Ostrovski, Stig Petersen, Charles Beattie, Amir Sadik, Ioannis Antonoglou, Helen King, Dharshan Kumaran, Daan Wierstra, Shane Legg, and Demis Hassabis. 2015. Human-level control through deep reinforcement learning. Nature 518, 7540 (Feb. 2015), 529–533. https://doi.org/10.1038/nature14236
- Narayan et al. (2017) Akshay Narayan, Zhuoru Li, and Tze-Yun Leong. 2017. SEAPoT-RL: selective exploration algorithm for policy transfer in RL. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 31.
- Narvekar et al. (2020) Sanmit Narvekar, Bei Peng, Matteo Leonetti, Jivko Sinapov, Matthew E Taylor, and Peter Stone. 2020. Curriculum Learning for Reinforcement Learning Domains: A Framework and Survey. J. of Machine Learning Research 21 (2020), 1–50.
- Narvekar et al. (2017) Sanmit Narvekar, Jivko Sinapov, and Peter Stone. 2017. Autonomous Task Sequencing for Customized Curriculum Design in Reinforcement Learning.. In IJCAI. 2536–2542.
- Peng et al. (2018) Xue Bin Peng, Marcin Andrychowicz, Wojciech Zaremba, and Pieter Abbeel. 2018. Sim-to-real transfer of robotic control with dynamics randomization. In 2018 IEEE Intl. Conf. on robotics and automation (ICRA). IEEE, 1–8.
- Qiao et al. (2018) Zhiqian Qiao, Katharina Muelling, John M Dolan, Praveen Palanisamy, and Priyantha Mudalige. 2018. Automatically generated curriculum based reinforcement learning for autonomous vehicles in urban environment. In 2018 IEEE Intelligent Vehicles Symposium (IV). IEEE, 1233–1238.
- Rostami et al. (2020) Mohammad Rostami, David Isele, and Eric Eaton. 2020. Using task descriptions in lifelong machine learning for improved performance and zero-shot transfer. Journal of Artificial Intelligence Research 67 (2020), 673–704.
- Sanger (1994) Terence D Sanger. 1994. Neural network learning control of robot manipulators using gradually increasing task difficulty. IEEE transactions on Robotics and Automation 10, 3 (1994), 323–333.
- Schulman et al. (2017) John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. 2017. Proximal Policy Optimization Algorithms. CoRR abs/1707.06347 (2017). arXiv:1707.06347 http://arxiv.org/abs/1707.06347
- Silva and Costa (2018) Felipe Leno Da Silva and Anna Helena Reali Costa. 2018. Object-oriented curriculum generation for reinforcement learning. In Proc.of the 17th Intl Conf. on Autonomous Agents and MultiAgent Systems. 1026–1034.
- Sinapov et al. (2015) Jivko Sinapov, Sanmit Narvekar, Matteo Leonetti, and Peter Stone. 2015. Learning inter-task transferability in the absence of target task samples. In Proc.of the 2015 Intl Conf. on Autonomous Agents and Multiagent Systems. 725–733.
- Sukhbaatar et al. (2018) Sainbayar Sukhbaatar, Zeming Lin, Ilya Kostrikov, Gabriel Synnaeve, Arthur Szlam, and Rob Fergus. 2018. Intrinsic Motivation and Automatic Curricula via Asymmetric Self-Play. In International Conference on Learning Representations.
- Taylor and Stone (2009) Matthew E Taylor and Peter Stone. 2009. Transfer learning for reinforcement learning domains: A survey. J. of Machine Learning Research 10, 7 (2009).
- Tobin et al. (2017) Josh Tobin, Rachel Fong, Alex Ray, Jonas Schneider, Wojciech Zaremba, and Pieter Abbeel. 2017. Domain randomization for transferring deep neural networks from simulation to the real world. In 2017 IEEE/RSJ Intl Conf. on Intelligent Robots and Systems (IROS). IEEE, 23–30.
- Williams (1992) Ronald J Williams. 1992. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning 8, 3-4 (1992), 229–256.
- Wu et al. (2018) Yuechen Wu, Wei Zhang, and Ke Song. 2018. Master-Slave Curriculum Design for Reinforcement Learning.. In IJCAI. 1523–1529.
- Zhang et al. (2020a) Yunzhi Zhang, Pieter Abbeel, and Lerrel Pinto. 2020a. Asymmetric self-play for automatic goal discovery in robotic manipulation. Advances in Neural Information Processing Systems Deep Reinforcement Learning Workshop (2020).
- Zhang et al. (2020b) Yunzhi Zhang, Pieter Abbeel, and Lerrel Pinto. 2020b. Automatic curriculum learning through value disagreement. Advances in Neural Information Processing Systems 33 (2020).