Adaptive Model Predictive Control with Data-driven Error Model for Quadrupedal Locomotion
Abstract
Model Predictive Control (MPC) relies heavily on the robot model for its control law. However, a gap always exists between the reduced-order control model with uncertainties and the real robot, which degrades its performance. To address this issue, we propose the controller of integrating a data-driven error model into traditional MPC for quadruped robots. Our approach leverages real-world data from sensors to compensate for defects in the control model. Specifically, we employ the Autoregressive Moving Average Vector (ARMAV) model to construct the state error model of the quadruped robot using data. The predicted state errors are then used to adjust the predicted future robot states generated by MPC. By such an approach, our proposed controller can provide more accurate inputs to the system, enabling it to achieve desired states even in the presence of model parameter inaccuracies or disturbances. The proposed controller exhibits the capability to partially eliminate the disparity between the model and the real-world robot, thereby enhancing the locomotion performance of quadruped robots. We validate our proposed method through simulations and real-world experimental trials on a large-size quadruped robot that involves carrying a 20 kg un-modeled payload (84% of body weight).
I INTRODUCTION
Quadruped robots’ promising application potential lets them become a research hotspot in the robotic field, and numerous research outcomes about it have sprung up in recent years [1] -[4]. For the model-based control of the quadruped robot, the controller is designed based on the robot’s dynamic model, which necessitates accurate model parameters. However, on the one hand, these parameters come from computer-aided design (CAD) software or simplified models due to computation costs in most real-world applications. On the other hand, certain parts of the system are challenging to include in physical models: 1) Friction in mechanical transmission; 2) Nonlinear output from the actuator; 3) Mechanical deformation under impact; 4) Unknown disturbances from the environment (such as un-modeled payload). These facts can result in inaccuracies in the control model. Although the controller’s robustness may enable it to operate despite the defect model, these constraints can negatively impact the locomotion performance of robots in real-world scenarios.
The objective of this paper is to employ real-world data to address the issue of model uncertainty in a model-based controller. The measurements extracted from onboard sensors can be considered as ground truth to some extent, and they reveal the defective part of the model. Thus, we propose to construct an error model by data-driven method in the view of time-series analysis, then use it to anticipate future errors and correct them proactively. In such ways, the real-world quadrupedal locomotion can be improved even under un-modeled payloads.


I-A Related Work
Model Predictive Control
Model-based control methods, particularly Model Predictive Control (MPC), have garnered significant attention in recent research on quadruped robot control. It has demonstrated impressive performance in controlling quadruped robots. For instance, the MIT Cheetah 3 and Mini-Cheetah, utilizing convex MPC, achieves robust locomotion in different gaits (e.g., trot, bound, gallop) [1], [2]. However, it is worth noting that their works are based on the simplifying assumption of a Single Rigid Body (SRB), due to the trade-off between model accuracy and computational cost in MPC. To address this, there are some researches about adopting a full-dynamic system model that implements Nonlinear Model Predictive Control (NMPC) in quadruped robots to improve control accuracy [5], [6].
Adaptive Control
This approach tackles the time-varying model by adjusting the model or control parameters online. To illustrate, the IIT group employs an offline and online identification algorithm on HyQ using a recursive approach [7]. Minniti et al. develop an adaptive Control Lyapunov Functions and Model Predictive Control (CLF-MPC) framework in ANYmal that ensures stability and allows for online convergence of the robot’s body inertial and mass parameters [8]. Sombolestan et al. present an adaptive force control for quadrupedal locomotion under uncertainties[9]. In addition, in [10], a robust model predictive control (RMPC) utilizes Reinforcement Learning (RL) to train a neural network that outputs uncertainties for a reduced-order model. Similarly, in the work by [11], an online training residual model is used to correct the nominal model in MPC, which enables the Unitree A1 robot to carry a 10 kg payload.
Physics-Data Hybrid Control
Due to the complexity of a real-world robotic system, some parts of it cannot be expressed by functions of physical laws. To solve this problem, some researchers have used data-driven models that describe these parts of the system and combined them with physics-based models to achieve better control of real-world robots [12] -[15].
I-B Contribution
The summary of our main contributions is as follows:
-
•
We use a data-driven method for quadrupedal locomotion by time-series data to tackle model uncertainties. Due to the periodic locomotion characteristic, the method exhibits a remarkable capability to provide highly accurate predictions for future data.
-
•
We propose a novel control framework for quadruped robots where the data-driven error model is combined with MPC. It can help the controller to have a better estimate of future robot states even under MPC with a defect model, then adjust desired inputs for the robot.
-
•
We validate our controller in various simulations and real-world experiments on our quadruped robot Sirius-belt. The hardware tests showcase that the robot with the proposed control framework is able to trot forward stably while carrying a 20 kg un-modeled payload (84% of body weight) as shown in Fig. 1. Our method can not only reduce tracking errors but also the vibration amplitude of robot states under dynamic uncertainties.
II MPC with Error Model
In this section, we present the integration of the error model, derived from the Autoregressive Moving Average Vector (ARMAV) model [16], into the traditional MPC framework for quadruped robots.
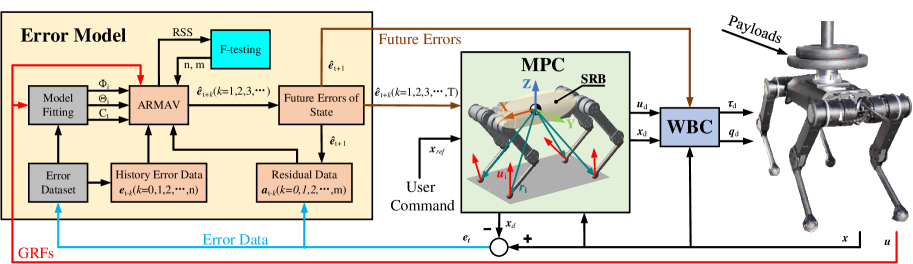
.
II-A Linearized Dynamic Model
In the context of Model Predictive Control (MPC) applied to quadruped robots, commonly the robot’s body is treated as a Single Rigid Body (SRB) and the state of the robot can be defined as follows:
| (1) |
Where are the Euler angles, positions, angle velocities, and linear velocities of robot body in the world frame, is the gravitational acceleration.
In each control cycle of the MPC algorithm, the future behavior of the robot is predicted using the floating base model, and its discrete-time formulation [1] is as follows:
| (2) |
Where is the states of the robot at time step , are Ground React Forces (GRFs) which are inputs of the system at time step , is the matrix related with states at time step , and is the matrix about inputs at time step .
The equation (2) is based on the model of the robot body after being linearized and simplified (ignoring the dynamic of legs). In real-world scenarios, practical robots inevitably exhibit deviations from this model as mentioned before.
II-B Integrating Error Model into MPC
The primary sensors commonly employed in quadruped robots are the inertial measurement unit (IMU) and encoders, which provide measurements of essential robot states, such as Euler angles and body height. These sensor measurements are reasonable approximations of the true values of these states. Consequently, our focus lies in constructing the error model based on these sensor data.
In this paper, An ARMAV error model fitted from sensor data is implemented in traditional MPC to compensate for errors of dynamics uncertainties. By using estimated GRFs as indicators to predict potential state errors, we modify the method to improve its performance in quadruped robot applications. The modified ARMAV() error model has the following form (derived from the procedure outlined in Section III-B and III-C):
| (3) |
Where is the error of robot state at time step , is autoregression (AR) parameters of the model, is the moving average (MA) parameters of the model, , are the matrix about AR and MA model respectively, is the matrix related with inputs in the error model.
Based on the error model (3) and obtaining predicted values of future state errors which is illustrated in Section III-A, the robot states after compensation are expressed as follows:
| (4) |
Where is the select matrix for error model.
Quadruped robot locomotion entails the critical task of regulating the position and orientation of the robot’s body, commonly referred to as robot states, in accordance with the desired commands. Based on the future states of the robot, MPC outputs the suitable GRFs to attain the desired robot states via optimization. This quadratic programming problem can be formulated as below:
| (5a) | ||||
| (5b) | ||||
| (5c) | ||||
| (5d) | ||||
| (5e) | ||||
Where is the predict horizon, is the stage quadratic cost function, is the current state at time step , is the predicted state at time step based on linear body dynamic, and are general equality, inequality constraints respectively.
The overall control framework is illustrated in Fig. 2. The procedure is that the error model is derived from the error data collected in the sensors on the robot within every control cycle and the model uses historical data to predict future state errors. Subsequently, the Controller leverages these prognostic state errors to effectuate compensatory adjustments, countering discrepancies arising from the control model. The compensation strategy is twofold: 1. The error model employs a multi-step prediction approach to mitigate disparities within the MPC; 2. One step-ahead prediction is used to compensate for the Whole-body Control (WBC).
III ARMAV Model
The objective of this section is to introduce the methodology of the ARMAV model based on time-series data.
III-A Model Structure
The ARMAV model[16] is a widely used statistical method for analyzing and predicting time series data. It has been successfully applied in various fields such as marketing prediction[17], manufacturing [18], resources management [19, 20], and so forth. One of its key strengths lies in its ability to capture and predict periodic behavior. Given that the locomotion of our quadruped robots exhibits periodic patterns, the ARMAV model is well-suited for error prediction in this context. The formulation of the ARMAV() model is presented below:
| (6) | |||
where represents the data sample at time step , is the residual modeling noise at time step , is the parameters matrix related with AR model and is the parameters matrix about MA model.
The update of and one-step ahead prediction of ARMAV() model can be obtained as the following equation:
| (7) | |||
| (8) |
Where is the predicted value for time step .
As for k-step ahead prediction, it is derived from iteration which means that the next predicted values are based on the before predicted values as well as real data:
| (9) | ||||
| (10) |
III-B Modeling Method
Due to the nonlinearity of the ARMAV() model, parameter estimation is a non-linear problem. A viable solution is to obtain the initial guess values through the inverse function of ARMAV():
| (11) |
Where is the inverse coefficient.
In the inverse function form of the ARMAV model, the relations in and expressed by the inverse coefficients are linear for an arbitrary ARMAV() model. Since coefficients are AR parameters of the infinite expansion of the ARMAV model, it can be estimated well by the Least-Squares (LS) approach.
Substituting for from equation (11) in equation (6), the relation between , and can be expressed as following:
| (12) |
Where is identity matrix and is back shift operator (for instance, ).
Equating the coefficients of equal powers of , the following is obtained:
| (13) |
Where it is assumed that for and for .
According to equation (13), for the particular case of it can be derived:
| (14) |
It is straightforward that once estimated values of inverse coefficients are known the initial values of AR parameters as well as MA parameters can be derived from equation (13) and (14). The initial guess of is given from pure AR() model:
| (15) |
Based on the estimates of in AR() model, is derived from equation (14). Then by substituting these in equation (13), the explicit solution of is got. Since the initial values of are derived from equation (14) that requires , for getting all the , it is reasonable to take the order of AR() model as:
| (16) |
III-C Checking Criterion
One of the reasons why the ARMAV model is so popular is that it is always possible to represent the dynamics of a stable stationary stochastic system with the ARMAV() model, which means that only if the order of system and increases can the error of the model decrease into as small as we want. This flexibility allows for fitting the data to different orders of the ARMAV model based on the complexity of the system and the desired level of accuracy.
The reduced trend of residual sum of squares (RSS) is a good indicator to evaluate the adequacy of the model, when RSS drops significantly which means that the model may not be enough and the order of ARMAV() should be increased. F checking criterion [16] is an indicator to evaluate the drop trend of RSS :
| (17) |
Where is the smaller RSS in the unrestricted model, is the larger RSS in the restricted model, is the number of restricted parameters, is the number of samples, is the number of estimated parameters, and is F-distribution with and degrees of freedom. If , RSS can be regarded as drop significantly with confidence .
The procedure of the F-testing method based on equation (17) is used to choose the order of the ARMAV model. The first step is to determine the AR order by comparing the RSS of ARMAV() and ARMAV() starting from . Then, the MA order is reduced to determine the desired value by a similar method. At last, the autocorrelation of residuals with lag should be confirmed:
| (18) |
IV Simulation
This section focuses on evaluating the performance of the proposed controller in an open-source simulation environment [21].
IV-A Inaccuracy Model Parameters Situation
In this case, to assess the performance of the proposed controller when model parameters are inaccurate, two groups have been established: 1. the control model is perfect (ground truth case); 2. the mass of the model is set to 34.7 kg (the real mass of the robot is 23.7 kg).
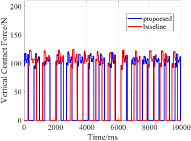
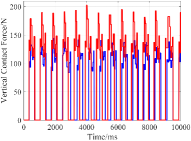
The locomotion performances of quadruped robots in two cases are compared based on the displacement of CoM and the GRFs in the vertical direction. The comparative outcomes are visually presented in Fig. 3 and Fig. 4.
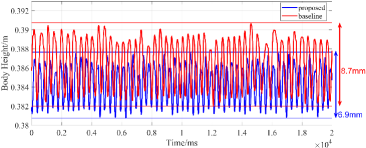
In the simulation, the robot’s desired body height is set to 0.38 m. Fig. 3 shows that the error model helps to bring the robot’s state closer to the desired value, and reduces the vibration amplitude of the body height for both cases. For the perfect model case, errors mostly arise from the model’s simplified and linearized process. Therefore, the error model only achieves a slight improvement of locomotion by reducing 21.7% vibration of CoM, from 8.7 mm to 6.9 mm. In the inaccurate mass case, there is an 11 kg gap in the mass parameter between the robot and the model. This is the reason why the body height vibrates largely. By adding the error model, this model inaccuracy is compensated and its CoM vertical vibration is decreased by 41.4%, from 18.6 mm to 10.9 mm. Fig. 4 shows that the error model helps MPC adjust the GRFs to achieve more suitable values for such improvement. In conclusion, the error model can improve the locomotion performance of the robot in both cases, and the improvement is more obvious under the inaccurate model parameter situation.
IV-B Un-modeled Payload Situation
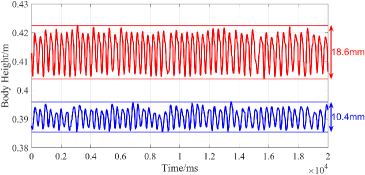
For the quadruped robot in the real world, transporting various payloads is one of its common applications. However, the parameters of payload such as mass are random depending on application scenarios and it is difficult to be included in the control model in advance. To simulate such a situation, in this part, an un-modeled payload is applied to the robot body.
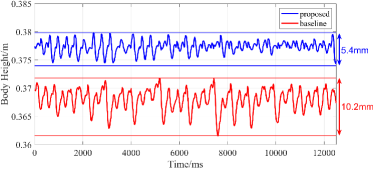
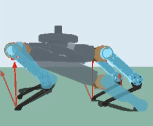
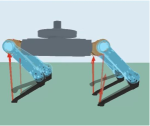
In the simulation, an 8 kg payload is exerted on the robot body, which is excluded from the control model. The vibration of body height under this situation is shown in Fig. 5(a). The baseline controller fails to restore the robot to the desired state, as the payload is not modeled, and the body height remains below the desired value of 0.38 m. On the other hand, the proposed controller has a noticeable effect in raising the body height to the desired value while simultaneously reducing the vibration by 47.1%. Additionally, as shown in Fig. 5(b) and Fig. 5(c), the performance of the robot with the baseline controller is less stable compared to the robot with the proposed controller and it falls down after 30 seconds of trotting. In conclusion, the proposed controller can make the robot attain the desired body height, reduce the vibration of CoM, and ensure stable trotting even under an unknown payload in the simulation.
V Experimental Results
In this section, we validate our proposed controller in real-world experiments by comparing it with linear MPC.
V-A Experimental Setup
The experiments are all implemented in our quadruped robot Sirius-Belt. Each leg of the robot consists of three degrees of freedom (DoFs) actuated by three electric motors. So Sirius-Belt has a total of 18 DoFs. The dimension (LengthWidthHeight) of the robot is m (fully standing). The maximum torque for knee joint actuators (Gear Ratio: 9 to 1) and hip joint actuators (Gear Ratio: 6 to 1) are 38 Nm and 30 Nm respectively. The controller runs in an onboard Upboard (ATOM x5-Z8350).
V-B Error Model Setup
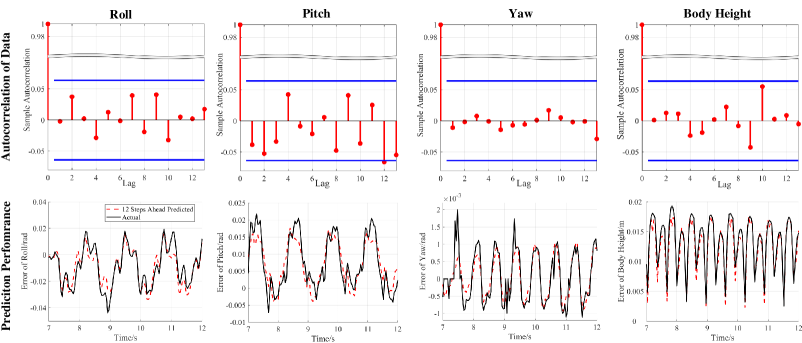
Real-world data are collected from the actual robotic system during trotting. By equation (18), the residuals autocorrelation of Euler angles and body height in the error model is depicted in the up part of Fig. 6. It can be seen that the autocorrelation of residuals between different times are all within the boundary of and (blue lines in Fig. 6), which can prove that residuals in error model can be regarded as uncorrelated data with mean zero and variance . The below part of Fig. 6 shows 12 (which is our MPC predicted horizon) steps ahead of predicted values from the error model in Euler angles and body height which are very close to the true values of the real-world robot.
V-C Results
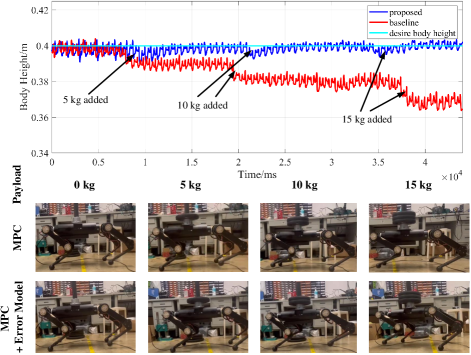
In the first hardware experiment, the payload from 5 kg to 15 kg is added on the Sirius-Belt during trotting in place one by one. Concurrently, the data of real robot states in the baseline controller and proposed controller are recorded to evaluate their performance. The body height of the robot during the experiment is shown in Fig. 7.
Table. I shows the performance of the proposed controller and baseline in the real-world experiment by Mean Absolute Error (MAE) and Mean Squared Error (MSE). It reveals that the proposed controller exhibits improved state tracking performance for roll, pitch, and body height in comparison to the baseline controller. However, it indicates that no significant effect is observed in the yaw state due to its pretty small errors.
| Method | Roll | Pitch | Yaw | Body Height |
|---|---|---|---|---|
| Baseline | 0.008 | 0.014 | 3e-4 | 5kg: 0.011(1.1e-4) |
| (1.6e-4) | (2.4e-4) | 10kg: 0.02(3.9e-4) | ||
| 15kg: 0.03(0.001) | ||||
| Proposed | 0.005 | 0.008 | 3e-4 | 5kg: 0.002(7.0e-6) |
| (4.6e-5) | (7.6e-5) | 10kg: 0.001(3.4e-6) | ||
| 15kg: 0.001(2.4e-6) |
The second experiment is to evaluate the performance of the proposed controller in the robot’s forward trotting. The results shown in Fig. 1 prove that the proposed controller enables the Sirius-Belt carrying a 20 kg un-modeled payload to achieve a stable forward trotting, where the mean of CoM height is 0.397 m (the desired value is 0.4 m) with standard deviation (STD) of 0.0011 m. However, the counterpart with the baseline controller is unstable even in a 10 kg payload (mean = 0.369 m and STD = 0.0035 m).
The obtained results validate the effectiveness of the proposed controller in facilitating stable trotting for the robot, even when confronted with un-modeled payloads. Notably, the robot with the proposed controller consistently maintains the desired body height throughout the experiments. This capability proves advantageous when the robot is tasked with carrying heavy loads, as it prevents excessive strain on the knee actuators.
VI CONCLUSIONS
In this paper, we present a novel controller that unifies MPC with a data-driven error model for improving the locomotion of quadruped robots. The error model is established based on the real data from sensors by the ARMAV model. This model has demonstrated an ability to accurately forecast forthcoming robot state errors by leveraging historical data and it proactively compensates for the state tracking of MPC and WBC. Besides, in the proposed controller, the error model runs concurrently with MPC, while it doesn’t change control laws in MPC. Through such ways, the error model can increase the state tracking performance of MPC and will not eliminate the MPC’s own robustness. The proposed controller can, to some degree, deal with the problems caused by the model’s inaccuracy, linearization, and simplification in MPC. The simulation results of Section IV show that the proposed controller significantly improves the locomotion performance of the quadruped robot during trotting both in situations of inaccurate model parameters and carrying payloads. Finally, the hardware test validate that the Sirius-Belt carrying a 20 kg un-modeled payload with the proposed controller can achieve more stable forward trotting compared with the baseline controller.
References
- [1] Di Carlo, Jared, et al. ”Dynamic locomotion in the MIT cheetah 3 through convex model-predictive control.” 2018 IEEE/RSJ international conference on intelligent robots and systems (IROS). IEEE, 2018.
- [2] Kim, Donghyun, et al. ”Highly dynamic quadruped locomotion via whole-body impulse control and model predictive control.” arXiv preprint arXiv:1909.06586 (2019).
- [3] Song, Zhitao, et al. ”An Optimal Motion Planning Framework for Quadruped Jumping.” 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2022.
- [4] Feng, Gilbert, et al. ”Genloco: Generalized locomotion controllers for quadrupedal robots.” Conference on Robot Learning. PMLR, 2023.
- [5] Neunert, Michael, et al. ”Whole-body nonlinear model predictive control through contacts for quadrupeds.” IEEE Robotics and Automation Letters 3.3 (2018): 1458-1465.
- [6] Meduri, Avadesh, et al. ”Biconmp: A nonlinear model predictive control framework for whole body motion planning.” IEEE Transactions on Robotics 39.2 (2023): 905-922.
- [7] Tournois, Guido, et al. ”Online payload identification for quadruped robots.” 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2017.
- [8] Minniti, Maria Vittoria, et al. ”Adaptive CLF-MPC with application to quadrupedal robots.” IEEE Robotics and Automation Letters 7.1 (2021): 565-572.
- [9] Sombolestan, Mohsen, Yiyu Chen, and Quan Nguyen. ”Adaptive force-based control for legged robots.” 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2021.
- [10] Pandala, Abhishek, et al. ”Robust predictive control for quadrupedal locomotion: Learning to close the gap between reduced-and full-order models.” IEEE Robotics and Automation Letters 7.3 (2022): 6622-6629.
- [11] Sun, Yu, et al. ”Online learning of unknown dynamics for model-based controllers in legged locomotion.” IEEE Robotics and Automation Letters 6.4 (2021): 8442-8449.
- [12] Yang, Wen-Shan, Wei-Chun Lu, and Pei-Chun Lin. ”Legged robot running using a physics-data hybrid motion template.” IEEE Transactions on Robotics 37.5 (2021): 1680-1695.
- [13] Fawcett, Randall T., et al. ”Toward a data-driven template model for quadrupedal locomotion.” IEEE Robotics and Automation Letters 7.3 (2022): 7636-7643.
- [14] Chang, Alexander H., et al. ”Learning to jump in granular media: Unifying optimal control synthesis with Gaussian process-based regression.” 2017 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2017.
- [15] Torrente, Guillem, et al. ”Data-driven MPC for quadrotors.” IEEE Robotics and Automation Letters 6.2 (2021): 3769-3776.
- [16] Pandit, Sudhakar Madhavrao, Shien‐Ming Wu, and Talivaldis I. Šmits. ”Time Series and System Analysis with Applications by Sudhakar Madhavrao Pandit and Shien‐Ming Wu.” (1984): 1924-1925.
- [17] Xu, Weijun, et al. ”Forecasting energy consumption using a new GM–ARMA model based on HP filter: The case of Guangdong Province of China.” Economic Modelling 45 (2015): 127-135.
- [18] Aghdam, B. H., M. Vahdati, and M. H. Sadeghi. ”Vibration-based estimation of tool major flank wear in a turning process using ARMA models.” The International Journal of Advanced Manufacturing Technology 76 (2015): 1631-1642.
- [19] Shafaei, Maryam, and Ozgur Kisi. ”Lake level forecasting using wavelet-SVR, wavelet-ANFIS and wavelet-ARMA conjunction models.” Water Resources Management 30 (2016): 79-97.
- [20] Erdem, Ergin, and Jing Shi. ”ARMA based approaches for forecasting the tuple of wind speed and direction.” Applied Energy 88.4 (2011): 1405-1414.
- [21] Di Carlo, Jared. Software and control design for the MIT Cheetah quadruped robots. Diss. Massachusetts Institute of Technology, 2020.