Adiabatic model of reactions with expicitly energy-dependent non-local potentials.
Abstract
We have developed an approximate way of dealing with explicit energy-dependence of non-local nucleon optical potentials as used to predict the cross sections within the adiabatic theory. Within this approximation, the non-local optical potentials have to be evaluated at an energy shifted from half the incident deuteron energy by the kinetic energy averaged over the range of the interaction and then treated as an energy-independent non-local potential. Thus the evaluation of the distorting potential in the incident channel is reduced to a problem solved in our previous work in [Phys. Rev. Lett. 110, 112501(2013) and Phys. Rev. C 87, 064610 (2013)]. We have demonstrated how our new model works for the case of 16OO, 36Ar(Ar and 40CaCa reactions and highlighted the need for a detailed understanding of energy-dependence of non-local potentials. We have also suggested a simple way of correcting the effective potentials for non-locality when the underlying energy-dependent non-local nucleon potentials are unknown but energy-dependent local phenomenological nucleon potentials are available.
pacs:
25.45.Hi, 21.10.JxI Introduction
In our two previous publications Tim13a ; Tim13b we have proposed a method for calculating cross sections when the interaction of the neutron and proton in deuteron with the target is energy-independent but non-local. This development has been motivated by the growing number of experiments performed at radioactive beams facilities with the aim of extracting spectroscopic information beyond the limits of -stability, including cases important for astrophysical applications. The reaction is known PTJT to be dominated by those components of the total wave functions in which the separation between the neutron and proton in the incoming deuteron is less than the range of the interaction. Such components are often calculated in the adiabatic distorted wave approximation (ADWA) where the effective deuteron potential is derived from neutron and proton optical potentials taken at some fixed energy JS ; HJ . Since the introduction of ADWA the fixed neutron and proton energies used to calculate the adabatic deuteron potential were always taken to be precisely half of the deuteron incident energy JS ; JT ; Joh05 . Such a prescription seemed to be reasonable from the intuitive point of view that appeals to the low binding energy of deuteron.
The first indications for a need to go beyond the approximation of fixed nucleon energies came from the Faddeev study of transfer reactions in Refs. Del09a ; Del09b . The energy dependence of the nucleon optical potentials assumed there were either explicit Del09a or a result of the non-locality of energy-independent nucleon potential Del09b . Given that the Faddeev formalism is too complicated for the routine analysis of deuteron stripping reactions we have suggested Tim13a ; Tim13b a practical way to account for the non-locality of nucleon optical potentials in the ADWA developed in JS ; JT . It turned out Tim13b that for energy-independent non-local potentials of the Perey-Buck type PB a simple adiabatic deuteron potential can be constructed as a solution of a transcendental equation, similar to the one obtained for nucleon scattering in PB . Moreover, for nuclei and isospin independent nucleon optical potentials this solution is related to the sum of nucleon potentials taken at an energy shifted with respect to the half the incident deuteron energy by about 40 MeV. We have shown that this large shift comes from the relative kinetic energy averaged over the short-range potential Tim13a ; Tim13b . The new effective deuteron potential is shallower than that traditionally used in the ADWA and this leads to a change in normalizaton of predicted cross sections with consequences for their interpretation in terms of nuclear structure quantities.
The simple prescription of Refs. Tim13a ; Tim13b to obtain the potential for reactions relies strongly on the assumption that the energy-dependence of nucleon optical potentials is a consequence of the non-locality of energy-independent potentials. However, the formal theory of optical potentials developed by Feshbach Fes58 shows that optical potentials are not only non-local but energy-dependent as well. The explicit energy dependence of Feshbach potentials comes from the coupling of channels with the target, , in its ground state to channels in which is excited, i.e, the mechanism that gives rise to the imaginary part of the optical potential when the excited channels are open. The result is that global local energy-dependent potentials derived from analysis of experimental data may not be of the Perey-Buck type. We have checked this for optical potentials taken from frequently-used global systematics CH89 CH89 . We found that only their real parts satisfy the Perey-Buck form with the usual non-locality range of 0.85 fm while the imaginary parts are definitely not of the Perey-Buck type and do not follow any immediately obvious systematic rule. Therefore, it is unclear how to treat explicit energy dependence of the popular CH89 global potential in the ADWA. This may be relevant to other energy-dependent global optical potentials available in the literature and used in reaction calculations.
In this paper we suggest an approximate practical way of dealing with explicitly energy-dependent non-local optical potentials. For this purpose we first consider in Sec. II the connection between three-body model and underlying many-body problem that leads to the energy dependence of optical potentials. Then in Sec. III we give formal expressions for optical potential operators in two- and three-body systems. We derive in Sec. IV the link between the adiabatic models with energy-dependent and energy-independent optical potentials making important comments in Sec. V. We apply in Sec. VI the new model to calculation of the cross sections of the same reactions considered earlier by us in Refs. Tim13b . We discuss our model and the results obtained making conclusions in Sec. VII. Important derivations are given in the Appendix.
II Connection between the three-body model of the system and the underlying many-body problem.
Explicit energy dependence of the nucleon optical potential arises as the result of internal structure of the target and the consequential possibility that the target can be excited. On the other hand, it is customary to model the reaction in terms of scattering state solutions of a three-body Schrödinger equation in which only the co-ordinates of the and appear explicitly. We can formalize this procedure by regarding the three-body wavefunction of the model as the projection, , of the full many-body wavefunction corresponding to a deuteron incident on a nucleus in its ground state, , onto the ground state of . This projection has outgoing waves that describe elastic deuteron scattering and elastic deuteron break-up exactly and outgoing waves in any open stripping channel in which has a non-neglible component with in its ground state. The complete many-body wavefunction has components in which is not in its ground state. The existence of coupling to these components influences the projection but we will base our analysis on a model in which their explicit contribution to the transition matrix is neglected.
Within this framework an exact expression for transition matrix is
| (1) |
where is the interaction and is a solution of the many-body Schrödinger equation corresponding to a proton with momentum incident on but with deleted. This expression for the exact amplitude differs from the widely used alternative expression in which the transition operator is given by Satchler and the bra-vector contains the product of the wave function of nucleus and the distorted wave in the channel generated by the (arbitrary) optical potential . The advantage of Eq. (1) is that it contains the short-ranged transition operator only, which allows a simple approximation for the to be developed. However, the final state wave function in this expression becomes more complicated. To further discuss this issue we restrict ourselves to a three-body model, , in which the internal degrees of freedom of are not treated explicitly. In this case is a solution of a three-body problem, but it is a very special one in which (i) two of the bodies, and , do not interact, and (ii) in practical applications to reactions is frequently much more massive than a nucleon. In fact, in the limit excitation of is impossible in this model and the exact solution for is the product of , a proton scattering wave function distorted by the proton-target potential , and the wave function of the final nucleus . The overlap of the latter with gives the neutron overlap function . Derivations of these results are given in RCJ09 where references to earlier work can be found. Corrections to this limit in the case of selected light nuclei have been evaluated in TJ99 using the adiabatic approximation to handle the excitation and break-up of by the recoil of and in Moro09 using the continuum-discretized coupled-channel method. It was shown in TJ99 how the recoil corrections modify the proton distorted wave, , by a factor that goes to unity for large leaving a three-body wave function with a range limited in space by the neutron overlap function. We refer to TJ99 and Moro09 for further quantitative discussion of these results which show that recoil contributions to can probably be ignored in the first instance except for the very lightest nuclei. The aim of the present paper is to clarify how a proper treatment of the wave function in the incident channel changes predictions when the wave function in the final channel is fixed. Although to date a complete solution to the problem of calculating for finite has not yet been obtained the results of TJ99 and Moro09 give sufficient grounds for ignoring the finite complications in for our purposes.
The emphasis will now be on the evaluation of , which by definition is a function of the coordinates of and . We will make heavy use of the fact that the evaluation of the amplitude (1) requires knowledge of this function within the range of only and we will make approximations that are inspired by this observation.
Using projection operator techniques originally given by Feshbach Fes58 it is possible to derive explicit expressions for the effective interactions that appear in the three-body Hamiltonian that drives . This effective Hamiltonian is
| (2) |
where is the three-body kinetic energy operator for in the centre of mass system and the bra-ket notation here implies integration over the target nucleus co-ordinates to leave an operator in and co-ordinates only. The interactions that appear in Eq. (2) depend only on the and coordinates, respectively, being diagonal in states of the target A, but otherwise arbitrary at this point. They have no influence on the ground state matrix elements of or on the three-body wave function. The importance of the introduction of the ’s in the present context is that their arbitrariness can be used to decouple the neutron and proton contributions to the complex many-body operator , at least as far as the lowest multiple scattering contributions are concerned. How this is done will be discussed in Sec. IV.
The many-body operator in Eq. (2) accounts for all the effects of the target nucleus degrees of freedom. It satisfies the integral equation (see Appendix A)
The operator projects onto excited states of the target and the energy denominator is given by
| (4) |
where and are the internal Hamiltonian and the ground state energy of the target , respectively. is the three-body energy related to the incident centre of mass kinetic energy and deuteron binding energy by .
A formal solution of Eq. (LABEL:U) is
sums up all processes via excited target states and the deuteron ground and break-up states that are coupled to the target ground state by and which begin and end on the target ground state. The expansion that appears on iteration of Eq. (LABEL:U) by repeated substitution for on the right-hand side makes this clear:
| (6) | |||||
When averaged over the target ground state, and added to , the first term on the right-hand-side of (6) will be recognised as providing an expression for the sum of the real nucleon optical potentials calculated in a folding model using the free-space interactions between and with the target nucleons. The second and higher order terms include the effect of target excitation. Because of the propagator they are complex and non-local in neutron and proton coordinates even when the nucleon-nucleon interactions are local. In addition there is an explicit dependence on the energy through the energy denominator . The purpose of this dependence is to link the three-body energy of the system to the thresholds of all relevant channels correctly. For example, if is less than the energy of a coupled intermediate excited state then the corresponding contribution to will be real (Hermitean); otherewise, a complex (non-Hermitean) contribution will result. This is the physical reason for expecting the effective interaction to be explicitly energy dependent.
Our aim is to make a connection between and the neutron and proton optical potentials and, in particular, to determine the energies at which phenomenological optical models should be taken to reproduce the main properties of for application to evaluation of the transition amplitude (1). We shall see that this can only be done approximately.
III Formal expressions for the nucleon optical potential in two- and three-body channels.
III.1 Multiple scattering expansion of operator .
The operator which is a complicated operator in the coordinates of , and , can be partially separated into its and contributions by using manipulations from multiple scattering theory (see Appendix B). We obtain
| (7) | |||||
where
| (8) |
and the dots in (7) are terms of third or higher order in and/or , always with an excited target (though not necessarily excited deuteron) as intermediate state.
We emphasize that although the target ground state matrix element is independent of the this is not true of the matrix elements . The underlying reason for this is that the denominator in depends both on and and, therefore, is not symmetric in and .
III.2 Two-body optical potential operator.
According to Feshbach Fes58 the optical model operator for a nucleon with kinetic energy satisfies the integral equation
| (9) |
where . In terms of the solution of this equation the optical potential, , for nucleon scattering by at energy is given by
| (10) |
Note that in the proton case we include Coulomb interactions in the NN potenital and, therefore, our proton optical potential includes a Coulomb potential .
To make a connection with the case of the last subsection we introduce a slightly modified definition of nucleon optical potential:
where
| (12) |
differs from by inclusion of the potential . The operators and have different matrix elements in general but their ground state expectation values are related by . The Feshbach optical potential is now given by
| (13) |
Using the same basic relation between the nucleon optical potential and the underlying many-body theory that we use here Buck and Lipperheide Buc81 ; Buc83 showed that a non-local and energy independent potential operator can be formally defined that generates the same projection of the many-body wavefunction on to the target ground state as does the explicitly energy dependent Eq. (13). However, the potential they derive as well as being non-Hermitean, as is also Eq. (13), does not satisfy a standard transformation under time reversal. When the underlying two-body interactions are invariant under time reversal, Feshbach’s (13) satisfies
| (14) |
where is the non-linear time reversal operator for the system. The operator defined by Buck and Lipperheide does not satisfy this relation. This results in a very clumsy discussion of reciprocity in reaction theories that make use of optical potentials and we therefore choose not to make use of the Buck-Lipperheide definition here.
III.3 Relation between the three-body and two-body optical potentials.
The three-body operator has contributions from the as leading term in the three-body Hamiltonian through Eqs.(2) and (7):
| (15) |
These quantities have a similar structure to the Feshbach form for the nucleon optical potential discussed in the last Section. Note however that the energy denominator which appears everywhere in the case is not the denominator that appears in the neutron operator (12).
In order to deal with this difference when calculating we proceed as follows:
(i) We neglect the higher order multiple scattering terms that appear on the right-hand-side of Eq. (7). These neglected terms involve and excitations that cannot be expressed in any obvious way as a sum of terms depending separately on the and coordinates. They remain to be investigated in future work. These contributions are neglected in all three-body models of the system with heavy targets. They will not be discussed further. This means our approximation for the effective interaction in the three-body Hamiltonian (2) in addition to is
| (16) |
where is or and the and are given by Eq. (8).
(ii) We consider only the limit of the infinite target mass so that the three-body kinetic energy operator, , can be separated into terms that depend on the individual neutron and proton coordinates relative to the target, , where and . This approximation seems to be essential if we are to obtain a three-body Hamiltonian which involves a sum of and potentials each of which only depend on the coordinates of one nucleon. The energy denominator is now
| (17) |
IV Distorting potentials for the adiabatic model of reactions
It has been shown PTJT that for a range of incident deuteron energies of current experimental interest the amplitude (1) is dominated by the first Weinberg component of , i.e.,
| (18) |
where is defined in terms of the - interaction by
| (19) |
in which is the deuteron ground state wavefunction. In (18), the integration is performed over the - relative coordinate, , resulting in a function of the - centre of mass coordinate, , only. The state restricts the - relative coordinate to be less than the range of the - interaction .
In the ADWA approximation JT the first Weinberg component of is determined by a distorted wave satisfying the equation
| (20) |
where is given by Eq. (16). We first consider the term in the expression for .
The dependence of the on the proton coordinates is solely through the presence in of the operators and . The values taken by influence the net neutron energy parameter in and hence determine the appropriate energy at which to choose the neutron optical potential. Our method here is to replace by an average value consistent with dominance of the first Weinberg component to the reaction. We deduce this value within the ADWA. Similarly, we will replace the operator in the term for by an average value.
The ADWA potential in Eq. (20) has energy dependence that comes through the energy denominators in which contains the matrix elements that are the functions of . The range of variable is restricted by the range of which is about 0.45 fm. Therefore, for most relevant for evaluating we have . Therefore, to a first approximation the operators in the numerator can be replaced by their form at . Then the only matrix element involving integration over is .
We show in Appendix C that within the ADWA we can consistently use the approximation
| (21) |
We consider the contribution from first. To evaluate the denominator in the right-hand-side of (21) we use definition (17) for and the result from Appendix D
| (22) |
where and are the kinetic energy operators associated with the coordinates and respectively and
| (23) |
We determine a reasonable value for the operator in Eq. (22) by recalling that it acts on the first Weinberg component . Using Eq. (20) we get
| (24) | |||||
We now recall that the potentials and are arbitrary provided that they commute with . We are therefore at liberty to choose
| (25) |
With this step Eq. (21) reduces to
| (26) |
where
| (27) |
The neutron contribution to the ADWA effective interaction (16) is given by
We see that the expression (LABEL:UADWeffn) is just the neutron contribution to the ADWA distorting potential calculated with a non-local neutron optical potential taken at energy . Similar conclusion can be made for proton contribution to the ADWA distorting potential. With the choice
| (29) |
we find in identical fashion that this contribution is obtained using the optical potential, including Coulomb terms, taken at the proton energy also equal to . We note that with the choices given by Eqs. (29) and (25) the neutron and proton contributions to the effective interaction of the three-body model in the single scattering approximation are independent of the . The choice (29) for will influence higher order multiple scattering terms in Eq. (7). We will not consider these terms further here.
V Comments
We have given arguments that suggest that for the purpose of calculating cross sections in the ADWA approximation when the nucleon optical potentials are explicitly energy dependent as well as non-local the neutron and proton kinetic energies used in the incident channel should be . This is acheved by averaging the proton kinetic energy in the incoming deuteron and adding the extra kinetic energy the neutron has because it must be close to proton in order to contribute to the amplitude. Thus the problem of calculating the ADWA amplitude for with energy-dependent nonlocal potentials is reduced to the problem of calculating this amplitude with energy-independent nonlocal potentials, the solution of which is found in Refs. Tim13a ; Tim13b . If a phenomenological non-local, explicitly energy dependent nucleon potential is available, the prescription of present paper together with that from Refs. Tim13a ; Tim13b can be used unambiguously.
The energy-independent non-local potential that replaces the original energy-dependent nonlocal potential is obtained from the latter by evaluating it at the energy shifted from the intuitively assumed value by one half of the average kinetic energy within the range of the potential, approximately equal to 57 MeV Tim13a . This value is close to, but not equal to, the energy shift MeV, identified in Refs. Tim13a ; Tim13b as the shift to the value that provides the appropriate energy of energy-dependent equivalents of nonlocal potentials to be used in ADWA.
For all known phenomenological optical potentials the underlying energy-dependent non-local potentials are not known. It may be tempting to use the conclusion of the previous section for choosing in the ADWA calculations the phenomenological local potentials taken at energies . This, however, would be a source of confusion and may lead to a wrong result. Indeed, if is the underlying energy-dependent non-local potential for the phenomenological local energy-dependent equivalent then the ADWA needs to use the energy-independent non-local potentials . This would give a different equivalent energy-dependent potential which then should be taken at the energy , as shown in Tim13a , Tim13b . The two potentials and are not the same. We will derive a link between them for a particular class of in the next section. However, more generally, further knowledge of energy-dependent non-local potentials is needed.
It is interesting to compare our treatment of explicit energy dependent optical potentials with that of Ref. Del09a . In that work the Faddeev approach was used to solve the three-body problem. Energy dependence is treated in Del09a by taking the neutron (proton) optical potential at an energy equal to the variable neutron (proton) energy parameter used in evaluating the neutron (proton) -matrix as it appears in the Faddeev equations. This seems physically plausible at first sight, but what kind of Schrödinger equation such an approach corresponds to is not clear. The Faddeev equations have been derived from the Schrödinger equation with energy-independent non-local pairwise potentials. We are not aware of a formal derivation of the Faddeev equations for explicitly energy-dependent pair potentials of the type that arise from many-body effects as discussed in Section II.
In our view, explicit energy dependence is an effect that can only be understood by explicitly recognising the internal degrees of freedom of the target as is done here and in Refs. Muk12 ; Joh05 . It should be added that the approximate prescription proposed here is intended for use only in the calculation of the incident channel distorting potential in a particular expression for the transition matrix and is not expected to be useful in any other context.
VI Applications to the , and reactions with global energy-dependent nonlocal optical potential
In this section we apply the formalism developed above to the ADWA calculation of the cross sections of the O, Ar and Ca reactions at , 9 and 11.8 MeV respectively. The cross sections of these reactions have been measured in o16 ; ar36 ; ca40 . These are the same reactions that have been considered in Ref. Tim13b using the energy-independent non-local nucleon optical potentials given by Giannini and Ricco (GR) systematics in Gia76 . The choice of targets made in Tim13b was to justify the use of the GR potential which is valid for nuclei only. In the present work, we first use the Giannini-Ricco-Zucchiatti (GRZ) nonlocal potential GRZ which has an energy-dependent imaginary part. Then we make a suggestion of how to account for non-locality when only energy-dependent local phenomenological potentials are known but the underlying energy-dependent non-local potentials are not known. As an example we use the widely used CH89 systematics CH89 .
VI.1 Giannini-Ricco-Zucchiatti potential
For targets, the GRZ potential is given by
| (30) |
with the nonlocality factor
| (31) |
determined by the non-locality range , where MeV-1 and is the nucleon-target reduced mass. The potential formfactor is defined as
| (32) |
It has one energy-dependent parameter, the depth of the imaginary part,
| (33) |
All other parameters are energy-independent and have the following values: the depth of the real potential MeV, the radius of both the real and imaginary potentials fm, the diffusseness fm and fm for the real and the imaginary potentials respectively. We neglect the spin-orbit term because its contributions to the cross sections at the chosen incident deuteron energies are small.
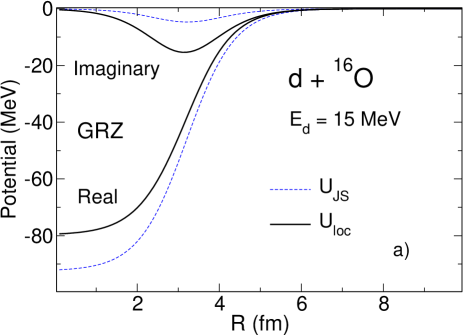
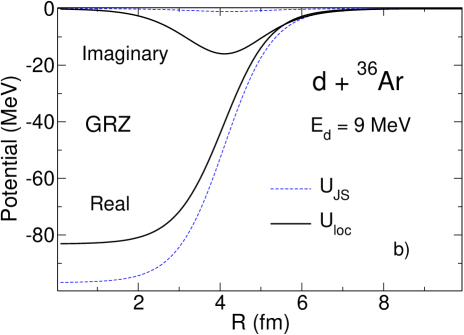
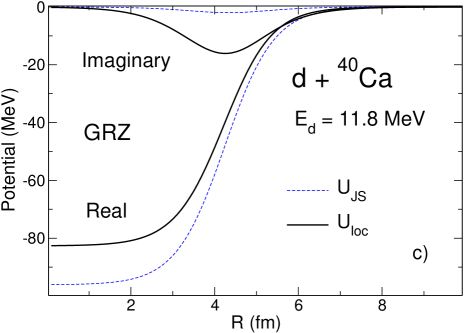
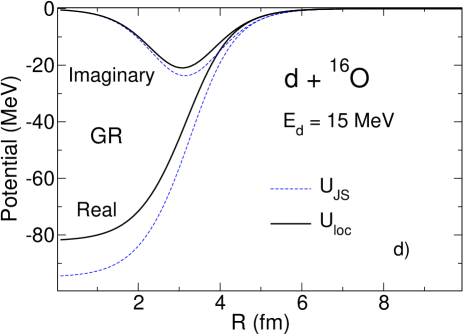
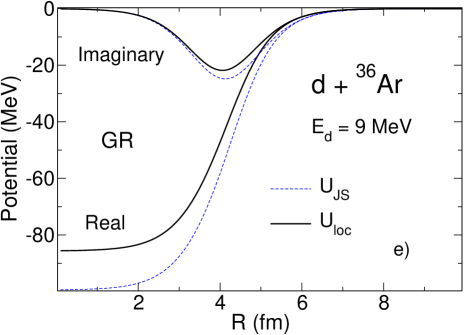
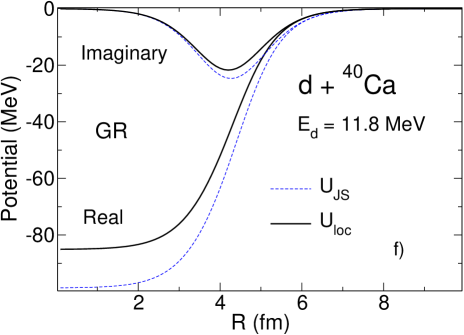
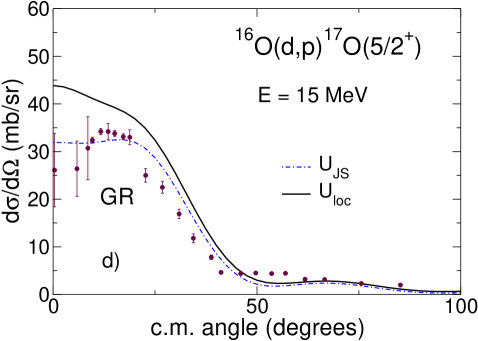
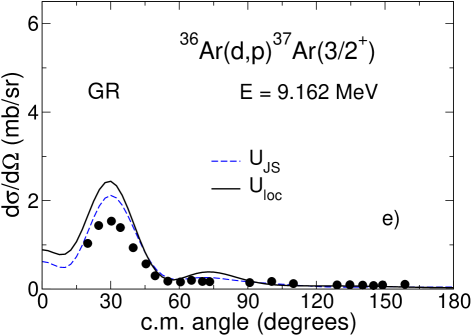
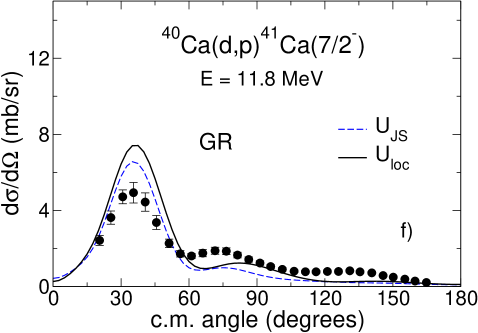
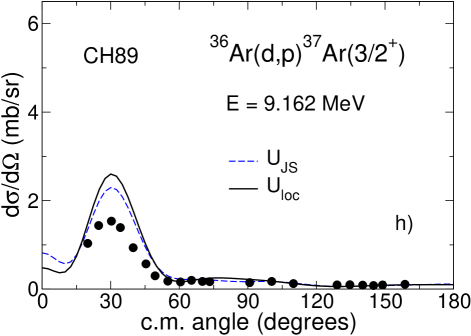
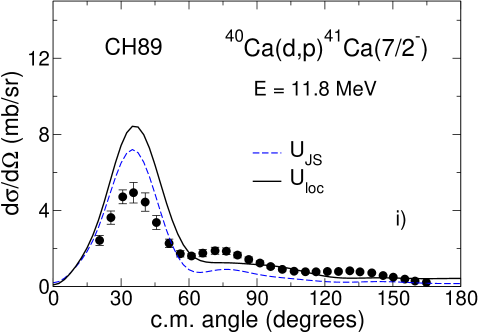
According to the prescription of Sec. IV we solve the three-body Schrödinger equation in the adiabatic approximation using energy-independent imaginary potential (33) evaluated at . For we use the value of 57 MeV obtained in Refs. Tim13a ; Tim13b for the Hultén potential. We also use MeV from Gia76 ; GRZ . As explained in Tim13a ; Tim13b , in the adiabatic approximation the deuteron distorted wave is found from a local-equivalent two-body model
| (34) |
where is the Coulomb potential and in the local-energy approximation the local potential is a solution of the transcendental equation
| (35) | |||||
In this equation is the deuteron- reduced mass and the constants and depend on and the nucleon non-locality range only. These constants are tabulated in Tim13b for the Hultén potential. The range has the meaning of an effective non-locality range for the deuteron-target interaction and is approximately equal to 0.46 which is close to . The moment is about 0.75 and its deviation from one determines the shift of energy at which the local equivalents of should be evaluated for use in Johnson-Tandy potential calculations. In this paper, we determine by solving the transcendental equation (35) directly without constructing the local equivalent of .
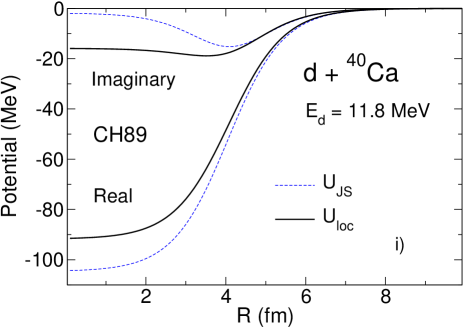
The local potentials obtained for O, Ar and Ca are shown in Fig. 1 (-). They are compared to the widely used Johnson-Soper potentials constructed from the energy-dependent local-equivalents of taken at :
| (36) | |||||
One can see that the real parts of the deuteron local potentials obtained with GRZ are shallower than the real parts of the corresponding Johnson-Soper potential . This is exactly what has been seen already for the energy-independent non-local potential GR in Tim13a ; Tim13b and is shown again Fig. 1 (-). This reflects the fact that the real part of GRZ is energy-independent. The imaginary parts of obtained with GRZ are much deeper than those of , which is completely opposite to what happens for the imaginary parts of and obtained with the energy-independent potential GR. This happens because the imaginary part of GRZ increases with and at MeV it takes on large values while the imaginary part of is constructed from nucleon potentials taken at MeV where is small. On the contrary, for the energy-independent potential GR the imaginary part of its local equivalent slowly decreases with . Taking this potential at leads to a smaller imaginary part. The different behaviour of the imaginary parts of compared to that of for GRZ and GR results in the difference manifestation of the non-local effects in the corresponding differential cross sections.
To calculate the angular distributions of reactions we used the framework (1) in which the remnant term is absent and the channel is described by the distorted wave obtained with the optical potential thus neglecting recoil excitation and breakup effects (note that in Refs. Tim13a ; Tim13b the optical potential was used which means that the remnant term was neglected). These optical potentials were obtained from the local model corresponding to either the GRZ or the GR potential. The local proton scattering wave function was multiplied by a Perey factor Per63 with the proton non-locality range appropriate to GRZ or GR. No Perey effect was considered in the deuteron channel. Such effects would arise from the linear terms in the expansion of the nucleon optical potentials near for which no averaging procedure has been developed. In the first place, these terms will influence the shape of the deuteron-target effective potential. The associated Perey effect will also modify the deuteron distorted wave, but only in the nuclear interior which does contribute significantly for the considered here where peripheral contributions dominate.
Both the proton equivalent local potentials and the effective deuteron potentials were read into the TWOFNR code 2FNR which was used to calculate the cross sections in the zero-range approximation. The overlap functions for 17O, 37Ar and 41Ca were represented by neutron single-particle wave functions obtained by fitting the Woods-Saxon potential wells to reproduce their corresponding neutron separation energies. The standard radius fm and diffusenness fm were used both for central and spin-orbit potentials while the depth of the spin-orbit potential was 5 MeV. No Perey effect was used for the neutron wave functions since we study only the relative change in the cross sections caused by replacing the Johnson-Soper potentials by our new adiabatic distorting deuteron potentials.
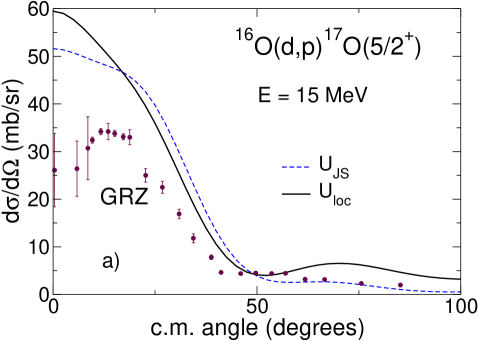
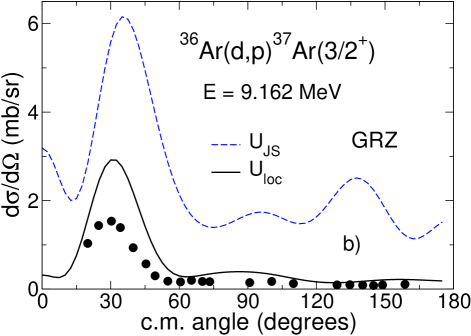
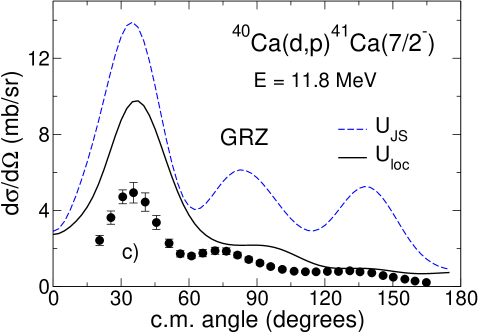
The cross sections calculated using deuteron distorting adiabatic potentials derived with GRZ and GR are shown in Fig. 2 ( and Fig. 2 respectively where they compared to the calculations, performed with the Johnson-Soper potentials derived with GR and GRZ, and with experimental data. The cross sections are plotted with the spectroscopic factor for 16O and 40Ca targets and for 36Ar. One can see that the influence of non-locality for GRZ and GR is completely different. While for the energy-independent potential GR the cross sections increase and their shapes change insignificantly compared to Johnson-Soper calculations, for energy-dependent potential GRZ the cross sections decrease and the changes in the shapes of the angular distributions are more noticeable. This happens because the Johnson-Soper potential corresponding to GRZ has much smaller imaginary part than that of so that reduction of absorption leads to large cross sections. For the GR potential, has less absorption than resulting in larger cross sections in comparison to the Johnson-Soper ones. While the difference between the Johnson-Soper cross sections calculated with GRZ and GR can almost reach a factor of three (for 36Ar), the difference of the cross sections obtained in non-local model with GRZ and GR is much smaller, in the main peak.
VI.2 Estimation of the deuteron distorting potential from phenomenological energy-dependent local nucleon optical potentials.
Suppose we know some phenomenological energy-dependent optical potential . We assume that its underlying energy-dependent non-local potential has the Perey-Buck form
| (38) |
where is given by Eq. (31) with some non-locality range . We suppose also that is related to by the Perey-Buck transformations given by (LABEL:PB). Then according to Sec. IV we need to use formfactors taken at the energy treating them as energy-independent. The local distorting potential is obtained from the transcendental equation (35) which can be rewritten as
| (39) |
where
| (40) |
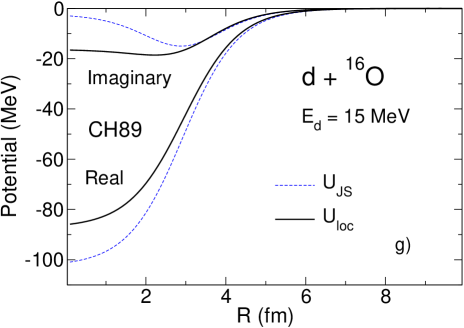
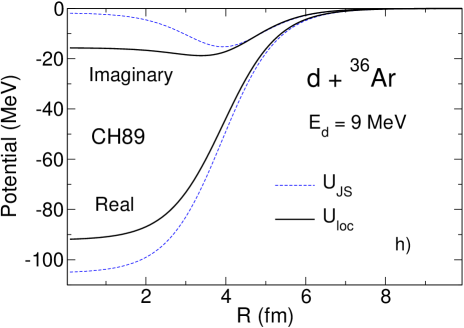
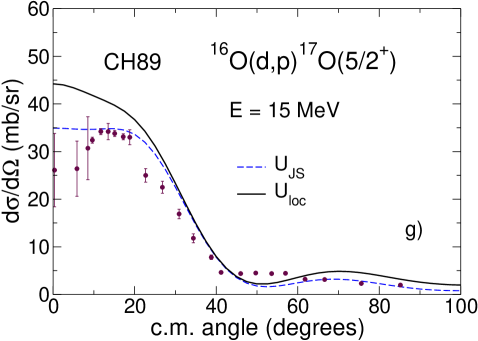
Thus, knowing phenomenological proton and neutron optical potentials we can calculate and find as a solution of Eq. (39). In Fig.1 () we have plotted these solutions for 16O, 36Ar and 40Ca + d using the CH89 systematics for and in comparison with the Johnson-Soper potential obtained also with CH89. We used fm since the real part of the CH89 potential seems to be consistent with Perey-Buck non-local potential of this range. The chosen value fm corresponds to fm and Tim13b . We have also solved Eq. (39) by expanding the exponential in its left-hand side up to second order terms but such solutions were not accurate enough.
Fig. 1 () shows that the distorting potential (CH89) generated from an energy-dependent phenomenological local potential has a smaller real part than (CH89), similar to the case of GR and GRZ. However, the imaginary part of (CH89) has more absorption in the internal nuclear region than has (CH89), while being similar outside the nucleus. This is the consequence of the interplay between the surface and volume absorption in CH89 and the fact that the imaginary part has to be evaluated at higher energies where the volume absorption grows. Nevertheless, the differential cross sections, plotted in Fig.2 () show a similar influence of non-locality to what has been observed with energy-independent potential GR. The cross sections increase in the main peak by 16, 10 and 18 for the 16O, 36Ar and 40Ca targets respectively. In comparison, an increase of 15 is obtained with GR. The absolute cross sections in the area of the main experimental peak obtained in non-local calculations with three different nucleon optical potentials differ by 20 in the case of 16O and 36Ar and by 30 in the case of 40Ca. This is comparable to the dependence on optical potential parameters found typically in distorted-wave Born approximation calculations.
VII Discussion and Conclusions
We have suggested an approximate practical way of dealing with explicitly energy-dependent non-local nucleon optical potentials when calculating the reactions within the model space. We have shown that within an approximation consistent with the adiabatic model of reactions the problem of using energy dependent nonlocal nucleon potentials is reduced to the problem of calculating the cross sections with energy-independent nonlocal potentials, the solution of which has been found in Tim13a ; Tim13b . It is important to note that in obtaining our results we have assumed that any explicit energy dependence of optical potentials arises from many-body effects. In our treatment we start from an approximate three-body Hamiltonian with non-local nucleon optical potential operators at an energy fixed by the incident deuteron energy. Our prescription is based on the identification of the particular feature of the amplitude (small separations) that is relevant to the calculation of a particular form of the many-body transition operator. It is not a prescription that is intended to be useful for the whole of configuration space. For example, it can not be used in calculations of elastic scattering.
It is also important to note that in deriving the three-body effective Hamiltonian we have ignored the terms in Eq. (7). These terms reflect the fact that the many-body problem asociated with the system cannot be mapped exactly onto a three-body model with Hamiltonian . The neglected terms are non-local energy dependent three-body forces that are a necessary consequence of the underlying many-body problem. They describe physical processes in which the target is excited by the incident neutron and de-excited by the proton and so on in higher orders. Terms in which successive target excitations are caused by the same nucleon are taken into account by the and operators. The quantitative significance of the terms is unknown.
The phenomenological optical potentials can be assumed to take antisymmetrization effects into account. These effects are believed to make important contributions to non-locality and are taken into account by the treatment of Timofeyuk and Johnson in Tim13a ; Tim13b . However, for the system there are additional antisymmetrization effects that cannot be taken into account in this way. For a discussion of their quantitative significance see Tostevin, Lopes and Johnson TLJ87 .
The prescription of the present paper is simple enough to be widely used in analysis of experiments. However, it requires knowledge of the energy-dependence of non-local optical potentials. At present, we are not aware of any potential of such a kind Mah13 except for the GRZ potential. While this potentials generates reasonable effective local potentials it clearly gives unphysical local Johnson-Soper potentials that strongly overestimate cross sections at the low incident deuteron energies frequently used at several modern radioactive beam facilities. This shows that more studies, using both phenomenological and microscopic models, are needed to pin down the energy-dependence of nucleon optical potentials.
We have also suggested a simple way of correcting the potentials for non-locality when the energy-dependence of non-local nucleon optical potentials is unknown but energy-dependent local systematics are available. We have shown that if a specific assumption about the form of energy-dependent non-local potentials is made, then the local distorting deuteron potentials for adiabatic calculations are obtained as solutions of a transcendental equation. While we believe that this assumption should be valid for the targets considered here, in general it may not be correct. For example, according to GRZ, the asymmetry term of the optical potential has much wider non-locality. Therefore, we can expect that for targets Eqs. (35) and (40) could be modified.
Finally, we did not intend to provide new values for the spectroscopic factors and asymptotic normalization coefficents obtained from the analysis of reactions using our new prescription. Our aim here is to clarify how the explicit energy-dependence of non-local optical potentials affects known results of adiabatic calculations. We do have preliminary ideas of what changes in spectroscopic factors and asymptotic normalization coefficients could be expected, but the details of any change will depend on how well we understand the energy dependence of non-local optical potentials. On the other hand, our study is not comprehensive and many issues remain outstanding. These include the influence of the deuteron -state on the effective potential, corrections to the approximate treatment of non-locality in Tim13a ,Tim13b , non-adiabatic corrections, additional antisymmetrization effects, multiple scattering etc. These questions present a challenge to the development of the reaction theory and answering them is important for the correct interpretation of measured cross sections in terms of the nuclear structure quantities.
VIII Acknowledgement
We greatfully acknowledge the support from the UK STFC ST/J000051/1 grant.
Appendix
VIII.1 The operator .
Here, we derive the formula (LABEL:U) from Section II for the operator whose matrix elements can be used to give formally exact expressions for projections of the many-body scattering state corresponding to a deuteron of momentum in its ground state incident on a target in its ground state , which we will assume has spin zero for simplicity here. The relevant projection operators and project onto the ground and excited states of nucleus respectively and satisfy
| (41) |
The state is obtained by taking the limit of the state that satisfies the equation
| (42) |
where is the Hamiltonian and is the total energy of the , which in the notations of Section II is
| (43) |
For the function is uniquely defined by the inhomogeneous Eq. (42). No further statements of boundary conditions are required. It follows from Eq. (42) that is square-integrable. As discussed in Goldberger and Watson, Ref. goldberger , Ch.5,“Formal Scattering Theory”, the function is used as a stepping stone to the calculation of transition matrices for all final channels using appropriate expressions in which the limit can be taken without ambiguity. They show that their methods can be justified by wave packet arguments.
Following Feshbach Fes58 we obtain equations coupling the and components of , defined as
| (44) |
by operating with and in turn on both sides of Eq. (42) to obtain
| (45) |
From the second equation we deduce
| (46) |
and substituting this result into the first of Eq. (45) we get an equation for alone:
where describes a plane wave deuteron in its ground state incident on in its ground state .
For a spin-zero target the projection will have the form . We obtain an equation for the function of and coordinates, , by taking the inner product of Eq. (LABEL:ExactEq4) with . Using the notation used in Eqs. (LABEL:U) and (4) we get
| (48) |
where and we have used the fact that commutes with and so that
We have also used the fact that because the operator 1/(denominator) in Eq. (48) appears with on either side then (i) only excited state eigenvalues of ever appear and (ii) is diagonal in the basis of states of . Therefore, we can replace by .
It is convenient here to define an operator in the complete many-body space by the equation
| (50) |
In terms of the Eq. (48) can be written as
| (51) |
We see that the wavefunction of the three-body model is determined by the target ground state matrix element of , .
We use the identity
| (52) |
where is an arbitrary operator. Identifying with we can show that satisfies the equation (LABEL:U) of Section II.
VIII.2 Derivation of a multiple scattering expansion for .
The operator is the unique solution of the equation
| (53) |
We derive the multiple scattering expansion of using the techniques of Watson goldberger . We introduce two new operators and defined in terms of by
| (54) |
By adding the formulae for and it can be seen that satisfies Eq. (53) and therefore
| (55) |
We next show how these operators are related to the operators used in the text and defined by
| (56) |
A useful way of expressing the solution of this equation is to take the second term on the right over to the left and deduce
| (57) |
Performing the analogous step in Eq. (54) with in turn and with replaced by we obtain
| (58) |
Substituting the formula into the right-hand-side of the equation and the formula into the right-hand-side of the we obtain the uncoupled equations
| (59) |
In the standard way we iterate both of these equations and then construct . The first few terms give the multiple scattering series discussed in Section III.
VIII.3 Derivation of the inversion formula, Eq. (21)
In order to understand the origin of the approximate inversion of the operator given in Eq. (21) it is first necessary to look at the ADWA from a different point of view from that customarily used.
In section II, Eq. (1) we introduced , the projection of the full many body wavefunction on to the ground state of . It is the limit of the function that satisfies
| (60) |
where is the effective three-body Hamiltonian,
| (61) |
with and some arbitrary interaction which can be an operator in the and degrees of freedom. A formal solution to Eq. (60) is
| (62) |
From this point of view we see that the solution of the three-body problem for is equivalent to inverting the operator . We now show that the ADWA can be regarded as an approximate inversion of this operator within the space of Weinberg states.
The Weinberg basis associated with was introduced by Johnson and Tandy JT as being well adapted to the evaluation of the components of that dominate the matrix element, Eq. (1) PTJT . The Weinberg states satisfy the orthonormality relation
| (63) |
and the components of in this basis are
| (64) |
The ADWA is obtained by multiplying Eq. (60) by on the left, integrating over and neglecting all couplings between and all other Weinberg components. This results in
| (65) |
where is the constant relating the first Weinberg state to the deuteron wave function by and satisfies JT . On the other hand, after multiplying Eq. (62) by on the left and integrating over we get:
| (66) |
Combining Eqs. (66) into (65) we get
| (67) | |||||
which is satisfied if
| (68) |
Taking Eq. (19) and into account in Eq. (68), we see that the approximation (21) follows from the same approximate inversion idea as used in the ADWA.
We now show how this approach can be made the basis for making systematic improvements to the ADWA. In the Weinberg basis an arbitary operator is represented by the matrix
| (69) |
Eq.(62) tells us that these components are given by
| (70) |
where
| (71) |
Note that each matrix element is an operator in the space of . Using the relation we have
| (72) |
and Eq. (70) reduces to
| (73) |
It was shown in PTJT that for reactions in a range of incident energies of current interest the transition matrix, Eq. (1), is dominated by the first Weinberg component . According to Eq. (73) an exact expression for this is
| (74) |
which only involves the single matrix element .
The evaluation of requires the inversion of the matrix
| (75) |
so that
| (76) |
By writing it is straightforward to show that an exact alternative to the condition (76) is
| (77) |
where
| (78) |
In particular
| (79) |
The essence of the ADWA is that it ignores all couplings between the first Weinberg component and all others JT . In this limit we deduce from Eq. (79) that
| (80) | |||||
in agreement with Eq. (68). The error is of second order in the off-diagonal elements with .
This approach can be developed by iteration of Eq. (77) to give corrections to the ADWA.
VIII.4 Averaging and
In Section IV we have shown that the expression for the ADWA distorting potential requires the evaluation of matrix element (21). The denominator in the neutron contribution contains the operator , as appears in the expression for neutron optical potential, and the operator for which we want to deduce an average value consistent with ADWA. Here we evaluate the average acting on . Since
| (81) |
we obtain
| (82) |
where the last line contains the quantity
| (83) |
introduced by Timofeyuk and Johnson in Tim13a . In obtaining the last line in Eq. (82) we have used that fact that and have the same parity and that . Using the exact result
| (84) |
we obtain
| (85) |
The same results is obtained for the average that is relevant to the calculation of the proton contribution to the distorting potential in the deuteron channel.
References
- (1) N.K. Timofeyuk and R.C. Johnson, Phys. Rev. Lett. 110, 112501 (2013)
- (2) N.K. Timofeyuk and R.C. Johnson, Phys. Rev. C 87,064610(2013)
- (3) D.Y. Pang, N.K. Timofeyuk,, R.C. Johnson and J.A. Tostevin, Phys. Rev. C 87, 064613 (2013)
- (4) R.C. Johnson and P.J.R. Soper, Phys. Rev. C 1, 976 (1970)
- (5) J.D. Harvey and R.C.Johnson, Phys. Rev. C 3, 636 (1971)
- (6) R. C. Johnson and P.C. Tandy, Nucl. Phys. A235, 56 (1974)
- (7) R.C.Johnson, APS Conf. Proc. 791, AIP, 2005, p. 128
- (8) A. Deltuva and A.C. Fonseca, Phys. Rev. C 79, 014606 (2009)
- (9) A. Deltuva, Phys. Rev. C 79, 021602 (2009)
- (10) F. Perey and B. Buck, Nucl. Phys. 32, 353 (1962)
- (11) H.Feshbach, Ann. Phys. 5, 357 (1958)
- (12) R.L. Varner et al, Phys. Rep. 201, 57 (1991)
- (13) G. R. Satchler, Direct Nuclear Reactions (Oxford University Press, New York, 1983).
- (14) R.C. Johnson, Phys.Rev.C 80,044616 (2009)
- (15) N.K.Timofeyuk and R.C. Johnson, Phys.Rev.C 59, 1545(1999)
- (16) A M Moro, F M Nunes and R C Johnson, Phys.Rev. C80, 064606(2009).
- (17) B. Buck and R. Lipperheide, Nucl. Phys. A368, 141 (1981)
- (18) B. Buck and R. Lipperheide, Phys. Lett. 123B, 1 (1983)
- (19) A.M. Mukhamedzhanov, V. Eremenko and A.I. Sattarov, Phys. Rev. C 86, 034001 (2012)
- (20) E. L. Keller, Phys. Rev. 121, 820 (1961).
- (21) S. Sen, C.L. Hellas and P. J. Ripley, Phys. Rev. 3, 2314 (1971)
- (22) U. Schmidt-Rohr, R. Stock and P. Turek, Nucl. Phys. 53, 77 (1964)
- (23) M.M. Gianinni and G. Ricco, Ann. Phys. 102,458 (1976)
- (24) M.M Giannini, G Ricco, A Zucchiatti, Ann. Phys. 124, 208 (1980)
- (25) F. Perey, Direct interactions and nuclear reaction mechanisms (Gordon and Breach, N.Y. 1963), p.125
- (26) J. A. Tostevin, University of Surrey version of the code TWOFNR (of M. Toyama, M. Igarashi and N.Kishida), http://www.nucleartheory.net/NPG/code.htm
- (27) J.A. Tostevin, M.H. Lopes and R.C. Johnson, Nuclear Phys A465 83 (1987).
- (28) After our was submitted for publication two preprints appeared on arXiv (M.H. Mahzoon et al, arXiv:1312.4886 and arXiv:1312.5209) where a phenomenological non-local energy-dependent potential for 40Ca has been found for the first time.
- (29) M.L. Goldberger and K.M. Watson, Collision Theory, Wiley, New York 1964 (Dover Publications, N.Y, 2004).