algorithm
Adjoint sharding for very long context training of state space models
Abstract
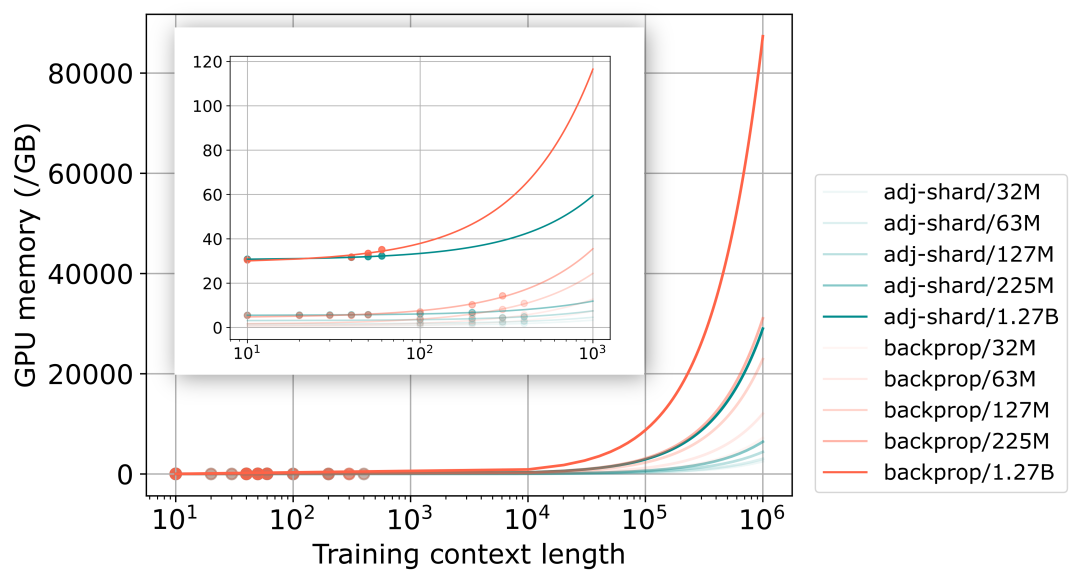
Despite very fast progress, efficiently training large language models (LLMs) in very long contexts remains challenging. Existing methods fall back to training LLMs with short contexts (a maximum of a few thousands tokens in training) and use inference time techniques when evaluating on long contexts (above 1M tokens context window at inference). As opposed to long-context-inference, training on very long context input prompts is quickly limited by GPU memory availability and by the prohibitively long training times it requires on state-of-the-art hardware. Meanwhile, many real-life applications require not only inference but also training/fine-tuning with long context on specific tasks. Such applications include, for example, augmenting the context with various sources of raw reference information for fact extraction, fact summarization, or fact reconciliation tasks. We propose adjoint sharding, a novel technique that comprises sharding gradient calculation during training to reduce memory requirements by orders of magnitude, making training on very long context computationally tractable. Adjoint sharding is based on the adjoint method and computes equivalent gradients to backpropagation. We also propose truncated adjoint sharding to speed up the algorithm while maintaining performance. We provide a distributed version, and a paralleled version of adjoint sharding to further speed up training. Empirical results show the proposed adjoint sharding algorithm reduces memory usage by up to 3X with a 1.27B parameter large language model on 1M context length training. This allows to increase the maximum context length during training or fine-tuning of a 1.27B parameter model from 35K tokens to above 100K tokens on a training infrastructure composed of five AWS P4 instances. 333Additional material for this paper can be found at: https://adjoint-sharding.github.io.
1 Introduction
Foundation models are a new paradigm in artificial intelligence research focused on building large, general-purpose models that adapt to different tasks [44, 40, 7, 51]. Extensive training on large datasets equips foundation models with broad capabilities, which are then fine-tuned on smaller datasets for specific applications. Foundation models commonly employ the transformer architecture [60]. Despite the immense success, training transformer-based models requires memory growing quadratically with the context length , limiting their applications on long context tasks [36]. Researchers developed various techniques to conquer this problem, ranging from inference time context window expansion [19, 18], IO-aware algorithms [16, 13, 55], and various linearly scaling language model architectures [23, 15, 49, 6]. On another note, distributed learning enables training large models with a big number of GPUs, and efficient training methods like activation checkpointing, model/gradient sharding, and mixed-precision computing have further reduced the memory requirement of training a large model [61, 69, 53, 41, 30]. However, current methodologies are entirely based on backpropagation and compute the gradient as a whole, inevitably requiring a memory growing rapidly with model size and context length [12]. Current sharding methods ignore the activations and only consider the model weights and optimizer states, constituting only a small fraction of the total memory cost [56]. Activation checkpointing is among the limited techniques that consider activation values. Activation checkpointing offloads necessary intermediate states to the CPU and recompute them on the fly, trading compute time for memory reduction [56, 52]. The substantial time required for offloading to the CPU hinders the effectiveness of activation checkpointing.
We propose adjoint sharding to dissemble gradient computation of residual and/or recurrent based models to achieve orders of magnitude lower memory usage during training.
Adjoint method
The adjoint sharding method is based on the adjoint method for recurrent models [8, 32]. Given an optimization problem of a parametric recurrent forward process, the adjoint method is concerned with computations of the gradients regarding the process’s parameters. Backpropagation saves intermediate states to calculate gradients, whereas the adjoint method relies on a backward adjoint process to compute gradients. The adjoint method is a constant-memory optimization technique for dynamical systems [9, 66]. In this paper, we are only concerned with the adjoint method for recurrent relations.
Vector-Jacobian product
Adjoint sharding dissembles the gradient computation of a large language model (LLM) into independent vector-Jacobian product (VJP) computations. By left-multiplying the Jacobian with a vector, it becomes unnecessary to compute the expensive Jacobian. Modern VJPs are as fast as a forward function call of the model, and can be thousands of times faster than Jacobian computations [2]. We speed up adjoint sharding by employing the VJPs.
Truncated adjoint sharding
Sharding the gradient computation allows us to prioritize the important gradients and disregard the rest, resulting in faster computation. We term this novel method truncated adjoint sharding, and empirically showcase its performance.
Distributed and parallel computation
In addition, we have developed a distributed multi-GPU variant of adjoint sharding to further improve the scalability of LLM training. We also analyze the memory cost of parallel computation of adjoint sharding, opening up directions for massive speedups.
State-space models and residual networks
Residual networks (ResNets) are a commonly applied neural network structure. We illustrate adjoint sharding assuming a ResNet structure [28]. State-space models (Mamba) have achieved performances on par with attention based models while possessing a linear scaling regarding the context length , a polynomial speedup compared to the scaling of transformers [60, 22].
2 Related works
Linear LLMs
[17, 5, 49] proposed LLM architectures with a linear inference time complexity. Each of them is formed by stacking residual layers together, where each layer has a recurrent relation. However, their temporal relationships are nonlinear, which limits the application of adjoint sharding to dissemble the gradients into independent vector-Jacobian products.
Backpropagation through time
Applying the adjoint method for recurrent models leads to backpropagation through time (BPTT) [64]. BPTT is a training algorithm developed for recurrent neural networks (RNNs). RNN models suffer from the exploding and vanishing gradient because of the term [46]. SSMs provide remedies with careful parameterization of the recurrent dynamics inspired by classical SSM theory [21, 24, 25, 27, 45, 33]. Linear temporal relations allow efficient evaluations of the model, while preserving universal approximation capabilities [63]. By a similar token, truncated adjoint sharding can be seen as a more general version of the truncated backpropagation through time [31, 57].
Neural ordinary differential equations
The adjoint method has also been applied to the optimization of continuous systems, especially the ordinary differential equations (ODEs) [9, 20]. Optimizing neural ODEs with autograd requires backpropagating through numerical solvers along every step, using an unrealistic amount of memory. The adjoint method does not backpropagate through the operations of the solver and uses a constant amount of memory. However, applying the adjoint method for continuous systems requires solving a costly ODE initial value problem with dimensionality of the number of parameters.
Low memory training methods
Researchers proposed various low memory training techniques to train big models in long contexts. ZERO provides data- and model-parallel training while retaining low communication volume, while eliminating memory redundancies [53]. PyTorch FSDP provides a streamline for model, gradient, and data parallelization [69]. Activation checkpointing discards intermediate values during the forward step, and recompute on the fly during the training phase [56]. CPU offloading scales large model training by offloading data and computations to the CPU, trading computing time for memory reduction [54]. Ring attention leverages the blockwise computation of self-attention and feedforward to distribute long sequences across multiple devices while fully overlapping the communication of key-value blocks with the computation of blockwise attention, enabling very-long context training of attention-based methods [38, 39]. The proposed adjoint sharding distributes state-space model computations across multiple devices as well as multiple multi-GPU-instances (MIG) to enable very-long context training of state-space models.
Context length extension methods
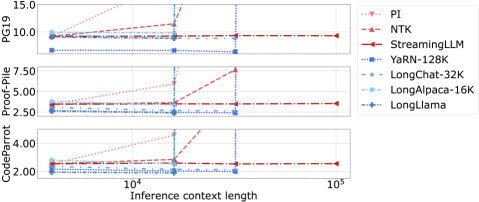
Existing context length extension method separate into two classes. The first type is fine-tuning free methods, including Positional Interpolation (PI) [10], the NTKAware Scale ROPE (NTK) [59], and StreamingLLM [65]. The second type is fine-tuning methods, including LongChat [35], LongAlpaca [11], YaRN [50], and LongLlama [11]. Additional methods such as activation beacon do tune a network seperate from the LLM [68]. As shown in Figure 3, fine-tuning methods achieve better performances than that of fine-tuning free methods at lengths that they have been fine-tuned on. However, fine-tuning methods suffer from a high computational cost and require a potentially intractable amount of GPU memory during fine-tuning.
3 Background
We first give a concise introduction to the state-space models, the residual networks, and the adjoint method.
3.1 State-space models
While our method generally applies to all recurrent models, we illustrate the idea using state-space models (s), which have shown performances at least on par with transformers at small to medium scale [14]. Given an input token sequence , the s first calculate the corresponding matrices , , and to evolve the dynamics as follows:
The s evolve a latent dynamics , whose initial condition is often assumed to be zero. With and defined, the dynamics evolves as:
The matrices then maps the latent dynamics back to token space as , with being the predicted token at . For a sequence of tokens, we denote:
In the most general case, we have , where is the hidden state dimension, and is the input/output dimension. We evolve the dynamics for , and assume that is a fixed and predefined constant.
The input to an is and , and the output is . We define as performing the following five steps:
-
1.
-
2.
-
3.
-
4.
-
5.
The input to the five steps is , and the output is . We can then write . SSMs decrease the quadratic computational complexity with sequence length on transformers to linear and decrease the large inference-time memory requirements from the key-value cache. SSM-based models at a small to medium scale have shown performances on par with or better than transformer-based models. For instance, [51, 1] shows that SSM-based mixture-of-experts (MOE) model outperforms baseline transformer-based MOE model on model sizes as big as 2400M parameters. [62] performed an extensive empirical study and found that while SSMs outperform transformers on various tasks, they underperform on tasks which require strong copying, in-context learning, or long-context reasoning abilities. [62] also experimented with a SSM-transformer hybrid model, which outperforms transformers and is up to eight times faster when generating tokens at inference time. [37] trained a 52B parameter model and further affirmed the hybrid models performances.
3.2 Residual Networks
In practice, we have s stacked together, and we have a large language head (LLH) , where is the number of all possible tokens. To predict a token, we have . Define , a ResNet computes as follows:
where and . Therefore, for a latent state at time we have .
3.3 Adjoint method
The adjoint method is concerned with optimizing with respect to , where is the solution to [8]. To employ gradient based algorithms like the stochastic gradient descent (SGD) or the Adam, we compute the derivative of regarding :
| (1) |
with being the total derivative, and being the partial derivative. The adjoint method converts computing to solving an adjoint equation. In our case, we need the adjoint method for recurrence relations, where is given by , and is given by
| (2) |
We have
| (3) |
Proposition 1
[8] When the states are defined as Equation 2, the gradient of with respect to is given as:
| (4) |
Equivalently, we have [32].
After computing adjoint states , the computation of the elements of are independent, allowing parallelism. This computation is a vector-Jacobian product (), with as the vector and as the Jacobian. s can be evaluated with the reverse-mode automatic differentiation and initializing the reverse phase with [3]. As each only requires saving their corresponding computation graph, and can be disposed after the computation, we can compute s in parallel on modern GPUs. We will discuss this in more details in subsection 4.5. Adjoint sharding aims to use the adjoint method to replace backpropagation, which solves:
The backpropagation requires a sequential accumulation of the gradients, computing from the outmost layer inwards, therefore needs to save the computation graph for computations at all time ’s and creates memory bottlenecks.
4 Adjoint sharding
We now introduce the adjoint sharding technique. We first illustrate the method assuming only one layer of , and generalize to layers.
4.1 Adjoint sharding for one SSM
Large scale neural networks are usually trained with the autograd framework [4, 47]. However, this framework suffers from a high memory cost when used with networks of recurrent nature [4]. Although activation checkpointing has been developed, which discards part of the intermediate values and recomputes them later on the fly, the memory cost is still high [30]. We employ the adjoint method for recurrence relations to further reduce the memory cost, and more importantly, to break the temporal dependencies of activations and parallelize their computations.
Define as ’s, ’s, and ’s parameters, for loss , in the context of a single-layer , we prove:
Proposition 2
The gradient is given as
| (5) |
where the adjoint state , , with being ’s parameters and being the index of , is the vector outer product, and is vector concatenation.
The proof of proposition 2 is in section A.1. The gradient for parameters of , and are each separated into , , and the gradient for parameters of only depend on inputs at time . After computing the adjoint states, these computations are separate from each other on both the network and the temporal level.
4.2 Adjoint sharding for multiple SSMs
We now generalize the results from subsection 4.1 to the general case of s concatenated together. As introduced in subsection 3.2, the outputs of each layer are added to the results of the last layer and normalized before it is fed into the next layer. Define the loss over all token predictions , using the residual structure we have
Combining with proposition 2, we have
Proposition 3
The gradient of the total loss with respect to the parameters is given as
| (6) |
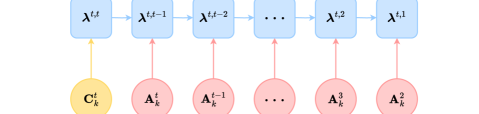
where the input to are computed with the k-th and the (the normalized output sequence of the (k-1)-th ). The adjoint state at layer is defined as .
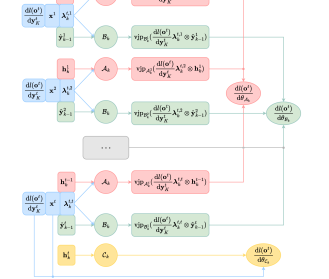
We provide the proof to proposition 3 in section A.2. Define , proposition 3 shows that the gradients of each network’s parameters computed with each token only correlate through the adjoint states . The adjoint states can be easily computed after a forward pass. The adjoint states can also be computed on the fly in the gradient computation phase, as it only depends on and and has no dependencies on the network Jacobians regarding the network parameters. The adjoint sharding method breaks down the backpropagation computation both layer-wise and token-wise into foundational computations that do not have any dependencies on each other.
4.3 Truncated adjoint sharding
One limitation of adjoint sharding is that the number of s performed increases polynomially regarding the number of tokens . In particular, adjoint sharding computes the for and times, and for times. When training large networks with many layers and long context length , applying adjoint sharding becomes computationally expensive. We propose truncated adjoint sharding, with which we argue that we can get similar results by computing a linearly growing number of s, and empirically showcase its performance.
Attention mechanisms have suffered from the complexities arising from the self-attention structure [60]. To enable training with longer context lengths, global-local attention has been proposed, where we divide the contexts into sections, and compute the attention between sections rather than tokens [67]. [57] proposed truncated backpropagation through time (T-BPTT) to avoid gradient explosion/vanishing when training with long contexts by only counting a fixed number of state transitions. Here, inspired by global-local attention and T-BPTT, instead of computing the full gradient given in Equation 11, we propose to train the s to depend on up to states:
| (7) |
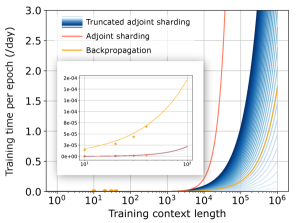
As shown in Equation 7 above, we perform the same computations for as before, and only perform the s back to the last states for . With truncated adjoint sharding, we perform s, which grows linearly. We show the number of s performed with and without truncated adjoint sharding in Figure 6. When , truncated adjoint sharding reduces of the s when training with a context length of .
The essence of the truncated adjoint sharding method is that we only explicitly count gradients related to the last states. As each state depends on its prior state, states still implicitly depend on all their prior states. We leave investigation of ’s impact on performances for future works.
4.4 Distributed training
We now discuss how to distribute the storage and compute of the adjoint sharding method, assuming that we have GPUs. Given the networks , initial tokens , and initial conditions (usually set to ), we can call algorithm 1 to get all necessary vectors for computing the gradient with adjoint sharding.
As shown in algorithm 3, to compute the s’ for token index and ResNet index , we only need . To compute all the gradients for layer , we only need , , and from the -th layer, and from the -th layer. Therefore, we can divide the layers into pieces, as shown in the appendix A.4.
As the computations are fully independent and we compute the gradients using only data on local devices, we additionally distribute the model and the gradients, as shown in Table 6, where represents the parameters of , , and , and represents the optimizer states for .
The complete training streamline is then as shown in algorithm 4. We fully distribute the activations, computations, gradients, and optimization states across devices. While the forward evaluation pass results across different devices, as shown in algorithm 1, the computation of gradients is parallel across the devices. This will speed up the training as the gradient computation takes most of the computation budget. We will also get a memory per GPU close to , with being the memory cost if we only have a single GPU. If we have devices, we can further speed up the forward evaluation by first evaluating , , in parallel, and then sequentially add them together on the distributed devices.
4.5 Parallel computing
Adjoint sharding converts the sequential process of backpropagation gradient computation into individual independent s, allowing for parallel computation. We analyze the time and memory cost of , , and .
has a similar time complexity as a forward pass, and a memory complexity of , where is the batch size, is the number of elements in the network output, and is the number of parameters [42]. We provide the memory and FLOPs required to compute the s in Table 1 [43].
| Unstructured SSM | Memory | |||
|---|---|---|---|---|
| FLOPs | ||||
| Diagonal SSM | Memory | |||
| FLOPs | ||||
| Scalar SSM | Memory | |||
| FLOPs | ||||
We analyze training with a dataset containing contexts of lengths , with NVIDIA H100 GPUs, and performing computations in FP16. We use a selective diagonal SSM with layers, and each , , and network is a single-layer multi-layer perceptron (MLP).
For each data point , we store and , which is FP16 numbers. We also save , , and , each taking FP16 numbers. We need to store FP16 numbers before computing the .
As computing all adjoint state sequences takes up to FLOPs, it takes FLOPs on average for each adjoint state. For large enough, , and we approximate the average FLOPs for each adjoint state with . Each then takes FLOPs of computation.
When computing with a selective diagonal SSM with , , and , while storing and performing computations in FP16, computing , , and each takes around memory and FLOPs. The capacity of a modern GPU is mostly characterized by FLOPs/sec, which measures the computation speed; GPU memory bandwidth, which is the rate at which a GPU can move data between its memory and processing cores; GPU Memory, which is the amount of data a GPU can hold; and number of Multi-Instance GPU (MIG) instances, which is the number of fully isolated GPU instances with its own high-bandwidth memory, cache, and compute cores a GPU can host.
An NVIDIA H100 Tensor Core GPU has a GPU memory bandwidth and performs tera FP16 FLOPS per second. Therefore, the memory bandwidth allows computing batches of s per second, and the computing speed allows computing batches of s per second. At the same time, since the H100 GPU has memory, it can hold up to batches of s at the same time if we do not consider any memory overhead. As each H100 GPU can hold up to instances in parallel, we perform the adjoint sharding algorithm with instances, offering as much as a 56x speedup on one AWS P4 instance (8 H100 GPUs). Such speedup cannot be achieved for backpropagation because of its sequential nature.
Limitation
The adjoint sharding method provides an alternative method of computing gradients to backpropagation. While we analytically proved that the gradients computed from adjoint sharding equals to that from backpropagation, adjoint sharding suffer from a time complexity polynomial regarding the training context length when computing equivalent gradients. We provided the truncated adjoint sharding as a linear time complexity alternative, and leave the analysis of its convergence and further improvements on it for future works. We also provided a distributed and parallel computing algorithm for performing adjoint sharding. However, the overhead of naïve implementation of such algorithm with multi-threading or multiprocessing overweights the speedups when the training context length is small. We leave efficient implementation of the parallel algorithm on a CUDA kernel for future work.
Conclusion
We introduced adjoint sharding, a distributed and parallel computing algorithm, to facilitate training of LLMs on long contexts. Unlike the sequential backpropagation, the adjoint sharding computes gradients of each LLM layer against each token independently through vector-Jacobian product, allowing for parallel computation. To avoid the limitation of s increasing polynomially regarding context length, we propose truncated adjoint sharding to focus on important gradients. We analyzed the memory and FLOP cost of each computation block in adjoint sharding and proposed a method to accelerate it through parallel computing. Empirical results suggest orders of magnitude of memory reduction in training while maintaining the same training results as backpropagation.
References
- Anthony et al. [2024] Quentin Anthony, Yury Tokpanov, Paolo Glorioso, and Beren Millidge. Blackmamba: Mixture of experts for state-space models, 2024. URL https://arxiv.org/abs/2402.01771.
- Balestriero and Baraniuk [2021] Randall Balestriero and Richard Baraniuk. Fast jacobian-vector product for deep networks, 2021. URL https://arxiv.org/abs/2104.00219.
- Baydin et al. [2018a] Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, and Jeffrey Mark Siskind. Automatic differentiation in machine learning: a survey, 2018a. URL https://arxiv.org/abs/1502.05767.
- Baydin et al. [2018b] Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, and Jeffrey Mark Siskind. Automatic differentiation in machine learning: a survey, 2018b. URL https://arxiv.org/abs/1502.05767.
- Beck et al. [2024] Maximilian Beck, Korbinian Pöppel, Markus Spanring, Andreas Auer, Oleksandra Prudnikova, Michael Kopp, Günter Klambauer, Johannes Brandstetter, and Sepp Hochreiter. xlstm: Extended long short-term memory, 2024. URL https://arxiv.org/abs/2405.04517.
- Beltagy et al. [2020] Iz Beltagy, Matthew E. Peters, and Arman Cohan. Longformer: The long-document transformer, 2020. URL https://arxiv.org/abs/2004.05150.
- Cai et al. [2024] Zheng Cai, Maosong Cao, Haojiong Chen, Kai Chen, Keyu Chen, Xin Chen, et al. Internlm2 technical report, 2024. URL https://arxiv.org/abs/2403.17297.
- Cao et al. [2002] Yang Cao, Shengtai Li, and Linda Petzold. Adjoint sensitivity analysis for differential-algebraic equations: algorithms and software. Journal of Computational and Applied Mathematics, 149(1):171–191, 2002. ISSN 0377-0427. doi: https://doi.org/10.1016/S0377-0427(02)00528-9. URL https://www.sciencedirect.com/science/article/pii/S0377042702005289. Scientific and Engineering Computations for the 21st Century - Me thodologies and Applications Proceedings of the 15th Toyota Conference.
- Chen et al. [2019] Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, and David Duvenaud. Neural ordinary differential equations, 2019. URL https://arxiv.org/abs/1806.07366.
- Chen et al. [2023] Shouyuan Chen, Sherman Wong, Liangjian Chen, and Yuandong Tian. Extending context window of large language models via positional interpolation, 2023. URL https://arxiv.org/abs/2306.15595.
- Chen et al. [2024] Yukang Chen, Shengju Qian, Haotian Tang, Xin Lai, Zhijian Liu, Song Han, and Jiaya Jia. Longlora: Efficient fine-tuning of long-context large language models, 2024. URL https://arxiv.org/abs/2309.12307.
- Damadi et al. [2023] Saeed Damadi, Golnaz Moharrer, and Mostafa Cham. The backpropagation algorithm for a math student, 2023. URL https://arxiv.org/abs/2301.09977.
- Dao [2023] Tri Dao. Flashattention-2: Faster attention with better parallelism and work partitioning, 2023. URL https://arxiv.org/abs/2307.08691.
- Dao and Gu [2024a] Tri Dao and Albert Gu. Transformers are ssms: Generalized models and efficient algorithms through structured state space duality, 2024a. URL https://arxiv.org/abs/2405.21060.
- Dao and Gu [2024b] Tri Dao and Albert Gu. Transformers are ssms: Generalized models and efficient algorithms through structured state space duality, 2024b. URL https://arxiv.org/abs/2405.21060.
- Dao et al. [2022] Tri Dao, Daniel Y. Fu, Stefano Ermon, Atri Rudra, and Christopher Ré. Flashattention: Fast and memory-efficient exact attention with io-awareness, 2022. URL https://arxiv.org/abs/2205.14135.
- De et al. [2024] Soham De, Samuel L. Smith, Anushan Fernando, Aleksandar Botev, George Cristian-Muraru, Albert Gu, Ruba Haroun, Leonard Berrada, Yutian Chen, Srivatsan Srinivasan, Guillaume Desjardins, Arnaud Doucet, David Budden, Yee Whye Teh, Razvan Pascanu, Nando De Freitas, and Caglar Gulcehre. Griffin: Mixing gated linear recurrences with local attention for efficient language models, 2024. URL https://arxiv.org/abs/2402.19427.
- Ding et al. [2024a] Yiran Ding, Li Lyna Zhang, Chengruidong Zhang, Yuanyuan Xu, Ning Shang, Jiahang Xu, Fan Yang, and Mao Yang. Longrope: Extending llm context window beyond 2 million tokens. arXiv preprint arXiv:2402.13753, 2024a.
- Ding et al. [2024b] Yiran Ding, Li Lyna Zhang, Chengruidong Zhang, Yuanyuan Xu, Ning Shang, Jiahang Xu, Fan Yang, and Mao Yang. Longrope: Extending llm context window beyond 2 million tokens, 2024b. URL https://arxiv.org/abs/2402.13753.
- Dupont et al. [2019] Emilien Dupont, Arnaud Doucet, and Yee Whye Teh. Augmented neural odes, 2019. URL https://arxiv.org/abs/1904.01681.
- Fu et al. [2023] Daniel Y. Fu, Tri Dao, Khaled K. Saab, Armin W. Thomas, Atri Rudra, and Christopher Ré. Hungry hungry hippos: Towards language modeling with state space models, 2023. URL https://arxiv.org/abs/2212.14052.
- Gu and Dao [2024a] Albert Gu and Tri Dao. Mamba: Linear-time sequence modeling with selective state spaces, 2024a. URL https://arxiv.org/abs/2312.00752.
- Gu and Dao [2024b] Albert Gu and Tri Dao. Mamba: Linear-time sequence modeling with selective state spaces, 2024b. URL https://arxiv.org/abs/2312.00752.
- Gu et al. [2021] Albert Gu, Isys Johnson, Karan Goel, Khaled Saab, Tri Dao, Atri Rudra, and Christopher Ré. Combining recurrent, convolutional, and continuous-time models with linear state-space layers, 2021. URL https://arxiv.org/abs/2110.13985.
- Gu et al. [2022] Albert Gu, Isys Johnson, Aman Timalsina, Atri Rudra, and Christopher Ré. How to train your hippo: State space models with generalized orthogonal basis projections, 2022. URL https://arxiv.org/abs/2206.12037.
- Guo et al. [2022] Meng-Hao Guo, Tian-Xing Xu, Jiang-Jiang Liu, Zheng-Ning Liu, Peng-Tao Jiang, Tai-Jiang Mu, Song-Hai Zhang, Ralph R Martin, Ming-Ming Cheng, and Shi-Min Hu. Attention mechanisms in computer vision: A survey. Computational visual media, 8(3):331–368, 2022.
- Gupta et al. [2023] Ankit Gupta, Harsh Mehta, and Jonathan Berant. Simplifying and understanding state space models with diagonal linear rnns, 2023. URL https://arxiv.org/abs/2212.00768.
- He et al. [2015] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition, 2015. URL https://arxiv.org/abs/1512.03385.
- He et al. [2016] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2016.
- Herrmann et al. [2019] Julien Herrmann, Olivier Beaumont, Lionel Eyraud-Dubois, Julien Hermann, Alexis Joly, and Alena Shilova. Optimal checkpointing for heterogeneous chains: how to train deep neural networks with limited memory, 2019. URL https://arxiv.org/abs/1911.13214.
- Jaeger [2005] Herbert Jaeger. A tutorial on training recurrent neural networks , covering bppt , rtrl , ekf and the ” echo state network ” approach - semantic scholar. In National Research Center for Information Technology, 2002, 2005. URL https://api.semanticscholar.org/CorpusID:192593367.
- Johnson [2007] Steven Johnson. Adjoint methods and sensitivity analysis for recurrence, 01 2007.
- Kaul [2020] Shiva Kaul. Linear dynamical systems as a core computational primitive. In H. Larochelle, M. Ranzato, R. Hadsell, M.F. Balcan, and H. Lin, editors, Advances in Neural Information Processing Systems, volume 33, pages 16808–16820. Curran Associates, Inc., 2020. URL https://proceedings.neurips.cc/paper_files/paper/2020/file/c3581d2150ff68f3b33b22634b8adaea-Paper.pdf.
- Kirillov et al. [2023] Alexander Kirillov, Eric Mintun, Nikhila Ravi, Hanzi Mao, Chloe Rolland, Laura Gustafson, Tete Xiao, Spencer Whitehead, Alexander C Berg, Wan-Yen Lo, et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 4015–4026, 2023.
- Li* et al. [2023] Dacheng Li*, Rulin Shao*, Anze Xie, Ying Sheng, Lianmin Zheng, Joseph E. Gonzalez, Ion Stoica, Xuezhe Ma, and Hao Zhang. How long can open-source llms truly promise on context length?, June 2023. URL https://lmsys.org/blog/2023-06-29-longchat.
- Li et al. [2024] Tianle Li, Ge Zhang, Quy Duc Do, Xiang Yue, and Wenhu Chen. Long-context llms struggle with long in-context learning, 2024. URL https://arxiv.org/abs/2404.02060.
- Lieber et al. [2024] Opher Lieber, Barak Lenz, Hofit Bata, Gal Cohen, Jhonathan Osin, Itay Dalmedigos, Erez Safahi, Shaked Meirom, Yonatan Belinkov, Shai Shalev-Shwartz, Omri Abend, Raz Alon, Tomer Asida, Amir Bergman, Roman Glozman, Michael Gokhman, Avashalom Manevich, Nir Ratner, Noam Rozen, Erez Shwartz, Mor Zusman, and Yoav Shoham. Jamba: A hybrid transformer-mamba language model, 2024. URL https://arxiv.org/abs/2403.19887.
- Liu et al. [2023] Hao Liu, Matei Zaharia, and Pieter Abbeel. Ring attention with blockwise transformers for near-infinite context, 2023. URL https://arxiv.org/abs/2310.01889.
- Liu et al. [2024] Hao Liu, Wilson Yan, Matei Zaharia, and Pieter Abbeel. World model on million-length video and language with blockwise ringattention, 2024. URL https://arxiv.org/abs/2402.08268.
- Meta et al. [2024] Meta et al. The llama 3 herd of models, 2024. URL https://arxiv.org/abs/2407.21783.
- Micikevicius et al. [2018] Paulius Micikevicius, Sharan Narang, Jonah Alben, Gregory Diamos, Erich Elsen, David Garcia, Boris Ginsburg, Michael Houston, Oleksii Kuchaiev, Ganesh Venkatesh, and Hao Wu. Mixed precision training, 2018. URL https://arxiv.org/abs/1710.03740.
- Novak et al. [2022] Roman Novak, Jascha Sohl-Dickstein, and Samuel S. Schoenholz. Fast finite width neural tangent kernel, 2022. URL https://arxiv.org/abs/2206.08720.
- NVIDIA [2024] NVIDIA. Matrix multiplication background user’s guide, 2024. URL https://docs.nvidia.com/deeplearning/performance/dl-performance-matrix-multiplication/index.html.
- OpenAI et al. [2024] OpenAI et al. Gpt-4 technical report, 2024. URL https://arxiv.org/abs/2303.08774.
- Orvieto et al. [2023] Antonio Orvieto, Samuel L Smith, Albert Gu, Anushan Fernando, Caglar Gulcehre, Razvan Pascanu, and Soham De. Resurrecting recurrent neural networks for long sequences, 2023. URL https://arxiv.org/abs/2303.06349.
- Pascanu et al. [2013] Razvan Pascanu, Tomas Mikolov, and Yoshua Bengio. On the difficulty of training recurrent neural networks, 2013. URL https://arxiv.org/abs/1211.5063.
- Paszke et al. [2019] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Köpf, Edward Yang, Zach DeVito, Martin Raison, Alykhan Tejani, Sasank Chilamkurthy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. Pytorch: An imperative style, high-performance deep learning library, 2019. URL https://arxiv.org/abs/1912.01703.
- Peebles and Xie [2023] William Peebles and Saining Xie. Scalable diffusion models with transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 4195–4205, 2023.
- Peng et al. [2023a] Bo Peng, Eric Alcaide, Quentin Anthony, Alon Albalak, Samuel Arcadinho, Stella Biderman, Huanqi Cao, Xin Cheng, Michael Chung, Matteo Grella, Kranthi Kiran GV, Xuzheng He, Haowen Hou, Jiaju Lin, Przemyslaw Kazienko, Jan Kocon, Jiaming Kong, Bartlomiej Koptyra, Hayden Lau, Krishna Sri Ipsit Mantri, Ferdinand Mom, Atsushi Saito, Guangyu Song, Xiangru Tang, Bolun Wang, Johan S. Wind, Stanislaw Wozniak, Ruichong Zhang, Zhenyuan Zhang, Qihang Zhao, Peng Zhou, Qinghua Zhou, Jian Zhu, and Rui-Jie Zhu. Rwkv: Reinventing rnns for the transformer era, 2023a. URL https://arxiv.org/abs/2305.13048.
- Peng et al. [2023b] Bowen Peng, Jeffrey Quesnelle, Honglu Fan, and Enrico Shippole. Yarn: Efficient context window extension of large language models, 2023b. URL https://arxiv.org/abs/2309.00071.
- Pióro et al. [2024] Maciej Pióro, Kamil Ciebiera, Krystian Król, Jan Ludziejewski, Michał Krutul, Jakub Krajewski, Szymon Antoniak, Piotr Miłoś, Marek Cygan, and Sebastian Jaszczur. Moe-mamba: Efficient selective state space models with mixture of experts, 2024. URL https://arxiv.org/abs/2401.04081.
- Rajbhandari et al. [2020a] Samyam Rajbhandari, Jeff Rasley, Olatunji Ruwase, and Yuxiong He. Zero: Memory optimizations toward training trillion parameter models, 2020a. URL https://arxiv.org/abs/1910.02054.
- Rajbhandari et al. [2020b] Samyam Rajbhandari, Jeff Rasley, Olatunji Ruwase, and Yuxiong He. Zero: Memory optimizations toward training trillion parameter models, 2020b. URL https://arxiv.org/abs/1910.02054.
- Ren et al. [2021] Jie Ren, Samyam Rajbhandari, Reza Yazdani Aminabadi, Olatunji Ruwase, Shuangyan Yang, Minjia Zhang, Dong Li, and Yuxiong He. Zero-offload: Democratizing billion-scale model training, 2021. URL https://arxiv.org/abs/2101.06840.
- Shah et al. [2024] Jay Shah, Ganesh Bikshandi, Ying Zhang, Vijay Thakkar, Pradeep Ramani, and Tri Dao. Flashattention-3: Fast and accurate attention with asynchrony and low-precision, 2024. URL https://arxiv.org/abs/2407.08608.
- Sohoni et al. [2022] Nimit S. Sohoni, Christopher R. Aberger, Megan Leszczynski, Jian Zhang, and Christopher Ré. Low-memory neural network training: A technical report, 2022. URL https://arxiv.org/abs/1904.10631.
- Tallec and Ollivier [2017] Corentin Tallec and Yann Ollivier. Unbiasing truncated backpropagation through time, 2017. URL https://arxiv.org/abs/1705.08209.
- Tworkowski et al. [2023] Szymon Tworkowski, Konrad Staniszewski, Mikołaj Pacek, Yuhuai Wu, Henryk Michalewski, and Piotr Miłoś. Focused transformer: Contrastive training for context scaling, 2023. URL https://arxiv.org/abs/2307.03170.
- users [2023] Reddit users. Ntk-aware scaled rope, 2023. URL https://www.reddit.com/r/LocalLLaMA/comments/14lz7j5/ntkaware_scaled_rope_allows_llama_models_to_have/.
- Vaswani et al. [2023] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. Attention is all you need, 2023. URL https://arxiv.org/abs/1706.03762.
- Verbraeken et al. [2020] Joost Verbraeken, Matthijs Wolting, Jonathan Katzy, Jeroen Kloppenburg, Tim Verbelen, and Jan S. Rellermeyer. A survey on distributed machine learning. ACM Computing Surveys, 53(2):1–33, March 2020. ISSN 1557-7341. doi: 10.1145/3377454. URL http://dx.doi.org/10.1145/3377454.
- Waleffe et al. [2024] Roger Waleffe, Wonmin Byeon, Duncan Riach, Brandon Norick, Vijay Korthikanti, Tri Dao, Albert Gu, Ali Hatamizadeh, Sudhakar Singh, Deepak Narayanan, Garvit Kulshreshtha, Vartika Singh, Jared Casper, Jan Kautz, Mohammad Shoeybi, and Bryan Catanzaro. An empirical study of mamba-based language models, 2024. URL https://arxiv.org/abs/2406.07887.
- Wang and Xue [2023] Shida Wang and Beichen Xue. State-space models with layer-wise nonlinearity are universal approximators with exponential decaying memory, 2023. URL https://arxiv.org/abs/2309.13414.
- Werbos [1990] P.J. Werbos. Backpropagation through time: what it does and how to do it. Proceedings of the IEEE, 78(10):1550–1560, 1990. doi: 10.1109/5.58337.
- Xiao et al. [2024] Guangxuan Xiao, Yuandong Tian, Beidi Chen, Song Han, and Mike Lewis. Efficient streaming language models with attention sinks, 2024. URL https://arxiv.org/abs/2309.17453.
- Xu et al. [2022] Xingzi Xu, Ali Hasan, Khalil Elkhalil, Jie Ding, and Vahid Tarokh. Characteristic neural ordinary differential equations, 2022. URL https://arxiv.org/abs/2111.13207.
- Yang et al. [2021] Jianwei Yang, Chunyuan Li, Pengchuan Zhang, Xiyang Dai, Bin Xiao, Lu Yuan, and Jianfeng Gao. Focal self-attention for local-global interactions in vision transformers, 2021. URL https://arxiv.org/abs/2107.00641.
- Zhang et al. [2024] Peitian Zhang, Zheng Liu, Shitao Xiao, Ninglu Shao, Qiwei Ye, and Zhicheng Dou. Soaring from 4k to 400k: Extending llm’s context with activation beacon, 2024. URL https://arxiv.org/abs/2401.03462.
- Zhao et al. [2023] Yanli Zhao, Andrew Gu, Rohan Varma, Liang Luo, Chien-Chin Huang, Min Xu, Less Wright, Hamid Shojanazeri, Myle Ott, Sam Shleifer, Alban Desmaison, Can Balioglu, Pritam Damania, Bernard Nguyen, Geeta Chauhan, Yuchen Hao, Ajit Mathews, and Shen Li. Pytorch fsdp: Experiences on scaling fully sharded data parallel, 2023. URL https://arxiv.org/abs/2304.11277.
Appendix A Appendix
A.1 Proof for proposition 2
Proof 1
Define , , and , , by plugging in the expression for from subsection 3.2, proposition 1 states that
In the context of , we have:
| (8) |
Plugging in these relations, we get:
| (9) |
Define the adjoint state , we have
Therefore, we have
Plug in everything, we have
where we define , with being ’s parameters and being the index of . Now, as , , and are separate, we have
| (10) |
where is vector concatenation.
A.2 Proof for proposition 3
Proof 2
First, using the structure of ResNet, we have
from proposiiton 2, we have proven that for a single SSM model, we have
so for the ResNet model, we have
| (11) |
where the input to are computed with the k-th and the (the normalized output sequence of the (k-1)-th ), and the adjoint state .
A.3 Proof of concept for VJP
As a proof of concept of why can computed with , we present an explicit and simple example. We have , , . We then have
With each . We have
where is vector dot product, is vector outer product, is element-wise product, and means summing all elements in a matrix.
A.4 Distributed tensors’ locations
We provide the specific location for each tensors in distributed training:
| GPU index | ||
|---|---|---|
| GPU index | |
|---|---|
| GPU index | |
|---|---|
| GPU index | |
|---|---|
| GPU index | ||
|---|---|---|