Adjusting inverse regression for predictors with clustered distribution

Sufficient dimension reduction (SDR) has attracted intensive research interest in the recent years due to the need of high-dimensional statistical data analysis. Usually, SDR assumes that the predictor $X$ affects the response $Y$ through a lower-dimensional $\beta^{\mbox{\tiny{\sf T}}}X$, that is,

where         means independence; and the research interest of SDR is to find the qualified $\beta^{\mbox{\tiny{\sf T}}}X$ as the subsequent predictor in a model-free manner, i.e. without parametric assumptions on $Y|\beta^{\mbox{\tiny{\sf T}}}X$. For identifiability, Cook (1998) introduced the central subspace, denoted by ${\mathcal{S}}_{\scriptscriptstyle Y|X}$, as the parameter of interest, whose arbitrary basis matrix satisfies (1) with minimal number of columns. This space is unique under fairly general conditions (Yin, Li and Cook, 2008).

When the research interest is focused on regression analysis, SDR is adjusted to find $\beta^{\mbox{\tiny{\sf T}}}X$ that only preserves the information about regression, i.e. $E(Y|X)$ being measurable with respect to $\beta^{\mbox{\tiny{\sf T}}}X$. Similar to ${\mathcal{S}}_{\scriptscriptstyle Y|X}$, the unique parameter of interest in this scenario is called the central mean subspace and denoted by ${\mathcal{S}}_{\scriptscriptstyle E(Y|X)}$ (Cook and Li, 2002). For ease of presentation, we do not distinguish the two parameters ${\mathcal{S}}_{\scriptscriptstyle E(Y|X)}$ and ${\mathcal{S}}_{\scriptscriptstyle Y|X}$ unless otherwise specified, and call both the central SDR subspace uniformly. Let $d$ be the dimension of the central SDR subspace and $\beta_{\scriptscriptstyle 0}\in\mathbb{R}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle p\times d$}}}$ be its arbitrary basis matrix.

In the literature, a major family of estimators for the central SDR subspace is called inverse regression, which includes the ordinary least squares (OLS; Li and Duan, 1989) and principal Hessian directions (pHd; Li, 1992) that estimate ${\mathcal{S}}_{\scriptscriptstyle E(Y|X)}$, and sliced inverse regression (SIR; Li, 1991), sliced average variance estimator (SAVE; Cook and Weisberg, 1991), and directional regression (DR; Li and Wang, 2007) that estimate ${\mathcal{S}}_{\scriptscriptstyle Y|X}$, etc. A common feature of the inverse regression methods is that they first use the moments of $X|Y$ to construct a matrix-valued parameter ${\Omega}$, whose columns fall in the central SDR subspace under certain parametric assumptions of $X$, and then use an estimate of ${\Omega}$ to recover the central SDR subspace. Suppose $X$ has zero mean and covariance matrix $\Sigma_{\scriptscriptstyle X}$. The forms of ${\Omega}$ for OLS, SIR, and SAVE are, respectively,

where $v^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle\otimes 2$}}}$ denotes $vv^{\mbox{\tiny{\sf T}}}$ for any matrix $v$. Clearly, ${\Omega}$ is readily estimable when $Y$ is discrete with limited number of outcomes. To ease the estimation for continuous $Y$ (except for OLS), the slicing technic is commonly applied to replace a univariate $Y$ in ${\Omega}$ with $Y_{\scriptscriptstyle S}=\textstyle\sum_{\scriptscriptstyle i=1}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle H$}}}iI(q_{\scriptscriptstyle i-1}<Y\leq q_{\scriptscriptstyle i})$, $H$ being a fixed integer and $q_{\scriptscriptstyle i}$ being the $(i/H)$th quantile of $Y$; the case of multivariate $Y$ follows similarly. Because the moments of $X|Y_{\scriptscriptstyle S}$ can be estimated by the sample moments within each slice $(q_{\scriptscriptstyle i},q_{\scriptscriptstyle i+1})$, a consistent estimator of ${\Omega}$, denoted by $\widehat{\Omega}$, can be readily constructed. The central SDR subspace is then estimated by the linear span of the leading left singular vectors of $\widehat{\Omega}$.

Despite their popularity in applications, the inverse regression methods are also commonly criticized for the aforementioned parametric assumptions on $X$. For example, the first-order inverse regression methods, i.e. OLS and SIR that only involve $E(X|Y)$ or its average $E(XY)$, require the linearity condition

where $P(\Sigma_{\scriptscriptstyle X},\beta)=\beta(\beta^{\mbox{\tiny{\sf T}}}\Sigma_{\scriptscriptstyle X}\beta)^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle-1$}}}\beta^{\mbox{\tiny{\sf T}}}\Sigma_{\scriptscriptstyle X}$ is the projection matrix onto the column space of $\beta$ under the inner product $\langle u,v\rangle=u^{\mbox{\tiny{\sf T}}}\Sigma_{\scriptscriptstyle X}v$. The second-order inverse regression methods that additionally involve $\mathrm{var}(X|Y)$, e.g. pHd, SAVE, and directional regression, require both the linearity condition (3) and the constant variance condition

Since both conditions adopt simple parametric forms on the moments of $X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$, they can be violated in practice. Moreover, as the central SDR subspace is unknown, both (3) and (4) are often strengthened to that they hold for any $\beta\in\mathbb{R}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle p\times d$}}}$. The strengthened linearity condition requires $X$ to be elliptically distributed (Li, 1991), and, together with the strengthened constant variance condition, $X$ must have a multivariate normal distribution (Cook and Weisberg, 1991). Hall and Li (1993) justified the approximate satisfaction of (3) for general $X$ as $p$ grows, but their theory is developed for diverging $p$, and, more importantly, it is built in a Bayesian sense that $\beta_{\scriptscriptstyle 0}$ follows a continuous prior distribution on $\mathbb{R}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle p\times d$}}}$. In the literature of high-dimensional SDR (Chen, Zou and Cook, 2010; Lin, Zhao and Liu, 2016; Zeng, Mai and Zhang, 2022), sparsity is commonly assumed on the central SDR subspace so that $\beta_{\scriptscriptstyle 0}$ only has a few nonzero rows. Thus, Hall and Li’s result is often inapplicable.

To enhance the applicability of inverse regression, multiple methods have been proposed to relax the linearity condition (3). Li and Dong (2009) and Dong and Li (2010) allow $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ to lie in a general finite-dimensional functional space, and they reformulate the inverse regression methods accordingly as minimizing certain objective functions. However, the non-convexity of the objective functions may complicate the implementation, and, unlike the connection between the linearity condition and the ellipticity of $X$, the relaxed linearity condition is lack of interpretability. Another effort specified for SIR can be found in Guan, Xie and Zhu (2017), which assumes $X$ to follow a mixture of skew-elliptical distributions with identical shape parameters up to multiplicative scalars. Guan, Xie and Zhu’s method can be easily implemented once the mixture model of $X$ is consistently fitted.

In a certain sense, the minimum average variance estimator (MAVE; Xia et al., 2002), a state-of-the-art SDR method that estimates the central mean subspace ${\mathcal{S}}_{\scriptscriptstyle E(Y|X)}$ by local linear regression, can also be regarded as relaxing the linearity condition (3) for OLS. Recall that OLS is commonly used to estimate the coefficients, i.e. the one-dimensional ${\mathcal{S}}_{\scriptscriptstyle E(Y|X)}$, of the linear model of $E(Y|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$. Thus, the linearity condition (3) on $X$ can be regarded as a surrogate to the assumption of linear $E(Y|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ for SDR estimation. As MAVE adopts and fits a linear $E(Y|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ in each local neighborhood of $X$, it equivalently adopts the linearity condition in these neighborhoods, which only requires the first-order Taylor expansion of $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ and thus is fairly general.

Following the same spirit as MAVE, the aggregate dimension reduction (ADR; Wang et al., 2020) conducts SIR in the local neighborhoods of $X$ and thus also relaxes the linearity condition. Recently, the idea of localization was also studied in Fertl and Bura (2022), who proposed both the cumulative covariance estimator (CVE) to recover ${\mathcal{S}}_{\scriptscriptstyle E(Y|X)}$ and the enemble CVE (eCVE) to recover ${\mathcal{S}}_{\scriptscriptstyle Y|X}$. For convenience, we call MAVE, ADR, CVE, eCVE, and other SDR methods based on localized estimation uniformly the MAVE-type methods. By the nature of localized estimation, these methods share the common limitation that they quickly lose consistency as $p$ grows.

Generally, the conjugate between the parametric assumptions on $X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$, i.e. (3) and (4), and the parametric assumptions on $Y|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$ can be formulated under the unified SDR framework proposed in Ma and Zhu (2012). In the population level, each SDR method in this framework solves the estimating equation

for certain $\alpha(X)$ and $g(Y,\beta^{\mbox{\tiny{\sf T}}}X)$, where $\mu_{\scriptscriptstyle\alpha}(\beta^{\mbox{\tiny{\sf T}}}X)$ and $\mu_{\scriptscriptstyle g}(\beta^{\mbox{\tiny{\sf T}}}X)$ are the working models for $E\{\alpha(X)|\beta^{\mbox{\tiny{\sf T}}}X\}$ and $E\{g(Y,\beta^{\mbox{\tiny{\sf T}}}X)|\beta^{\mbox{\tiny{\sf T}}}X\}$, respectively. Ma and Zhu (2012) justified a double-robust property that, as long as either $\mu_{\scriptscriptstyle\alpha}(\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ or $\mu_{\scriptscriptstyle g}(\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ truly specifies the corresponding regression function when $\beta$ is fixed at $\beta_{\scriptscriptstyle 0}$, any minimal solution to (5) must be included in the central SDR subspace. Up to asymptotically negligible errors, (5) incorporates a large family of SDR methods. For example, with $\alpha(X)=X$ and the linearity condition (3), one can take linear $\mu_{\scriptscriptstyle\alpha}(\beta^{\mbox{\tiny{\sf T}}}X)$ and force $\mu_{\scriptscriptstyle g}(\beta^{\mbox{\tiny{\sf T}}}X)$ to be zero, and solving (5) delivers OLS if $g(Y,\beta^{\mbox{\tiny{\sf T}}}X)$ is $Y$ and delivers SIR if it is $(I(Y_{\scriptscriptstyle S}=1),\ldots,I(Y_{\scriptscriptstyle S}=H))$.

The double-robustness property for (5) illuminates the tradeoff for general SDR methods: if we choose to avoid parametric assumptions or nonparametric estimation on $Y|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$, then we must adopt those on $X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$ instead. In principle, like the rich literature for modeling $Y|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$, numerous assumptions can be adopted on $X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$ to represent different balances between parsimoniousness and flexibility. Nonetheless, under the unified framework (5), only the two extremes have been widely studied in the SDR literature: the most aggressive parametric models (3) and (4) in inverse regression, and the most conservative nonparametric model in MAVE. Although a compromise between the two was discussed by Li and Dong (2009) and Dong and Li (2010) as mentioned above, there is lack of parametric learning of $X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$ that specifies easily interpretable conditional moments and is often satisfied in practice.

In this paper, we adjust both the first- and second-order inverse regression methods by approximating the distribution of $X$ with mixture models, where we allow each mixture component to differ in either center or shape but it must satisfy the linearity condition (3) and the constant variance condition (4). The mixture model approximation has been widely used in applications to fit generally unknown distributions (Lindsay, 1995; Everitt, 2013), especially those with clustered sample support, and it permits estimating each of $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ and $\mathrm{var}(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ by one of multiple commonly seen parametric models chosen in a data-driven manner. As supported by numerical studies, the proposed methods also have a consistent sample performance under more complex settings, for example, if $X$ has a unimodal but curved sample support. Compared with the MAVE-type methods, our approach is more robust to the dimensionality and in particular effective under the high-dimensional settings. Compared with Guan, Xie and Zhu (2017), it allows the mixture components to have different shapes and is applicable for all the second-order inverse regression methods. It also alleviates the issue of non-exhaustive recovery of the central SDR subspace that persists in OLS and SIR, in a similar fashion to MAVE and ADR that capture the local patterns of data.

The rest of the paper is organized as follows. Throughout the theoretical development, we assume $X$ to be continuous and follow a mixture model, under which the parametric forms of the moments of $X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$ are studied in Section $2$. We adjust SIR in Section $3$, and further modify it towards sparsity under the high-dimensional settings in Section 4. Section 5 is devoted for the adjustment of SAVE. The simulation studies are presented in Section 6, where we evaluate the performance of the proposed methods under various settings, including the cases where $X$ does not follow a mixture model. A real data example is investigated in Section 7. The adjustment for OLS is omitted for its similarity to SIR. The adjustments of other second-order inverse regression methods, as well as the detailed implementation and complementery simulation studies, are deferred to the Appendix. R code for implementing the proposed methods can be downloaded at https://github.com/Yan-Guo1120/IRMN. For convenience, we focus on continuous $Y$ whose sample slices have an equal size, and we regard the dimension $d$ of the central SDR subspace as known a priori. The generality of the latter is briefly justified in Section 2, given the consistent estimation of $d$ discussed in Sections 3 and 5.

We first clarify the notations. Suppose $X=(X_{\scriptscriptstyle 1},\ldots,X_{\scriptscriptstyle p})^{\mbox{\tiny{\sf T}}}$. For any matrix $\beta\in\mathbb{R}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle p\times d$}}}$, let ${\mathcal{S}}({\beta})$ be the column space of $\beta$ and let ${\mathrm{vec}}(\beta)$ be the vector that stacks the columns of $\beta$ together. Like $\beta^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle\otimes 2$}}}$ in (2), sometimes we also denote $\beta$ itself by $\beta^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle\otimes 1$}}}$. We expand $P(\Sigma_{\scriptscriptstyle X},\beta)$ in (3) to $P(\Lambda,\beta)$ for any positive definite matrix $\Lambda$, and, with $\mathrm{I}_{\scriptscriptstyle p}$ being the identity matrix, we denote $\mathrm{I}_{\scriptscriptstyle p}-P(\Lambda,\beta)$ by $Q(\Lambda,\beta)$. For a set of matrices $\{{\Omega}_{\scriptscriptstyle i}:i\in\{1,\ldots,k\}\}$ with equal number of rows, we denote the ensemble matrix $({\Omega}_{\scriptscriptstyle 1},\ldots,{\Omega}_{\scriptscriptstyle k})$ by $({\Omega}_{\scriptscriptstyle i})_{\scriptscriptstyle i\in\{1,\ldots,k\}}$.

In the literature, the mixture model has been widely employed to approximate unknown distributions (Lindsay, 1995; Everitt, 2013), both clustered and non-clustered, as it provides a wide range of choices to balance between the estimation efficiency and the modeling flexibility, especially for the local patterns of data. Application fields include, for example, astronomy, bioinformatics, ecology, and economics (Marin, Mengersen and Robert, 2005, Subsection 1.1). Given a parametric family of probability density functions ${\mathcal{F}}=\{f(x,\alpha)\}$ on $\mathbb{R}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle p$}}}$, a mixture model for $X$ means

where $q$ is an unknown integer, each mixture component $Z^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(i)$}}}$ is generated from $f(\cdot,\alpha_{\scriptscriptstyle i})\in{\mathcal{F}}$, $W$ is a latent variable that follows a multinomial distribution with support $\{1,\ldots,q\}$ and probabilities $\pi_{\scriptscriptstyle 1},\ldots,\pi_{\scriptscriptstyle q}$, and $W,Z^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(1)$}}},\ldots,Z^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(q)$}}}$ are mutually independent. For the identifiability of (6), we require each $\pi_{\scriptscriptstyle i}$ to be positive and each $\alpha_{\scriptscriptstyle i}$ to be distinct, as well as additional regularity conditions on ${\mathcal{F}}$. The latter can be found in Titterington, Smith and Makov (1985), details omitted. As a special case, when ${\mathcal{F}}$ is the family of multivariate normal distributions, (6) becomes a mixture multivariate normal distribution with $\alpha_{\scriptscriptstyle i}$ being $(\mu_{\scriptscriptstyle i},\Sigma_{\scriptscriptstyle i})$, the mean and the covariance matrix of the $i$th mixture component. Here, we allow $\Sigma_{\scriptscriptstyle i}$’s to differ.

For the most flexibility of the mixture model (6), one can allow the number of mixture components $q$ to be relatively large or even diverge with $n$ in practice, so that it can “facilitate much more careful description of complex systems” (Marin, Mengersen and Robert, 2005, Subsection 1.2.3), including those distributions who convey non-clustered sample supports. An extreme case is the kernel density estimation that uses an average of $n$ multivariate normal distributions to approximate a general distribution, which can be regarded as a mixture multivariate normal distribution mentioned above but with $q=n$. For simplicity, we set $q$ to be fixed as $n$ grows throughout the theoretical development, by which (6) is a parametric analogue of kernel density estimation, with each mixture component being a “global” neighborhood of $X$. The setting of non-clustered $X$ approximated by mixture model will be investigated numerically in Section $6$.

Given that ${\mathcal{F}}$ truly specifies the distributions of the mixture components, the consistency of the mixture model (6) hinges on the true determination of $q$. This can be achieved by multiple methods, such as the Bayesian information criterion (BIC; Zhao, Hautamaki and Fränti, 2008), the integrated completed likelihood (Biernacki, Celeux and Govaert, 2000), the sequential testing procedure (McLachlan, Lee and Rathnayake, 2019a), and the recently proposed method based on data augmentation (Luo, 2022). In the presence of these estimators, we regard $q$ as known a priori throughout the theoretical study to ease the presentation. The generality of doing so is justified in the following lemma, which shows that the asymptotic properties of any statistic that involves $q$ will be invariant if $q$ is replaced with its arbitrary consistent estimator $\widehat{q}$. The same invariance property also holds for using the true value of the dimension $d$ of the central SDR subspace in place of its consistent estimator, which justifies the generality of assuming $d$ known mentioned at the end of the Introduction.

Given $q$, the marginal density of $X$ is $\textstyle\sum_{\scriptscriptstyle i=1}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle q$}}}\pi_{\scriptscriptstyle i}f(x,\alpha_{\scriptscriptstyle i})$ up to the unknown $(\pi_{\scriptscriptstyle i},\alpha_{\scriptscriptstyle i})$’s, which generates a maximal likelihood approach to estimate these parameters using the EM algorithm; see Cai, Ma and Zhang (2019) and McLachlan, Lee and Rathnayake (2019b) for the relative literature. Hereafter, we treat the estimators $\widehat{\pi}_{\scriptscriptstyle i}$ and $\widehat{\alpha}_{\scriptscriptstyle i}$ as granted, and assume their $n^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle 1/2$}}}$-consistency and asymptotic normality whenever needed. The same applies to $\mu_{\scriptscriptstyle i}$ and $\Sigma_{\scriptscriptstyle i}$ defined above, where $\widehat{\mu}_{\scriptscriptstyle i}$ and $\widehat{\Sigma}_{\scriptscriptstyle i}$ for general parametric family ${\mathcal{F}}$ can be derived by appropriate transformations of $\widehat{\alpha}_{\scriptscriptstyle i}$.

To connect the mixture model (6) with a parametric model on the moments of $X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$, we assume that the linearity condition and the constant variance condition holds for each mixture component; that is, for $i\in\{1,\ldots,q\}$,

Referring to the discussion about (3) and (4) in the Introduction, this includes but is not limited to the cases where each mixture component of $X$ is multivariate normal. For clarification, hereafter we call (3) the overall linearity condition and call (7) the mixture component-wise linearity condition whenever necessary, and likewise call (4) and (8) the overall and the mixture component-wise constant variance conditions, respectively. Because $W$ is latent, we next provide two useful derivations of (7). For each $i\in\{1,\ldots,q\}$, let $\pi_{\scriptscriptstyle i}(X)$ be $\mathrm{prob}(W=i|X)$, which is a known function up to $(\pi_{\scriptscriptstyle i},\alpha_{\scriptscriptstyle i})$’s, and let $\pi_{\scriptscriptstyle i}(\beta^{\mbox{\tiny{\sf T}}}X)$ be $\mathrm{prob}(W=i|\beta^{\mbox{\tiny{\sf T}}}X)$ for any $\beta\in\mathbb{R}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle p\times d$}}}$. Generally, $\pi_{\scriptscriptstyle i}(\beta^{\mbox{\tiny{\sf T}}}X)$ differs from $\pi_{\scriptscriptstyle i}(X)$ unless in the extreme case $W\;\,\rule[0.0pt]{0.29999pt}{6.00006pt}\rule[0.0pt]{6.49994pt}{0.29999pt}\rule[0.0pt]{0.29999pt}{6.00006pt}\;\,X|\beta^{\mbox{\tiny{\sf T}}}X$. The latter is not assumed in this article. The estimators $\widehat{\pi}_{\scriptscriptstyle i}(X)$ and $\widehat{\pi}_{\scriptscriptstyle i}(\beta^{\mbox{\tiny{\sf T}}}X)$ are readily derived from the mixture model fit.

From the proof of Lemma 2, $\pi_{\scriptscriptstyle i}(X)$ in $E_{\scriptscriptstyle i}(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ can be replaced with the indicator $I(W=i)$, so (9) resembles the mixture component-wise linearity condition (7) for a single mixture component of $X$. Similarly, (10) is an ensemble of (7) across all the mixture components of $X$.

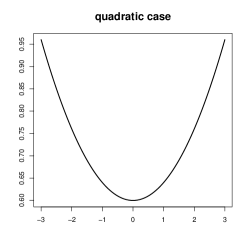
Depending on how $\pi_{\scriptscriptstyle i}(\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ is distributed, that is, how $W$ is associated with $\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$, the functional form of $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ in (10) can be approximated by various parametric models. In this sense, (10) relaxes the overall linearity condition (3) to numerous parametric models, among which the most appropriate is automatically chosen by the data. For example, if the mixture components of $\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$ are well separate, then each $\pi_{\scriptscriptstyle i}(\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ is close to a Bernoulli distribution and thus $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ is nearly a linear spline of $\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$. This is illustrated by $E(X_{\scriptscriptstyle 1}|X_{\scriptscriptstyle 2})$ in the upper-left and upper-middle panels of Figure 1, where $X$ is a balanced mixture of $N((0,2)^{\mbox{\tiny{\sf T}}},(r_{\scriptscriptstyle 1}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle|i-j|$}}}))$ and $N((0,-2)^{\mbox{\tiny{\sf T}}},(r_{\scriptscriptstyle 2}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle|i-j|$}}}))$, with $r_{\scriptscriptstyle 1}=.5$ and $r_{\scriptscriptstyle 2}=-.5$ in the former and both equal to $.5$ in the latter. In the other extreme, if $\pi_{\scriptscriptstyle i}(\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$’s are degenerate, which occurs if the mixture components of $X$ are identical along the directions in $\beta_{\scriptscriptstyle 0}$, then $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ reduces to satisfy the overall linearity condition (3). When $\pi_{\scriptscriptstyle i}(\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$’s are continuously distributed, $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ conveys other forms, such as a quadratic function if we change $\mu_{\scriptscriptstyle 1}$ and $\mu_{\scriptscriptstyle 2}$ in the upper-left panel to $\mu_{\scriptscriptstyle 1}=-\mu_{\scriptscriptstyle 2}=(0,.2)^{\mbox{\tiny{\sf T}}}$, as depicted in the upper-right panel of Figure 1.

Similar to (7), the mixture component-wise constant variance condition (8) can also be modified in two directions towards practical use, with the aid of $\pi_{\scriptscriptstyle i}(X)$ and $\pi_{\scriptscriptstyle i}(\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$, respectively.

Same as $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ in (10), the functional form of $\mathrm{var}(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ in (12) can be approximated by various commonly seen parametric models. This is illustrated in the lower panels of Figure 1, where we again set $X$ to be a balanced mixture of $N(\mu_{\scriptscriptstyle 1},(r_{\scriptscriptstyle 1}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle|i-j|$}}}))$ and $N(-\mu_{\scriptscriptstyle 1},(r_{\scriptscriptstyle 2}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle|i-j|$}}}))$, with $(\mu_{\scriptscriptstyle 1}^{\mbox{\tiny{\sf T}}},r_{\scriptscriptstyle 1},r_{\scriptscriptstyle 2})$ being $((0,2),.4,.8)$, $((0,.8),.5,-.5)$, and $((0,0),.4,.8)$, respectively. The resulting $\mathrm{var}(X_{\scriptscriptstyle 1}|X_{\scriptscriptstyle 2})$ approximates to a piecewise constant function and a trigonometric function in the first two cases. In the third case, $\pi_{\scriptscriptstyle i}(X_{\scriptscriptstyle 2})$ is degenerate, and, by (12), $\mathrm{var}(X_{\scriptscriptstyle 1}|X_{\scriptscriptstyle 2})$ is exactly a quadratic function. As mentioned below Lemma 2, the overall linearity condition (3) is satisfied for $E(X_{\scriptscriptstyle 1}|X_{\scriptscriptstyle 2})$ in this case. A relative discussion about the inverse regression methods under linear $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ and quadratic $\mathrm{var}(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$, but with elliptically distributed $X$, can be found in Luo (2018).

Compared with the general parametric families of $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ discussed in Li and Dong (2009) and Dong and Li (2010), the proposed parametric form (10) has a clear interpretation; that is, it is most suitable to use if the sample distribution of $X$ conveys a clustered pattern. In addition, because we model $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ by averaging a few linear functions of $\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$, the result is relatively robust to the outliers of $X$. The functional form of $\mathrm{var}(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ is also relaxed in our work, whereas it is fixed as a constant in Dong and Li (2010).

Recall that the MAVE-type methods adopt the linearity condition in the local neighborhoods of $X$, and that each mixture component in the mixture model (6) can be regarded as a global neighborhood of $X$. Since we adopt the linearity condition and the constant variance condition for each mixture component of $X$, a corresponding modification of the inverse regression methods will naturally serve as a bridge, or a compromise, that connects inverse regression with the MAVE-type methods. This modification will also inherit the advantages of both sides, including the $n^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle 1/2$}}}$-consistency and the exhaustive recovery of the central SDR subspace, etc., as seen next.

Based on the discussions in Section 2, there are two intuitive strategies for adjusting inverse regression for $X$ that follows a mixture model. First, one can conduct inverse regression on each mixture component of $X$ using (9) and (11), and then merge the SDR results. Second, one can construct and solve an appropriate estimation equation (5) with the aid of the functional forms (10) for $E(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$ and (12) for $\mathrm{var}(X|\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$. Because these two strategies use the terms $\pi_{\scriptscriptstyle i}(X)$ and $\pi_{\scriptscriptstyle i}(\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X)$, respectively, which characterize the “global” neighborhoods of $X$ and $\beta_{\scriptscriptstyle 0}^{\mbox{\tiny{\sf T}}}X$, they can be parallelized with MAVE and its refined version (Xia et al., 2002). We start with adjusting SIR in this section, and discuss both strategies sequentially.

To formulate the first strategy, we first parametrize the SDR result specified for an individual mixture component of $X$ as the conditional central subspace on $W=i$, which is the unique subspace of $\mathbb{R}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle p$}}}$ that satisfies

with minimal dimension. Denote this space by ${\mathcal{S}}_{\scriptscriptstyle Y|X}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(i)$}}}$. For a general non-latent variable $W$, the space spanned by the union of ${\mathcal{S}}_{\scriptscriptstyle Y|X}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(i)$}}}$’s, denoted by ${\mathcal{S}}({\bigcup_{\scriptscriptstyle i=1}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle q$}}}{\mathcal{S}}_{\scriptscriptstyle Y|X}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(i)$}}}})$, is called the partial central subspace in Chiaromonte, Cook and Li (2002). Naturally, the first strategy aims to estimate ${\mathcal{S}}({\bigcup_{\scriptscriptstyle i=1}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle q$}}}{\mathcal{S}}_{\scriptscriptstyle Y|X}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(i)$}}}})$, so it recovers ${\mathcal{S}}_{\scriptscriptstyle Y|X}$ if

Because $W$ is the latent variable constructed for the convenience of modeling the distribution of $X$, we can naturally assume that $W$ is uninformative to $Y$ given $X$. Intuitively, this means that the term $W=i$ can be removed from (13), by which ${\mathcal{S}}_{\scriptscriptstyle Y|X}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(i)$}}}$ becomes identical to ${\mathcal{S}}_{\scriptscriptstyle Y|X}$. The only issue is that the support of $X|W=i$ can be a proper subset of the support of $X$, under which ${\mathcal{S}}_{\scriptscriptstyle Y|X}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(i)$}}}$ may only capture a local pattern of $Y|X$ and becomes a proper subspace of ${\mathcal{S}}_{\scriptscriptstyle Y|X}$. Nonetheless, since the supports of $X|W=i$ for $i=1,\ldots,q$ must together cover the support of $X$, the union of ${\mathcal{S}}_{\scriptscriptstyle Y|X}^{\raisebox{1.2pt}{\mbox{$\scriptscriptstyle(i)$}}}$’s must span the entire ${\mathcal{S}}_{\scriptscriptstyle Y|X}$. This reasoning is rigorized in the following lemma, which justifies (14) and thus justifies the consistency of the first strategy.