AdS Ellis wormholes with scalar field
Abstract
In this paper, we study the spherically symmetric traversable wormholes with a scalar field supported by a phantom field in the anti-de Sitter (AdS) asymptotic spacetime. Despite coupling the scalar matter field, these wormholes remain massless and symmetric for reflection of the radial coordinate . The solution possesses a finite Noether charge , which varies as a function of frequency with changes in the cosmological constant and the throat size . Under specific conditions, an approximate “event horizon” will appear at the throat.
I INTRODUCTION
The wormhole is a spacetime structure that can connect two different universes or distant regions in the same universe, it is featured by a minimal surface called “throat”. Wormholes represent one of the most intriguing solutions in General Relativity (GR). In 1935, A. Einstein and his collaborator N. Rosen formally developed the wormhole theory, which was known as the “Einstein-Rosen bridge”Einstein:1935tc . We now understand that this solution is actually a part of the Kruskal extension of the Schwarzschild metric, and the “Einstein-Rosen bridge” is not traversable Kruskal:1959vx ; Fuller:1962zza . After that, the field fell silent for more than twenty years. Interest in this work was rekindled by J.A. Wheeler in the 1950s, he and C. W. Misner mentioned the word “wormhole” for the first time in 1957 Misner:1957mt . To achieve traversable wormholes, a violation of the null energy condition seems necessary Visser:1989kh . The earliest traversable wormholes were discovered in Ellis:1973yv ; Ellis:1979bh ; Bronnikov:1973fh ; Kodama:1978dw , with further insights provided by Morris and Thorne in 1988 Morris:1988cz . Among the many traversable wormhole solutions, the “Ellis wormhole” involves using a phantom field with an opposite sign in front of the kinetic energy term Lobo:2005us ; Sushkov:2005kj ; Lobo:2005yv ; Bronnikov:2012ch ; Kleihaus:2014dla . Additionally, the more general “Ellis-Bronnikov wormhole” has been extensively studied Novikov:2009vn ; Bronnikov:2013coa ; Cremona:2018wkj ; Huang:2020qmn . Moreover, many traversable wormhole solutions do not require the exotic matter with negative energy density Bronnikov:2002rn ; Kanti:2011jz ; Maldacena:2020sxe ; Blazquez-Salcedo:2020czn ; Konoplya:2021hsm ; Kain:2023pvp ; Klinkhamer:2022rsj .
The previously mentioned solutions all exist in the background of asymptotically flat spacetime without cosmological constants. The advent of AdS/CFT correspondence Maldacena:1997re has aroused great interest in the anti-de Sitter (AdS) spacetime with negative cosmological constants. Particularly within this framework, the ER=EPR Maldacena:2013xja proposal has underscored the importance of studying wormhole solutions in AdS spacetime Gao:2016bin ; Maldacena:2017axo ; vanBreukelen:2017dul ; Maldacena:2018lmt ; Dai:2020ffw ; Bintanja:2021xfs ; Kundu:2021nwp ; Kain:2023ore . However, the exact wormhole solutions are elusive in AdS spacetime, contrary to the asymptotically flat case, and so far, not so many fully-fledged examples of AdS wormhole solutions are available in the literature. Notable examples include solutions obtained via the cut-and-paste technique Lemos:2003jb ; Lemos:2004vs , the modified gravity solution Maeda:2008nz , the dynamical solution Maeda:2012fr , the Ricci-flat/AdS correspondence solution Wu:2022gpm , the Ads solution generated from flat spacetime Nozawa:2020gzz , and the asymptotically locally AdS solution Anabalon:2018rzq . Moreover, intriguing investigations into the properties of AdS wormholes have been conducted Korolev:2014hwa ; Franciolini:2018aad ; Chatzifotis:2020oqr ; Blazquez-Salcedo:2020nsa . It is worth noting that in Blazquez-Salcedo:2020nsa , the AdS asymptotic Ellis wormhole was successfully constructed, and the properties of this solution were explored through numerical methods.
On the other hand, the attempts to combine the matter fields with GR to find an exact solution can be traced back to 1955. J. A. Wheeler got an unstable solution by coupling the classical fields of electromagnetism with general relativity and he named these objects “geons”Wheeler:1955zz ; Power:1957zz . Later, Kaup et al. obtained Klein-Gordon geons (i.e., boson stars) by replacing the massless vector field with a massive complex scalar field Kaup:1968zz . Ruffini also independently studied boson stars by considering quantized real scalar fields Ruffini:1969qy . And now, the enthusiasm for the study of Boson stars has grown day by day, except that the original boson stars are spherically symmetric and composed of free scalar fields with fundamental configurations. It is generalized to the cases of rotation Schunck:1996he ; Yoshida:1997qf , the excited BSs Bernal:2009zy ; Collodel:2017biu ; Wang:2018xhw , static multipolar BSs Herdeiro:2021mol and the AdS asymptotic BSs Astefanesei:2003qy ; Buchel:2013uba ; Maliborski:2013ula ; Fodor:2015eia ; Brihaye:2013hx ; Liu:2020uaz . Recently, in Dzhunushaliev:2014bya ; Hoffmann:2017jfs ; Yue:2023ela ; Ding:2023syj ; Hao:2023igi ; Su:2023xxk , the solutions of Ellis wormholes coupling scalar field, Proca fields, and Dirac fields were constructed respectively. These solutions not only reveal how nontrivial topological spacetime impacts the physical properties of the matter fields but also demonstrate intriguing “extreme” behavior under a specific parameter range. In this study, we extend the Ellis wormhole solution with a scalar field to AdS spacetime, investigating its geometric structure and properties. The solution possesses a finite Noether charge , which varies as a function of frequency with changes in the cosmological constant and the throat size . Under specific conditions, an approximate “event horizon” will appear at the throat.
The paper is organized as follows. In Sec. II, we present the model of four-dimensional Einstein’s gravity coupled to a phantom field and a scalar field in the anti-de Sitter (AdS) asymptotic spacetime. In Sec. III, the boundary conditions are studied. We perform the series expansion for the equations of the metric and the scalar field to study the asymptotic behavior. The numerical results of the solution are discussed in Sec. IV. We conclude in Sec. V with a summary and illustrate the range for future work.
II THE MODEL
II.1 Action
We consider the Einstein-Hilbert action including the Lagrangian for two massive Dirac fields and the phantom scalar field, the action is given by
| (1) |
where is the Ricci scalar. The term and are the Lagrangians defined by with
| (2) | |||||
| (3) |
Here and represent the complex scalar field and the phantom field, respectively. By varying the action (1) with respect to the metric, we can obtain the Einstein equations
| (4) |
with stress-energy tensor
| (5) |
and the matter field equations by varying with respect to the phantom field and Dirac fields.
| (6) |
and
| (7) |
II.2 Ansatze
We consider the general static spherically symmetric solution with a wormhole, and adopt the Ansatzes as follows, see e.g. Blazquez-Salcedo:2020nsa :
| (8) |
here , with the throat parameter , and ranges from positive infinity to negative infinity. It should be emphasized that the two limits correspond to two distinct asymptotically flat spacetime and in the pure Einstein gravity (), the above metric describes a static symmetric Ellis wormhole with scalar field Dzhunushaliev:2014bya ; Ding:2023syj . Furthermore, we assume stationary complex scalar field and phantom field in the form
| (9) |
Here, is only a real function of the radial coordinate , and the constant is referred to as the synchronization frequency. Moreover, the phantom field is also a real function and is independent of the time coordinate .
Variation of the action with respect to the complex scalar field and the phantom field leads to the equations
| (10) |
| (11) |
Substituting the above Ansatzes into the Einstein equations leads to the following field equations
| (12) |
| (13) |
| (14) |
These five equations are divided into three groups: three of these equations (10), (12), and (13) are solved together, by solving these OED equations numerically, we can get all information about metric functions and , field . The remaining one equation (14) is treated as the constraint and used to check the numerical accuracy of the method. Furthermore, as the derivative in Eq. (11) happens to be zero, we can transform the last expression into the following form
| (15) |
the is a constant that represents the scalar charge of the phantom field and can be used to check the accuracy of numerical calculations. Its value as a function of frequency should be the same at different locations while fixing or . We give the expression of scalar charge by taking the above Eq. (15) into the Eq. (14)
| (16) |
III BOUNDARY CONDITIONS
Before numerically solving the differential equations instead of seeking the analytical solutions, we should obtain the asymptotic behaviors of the three functions , , which is equivalent to giving the boundary conditions we need.
For our work, the solution is symmetric and continuous at the origin, and we can get the solution in the whole spacetime at once, which means there is no need to limit the boundary conditions at the origin. To study the asymptotic behavior of the metric functions in the limit , we perform the series expansion for Eqs. (12) and (13) to obtain the asymptotic expansion for the functions
| (17) |
| (18) |
Obviously, the odd terms vanish identically and we can get the large- expansions of for this wormhole solution
| (19) |
The odd terms vanish, and the metric functions have the same asymptotic behaviors at and , they all return to the Minkowski spacetime. The appropriate boundary conditions to be imposed on the metric functions and scalar field function at infinity are given by
| (20) |
| (21) |
Meanwhile, considering the expression for the mass of the wormholes, obtained from the ADM formalism, the vanishing of the term also implies that the mass of these symmetric wormholes vanishes, this has not changed with the addition of the scalar matter field. Interestingly, when the cosmological constant is 0, this solution degenerates back to the Ellis wormhole with a scalar field and has finite ADM mass, which is encoded in the asymptotic expansion of metric components (which means odd terms reappear)
| (22) |
On the other hand, the action of the complex scalar field is invariant under the transformation with a constant . According to Noether’s theorem, there is a conserved current corresponding to the complex scalar field:
| (23) |
Integrating the timelike component of the above-conserved currents on a spacelike hypersurface , one could obtain the Noether charge in the symmetric case:
| (24) | |||||
IV NUMERICAL RESULTS
In this work, all the numbers are dimensionless as follows
| (25) |
Without loss of generality, we can fix the specific parameters as and . To facilitate numerical calculations, we transform the radial coordinates by the following equation
| (26) |
map the infinite region (,) to the finite region (-1,1). This allows the ordinary differential equations to be approximated by algebraic equations. The grid with 2000 points covers the integration region and the relative errors are less .
We focus on two variable parameters: the cosmological constant and the throat size . In the subsequent presentation of results, we will keep one of these parameters constant while varying the other to investigate solution properties. Furthermore, the symmetry of the solution means that the throat is located at the center of the wormhole, at . Without loss of generality, we only show the results for the cosmological constant from 0 to -10, it can take any value less than 0.
IV.1 The cosmological constant
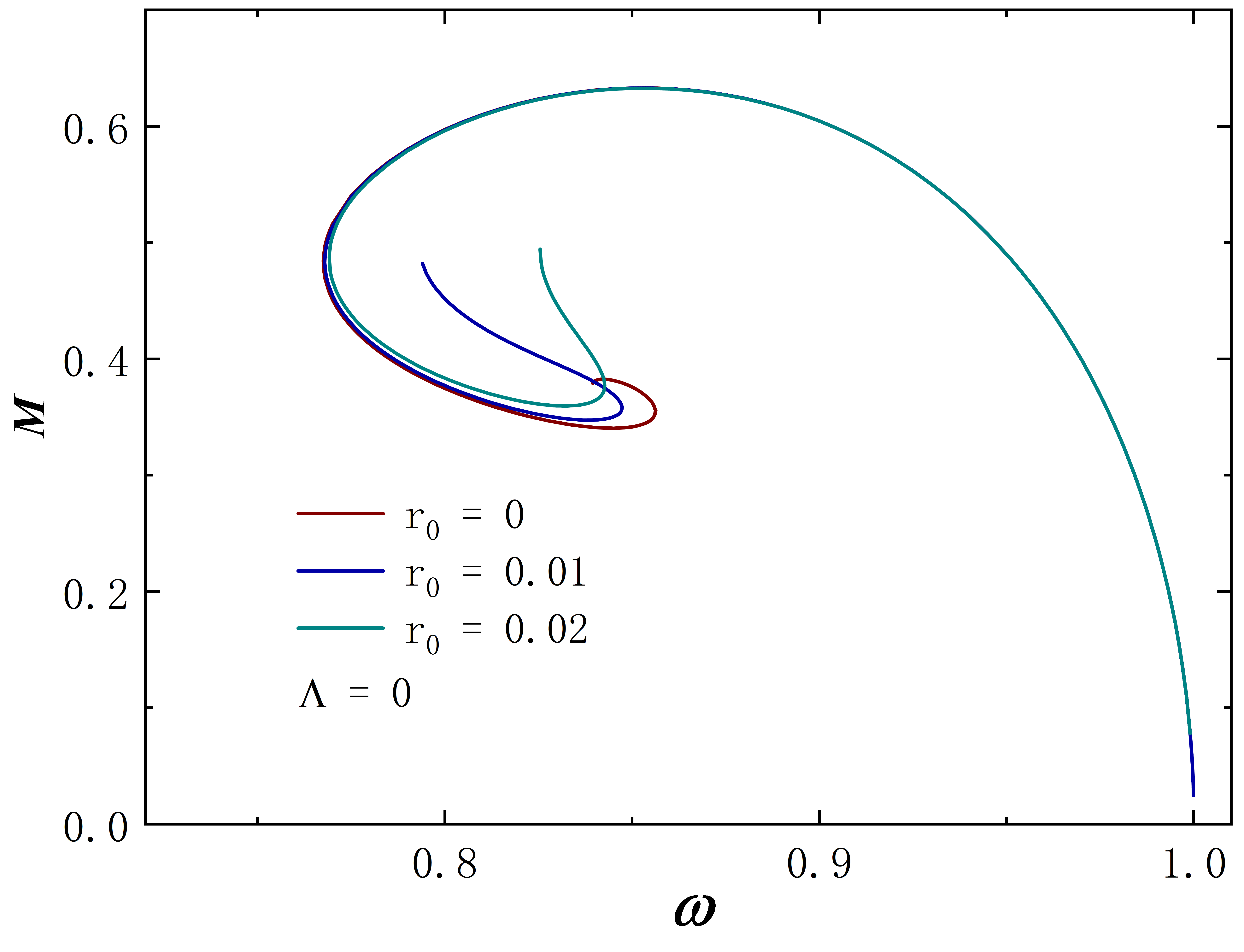
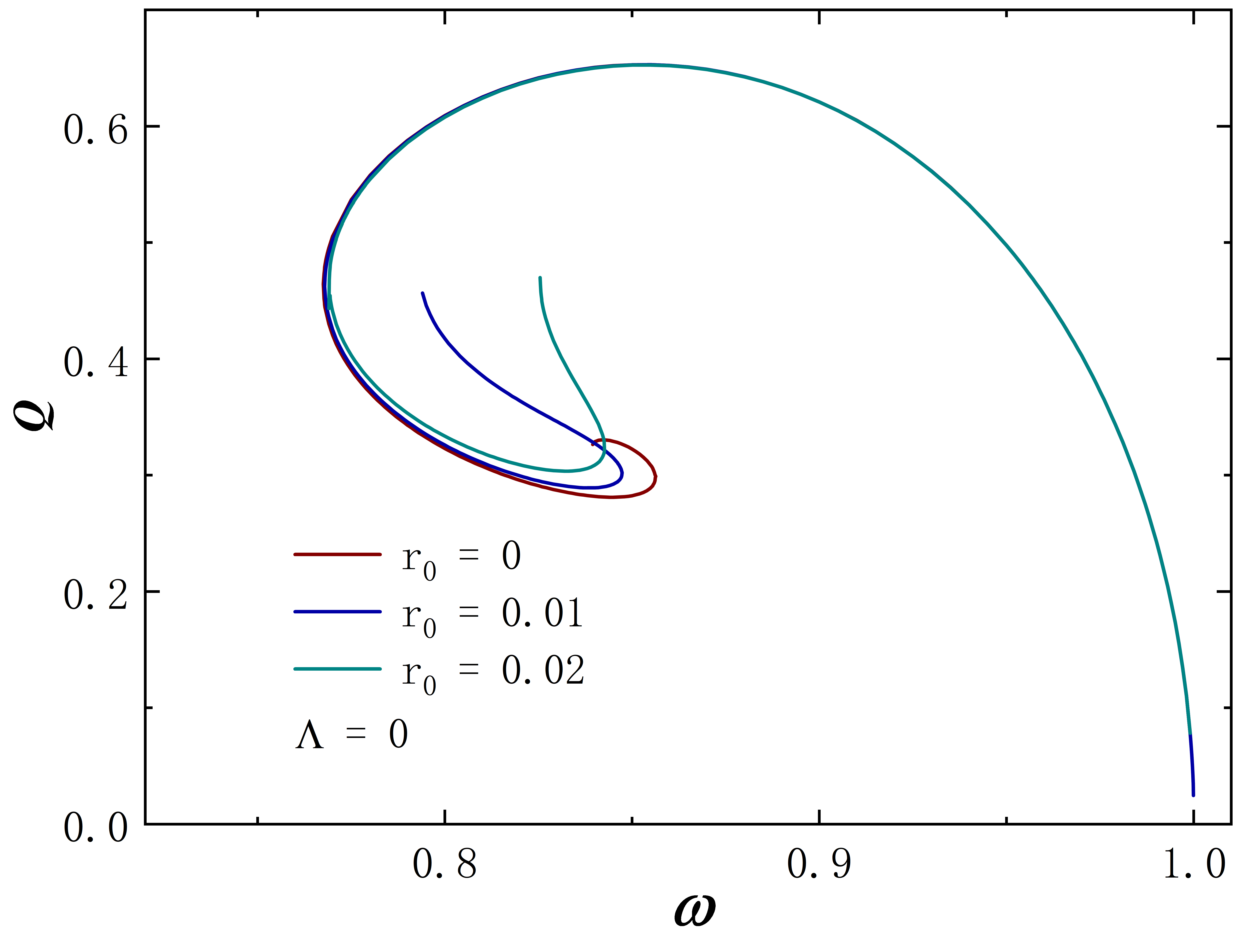
When the cosmological constant , the solution degenerates to the static symmetric Ellis wormhole with a scalar field. At this juncture, we show the ADM mass and Noether charge for this solution in Fig.1, and the numerical results are aligned with the Ding:2023syj . When is small, the solution will be limited in a tight range of , and the curve shapes are just like the well-known spiral curve of Bonson stars. As increases, the spiral curve configuration gradually unfolds, eventually resulting in a single branch, such as the case of . Notably, the mass and charge at this time will sharply grow almost linearly as decreases, so we do not show the data when is very small. Further properties of this solution without cosmological constants will not be presented. Interested readers are encouraged to refer to the Ding:2023syj for additional details.
IV.2 The cosmological constant
In the context of a negative cosmological constant, the odd terms in the metric expansion vanish, implying that the ADM mass of the solution becomes zero. To investigate the solution’s properties, we study the functional relationship between the Noether charge and frequency under varying cosmological constant for three distinct throat size groups, ranging from small to large.
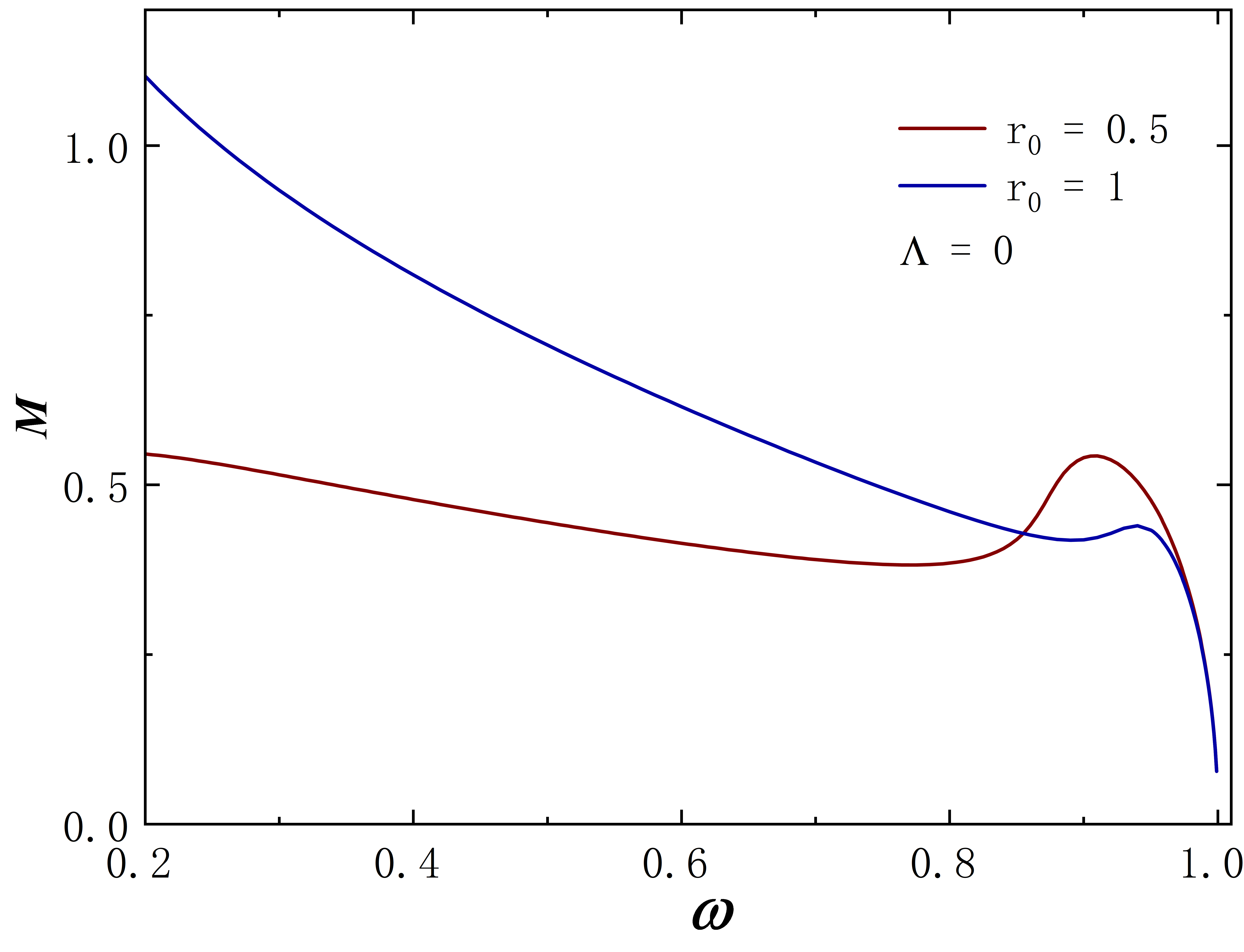
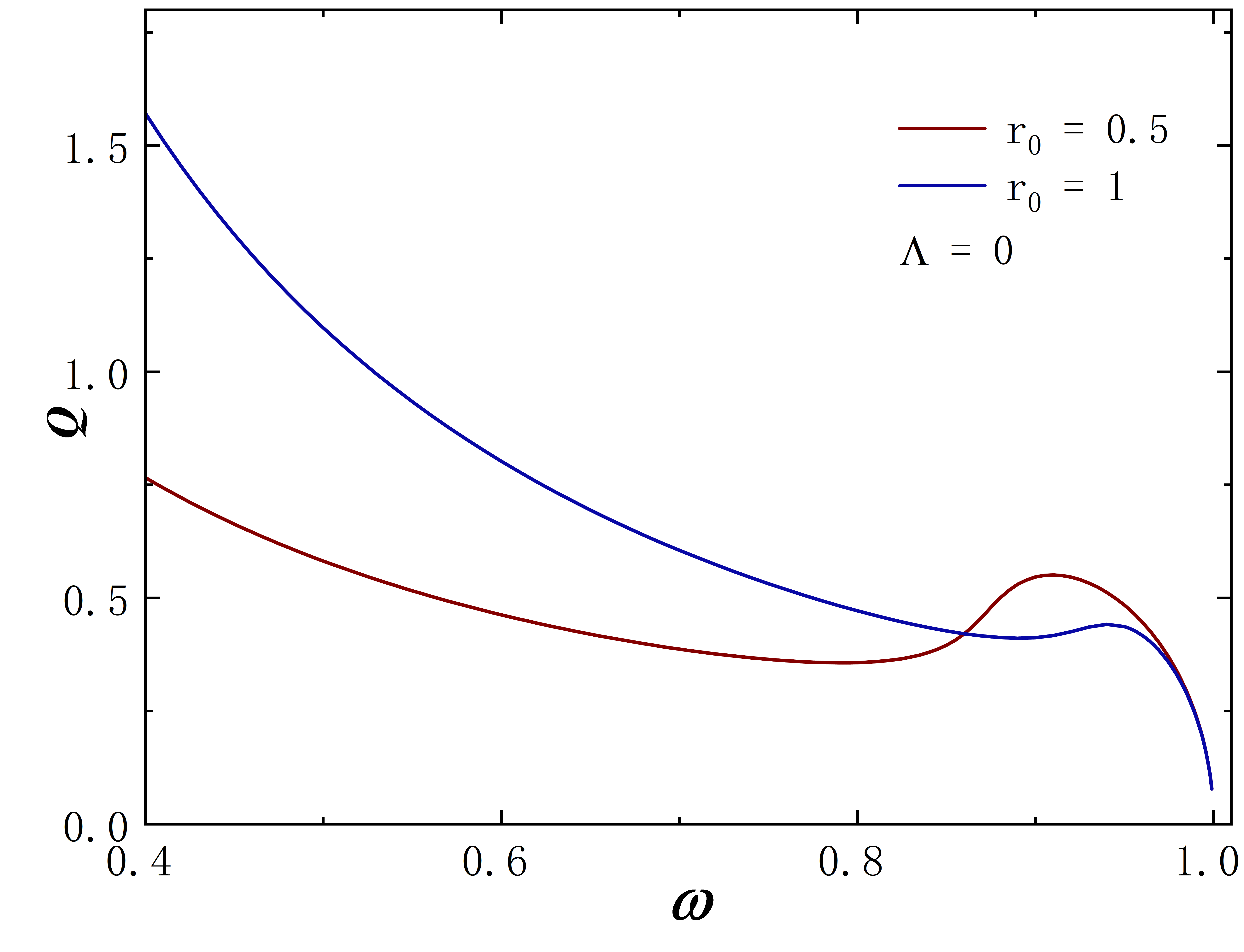
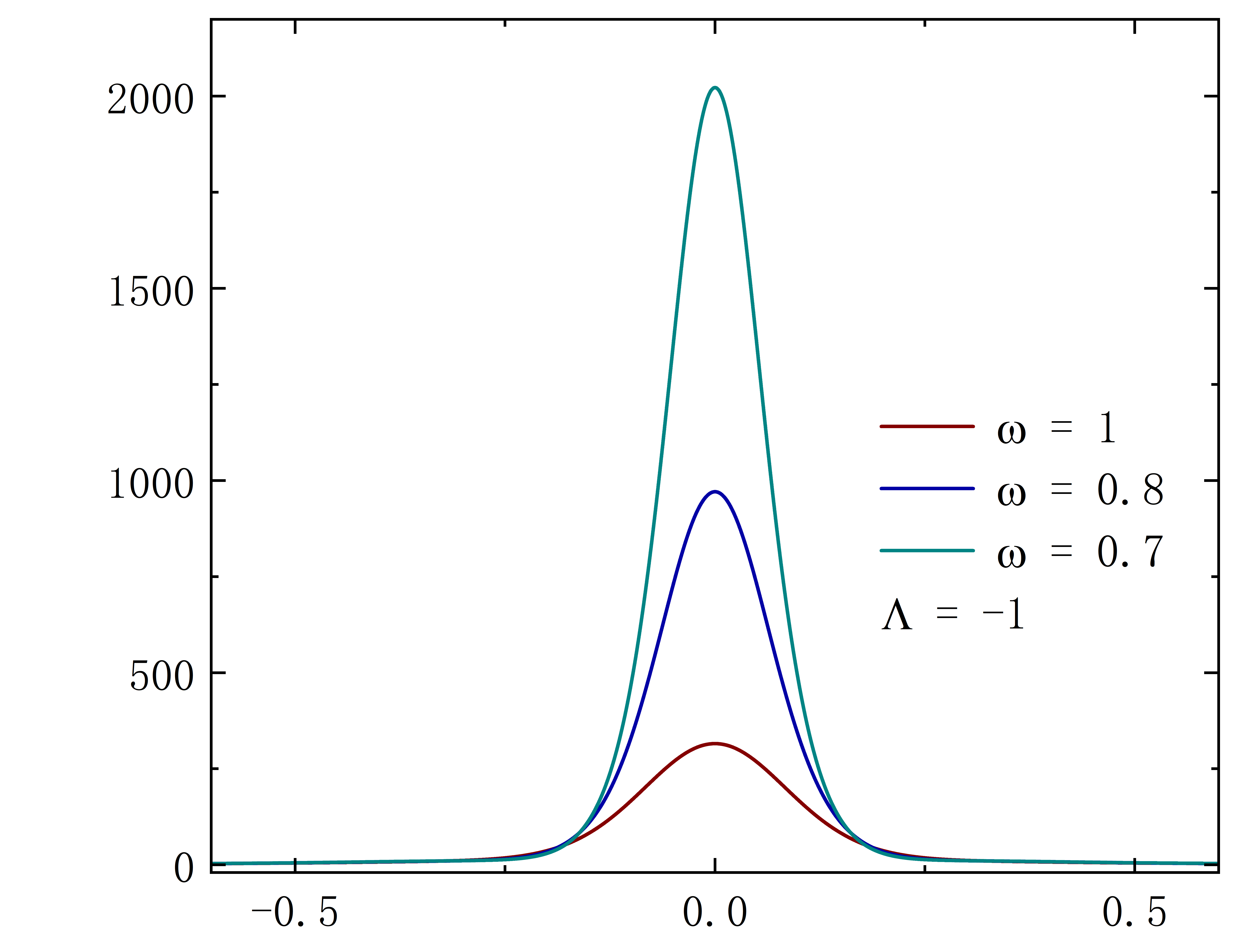
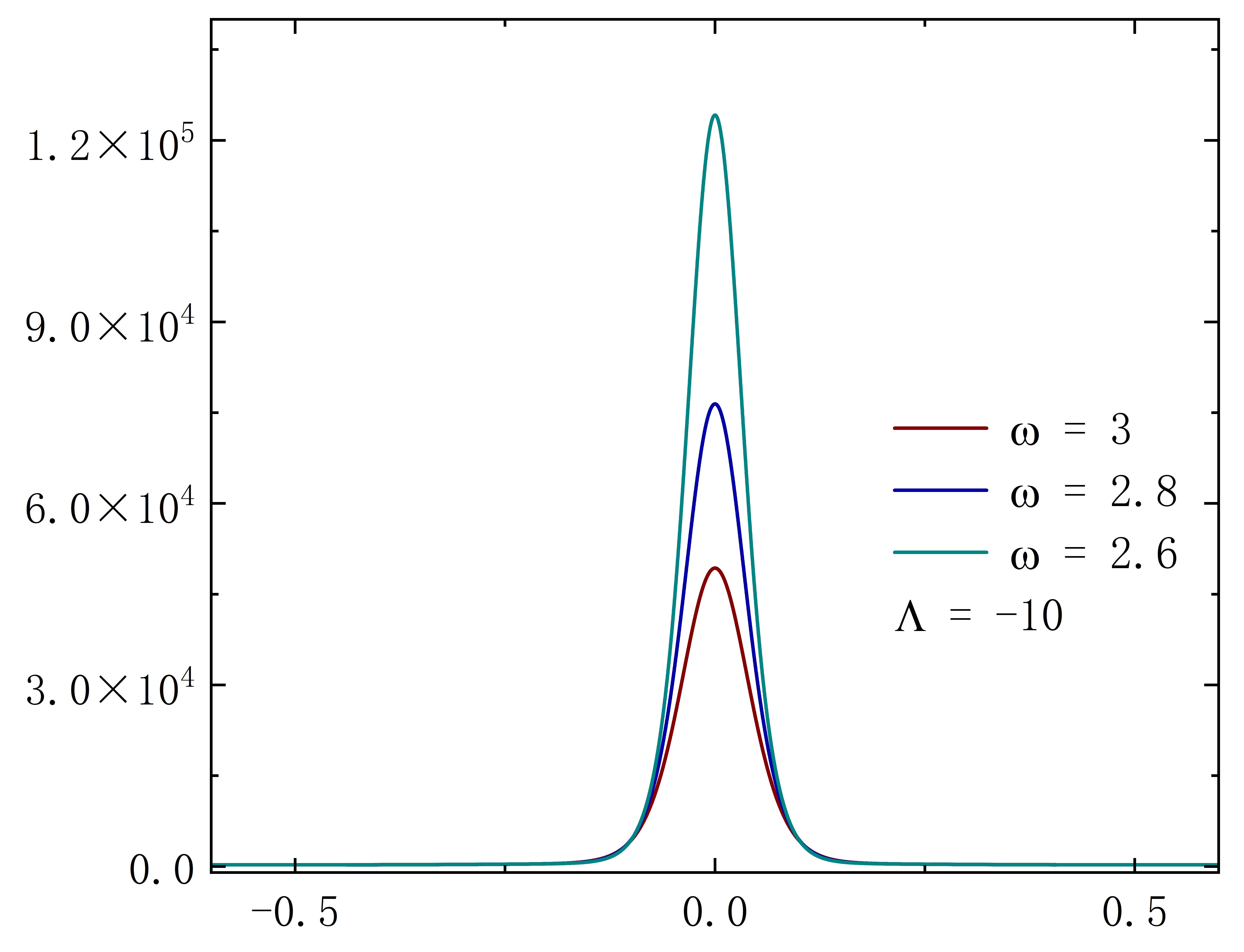
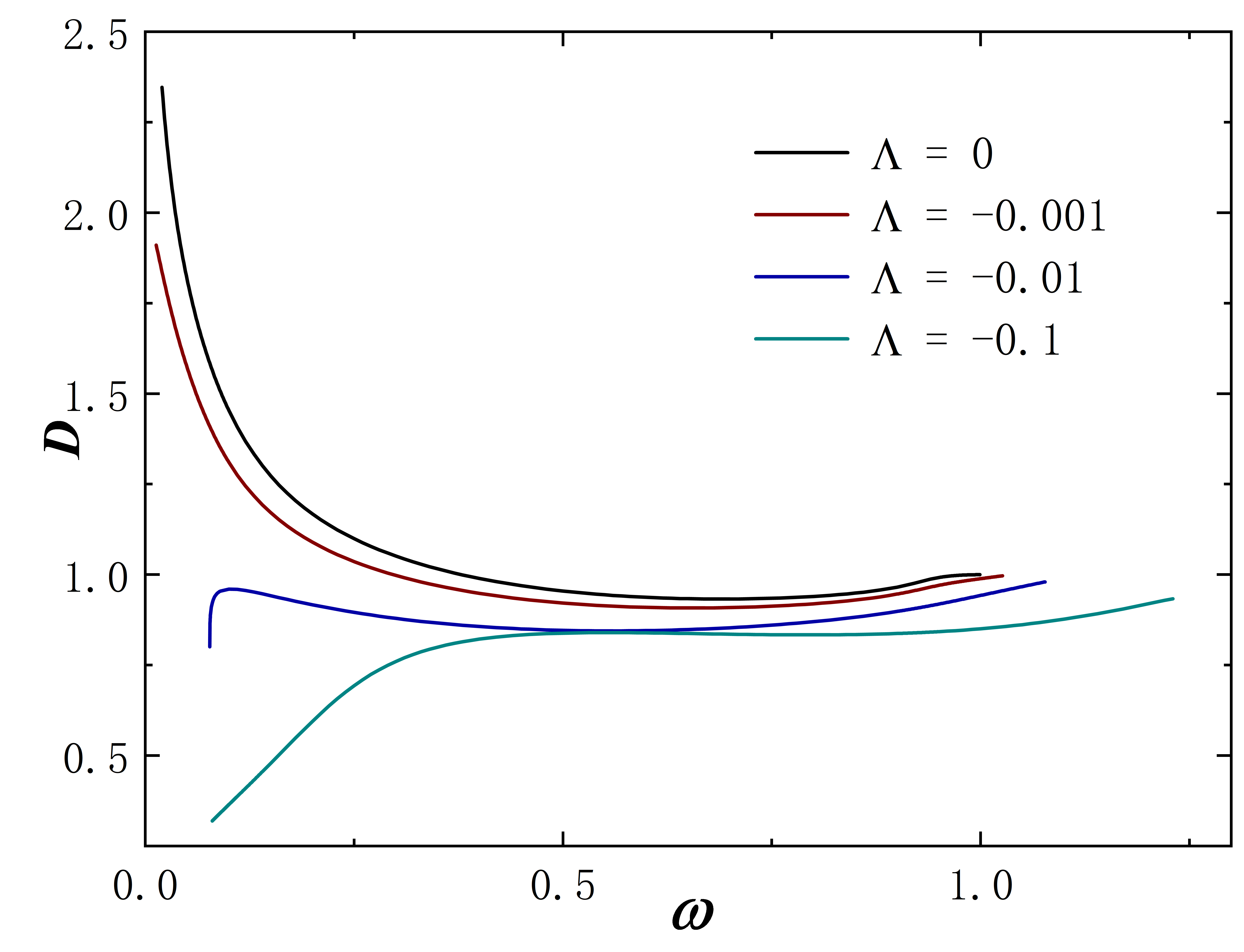
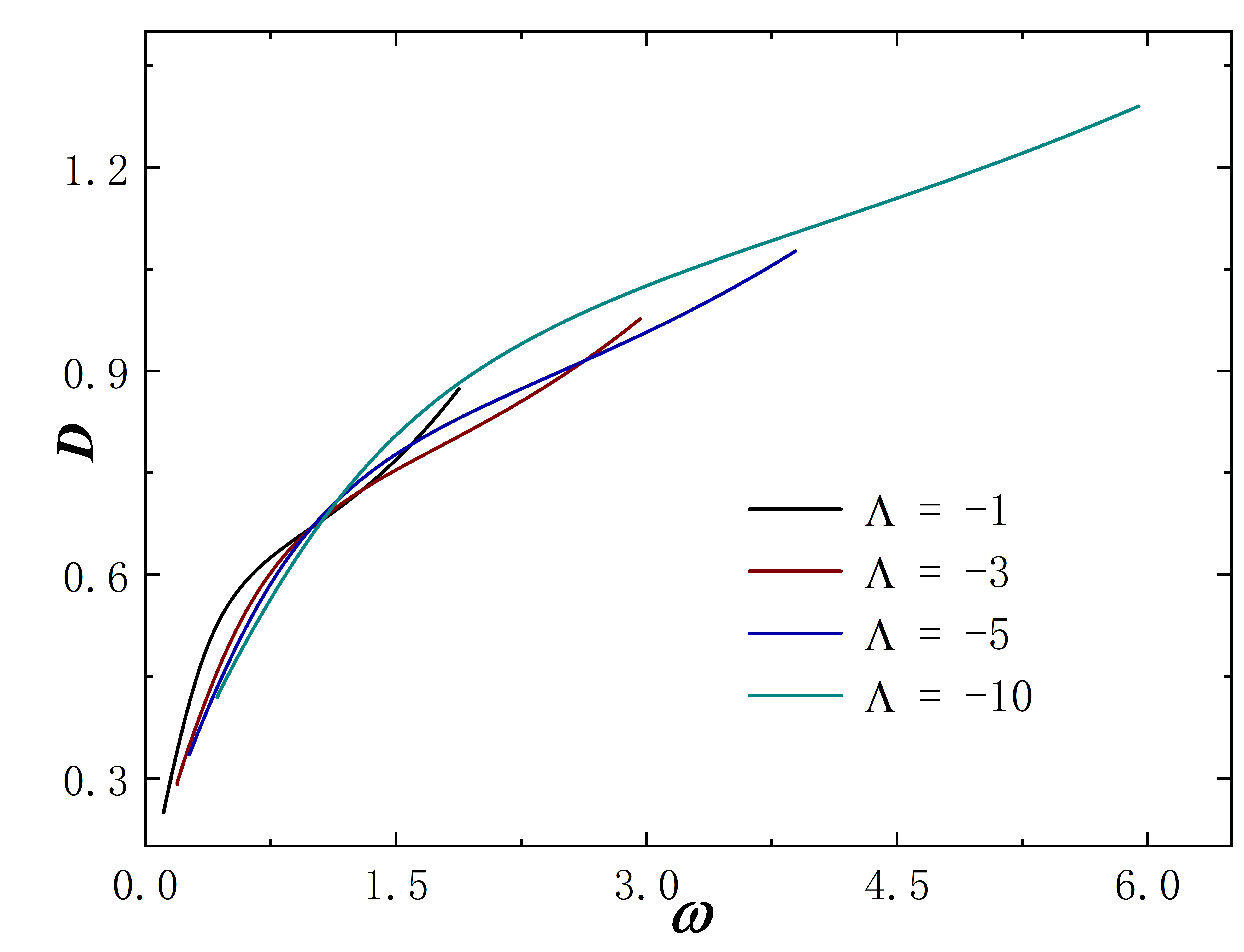
The Noether charge as a function of frequency is shown in Fig.2. When the cosmological constant approaches zero, the solutions exhibit minimal deviation from . This behavior is evident both in the curve shape and the magnitude of the Noether charge . As decreases further, gradual changes in solution properties become apparent. Specifically, for , the reduction in the leads to fewer solution branches, the gradual unfolding of the corresponding spiral curve, and a decrease in the value of . The situation of exhibits similar behavior. However, for larger throat sizes, such as , the situation diverges. At this time, the solution exhibits no branches regardless of the cosmological constant’s value and the Noether charge does not exhibit an obvious monotonic change as decreases. Furthermore, the presence of a negative cosmological constant alters the solution’s existence domain, which is manifested in that as decreases, the frequency range of the solution expands and gradually shifts to the right.
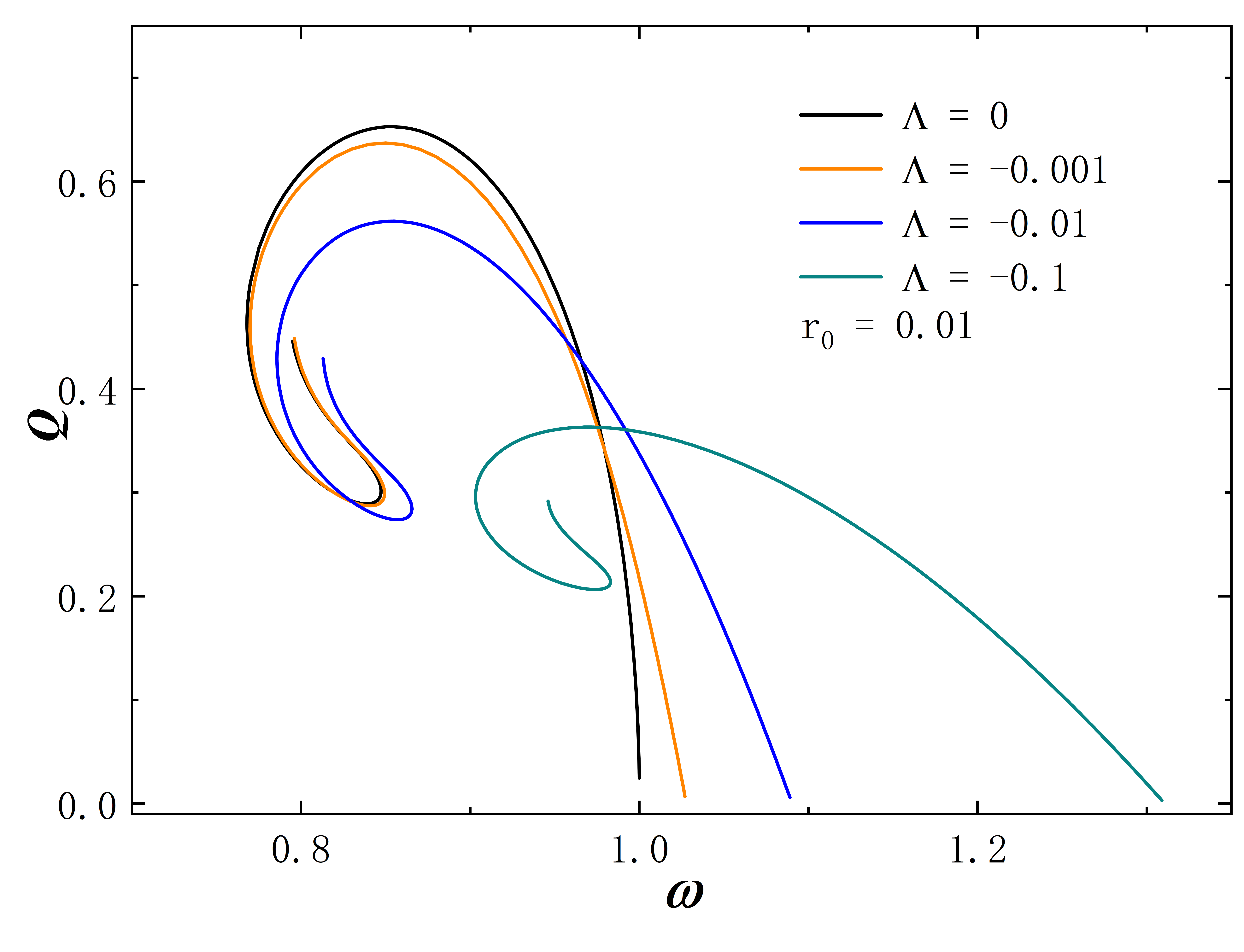
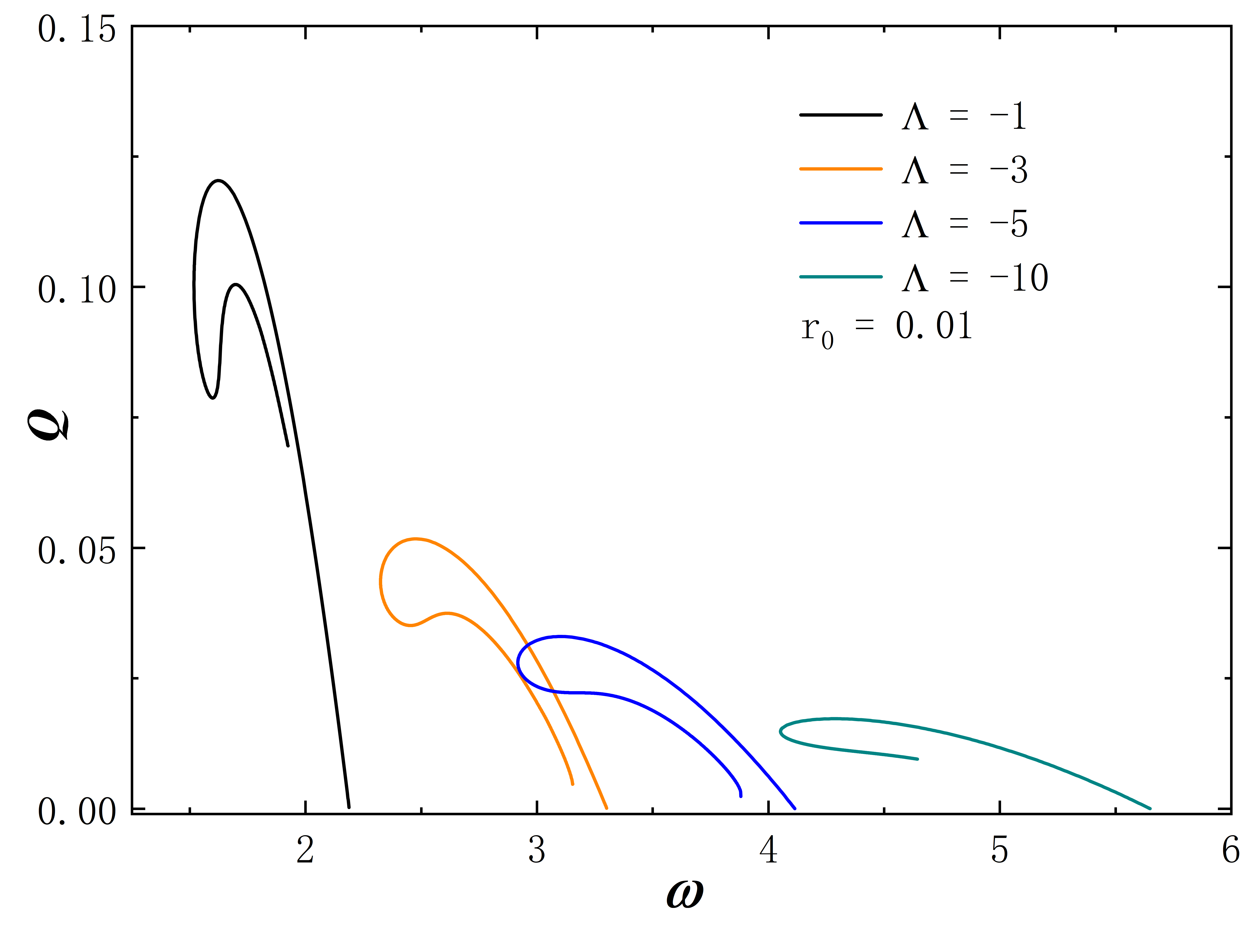
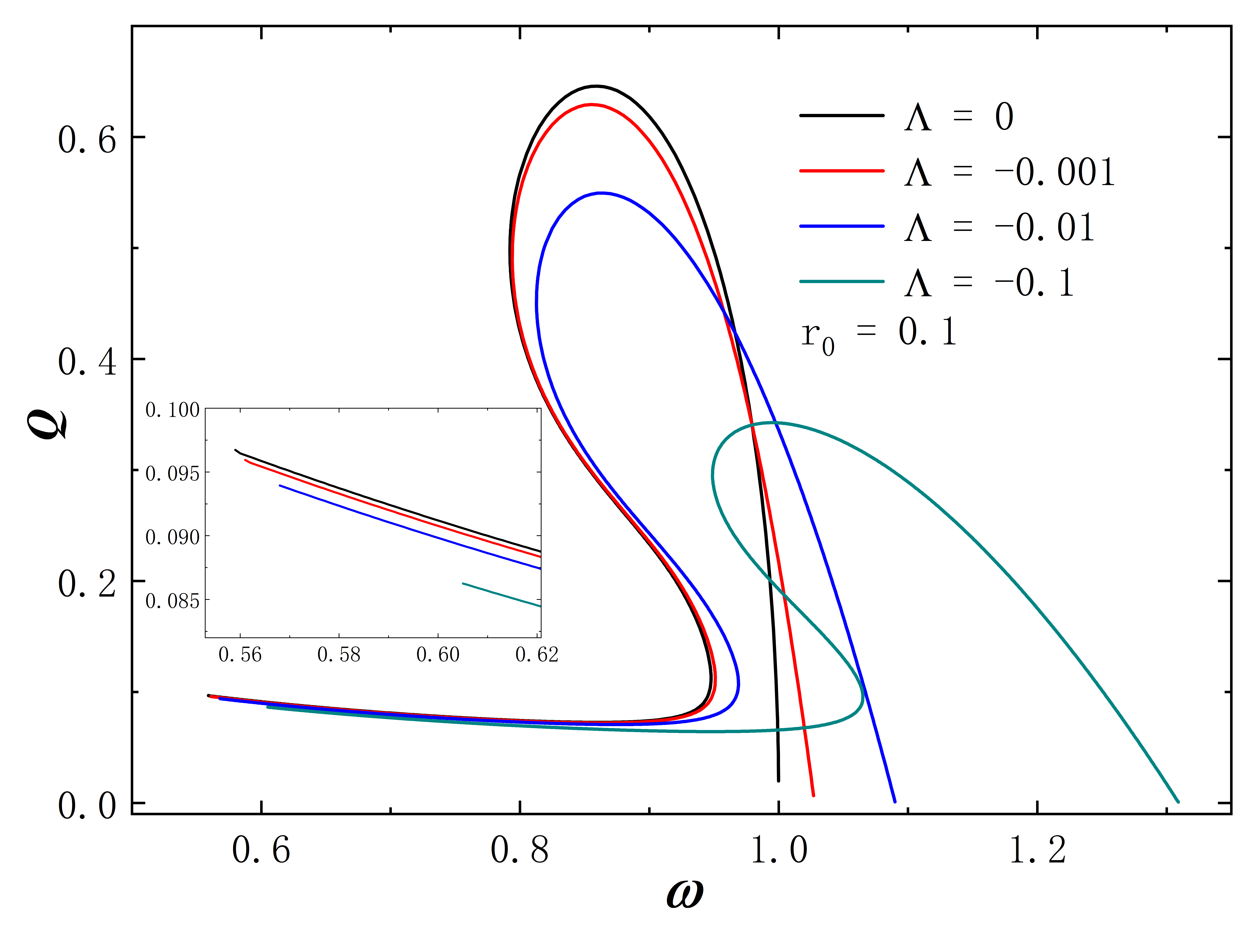
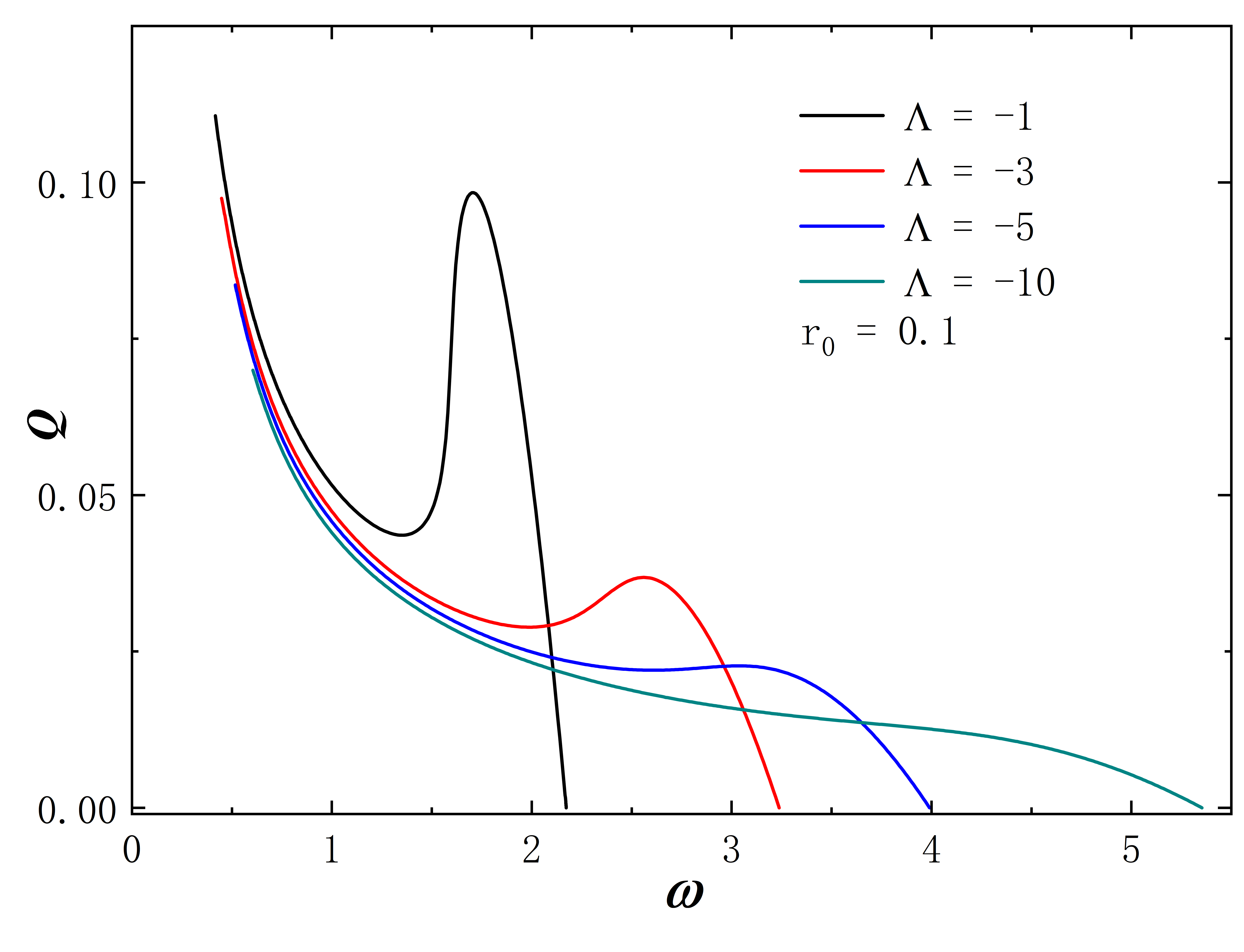
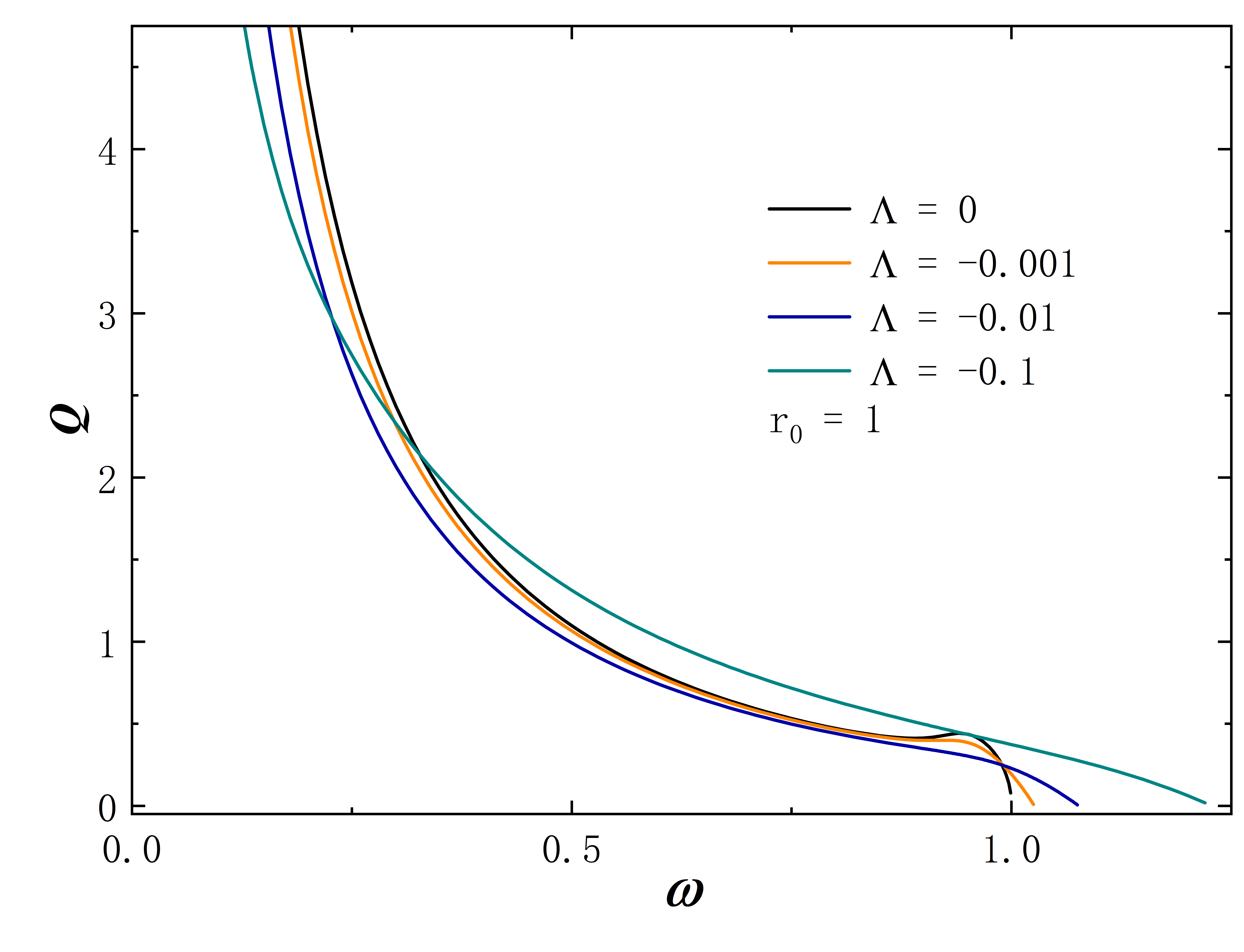
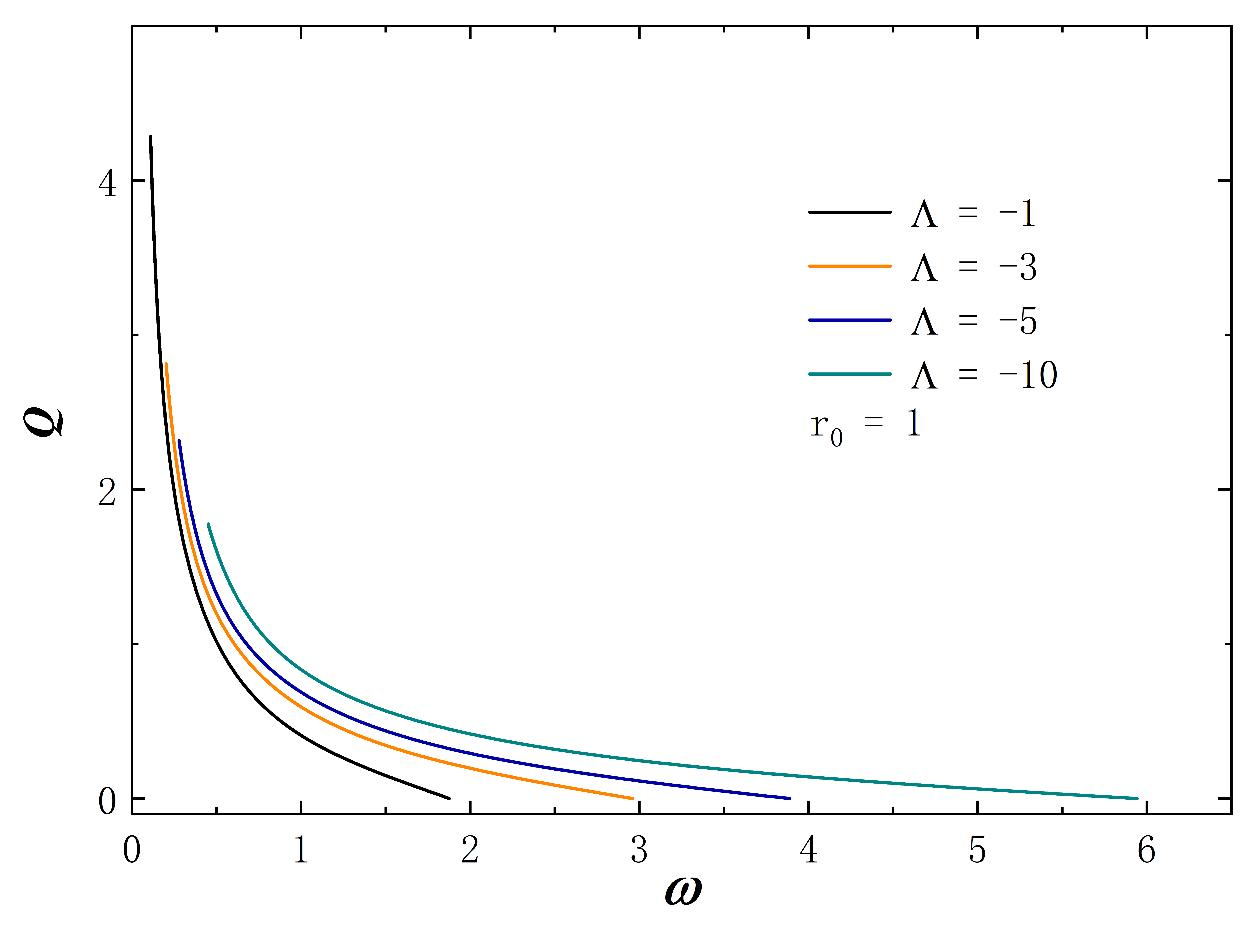
Without loss of generality, we set for all subsequent numerical results. The metric functions and characterize the spacetime properties of the solution, as depicted in Fig. 3. First, we fix the frequency at 0.6 and explore a range of different values, and the corresponding results are depicted in the figure on the first line. When takes 0, the solution aligns with the scenario described in Ding:2023syj . As decreases, the value at gradually approaches 0. In terms of the Eq. (8) line element, this signifies the emergence of an approximate “event horizon”. In addition, taking the frequency to the right limit of the solution signifies the disappearance of the scalar field, causing the solution to degenerate back into the wormhole described in Blazquez-Salcedo:2020nsa . In the second row of the figure, the cosmological constant is fixed at -10, and we investigate the variation of the metric functions with frequency . As gradually decreases (approaching the left limit of the solution), the value of at once again approaches 0. The “extreme” behavior of the approximate “event horizon”, resulting from parameter variations in the solution, has been investigated in Hao:2023igi ; Su:2023xxk . This phenomenon bears a resemblance to the appearance of “one-way traversable wormholes” due to parameter changes in the metric within the context of “black-bounce” scenarios Simpson:2018tsi ; Lobo:2020ffi .
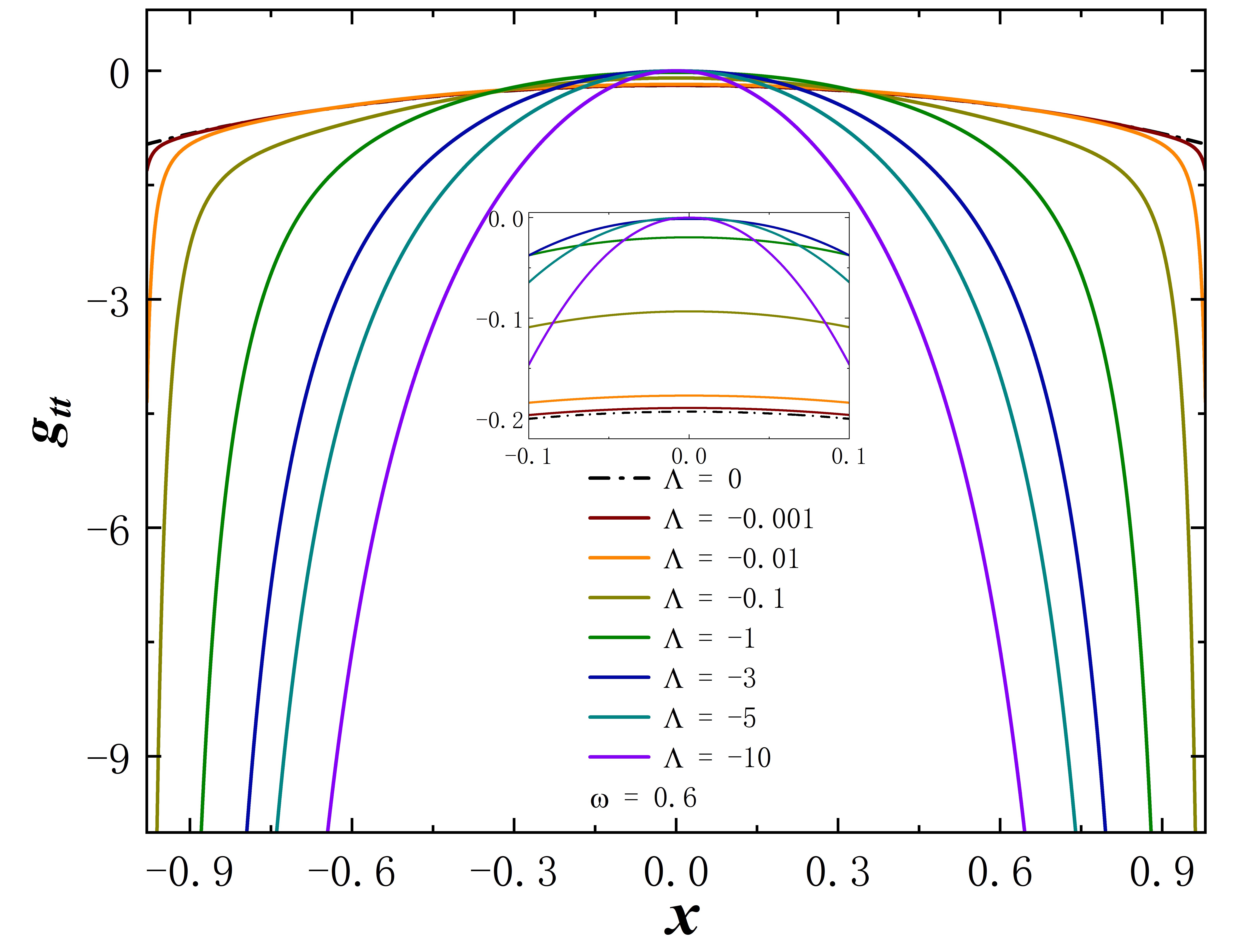
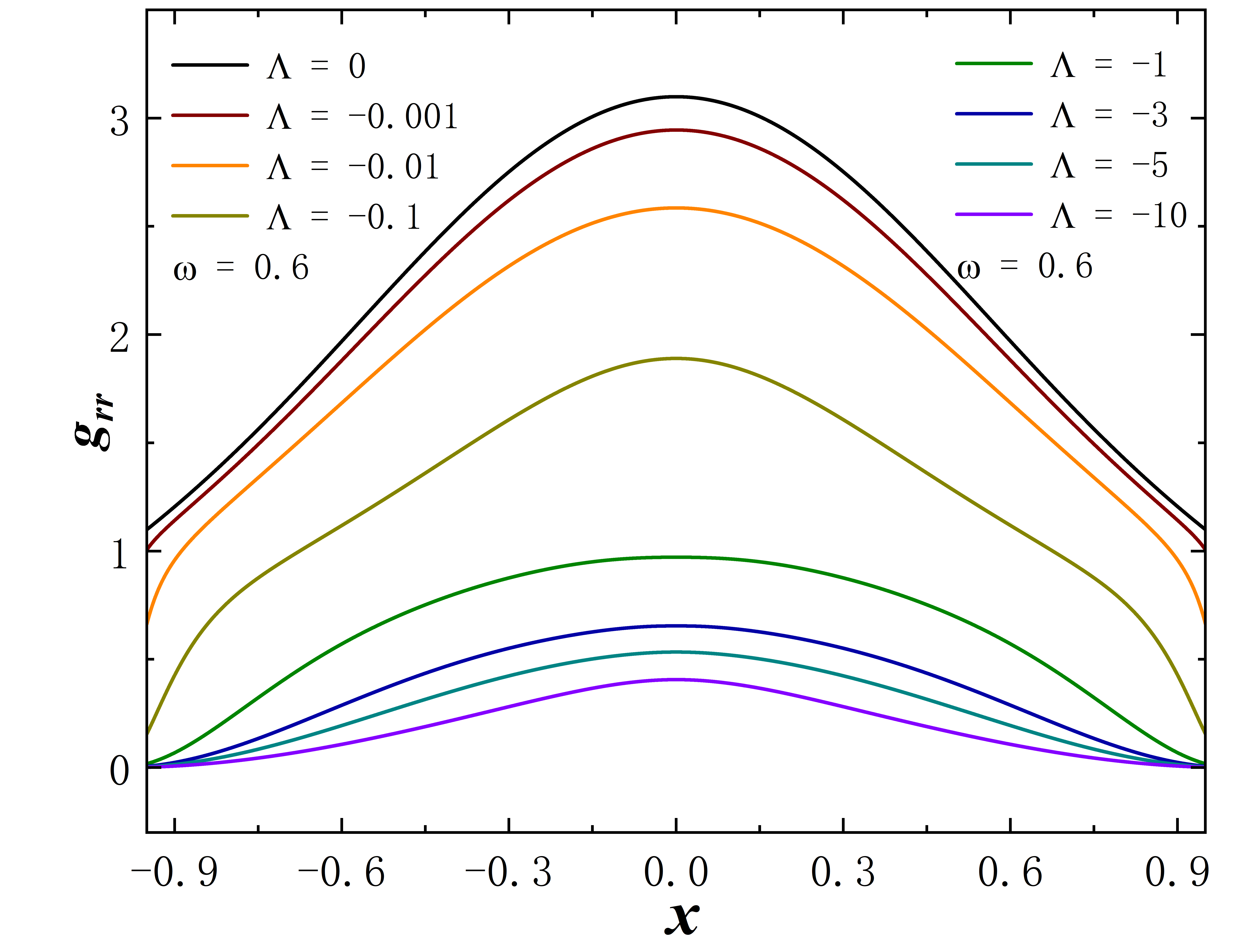
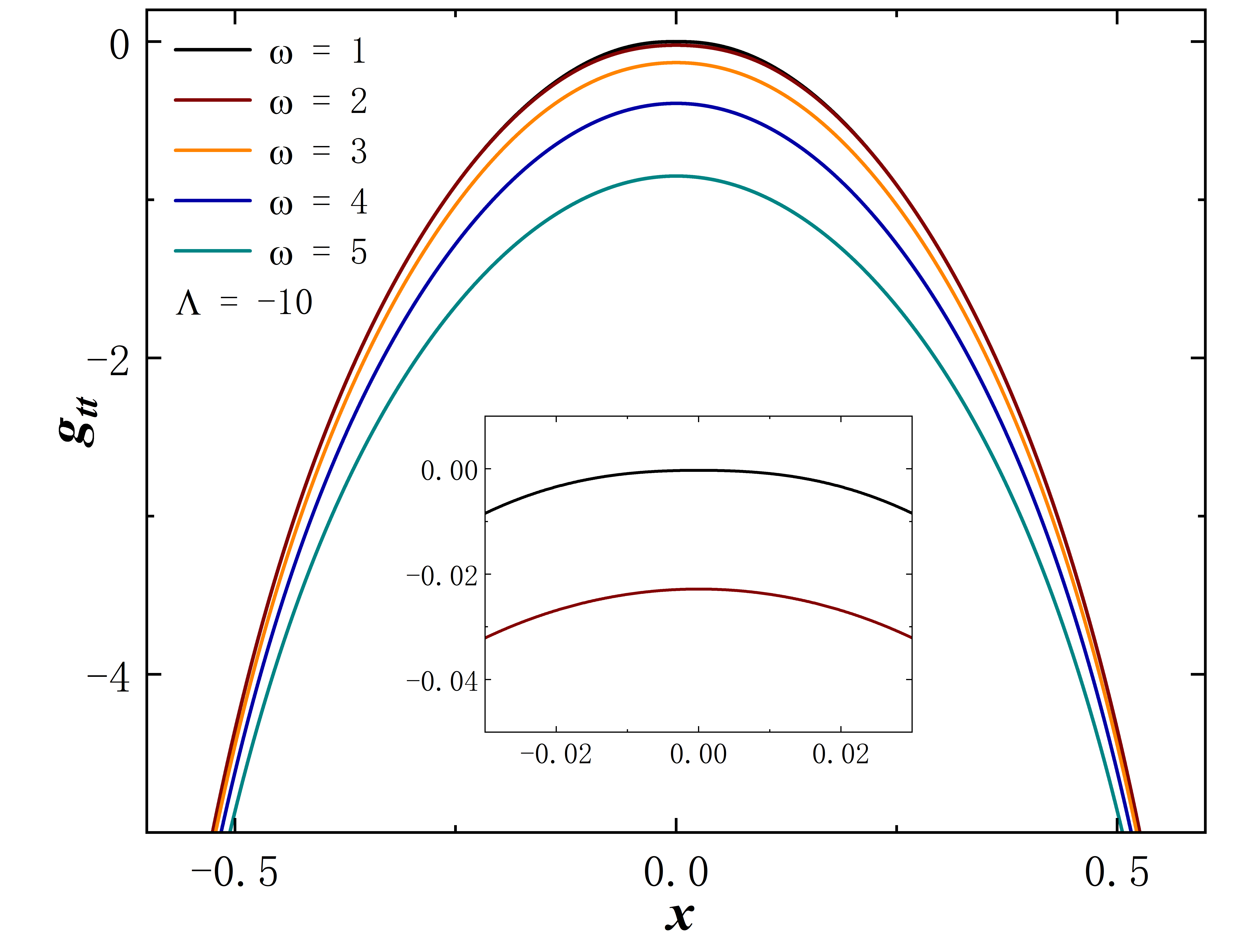
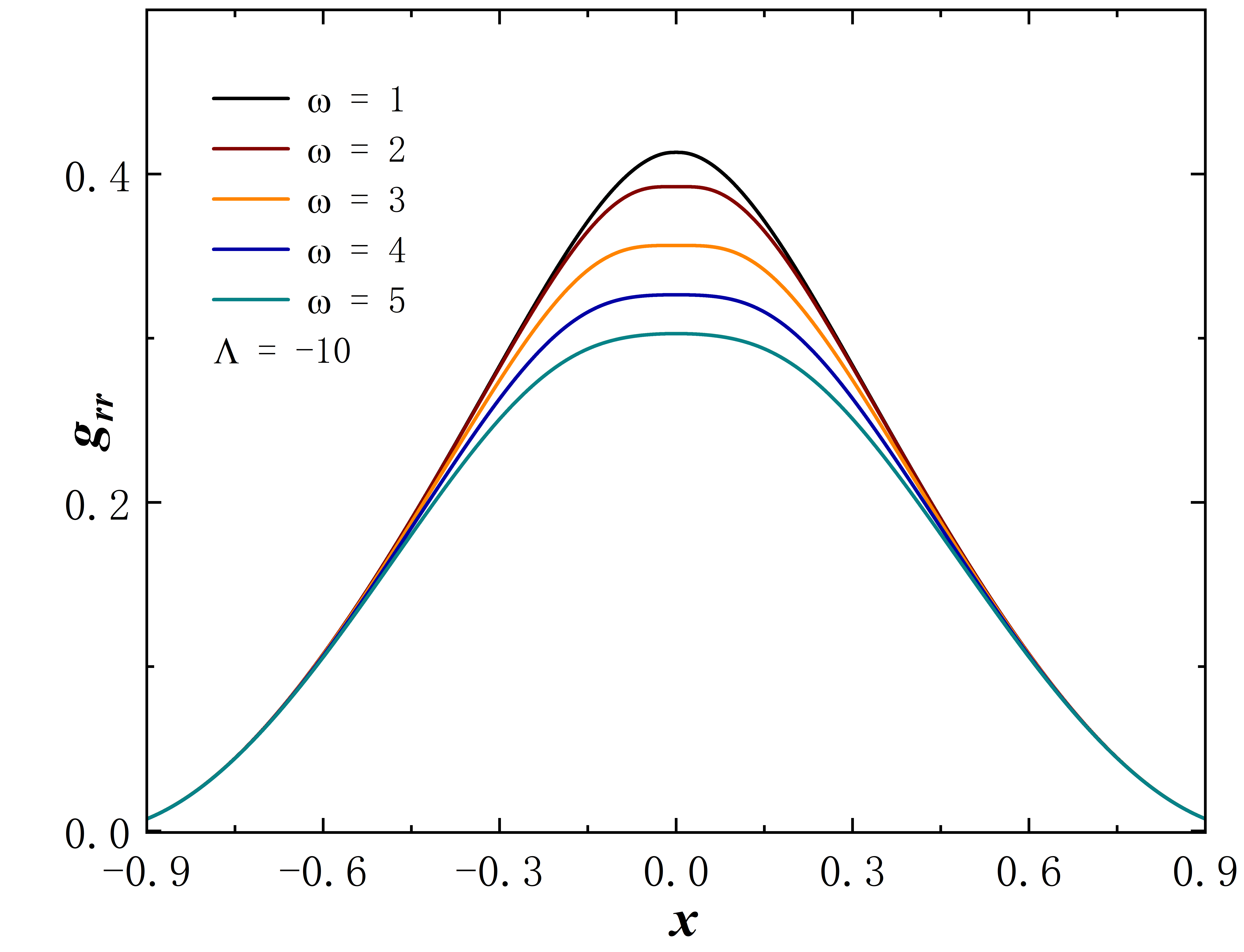
To better capture the behavior of the metric function at the throat approaching zero, we employ Tab. 1 and Tab. 2 to denote the value of at under decreasing cosmological constants or frequencies. It is evident that for sufficiently small values of or , the minimum value of can approach or even smaller.
| -3 () | -5 () | -10 () | |
|---|---|---|---|
| 1.5 () | 1 () | 0.6 () | |
|---|---|---|---|
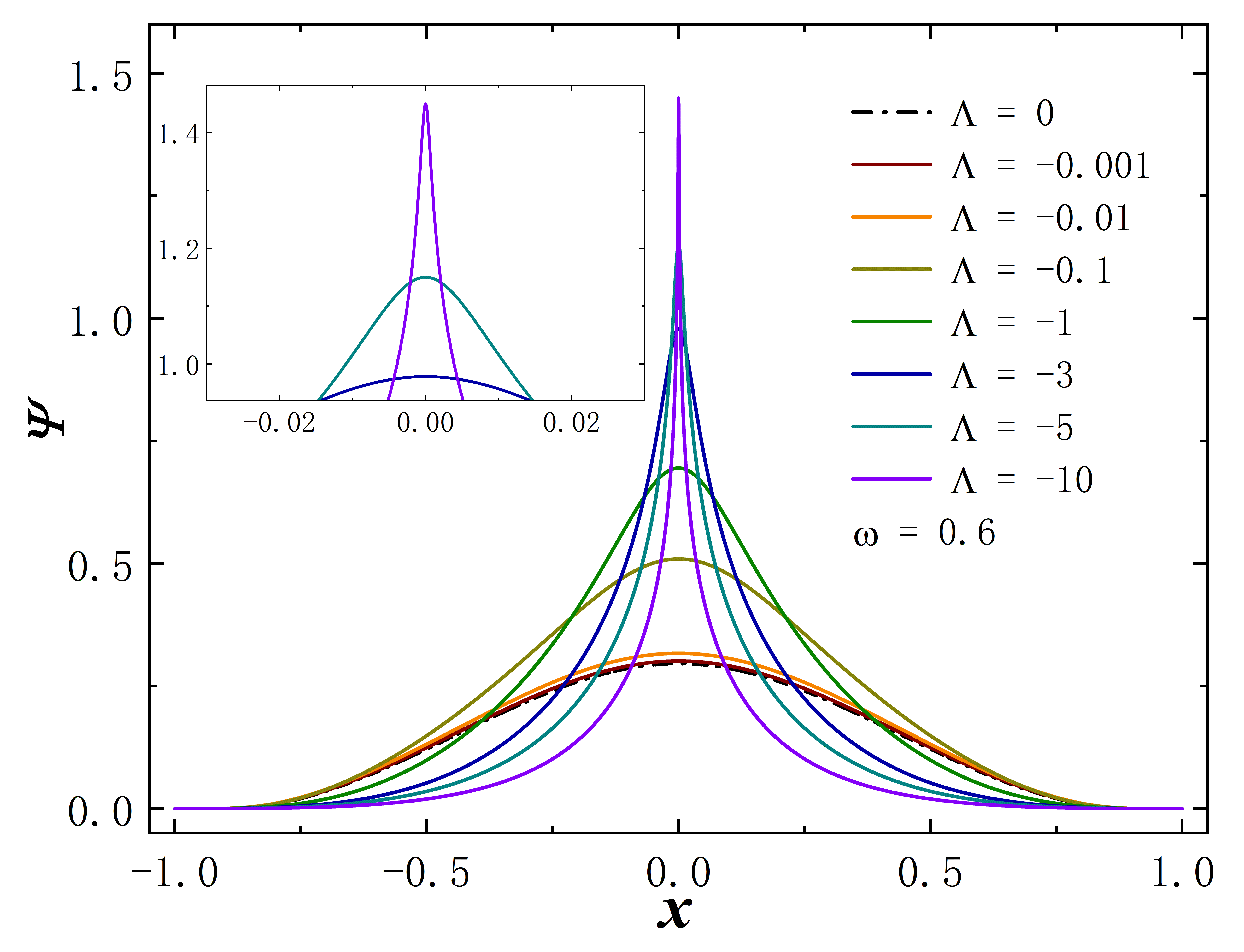
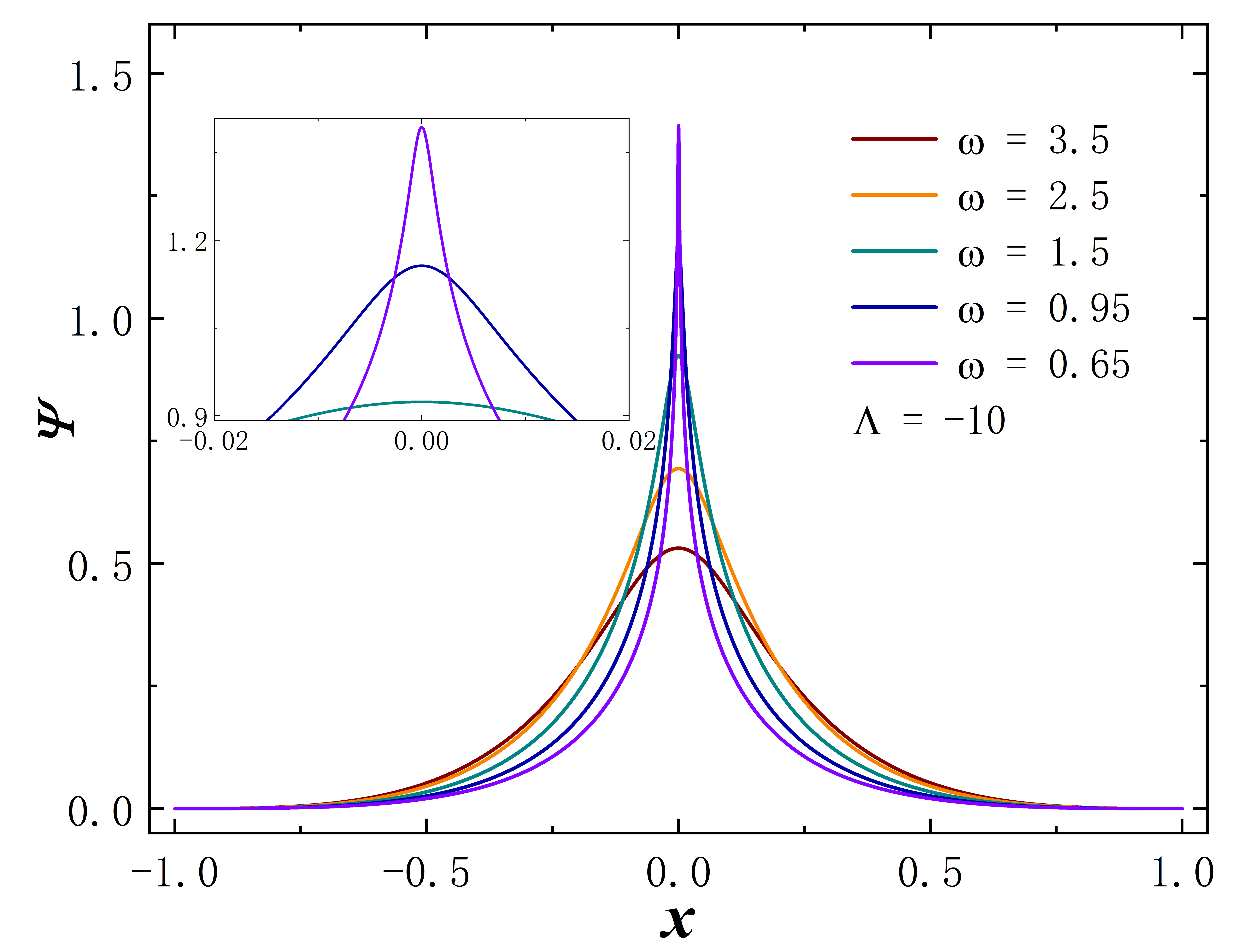
Given that this traversable wormhole solution is coupled with a scalar field, investigating the properties of the scalar field becomes highly relevant. Analogous to our previous approach, we fix the frequency at 0.6 or set the cosmological constant to -10. Subsequently, we explore the effects of varying or on the matter field within these two scenarios Fig. 4. Remarkably, we observe a recurring “extreme” behavior. As or decreases, the scalar field distribution near becomes highly concentrated, while the distribution in other regions of spacetime diminishes significantly. This property enables us to investigate the distribution of the Kretschmann scalar further. Fig. 5 illustrates the Kretschmann scalar distribution when remains constant while varying . When remains constant, decreasing leads to an increased value of the Kretschmann scalar, concentrating it near . Similarly, reducing at the same frequency produces a similar effect. The concentrated distribution of the matter field at the center of the wormhole, along with the nearly divergent Kretschmann scalar, suggests that within the parameter range where this “extreme” behavior occurs, the wormhole becomes untraversable.
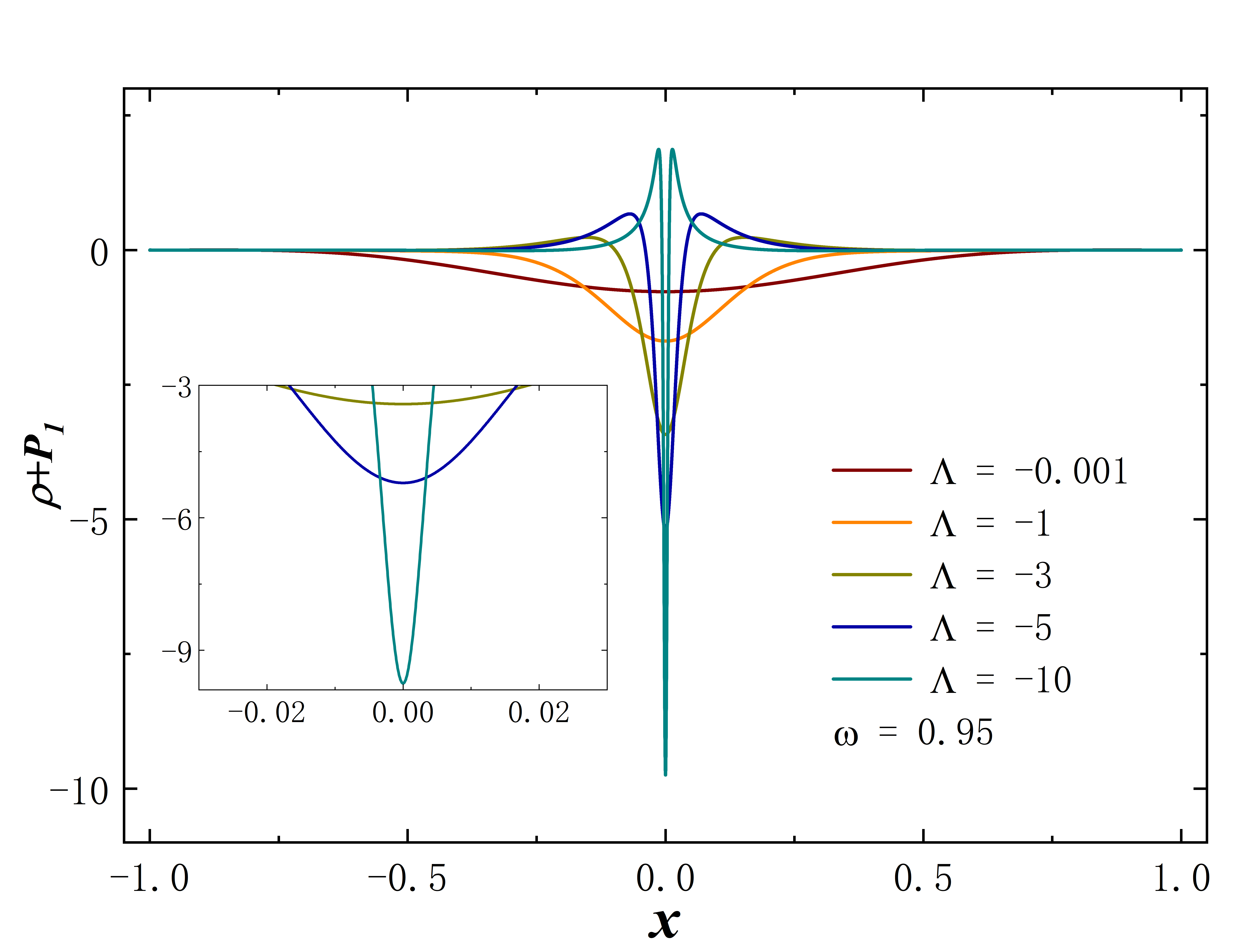
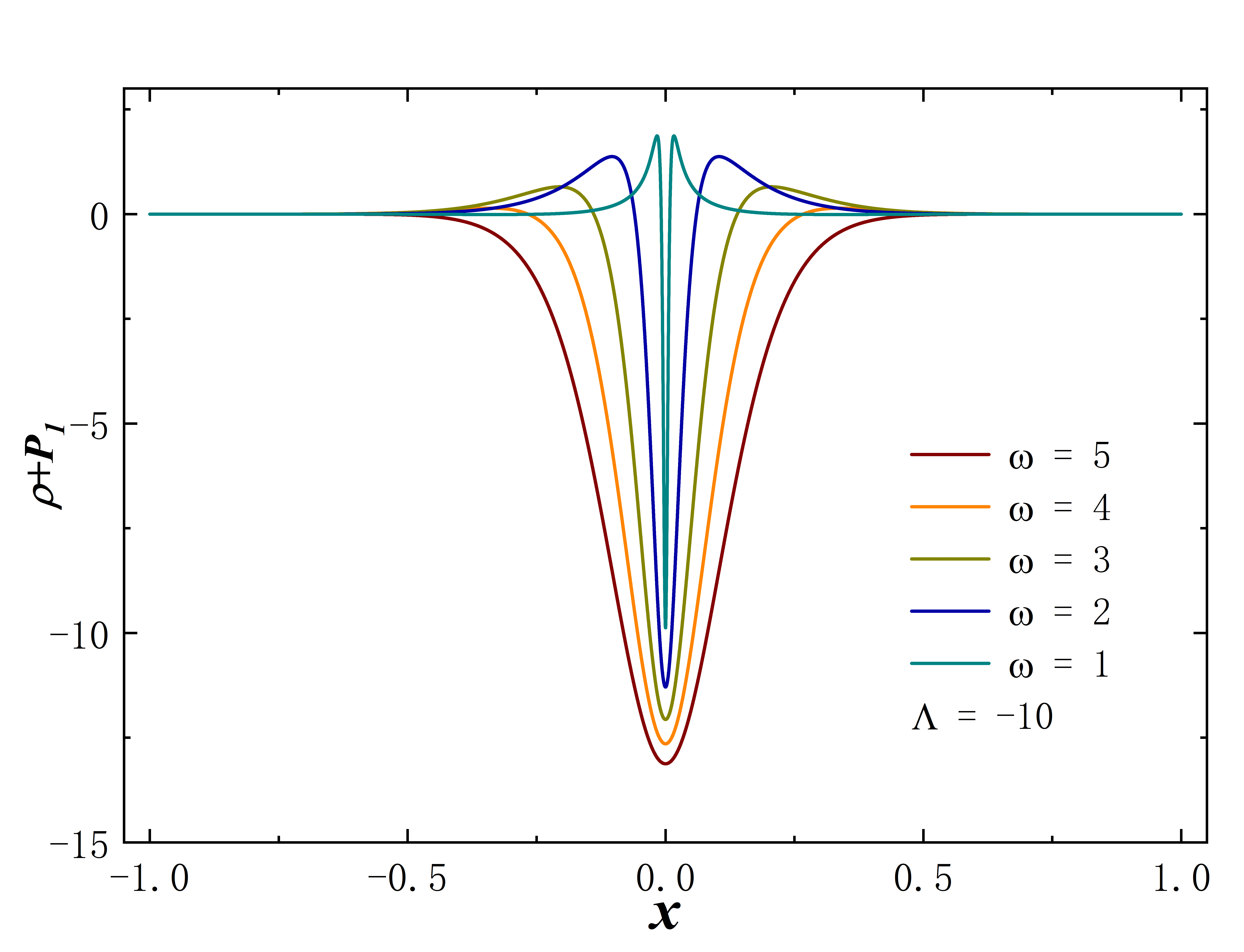
Ellis wormholes devoid of matter fields violate the null energy condition (NEC) due to the presence of a phantom field. However, what happens when a scalar field is coupled? We examine the sum of energy density and radial pressure in the context of varying the cosmological constant at a fixed frequency or altering the frequency while keeping the cosmological constant Fig. 6. While the violation of the null energy condition (NEC) persists at the wormhole throat, the degree of violation intensifies as decreases or increases. However, it is noteworthy that when the cosmological constant or frequency becomes small (specifically when or in the figure), two small regions symmetrically appear on both sides of the throat. Remarkably, within these spacetime regions, the NEC remains unviolated. This effect may arise from the contribution of a scalar field with positive energy density.
In the previous article, we defined the constant to reflect the scalar charge of the phantom field and to test the accuracy of numerical calculations. Its value, fixed at as a function of frequency , should be consistent at different positions, as shown in Fig. 7. Considering points at radial coordinates , the difference in is smaller than . Analogously, if we concentrate solely on the value of when the frequency is at its right limit (where the scalar field vanishes) in each scenario, the outcomes align with those observed in Blazquez-Salcedo:2020nsa . With decreasing , the constant at first decreases slightly to a minimum value and then increases as decreases further.
IV.3 The geometry properties
Finally, we study the geometric properties of the wormhole. We can make use of a geometrical embedding diagram by fixing and . The resulting two-dimensional spatial hypersurface of the wormhole spacetime can then be embedded in a three-dimensional Euclidean space, where the embedding diagram can be used to visualize the wormhole geometry. This technique allows us to better understand the topology and properties of the wormhole solution.
The specific method is: we begin by constructing the embeddings of planes with , and then use the cylindrical coordinates , the metric on this plane can be expressed by the following formula
| (27) | ||||
| (28) |
Comparing the two equations above, we then obtain the expression for and
| (29) |
Here corresponds to the circumferential radius, which corresponds to the radius of a circle located in the equatorial plane and having a constant coordinate . The function has extreme points, where the first derivative is zero. When the second derivative of the extreme point is greater than zero, we call this point a throat, which corresponds to a minimal surface. When the second derivative of the extreme point is less than zero, we call this point an equator, which corresponds to a maximal surface.
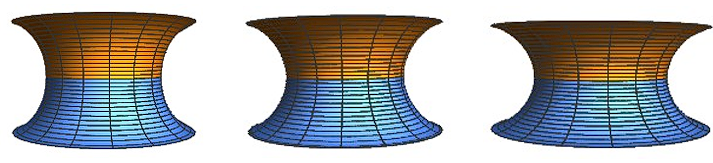
In Fig. 8, we present two sets of wormhole embedding diagrams. In the first row of figures, the frequency is fixed at 0.95, while the cosmological constants are varied as -0.001, -1, and -10. In the second row, the remains fixed at -1, and we explore three frequencies: 0.5, 0.9, and 1.5. Wormholes exhibit inherent symmetry and consistently possess a single throat without an equatorial plane. Decreasing the cosmological constant gradually widens the wormhole’s throat, whereas alterations in frequency have minimal impact on its geometric properties.
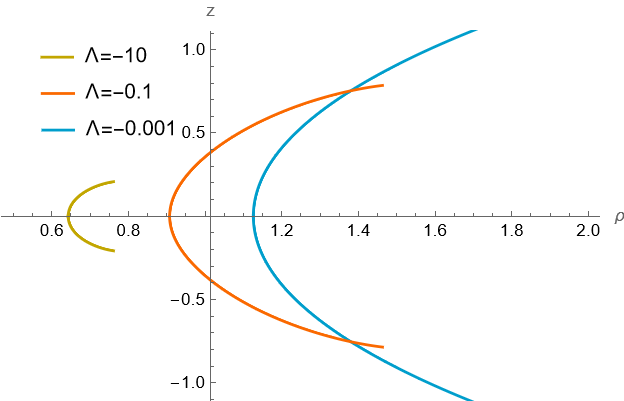
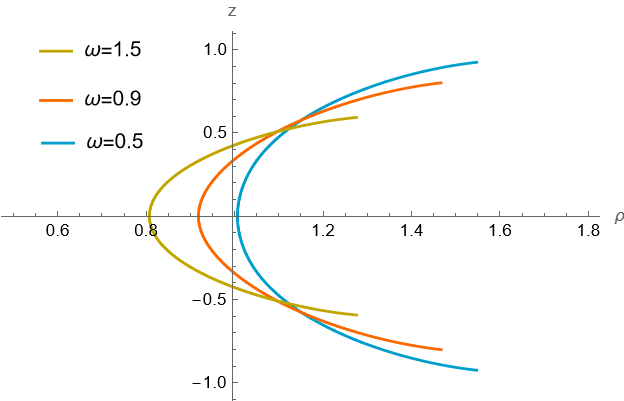

V CONCLUSION AND OUTLOOK
We have numerically constructed the solutions of Ellis wormholes with a scalar field in the anti-de Sitter (AdS) asymptotic spacetime. The wormhole solutions are symmetric with respect to and consequently massless. The wormholes possess a single throat which, because of the symmetry and the radial coordinate that we have used, is located at the position . The solutions can exist for any value of the negative cosmological constant, in this work, we have focused on discussion on the range . Through the computation of the Noether charge of different cosmological constants under different cases, we have elucidated the properties of the matter field within this solution. Additionally, by analyzing the metric functions and , we reveal the characteristics of spacetime. Notably, the most intriguing aspect lies in the “extreme” behavior observed within specific parameter ranges. At this juncture, the value of at the throat tends toward zero, signifying the emergence of an approximate “event horizon”. The scalar field distribution in the throat also exhibits high concentration, as reflected in the distribution of the Kretschmann scalar.
In addition, despite the persistent violation of the Null Energy Condition (NEC) at the wormhole throat, the introduction of scalar field results in NEC compliance within specific symmetry regions on both sides of the throat, subject to certain parameter ranges. Notably, wormholes exhibit geometric symmetry, featuring single throats without equatorial planes. However, variations in cosmological constants and frequencies lead to modifications in the wormhole embedding diagram. Finally, the substantial overlap in the values of across various positions indicates that our numerical calculations exhibit minimal error.
Let us end with two related outlooks. The stability of wormholes with a phantom field has always been of concern. At present, it is known that both pure Ellis wormholes and Ellis wormholes coupled with matter fields are unstable Gonzalez:2008wd ; Bronnikov:2011if ; Dzhunushaliev:2014bya , the asymptotically AdS wormholes are also unstable against radial linear perturbations Blazquez-Salcedo:2020nsa . So what if the AdS asymptotic Ellis wormhole is coupled to the material field? We defer the investigation of stability for future work.
While it is expected that an AdS asymptotic Ellis wormhole constructed solely from a massless phantom field remains massless, our results indicate that even when coupled with a scalar matter field, this wormhole lacks ADM mass. Notably, in Lu:2015cqa ; Hao:2023kvf , the ADM mass of black hole or wormhole spacetime transitions from positive to negative, with a solution also existing at a mass of 0. The solution obtained in this study exhibits radial symmetry, which explains the absence of ADM mass. Our future goal is to explore the possibility of finding an asymmetric AdS asymptotic wormhole solution coupled with matter.
Acknowledgements
This work is supported by the National Key Research and Development Program of China (Grant No. 2022YFC2204101 and 2020YFC2201503) and the National Natural Science Foundation of China (Grant No. 12275110 and No. 12247101).
References
- (1) A. Einstein and N. Rosen, The Particle Problem in the General Theory of Relativity, Phys. Rev. 48 (1935), 73-77 doi:10.1103/PhysRev.48.73
- (2) M. D. Kruskal, Maximal extension of Schwarzschild metric, Phys. Rev. 119 (1960), 1743-1745 doi:10.1103/PhysRev.119.1743
- (3) R. W. Fuller and J. A. Wheeler, Causality and Multiply Connected Space-Time, Phys. Rev. 128 (1962), 919-929 doi:10.1103/PhysRev.128.919
- (4) C. W. Misner and J. A. Wheeler, Classical physics as geometry: Gravitation, electromagnetism, unquantized charge, and mass as properties of curved empty space, Annals Phys. 2 (1957), 525-603 doi:10.1016/0003-4916(57)90049-0
- (5) M. Visser, Traversable wormholes: Some simple examples, Phys. Rev. D 39 (1989), 3182-3184 doi:10.1103/PhysRevD.39.3182 [arXiv:0809.0907 [gr-qc]].
- (6) H. G. Ellis, Ether flow through a drainhole - a particle model in general relativity, J. Math. Phys. 14 (1973), 104-118 doi:10.1063/1.1666161
- (7) H. G. Ellis, THE EVOLVING, FLOWLESS DRAIN HOLE: A NONGRAVITATING PARTICLE MODEL IN GENERAL RELATIVITY THEORY, Gen. Rel. Grav. 10 (1979), 105-123 doi:10.1007/BF00756794
- (8) K. A. Bronnikov, Scalar-tensor theory and scalar charge, Acta Phys. Polon. B 4 (1973), 251-266
- (9) T. Kodama, General Relativistic Nonlinear Field: A Kink Solution in a Generalized Geometry, Phys. Rev. D 18 (1978), 3529-3534 doi:10.1103/PhysRevD.18.3529
- (10) M. S. Morris and K. S. Thorne, Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity, Am. J. Phys. 56 (1988), 395-412 doi:10.1119/1.15620
- (11) F. S. N. Lobo, Phys. Rev. D 71 (2005), 084011 doi:10.1103/PhysRevD.71.084011 [arXiv:gr-qc/0502099 [gr-qc]].
- (12) S. V. Sushkov, Phys. Rev. D 71 (2005), 043520 doi:10.1103/PhysRevD.71.043520 [arXiv:gr-qc/0502084 [gr-qc]].
- (13) F. S. N. Lobo, Phys. Rev. D 71 (2005), 124022 doi:10.1103/PhysRevD.71.124022 [arXiv:gr-qc/0506001 [gr-qc]].
- (14) K. A. Bronnikov, R. A. Konoplya and A. Zhidenko, Phys. Rev. D 86 (2012), 024028 doi:10.1103/PhysRevD.86.024028 [arXiv:1205.2224 [gr-qc]].
- (15) B. Kleihaus and J. Kunz, Phys. Rev. D 90 (2014), 121503 doi:10.1103/PhysRevD.90.121503 [arXiv:1409.1503 [gr-qc]].
- (16) D. I. Novikov, A. G. Doroshkevich, I. D. Novikov and A. A. Shatskiy, Astron. Rep. 53 (2009), 1079-1085 doi:10.1134/S1063772909120014 [arXiv:0911.4456 [gr-qc]].
- (17) K. A. Bronnikov, L. N. Lipatova, I. D. Novikov and A. A. Shatskiy, Grav. Cosmol. 19 (2013), 269-274 doi:10.1134/S0202289313040038 [arXiv:1312.6929 [gr-qc]].
- (18) F. Cremona, F. Pirotta and L. Pizzocchero, Gen. Rel. Grav. 51 (2019) no.1, 19 doi:10.1007/s10714-019-2501-x [arXiv:1805.02602 [gr-qc]].
- (19) H. Huang, H. Lü and J. Yang, Class. Quant. Grav. 39 (2022) no.18, 185009 doi:10.1088/1361-6382/ac8266 [arXiv:2010.00197 [gr-qc]].
- (20) K. A. Bronnikov and S. W. Kim, Possible wormholes in a brane world, Phys. Rev. D 67 (2003), 064027 doi:10.1103/PhysRevD.67.064027 [arXiv:gr-qc/0212112 [gr-qc]].
- (21) P. Kanti, B. Kleihaus and J. Kunz, Wormholes in Dilatonic Einstein-Gauss-Bonnet Theory Phys. Rev. Lett. 107 (2011), 271101 doi:10.1103/PhysRevLett.107.271101 [arXiv:1108.3003 [gr-qc]].
- (22) J. Maldacena and A. Milekhin, Humanly traversable wormholes Phys. Rev. D 103 (2021) no.6, 066007 doi:10.1103/PhysRevD.103.066007 [arXiv:2008.06618 [hep-th]].
- (23) J. L. Blázquez-Salcedo, C. Knoll and E. Radu, Traversable wormholes in Einstein-Dirac-Maxwell theory, Phys. Rev. Lett. 126 (2021) no.10, 101102 doi:10.1103/PhysRevLett.126.101102 [arXiv:2010.07317 [gr-qc]].
- (24) R. A. Konoplya and A. Zhidenko, Traversable Wormholes in General Relativity, Phys. Rev. Lett. 128 (2022) no.9, 091104 doi:10.1103/PhysRevLett.128.091104 [arXiv:2106.05034 [gr-qc]].
- (25) B. Kain, Einstein-Dirac-Maxwell wormholes in quantum field theory, [arXiv:2308.00049 [gr-qc]].
- (26) F. R. Klinkhamer, Defect Wormhole: A Traversable Wormhole Without Exotic Matter, Acta Phys. Polon. B 54 (2023) no.5, 5-A3 doi:10.5506/APhysPolB.54.5-A3 [arXiv:2301.00724 [gr-qc]].
- (27) J. M. Maldacena, Adv. Theor. Math. Phys. 2 (1998), 231-252 doi:10.4310/ATMP.1998.v2.n2.a1 [arXiv:hep-th/9711200 [hep-th]].
- (28) J. Maldacena and L. Susskind, Fortsch. Phys. 61 (2013), 781-811 doi:10.1002/prop.201300020 [arXiv:1306.0533 [hep-th]].
- (29) P. Gao, D. L. Jafferis and A. C. Wall, JHEP 12 (2017), 151 doi:10.1007/JHEP12(2017)151 [arXiv:1608.05687 [hep-th]].
- (30) J. Maldacena, D. Stanford and Z. Yang, Fortsch. Phys. 65 (2017) no.5, 1700034 doi:10.1002/prop.201700034 [arXiv:1704.05333 [hep-th]].
- (31) R. van Breukelen and K. Papadodimas, JHEP 08 (2018), 142 doi:10.1007/JHEP08(2018)142 [arXiv:1708.09370 [hep-th]].
- (32) J. Maldacena and X. L. Qi, [arXiv:1804.00491 [hep-th]].
- (33) D. C. Dai, D. Minic, D. Stojkovic and C. Fu, Phys. Rev. D 102 (2020) no.6, 066004 doi:10.1103/PhysRevD.102.066004 [arXiv:2002.08178 [hep-th]].
- (34) S. Bintanja, R. Espíndola, B. Freivogel and D. Nikolakopoulou, JHEP 10 (2021), 173 doi:10.1007/JHEP10(2021)173 [arXiv:2102.06628 [hep-th]].
- (35) A. Kundu, Eur. Phys. J. C 82 (2022) no.5, 447 doi:10.1140/epjc/s10052-022-10376-z [arXiv:2110.14958 [hep-th]].
- (36) B. Kain, Phys. Rev. Lett. 131 (2023) no.10, 101001 doi:10.1103/PhysRevLett.131.101001 [arXiv:2309.03314 [hep-th]].
- (37) J. P. S. Lemos, F. S. N. Lobo and S. Quinet de Oliveira, Phys. Rev. D 68 (2003), 064004 doi:10.1103/PhysRevD.68.064004 [arXiv:gr-qc/0302049 [gr-qc]].
- (38) J. P. S. Lemos and F. S. N. Lobo, Phys. Rev. D 69 (2004), 104007 doi:10.1103/PhysRevD.69.104007 [arXiv:gr-qc/0402099 [gr-qc]].
- (39) H. Maeda and M. Nozawa, Phys. Rev. D 78 (2008), 024005 doi:10.1103/PhysRevD.78.024005 [arXiv:0803.1704 [gr-qc]].
- (40) H. Maeda, Phys. Rev. D 86 (2012), 044016 doi:10.1103/PhysRevD.86.044016 [arXiv:1204.4472 [gr-qc]].
- (41) T. Wu, Phys. Rev. D 108 (2023) no.4, 044001 doi:10.1103/PhysRevD.108.044001 [arXiv:2209.02278 [gr-qc]].
- (42) M. Nozawa, Phys. Rev. D 103 (2021) no.2, 024005 doi:10.1103/PhysRevD.103.024005 [arXiv:2010.07561 [gr-qc]].
- (43) A. Anabalón and J. Oliva, JHEP 04 (2019), 106 doi:10.1007/JHEP04(2019)106 [arXiv:1811.03497 [hep-th]].
- (44) R. V. Korolev and S. V. Sushkov, Phys. Rev. D 90 (2014), 124025 doi:10.1103/PhysRevD.90.124025 [arXiv:1408.1235 [gr-qc]].
- (45) G. Franciolini, L. Hui, R. Penco, L. Santoni and E. Trincherini, JHEP 01 (2019), 221 doi:10.1007/JHEP01(2019)221 [arXiv:1811.05481 [hep-th]].
- (46) N. Chatzifotis, G. Koutsoumbas and E. Papantonopoulos, Phys. Rev. D 104 (2021) no.2, 024039 doi:10.1103/PhysRevD.104.024039 [arXiv:2011.08770 [gr-qc]].
- (47) J. L. Blázquez-Salcedo, X. Y. Chew, J. Kunz and D. H. Yeom, Eur. Phys. J. C 81 (2021) no.9, 858 doi:10.1140/epjc/s10052-021-09645-0 [arXiv:2012.06213 [gr-qc]].
- (48) J. A. Wheeler, Phys. Rev. 97 (1955), 511-536 doi:10.1103/PhysRev.97.511
- (49) E. A. Power and J. A. Wheeler, Rev. Mod. Phys. 29 (1957), 480-495 doi:10.1103/RevModPhys.29.480
- (50) D. J. Kaup, Phys. Rev. 172 (1968), 1331-1342 doi:10.1103/PhysRev.172.1331
- (51) R. Ruffini and S. Bonazzola, Phys. Rev. 187 (1969), 1767-1783 doi:10.1103/PhysRev.187.1767
- (52) F. E. Schunck and E. W. Mielke, Phys. Lett. A 249 (1998), 389-394 doi:10.1016/S0375-9601(98)00778-6
- (53) S. Yoshida and Y. Eriguchi, Phys. Rev. D 56 (1997), 762-771 doi:10.1103/PhysRevD.56.762
- (54) A. Bernal, J. Barranco, D. Alic and C. Palenzuela, Phys. Rev. D 81 (2010), 044031 doi:10.1103/PhysRevD.81.044031 [arXiv:0908.2435 [gr-qc]].
- (55) L. G. Collodel, B. Kleihaus and J. Kunz, Phys. Rev. D 96 (2017) no.8, 084066 doi:10.1103/PhysRevD.96.084066 [arXiv:1708.02057 [gr-qc]].
- (56) Y. Q. Wang, Y. X. Liu and S. W. Wei, Phys. Rev. D 99 (2019) no.6, 064036 doi:10.1103/PhysRevD.99.064036 [arXiv:1811.08795 [gr-qc]].
- (57) C. A. R. Herdeiro, J. Kunz, I. Perapechka, E. Radu and Y. Shnir, Phys. Rev. D 103 (2021) no.6, 065009 doi:10.1103/PhysRevD.103.065009 [arXiv:2101.06442 [gr-qc]].
- (58) D. Astefanesei and E. Radu, Nucl. Phys. B 665 (2003), 594-622 doi:10.1016/S0550-3213(03)00482-6 [arXiv:gr-qc/0309131 [gr-qc]].
- (59) A. Buchel, S. L. Liebling and L. Lehner, Phys. Rev. D 87 (2013) no.12, 123006 doi:10.1103/PhysRevD.87.123006 [arXiv:1304.4166 [gr-qc]].
- (60) M. Maliborski and A. Rostworowski, [arXiv:1307.2875 [gr-qc]].
- (61) G. Fodor, P. Forgács and P. Grandclément, Phys. Rev. D 92 (2015) no.2, 025036 doi:10.1103/PhysRevD.92.025036 [arXiv:1503.07746 [gr-qc]].
- (62) Y. Brihaye, B. Hartmann and S. Tojiev, Class. Quant. Grav. 30 (2013), 115009 doi:10.1088/0264-9381/30/11/115009 [arXiv:1301.2452 [hep-th]].
- (63) H. S. Liu, H. Lu and Y. Pang, Phys. Rev. D 102 (2020) no.12, 126008 doi:10.1103/PhysRevD.102.126008 [arXiv:2007.15017 [hep-th]].
- (64) V. Dzhunushaliev, V. Folomeev, C. Hoffmann, B. Kleihaus and J. Kunz, Phys. Rev. D 90 (2014) no.12, 124038 doi:10.1103/PhysRevD.90.124038 [arXiv:1409.6978 [gr-qc]].
- (65) C. Hoffmann, T. Ioannidou, S. Kahlen, B. Kleihaus and J. Kunz, Phys. Rev. D 95 (2017) no.8, 084010 doi:10.1103/PhysRevD.95.084010 [arXiv:1703.03344 [gr-qc]].
- (66) Y. Yue, P. B. Ding and Y. Q. Wang, Eur. Phys. J. C 83 (2023) no.8, 732 doi:10.1140/epjc/s10052-023-11914-z [arXiv:2305.04496 [gr-qc]].
- (67) P. B. Ding, T. X. Ma and Y. Q. Wang, [arXiv:2305.19819 [gr-qc]].
- (68) C. H. Hao, S. X. Sun, L. X. Huang, R. Zhang, X. Su and Y. Q. Wang, [arXiv:2309.16379 [gr-qc]].
- (69) X. Su, C. H. Hao, J. R. Ren and Y. Q. Wang, [arXiv:2311.17557 [gr-qc]].
- (70) A. Simpson and M. Visser, Black-bounce to traversable wormhole, JCAP 02 (2019), 042 doi:10.1088/1475-7516/2019/02/042 [arXiv:1812.07114 [gr-qc]].
- (71) F. S. N. Lobo, M. E. Rodrigues, M. V. de Sousa Silva, A. Simpson and M. Visser, Novel black-bounce spacetimes: wormholes, regularity, energy conditions, and causal structure, Phys. Rev. D 103 (2021) no.8, 084052 doi:10.1103/PhysRevD.103.084052 [arXiv:2009.12057 [gr-qc]].
- (72) J. A. Gonzalez, F. S. Guzman and O. Sarbach, Class. Quant. Grav. 26 (2009), 015010 doi:10.1088/0264-9381/26/1/015010 [arXiv:0806.0608 [gr-qc]].
- (73) K. A. Bronnikov, J. C. Fabris and A. Zhidenko, Eur. Phys. J. C 71 (2011), 1791 doi:10.1140/epjc/s10052-011-1791-2 [arXiv:1109.6576 [gr-qc]].
- (74) H. Lu, A. Perkins, C. N. Pope and K. S. Stelle, Phys. Rev. Lett. 114 (2015) no.17, 171601 doi:10.1103/PhysRevLett.114.171601 [arXiv:1502.01028 [hep-th]].
- (75) C. H. Hao, L. X. Huang, X. Su and Y. Q. Wang, [arXiv:2312.03800 [gr-qc]].