All bipartite circulants are dispersable

Shannon Overbay, Samuel Joslin, Paul C. Kainen

Abstract

We show that a cyclic vertex order due to Yu, Shao and Li gives a dispersable book embedding for any bipartite circulant.

Keywords: edge-coloring, graph drawing, 05C10, 05C15, 05C78.

It has been conjectured [2] that vertex transitive bipartite graphs can be laid out with vertices on the unit circle, with edges as chords, such that there is a Vizing type-1 edge-coloring where no crossings are monochromatic. Such a drawing and coloring is a dispersable book embedding [3].

We proposed this in 1979, omitting vertex transitivity [3], but in 2018, Alam et al [1] found two counterexamples and later Alam et al. [2] showed the existence of an infinite family of regular bipartite graphs, of fixed degree, which require an arbitrarily large number of edge colors to avoid monochrome edge-crossings.

Based on their examples, Alam et al [2] added the qualification of vertex transitivity, and we further conjectured in [12] that vertex transitive non-bipartite graphs have a type-2 edge coloring (i.e., are nearly dispersable). See [9, 11, 14, 16, 15] which support both conjectures.

In [17, Theorem 4.1], Yu, Shao and Li found what we call the YSL-order; see Fig. 1. They used it only for bipartite degree 3 and 4 circulants. In contrast, we show that the following holds and give a short proof.

Theorem 1.

Any bipartite circulant with the YSL-order is dispersable.

The theorem is additional evidence for the conjecture of [2]. Circulants have been one of the more widely used graph-types and so the theorem might have interesting applications. See, e.g., [5, 7, 8, 10].

In fact, the YSL-order also gives dispersable embeddings for the Franklin and Heawood graphs but not for the Desargues graph.

We now briefly sketch some definitions for the reader’s convenience.

A graph $G=(V,E)$ is a circulant if $V=\{1,\ldots,n\}$ , $n\geq 3$ , and there exists $S\subseteq\{1,2,\ldots,\lfloor n/2\rfloor\}$ such that $E=\{ij:j=i+s,s\in S\}$ , where addition is mod $n$ . Such a circulant is denoted $C(n,S)$ and the elements in $S$ are the jump-lengths. The ${\bf C}_{\bf n}$ -distance between two vertices $u,w$ of a circulant $C(n,S)$ is the graph-theoretic distance in $C_{n}$ ; for instance, the $C_{16}$ -distance from 2 to 13 is 5.

A graph $G$ is dispersable [3] if it has an outerplane drawing (crossings allowed) and an edge-coloring with $\Delta(G)$ colors ( $\Delta=$ maximum degree) such that two edges of the same color neither cross nor share an endpoint. The color-classes (or pages) are matchings for this book embedding.

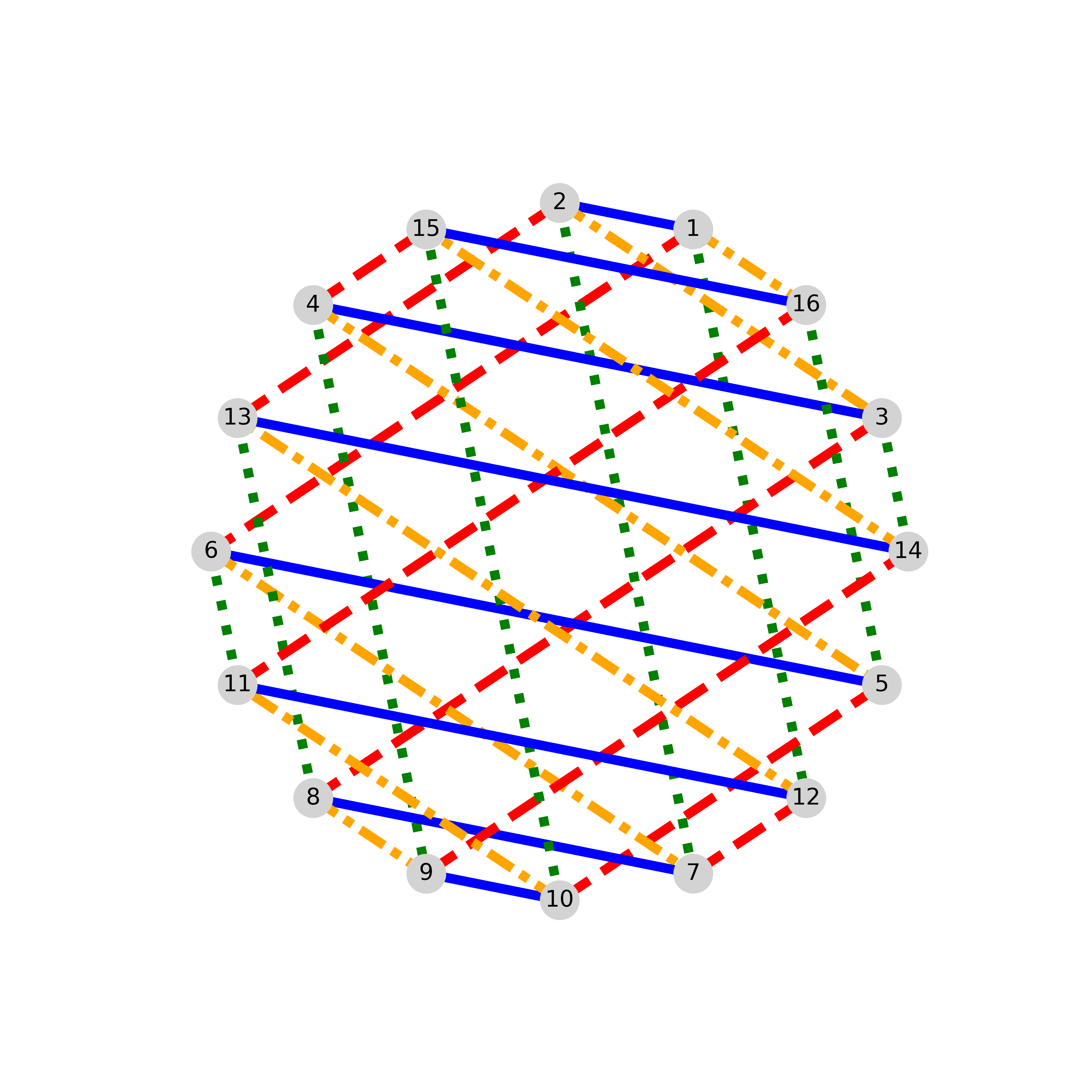
Refer to caption — Figure 1: YSL-order for $C(16,\{1,3,5,7\})$ . Only 1 and 5 are shown.

In a YSL-order, the natural clockwise cyclic order $1,2,\ldots,2k$ is permuted so that the odd vertices remain, in clockwise order, at the odd positions, while the even vertices are placed at the even-indexed positions but in counterclockwise order. Our argument below shows that it doesn’t matter where 2 is placed. In [17], Yu et al put 2 immediately counterclockwise of 1, so in clockwise direction, their order is

\dots,2k-3,4,2k-1,2,1,2k,3,2k-2,5,\ldots

Using characterizations of bipartite circulants by Heuberger [6] and of connected circulants by Boesch and Tindell [4], and the fact that a disjoint union of identical subgraphs is dispersable if the subgraph is dispersable, one sees that to prove Theorem 1, it suffices to show the following.

Theorem 2.

Let $n=2k$ , $k\geq 2$ , and let $\mu(k)$ be the largest odd number not exceeding $k$ . Then $C=C(n,\{1,3,\ldots,\mu(k)\})$ is dispersable under a YSL order, and the edges in each page correspond to a single jump-length.

Proof.

Each page consists of a maximal parallel family of edges which we enumerate $1,\ldots,k$ in the order they intersect some orthogonal line. We show that (i) the $C_{n}$ -distance between the endpoints of edge 1 and edge 2 are equal and (ii) the same holds for edge $j$ and edge $j+2$ , $1\leq j\leq n-2$ .

For (i), suppose that $ab$ and $a^{\prime}b^{\prime}$ are edges 1 and 2, with $(a^{\prime},a,b,b^{\prime})$ occurring consecutively clockwise. Then $a^{\prime}=b\pm 2$ and $b^{\prime}=a\pm 2$ , where the signs agree because vertices alternate odd/even and the ordering is opposite for the two parities. Hence, the $C_{n}$ distance from $a$ to $b$ is the same as the $C_{n}$ distance from $b^{\prime}$ to $a^{\prime}$ . But distance is symmetric.

For (ii), suppose that $ab$ and $a^{\prime}b^{\prime}$ are edges $j$ and $j+2$ , with

(a^{\prime},x,a,\ldots,b,y,b^{\prime})

occurring consecutively clockwise but $a$ and $b$ can be nonconsecutive. Then $a^{\prime}=a\pm 2$ and $b^{\prime}=b\pm 2$ , where again both signs must be equal. ∎

For the reader’s convenience, here are the cited theorems.

Theorem 3 (Heuberger [6]).

Let $C:=C(n,\{a_{1},\ldots,a_{m}\})$ . Then $C$ is bipartite if and only if there exists $\ell\in\mathbb{N}$ such that $2^{\ell}|a_{1},\ldots,a_{m}$ , $2^{\ell+1}|n$ , but $2^{\ell+1}$ does not divide any of the $a_{j}$ .

For $t$ a positive integer, let $tH$ denote $t$ disjoint copies of graph $H$ .

Theorem 4 (Boesch & Tindell [4]).

Let $C:=C(n,\{a_{1},\ldots,a_{m}\})$ be a circulant. Then $C=r\,C(n/r,\{a_{1}/r,\ldots,a_{m}/r\})$ , $r:=\gcd(n,a_{1},\dots,a_{m})$ .

If $C$ is bipartite, then $r=2^{\ell}u$ for $u$ odd, with $\ell$ as in Theorem 3.

Each maximal family of parallel edges, under the YSL ordering, has constant jump-length which could represent delay, allowing delay to depend on direction. In contrast, for Overbay’s ordering [13, p 82], for a family of parallel edges, jump-lengths vary palindromically and unimodally $1,3,\ldots,\mu(k),\ldots,3,1$ , with $\mu(k)$ repeated if and only if $k$ is even, as one traverses them with respect to a perpendicular line. See Fig. 2.

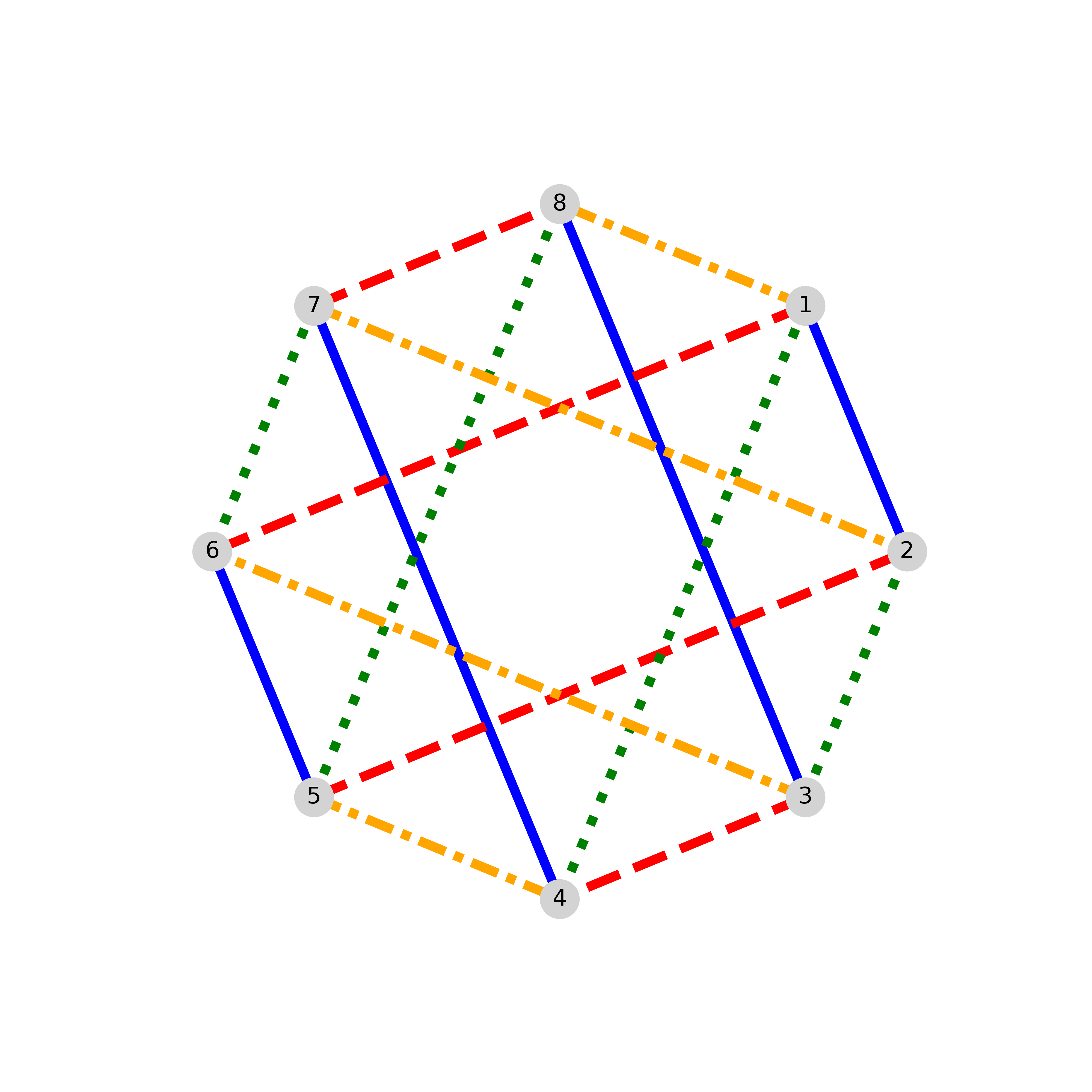
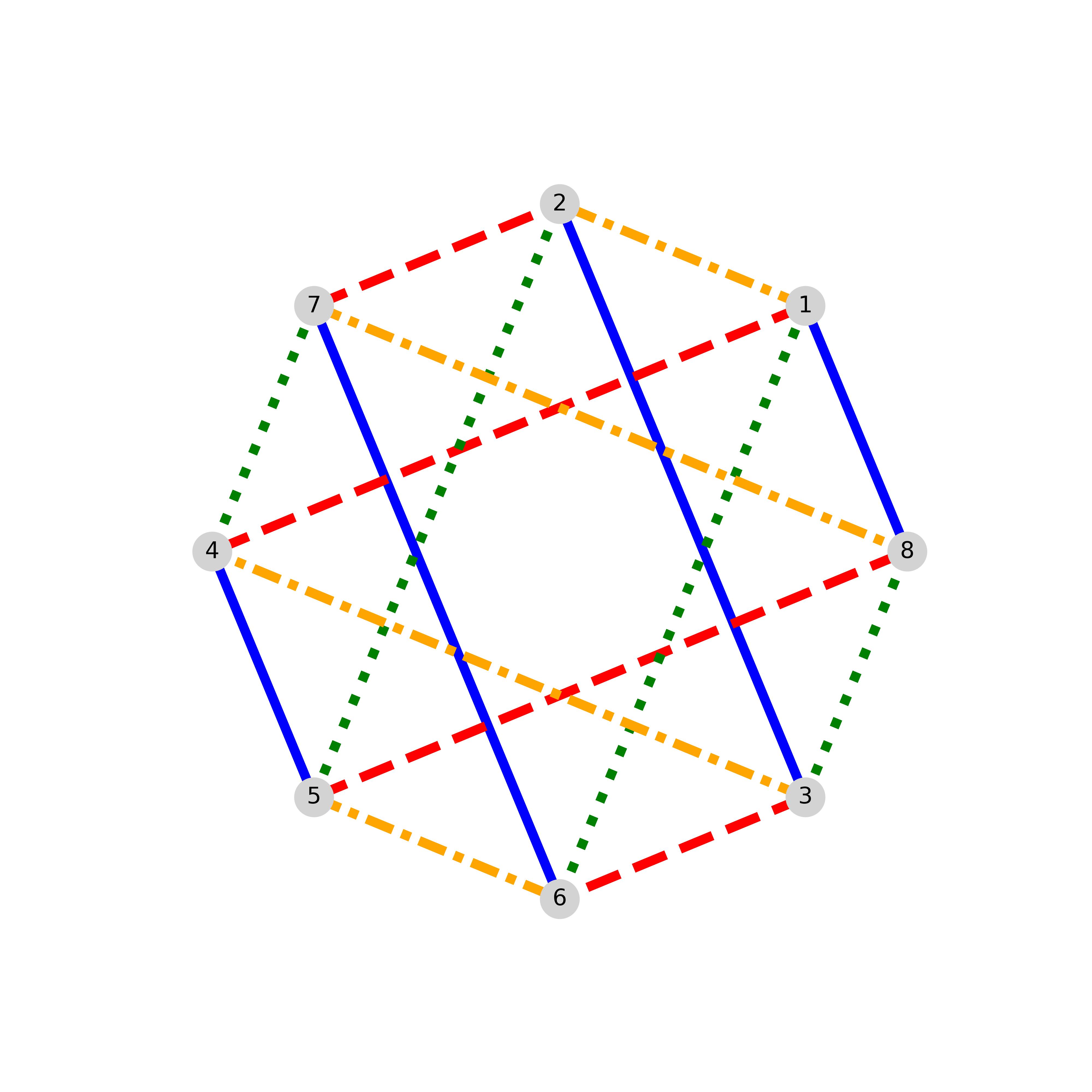
In applications, the bipartition could be input and output vertices.

References

[1] J. Md. Alam, M. A. Bekos, M. Gronemann, M. Kaufmann & S. Pupyrev, On dispersable book embeddings, Graph-theoretic Concepts in Computer Science (44th International Workshop, WG 2018, Cottbus, Germany), A. Brandestädt, E. Köhler, & K. Meer, Eds., LNCS 11159 (2018) 1–14, Springer, Cham, Switzerland.
[2] J. Md. Alam, M. A. Bekos, V. Dujmovič, M. Gronemann, M. Kaufmann & S. Pupyrev, On dispersable book embeddings, Theor. Computer Sci. 861 (2021) 1–22.
[3] F. R. Bernhart & P. C. Kainen, The book thickness of a graph, J. Comb. Th. B 27 (1979) 320–331.
[4] F. Boesch & R. Tindell, Circulants and their connectivities, J. Graph Theory 8 (1984) 487–499.
[5] F. Harary, The maximum connectivity of a graph, Proc. National Acad. of Sci. 48 (1962) 1142–1146.
[6] C. Heuberger, On planarity and colorability of circulant graphs, Discr. Math. 268 (2003) 153–169.
[7] X. Huang, A. F. Ramos, & Y. Deng, Optimal circulant graphs as low-latency network topologies, J Supercomput 78(2022) 13491–13510 (2022). https://doi.org/10.1007/s11227-022-04396-5
[8] F.K. Hwang, A survey on multi-loop networks, Theor. Comp. Science 299 (2003) 107–121.
[9] S. Joslin, P. C. Kainen & S. Overbay, Dispersability of some cycle products, Missouri J. Math. Sci. 33(2) (2021) 206–213
[10] S. Joslin, S. Overbay & P. C. Kainen, Information as order (?).
[11] P. C. Kainen. Complexity of products of even cycles, Bull. Inst. Comb. and Its Appl. 62 (2011) 95–102.
[12] P. C. Kainen, S. Joslin & S. Overbay, On dispersability of some circulants, J Graph Algor. & Appl., to appear.
[13] S. Overbay, Generalized book embeddings, Ph.D. Dissertation, Fort Collins: Colorado State University, 1998.
[14] Z. Shao, H. Geng, Z. Li, Matching book thickness of generalized Petersen graphs, Elec. J. Graph Theory and Appl., 10(1) (2022) 173–180.
[15] Z. Shao, Y. Liu, Z. Li. Matching book embedding of the Cartesian product of a complete graph and a cycle, Ars Combinatoria 153 (2020) 89–97.
[16] Z. Shao, X. Yu, & Z. Li, On the dispersability of toroidal grids, Appl. Math. & Computation 453 (2023) 128087.
[17] X. Yu, Z. Shao & Z. Li, On the classification and dispersability of circulant graphs with two jump lengths, arXiv:2310.06612 10 Oct 2023.