Alternatives to the Scaled Dot Product for Attention in the Transformer Neural Network Architecture

A scalar attention function is a function $a:\mathbb{R}^{d}\times\mathbb{R}^{d}\to\mathbb{R}$ for some $d$. The first argument of $a$ is called a $query$ and the second argument a $key$. For $q,k\in\mathbb{R}^{d}$, we will call the real number $a(q,k)$ the scalar attention of $q$ on $k$.

Given an attention function $a:\mathbb{R}^{d}\times\mathbb{R}^{d}\to\mathbb{R}$ and a finite ordered set $\mathcal{K}$ of keys $k_{1},\ldots,k_{n}\in\mathbb{R}^{d}$, we can define a function $a_{\mathcal{K}}:\mathbb{R}^{d}\to\mathbb{R}^{n}$, which we will call the vector attention function associated with $\mathcal{K}$ and based on $a$, by:

$$a_{\mathcal{K}}(q)=\begin{bmatrix}a(q,k_{1})\\ a(q,k_{2})\\ \vdots\\ a(q,k_{n})\end{bmatrix}.$$

We will call $a_{\mathcal{K}}(q)$ the vector attention of $q$ on $\mathcal{K}$.

Suppose that, for this set $\mathcal{K}$ of $n$ keys, we have a function $s_{\mathcal{K}}:\mathbb{R}^{n}\to\Delta^{n-1}$, where $\Delta^{n-1}$ is the standard $(n-1)$-simplex in $\mathbb{R}^{n}$:

$$\Delta^{n-1}=\{\begin{bmatrix}x_{1}\\ x_{2}\\ \vdots\\ x_{n}\end{bmatrix}\in\mathbb{R}^{n}\ |\ \sum_{i=1}^{n}x_{i}=1\ \text{and}\ \forall i\ x_{i}\geq 0\}.$$

We will call such a function $s_{\mathcal{K}}$ a rescaling function.

With a rescaling function, we can then define the rescaled vector attention function $A_{\mathcal{K}}:\mathbb{R}^{d}\to\Delta^{n-1}$ based on $a$, $\mathcal{K}$, and $s_{\mathcal{K}}$ by:

$$A_{\mathcal{K}}=s_{\mathcal{K}}\circ a_{\mathcal{K}}.$$

In the context of “Attention Is All You Need” [1], the authors describe what we have termed their scalar attention function as a “scaled dot product”:

$$a(q,k)=\frac{q\cdot k}{\sqrt{d}}.$$

For each set $\mathcal{K}$ of keys $k_{1},\ldots,k_{n}$, they use $\text{softmax}_{n}:\mathbb{R}^{n}\to\Delta^{n-1}$ as what we have called a rescaling function, defined by:

$$\text{softmax}_{n}(\begin{bmatrix}x_{1}\\ x_{2}\\ \vdots\\ x_{n}\end{bmatrix})=\frac{1}{\sum_{i=1}^{n}\exp(x_{i})}\begin{bmatrix}\exp(x_{1})\\ \exp(x_{2})\\ \vdots\\ \exp(x_{n})\end{bmatrix}.$$

This produces the following rescaled vector attention function $A_{\mathcal{K}}:\mathbb{R}^{d}\to\mathbb{R}^{n}$:

$$A_{\mathcal{K}}(q)=\frac{1}{\sum_{i=1}^{n}\exp(q\cdot k_{i}/\sqrt{d})}\begin{bmatrix}\exp(q\cdot k_{1}/\sqrt{d})\\ \exp(q\cdot k_{2}/\sqrt{d})\\ \vdots\\ \exp(q\cdot k_{n}/\sqrt{d})\end{bmatrix}.$$

Their paper also includes some additional aspects of attention that are important for its implementation in the transformer architecture, but that we mention only briefly here:

1. 1.

   In addition to keys $k_{1},\ldots,k_{n}\in\mathbb{R}^{d}$, they also have a finite ordered set of values $v_{1},\ldots,v_{n}\in\mathbb{R}^{t}$. (Since keys and values are to be thought of as pairs, the number of keys and values must be the same. However, the dimensions of the spaces where they reside may be different.) To arrive at what they term their “Attention” function, they first apply the above rescaled vector attention function and then apply a linear transformation $T:\mathbb{R}^{n}\to\mathbb{R}^{t}$ (restricted to the domain $\Delta_{n-1}$) given by

   $$T(\begin{bmatrix}x_{1}\\ x_{2}\\ \vdots\\ x_{n}\end{bmatrix})=\sum_{i=1}^{n}x_{i}v_{i}.$$

   This produces a vector in the convex hull of $v_{1},\ldots,v_{n}$.

2. 2.

   Also, they write their “Attention” function in terms of a set of (row vector) queries $q_{1},\ldots,q_{m}\in\mathbb{R}^{d}$ that form the rows of a matrix, rather than in terms of individual queries.

These aspects are important for the implementation of attention in the transformer architecture but not for our discussion here.

The authors of “Attention Is All You Need” [1] explain their reason for dividing the dot product by $\sqrt{d}$ (or $\sqrt{d_{k}}$ in their notation) in what we have termed their scalar attention function: “We suspect that for large values of $d_{k}$, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients. To counteract this effect, we scale the dot products by $1/\sqrt{d_{k}}$.” They elaborate further in a footnote that the issue can be observed by noting that if the components of the queries and keys are independent random variables with mean $0$ and variance $1$, then their dot products have mean $0$ and variance $d$.

Their explanation can be further illustrated through some simulations, and understanding these simulations will also be helpful when we use similar simulations to compare alternative rescalings later in this paper.

For each of the plots in Figure 1, we simulate all the components of every query and key as being independent and standard normally distributed. We generate a set of $32$ keys, and we give them a very small dimension of $16$. (The effect we are illustrating is so large that even such a small dimension shows it strongly.) To compute attentions, we generate $500$ queries, also each of dimension $16$. We then make a kernel density estimate plot of just the first component of the rescaled vector attention function applied to all the queries. By symmetry, the other components should look similar, and this approach avoids any issues with displaying (in the same kernel density estimate plot) multiple components of the rescaled vector attention, which lack independence.

In these three plots, each point represents the following:

1. a.

   In (a), a single unscaled dot product.

2. b.

   In (b), a single unscaled dot product after softmax has been applied to it.

3. c.

   In (c), a single scaled dot product (scaled by $1/\sqrt{d}$) after softmax has been applied to it.

Comparing the three plots in Figure 1, we can see how softmax, with and without scaling, distorts the shape of the original distribution of unscaled dot products.

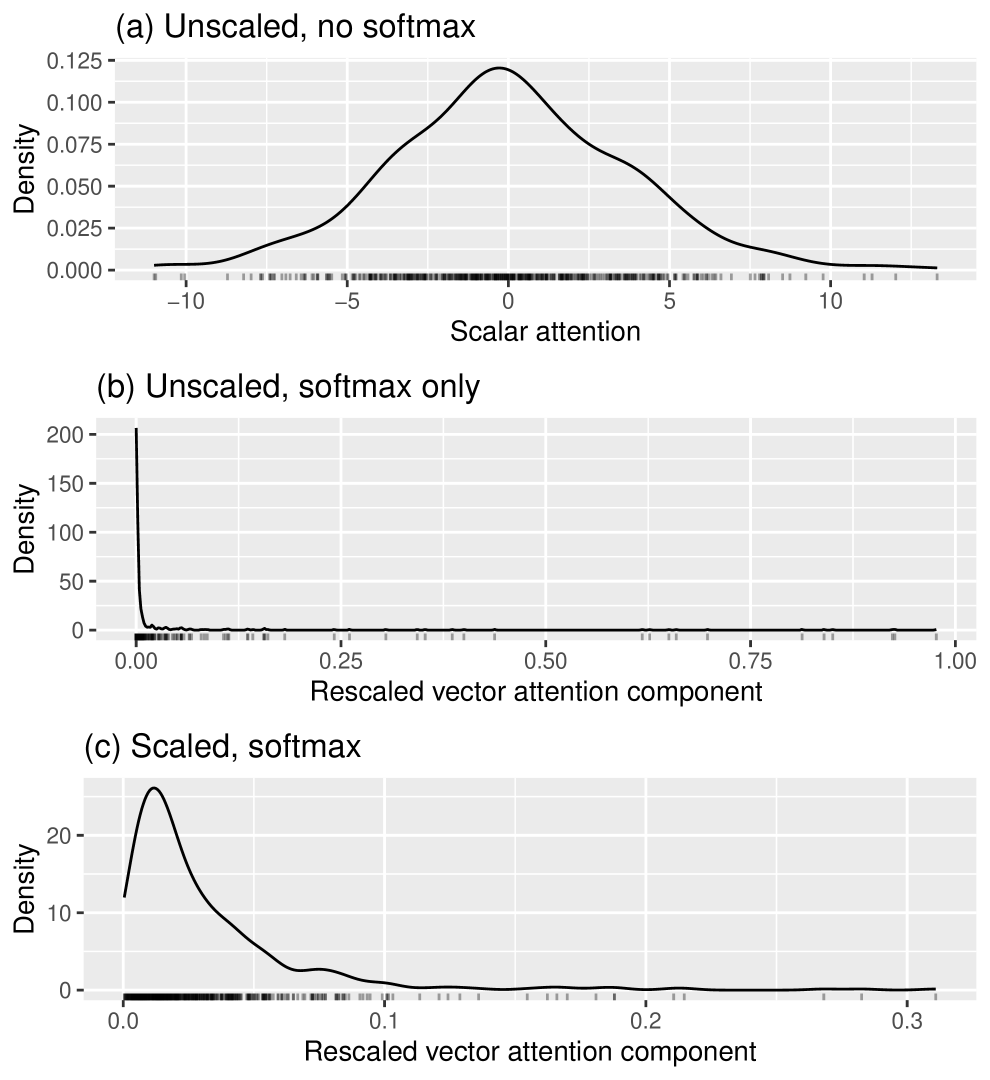
Even with such a small key dimension as $16$, Figure 1(b) shows that applying softmax without scaling severely distorts the shape of the distribution of the original dot products. Because the shape after applying softmax is weighted heavily near $0$ and has a pronounced right skew, it is apparent that applying softmax to the unscaled dot product would be prone to vanishing gradient issues.

Although Figure 1(c) shows a mild right skew that was not present in the distribution before softmax was applied, from the plot it is clear that dividing the dot products by $\sqrt{d}$ before applying softmax did indeed help preserve the general shape of the distribution compared to not scaling at all. Correspondingly, this method helps alleviate the vanishing gradient issue with softmax (as has also been demonstrated time and again in its widespread use).

However, there are two things to think about here:

1. 1.

   The choice to divide by $\sqrt{d}$ was based on the absolute values of the query and key dot products growing too large because of their dimension, but there are other reasons besides the dimension why the absolute value of these dot products might grow large. It would be good to compensate for those too.

2. 2.

   The reason why we want to compensate for the size of the dot products is that we are planning to apply softmax, but notice that it is impossible to apply softmax without knowing how many keys are in $\mathcal{K}$. As such, we might not be able to avoid all of the softmax-related difficulties by adjusting the scalar attention function, since this function has nothing to do with $\mathcal{K}$, only with individual keys. Instead we might want to adjust the rescaling function, which does depend on the choice of $\mathcal{K}$.

These considerations lead us to rethink the way we view dividing by $\sqrt{d}$ in the transformer neural network architecture. Instead of thinking of the “scaled dot product” $(q\cdot k)/\sqrt{d}$ as the scalar attention function and softmax as the rescaling function, we view the scalar attention function as the ordinary dot product $q\cdot k$ and the rescaling function as what might be called a “prescaled softmax function” $s_{\mathcal{K}}:\mathbb{R}^{n}\to\Delta_{n-1}$:

$$s_{\mathcal{K}}(\begin{bmatrix}x_{1}\\ x_{2}\\ \vdots\\ x_{n}\end{bmatrix})=\frac{1}{\sum_{i=1}^{n}\exp(x_{i}/\sqrt{d})}\begin{bmatrix}\exp(x_{1}/\sqrt{d})\\ \exp(x_{2}/\sqrt{d})\\ \vdots\\ \exp(x_{n}/\sqrt{d})\end{bmatrix}.$$

This minor shift in perspective is unimportant for using the “Attention” function directly as formulated in “Attention Is All You Need” [1]. However, for our purposes here it is crucial. It suggests that the ordinary, unscaled dot product (as used already in [3]) is actually a good scalar attention function; rescaling follows it only because of how it is to be used in a particular neural network context. This might seem like a small change, but it opens up the possibility that the rescaling might depend not solely on the dimension of the keys (as with dividing by $\sqrt{d}$) but possibly on the number of keys in $\mathcal{K}$ (as softmax does), or even on the keys $k_{1},\ldots,k_{n}$ themselves.

In light of the above considerations, we take the following as our starting point: the ordinary, unscaled dot product is a good scalar attention function for the transformer architecture, and our task is to figure out a suitable rescaling function $s_{\mathcal{K}}:\mathbb{R}^{n}\to\Delta_{n-1}$ that preserves as much of the overall shape of the distribution of the unscaled dot products as possible.

Note that the rescaling function doesn’t interact with queries directly, so in this approach, it can’t be helped if $\|q\|$ gets large and so makes the dot product large. If we were modifying the scalar attention function, it might be tempting to divide it by $\|q\|$, but (even ignoring the possibility of this being $0$) that would make the scalar attention function independent of $\|q\|$, which seems undesirable. It might be worth thinking about whether anything different should be done with $q$ in the scalar attention function, but for our purposes here we are leaving $q$ out of the investigation and focusing solely on finding a rescaling function.

Suppose then that we have the dot product as our scalar attention function $a:\mathbb{R}^{d}\times\mathbb{R}^{d}\to\mathbb{R}$:

$$a(q,k)=q\cdot k.$$

Also suppose that we are given a finite ordered set $\mathcal{K}$ of keys $k_{1},\ldots,k_{n}\in\mathbb{R}^{d}$. We can then define the vector attention function $a_{\mathcal{K}}:\mathbb{R}^{d}\times\mathbb{R}^{d}\to\mathbb{R}^{n}$ by:

$$a_{\mathcal{K}}(q)=\begin{bmatrix}q\cdot k_{1}\\ q\cdot k_{2}\\ \vdots\\ q\cdot k_{n}\end{bmatrix}.$$

Our task is to find a suitable rescaling function $s_{\mathcal{K}}:\mathbb{R}^{n}\to\Delta_{n-1}$.

A natural idea for a rescaling function would be $\text{softmax}_{n}:\mathbb{R}^{n}\to\Delta_{n-1}$, but as discussed above and in “Attention Is All You Need” [1], this function by itself is prone to vanishing gradients because the absolute values of the dot products that make up each component can easily get very large as the dimension $d$ of the keys and queries does. The authors of “Attention Is All You Need” [1] suggest pre-dividing by $\sqrt{d}$ before applying softmax, which works well for avoiding this problem.

However, as also discussed above, there are other reasons why the absolute values of the dot products might get large besides just the dimension of the key space. Keeping in mind that the function $s_{\mathcal{K}}$ can’t depend on the queries but that it can depend on $k_{1},\ldots,k_{n}$, some thought and experimentation suggests pre-dividing by $k_{total}$, the sum of the key lengths:

$$k_{total}=\sum_{i=1}^{n}\|k_{i}\|.$$

(Note that $k_{total}$ should indeed be nonzero in all practical applications.) In other words, as a rescaling function $s_{\mathcal{K}}:\mathbb{R}^{n}\to\Delta_{n-1}$, we propose:

$$s_{\mathcal{K}}(\begin{bmatrix}x_{1}\\ x_{2}\\ \vdots\\ x_{n}\end{bmatrix})=\frac{1}{\sum_{i=1}^{n}\exp(x_{i}/k_{total})}\begin{bmatrix}\exp(x_{1}/k_{total})\\ \exp(x_{2}/k_{total})\\ \vdots\\ \exp(x_{n}/k_{total})\end{bmatrix}.$$

Some of the intuition behind this is that, by the Cauchy-Schwarz inequality,

$$\frac{|k_{i}\cdot q|}{k_{total}}\leq\frac{\|k_{i}\|}{k_{total}}\|q\|\leq\|q\|.$$

As discussed earlier, the rescaling function doesn’t interact directly with the queries themselves. But the previous inequality shows that as long as the lengths of the queries don’t get too large, then the relative sizes of the components of the vectors to which softmax is applied won’t be distorted too much.

We now use simulations to compare this rescaling function to the one used (with a slightly different point of view, as discussed above) in “Attention Is All You Need” [1]. Both are of the following form:

$$s_{\mathcal{K}}(\begin{bmatrix}x_{1}\\ x_{2}\\ \vdots\\ x_{n}\end{bmatrix})=\frac{1}{\sum_{i=1}^{n}\exp(x_{i}/c_{\mathcal{K}})}\begin{bmatrix}\exp(x_{1}/c_{\mathcal{K}})\\ \exp(x_{2}/c_{\mathcal{K}})\\ \vdots\\ \exp(x_{n}/c_{\mathcal{K}})\end{bmatrix},$$

and $c_{\mathcal{K}}$ equals either $\sqrt{d}$ or $k_{total}$.

In each of the plots in Figure 2, we simulate all the components of every query and key as being independent and standard normally distributed. We generate a set of $32$ keys, each of dimension $256$. To compute the vector attentions, we generate $500$ queries, also each of dimension $256$. We then make a kernel density estimate plot of just the first component of either the vector attention function or the rescaled vector attention function applied to all the queries. By symmetry, the other components should look similar, and as before, this approach avoids any issues with displaying (in the same kernel density estimate plot) multiple components of the rescaled vector attention, which lack independence.

Each point in the three plots in Figure 2 represents:

1. a.

   In (a), a single unscaled dot product.

2. b.

   In (b), a dot product which has been rescaled by the above $s_{\mathcal{K}}$ with $c_{\mathcal{K}}=\sqrt{d}$, as in “Attention Is All You Need” [1],

3. c.

   In (c), a dot product which has been rescaled by the above $s_{\mathcal{K}}$ with $c_{\mathcal{K}}=k_{total}=\sum_{i=1}^{n}\|k_{i}\|$.

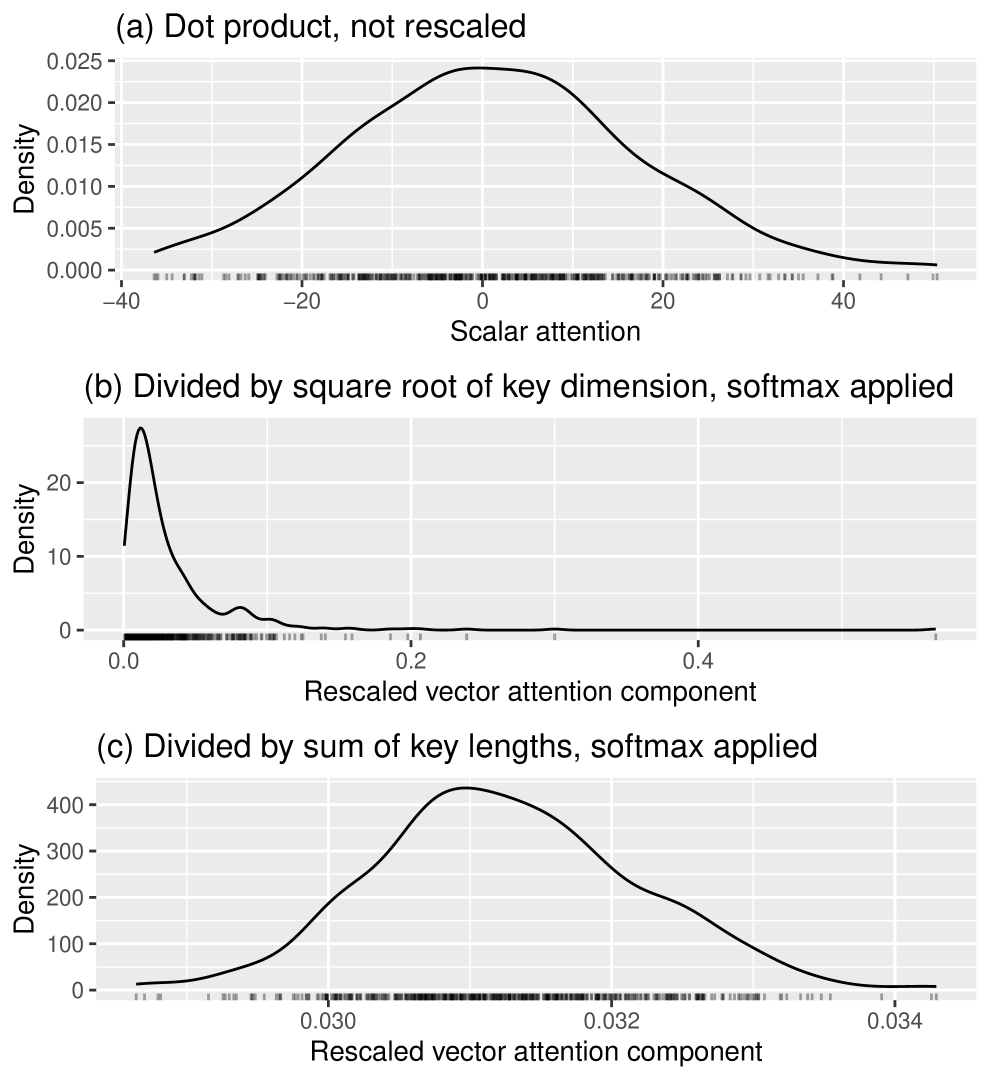
The axes on all three plots are on completely different scales, but we have displayed them in this way (using the default scales chosen by the computer) in order to be able to compare the shapes of the distributions. In these plots, it is apparent that pre-dividing by $k_{total}$ before applying softmax preserves the shape of the distribution much better than pre-dividing by $\sqrt{d}$.

These simulations have used an independent standard normal distribution for each component of the queries and keys. Further experimentation readily shows that when normal distribution means and variances change (and even more so when distribution families change), pre-dividing by $\sqrt{d}$ leads to greater distortions of the distribution shape than pre-dividing by $k_{total}$. Also, these patterns persist even when $d$ and $n$ vary over a wide range.

To explore these variations further, the R package that the author wrote to generate the simulations and plots for this paper can be used. It is available at https://github.com/James-Bernhard/attnsims.

Once we view dividing the dot product by $\sqrt{d}$ in the transformer architecture as part of the rescaling function rather than as a modification of the dot product in the scalar attention function, many other rescaling possibilities arise. In our explorations, pre-dividing by $k_{total}$ has appeared to decrease the distortion by the softmax function and help avoid the issue of vanishing gradients, but some other possibilities that might also be considered are:

• •

  dividing by $\sum_{i=1}^{n}\|k_{i}\|/n$,

• •

  dividing by $\sqrt{\sum_{i=1}^{n}\|k_{i}\|^{2}}$,

• •

  more generally, dividing by $\left(\sum_{i=1}^{n}\|k_{i}\|^{p}\right)^{1/p}$.

These are more complicated, and in the author’s explorations, none of them seemed to perform as well as dividing by $k_{total}$. But perhaps there are other possibilities that do.

It is also possible that different rescalings might be more effective in different contexts. As such, it would be good to consider rescaling functions other than just the ones described here. If it is feasible, multiple possible rescaling functions might even be tested in the specific context in which they are to be applied.

It is worth noting that dividing by $n\sqrt{d}$ seems to exhibit similar behavior to dividing by $k_{total}$ for independent standard normally distributed key and query components. If it is impractical to compute $k_{total}$ in a particular situation, perhaps dividing by $n\sqrt{d}$ could be substituted for it. As might be expected though, dividing by $n\sqrt{d}$ doesn’t appear to behave as well for distributions other than standard normal.

Vanishing gradients arise when individual components resulting from applying softmax approach $0$ or $1$, and this issue can be seen in the distortion of the shapes of the distributions of the vector attention components. Dividing by the square root of the key dimension alleviates this distortion well, but, judging from simulations, in many situations dividing by the sum of the key lengths appears to preserve the shape of the distribution even better.

Of course, the real test of the utility of dividing by the sum of the key lengths lies in how it performs in its intended setting in the transformer neural network architecture. Although further and more systematic testing is still needed, the author has conducted preliminary experiments using this modified transformer architecture and it appears to perform well.

The simulations and plots in this paper were generated using R version 4.3.0 [4] and the R packages ggplot2 [5] and rlang [6]. The R package that the author wrote to generate the simulations and plots in this paper is available at https://github.com/James-Bernhard/attnsims.

re [1] A. Vaswani et al., “Attention is all you need.” 2017. doi: 10.48550/arXiv.1706.03762. Available: https://arxiv.org/abs/1706.03762

pre [2] D. Bahdanau, K. Cho, and Y. Bengio, “Neural machine translation by jointly learning to align and translate.” 2014. doi: 10.48550/arXiv.1409.0473. Available: https://arxiv.org/abs/1409.0473

pre [3] M.-T. Luong, H. Pham, and C. D. Manning, “Effective approaches to attention-based neural machine translation.” 2015. doi: 10.48550/arXiv.1508.04025. Available: https://arxiv.org/abs/1508.04025

pre [4] R Core Team, R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing, 2023. Available: https://www.R-project.org/

pre [5] H. Wickham, ggplot2: Elegant graphics for data analysis. Springer-Verlag New York, 2016. Available: https://ggplot2.tidyverse.org

pre [6] L. Henry and H. Wickham, Rlang: Functions for base types and core r and ’tidyverse’ features. 2023. Available: https://CRAN.R-project.org/package=rlang

p