This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

\SmartPairedDelimiter

hopen[) \defineshorthand” \babelhyphennobreak \useshorthands” \titlehead[Uncaptioned image]

An alternating colouring function on strings

Jonathan Garbe
Lund University
(2024)
Abstract

An alternating colouring function is defined on strings over the alphabet \crl​\bm​0,\bm​1\crl{\bm 0,\bm 1}. It divides the strings in colourable and non-colourable ones. The points in the subshift of finite type defined by forbidding all non-colourable strings of a certain length alternate between states of one colour and states of the other colour. In other words, the points in the 2nd power shifts all have the same colour.

The number KnK_{n} of non-colourable strings of length n≥2n\geq 2 is shown to be 2⋅\p​Jn−2+12\cdot\p{J_{n-2}+1} where JJ is the sequence of Jacobsthal numbers. The number of sources and sinks in the de Bruijn graph of dimension n≥3n\geq 3 with non-colourable edges removed is shown each to be Kn−4K_{n}-4.

\addsec

Preface

This paper is an extract from my master thesis ([(2)]) that I wrote during the spring semester 2020. As many will remember, that was when the covid-19 pandemic hit the world. I was lucky that all I had left to complete my major was the thesis while fellow students struggled with improvised online teaching as even Swedish universities closed their doors to mitigate the spread of the virus.

I started with a research question in the area of dynamical systems that I tried to tackle by looking at de Bruijn sequences. (They are named after Nicolaas Govert de Bruijn who 1 published his famous result regarding their number.) After a time however I noticed some symmetries of de Bruijn graphs that I tried to formalise. In particular, I noticed that by deleting palindromes I could categorise the remaining edges such that in any path an edge of one category would follow an edge of the other.

In the following weeks I was able to formalise that notion by defining the function ψ\psi. Theorem \zarabicsection.\zarabicthrm shows it actually has the property I was looking for. It can therefore be seen as the most important result, but it is not surprising as ψ\psi was made to fulfil that property. However, observation \zarabicsection.\zarabicthrm came as a disappointment: The set of strings that ψ\psi does not assign a colour to is identical with the set of palindromes only up to a string length of 55 and theorem \zarabicsection.\zarabicthrm shows that the definition of ψ\psi cannot easily be improved. Corollary \zarabicsection.\zarabicthrm instead shows that in the limit 16\frac{1}{6} of all strings are not colourable. Surprisingly however, the number of non-colourable strings of certain length turns out to be an integer sequence so far unknown even to the On-Line Encyclopedia of Integer Sequences oeis (3) that had been a great help in finding that sequence.

While for strings of even length the definition of ψ\psi is rather straight-forward, for strings of odd length the definition first requires two other functions ϕ\phi and ξ\xi. Those two functions feature some remarkable relations. Theorem \zarabicsection.\zarabicthrm, which establishes a relation between ϕ\phi and ξ\xi being equal to zero, to me is the most surprising result of my master thesis.

For personal reasons some time has passed between my master thesis and this paper. I beg pardon for the delay. I am grateful for my supervisor Jörg Schmeling for having introduced me into the subject and especially for my examiner Tomas Persson who has put more effort in supporting the production of my thesis and this paper than I would have dared to ask for.

Cologne, Autumn 2024

Jonathan Garbe

\zarabicsection Notation

Notation.

Define ††margin: – ll, rr, mm, RR, CC, TT, C​TCT l,r:𝒜2≥1→𝒜2∗,m:𝒜2≥2→𝒜2∗,R,C:𝒜2∗→𝒜2∗,T,C​T:\N→𝒜2∗l,r:\mathcal{A}_{2}^{\geq 1}\to\mathcal{A}_{2}^{*},m:\mathcal{A}_{2}^{\geq 2}\to\mathcal{A}_{2}^{*},R,C:\mathcal{A}_{2}^{*}\to\mathcal{A}_{2}^{*},T,CT:\N\to\mathcal{A}_{2}^{*} by

l​\p​w\displaystyle l\p w =w[0,#​w−1)\displaystyle=w_{[0,\#w-1)}
r​\p​w\displaystyle r\p w =w[1,#​w)\displaystyle=w_{[1,\#w)}
m\displaystyle m =l∘r\displaystyle=l\circ r
R​\p​w0​…​w#​w−1\displaystyle R\p{w_{0}\dots w_{\#w-1}} =w#​w−1​…​w0\displaystyle=w_{\#w-1}\dots w_{0}
C​\p​w0​…​w#​w−1\displaystyle C\p{w_{0}\dots w_{\#w-1}} =C​\p​w0​…​C​\p​w#​w−1​, where ​C​\p​\bm​0=\bm​1∧C​\p​\bm​1=\bm​0\displaystyle=C\p{w_{0}}\dots C\p{w_{\#w-1}}\text{, where }C\p\bm 0=\bm 1\land C\p\bm 1=\bm 0
Tn\displaystyle T^{n} ={\upepsilonif ​n=0Tn−1​\bm​0if ​n​ oddTn−1​\bm​1if ​n​ even>0\displaystyle=\begin{cases}\upepsilon&\text{if }n=0\\ T^{n-1}\bm 0&\text{if }n\text{ odd}\\ T^{n-1}\bm 1&\text{if }n\text{ even}>0\end{cases}
C​Tn\displaystyle CT^{n} =C​\p​Tn.\displaystyle=C\p{T^{n}}.
Remark.

l​\p​w,r​\p​wl\p w,r\p w are prefix and suffix with length #​w−1\#w-1 of ww. m​\p​wm\p w is the proper infix of length #​w−2\#w-2. R​\p​wR\p w is the reverse of ww (meaning that ww is a palindrome if and only if R​\p​w=wR\p w=w) while C​\p​wC\p w is its complement. Tn,C​TnT^{n},CT^{n} are the strings of length nn starting with \bm​0,\bm​1\bm 0,\bm 1 respectively and alternating between \bm​0\bm 0 and \bm​1\bm 1.

Example.
l​\p​\bm​0010110\displaystyle l\p{\bm{0010110}} =\bm​001011\displaystyle=\bm{001011}
r​\p​\bm​0010110\displaystyle r\p{\bm{0010110}} =\bm​010110\displaystyle=\bm{010110}
m​\p​\bm​0010110\displaystyle m\p{\bm{0010110}} =\bm​01011\displaystyle=\bm{01011}
R​\p​\bm​0010110\displaystyle R\p{\bm{0010110}} =\bm​0110100\displaystyle=\bm{0110100}
C​\p​\bm​0010110\displaystyle C\p{\bm{0010110}} =\bm​1101001\displaystyle=\bm{1101001}
T7\displaystyle T^{7} =\bm​0101010\displaystyle=\bm{0101010}
C​T7\displaystyle CT^{7} =\bm​1010101\displaystyle=\bm{1010101}
Observation \zarabicsection.\zarabicthrm.
l∘r\displaystyle l\circ r =r∘l\displaystyle=r\circ l (\zarabicsection-\zarabicequation)
l∘m=m∘l\displaystyle l\circ m=m\circ l ∧r∘m=m∘r\displaystyle\land r\circ m=m\circ r (\zarabicsection-\zarabicequation)
R∘l=r∘R\displaystyle R\circ l=r\circ R ∧R∘r=l∘R\displaystyle\land R\circ r=l\circ R (\zarabicsection-\zarabicequation)
R∘m\displaystyle R\circ m =m∘R\displaystyle=m\circ R (\zarabicsection-\zarabicequation)
C∘l=l∘C\displaystyle C\circ l=l\circ C ∧C∘r=r∘C\displaystyle\land C\circ r=r\circ C (\zarabicsection-\zarabicequation)
C∘m\displaystyle C\circ m =m∘C\displaystyle=m\circ C (\zarabicsection-\zarabicequation)
R∘C\displaystyle R\circ C =C∘R\displaystyle=C\circ R (\zarabicsection-\zarabicequation)

\zarabicsection The function ξ\xi

Definition.
††margin: – the function ξ\xi

ξ\xi:𝒜2∗→\crl−1,0,1:\mathcal{A}_{2}^{*}\to\crl{-1,0,1} is defined recursively by

ξ​\p​w\displaystyle\xi\p w ={0if ​w=\upepsilon1if ​w∈\crl​Teven≥0−1if ​w∈\crl​C​Teven≥0\sgn​\p​ξ​\p​l​\p​w+ξ​\p​r​\p​welse.\displaystyle=\begin{cases}0&\text{if }w=\upepsilon\\ 1&\text{if }w\in\crl T^{\mathrm{even}\geq 0}\\ -1&\text{if }w\in\crl{CT}^{\mathrm{even}\geq 0}\\ \sgn\p{\xi\p{l\p w}+\xi\p{r\p w}}&\text{else}.\end{cases}
ww \upepsilon\upepsilon \bm​0\bm 0 \bm​1\bm 1 \bm​00\bm{00} \bm​01\bm{01} \bm​10\bm{10} \bm​11\bm{11}
ξ​\p​w\xi\p w 0 0 0 0 1 -1 0
ww \bm​000\bm{000} \bm​001\bm{001} \bm​010\bm{010} \bm​011\bm{011} \bm​100\bm{100} \bm​101\bm{101} \bm​110\bm{110} \bm​111\bm{111}
ξ​\p​w\xi\p w 0 1 0 1 -1 0 -1 0
Table \zarabictable: ξ​\p​w\xi\p w for w∈𝒜2≤3w\in\mathcal{A}_{2}^{\leq 3}

 

Remark.

The function ξ\xi tells on which side of the vertical axis a vertex appears in a de Bruijn graph when drawn as is done in the examples given in this thesis. In figures \zarabicfigure to \zarabicfigure the background is coloured according to the value of ξ\xi evaluated on the vertices. The vertices ww for which ξ​\p​w=0\xi\p w=0 are found in the centre. The letter ξ\xi was chosen with the word x-axis in mind.

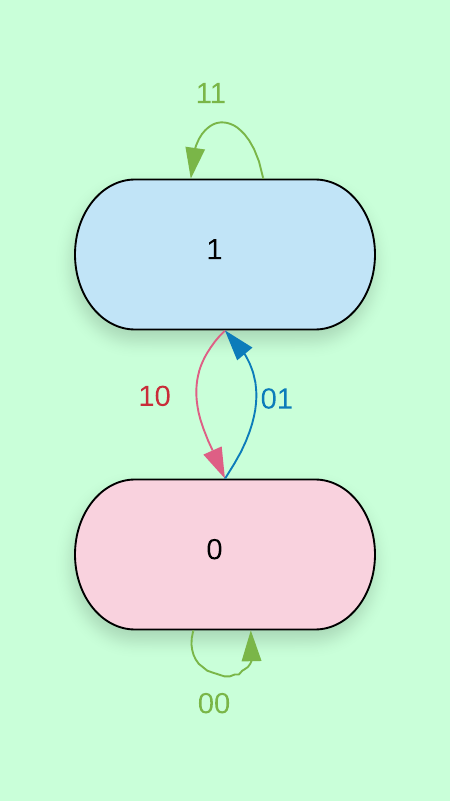
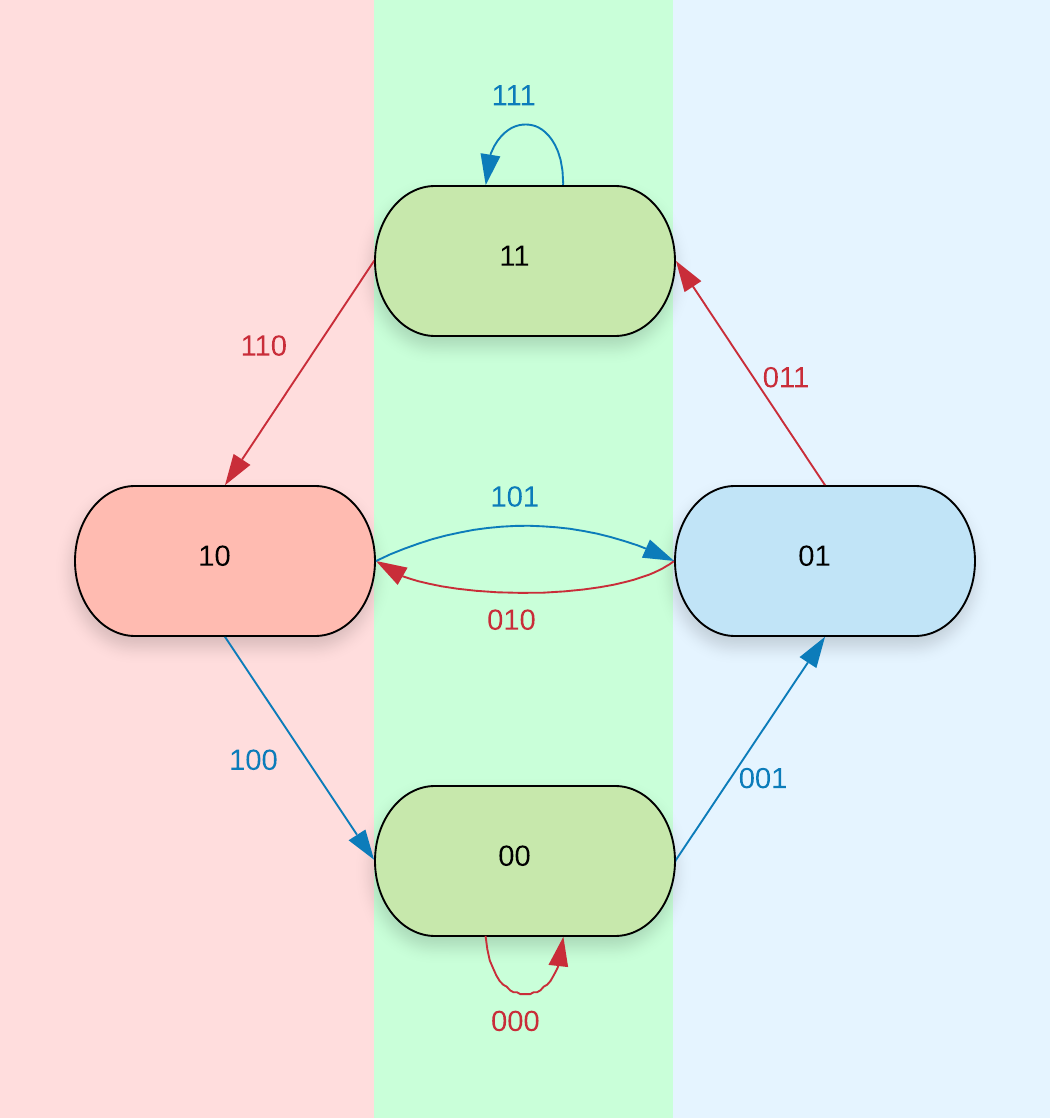
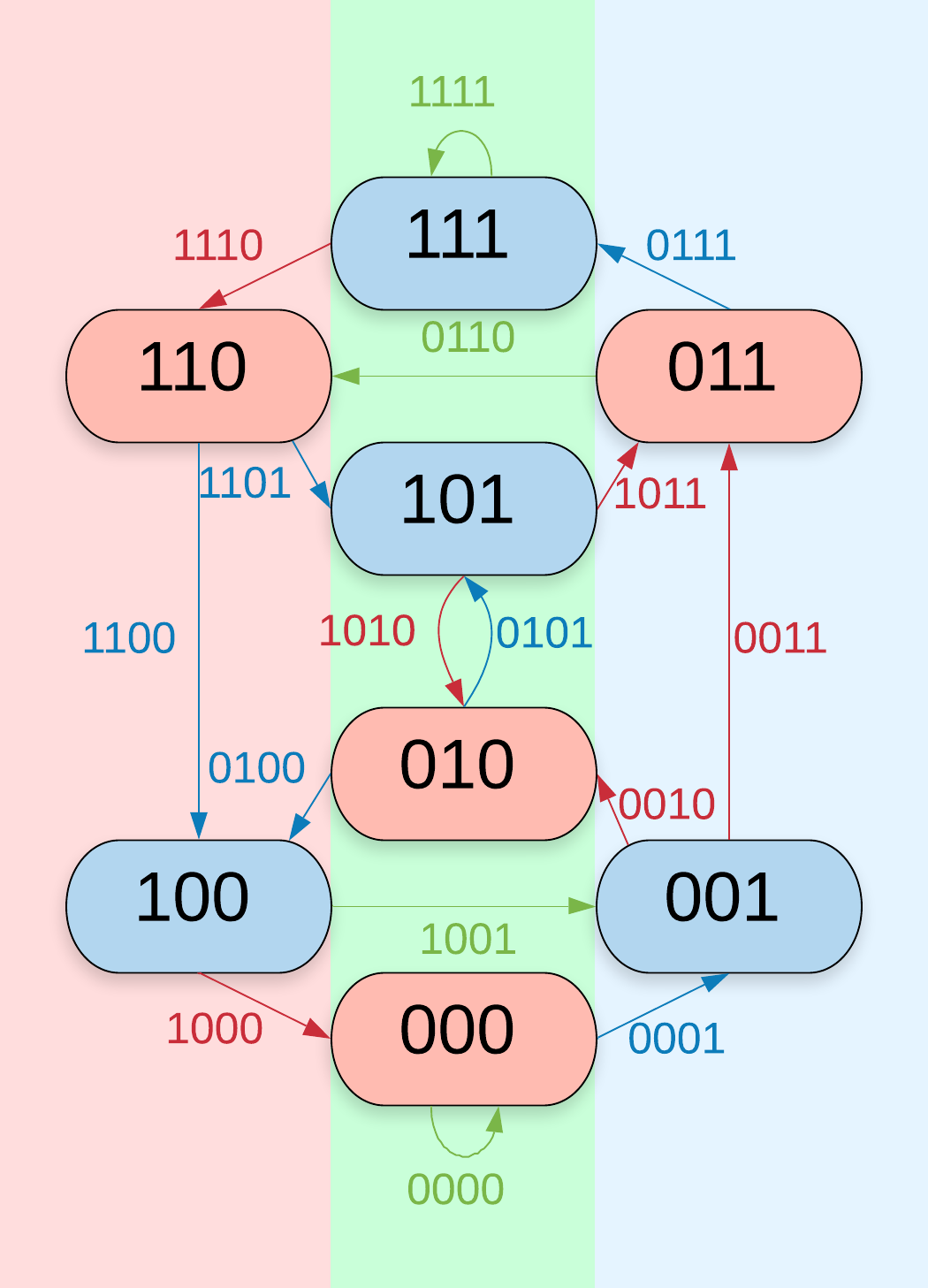
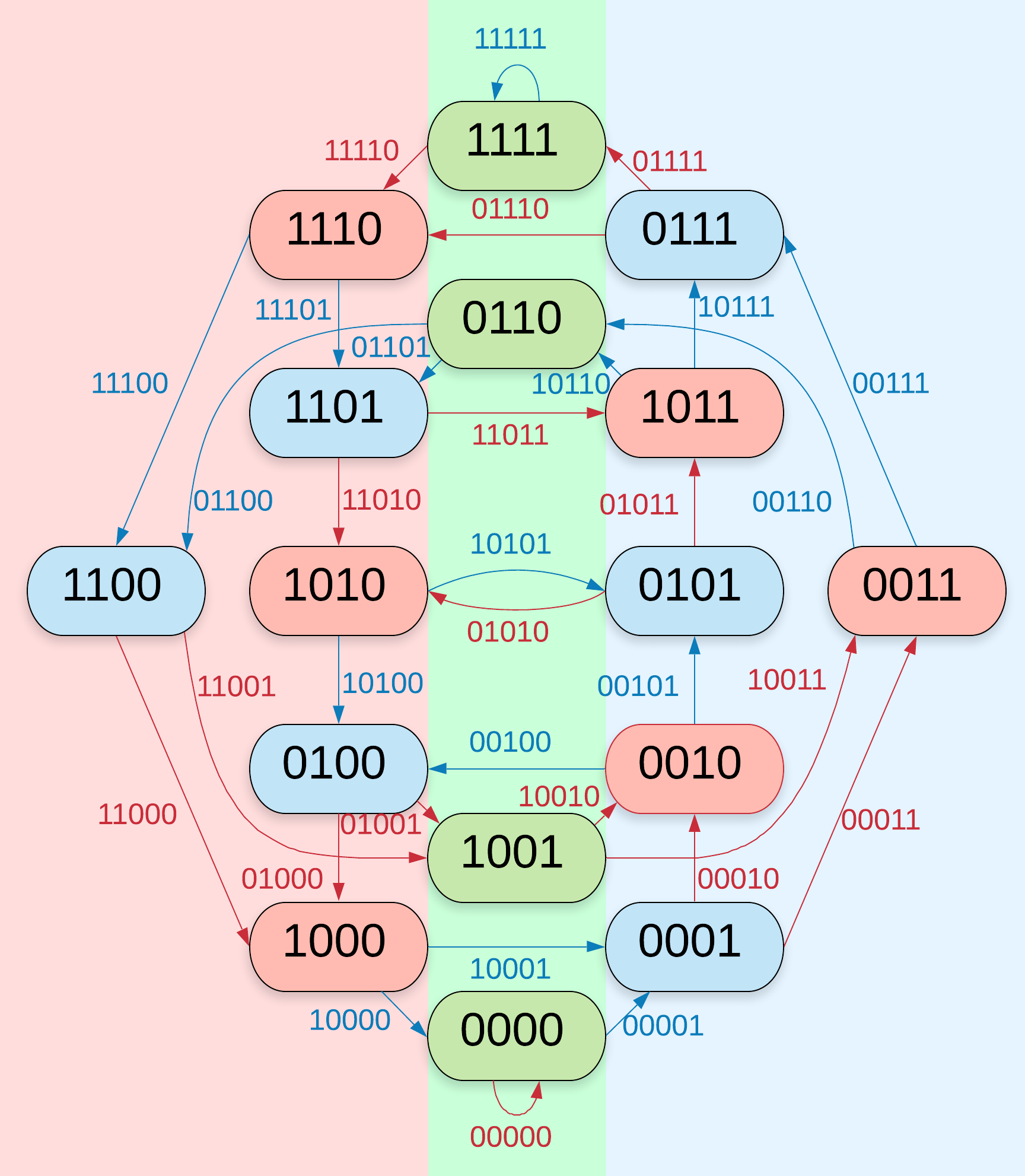
Refer to caption
Figure \zarabicfigure: The 11-dimensional de Bruijn graph. The vertex \bm​0\bm 0 and the edge \bm​10\bm{10} are coloured red indicating that ϕ​\p​\bm​0=ϕ​\p​\bm​10=−1\phi\p\bm 0=\phi\p{\bm{10}}=-1 while the vertex \bm​1\bm 1 and the edge \bm​01\bm{01} are coloured blue indicating ϕ​\p​\bm​1=ϕ​\p​\bm​01=1\phi\p\bm 1=\phi\p{\bm{01}}=1. The edges \bm​00,\bm​11\bm{00},\bm{11} and the background are coloured green because ξ​\p​\bm​0=ξ​\p​\bm​1=ϕ​\p​\bm​00=ϕ​\p​\bm​11=0\xi\p\bm 0=\xi\p\bm 1=\phi\p{\bm{00}}=\phi\p{\bm{11}}=0.

 

Refer to caption
Figure \zarabicfigure: The 22-dimensional de Bruijn graph. The vertices and edges are coloured red if ϕ=−1\phi=-1, green if ϕ=0\phi=0 and blue if ϕ=1\phi=1. The background of the vertex \bm​10\bm{10} is painted red because ξ​\p​\bm​10=−1\xi\p{\bm{10}}=-1. In the centre the background is green because ξ​\p​\bm​00=ξ​\p​\bm​11=0\xi\p{\bm{00}}=\xi\p{\bm{11}}=0 and for the vertex \bm​01\bm{01} it is blue because ξ​\p​\bm​01=1\xi\p{\bm{01}}=1.

 

Refer to caption
Figure \zarabicfigure: The 33-dimensional de Bruijn graph. The vertices and edges are coloured red if ϕ=−1\phi=-1, green if ϕ=0\phi=0 and blue if ϕ=1\phi=1. The background of the vertices is painted red where ξ=−1\xi=-1, green where ξ=0\xi=0 and blue where ξ=1\xi=1. Note that since the vertices have odd length, none of them is green.

 

Refer to caption
Figure \zarabicfigure: The 44-dimensional de Bruijn graph. The vertices and edges are coloured red if ϕ=−1\phi=-1, green if ϕ=0\phi=0 and blue if ϕ=1\phi=1. The background of the vertices is painted red where ξ=−1\xi=-1, green where ξ=0\xi=0 and blue where ξ=1\xi=1. Note that since the edges have odd length, none of them is green while the green vertices are exactly those that also have green background.

 

Lemma \zarabicsection.\zarabicthrm.
ξ∘C=ξ∘R=−ξ\displaystyle\xi\circ C=\xi\circ R=-\xi (\zarabicsection-\zarabicequation)
Proof.

By induction on #​w\#w.

ξ​\p​C​\p​\upepsilon\displaystyle\xi\p{C\p\upepsilon} =−ξ​\p​\upepsilon=ξ​\p​R​\p​\upepsilon=0\displaystyle=-\xi\p\upepsilon=\xi\p{R\p\upepsilon}=0

Now assume, the statement holds for #​w<n\#w<n. Let #​w=n\#w=n.

If w∈\crl​Teven∪\crl​C​Tevenw\in\crl{T}^{\mathrm{even}}\cup\crl{CT}^{\mathrm{even}}, the statement follows directly from the definition of ξ\xi. Otherwise,

\p​ξ∘C​\p​w​\by​[=]\sgn​\p​\p​ξ∘l∘C​\p​w+\p​ξ∘r∘C​\p​w\by​(​\zarabicsection-\zarabicequation​)\sgn​\p​\p​ξ∘C∘l​\p​w+\p​ξ∘C∘r​\p​w\by​(​\zarabicsection-\zarabicequation​)−\sgn​\p​\p​ξ∘l​\p​w+\p​ξ∘r​\p​w\by​[=]−ξ​\p​w\displaystyle\begin{split}\p{\xi\circ C}\p w\makebox[0.0pt][c]{$\by[=]{}$}&\sgn\p{\p{\xi\circ l\circ C}\p w+\p{\xi\circ r\circ C}\p w}\\ \by{\eqref{eq:CllCCrrC}}&\sgn\p{\p{\xi\circ C\circ l}\p w+\p{\xi\circ C\circ r}\p w}\\ \by{\eqref{eq:xiCxiR}}&-\sgn\p{\p{\xi\circ l}\p w+\p{\xi\circ r}\p w}\\ \makebox[0.0pt][c]{$\by[=]{}$}&-\xi\p w\end{split}
\p​ξ∘R​\p​w​\by​[=]\sgn​\p​\p​ξ∘l∘R​\p​w+\p​ξ∘r∘R​\p​w\by​(​\zarabicsection-\zarabicequation​)\sgn​\p​\p​ξ∘R∘r​\p​w+\p​ξ∘R∘l​\p​w\by​(​\zarabicsection-\zarabicequation​)−\sgn​\p​\p​ξ∘r​\p​w+\p​ξ∘l​\p​w\by​[=]−ξ​\p​w.\displaystyle\begin{split}\p{\xi\circ R}\p w\makebox[0.0pt][c]{$\by[=]{}$}&\sgn\p{\p{\xi\circ l\circ R}\p w+\p{\xi\circ r\circ R}\p w}\\ \by{\eqref{eq:RlrRRrlR}}&\sgn\p{\p{\xi\circ R\circ r}\p w+\p{\xi\circ R\circ l}\p w}\\ \by{\eqref{eq:xiCxiR}}&-\sgn\p{\p{\xi\circ r}\p w+\p{\xi\circ l}\p w}\\ \makebox[0.0pt][c]{$\by[=]{}$}&-\xi\p w.\end{split}

∎

Corollary \zarabicsection.\zarabicthrm.

Let w∈𝒜2∗w\in\mathcal{A}_{2}^{*} be a palindrome. Then

ξ​\p​w=0.\displaystyle\xi\p w=0. (\zarabicsection-\zarabicequation)
Proof.

Since for a palindrome ww, R​\p​w=wR\p w=w, equation (\zarabicsection-\zarabicequation) becomes

ξ​\p​w\displaystyle\xi\p w =−ξ​\p​w\displaystyle=-\xi\p w

which establishes the statement. ∎

Counterexample.

\bm​001101\bm{001101} is an example for a string that is not a palindrome although

ξ​\p​\bm​001101=0.\xi\p{\bm{001101}}=0.
Corollary \zarabicsection.\zarabicthrm.

Let kk be odd. Then

ξ​\p​Tk=ξ​\p​C​Tk=0.\displaystyle\xi\p{T^{k}}=\xi\p{CT^{k}}=0. (\zarabicsection-\zarabicequation)
Proof.

Since Tk,C​TkT^{k},CT^{k} are palindromes the statement follows directly from corollary  \zarabicsection.\zarabicthrm. ∎

Observation \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥1w\in\mathcal{A}_{2}^{\geq 1}.

ξ​\p​w=0\displaystyle\xi\p w=0 ⇔w∉\crl​Teven∪\crl​C​Teven∧ξ​\p​l​\p​w=−ξ​\p​r​\p​w\displaystyle\iff w\notin\crl{T}^{\mathrm{even}}\cup\crl{CT}^{\mathrm{even}}\land\xi\p{l\p w}=-\xi\p{r\p w} (\zarabicsection-\zarabicequation)
Corollary \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥1w\in\mathcal{A}_{2}^{\geq 1} such that ξ​\p​l​\p​w,ξ​\p​r​\p​w≠0\xi\p{l\p w},\xi\p{r\p w}\neq 0. Then

ξ​\p​w=0⇔ξ​\p​l​\p​w≠ξ​\p​r​\p​w\displaystyle\xi\p w=0\iff\xi\p{l\p w}\neq\xi\p{r\p w} (\zarabicsection-\zarabicequation)
Proof.

From corollary  \zarabicsection.\zarabicthrm it follows that w∉\crl​Teven∪\crl​C​Tevenw\notin\crl{T}^{\mathrm{even}}\cup\crl{CT}^{\mathrm{even}}, so the statement follows from observation \zarabicsection.\zarabicthrm. ∎

Remark.

When ξ​\p​l​\p​w,ξ​\p​r​\p​w≠0\xi\p{l\p w},\xi\p{r\p w}\neq 0, it is equivalent to say ξ​\p​l​\p​w=−ξ​\p​r​\p​w\xi\p{l\p w}=-\xi\p{r\p w} or ξ​\p​l​\p​w≠ξ​\p​r​\p​w\xi\p{l\p w}\neq\xi\p{r\p w}. For aesthetic reasons, the latter formulation will be preferred, also in future occasions.

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥1w\in\mathcal{A}_{2}^{\geq 1} such that ξ​\p​w≠0\xi\p{w}\neq 0. Then

ξ​\p​l​\p​w≠0\displaystyle\xi\p{l\p{w}}\neq 0 ⟹ξ​\p​w=ξ​\p​l​\p​w\displaystyle\implies\xi\p{w}=\xi\p{l\p w} (\zarabicsection-\zarabicequation)
ξ​\p​r​\p​w≠0\displaystyle\xi\p{r\p{w}}\neq 0 ⟹ξ​\p​w=ξ​\p​r​\p​w.\displaystyle\implies\xi\p{w}=\xi\p{r\p w}. (\zarabicsection-\zarabicequation)
Proof.

From ξ​\p​l​\p​w≠0∨ξ​\p​r​\p​w≠0\xi\p{l\p w}\neq 0\lor\xi\p{r\p w}\neq 0 it follows that w​\by​[∉]​(​\zarabicsection-\zarabicequation​)​\crl​Teven∪\crl​C​Tevenw\by[\notin]{\eqref{eq:xiTodd}}\crl T^{\mathrm{even}}\cup\crl{CT}^{\mathrm{even}}, so

ξ​\p​w=\sgn​\p​ξ​\p​l​\p​w+ξ​\p​r​\p​w.\displaystyle\xi\p w=\sgn\p{\xi\p{l\p w}+\xi\p{r\p w}}.

Now if one of the summands is non-zero, ξ​\p​w\xi\p w must either equal that summand or be zero. ∎

Lemma \zarabicsection.\zarabicthrm.

Let ı,ȷ≥1\imath,\jmath\geq 1. Then

ξ​\p​\bm​0ı​\bm​1ȷ=1.\displaystyle\xi\p{\bm 0^{\imath}\bm 1^{\jmath}}=1. (\zarabicsection-\zarabicequation)
Proof.

Induction on ı+ȷ\imath+\jmath. ξ​\p​\bm​01=1\xi\p{\bm{01}}=1, which establishes the statement for ı+ȷ=2\imath+\jmath=2. Now assume the statement holds for ı+ȷ<n∈\N\imath+\jmath<n\in\N. Let ı+ȷ=n\imath+\jmath=n.

ξ​\p​\bm​0ı​\bm​1ȷ=\sgn​\p​ξ​\p​\bm​0ı​\bm​1ȷ−1+ξ​\p​\bm​0ı−1​\bm​1ȷ,\displaystyle\xi\p{\bm 0^{\imath}\bm 1^{\jmath}}=\sgn\p{\xi\p{\bm 0^{\imath}\bm 1^{\jmath-1}}+\xi\p{\bm 0^{\imath-1}\bm 1^{\jmath}}},

where by the induction hypothesis at least one of the summands is 1 while the other cannot be negative either. The statement follows. ∎

Corollary \zarabicsection.\zarabicthrm.
ξ​\p​\bm​1ȷ​\bm​0ı=−1\displaystyle\xi\p{\bm 1^{\jmath}\bm 0^{\imath}}=-1 (\zarabicsection-\zarabicequation)
Proof.
ξ​\p​\bm​1ȷ​\bm​0ı​\by​(​\zarabicsection-\zarabicequation​)−ξ​\p​\bm​0ı​\bm​1ȷ​\by​(​\zarabicsection-\zarabicequation​)−1\displaystyle\xi\p{\bm 1^{\jmath}\bm 0^{\imath}}\by{\eqref{eq:xiCxiR}}-\xi\p{\bm 0^{\imath}\bm 1^{\jmath}}\by{\eqref{eq:xi0i1j}}-1

∎

Lemma \zarabicsection.\zarabicthrm.

Let k≥2k\geq 2. Then

ξ​\p​Tk​\bm​0\displaystyle\xi\p{T^{k}\bm 0} ={0if ​k​ is even−1if ​k​ is odd\displaystyle=\begin{cases}0&\text{if }k\text{ is even{}}\\ -1&\text{if }k\makebox[0.0pt][l]{$\text{ is odd{}}$}\end{cases} (\zarabicsection-\zarabicequation)
ξ​\p​Tk​\bm​1\displaystyle\xi\p{T^{k}\bm 1} =1\displaystyle=1 (\zarabicsection-\zarabicequation)
ξ​\p​C​Tk​\bm​0\displaystyle\xi\p{CT^{k}\bm 0} =−1\displaystyle=-1 (\zarabicsection-\zarabicequation)
ξ​\p​C​Tk​\bm​1\displaystyle\xi\p{CT^{k}\bm 1} ={0if ​k​ is even1if ​k​ is odd.\displaystyle=\begin{cases}0&\text{if }k\text{ is even{}}\\ 1&\text{if }k\makebox[0.0pt][l]{$\text{ is odd{.}}$}\end{cases} (\zarabicsection-\zarabicequation)
Proof.

By induction on kk. Note first, that the statement holds for k=2k=2. Assume then that it holds for a certain k≥2k\geq 2.

Case kk is even:

ξ​\p​Tk+1​\bm​0\displaystyle\xi\p{T^{k+1}\bm 0} =\sgn​\p​ξ​\p​Tk+1+ξ​\p​C​Tk​\bm​0​\by​(​\zarabicsection-\zarabicequation​),(​\zarabicsection-\zarabicequation​)​\sgn​\p​0−1=−1\displaystyle=\sgn\p{\xi\p{T^{k+1}}+\xi{\p{CT^{k}\bm 0}}}\by{\eqref{eq:xiTodd},\eqref{eq:xiCTk0}}\sgn\p{0-1}=-1
ξ​\p​Tk+1​\bm​1\displaystyle\xi\p{T^{k+1}\bm 1} =ξ​\p​Tk+2=1\displaystyle=\xi\p{T^{k+2}}=1
ξ​\p​C​Tk+1​\bm​0\displaystyle\xi\p{CT^{k+1}\bm 0} =ξ​\p​C​Tk+2=−1\displaystyle=\xi\p{CT^{k+2}}=-1
ξ​\p​C​Tk+1​\bm​1\displaystyle\xi\p{CT^{k+1}\bm 1} =\sgn​\p​ξ​\p​C​Tk+1+ξ​\p​Tk​\bm​1​\by​(​\zarabicsection-\zarabicequation​),(​\zarabicsection-\zarabicequation​)​\sgn​\p​0+1=1\displaystyle=\sgn\p{\xi\p{CT^{k+1}}+\xi{\p{T^{k}\bm 1}}}\by{\eqref{eq:xiTodd},\eqref{eq:xiTk1}}\sgn\p{0+1}=1

Case kk is odd:

ξ​\p​Tk+1​\bm​0\displaystyle\xi\p{T^{k+1}\bm 0} =ξ​\p​Tk+2​\by​(​\zarabicsection-\zarabicequation​)​0\displaystyle=\xi\p{T^{k+2}}\by{\eqref{eq:xiTodd}}0
ξ​\p​Tk+1​\bm​1\displaystyle\xi\p{T^{k+1}\bm 1} =\sgn​\p​ξ​\p​Tk+1+ξ​\p​C​Tk​\bm​1​\by​(​\zarabicsection-\zarabicequation​)​\sgn​\p​1+1=1\displaystyle=\sgn\p{\xi\p{T^{k+1}}+\xi{\p{CT^{k}\bm 1}}}\by{\eqref{eq:xiCTk1}}\sgn\p{1+1}=1
ξ​\p​C​Tk+1​\bm​0\displaystyle\xi\p{CT^{k+1}\bm 0} =\sgn​\p​ξ​\p​C​Tk+1+ξ​\p​Tk​\bm​0​\by​(​\zarabicsection-\zarabicequation​)​\sgn​\p−1−1=−1\displaystyle=\sgn\p{\xi\p{CT^{k+1}}+\xi{\p{T^{k}\bm 0}}}\by{\eqref{eq:xiTk0}}\sgn\p{-1-1}=-1
ξ​\p​C​Tk+1​\bm​1\displaystyle\xi\p{CT^{k+1}\bm 1} =ξ​\p​C​Tk+2​\by​(​\zarabicsection-\zarabicequation​)​0\displaystyle=\xi\p{CT^{k+2}}\by{\eqref{eq:xiTodd}}0

∎

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥1w\in\mathcal{A}_{2}^{\geq 1} such that ξ​\p​l​\p​w=ξ​\p​r​\p​w=0\xi\p{l\p w}=\xi\p{r\p w}=0. Then

ξ​\p​w=0\displaystyle\xi\p w=\makebox[0.0pt][r]{$0$} ⟹w∈\crl​\bm​0∗∪\crl​\bm​1∗\displaystyle\implies w\in\crl\bm 0^{*}\cup\crl\bm 1^{*} (\zarabicsection-\zarabicequation)
ξ​\p​w=1\displaystyle\xi\p w=\makebox[0.0pt][r]{$1$} ⟹w∈\crl​Teven\displaystyle\implies w\in\crl{T}^{\mathrm{even}} (\zarabicsection-\zarabicequation)
ξ​\p​w=−1\displaystyle\xi\p w=-1 ⟹w∈\crl​C​Teven.\displaystyle\implies w\in\crl{CT}^{\mathrm{even}}. (\zarabicsection-\zarabicequation)
Proof.

Induction on #​w\#w. For #​w≤2\#w\leq 2 there are only finitely many cases to consider. Now assume the statements holds for #​w<n\#w<n. Let #​w=n≥3∧ξ​\p​l​\p​w=ξ​\p​r​\p​w=0\#w=n\geq 3\land\xi\p{l\p w}=\xi\p{r\p w}=0, which means that by observation \zarabicsection.\zarabicthrm

ξ​\p​l2​\p​w=−ξ​\p​m​\p​w=ξ​\p​r2​\p​w.\displaystyle\xi\p{l^{2}\p w}=-\xi\p{m\p w}=\xi\p{r^{2}\p w}.

If m​\p​w∈\crl​Teven∪\crl​C​Tevenm\p w\in\crl{T}^{\mathrm{even}}\cup\crl{CT}^{\mathrm{even}}, the statement follows from lemma \zarabicsection.\zarabicthrm. Otherwise, the above equation can be rewritten the following way:

\sgn​\p​\p​ξ∘l3​\p​w+\p​ξ∘l2∘r​\p​w=−\sgn​\p​\p​ξ∘l2∘r​\p​w+\p​ξ∘l∘r2​\p​w=\sgn​\p​\p​ξ∘l∘r2​\p​w+\p​ξ∘r3​\p​w\displaystyle\begin{split}&\sgn\p{\p{\xi\circ l^{3}}\p w+\p{\xi\circ l^{2}\circ r}\p w}\\ =-&\sgn\p{\p{\xi\circ l^{2}\circ r}\p w+\p{\xi\circ l\circ r^{2}}\p w}\\ =\phantom{-}&\sgn\p{\p{\xi\circ l\circ r^{2}}\p w+\p{\xi\circ r^{3}}\p w}\end{split}

Some playing with the minus sign yields:

\sgn​\p​\p​ξ∘l3​\p​w−\p−ξ∘l2∘r​\p​w=\sgn​\p​\p−ξ∘l2∘r​\p​w−\p​ξ∘l∘r2​\p​w=\sgn​\p​\p​ξ∘l∘r2​\p​w−\p−ξ∘r3​\p​w\displaystyle\begin{split}&\sgn\p{\p{\xi\circ l^{3}}\p w-\p{-\xi\circ l^{2}\circ r}\p w}\\ =&\sgn\p{\p{-\xi\circ l^{2}\circ r}\p w-\p{\xi\circ l\circ r^{2}}\p w}\\ =&\sgn\p{\p{\xi\circ l\circ r^{2}}\p w-\p{-\xi\circ r^{3}}\p w}\end{split}

Hence, one of the following three statements must hold:

\p​ξ∘l3​\p​w<\p−ξ∘l2∘r​\p​w\displaystyle\p{\xi\circ l^{3}}\p w<\p{-\xi\circ l^{2}\circ r}\p w <\p​ξ∘l∘r2​\p​w<\p−ξ∘r3​\p​w\displaystyle<\p{\xi\circ l\circ r^{2}}\p w<\p{-\xi\circ r^{3}}\p w
∨\p​ξ∘l3​\p​w=\p−ξ∘l2∘r​\p​w\displaystyle\lor\quad\p{\xi\circ l^{3}}\p w=\p{-\xi\circ l^{2}\circ r}\p w =\p​ξ∘l∘r2​\p​w=\p−ξ∘r3​\p​w\displaystyle=\p{\xi\circ l\circ r^{2}}\p w=\p{-\xi\circ r^{3}}\p w
∨\p​ξ∘l3​\p​w>\p−ξ∘l2∘r​\p​w\displaystyle\lor\quad\p{\xi\circ l^{3}}\p w>\p{-\xi\circ l^{2}\circ r}\p w >\p​ξ∘l∘r2​\p​w>\p−ξ∘r3​\p​w\displaystyle>\p{\xi\circ l\circ r^{2}}\p w>\p{-\xi\circ r^{3}}\p w

However, since \img​ξ=\crl−1,0,1\img\xi=\crl{-1,0,1}, the strict inequalities cannot hold, meaning that the equality does. Then

ξ​\p​l2​\p​w=ξ​\p​m​\p​w=ξ​\p​r2​\p​w=0,\displaystyle\xi\p{l^{2}\p w}=\xi\p{m\p w}=\xi\p{r^{2}\p w}=0,

so by the induction hypothesis

l​\p​w,r​\p​w∈\crl​\bm​0∗∪\crl​\bm​1∗\displaystyle l\p w,r\p w\in\crl\bm 0^{*}\cup\crl\bm 1^{*}

and since #​w≥3\#w\geq 3,

w∈\crl​\bm​0∗∪\crl​\bm​1∗.\displaystyle w\in\crl\bm 0^{*}\cup\crl\bm 1^{*}.

∎

Remark.

The argument used in this proof, considering l3,l2∘r,l∘r2l^{3},l^{2}\circ r,l\circ r^{2} and r3r^{3} of a certain string and using the fact that the functions ξ\xi and ϕ\phi only attain three different values will be important also for the proof of lemma \zarabicsection.\zarabicthrm.

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥2w\in\mathcal{A}_{2}^{\geq 2} such that ξ​\p​w=0\xi\p w=0. Then

ξ​\p​m​\p​w=0.\displaystyle\xi\p{m\p w}=0. (\zarabicsection-\zarabicequation)
Proof.

If m​\p​w∈\crl​Todd∪\crl​C​Toddm\p w\in\crl T^{\mathrm{odd}}\cup\crl{CT}^{\mathrm{odd}} the statement follows from corollary \zarabicsection.\zarabicthrm so assume it is not. ξ​\p​w=0\xi\p w=0 by observation \zarabicsection.\zarabicthrm implies that ξ​\p​l​\p​w=−ξ​\p​r​\p​w\xi\p{l\p w}=-\xi\p{r\p w}. By lemma \zarabicsection.\zarabicthrm either w∈\crl​Teven∪\crl​C​Tevenw\in\crl{T}^{\mathrm{even}}\cup\crl{CT}^{\mathrm{even}} or w∈\crl​\bm​0∗∪\crl​\bm​1∗w\in\crl\bm 0^{*}\cup\crl\bm 1^{*} or ξ​\p​l​\p​w=−ξ​\p​r​\p​w≠0\xi\p{l\p w}=-\xi\p{r\p w}\neq 0. However, the first case can be excluded since ξ​\p​w=0\xi\p w=0. In the second case, ξ​\p​m​\p​w​\by​(​\zarabicsection-\zarabicequation​)​0\xi\p{m\p w}\by{\eqref{eq:xipalindrome}}0. In the third case

\sgn​\p​ξ​\p​l2​\p​w+ξ​\p​m​\p​w=−\sgn​\p​ξ​\p​m​\p​w+ξ​\p​r2​\p​w≠0,\displaystyle\sgn\p{\xi\p{l^{2}\p w}+\xi\p{m\p w}}=-\sgn\p{\xi\p{m\p w}+\xi\p{r^{2}\p w}}\neq 0,

which can be reformulated to

\sgn​\p​ξ​\p​m​\p​w−\p−ξ​\p​l2​\p​w=\sgn​\p​\p−ξ​\p​r2​\p​w−ξ​\p​m​\p​w≠0,\displaystyle\sgn\p{\xi\p{m\p w}-\p{-\xi\p{l^{2}\p w}}}=\sgn\p{\p{-\xi\p{r^{2}\p w}}-\xi\p{m\p w}}\neq 0,

so

−ξ\pl2\pw<ξ\pm\pw<−ξ\pr2\pw∨−ξ\pl2\pw>ξ\pm\pw>−ξ\pr2\pw.\displaystyle-\xi\p{l^{2}\p w}<\xi\p{m\p w}<-\xi\p{r^{2}\p w}\lor-\xi\p{l^{2}\p w}>\xi\p{m\p w}>-\xi\p{r^{2}\p w}.

It follows that ξ​\p​m​\p​w=0\xi\p{m\p w}=0. ∎

Remark.

The number \zarabicsection is omitted in numbering the results to keep section \zarabicsection and \zarabicsection having the same structure. There is nothing equivalent to say about the function ξ\xi as is said about the function ϕ\phi in corollary \zarabicsection.\zarabicthrm.

Theorem \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥2w\in\mathcal{A}_{2}^{\geq 2} such that ξ​\p​l2​\p​w=ξ​\p​r2​\p​w≠0\xi\p{l^{2}\p w}=\xi\p{r^{2}\p w}\neq 0. Then

ξ​\p​m​\p​w≠0.\displaystyle\xi\p{m\p w}\neq 0. (\zarabicsection-\zarabicequation)
Proof.

First of all, note that #​w≥4\#w\geq 4, as otherwise ξ​\p​l2​\p​w=0\xi\p{l^{2}\p w}=0. For #​w=4\#w=\nolinebreak 4, w∈\crl​T4,C​T4w\in\crl{T^{4},CT^{4}}, so ξ​\p​m​\p​w≠0\xi\p{m\p w}\neq 0. Assume now that #​w≥5\#w\geq 5 and start with considering the case l2​\p​w∈\crl​Tevenl^{2}\p w\in\crl T^{\mathrm{even}}. Then m​\p​w∈\crl​C​T#​w−3​\bm​0,C​T#​w−3​\bm​1m\p w\in\crl{CT^{\#w-3}\bm 0,CT^{\#w-3}\bm 1}, so ξ​\p​m​\p​w​\by​[≠]​(​\zarabicsection-\zarabicequation​),(​\zarabicsection-\zarabicequation​)​0\xi\p{m\p w}\by[\neq]{\eqref{eq:xiCTk0},\eqref{eq:xiCTk1}}0. Similarly, the cases l2​\p​w∈\crl​C​Teven∨r2​\p​w∈\crl​Teven∪\crl​C​Tevenl^{2}\p w\in\crl{CT}^{\mathrm{even}}\lor r^{2}\p w\in\crl{T}^{\mathrm{even}}\cup\crl{CT}^{\mathrm{even}} can be considered. In all other cases, assume ξ​\p​m​\p​w=0\xi\p{m\p w}=0. Then

\p​ξ∘l2∘r​\p​w​\by​(​\zarabicsection-\zarabicequation​)​\p−ξ∘l∘r2​\p​w,\displaystyle\p{\xi\circ l^{2}\circ r}\p w\by{\eqref{eq:xi0}}\p{-\xi\circ l\circ r^{2}}\p w, (\zarabicsection-\zarabicequation)

so

ξ​\p​l2​\p​w=ξ​\p​r2​\p​w≠0⇔\sgn​\p​\p​ξ∘l3​\p​w+\p​ξ∘l2∘r​\p​w=\sgn​\p​\p​ξ∘l∘r2​\p​w+\p​ξ∘r3​\p​w≠0\by​[⇔]​(​\zarabicsection-\zarabicequation​)\sgn​\p​\p​ξ∘l3​\p​w+\p​ξ∘l2∘r​\p​w=\sgn​\p​\p​ξ∘r3​\p​w−\p​ξ∘l2∘r​\p​w≠0⟹\p​ξ∘l2∘r​\p​w=0.\displaystyle\begin{split}\xi\p{l^{2}\p w}=\xi\p{r^{2}\p w}\neq 0\iff&\\ \sgn\p{\p{\xi\circ l^{3}}\p w+\p{\xi\circ l^{2}\circ r}\p w}=&\sgn\p{\p{\xi\circ l\circ r^{2}}\p w+\p{\xi\circ r^{3}}\p w}\neq 0\\ \by[\iff]{\eqref{eq:proof:xil2rxilr2}}&\\ \sgn\p{\p{\xi\circ l^{3}}\p w+\p{\xi\circ l^{2}\circ r}\p w}=&\sgn\p{\p{\xi\circ r^{3}}\p w-\p{\xi\circ l^{2}\circ r}\p w}\neq 0\\ \implies&\p{\xi\circ l^{2}\circ r}\p w=0.\end{split}

From \p​ξ∘m​\p​w=\p​ξ∘l2∘r​\p​w=\p​ξ∘l∘r2​\p​w=0\p{\xi\circ m}\p w=\p{\xi\circ l^{2}\circ r}\p w=\p{\xi\circ l\circ r^{2}}\p w=0 it follows by lemma \zarabicsection.\zarabicthrm that m​\p​w∈\crl​\bm​0∗∪\crl​\bm​1∗m\p w\in\crl\bm 0^{*}\cup\crl\bm 1^{*}. However, then

ξ​\p​l2​\p​w≤0≤ξ​\p​r2​\p​w,\displaystyle\xi\p{l^{2}\p w}\leq 0\leq\xi\p{r^{2}\p w},

a contradiction. ∎

Remark.

One could try to redefine ξ\xi in an attempt to shrink the subset of 𝒜2∗\mathcal{A}_{2}^{*} on which ξ\xi is 0. However theorem \zarabicsection.\zarabicthrm shows that that is not easily possible: Already now ξ\xi is zero only for vertices in the de Bruijn graph that have preceding and succeeding vertices with different ξ\xi-value.

Lemma \zarabicsection.\zarabicthrm.

Let n≥2,w∈𝒜2nn\geq 2,w\in\mathcal{A}_{2}^{n} such that ξ​\p​m​\p​w=0\xi\p{m\p w}=0. Then

ξ​\p​l​\p​w=ξ​\p​r​\p​w=0⇔w∈\crl​\bm​0n,\bm​1n\displaystyle\xi\p{l\p w}=\xi\p{r\p w}=\makebox[0.0pt][r]{$0$}\iff w\in\crl{\bm 0^{n},\bm 1^{n}} (\zarabicsection-\zarabicequation)
ξ​\p​l​\p​w=ξ​\p​r​\p​w=1⇔w∈\crl​\bm​0​Tn−1,Tn−1​\bm​1∧n​ is odd\displaystyle\xi\p{l\p w}=\xi\p{r\p w}=\makebox[0.0pt][r]{$1$}\iff w\in\crl{\bm 0T^{n-1},T^{n-1}\bm 1}\land n\makebox[0.0pt][l]{$\text{ is odd{}}$} (\zarabicsection-\zarabicequation)
ξ​\p​l​\p​w=ξ​\p​r​\p​w=−1⇔w∈\crl​C​Tn−1​\bm​0,\bm​1​C​Tn−1∧n​ is odd\displaystyle\xi\p{l\p w}=\xi\p{r\p w}=-1\iff w\in\crl{CT^{n-1}\bm 0,\bm 1CT^{n-1}}\land n\makebox[0.0pt][l]{$\text{ is odd{}}$} (\zarabicsection-\zarabicequation)
ξ​\p​l​\p​w=0∧ξ​\p​r​\p​w=1⇔w=\bm​0n−1​\bm​1\displaystyle\xi\p{l\p w}=\makebox[0.0pt][r]{$0$}\land\xi\p{r\p w}=\makebox[0.0pt][r]{$1$}\iff w=\bm 0^{n-1}\bm 1 (\zarabicsection-\zarabicequation)
ξ​\p​l​\p​w=0∧ξ​\p​r​\p​w=−1⇔w=\bm​1n−1​\bm​0\displaystyle\xi\p{l\p w}=\makebox[0.0pt][r]{$0$}\land\xi\p{r\p w}=-1\iff w=\bm 1^{n-1}\bm 0 (\zarabicsection-\zarabicequation)
ξ​\p​l​\p​w=1∧ξ​\p​r​\p​w=0⇔w=\bm​0​\bm​1n−1\displaystyle\xi\p{l\p w}=\makebox[0.0pt][r]{$1$}\land\xi\p{r\p w}=\makebox[0.0pt][r]{$0$}\iff w=\bm 0\bm 1^{n-1} (\zarabicsection-\zarabicequation)
ξ​\p​l​\p​w=−1∧ξ​\p​r​\p​w=0⇔w=\bm​1​\bm​0n−1.\displaystyle\xi\p{l\p w}=-1\land\xi\p{r\p w}=\makebox[0.0pt][r]{$0$}\iff w=\bm 1\bm 0^{n-1}. (\zarabicsection-\zarabicequation)
Proof.
(\zarabicsection-\zarabicequation), (\zarabicsection-\zarabicequation), (\zarabicsection-\zarabicequation)

From ξ​\p​l​\p​w=ξ​\p​m​\p​w=0\xi\p{l\p w}=\xi\p{m\p w}=0 it follows that

ξ​\p​l2​\p​w=0.\xi\p{l^{2}\p w}=0.

Hence by lemma \zarabicsection.\zarabicthrm l​\p​w∈\crl​\bm​0n−1,\bm​1n−1l\p w\in\crl{\bm 0^{n-1},\bm 1^{n-1}}

(\zarabicsection-\zarabicequation), (\zarabicsection-\zarabicequation)

Similarly one finds in these cases that r​\p​w∈\crl​\bm​0n−1,\bm​1n−1r\p w\in\crl{\bm 0^{n-1},\bm 1^{n-1}}.

(\zarabicsection-\zarabicequation), (\zarabicsection-\zarabicequation)

Assume m​\p​w∉\crl​Todd∪\crl​C​Toddm\p w\notin\crl T^{\mathrm{odd}}\cup\crl{CT}^{\mathrm{odd}}. Then

ξ​\p​l2​\p​w=ξ​\p​r2​\p​w≠0\xi\p{l^{2}\p w}=\xi\p{r^{2}\p w}\neq 0

which according to theorem \zarabicsection.\zarabicthrm implies that m​\p​w≠0m\p w\neq 0, a contradiction. Also, ww must not be a palindrome, leaving exactly these four cases.

∎

Remark.

Already at this point, #​\crl​w∈𝒜2n;ξ​\p​w=0\#\crl{w\in\mathcal{A}_{2}^{n};\xi\p w=0} could be investigated. However, that result shall be postponed until section \zarabicsection, as the relevance of that set and its size will be more obvious by then.

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥4w\in\mathcal{A}_{2}^{\geq 4} such that ξ​\p​l​\p​w≠ξ​\p​m​\p​w=−1≠ξ​\p​r​\p​w\xi\p{l\p w}\neq\xi\p{m\p w}=-1\neq\xi\p{r\p w}. Then w∈\crl​Tevenw\in\crl T^{\mathrm{even}}.

Proof.

Note that ξ​\p​l​\p​w=ξ​\p​r​\p​w=0\xi\p{l\p w}=\xi\p{r\p w}=0 as anything else would contradict lemma \zarabicsection.\zarabicthrm. By lemma \zarabicsection.\zarabicthrm

w∈\crl​\bm​0∗∪\crl​\bm​1∗∪\crl​Teven∪\crl​C​Teven,w\in\crl\bm 0^{*}\cup\crl\bm 1^{*}\cup\crl T^{\mathrm{even}}\cup\crl{CT}^{\mathrm{even}},

but only w∈\crl​Tevenw\in\crl T^{\mathrm{even}} satisfies ξ​\p​m​\p​w=−1\xi\p{m\p w}=-1. ∎

Theorem \zarabicsection.\zarabicthrm.

Let k,n∈\Nk,n\in\N and w∈𝒜2k+nw\in\mathcal{A}_{2}^{k+n} be such that

w\hopen​0,n=w\hopen​k,k+n∧∃ı<kξ​\p​w\hopen​ı,ı+n=1.w_{\hopen{0,n}}=w_{\hopen{k,k+n}}\land\exists\imath<k\quad\xi\p{w_{\hopen{\imath,\imath+n}}}=1.

Then

∃ȷ<kξ​\p​w\hopen​ȷ,ȷ+n=−1.\displaystyle\exists\jmath<k\quad\xi\p{w_{\hopen{\jmath,\jmath+n}}}=-1.
Proof.

Induction on nn. As it suffices to consider cycles in the nn” dimensional de Bruijn graph (instead of any closed walk ww represents), there are only finitely many cases to consider for n∈\crl​0,1,2n\in\crl{0,1,2}. Now assume the statement holds for a certain nn. Let w∈𝒜2k+n+1w\in\mathcal{A}_{2}^{k+n+1} such that

w\hopen​0,n+1=w\hopen​k,k+n+1∧∃ı<kξ​\p​w\hopen​ı,ı+n+1=1.w_{\hopen{0,n+1}}=w_{\hopen{k,k+n+1}}\land\exists\imath<k\quad\xi\p{w_{\hopen{\imath,\imath+n+1}}}=1.

If w\hopen​ı,ı+n+2∈\crl​Toddw_{\hopen{\imath,\imath+n+2}}\in\crl T^{\mathrm{odd}} then ξ​\p​w\hopen​ı+1,ı+n+2=−1\xi\p{w_{\hopen{\imath+1,\imath+n+2}}}=-1, which would already establish the statement and if w\hopen​ı,ı+n+2=Tn+1​\bm​1w_{\hopen{\imath,\imath+n+2}}=T^{n+1}\bm 1 then ξ​\p​w\hopen​ı+2,ı+n+2=1\xi\p{w_{\hopen{\imath+2,\imath+n+2}}}=1. Otherwise w\hopen​ı,ı+n+1∉\crl​Tevenw_{\hopen{\imath,\imath+n+1}}\notin\crl T^{\mathrm{even}} so either ξ​\p​w\hopen​ı,ı+n=1∨ξ​\p​w\hopen​ı+1,ı+n+1=1\xi\p{w_{\hopen{\imath,\imath+n}}}=1\lor\xi\p{w_{\hopen{\imath+1,\imath+n+1}}}=1. In any case either the statement is already established or there is a substring of length nn to which ξ\xi assigns the value 11.

Define w~\tilde{w} by replacing any occurrence of Tn+2T^{n+2} in ww by TnT^{n}, meaning that Tn+2T^{n+2} is not a substring of w~\tilde{w}. Set k~=#​w~−\p​n+1\tilde{k}=\#\tilde{w}-\p{n+1}. Note that

\crl​w~\hopen​ı,ı+n;ı<k~⊆\crl​w\hopen​ı,ı+n;ı<k\crl{\tilde{w}_{\hopen{\imath,\imath+n}};\imath<\tilde{k}}\subseteq\crl{w_{\hopen{\imath,\imath+n}};\imath<k}

(in words: any substring of length nn of w~\tilde{w} is also a substring of ww), however

\crl​w\hopen​ı,ı+n;ı<k⊆\crl​w~\hopen​ı,ı+n;ı<k~∪\crl​C​Tn.\crl{w_{\hopen{\imath,\imath+n}};\imath<k}\subseteq\crl{\tilde{w}_{\hopen{\imath,\imath+n}};\imath<\tilde{k}}\cup\crl{CT^{n}}.

(In words: the only substring of length nn that has been removed by constructing w~\tilde{w} from ww is C​TnCT^{n}.) Since ξ​\p​C​Tn≠1\xi\p{CT^{n}}\neq 1, it follows that still ∃ı<k~ξ​\p​w~\hopen​ı,ı+n=1\exists\imath<\tilde{k}\quad\xi\p{\tilde{w}_{\hopen{\imath,\imath+n}}}=1. This also shows that k~≥1\tilde{k}\geq 1 and hence #​w~≥n+2\#\tilde{w}\geq n+2.

First, consider the case w~\hopen​0,n≠w~\hopen​k~,k~+n\tilde{w}_{\hopen{0,n}}\neq\tilde{w}_{\hopen{\tilde{k},\tilde{k}+n}}. That implies w~\hopen​k~,k~+n+1≠w\hopen​k,k+n+1\tilde{w}_{\hopen{\tilde{k},\tilde{k}+n+1}}\neq w_{\hopen{k,k+n+1}}, which is possible only if w\hopen​k−1,k+n+1=Tn+2w_{\hopen{k-1,k+n+1}}=T^{n+2}, so w\hopen​0,n+1=w\hopen​k,k+n+1=C​Tn+1w_{\hopen{0,n+1}}=w_{\hopen{k,k+n+1}}=CT^{n+1} and hence w~\hopen​1,n+1=w~\hopen​k~+1,k~+n+1=Tn\tilde{w}_{\hopen{1,n+1}}=\tilde{w}_{\hopen{\tilde{k}+1,\tilde{k}+n+1}}=T^{n}. By the induction hypothesis,

∃ȷ1≤ȷ<k~+1∧ξ​\p​w~\hopen​ȷ,ȷ+n=−1.\displaystyle\exists\jmath\quad 1\leq\jmath<\tilde{k}+1\land\xi\p{\tilde{w}_{\hopen{\jmath,\jmath+n}}}=-1. (\zarabicsection-\zarabicequation)

If w~\hopen​0,n=w~\hopen​k~,k~+n\tilde{w}_{\hopen{0,n}}=\tilde{w}_{\hopen{\tilde{k},\tilde{k}+n}}, the induction hypothesis directly gives ∃ȷ<k~ξ​\p​w~\hopen​ȷ,ȷ+n=−1\exists\jmath<\tilde{k}\quad\xi\p{\tilde{w}_{\hopen{\jmath,\jmath+n}}}=-1. If ȷ=0\jmath=0, one can also pick ȷ=k~\jmath=\tilde{k}, so also in this case equation (\zarabicsection-\zarabicequation) holds.

Then by lemma \zarabicsection.\zarabicthrm

ξ​\p​w~\hopen​ȷ−1,ȷ+n=−1∨ξ​\p​w~\hopen​ȷ,ȷ+n+1=−1∨w~\hopen​ȷ−1,ȷ+n+1=Tn+2,\displaystyle\xi\p{\tilde{w}_{\hopen{\jmath-1,\jmath+n}}}=-1\lor\xi\p{\tilde{w}_{\hopen{\jmath,\jmath+n+1}}}=-1\lor\tilde{w}_{\hopen{\jmath-1,\jmath+n+1}}=T^{n+2},

where the third option is excluded by the definition of w~\tilde{w}. The statement now follows from the fact that

\crl​w~\hopen​ı,ı+n+1;ı<k~⊆\crl​w\hopen​ı,ı+n+1;ı<k.\displaystyle\crl{\tilde{w}_{\hopen{\imath,\imath+n+1}};\imath<\tilde{k}}\subseteq\crl{w_{\hopen{\imath,\imath+n+1}};\imath<k}.

(In words: any substring of length n+1n+1 of w~\tilde{w} is also a substring of ww.) ∎

Remark.

The statement also holds when switching the rolls of 11 and −1-1; the proof is analogous.

Using the notion of ξ\xi as defining a left, a centre and a right part of the de Bruijn graph, theorem \zarabicsection.\zarabicthrm tells that there are no non-empty closed walks in the right part. Figure \zarabicfigure does not contain non-trivial closed walks in the blue (or red) highlighted area.

The proof idea is simpler than it seems: A string representing a walk in a certain de Bruijn graph also represents a walk in the de Bruijn graph one dimension lower. If a walk passes a vertex vv for which ξ​\p​v=−1\xi\p v=-1 of a graph by the construction of the ξ\xi function it will also do so in a higher dimensional de Bruijn graph – with one notable exception: The vertex C​TnCT^{n} for even nn. Take for example the walk \bm​0101\bm{0101} in the 22-dimensional de Bruijn graph. Glancing at figure \zarabicfigure shows that this walk passes both the area with blue and the area with red background. Now consider the same string a walk through the 33-dimensional de Bruijn graph. A look at figure \zarabicfigure tells that the graph does not pass the area with red background. This one exception is what makes the construction of w~\tilde{w} necessary.

Corollary \zarabicsection.\zarabicthrm.

Let n∈\Nn\in\N. The sft generated by prohibiting the strings in

\crl​w∈𝒜2n;ξ​\p​w≠1\crl{w\in\mathcal{A}_{2}^{n};\xi\p w\neq 1}

is empty.

Proof.

Assume, there were a point uu in the sft. Pick ı<ȷ∈\N\imath<\jmath\in\N such that u\hopen​ı,ı+n=u\hopen​ȷ,ȷ+nu_{\hopen{\imath,\imath+n}}=u_{\hopen{\jmath,\jmath+n}}. By definition of the sft, ξ​\p​u\hopen​ı,ı+n=1\xi\p{u_{\hopen{\imath,\imath+n}}}=1. Set w=u\hopen​ı,ȷ+nw=u_{\hopen{\imath,\jmath+n}} and k=ȷ−ık=\jmath-\imath. Then theorem \zarabicsection.\zarabicthrm contradicts the definition of the sft. ∎

\zarabicsection The function ϕ\phi

Remark.

Section \zarabicsection has the same structure as the previous one. Each result but corollary \zarabicsection.\zarabicthrm can be compared with the result of the same number in section \zarabicsection. Often the proofs are similar.

Definition.
††margin: – the function ϕ\phi

ϕ\phi:𝒜2∗→\crl−1,0,1:\mathcal{A}_{2}^{*}\to\crl{-1,0,1} is defined recursively by

ϕ​\p​w\displaystyle\phi\p w ={0if ​w=\upepsilon−1if ​w∈\crl​\bm​0odd1if ​w∈\crl​\bm​1odd\sgn​\p​ϕ​\p​r​\p​w−ϕ​\p​l​\p​welse.\displaystyle=\begin{cases}0&\text{if }w=\upepsilon\\ -1&\text{if }w\in\crl\bm 0^{\mathrm{odd}}\\ 1&\text{if }w\in\crl\bm 1^{\mathrm{odd}}\\ \sgn\p{\phi\p{r\p w}-\phi\p{l\p w}}&\text{else}.\end{cases}
Remark.

In figures \zarabicfigure to \zarabicfigure the vertices and edges are coloured according to the value ϕ\phi assigns to them.

ww \upepsilon\upepsilon \bm​0\bm 0 \bm​1\bm 1 \bm​00\bm{00} \bm​01\bm{01} \bm​10\bm{10} \bm​11\bm{11}
ϕ​\p​w\phi\p w 0 -1 1 0 1 -1 0
ww \bm​000\bm{000} \bm​001\bm{001} \bm​010\bm{010} \bm​011\bm{011} \bm​100\bm{100} \bm​101\bm{101} \bm​110\bm{110} \bm​111\bm{111}
ϕ​\p​w\phi\p w -1 1 -1 -1 1 1 -1 1
Table \zarabictable: ϕ​\p​w\phi\p w for w∈𝒜2≤3w\in\mathcal{A}_{2}^{\leq 3}

 

Lemma \zarabicsection.\zarabicthrm.
ϕ∘C\displaystyle\phi\circ C =−ϕ\displaystyle=-\phi \p​ϕ∘R​\p​w\displaystyle\p{\phi\circ R}\p w =\p−1#​w+1⋅ϕ​\p​w\displaystyle=\p{-1}^{\#w+1}\cdot\phi\p w (\zarabicsection-\zarabicequation)
Proof.

By induction on #​w\#w.

ϕ​\p​C​\p​\upepsilon\displaystyle\phi\p{C\p\upepsilon} =−ϕ​\p​\upepsilon=ϕ​\p​R​\p​\upepsilon=\p−10+1⋅ϕ​\p​\upepsilon=0\displaystyle=-\phi\p\upepsilon=\phi\p{R\p\upepsilon}=\p{-1}^{0+1}\cdot\phi\p\upepsilon=0

Now assume, the statement holds for #​w<n\#w<n. Let #​w=n\#w=n.

If w∈\crl​\bm​0odd∪\crl​\bm​1oddw\in\crl\bm 0^{\mathrm{odd}}\cup\crl\bm 1^{\mathrm{odd}}, the statement follows directly from the definition of ϕ\phi. Otherwise,

\p​ϕ∘C​\p​w=\sgn​\p​\p​ϕ∘r∘C​\p​w−\p​ϕ∘l∘C​\p​w=\sgn​\p​\p​ϕ∘C∘r​\p​w−\p​ϕ∘C∘l​\p​w=−\sgn​\p​\p​ϕ∘r​\p​w−\p​ϕ∘l​\p​w=−ϕ​\p​w\displaystyle\begin{split}\p{\phi\circ C}\p w&=\sgn\p{\p{\phi\circ r\circ C}\p w-\p{\phi\circ l\circ C}\p w}\\ &=\sgn\p{\p{\phi\circ C\circ r}\p w-\p{\phi\circ C\circ l}\p w}\\ &=-\sgn\p{\p{\phi\circ r}\p w-\p{\phi\circ l}\p w}\\ &=-\phi\p w\end{split}
\p​ϕ∘R​\p​w=\sgn​\p​\p​ϕ∘r∘R​\p​w−\p​ϕ∘l∘R​\p​w=\sgn​\p​\p​ϕ∘R∘l​\p​w−\p​ϕ∘R∘r​\p​w=\p−1n⋅\sgn​\p​\p​ϕ∘l​\p​w−\p​ϕ∘r​\p​w=\p−1n+1⋅ϕ​\p​w\displaystyle\begin{split}\p{\phi\circ R}\p w&=\sgn\p{\p{\phi\circ r\circ R}\p w-\p{\phi\circ l\circ R}\p w}\\ &=\sgn\p{\p{\phi\circ R\circ l}\p w-\p{\phi\circ R\circ r}\p w}\\ &=\p{-1}^{n}\cdot\sgn\p{\p{\phi\circ l}\p w-\p{\phi\circ r}\p w}\\ &=\p{-1}^{n+1}\cdot\phi\p w\end{split}

∎

Corollary \zarabicsection.\zarabicthrm.

Let w∈𝒜2evenw\in\mathcal{A}_{2}^{\mathrm{even}} be a palindrome. Then

ϕ​\p​w=0.\displaystyle\phi\p w=0.
Proof.

For a palindrome ww of even length, equation (\zarabicsection-\zarabicequation) becomes

ϕ​\p​w\displaystyle\phi\p w =−ϕ​\p​w,\displaystyle=-\phi\p w,

which establishes the statement. ∎

Corollary \zarabicsection.\zarabicthrm.

Let kk be even. Then

ϕ​\p​\bm​0k=ϕ​\p​\bm​1k=0\displaystyle\phi\p{\bm 0^{k}}=\phi\p{\bm 1^{k}}=0 (\zarabicsection-\zarabicequation)
Proof.

Since \bm​0k,\bm​1k\bm 0^{k},\bm 1^{k} are palindromes, the statement follows directly from corollary  \zarabicsection.\zarabicthrm. ∎

Observation \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥1w\in\mathcal{A}_{2}^{\geq 1}.

ϕ​\p​w=0\displaystyle\phi\p w=0 ⇔w∉\crl​\bm​0odd∪\crl​\bm​1odd∧ϕ​\p​l​\p​w=ϕ​\p​r​\p​w\displaystyle\iff w\notin\crl\bm 0^{\mathrm{odd}}\cup\crl\bm 1^{\mathrm{odd}}\land\phi\p{l\p w}=\phi\p{r\p w} (\zarabicsection-\zarabicequation)
Corollary \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥1w\in\mathcal{A}_{2}^{\geq 1} such that ϕ​\p​l​\p​w,ϕ​\p​r​\p​w≠0\phi\p{l\p w},\phi\p{r\p w}\neq 0. Then

ϕ​\p​w=0⇔ϕ​\p​l​\p​w=ϕ​\p​r​\p​w\displaystyle\phi\p w=0\iff\phi\p{l\p w}=\phi\p{r\p w} (\zarabicsection-\zarabicequation)
Proof.

From corollary  \zarabicsection.\zarabicthrm it follows that w∉\crl​\bm​0odd∪\crl​\bm​1oddw\notin\crl\bm 0^{\mathrm{odd}}\cup\crl\bm 1^{\mathrm{odd}}, so the statement follows from observation \zarabicsection.\zarabicthrm. ∎

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥1w\in\mathcal{A}_{2}^{\geq 1} such that ϕ​\p​w≠0\phi\p{w}\neq 0. Then

ϕ​\p​r​\p​w≠0\displaystyle\phi\p{r\p{w}}\neq 0 ⟹ϕ​\p​w=ϕ​\p​r​\p​w\displaystyle\implies\phi\p{w}=\phi\p{r\p w} (\zarabicsection-\zarabicequation)
ϕ​\p​l​\p​w≠0\displaystyle\phi\p{l\p{w}}\neq 0 ⟹ϕ​\p​w≠ϕ​\p​l​\p​w.\displaystyle\implies\phi\p{w}\neq\phi\p{l\p w}. (\zarabicsection-\zarabicequation)
Proof.

From ϕ​\p​r​\p​w≠0∨ϕ​\p​l​\p​w≠0\phi\p{r\p w}\neq 0\lor\phi\p{l\p w}\neq 0 it follows that w∉\crl​\bm​0odd∪\crl​\bm​1oddw\notin\crl\bm 0^{\mathrm{odd}}\cup\crl\bm 1^{\mathrm{odd}}, so

ϕ​\p​w=\sgn​\p​ϕ​\p​r​\p​w+\p−ϕ​\p​l​\p​w.\displaystyle\phi\p w=\sgn\p{\phi\p{r\p w}+\p{-\phi\p{l\p w}}}.

Now if one of the summands is non-zero ϕ​\p​w\phi\p w must either equal that summand or be zero. ∎

Lemma \zarabicsection.\zarabicthrm.

Let ı,ȷ≥1\imath,\jmath\geq 1. Then

ϕ​\p​\bm​0ı​\bm​1ȷ=\p−1ȷ+1.\displaystyle\phi\p{\bm 0^{\imath}\bm 1^{\jmath}}=\p{-1}^{\jmath+1}. (\zarabicsection-\zarabicequation)
Proof.

Induction on ı+ȷ\imath+\jmath. ϕ​\p​\bm​0​\bm​1=1\phi\p{\bm 0\bm 1}=1 which establishes the statement for ı+ȷ=2\imath+\jmath=2. Now assume the statement holds for ı+ȷ<n∈\N\imath+\jmath<n\in\N. Let ı+ȷ=n\imath+\jmath=n. Then

ϕ​\p​\bm​0ı​\bm​1ȷ=\sgn​\p​ϕ​\p​\bm​0ı−1​\bm​1ȷ−ϕ​\p​\bm​0ı​\bm​1ȷ−1,\displaystyle\phi\p{\bm 0^{\imath}\bm 1^{\jmath}}=\sgn\p{\phi\p{\bm 0^{\imath-1}\bm 1^{\jmath}}-\phi\p{\bm 0^{\imath}\bm 1^{\jmath-1}}},

where

ȷ​ is even\displaystyle\jmath\text{ is even{}} ⟹ϕ​\p​\bm​0ı−1​\bm​1ȷ≤0∧ϕ​\p​\bm​0ı​\bm​1ȷ−1=1\displaystyle\implies\phi\p{\bm 0^{\imath-1}\bm 1^{\jmath}}\leq 0\land\phi\p{\bm 0^{\imath}\bm 1^{\jmath-1}}=1
ȷ​ is odd\displaystyle\jmath\makebox[0.0pt][l]{$\text{ is odd{}}$} ⟹ϕ​\p​\bm​0ı−1​\bm​1ȷ=1∧ϕ​\p​\bm​0ı​\bm​1ȷ−1≤0.\displaystyle\implies\phi\p{\bm 0^{\imath-1}\bm 1^{\jmath}}=1\land\phi\p{\bm 0^{\imath}\bm 1^{\jmath-1}}\leq 0.

In both cases the statement holds. ∎

Corollary \zarabicsection.\zarabicthrm.
ϕ​\p​\bm​1ȷ​\bm​0ı=\p−1ı\displaystyle\phi\p{\bm 1^{\jmath}\bm 0^{\imath}}=\p{-1}^{\imath}
Proof.
ϕ​\p​\bm​1ȷ​\bm​0ı​\by​(​\zarabicsection-\zarabicequation​)​\p−1ı+ȷ+1⋅ϕ​\p​\bm​0ı​\bm​1ȷ​\by​(​\zarabicsection-\zarabicequation​)​\p−1ı+ȷ+1+ȷ+1=\p−1ı\displaystyle\phi\p{\bm 1^{\jmath}\bm 0^{\imath}}\by{\eqref{eq:phiCphiR}}\p{-1}^{\imath+\jmath+1}\cdot\phi\p{\bm 0^{\imath}\bm 1^{\jmath}}\by{\eqref{eq:phi0i1j}}\p{-1}^{\imath+\jmath+1+\jmath+1}=\p{-1}^{\imath}

∎

Lemma \zarabicsection.\zarabicthrm.

Let k>0k>0. Then ϕ​\p​Tk=\p−1k\phi\p{T^{k}}=\p{-1}^{k}.

Proof.

Induction on kk. ϕ​\p​T1=ϕ​\p​\bm​0=−1\phi\p{T^{1}}=\phi\p\bm 0=-1. Now assume the statement holds for a certain kk. Then

ϕ​\p​Tk+1=\sgn​\p​ϕ​\p​C​Tk−ϕ​\p​Tk​\by​(​\zarabicsection-\zarabicequation​)​\sgn​\p−2⋅ϕ​\p​Tk=−ϕ​\p​Tk=\p−1k+1.\displaystyle\phi\p{T^{k+1}}=\sgn\p{\phi\p{CT^{k}}-\phi\p{T^{k}}}\by{\eqref{eq:phiCphiR}}\sgn\p{-2\cdot\phi\p{T^{k}}}=-\phi\p{T^{k}}=\p{-1}^{k+1}.

∎

Lemma \zarabicsection.\zarabicthrm.
∀w∈𝒜2≥1ϕ​\p​l​\p​w=ϕ​\p​r​\p​w=0⟹w∈\crl​\bm​0odd∪\crl​\bm​1odd\forall w\in\mathcal{A}_{2}^{\geq 1}\quad\phi\p{l\p w}=\phi\p{r\p w}=0\implies w\in\crl\bm 0^{\mathrm{odd}}\cup\crl\bm 1^{\mathrm{odd}}
Proof.

Induction on #​w\#w. For #​w≤2\#w\leq 2 there are only finitely many cases. Now assume the statement holds for #​w<n\#w<n. Let #​w=n≥3\#w=n\geq 3 and ϕ​\p​l​\p​w=ϕ​\p​r​\p​w=0\phi\p{l\p w}=\phi\p{r\p w}=0, which means that

ϕ​\p​l2​\p​w=ϕ​\p​m​\p​w=ϕ​\p​r2​\p​w.\displaystyle\phi\p{l^{2}\p w}=\phi\p{m\p w}=\phi\p{r^{2}\p w}.

By the argument used in the proof of lemma \zarabicsection.\zarabicthrm, one gets that in fact

ϕ​\p​l2​\p​w=ϕ​\p​m​\p​w=ϕ​\p​r2​\p​w=0,\displaystyle\phi\p{l^{2}\p w}=\phi\p{m\p w}=\phi\p{r^{2}\p w}=0,

so by the induction hypothesis,

l​\p​w,r​\p​w∈\crl​\bm​0∗∪\crl​\bm​1∗\displaystyle l\p w,r\p w\in\crl\bm 0^{*}\cup\crl\bm 1^{*}

and since #​w≥3\#w\geq 3,

w∈\crl​\bm​0∗∪\crl​\bm​1∗.\displaystyle w\in\crl\bm 0^{*}\cup\crl\bm 1^{*}.

#​w\#w must be odd because otherwise ϕ​\p​l​\p​w≠0\phi\p{l\p w}\neq 0. ∎

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥2w\in\mathcal{A}_{2}^{\geq 2} such that ϕ​\p​w=0\phi\p w=0. Then

ϕ​\p​m​\p​w=0.\displaystyle\phi\p{m\p w}=0. (\zarabicsection-\zarabicequation)
Proof.

If m​\p​w∈\crl​\bm​0even∪\crl​\bm​1evenm\p w\in\crl\bm 0^{\mathrm{even}}\cup\crl\bm 1^{\mathrm{even}} the statement follows from corollary \zarabicsection.\zarabicthrm so assume that it is not. ϕ​\p​w=0\phi\p w=0 implies that ϕ​\p​l​\p​w=ϕ​\p​r​\p​w\phi\p{l\p w}=\phi\p{r\p w}. By lemma \zarabicsection.\zarabicthrm either w∈\crl​\bm​0odd∪\crl​\bm​1oddw\in\crl\bm 0^{\mathrm{odd}}\cup\crl\bm 1^{\mathrm{odd}} or ϕ​\p​l​\p​w=ϕ​\p​r​\p​w≠0\phi\p{l\p w}=\phi\p{r\p w}\neq 0. However, the first case can be excluded since ϕ​\p​w=0\phi\p w=0. Hence

\sgn​\p​ϕ​\p​m​\p​w−ϕ​\p​l2​\p​w=\sgn​\p​ϕ​\p​r2​\p​w−ϕ​\p​m​\p​w≠0,\displaystyle\sgn\p{\phi\p{m\p w}-\phi\p{l^{2}\p w}}=\sgn\p{\phi\p{r^{2}\p w}-\phi\p{m\p w}}\neq 0,

so

ϕ​\p​l2​\p​w<ϕ​\p​m​\p​w<ϕ​\p​r2​\p​w∨ϕ​\p​l2​\p​w>ϕ​\p​m​\p​w>ϕ​\p​r2​\p​w.\displaystyle\phi\p{l^{2}\p w}<\phi\p{m\p w}<\phi\p{r^{2}\p w}\quad\lor\quad\phi\p{l^{2}\p w}>\phi\p{m\p w}>\phi\p{r^{2}\p w}.

In both cases it follows that ϕ​\p​m​\p​w=0\phi\p{m\p w}=0. ∎

Corollary \zarabicsection.\zarabicthrm.

Let w∈𝒜2oddw\in\mathcal{A}_{2}^{\mathrm{odd}}. Then

ϕ​\p​w≠0.\displaystyle\phi\p w\neq 0. (\zarabicsection-\zarabicequation)
Proof.

Induction on #​w\#w. For #​w=1\#w=1 there are only finitely many cases to consider. Assume now, the statement is true for #​w<n\#w<n. Let #​w=n\#w=n and ϕ​\p​w=0\phi\p w=0. Then ϕ​\p​m​\p​w=0\phi\p{m\p w}=0, so n−2n-2 is odd. ∎

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥2w\in\mathcal{A}_{2}^{\geq 2} such that ϕ​\p​l2​\p​w=ϕ​\p​r2​\p​w≠0\phi\p{l^{2}\p w}=\phi\p{r^{2}\p w}\neq 0. Then

ϕ​\p​m​\p​w≠0.\displaystyle\phi\p{m\p w}\neq 0.
Proof.

#​w=2⟹ϕ​\p​l2​\p​w=0\#w=2\implies\phi\p{l^{2}\p w}=0. Now let #​w≥3\#w\geq 3 and ϕ​\p​m​\p​w=0\phi\p{m\p w}=0. Then

\p​ϕ∘l2∘r​\p​w​\by​(​\zarabicsection-\zarabicequation​)​\p​ϕ∘l∘r2​\p​w\displaystyle\p{\phi\circ l^{2}\circ r}\p w\by{\eqref{eq:phi0}}\p{\phi\circ l\circ r^{2}}\p w (\zarabicsection-\zarabicequation)

and by corollary \zarabicsection.\zarabicthrm #​w\#w is even so l2​\p​w,r2​\p​w∉\crl​\bm​0odd∪\crl​\bm​1oddl^{2}\p w,r^{2}\p w\notin\crl\bm 0^{\mathrm{odd}}\cup\crl\bm 1^{\mathrm{odd}}. Hence

ϕ​\p​l2​\p​w=ϕ​\p​r2​\p​w≠0⇔\sgn​\p​\p​ϕ∘l2∘r​\p​w−\p​ϕ∘l3​\p​w=\sgn​\p​\p​ϕ∘r3​\p​w−\p​ϕ∘l∘r2​\p​w≠0\by​[⇔]​(​\zarabicsection-\zarabicequation​)\sgn​\p​\p−ϕ∘l3​\p​w+\p​ϕ∘l2∘r​\p​w=\sgn​\p​\p​ϕ∘r3​\p​w−\p​ϕ∘l2∘r​\p​w≠0⟹\p​ϕ∘l2∘r​\p​w=0,\displaystyle\begin{split}\phi\p{l^{2}\p w}=\phi\p{r^{2}\p w}\neq 0\iff&\\ \sgn\p{\p{\phi\circ l^{2}\circ r}\p w-\p{\phi\circ l^{3}}\p w}=&\sgn\p{\p{\phi\circ r^{3}}\p w-\p{\phi\circ l\circ r^{2}}\p w}\neq 0\\ \by[\iff]{\eqref{eq:proof:phil2rphilr2}}&\\ \sgn\p{\p{-\phi\circ l^{3}}\p w+\p{\phi\circ l^{2}\circ r}\p w}=&\sgn\p{\p{\phi\circ r^{3}}\p w-\p{\phi\circ l^{2}\circ r}\p w}\neq 0\\ \implies&\p{\phi\circ l^{2}\circ r}\p w=0,\end{split}

which is impossible because #​\p​\p​l2∘r​\p​w\#\p{\p{l^{2}\circ r}\p w} is odd. ∎

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜22w\in\mathcal{A}_{2}^{2} such that ϕ​\p​m​\p​w=0\phi\p{m\p w}=0. Then

ϕ\pw≠0⇔w∈Λ≥2=⋃n≥1\crl\bm0n\bm1,\bm0\bm1n,\bm1\bm0n,\bm1n\bm0.\displaystyle\phi\p w\neq 0\iff w\in\Lambda^{\geq 2}=\bigcup_{n\geq 1}\crl{\bm 0^{n}\bm 1,\bm 0\bm 1^{n},\bm 1\bm 0^{n},\bm 1^{n}\bm 0}.
Proof.

⟸\impliedby is established in lemma \zarabicsection.\zarabicthrm and corollary \zarabicsection.\zarabicthrm. To show ⟹\implies assume w∉Λ≥2w\notin\Lambda^{\geq 2} but ϕ​\p​m​\p​w=0\phi\p{m\p w}=0. Then l​\p​w,r​\p​w∉\crl​\bm​0odd∪\crl​\bm​1oddl\p w,r\p w\notin\crl\bm 0^{\mathrm{odd}}\cup\crl\bm 1^{\mathrm{odd}} and by corollary \zarabicsection.\zarabicthrm #​w\#w is even, so neither is ww. Hence

ϕ​\p​l​\p​w\displaystyle\phi\p{l\p w} =\sgn​\p​ϕ​\p​m​\p​w−ϕ​\p​l2​\p​w=−ϕ​\p​l2​\p​w\displaystyle=\sgn\p{\phi\p{m\p w}-\phi\p{l^{2}\p w}}=-\phi\p{l^{2}\p w}
ϕ​\p​r​\p​w\displaystyle\phi\p{r\p w} =\sgn​\p​ϕ​\p​r2​\p​w−ϕ​\p​m​\p​w=ϕ​\p​r2​\p​w\displaystyle=\sgn\p{\phi\p{r^{2}\p w}-\phi\p{m\p w}}=\phi\p{r^{2}\p w}
ϕ​\p​w\displaystyle\phi\p w =\sgn​\p​ϕ​\p​r​\p​w−ϕ​\p​l​\p​w=\sgn​\p​ϕ​\p​r2​\p​w+ϕ​\p​l2​\p​w.\displaystyle=\sgn\p{\phi\p{r\p w}-\phi\p{l\p w}}=\sgn\p{\phi\p{r^{2}\p w}+\phi\p{l^{2}\p w}}.

Since #​\p​l​\p​w\#\p{l\p w} and #​\p​r​\p​w\#\p{r\p w} are odd, both summands are non-zero. However, by lemma \zarabicsection.\zarabicthrm they cannot be equal either. Hence ϕ​\p​w=0\phi\p w=0. ∎

\zarabicsection Relations between ξ\xi and ϕ\phi

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥2w\in\mathcal{A}_{2}^{\geq 2} such that ϕ​\p​m​\p​w=ξ​\p​m​\p​w=0\phi\p{m\p w}=\xi\p{m\p w}=0. Then

ϕ​\p​w=ξ​\p​w.\displaystyle\phi\p w=\xi\p w. (\zarabicsection-\zarabicequation)
Proof.

By corollary \zarabicsection.\zarabicthrm #​w\#w is even. Then by lemmata \zarabicsection.\zarabicthrm and \zarabicsection.\zarabicthrm

ξ​\p​w≠0⇔ϕ​\p​w≠0⇔w∈Λ≥2.\displaystyle\xi\p w\neq 0\iff\phi\p w\neq 0\iff w\in\Lambda^{\geq 2}.

Set k=#​w−1k=\#w-1. According to lemmata \zarabicsection.\zarabicthrm, \zarabicsection.\zarabicthrm, corollaries \zarabicsection.\zarabicthrm and \zarabicsection.\zarabicthrm

ξ​\p​\bm​0k​\bm​1\displaystyle\xi\p{\bm 0^{k}\bm 1} =ξ​\p​\bm​0​\bm​1k=ϕ​\p​\bm​0k​\bm​1=ϕ​\p​\bm​0​\bm​1k=1\displaystyle=\xi\p{\bm 0\bm 1^{k}}=\phi\p{\bm 0^{k}\bm 1}=\phi\p{\bm 0\bm 1^{k}}=1
ξ​\p​\bm​1k​\bm​0\displaystyle\xi\p{\bm 1^{k}\bm 0} =ξ​\p​\bm​1​\bm​0k=ϕ​\p​\bm​1k​\bm​0=ϕ​\p​\bm​1​\bm​0k=−1.\displaystyle=\xi\p{\bm 1\bm 0^{k}}=\phi\p{\bm 1^{k}\bm 0}=\phi\p{\bm 1\bm 0^{k}}=-1.

∎

Theorem \zarabicsection.\zarabicthrm.

Let w∈𝒜2∗w\in\mathcal{A}_{2}^{*}.

ϕ​\p​w=0⇔#​w​ is even∧ξ​\p​w=0\displaystyle\phi\p w=0\iff\#w\text{ is even{}}\land\xi\p w=0 (\zarabicsection-\zarabicequation)
Proof.

Induction on #​w\#w. For #​w≤1\#w\leq 1 there are only finitely many cases to consider. Now assume, the statement holds for #​w<n\#w<n. Let #​w=n\#w=n.

ϕ​\p​w=0​\by​[⟹]​(​\zarabicsection-\zarabicequation​)\displaystyle\phi\p w=0\by[\implies]{\eqref{eq:phiodd}} #​w​ is even\displaystyle\#w\text{ is even{}}
ϕ​\p​w=0​\by​[⟹]​(​\zarabicsection-\zarabicequation​)ϕ​\p​m​\p​w=0\by​[⟹]​(​\zarabicsection-\zarabicequation​)ξ​\p​m​\p​w=0\by​[⟹]​(​\zarabicsection-\zarabicequation​)ξ​\p​w=ϕ​\p​w=0\displaystyle\begin{split}\phi\p w=0\by[\implies]{\eqref{eq:phimw0}}&\phi\p{m\p w}=0\\ \by[\implies]{\eqref{eq:phi0xi0}}&\xi\p{m\p w}=0\\ \by[\implies]{\eqref{eq:phimwximw0}}&\xi\p w=\phi\p w=0\end{split}
#​w​ is even∧ξ​\p​w=0​\by​[⟹]​(​\zarabicsection-\zarabicequation​)#​w​ is even∧ξ​\p​m​\p​w=0\by​[⟹]​(​\zarabicsection-\zarabicequation​)ϕ​\p​m​\p​w=0\by​[⟹]​(​\zarabicsection-\zarabicequation​)ϕ​\p​w=ξ​\p​w=0\displaystyle\begin{split}\#w\text{ is even{}}\land\xi\p w=0\by[\implies]{\eqref{eq:xi0xim0}}&\#w\text{ is even{}}\land\xi\p{m\p w}=0\\ \by[\implies]{\eqref{eq:phi0xi0}}&\phi\p{m\p w}=0\\ \by[\implies]{\eqref{eq:phimwximw0}}&\phi\p w=\xi\p w=0\end{split}

∎

Corollary \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥1w\in\mathcal{A}_{2}^{\geq 1} be such that ξ​\p​l​\p​w,ξ​\p​r​\p​w≠0\xi\p{l\p w},\xi\p{r\p w}\neq 0. Then

ϕ​\p​l​\p​w=ϕ​\p​r​\p​w⇔#​w​ is even∧ξ​\p​l​\p​w≠ξ​\p​r​\p​w\displaystyle\phi\p{l\p w}=\phi\p{r\p w}\iff\#w\text{ is even{}}\land\xi\p{l\p w}\neq\xi\p{r\p w} (\zarabicsection-\zarabicequation)
Proof.
ϕ​\p​l​\p​w=ϕ​\p​r​\p​w\displaystyle\phi\p{l\p w}=\phi\p{r\p w} \by​[⇔]​(​\zarabicsection-\zarabicequation​)​ϕ​\p​w=0\displaystyle\by[\iff]{\eqref{eq:phi0*}}\phi\p w=0
\by​[⇔]​(​\zarabicsection-\zarabicequation​)​#​w​ is even∧ξ​\p​w=0\displaystyle\by[\iff]{\eqref{eq:phi0xi0}}\#w\text{ is even{}}\land\xi\p w=0
\by​[⇔]​(​\zarabicsection-\zarabicequation​)​#​w​ is even∧ξ​\p​l​\p​w≠ξ​\p​r​\p​w\displaystyle\by[\iff]{\eqref{eq:xi0*}}\#w\text{ is even{}}\land\xi\p{l\p w}\neq\xi\p{r\p w}

∎

Remark.

By giving a necessary and sufficient condition for the exceptions, corollary  \zarabicsection.\zarabicthrm shows that usually ϕ​\p​l​\p​w≠ϕ​\p​r​\p​w\phi\p{l\p w}\neq\phi\p{r\p w}. Later the alternating colouring function ψ\psi shall be introduced as an improvement of ϕ\phi for which the inequality always hold.

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥2w\in\mathcal{A}_{2}^{\geq 2} such that

ξ​\p​l2​\p​w,ξ​\p​r2​\p​w≠0=ξ​\p​m​\p​w.\displaystyle\xi\p{l^{2}\p w},\xi\p{r^{2}\p w}\neq 0=\xi\p{m\p w}. (\zarabicsection-\zarabicequation)

Then

ϕ​\p​l2​\p​w=ϕ​\p​r2​\p​w⇔#​w​ is odd.\displaystyle\phi\p{l^{2}\p w}=\phi\p{r^{2}\p w}\iff\#w\makebox[0.0pt][l]{$\text{ is odd{}}$}. (\zarabicsection-\zarabicequation)
Proof.

Note that l​\p​w,r​\p​w​\by​[∉]​(​\zarabicsection-\zarabicequation​)​\crl​Teven∪\crl​C​Teven∪\crl​\bm​0∗∪\crl​\bm​1∗l\p w,r\p w\by[\notin]{\eqref{eq:cond:phillphirrxim0}}\crl T^{\mathrm{even}}\cup\crl{CT}^{\mathrm{even}}\cup\crl\bm 0^{*}\cup\crl\bm 1^{*}, so

ξ​\p​l​\p​w=\displaystyle\xi\p{l\p w}= \sgn​\p​ξ​\p​l2​\p​w+ξ​\p​m​\p​w​\by​(​\zarabicsection-\zarabicequation​)​ξ​\p​l2​\p​w\displaystyle\sgn\p{\xi\p{l^{2}\p w}+\xi\p{m\p w}}\by{\eqref{eq:cond:phillphirrxim0}}\xi\p{l^{2}\p w} (\zarabicsection-\zarabicequation)
ξ​\p​r​\p​w=\displaystyle\xi\p{r\p w}= \sgn​\p​ξ​\p​m​\p​w+ξ​\p​r2​\p​w​\by​(​\zarabicsection-\zarabicequation​)​ξ​\p​r2​\p​w\displaystyle\sgn\p{\xi\p{m\p w}+\xi\p{r^{2}\p w}}\by{\eqref{eq:cond:phillphirrxim0}}\xi\p{r^{2}\p w} (\zarabicsection-\zarabicequation)
ϕ​\p​l​\p​w=\displaystyle\phi\p{l\p w}= \sgn​\p​ϕ​\p​m​\p​w−ϕ​\p​l2​\p​w​\by​(​\zarabicsection-\zarabicequation​)−ϕ​\p​l2​\p​w\displaystyle\sgn\p{\phi\p{m\p w}-\phi\p{l^{2}\p w}}\by{\eqref{eq:cond:phillphirrxim0}}-\phi\p{l^{2}\p w} (\zarabicsection-\zarabicequation)
ϕ​\p​r​\p​w=\displaystyle\phi\p{r\p w}= \sgn​\p​ϕ​\p​r2​\p​w−ϕ​\p​m​\p​w​\by​(​\zarabicsection-\zarabicequation​)​ϕ​\p​r2​\p​w.\displaystyle\sgn\p{\phi\p{r^{2}\p w}-\phi\p{m\p w}}\by{\eqref{eq:cond:phillphirrxim0}}\phi\p{r^{2}\p w}. (\zarabicsection-\zarabicequation)

Hence

ϕ​\p​l2​\p​w=ϕ​\p​r2​\p​w​\by​[⇔]​(​\zarabicsection-\zarabicequation​),(​\zarabicsection-\zarabicequation​)\displaystyle\phi\p{l^{2}\p w}=\phi\p{r^{2}\p w}\by[\iff]{\eqref{eq:proof:phillphirrphil},\eqref{eq:proof:phillphirrphir}} ϕ​\p​l​\p​w≠ϕ​\p​r​\p​w\displaystyle\phi\p{l\p w}\neq\phi\p{r\p w}
\by​[⇔]​(​\zarabicsection-\zarabicequation​)\by[\iff]{\eqref{eq:philphir}} #​w​ is odd∨ξ​\p​l​\p​w=ξ​\p​r​\p​w\displaystyle\#w\makebox[0.0pt][l]{$\text{ is odd{}}$}\lor\xi\p{l\p w}=\xi\p{r\p w}
\by​[⇔]​(​\zarabicsection-\zarabicequation​),(​\zarabicsection-\zarabicequation​)\displaystyle\by[\iff]{\eqref{eq:proof:phillphirrxil},\eqref{eq:proof:phillphirrxir}} #​w​ is odd∨ξ​\p​l2​\p​w=ξ​\p​r2​\p​w\displaystyle\#w\makebox[0.0pt][l]{$\text{ is odd{}}$}\lor\xi\p{l^{2}\p w}=\xi\p{r^{2}\p w}
\by​[⇔]​(​\zarabicsection-\zarabicequation​)\by[\iff]{\eqref{eq:xillxirrxim0}} #​w​ is odd.\displaystyle\#w\makebox[0.0pt][l]{$\text{ is odd{.}}$}

∎

Lemma \zarabicsection.\zarabicthrm.

Let k,n∈\N,w∈𝒜2\Nk,n\in\N,w\in\mathcal{A}_{2}^{\N} such that k≥1k\geq 1 and

∀ȷ≤k\p​ξ​\p​w\hopen​ȷ,ȷ+n≠0⇔ȷ∈\crl​0,k.\displaystyle\forall\jmath\leq k\quad\p{\xi\p{w_{\hopen{\jmath,\jmath+n}}}\neq 0\iff\jmath\in\crl{0,k}}.

Then

ϕ​\p​w\hopen​0,n=ϕ​\p​w\hopen​k,k+n⇔n​ is odd∧ξ​\p​w\hopen​0,n≠ξ​\p​w\hopen​k,k+n.\displaystyle\phi\p{w_{\hopen{0,n}}}=\phi\p{w_{\hopen{k,k+n}}}\iff n\makebox[0.0pt][l]{$\text{ is odd{}}$}\land\xi\p{w_{\hopen{0,n}}}\neq\xi\p{w_{\hopen{k,k+n}}}. (\zarabicsection-\zarabicequation)
Proof.

Since ξ​\p​w\hopen​0,n≠0\xi\p{w_{\hopen{0,n}}}\neq 0, actually n≥2n\geq 2. The cases k∈\crl​1,2k\in\crl{1,2} are covered by corollary \zarabicsection.\zarabicthrm and lemma \zarabicsection.\zarabicthrm respectively. Now let k≥3k\geq 3. Then by lemma \zarabicsection.\zarabicthrm

m​\p​w∈\crl​\bm​0k+n−2,\bm​1k+n−2∨n​ is odd∧m​\p​w∈\crl​Tk+n−2,C​Tk+n−2\displaystyle m\p w\in\crl{\bm 0^{k+n-2},\bm 1^{k+n-2}}\lor n\makebox[0.0pt][l]{$\text{ is odd{}}$}\land m\p w\in\crl{T^{k+n-2},CT^{k+n-2}}

Taking into account the condition ξ​\p​w\hopen​0,n,ξ​\p​w\hopen​k,k+n≠0\xi\p{w_{\hopen{0,n}}},\xi\p{w_{\hopen{k,k+n}}}\neq 0 gives

w\displaystyle w ∈\crl​\bm​1​\bm​0k+n−2​\bm​1,\bm​0​\bm​1k+n−2​\bm​0\displaystyle\in\crl{\bm 1\bm 0^{k+n-2}\bm 1,\bm 0\bm 1^{k+n-2}\bm 0}
∨w\displaystyle{}\lor w ∈\crl​\bm​0​Tk+n−2​\bm​0,\bm​1​C​Tk+n−2​\bm​1∧k​ is even∧n​ is odd\displaystyle\in\crl{\bm 0T^{k+n-2}\bm 0,\bm 1CT^{k+n-2}\bm 1}\land{}k\text{ is even{}}{}\land{}n\makebox[0.0pt][l]{$\text{ is odd{}}$}
∨w\displaystyle{}\lor w ∈\crl​\bm​0​Tk+n−2​\bm​1,\bm​1​C​Tk+n−2​\bm​0∧k​ is odd∧n​ is odd.\displaystyle\in\crl{\bm 0T^{k+n-2}\bm 1,\bm 1CT^{k+n-2}\bm 0}\land{}k\makebox[0.0pt][l]{$\text{ is odd{}}$}\land{}n\makebox[0.0pt][l]{$\text{ is odd{.}}$}

In each of these cases the statement holds. ∎

Remark.

The proof idea is to determine those spots in the de Bruijn graph where several edges ww for which ξ​\p​w=0\xi\p w=0 follow upon each other. By looking at the graphs one gets the impression that happens only around \bm​0n\bm 0^{n}, \bm​1n\bm 1^{n} and around the centre of odd-dimensional de Bruijn graphs, which lemma \zarabicsection.\zarabicthrm confirms. In all other cases the statement is already established by corollary \zarabicsection.\zarabicthrm and lemma \zarabicsection.\zarabicthrm.

\zarabicsection The alternating colouring function ψ\psi

Definition.

Define ψ:𝒜2∗→\crl−1,0,1\psi:\mathcal{A}_{2}^{*}\to\crl{-1,0,1} by

ψ​\p​w\displaystyle\psi\p w =\p​ξ​\p​w#​w⋅ϕ​\p​w.\displaystyle=\p{\xi\p w}^{\#w}\cdot\phi\p w. (\zarabicsection-\zarabicequation)

ψ\psi is called the ††margin: – alternating colouring function ψ\psi alternating colouring function.

w∈𝒜2∗w\in\mathcal{A}_{2}^{*} is called ††margin: – colourable string colourable if ψ​\p​w≠0\psi\p w\neq 0. For n≥2n\geq 2 the sft generated by prohibiting the strings in \crl​w∈𝒜2n;ψ​\p​w=0\crl{w\in\mathcal{A}_{2}^{n};\psi\p w=0} is called the ††margin: – maximal nn” colourable shift maximal nn” colourable shift. Any subshift of the maximal nn” colourable shift is called ††margin: – nn-colourable shift nn” colourable.

Remark.

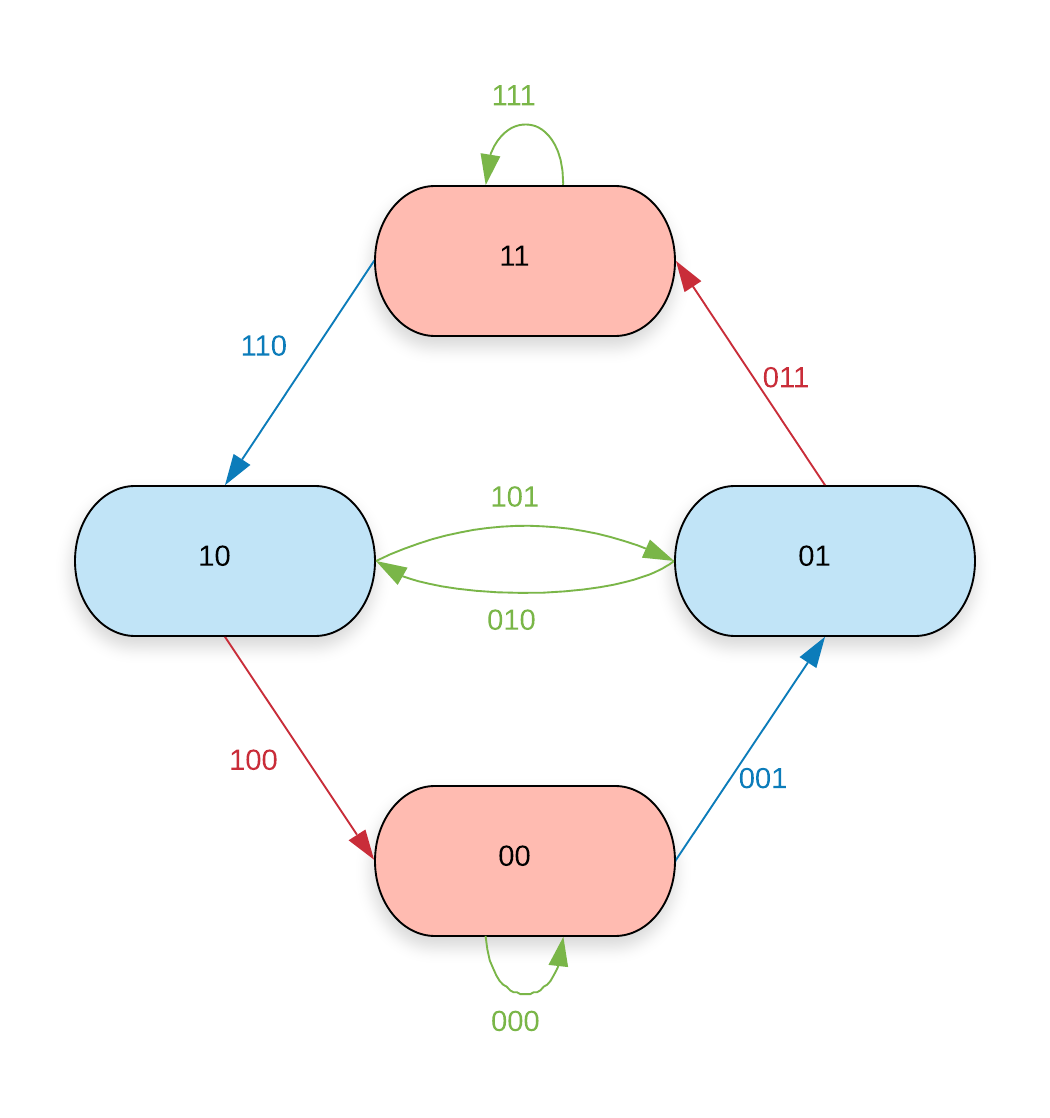
In figures \zarabicfigure to \zarabicfigure the vertices and edges are coloured according to the value ψ\psi assigns to them. Colourable are those vertices and edges that are coloured blue or red.

The maximal nn-colourable shift is the edge shift of the \p​n−1\p{n-1}-dimensional de Bruijn graph of which all the non-colourable edges (the green ones in figures \zarabicfigure to \zarabicfigure that is) have been removed. Equivalently it is the vertex shift of the nn-dimensional de Bruijn graph of which all non-colourable vertices have been removed.

ww \upepsilon\upepsilon \bm​0\bm 0 \bm​1\bm 1 \bm​00\bm{00} \bm​01\bm{01} \bm​10\bm{10} \bm​11\bm{11}
ψ​\p​w\psi\p w 0 0 0 0 1 -1 0
ww \bm​000\bm{000} \bm​001\bm{001} \bm​010\bm{010} \bm​011\bm{011} \bm​100\bm{100} \bm​101\bm{101} \bm​110\bm{110} \bm​111\bm{111}
ψ​\p​w\psi\p w 0 1 0 -1 -1 0 1 0
Table \zarabictable: The values ψ​\p​w\psi\p w of the alternating colouring for w∈𝒜2≤3w\in\mathcal{A}_{2}^{\leq 3}

 

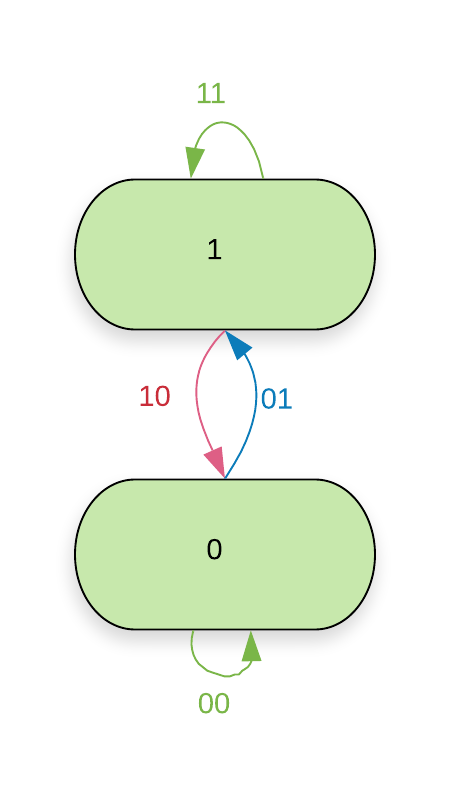
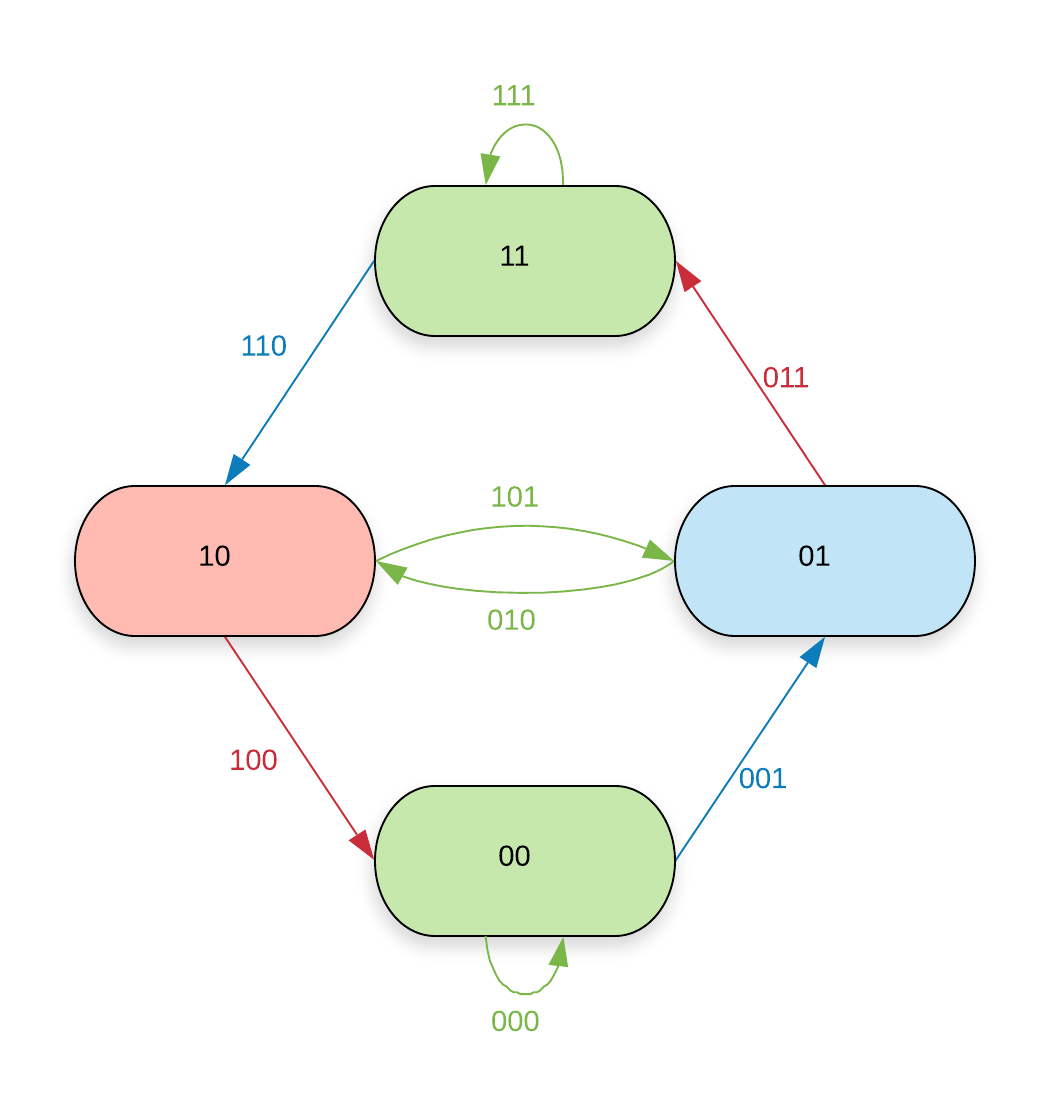
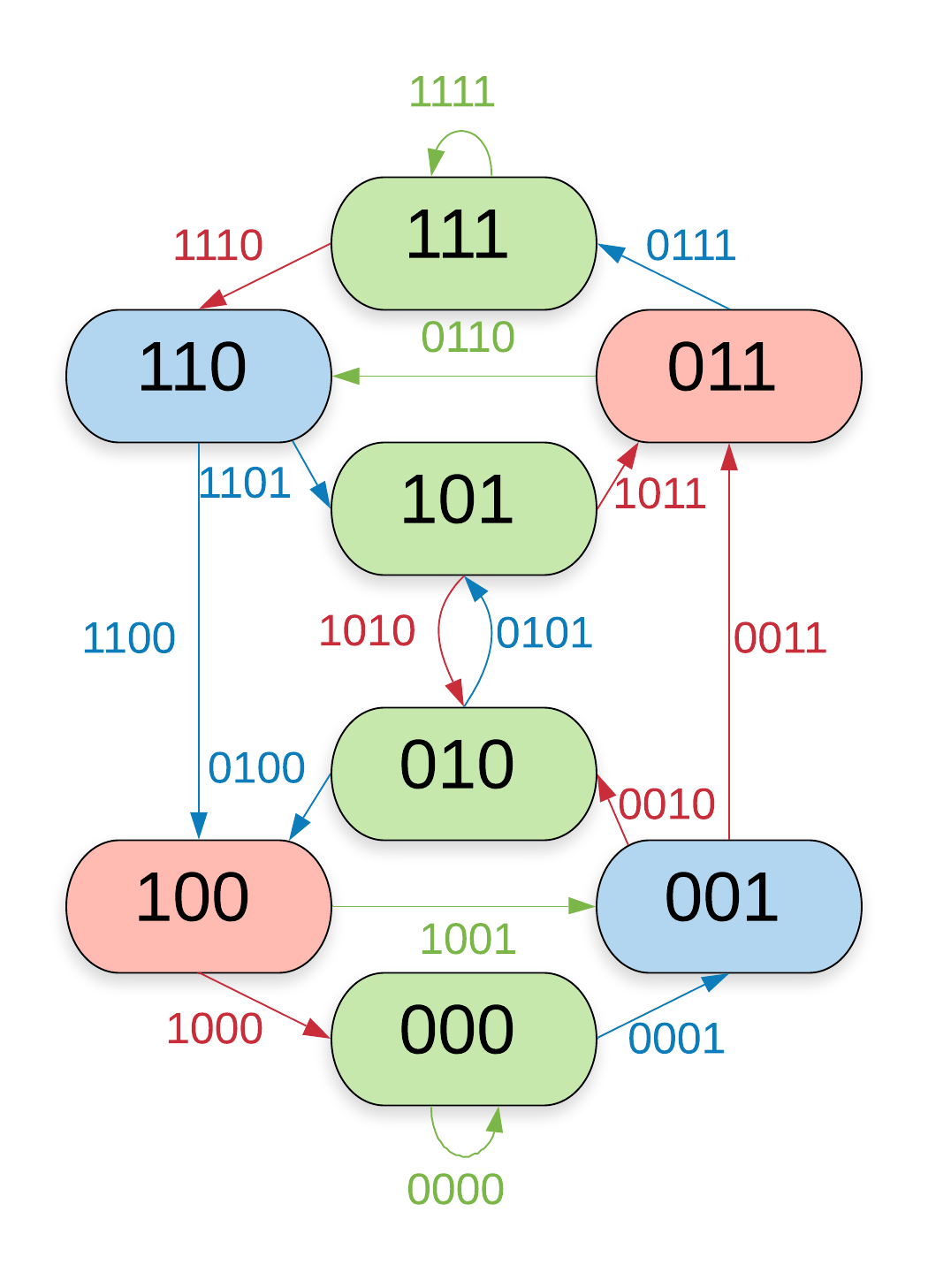
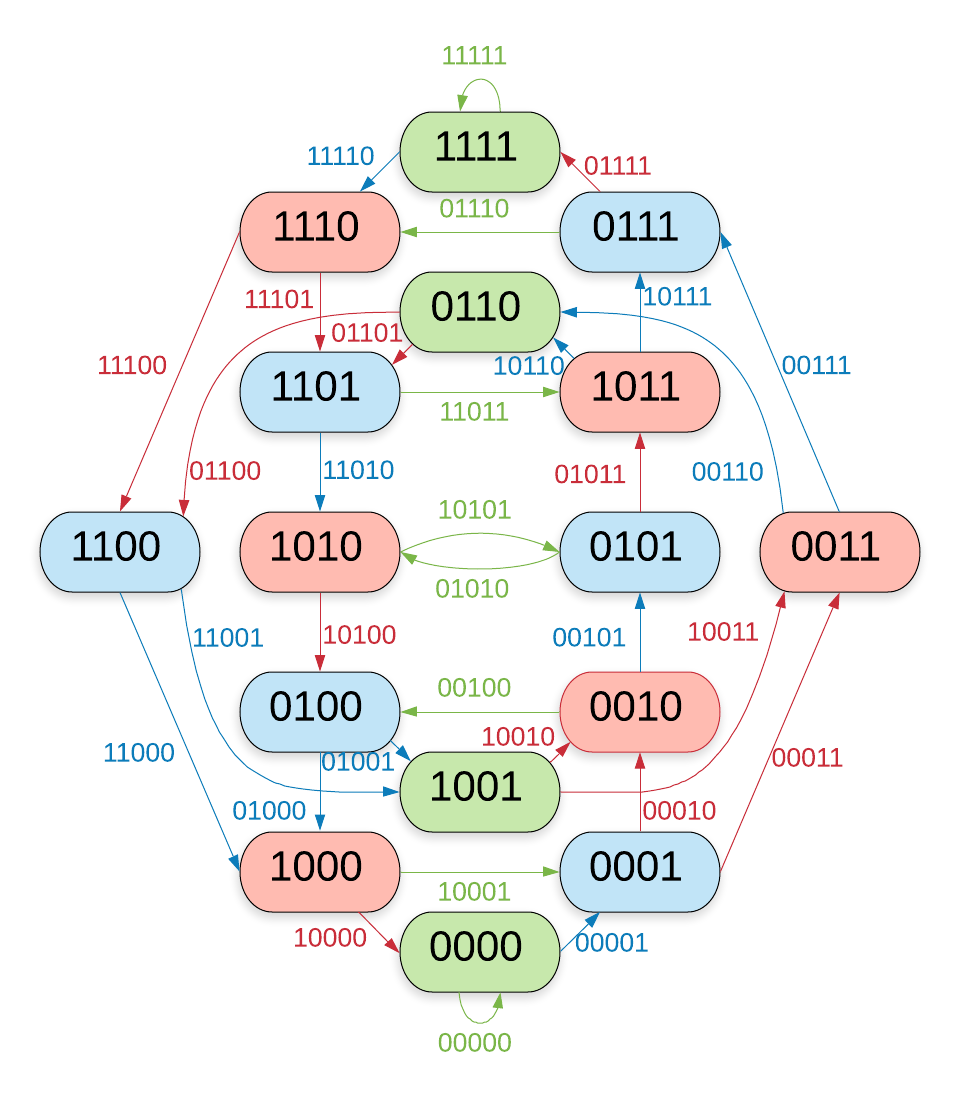
Refer to caption
Figure \zarabicfigure: The 11-dimensional de Bruijn graph. The edges \bm​01\bm{01} and \bm​10\bm{10} are coloured blue and red respectively indicating that ψ​\p​\bm​01=1∧ψ​\p​\bm​10=−1\psi\p{\bm{01}}=1\land\psi\p{\bm{10}}=-1. The other two edges and the vertices are coloured green because ψ\psi is 0 there.

 

Refer to caption
Figure \zarabicfigure: The 22-dimensional de Bruijn graph. The vertices and edges are coloured red if ψ=−1\psi=-1, green if ψ=0\psi=0 and blue if ψ=1\psi=1.

 

Refer to caption
Figure \zarabicfigure: The 33-dimensional de Bruijn graph. The vertices and edges are coloured red if ψ=−1\psi=-1, green if ψ=0\psi=0 and blue if ψ=1\psi=1.

 

Refer to caption
Figure \zarabicfigure: The 44-dimensional de Bruijn graph. The vertices and edges are coloured red if ψ=−1\psi=-1, green if ψ=0\psi=0 and blue if ψ=1\psi=1.

 

Lemma \zarabicsection.\zarabicthrm.
\p​ψ∘C​\p​w=\p−1#​w+1⋅ψ​\p​w\displaystyle\p{\psi\circ C}\p w=\p{-1}^{\#w+1}\cdot\psi\p w ψ∘R=−ψ\displaystyle\psi\circ R=-\psi (\zarabicsection-\zarabicequation)
Proof.
\p​ψ∘C​\p​w\by​[=]​(​\zarabicsection-\zarabicequation​)\p​ξ​\p​C​\p​w#​w⋅ϕ​\p​C​\p​w\by​(​\zarabicsection-\zarabicequation​),(​\zarabicsection-\zarabicequation​)\p−ξ\pw#​w⋅−ϕ\pw\by​[=]​(​\zarabicsection-\zarabicequation​)\p−1#​w+1⋅ψ​\p​w\displaystyle\begin{split}&\p{\psi\circ C}\p w\\ \makebox[0.0pt][c]{$\by[=]{\eqref{eq:psi}}$}&\p{\xi\p{C\p w}}^{\#w}\cdot\phi\p{C\p w}\\ \by{{\eqref{eq:xiCxiR}},{\eqref{eq:phiCphiR}}}&\p{-\xi\p w}^{\#w}\cdot-\phi\p w\\ \makebox[0.0pt][c]{$\by[=]{\eqref{eq:psi}}$}&\p{-1}^{\#w+1}\cdot\psi\p w\end{split} |\displaystyle\Bigg{|} \p​ψ∘R​\p​w\by​[=]​(​\zarabicsection-\zarabicequation​)\p​ξ​\p​R​\p​w#​w⋅ϕ​\p​R​\p​w\by​(​\zarabicsection-\zarabicequation​),(​\zarabicsection-\zarabicequation​)\p−ξ​\p​w#​w⋅\p−1#​w+1⋅ϕ​\p​w\by​[=]​(​\zarabicsection-\zarabicequation​)−ψ​\p​w\displaystyle\begin{split}&\p{\psi\circ R}\p w\\ \makebox[0.0pt][c]{$\by[=]{\eqref{eq:psi}}$}&\p{\xi\p{R\p w}}^{\#w}\cdot\phi\p{R\p w}\\ \by{{\eqref{eq:xiCxiR}},{\eqref{eq:phiCphiR}}}&\p{-\xi\p w}^{\#w}\cdot\p{-1}^{\#w+1}\cdot\phi\p w\\ \makebox[0.0pt][c]{$\by[=]{\eqref{eq:psi}}$}&-\psi\p w\end{split}

∎

Lemma \zarabicsection.\zarabicthrm.

Let w∈𝒜2∗w\in\mathcal{A}_{2}^{*}. Then

ψ​\p​w=0⇔ξ​\p​w=0.\displaystyle\psi\p w=0\iff\xi\p w=0. (\zarabicsection-\zarabicequation)
Proof.
ψ​\p​w=0​\by​[⇔]​(​\zarabicsection-\zarabicequation​)​ξ​\p​w=0∨ϕ​\p​w=0​\by​[⇔]​(​\zarabicsection-\zarabicequation​)​ξ​\p​w=0\displaystyle\psi\p w=0\by[\iff]{\eqref{eq:psi}}\xi\p w=0\lor\phi\p w=0\by[\iff]{\eqref{eq:phi0xi0}}\xi\p w=0

∎

Remark.

Lemma \zarabicsection.\zarabicthrm will often be used without explicit reference. Saying that ww is colourable should always be understood as ξ​\p​w,ψ​\p​w≠0\xi\p w,\psi\p w\neq 0. To show colourability, of course the easier condition ξ​\p​w≠0\xi\p w\neq 0 will be used.

Corollary \zarabicsection.\zarabicthrm.

Let w∈𝒜2evenw\in\mathcal{A}_{2}^{\mathrm{even}}. Then

ψ​\p​w=ϕ​\p​w.\displaystyle\psi\p w=\phi\p w. (\zarabicsection-\zarabicequation)
Proof.

The statement follows directly from lemma \zarabicsection.\zarabicthrm and the definition of ψ\psi. ∎

Theorem \zarabicsection.\zarabicthrm.

Let k,n∈\N,w∈𝒜2\Nk,n\in\N,w\in\mathcal{A}_{2}^{\N} such that k≥1k\geq 1 and

w\hopen​ȷ,ȷ+n​ is colourable⇔ȷ∈\crl​0,k.\displaystyle w_{\hopen{\jmath,\jmath+n}}\text{ is colourable}\iff\jmath\in\crl{0,k}.

Then

ψ​\p​w\hopen​0,n≠ψ​\p​w\hopen​k,k+n.\displaystyle\psi\p{w_{\hopen{0,n}}}\neq\psi\p{w_{\hopen{k,k+n}}}. (\zarabicsection-\zarabicequation)
Proof.

The statement can be seen as a corollary to lemma \zarabicsection.\zarabicthrm. First let nn be even. Then

ψ​\p​w\hopen​0,n​\by​(​\zarabicsection-\zarabicequation​)​ϕ​\p​w\hopen​0,n​\by​[≠]​(​\zarabicsection-\zarabicequation​)​ϕ​\p​w\hopen​k,k+n​\by​(​\zarabicsection-\zarabicequation​)​ψ​\p​w\hopen​k,k+n.\displaystyle\psi\p{w_{\hopen{0,n}}}\by{\eqref{eq:psiphi}}\phi\p{w_{\hopen{0,n}}}\by[\neq]{\eqref{eq:philllphirrr}}\phi\p{w_{\hopen{k,k+n}}}\by{\eqref{eq:psiphi}}\psi\p{w_{\hopen{k,k+n}}}.

Now let nn be odd. Then

ψ​\p​w\hopen​0,n​\by​(​\zarabicsection-\zarabicequation​)\displaystyle\psi\p{w_{\hopen{0,n}}}\by{\eqref{eq:psi}} ξ​\p​w\hopen​0,n⋅ϕ​\p​w\hopen​0,n\displaystyle\xi\p{w_{\hopen{0,n}}}\cdot\phi\p{w_{\hopen{0,n}}}
\by​[≠]​(​\zarabicsection-\zarabicequation​)\displaystyle\by[\neq]{\eqref{eq:philllphirrr}} ξ​\p​w\hopen​k,k+n⋅ϕ​\p​w\hopen​k,k+n\displaystyle\xi\p{w_{\hopen{k,k+n}}}\cdot\phi\p{w_{\hopen{k,k+n}}}
\by​(​\zarabicsection-\zarabicequation​)\displaystyle\by{\eqref{eq:psi}} ψ​\p​w\hopen​k,k+n.\displaystyle\psi\p{w_{\hopen{k,k+n}}}.

∎

Remark.

Theorem \zarabicsection.\zarabicthrm states that in an infinite string, a colourable substring always has a different ψ\psi” colour than the preceding colourable substring of the same length – no matter how many non-colourable substrings there are in between.

\bm​0​1​0​0​11​1​1​1​0​0​0​1​101​…\displaystyle\bm{{\color[rgb]{0,0,1}{0}}{\color[rgb]{0,1,0}{1}}{\color[rgb]{1,0,0}{0}}{\color[rgb]{0,0,1}{0}}{\color[rgb]{0,1,0}{1}}{\color[rgb]{0,1,0}{1}}{\color[rgb]{1,0,0}{1}}{\color[rgb]{0,0,1}{1}}{\color[rgb]{1,0,0}{1}}{\color[rgb]{0,0,1}{0}}{\color[rgb]{1,0,0}{0}}{\color[rgb]{0,1,0}{0}}{\color[rgb]{0,0,1}{1}}101...}
Figure \zarabicfigure: The beginning of an infinite string w∈𝒜2\Nw\in\mathcal{A}_{2}^{\N}. For k∈\Nk\in\N the character on place kk has been coloured red if ψ​\p​w\hopen​k,k+4=−1\psi\p{w_{\hopen{k,k+4}}}=-1, green if ψ​\p​w\hopen​k,k+4=0\psi\p{w_{\hopen{k,k+4}}}=0 and blue if ψ​\p​w\hopen​k,k+4=1\psi\p{w_{\hopen{k,k+4}}}=1. The first character is blue because ψ​\p​\bm​0100=1\psi\p{\bm{0100}}=1; the second one is green because ψ​\p​\bm​1001=0\psi\p{\bm{1001}}=0. The last three characters are printed black because their colour depends on the upcoming characters that are not given here. Ignoring the green characters, always a blue character follows on a red and vice versa. The fact that there are green characters means that this ww cannot be a point in a 44-colourable shift.

 

Corollary \zarabicsection.\zarabicthrm.

Let w∈𝒜2≥1w\in\mathcal{A}_{2}^{\geq 1} be such that l​\p​w,r​\p​wl\p w,r\p w are colourable. Then ψ​\p​l​\p​w≠ψ​\p​r​\p​w\psi\p{l\p w}\neq\psi\p{r\p w}.

Proof.

The statement follows from theorem \zarabicsection.\zarabicthrm by regarding ww as the beginning of an infinite string and setting k=1,n=#​w−1k=1,n=\#w-1. ∎

Remark.

Compare corollary  \zarabicsection.\zarabicthrm with corollary  \zarabicsection.\zarabicthrm. While there were some special cases in which ϕ​\p​l​\p​w≠ϕ​\p​r​\p​w\phi\p{l\p w}\neq\phi\p{r\p w} would not hold, ψ​\p​l​\p​w≠ψ​\p​r​\p​w\psi\p{l\p w}\neq\psi\p{r\p w} always does.

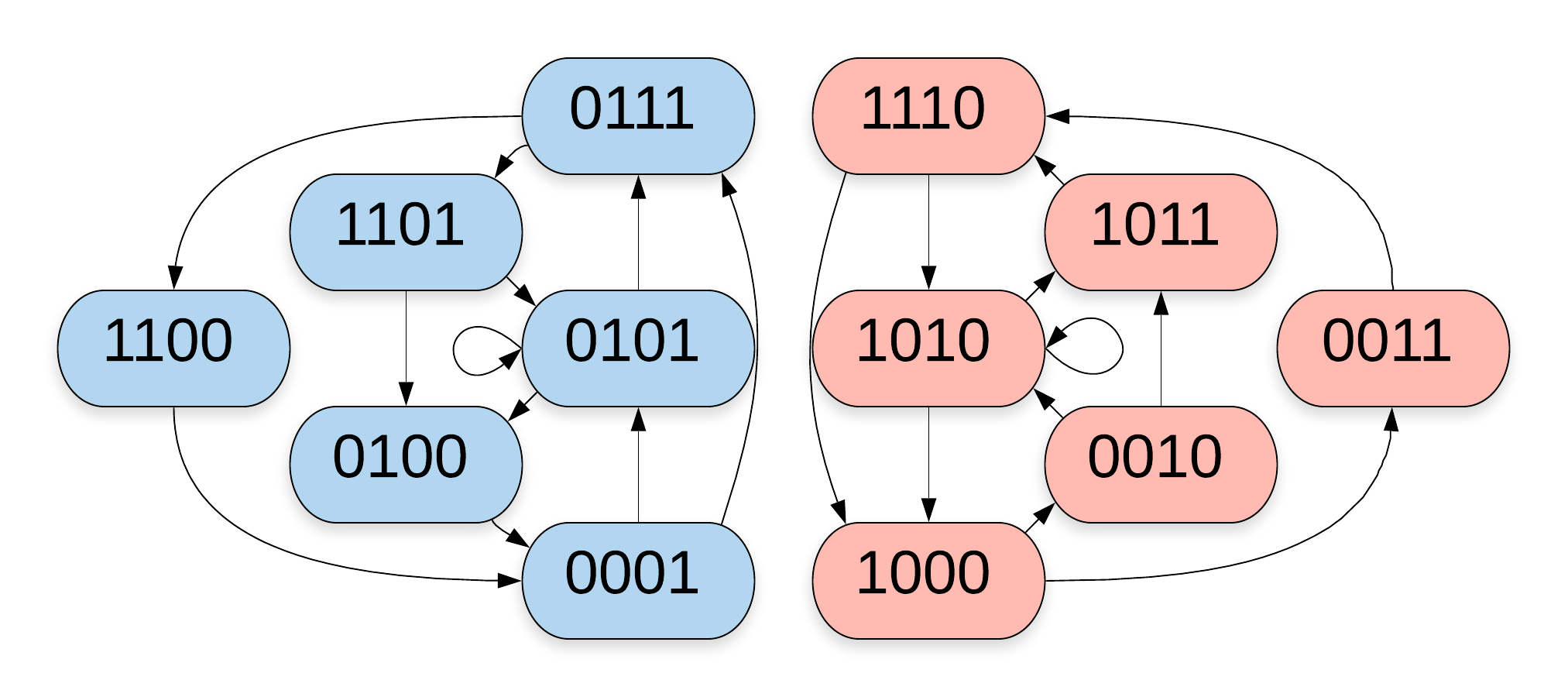
Refer to caption
Figure \zarabicfigure: The \nth2 power graph of the 44-dimensional de Bruijn graph. The vertices whose ξ\xi-value is zero are omitted as are the edges that represent walks which would have passed an omitted edge. The vertices are coloured red if ξ=−1\xi=-1 and blue if ξ=1\xi=1.

 

Remark.

Consider a de Bruijn graph of which all non-colourable vertices have been removed. Corollary \zarabicsection.\zarabicthrm states that the colour of the vertices a walk passes alternates between blue and red. For the resulting vertex shift that result will be expressed in corollary \zarabicsection.\zarabicthrm.

In the even powers of such a graph there are only walks from vertices of one colour to vertices of the same colour. Figure \zarabicfigure shows the \nth2 power of the 44-dimensional de Bruijn subgraph without non-colourable edges.

Corollary \zarabicsection.\zarabicthrm.

Let k,n∈\N,w∈𝒜2\Nk,n\in\N,w\in\mathcal{A}_{2}^{\N} such that w\hopen​0,n,w\hopen​k,k+n{w_{\hopen{0,n}}},{w_{\hopen{k,k+n}}} are colourable. Set

z=#​\crl​ȷ<k;w\hopen​ȷ,ȷ+n​ is not colourable.z=\#\crl{\jmath<k;w_{\hopen{\jmath,\jmath+n}}\text{ is not colourable}}.

Then

ψ​\p​w\hopen​k,k+n=\p−1k−z⋅ψ​\p​w\hopen​0,n.\displaystyle\psi\p{w_{\hopen{k,k+n}}}=\p{-1}^{k-z}\cdot\psi\p{w_{\hopen{0,n}}}. (\zarabicsection-\zarabicequation)
Proof.

Strong induction on kk. For k=0k=0 the statement is trivial. Now assume the statement holds whenever k<Kk<K for a certain K∈\NK\in\N. Set

Z=\displaystyle Z= #\crl​ȷ<K;w\hopen​ȷ,ȷ+n​ is not colourable,\displaystyle\makebox[0.0pt][r]{$\#$}\crl{\jmath<K;w_{\hopen{\jmath,\jmath+n}}\text{ is not colourable}},
k=\displaystyle k= max⁡\crl​ȷ<K;w\hopen​ȷ,ȷ+n​ is colourable,\displaystyle\max\crl{\jmath<K;w_{\hopen{\jmath,\jmath+n}}\text{ is colourable}},
z=\displaystyle z= #\crl​ȷ<k;w\hopen​ȷ,ȷ+n​ is not colourable.\displaystyle\makebox[0.0pt][r]{$\#$}\crl{\jmath<k;w_{\hopen{\jmath,\jmath+n}}\text{ is not colourable}}.

Note that Z−z=K−k−1Z-z=K-k-1, so

k−z=K−Z−1.\displaystyle k-z=K-Z-1. (\zarabicsection-\zarabicequation)

Hence

ψ​\p​w\hopen​K,K+n​\by​(​\zarabicsection-\zarabicequation​)\displaystyle\psi\p{w_{\hopen{K,K+n}}}\by{\eqref{eq:psilllpsirrr}} −ψ​\p​w\hopen​k,k+n\displaystyle-\psi\p{w_{\hopen{k,k+n}}}
\by​(​\zarabicsection-\zarabicequation​)\displaystyle\by{\eqref{eq:psilllpsirrr}} −\p−1k−z⋅ψ​\p​w\hopen​0,n\displaystyle-\p{-1}^{k-z}\cdot\psi\p{w_{\hopen{0,n}}}
\by​(​\zarabicsection-\zarabicequation​)\displaystyle\by{\eqref{eq:proof:JZ}} \p−1K−Z⋅ψ​\p​w\hopen​0,n.\displaystyle\p{-1}^{K-Z}\cdot\psi\p{w_{\hopen{0,n}}}.

∎

Corollary \zarabicsection.\zarabicthrm.

Take k,n,w,zk,n,w,z as in corollary \zarabicsection.\zarabicthrm.

Let ψ​\p​w\hopen​0,n=ψ​\p​w\hopen​k,k+n\psi\p{w_{\hopen{0,n}}}=\psi\p{w_{\hopen{k,k+n}}}. Then

k​ is even⇔z​ is even.\displaystyle k\text{ is even{}}\iff z\text{ is even{.}}
Proof.

By corollary \zarabicsection.\zarabicthrm \p−1k−z=1\p{-1}^{k-z}=1. ∎

Corollary \zarabicsection.\zarabicthrm.

Let n∈\Nn\in\N and ww be a point in an nn” colourable shift. Then

∀k∈\Nψ​\p​w[k,k+n)=\p−1k⋅ψ​\p​w[0,n).\displaystyle\forall k\in\N\quad\psi\p{w_{[k,k+n)}}=\p{-1}^{k}\cdot\psi\p{w_{[0,n)}}. (\zarabicsection-\zarabicequation)
Proof.

The statement follows directly from corollary \zarabicsection.\zarabicthrm by noting that for an nn” colourable shift, z=0z=0. ∎

Remark.

Corollary \zarabicsection.\zarabicthrm motivates the term alternating colouring.

\bm​0​0​0​1​0​1​1​1​0​0​0​1​1​1​0​1​…\displaystyle\bm{{\color[rgb]{0,0,1}{0}}{\color[rgb]{1,0,0}{0}}{\color[rgb]{0,0,1}{0}}{\color[rgb]{1,0,0}{1}}{\color[rgb]{0,0,1}{0}}{\color[rgb]{1,0,0}{1}}{\color[rgb]{0,0,1}{1}}{\color[rgb]{1,0,0}{1}}{\color[rgb]{0,0,1}{0}}{\color[rgb]{1,0,0}{0}}{\color[rgb]{0,0,1}{0}}{\color[rgb]{1,0,0}{1}}{\color[rgb]{0,0,1}{1}}{\color[rgb]{1,0,0}{1}}{\color[rgb]{0,0,1}{0}}{\color[rgb]{1,0,0}{1}}{\color[rgb]{0,0,1}{.}}{\color[rgb]{1,0,0}{.}}{\color[rgb]{0,0,1}{.}}}
Figure \zarabicfigure: The beginning of a point ww in a 44-colourable shift. For k∈\Nk\in\N the character on place kk has been coloured blue if ψ​\p​w\hopen​k,k+4=1\psi\p{w_{\hopen{k,k+4}}}=1 and red if ψ​\p​w\hopen​k,k+4=−1\psi\p{w_{\hopen{k,k+4}}}=-1. The sequence alternates between blue and red, a visualisation of the alternating colouring.

 

Corollary \zarabicsection.\zarabicthrm.

Let k,n∈\Nk,n\in\N and ww be a point in an nn” colourable shift such that w\hopen​0,n=w\hopen​k,k+nw_{\hopen{0,n}}=w_{\hopen{k,k+n}}. Then kk is even.

Proof.

By corollary \zarabicsection.\zarabicthrm \p−1k=1\p{-1}^{k}=1. ∎

Remark.

Corollary \zarabicsection.\zarabicthrm states that any closed walk among the colourable edges of a de Bruijn graph has even length.

Corollary \zarabicsection.\zarabicthrm.

Let n∈\Nn\in\N. A non-empty, nn” colourable shift is not mixing.

Proof.

For any natural number there is a larger odd number, but by corollary \zarabicsection.\zarabicthrm there is no walk of odd length from a word back to itself. ∎

\zarabicsection Counting the non-colourable strings

Observation \zarabicsection.\zarabicthrm.

A string of length ≤5\leq 5 is colourable if and only if it is not a palindrome.

Lemma \zarabicsection.\zarabicthrm.

Let n≥4n\geq 4. Then

#​\crl​w∈𝒜2n;ξ​\p​m​\p​w=0∧ξ​\p​w≠0=6−2⋅\p−1n\displaystyle\#\crl{w\in\mathcal{A}_{2}^{n};\xi\p{m\p w}=0\land\xi\p w\neq 0}=6-2\cdot\p{-1}^{n} (\zarabicsection-\zarabicequation)
Proof.

The statement can be seen as a corollary to lemma \zarabicsection.\zarabicthrm. Set

W=\crl​w∈𝒜2n;ξ​\p​m​\p​w=0.W=\crl{w\in\mathcal{A}_{2}^{n};\xi\p{m\p w}=0}.

Then

#​\crl​w∈𝒜2n;ξ​\p​m​\p​w=0∧ξ​\p​w≠0\displaystyle\#\crl{w\in\mathcal{A}_{2}^{n};\xi\p{m\p w}=0\land\xi\p w\neq 0}
\by​[=]\displaystyle\by[=]{\phantom{\eqref{eq:ximw0w0n11}}} #​\crl​w∈W;ξ​\p​w≠0\displaystyle\#\crl{w\in W;\xi\p w\neq 0}
\by​[=]\displaystyle\by[=]{\phantom{\eqref{eq:ximw0w0n11}}} #​\crl​w∈W;ξ​\p​l​\p​w=0∧ξ​\p​r​\p​w≠0\displaystyle\#\crl{w\in W;\xi\p{l\p w}=0\land\xi\p{r\p w}\neq 0}
+\displaystyle{}+{} #​\crl​w∈W;ξ​\p​l​\p​w≠0∧ξ​\p​r​\p​w=0\displaystyle\#\crl{w\in W;\xi\p{l\p w}\neq 0\land\xi\p{r\p w}=0}
+\displaystyle{}+{} #​\crl​w∈W;ξ​\p​l​\p​w=ξ​\p​r​\p​w≠0\displaystyle\#\crl{w\in W;\xi\p{l\p w}=\xi\p{r\p w}\neq 0}
\by​[=]​(​\zarabicsection-\zarabicequation​)\displaystyle\by[=]{\eqref{eq:ximw0w0n11}} 2​\by​[+]​(​\zarabicsection-\zarabicequation​)​2​\by​[+]​(​\zarabicsection-\zarabicequation​),(​\zarabicsection-\zarabicequation​)​2⋅\p​1−\p−1n\displaystyle 2\by[+]{\eqref{eq:ximw0w01n1}}2\by[+]{\eqref{eq:ximw0w0Tn1Tn11},\eqref{eq:ximw0wCTn101CTn1}}2\cdot\p{1-\p{-1}^{n}}
\by​[=]\displaystyle\by[=]{\phantom{\eqref{eq:ximw0w0n11}}} 6−2⋅\p−1n.\displaystyle 6-2\cdot\p{-1}^{n}.

∎

Corollary \zarabicsection.\zarabicthrm.

For n∈\Nn\in\N set Kn=#​\crl​w∈𝒜2n;ψ​\p​w=0K_{n}=\#\crl{w\in\mathcal{A}_{2}^{n};\psi\p w=0}. Let n≥4n\geq 4. Then

Kn=4⋅Kn−2−6+2⋅\p−1n.\displaystyle K_{n}=4\cdot K_{n-2}-6+2\cdot\p{-1}^{n}. (\zarabicsection-\zarabicequation)
Proof.
Kn​\by​(​\zarabicsection-\zarabicequation​)​#​\crl​w∈𝒜2n;ξ​\p​w=0​\by​(​\zarabicsection-\zarabicequation​)\displaystyle K_{n}\by{\eqref{eq:psi0xi0}}\#\crl{w\in\mathcal{A}_{2}^{n};\xi\p w=0}\by{\eqref{eq:xi0xim0}} #​\crl​w∈𝒜2n;ξ​\p​m​\p​w=0\displaystyle\#\crl{w\in\mathcal{A}_{2}^{n};\xi\p{m\p w}=0}
−\displaystyle{}-{} #​\crl​w∈𝒜2n;ξ​\p​m​\p​w=0∧ξ​\p​w≠0\displaystyle\#\crl{w\in\mathcal{A}_{2}^{n};\xi\p{m\p w}=0\land\xi\p w\neq 0}
\by​(​\zarabicsection-\zarabicequation​)\displaystyle\by{\eqref{eq:hashxm0xn0}} 4⋅Kn−2−6+2⋅\p−1n.\displaystyle 4\cdot K_{n-2}-6+2\cdot\p{-1}^{n}.

∎

Definition.

For n∈\Nn\in\N the ††margin: – Jacobsthal number Jacobsthal number JnJ_{n} is defined as

Jn=2n−\p−1n3.\displaystyle J_{n}=\frac{2^{n}-\p{-1}^{n}}{3}. (\zarabicsection-\zarabicequation)
nn 0 1 2 3 4 5 6 7 8 9 10 11
JnJ_{n} 0 1 1 3 5 11 21 43 85 171 341 683
Table \zarabictable: The first Jacobsthal numbers

 

Fact \zarabicsection.\zarabicthrm.

Let n∈\Nn\in\N.

Jn+1\displaystyle J_{n+1} =2⋅Jn+\p−1n\displaystyle=2\cdot J_{n}+\p{-1}^{n} (\zarabicsection-\zarabicequation)
Jn+2\displaystyle J_{n+2} =Jn+1+2⋅Jn\displaystyle=J_{n+1}+2\cdot J_{n} (\zarabicsection-\zarabicequation)
Remark.

The definition of the Jacobsthal numbers, the values in table \zarabictable and fact \zarabicsection.\zarabicthrm have been taken from wiki:jacobsthal (4).

Theorem \zarabicsection.\zarabicthrm.

Let n∈\Nn\in\N.

Kn+2=2⋅\p​Jn+1.\displaystyle K_{n+2}=2\cdot\p{J_{n}+1}. (\zarabicsection-\zarabicequation)
Proof.

By induction on nn. For n≤1n\leq 1 there are only two cases to consider. Now assume the statement holds for a certain nn.

Kn+4​\by​(​\zarabicsection-\zarabicequation​)\displaystyle K_{n+4}\by{\eqref{eq:KnKn2}} 4⋅Kn+2−6+2⋅\p−1n\displaystyle 4\cdot K_{n+2}-6+2\cdot\p{-1}^{n}
\by​(​\zarabicsection-\zarabicequation​)\displaystyle\by{\eqref{eq:Kn2}} 8⋅\p​Jn+1−6+2⋅\p−1n\displaystyle 8\cdot\p{J_{n}+1}-6+2\cdot\p{-1}^{n}
\by\displaystyle\by{\phantom{\eqref{eq:Kn2}}} 2⋅\p​2⋅Jn+\p−1n+4⋅Jn+2\displaystyle 2\cdot\p{2\cdot J_{n}+\p{-1}^{n}}+4\cdot J_{n}+2
\by​(​\zarabicsection-\zarabicequation​)\displaystyle\by{\eqref{eq:Jn1}} 2⋅Jn+1+4⋅Jn+2\displaystyle 2\cdot J_{n+1}+4\cdot J_{n}+2
\by​(​\zarabicsection-\zarabicequation​)\displaystyle\by{\eqref{eq:Jn2}} 2⋅\p​Jn+2+1\displaystyle 2\cdot\p{J_{n+2}+1}

∎

nn 0 1 2 3 4 5 6 7 8 9 10 11
KnK_{n} 1 2 2 4 4 8 12 24 44 88 172 344
Table \zarabictable: The number KnK_{n} of non-colourable strings in 𝒜2n\mathcal{A}_{2}^{n}

 

Corollary \zarabicsection.\zarabicthrm.

Let n≥2n\geq 2. Then

n​ is even⟹\displaystyle n\text{ is even{}}\implies Kn=2n+86\displaystyle K_{n}=\frac{2^{n}+\makebox[0.0pt][r]{$8$}}{6} (\zarabicsection-\zarabicequation)
n​ is odd⟹\displaystyle n\makebox[0.0pt][l]{$\text{ is odd{}}$}\implies Kn=2n+166.\displaystyle K_{n}=\frac{2^{n}+16}{6}. (\zarabicsection-\zarabicequation)
Proof.
Kn​\by​(​\zarabicsection-\zarabicequation​)​2⋅\p​Jn−2+1​\by​(​\zarabicsection-\zarabicequation​)​2⋅\p​2n−2−\p−1n3+1=2n+12−4⋅\p−1n6\displaystyle K_{n}\by{\eqref{eq:Kn2}}2\cdot\p{J_{n-2}+1}\by{\eqref{eq:Jn}}2\cdot\p{\frac{2^{n-2}-\p{-1}^{n}}{3}+1}=\frac{2^{n}+12-4\cdot\p{-1}^{n}}{6}

∎

Corollary \zarabicsection.\zarabicthrm.

Let nn be even. Then

Kn+1=2⋅Kn.\displaystyle K_{n+1}=2\cdot K_{n}. (\zarabicsection-\zarabicequation)
Proof.
Kn+1​\by​(​\zarabicsection-\zarabicequation​)​2n+1+166=2⋅2n+86​\by​(​\zarabicsection-\zarabicequation​)​2⋅Kn\displaystyle K_{n+1}\by{\eqref{eq:Knodd}}\frac{2^{n+1}+16}{6}=2\cdot\frac{2^{n}+8}{6}\by{\eqref{eq:Kneven}}2\cdot K_{n}

∎

Corollary \zarabicsection.\zarabicthrm.
limn→∞Kn2n=16\displaystyle\lim_{n\to\infty}\frac{K_{n}}{2^{n}}=\frac{1}{6}
Proof.

This follows immediately from corollary  \zarabicsection.\zarabicthrm. ∎

Remark.

Since there are 2n2^{n} strings of length nn, corollary  \zarabicsection.\zarabicthrm tells that in the limit 1 out of 6 strings is not colourable.

Corollary \zarabicsection.\zarabicthrm.

Let n≥2n\geq 2. Then

Kn+4=5⋅Kn+2−4⋅Kn.\displaystyle K_{n+4}=5\cdot K_{n+2}-4\cdot K_{n}.
Proof.

Let c∈\Nc\in\N. The statement follows from corollary  \zarabicsection.\zarabicthrm and the observation that

5⋅2n+2+c6−4⋅2n+c6=5⋅2n+2−2n+2+c6=2n+4+c6.\displaystyle 5\cdot\frac{2^{n+2}+c}{6}-4\cdot\frac{2^{n}+c}{6}=\frac{5\cdot 2^{n+2}-2^{n+2}+c}{6}=\frac{2^{n+4}+c}{6}.

∎

\zarabicsection Colourability sources and sinks

Definition.

Let w∈𝒜2∗w\in\mathcal{A}_{2}^{*}. If w​\bm​0,w​\bm​1w\bm 0,w\bm 1 are not colourable, ww is called a ††margin: – colourability sink colourability sink; if \bm​0​w,\bm​1​w\bm 0w,\bm 1w are not colourable, ww is called a ††margin: – colourability source colourability source. \upepsilon\upepsilon is called the ††margin: – trivial colourability sink and source trivial colourability sink and source.

Observation \zarabicsection.\zarabicthrm.

The reverse of a colourability source is a colourability sink and vice versa.

Corollary \zarabicsection.\zarabicthrm.

Let n∈\Nn\in\N. There are equally many colourability sinks as sources in 𝒜2n\mathcal{A}_{2}^{n}.

Proof.

If w∈𝒜2nw\in\mathcal{A}_{2}^{n} is a colourability sink, R​\p​wR\p w is a colourability source and vice versa. Since RR is bijective, the statement follows. ∎

Lemma \zarabicsection.\zarabicthrm.

If w∈𝒜2∗w\in\mathcal{A}_{2}^{*} is a colourability sink \bm​0​w,\bm​1​w\bm 0w,\bm 1w are colourable. If ww is a colourability source w​\bm​0,w​\bm​1w\bm 0,w\bm 1 are colourable.

Proof.

Assume the contrary, say ξ​\p​w​\bm​0=ξ​\p​\bm​0​w=0\xi\p{w\bm 0}=\xi\p{\bm 0w}=0. Then by lemma \zarabicsection.\zarabicthrm \bm​0​w​\bm​0∈\crl​\bm​0∗\bm 0w\bm 0\in\crl\bm 0^{*}, so w∈\crl​\bm​0∗w\in\crl\bm 0^{*}. Hence ξ​\p​\bm​1​w,ξ​\p​w​\bm​1​\by​[≠]​(​\zarabicsection-\zarabicequation​),(​\zarabicsection-\zarabicequation​)​0,\xi\p{\bm 1w},\xi\p{w\bm 1}\by[\neq]{\eqref{eq:xi0i1j},\eqref{eq:xi1j0i}}0, a contradiction. Similarly if ξ​\p​w​\bm​1=ξ​\p​\bm​1​w=0\xi\p{w\bm 1}=\xi\p{\bm 1w}=0 one gets that ξ​\p​\bm​0​w,ξ​\p​w​\bm​0≠0\xi\p{\bm 0w},\xi\p{w\bm 0}\neq 0. ∎

Corollary \zarabicsection.\zarabicthrm.

The only string that is both a colourability sink and a colourability source is \upepsilon\upepsilon.

Proof.

Any non-trivial colourability sink is by lemma \zarabicsection.\zarabicthrm not a colourability source. ∎

Remark.

Corollary  \zarabicsection.\zarabicthrm means that removing the non-colourable edges of a de Bruijn graph does not leave isolated vertices.

Lemma \zarabicsection.\zarabicthrm.

Any non-trivial colourability sink is colourable.

Proof.

Let w∈𝒜2∗w\in\mathcal{A}_{2}^{*} not be colourable.

ξ​\p​w=ξ​\p​w​\bm​0=0​\by​[⟹]​(​\zarabicsection-\zarabicequation​)\displaystyle\xi\p w=\xi\p{w\bm 0}=0\makebox[0.0pt][c]{$\by[\implies]{\eqref{eq:xi0}}$} ξ​\p​w=ξ​\p​r​\p​w​\bm​0=ξ​\p​w​\bm​0=0\displaystyle\xi\p w=\xi\p{r\p w\bm 0}=\xi\p{w\bm 0}=0
\by​[⟹]​(​\zarabicsection-\zarabicequation​)\displaystyle\by[\implies]{\eqref{eq:xilr0xi0}} w​\bm​0∈\crl​\bm​0∗∪\crl​\bm​1∗\displaystyle w\bm 0\in\crl\bm 0^{*}\cup\crl\bm 1^{*}
\by​[⟹]\by[\implies]{} w∈\crl​\bm​0∗\displaystyle w\in\crl\bm 0^{*}

but similarly

ξ​\p​w=ξ​\p​w​\bm​1=0⟹w∈\crl​\bm​1∗,\displaystyle\xi\p w=\xi\p{w\bm 1}=0\implies w\in\crl\bm 1^{*},

so w=\upepsilonw=\upepsilon. ∎

Corollary \zarabicsection.\zarabicthrm.

Any non-trivial colourability source is colourable.

Proof.

Since the reverse of a colourability source is a colourability sink, the statement follows directly from lemmata \zarabicsection.\zarabicthrm and \zarabicsection.\zarabicthrm. ∎

Lemma \zarabicsection.\zarabicthrm.

If w∈𝒜2∗w\in\mathcal{A}_{2}* is a colourability sink,

ξ​\p​\bm​0​w\displaystyle\xi\p{\bm 0w} =ξ​\p​\bm​1​w=ξ​\p​w\displaystyle=\xi\p{\bm 1w}=\xi\p w (\zarabicsection-\zarabicequation)
ϕ​\p​\bm​0​w\displaystyle\phi\p{\bm 0w} =ϕ​\p​\bm​1​w=ϕ​\p​w\displaystyle=\phi\p{\bm 1w}=\phi\p w (\zarabicsection-\zarabicequation)
ψ​\p​\bm​0​w\displaystyle\psi\p{\bm 0w} =ψ​\p​\bm​1​w=ξ​\p​w⋅ψ​\p​w.\displaystyle=\psi\p{\bm 1w}=\xi\p w\cdot\psi\p w. (\zarabicsection-\zarabicequation)

If ww is a colourability source,

ξ​\p​w​\bm​0\displaystyle\xi\p{w\bm 0} =ξ​\p​w​\bm​1=ξ​\p​w\displaystyle=\xi\p{w\bm 1}=\xi\p w (\zarabicsection-\zarabicequation)
ϕ​\p​w​\bm​0\displaystyle\phi\p{w\bm 0} =ϕ​\p​w​\bm​1=−ϕ​\p​w\displaystyle=\phi\p{w\bm 1}=-\phi\p w (\zarabicsection-\zarabicequation)
ψ​\p​w​\bm​0\displaystyle\psi\p{w\bm 0} =ψ​\p​w​\bm​1=−ξ​\p​w⋅ψ​\p​w.\displaystyle=\psi\p{w\bm 1}=-\xi\p w\cdot\psi\p w. (\zarabicsection-\zarabicequation)
Proof.

Consider lemma \zarabicsection.\zarabicthrm, lemma \zarabicsection.\zarabicthrm and corollary \zarabicsection.\zarabicthrm. For (\zarabicsection-\zarabicequation) and (\zarabicsection-\zarabicequation) combine them with lemma \zarabicsection.\zarabicthrm, for (\zarabicsection-\zarabicequation) and (\zarabicsection-\zarabicequation) with lemma \zarabicsection.\zarabicthrm. The following establishes (\zarabicsection-\zarabicequation):

ψ​\p​\bm​0​w=\p​ξ​\p​\bm​0​w#​w+1⋅ϕ​\p​\bm​0​w​\by​(​\zarabicsection-\zarabicequation​)ψ​\p​\bm​1​w=\p​ξ​\p​\bm​1​w#​w+1⋅ϕ​\p​\bm​1​w​\by​(​\zarabicsection-\zarabicequation​)​\p​ξ​\p​w#​w+1⋅ϕ​\p​w=ξ​\p​w⋅ψ​\p​w\displaystyle\begin{split}\psi\p{\bm 0w}&=\p{\xi\p{\bm 0w}}^{\#w+1}\cdot\phi\p{\bm 0w}\by{\eqref{eq:xi0sinkxi1sink}}\\ \psi\p{\bm 1w}&=\p{\xi\p{\bm 1w}}^{\#w+1}\cdot\phi\p{\bm 1w}\by{\eqref{eq:phi0sinkphi1sink}}\end{split}\p{\xi\p w}^{\#w+1}\cdot\phi\p w=\xi\p w\cdot\psi\p w

and the following (\zarabicsection-\zarabicequation):

ψ​\p​w​\bm​0=\p​ξ​\p​w​\bm​0#​w+1⋅ϕ​\p​w​\bm​0​\by​(​\zarabicsection-\zarabicequation​)ψ​\p​w​\bm​1=\p​ξ​\p​w​\bm​1#​w+1⋅ϕ​\p​w​\bm​1​\by​(​\zarabicsection-\zarabicequation​)​\p​ξ​\p​w#​w+1⋅\p−ϕ​\p​w=−ξ​\p​w⋅ψ​\p​w.\displaystyle\begin{split}\psi\p{w\bm 0}&=\p{\xi\p{w\bm 0}}^{\#w+1}\cdot\phi\p{w\bm 0}\by{\eqref{eq:xisource0xisource1}}\\ \psi\p{w\bm 1}&=\p{\xi\p{w\bm 1}}^{\#w+1}\cdot\phi\p{w\bm 1}\by{\eqref{eq:phisource0phisource1}}\end{split}\p{\xi\p w}^{\#w+1}\cdot\p{-\phi\p w}=-\xi\p w\cdot\psi\p w.

∎

Theorem \zarabicsection.\zarabicthrm.

Let w∈𝒜2∗w\in\mathcal{A}_{2}^{*}. Then

w​\bm​0,w​\bm​1​ are colourable\displaystyle w\bm 0,w\bm 1\text{ are colourable} ⟹ψ​\p​w​\bm​0=ψ​\p​w​\bm​1\displaystyle\implies\psi\p{w\bm 0}=\psi\p{w\bm 1}
\bm​0​w,\bm​1​w​ are colourable\displaystyle\bm 0w,\bm 1w\text{ are colourable} ⟹ψ​\p​\bm​0​w=ψ​\p​\bm​1​w\displaystyle\implies\psi\p{\bm 0w}=\psi\p{\bm 1w}
Proof.

If ww is a colourability sink or source, the statement is proven in lemma \zarabicsection.\zarabicthrm. Otherwise it follows from corollary \zarabicsection.\zarabicthrm. ∎

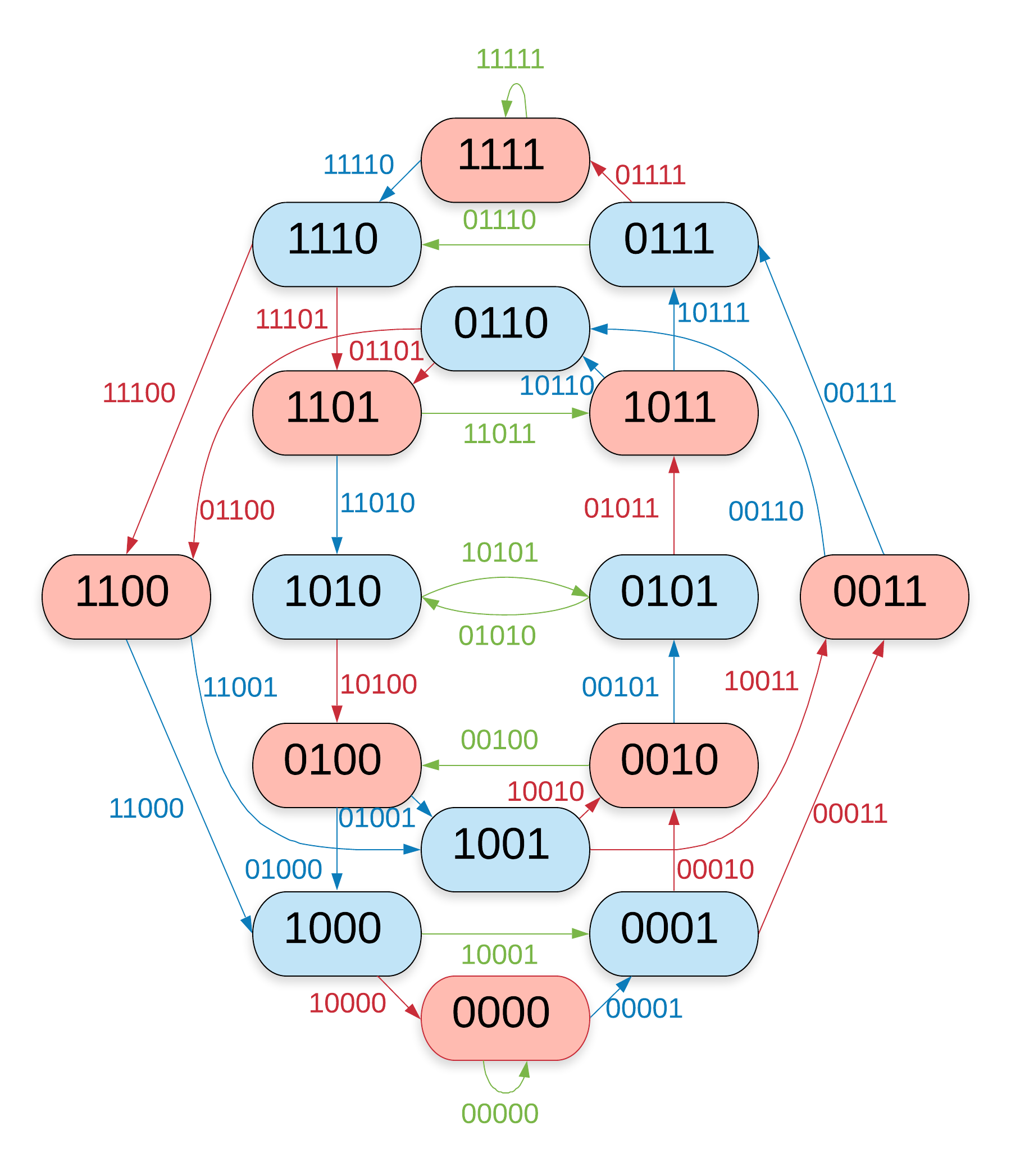
Refer to caption
Figure \zarabicfigure: The 22-dimensional de Bruijn graph. As in figure \zarabicfigure the edges are coloured according to the value ψ\psi assigns to them. The colour of the vertices coincides with the colour of the incoming edges and differs from the colour of the outgoing ones.

 

Refer to caption
Figure \zarabicfigure: The 44-dimensional de Bruijn graph. As in figure \zarabicfigure the edges are coloured according to the value ψ\psi assigns to them. The colour of the vertices coincides with the colour of the incoming edges and differs from the colour of the outgoing ones.

 

Remark.

Theorem \zarabicsection.\zarabicthrm makes it possible to define a function that assigns to the vertices of a de Bruijn graph a colour that corresponds to the colour of the incoming edges while differing from the colour of the outgoing ones. Lemma \zarabicsection.\zarabicthrm and corollary \zarabicsection.\zarabicthrm show that for odd-dimensional de Bruijn graphs that function is just ϕ\phi. Figures \zarabicfigure and \zarabicfigure give examples for even-dimensional de Bruijn graphs.

Observation \zarabicsection.\zarabicthrm.

In 𝒜2≤4\mathcal{A}_{2}^{\leq 4} there are no non-trivial colourability sinks or sources.

Theorem \zarabicsection.\zarabicthrm.

For n∈\Nn\in\N let SnS_{n} be the number of colourability sinks in 𝒜2n\mathcal{A}_{2}^{n}. If n≥3n\geq 3,

Sn=Kn−4.S_{n}=K_{n}-4.
Proof.

Let n≥3n\geq 3 and w∈𝒜2nw\in\mathcal{A}_{2}^{n} be a colourability sink. Then by lemma \zarabicsection.\zarabicthrm ξ​\p​r​\p​w=0\xi\p{r\p w}=0. First, let nn be odd. By lemma \zarabicsection.\zarabicthrm

ξ\pw\bm0=ξ\pw\bm1=0⇔ξ\pr\pw=0∧w∉\crl\bm0n,\bm0\bm1n−1,\bm1\bm0n−1,\bm1n,\displaystyle\xi\p{w\bm 0}=\xi\p{w\bm 1}=0\iff\xi\p{r\p w}=0\land w\notin\crl{\bm 0^{n},\bm 0\bm 1^{n-1},\bm 1\bm 0^{n-1},\bm 1^{n}},

so

Sn=#​\crl​w∈𝒜2n;ξ​\p​r​\p​w=0−4=2⋅Kn−1−4​\by​(​\zarabicsection-\zarabicequation​)​Kn−4.\displaystyle S_{n}=\#\crl{w\in\mathcal{A}_{2}^{n};\xi\p{r\p w}=0}-4=2\cdot K_{n-1}-4\by{\eqref{eq:Kn1Kneven}}K_{n}-4.

Now let nn be even. Then by lemma \zarabicsection.\zarabicthrm

ξ​\p​w​\bm​0=ξ​\p​w​\bm​1=0\displaystyle\xi\p{w\bm 0}=\xi\p{w\bm 1}=0
⇔\displaystyle\iff ξ​\p​r​\p​w=0∧w∉\crl​\bm​0n,\bm​0​Tn−1,Tn,\bm​0​\bm​1n−1,\bm​1​\bm​0n−1,C​Tn,\bm​1​C​Tn−1,\bm​1n,\displaystyle\xi\p{r\p w}=0\land w\notin\crl{\bm 0^{n},\bm 0T^{n-1},T^{n},\bm 0\bm 1^{n-1},\bm 1\bm 0^{n-1},CT^{n},\bm 1CT^{n-1},\bm 1^{n}},

so

Sn​\by\displaystyle S_{n}\by{\phantom{\eqref{eq:Kneven}}} #​\crl​w∈𝒜2n;ξ​\p​r​\p​w=0−8\displaystyle\#\crl{w\in\mathcal{A}_{2}^{n};\xi\p{r\p w}=0}-8
\by\displaystyle\by{\phantom{\eqref{eq:Kneven}}} 2⋅Kn−1−8\displaystyle 2\cdot K_{n-1}-8
\by​(​\zarabicsection-\zarabicequation​)\displaystyle\by{\eqref{eq:Knodd}} 2⋅2n−1+166−8\displaystyle 2\cdot\frac{2^{n-1}+16}{6}-8
\by\displaystyle\by{\phantom{\eqref{eq:Kneven}}} 2n+86−4\displaystyle\frac{2^{n}+8}{6}-4
\by​(​\zarabicsection-\zarabicequation​)\displaystyle\by{\eqref{eq:Kneven}} Kn−4.\displaystyle K_{n}-4.

∎

nn 0 1 2 3 4 5 6 7 8 9 10 11
SnS_{n} 1 0 0 0 0 4 8 20 40 84 168 340
Table \zarabictable: The number SnS_{n} of colourability sinks in 𝒜2n\mathcal{A}_{2}^{n}. There are equally many colourability sources as sinks.

 

Remark.

Theorem \zarabicsection.\zarabicthrm is a little bit more surprising than it looks at first glance: Due to the definition of a colourability sink focusing on w​\bm​0w\bm 0 and w​\bm​1w\bm 1, SnS_{n} rather says something about 𝒜2n+1\mathcal{A}_{2}^{n+1} than about 𝒜2n\mathcal{A}_{2}^{n}. KnK_{n} in contrast should be seen as an information about 𝒜2n\mathcal{A}_{2}^{n}.

References