An Alternative Paradigm for Developing and Pricing Storage on Smart Contract Platforms

Bitcoin ([1]) revolutionized the world of digital payments by allowing untrusted entities to transact securely without relying on trusted, third parties. Its operation is based on a distributed network of peers with open membership that maintains a highly replicated, auditable, append-only log of transactions, which is commonly referred to as a blockchain. A second generation of blockchains allows the development of smart contracts ([2]), i.e., digital agents that encode, execute and enforce arbitrary agreements. Smart contract platforms provide the means of developing diverse and important distributed applications (dApps) in a simple manner that, prior to their introduction, was challenging to implement.

Ethereum ([3]) is probably the most notable smart contract platform. Its live chain features dApps that implement naming services ([4]), multisignature wallets ([5]), a large variety of fungible tokens ([6]) and even crypto-collectibles ([7]), all in just a few lines of code. The simplicity of developing dApps on top of these platforms stems from the inherent utility of employing the state of smart contracts to store, query and verify the validity of application data. For instance, all implementations of the most widely deployed standard for fungible tokens, i.e., the ERC20 token standard ([8]), store each account’s token balance on the contract’s state.

Today, Ethereum’s cost model does not adequately take into account the amount of storage consumed by smart contracts. This is problematic for several reasons. First, in Ethereum, storing data on the state of smart contracts requires paying one, non-recurring fee at the time the data is stored. Thus, regardless of the amount of state that they consume, contracts have zero maintenance costs and can be part of Ethereum’s state forever. Second, storage-related operations are underpriced, as stated by Ethereum’s creator, Vitalik Buterin, in one of his recent talks ([9]). These two factors facilitate contracts that gain utility from storing small amounts of data per user and have low computational complexity, such as ERC20 tokens. As a result, such contracts have very low transaction fees for their operations. Third and most importantly, Ethereum’s state must be maintained by all full nodes, yet there is no incentive mechanism in place for freeing storage. If left unchecked, this can have serious consequences. It will diminish the mining population as proportionally fewer and fewer miners will be able to contribute to the network. This will lead to centralization and may prohibit new nodes from joining and syncing to the network. This will have a direct impact on Ethereum’s security and, utlimately, its longevity.

In this work, we introduce an alternative paradigm for developing dApps on top of smart contract platforms by decoupling the issue of storage from verifying the validity of data. The former is handled by an external, potentially unreliable, storage network that allows efficient access to the application’s data. To verify the validity of data obtained from the storage network, we maintain cryptographic accumulators in the smart contract’s state. These are data structures that provide a constant-sized representation of a set of elements and allow for verifiable (non) membership proofs. To evaluate our approach, we present a case study of an accumulator-based implementation of the ERC20 token standard. We choose this standard because it is the most widely deployed token standard for fungible tokens, numbering over 130,000 compliant contracts on Ethereum’s live chain ([6]). Via minor modifications, our construction can be modified to fit other, upcoming standards, such as the ERC721 standard ([10]) for non-fungible tokens. However, we stress that our approach can be adapted to any application that requires a verifiable representation of its application data, e.g., naming services, voting systems or any kind of key-value store.

By requiring only minimal (constant-sized) state to be stored in the contract, our accumulator-based approach promotes diversity, scalability, and security of the Ethereum network. Yet, we show that under Ethereum’s current cost model, this accumulator-based approach is penalized for the security properties it provides; it is much more (almost prohibitively) costly than the approach of storing each account’s token balance in the contract state. This illustrates one of Ethereum’s main incentive misalignments. To address this, we revisit Ethereum’s storage cost model and propose modifications that: 1) price storage-related operations based on the effort that miners have to expend to execute them, 2) ensure that contracts pay recurring fees proportionate to the amount of storage they consume and the system’s overall capacity and, 3) free space consumed by unused/stale contracts. We show that under such a pricing scheme, our accumulator-based ERC20 token construction reduces the incurred transaction fees by up to an order of magnitude. With these modifications, we hope the Ethereum developer community will be encouraged to exercise economy in the state consumed by the smart contracts they develop.

Ethereum is a blockchain-based, 32-byte word, global computer that allows the development of smart contracts, i.e., stateful agents that “live” in the blockchain and can execute arbitrary state transition functions. Smart contract code is written in a high-level, Turing-complete programming language (e.g., Solidity [11]), which is then compiled-down to Ethereum Virtual Machine (EVM) initialization code. Contracts are deployed by wrapping their initialization code in a transaction, signing it and broadcasting it to the network. Users can interact with smart contracts by broadcasting appropriately formatted transactions. Smart contracts are “passive” entities that, as a result of a user’s transaction, can issue message calls, i.e., call functions of other contracts. Ethereum’s cryptocurrency is called ether and serves as a means to incentivize participants (miners) to engage in the protocol. Transactions fees are measured in a unit called gas and are a function of the byte size and the complexity of the code invoked by transactions (if any). Each transaction byte and EVM operation costs some predefined amount of gas ([3]). Transactions specify a gas price, which converts ether to gas and influences the incentive of miners to include it in their next block. A transaction that consumes $g_{cost}$ gas and specifies a gas price of $g_{price}$ will cost $E=g_{cost}\times g_{price}$ units of ether. Lastly, transactions and message calls, specify an upper bound on the amount of gas that they can consume. This protects miners from, e.g., getting stuck in an infinite loop, an issue that stems from Ethereum’s Turing-completeness.

Cryptographic accumulators provide a constant representation of a set of elements and allow for verifiable membership queries. Universal accumulators also allow for verifiable non membership queries. Proving statements (e.g., element membership) is facilitated via values that are referred to as witnesses. Informally, the security property of accumulators states that an adversary is unable to generate a valid witness value for a false statement, except with negligible probability. For instance, an adversary is not able to generate a valid membership witness for an element $x$ that is not part of the accumulated set of elements $X$. It is common to refer to the party that maintains and manages the accumulator as the accumulator manager. In our accumulator-based ERC20 token, this role is played by the smart contract.

In the following, we provide a high level description of the hash tree, universal accumulator of Camacho et al. [12], whose security is based on collision-resistant hash functions. This accumulator employs a public data structure $m=(T,X)$ (referred to as memory), where $X=\{x_{1},...,x_{n}\}$ is the set of accumulated elements and $T$ is a binary, balanced hash tree. The accumulator’s value (denoted as $Acc$) is the hash of $T$’s root node. Camacho et al. [12] model their accumulator as a tuple of the following algorithms:

• •

  $\mathsf{Setup}\mathsf{(k)}:$ On input the security parameter $k\in\mathbb{N}$, it outputs the accumulator’s initial value $Acc_{0}\in\{0,1\}^{k}$, which corresponds to the set $X=\emptyset$, and an initialized memory $m_{0}$.

• •

  $\mathsf{Witness}\mathsf{(Acc,m,x)}:$ This algorithm outputs a membership or a non membership witness $W$, if $x\in X$ or if $x\notin X$, respectively.

• •

  $\mathsf{Belongs}\mathsf{(Acc,x,W)}:$ This algorithm outputs $1$, if $W$ is a valid witness for $x\in X$, $0$, if $W$ is a valid witness for $x\notin X$, or $\perp$ otherwise.

• •

  $\mathsf{Update_{op}}\mathsf{(Acc_{\mathsf{before}},m_{\mathsf{before}},x)}:$ This algorithm updates the accumulator’s value by either adding ($\mathsf{op=add}$) or removing ($\mathsf{op=del}$) the element $x$ to/from the accumulated set $X$. It outputs the updated values of the accumulator ($\mathsf{Acc_{after}}$) and its memory ($\mathsf{m_{after}}$), as well as, an update witness $\mathsf{W_{op}}$.

• •

  $\mathsf{CheckUpdate}\mathsf{(Acc_{\mathsf{before}},Acc_{\mathsf{after}},x,W_{\mathsf{op}})}:$ This algorithm outputs $1$, if $W_{op}$ is a valid witness for an update operation ($\mathsf{op\in\{add,del\}}$) pertaining element $x$, which updated the accumulator’s value from $\mathsf{Acc_{before}}$ to $\mathsf{Acc_{after}}$, otherwise, it outputs $0$.

This accumulator is strong, i.e., it does not require a trusted setup nor a trusted accumulator manager. It allows for updates (additions and deletions) that can be performed without having access to secret information and are publicly verifiable. The latter is accomplished via the $\mathsf{CheckUpdate}$ algorithm which, on input a witness returned by $\mathsf{Update_{op}}$ and the accumulator’s values before and after the update, outputs 1, if the update was performed honestly, and 0, otherwise. In this accumulator, (non) membership and update witnesses are hash path(s) starting from some node(s) in $T$ (not necessarily leaf node(s)) that lead all the way up to the root node. Thus, their size is $\mathcal{O}(k\log_{2}(n))$, where $n=|X|$.

The ERC20 token standard ([8]) describes the functions and events that facilitate the exchange of arbitrary crypto-assets. Each token holder’s account is associated with an Ethereum $\mathbf{address}$ data type. The token balance of each account is commonly represented as a $\mathbf{uint}$ data type, i.e., an unsigned integer. The ERC20 token interface is comprised of the following functions:

1. 1.

   $\mathbf{totalSupply}\mathbf{()\!:}$ Outputs the total supply of tokens accross all accounts.

2. 2.

   $\mathbf{balanceOf}\mathbf{(address\;owner)\!:}$ Outputs the token balance of the input account.

3. 3.

   $\mathbf{approve}\mathbf{(address\;spender,uint\;tokens)\!:}$ The account that issues the call (transaction) to this function authorizes the “$\mathbf{spender}$” account to transfer the specified number of $\mathbf{tokens}$ from her account.

4. 4.

   $\mathbf{allowance}\mathbf{(address\;owner,address\;spender):}$ Outputs the number of tokens that the spender’s account is $\mathbf{approve}$’d to transfer from the owner’s account.

5. 5.

   $\mathbf{transfer}\mathbf{(address\;to,uint\;tokens)\!:}$ The account that issues the call (transaction) to this function transfers the specified number of tokens to the “$\mathbf{to}$” account.

6. 6.

   $\begin{aligned} &\mathbf{transferFrom}\mathbf{(address\;from,address\;to,uint}\\[-2.84526pt] &\mathbf{tokens):}\end{aligned}$
   
          Transfers the specified number of $\mathbf{tokens}$ from account ”$\mathbf{from}$“ to the $\mathbf{approve}$’d account ”$\mathbf{to}$“.

To facilitate the aforementioned functionality, ERC20 compliant smart contracts store two mappings in their state: 1) balances, which maps account addresses to token balances and, 2) allowed, which maps account addresses to another mapping where, the latter, maintains the balance that each $\mathbf{approve}$’d account is allowed to transfer from the token owner’s account.

We now illustrate how we employ the hash tree, universal accumulator of Camacho et al. [12] (Section III), to realize an accumulator-based ERC20 token. The core idea is to replace each aforementioned mapping with one accumulator. We replace the balances mapping with an accumulator, balancesAcc, that accumulates (owner,tokens) tuples and allows clients to infer each account’s token balance. For the allowed mapping, which is a “double” mapping, we need two accumulators. The first accumulator, allowedAddressesAcc, accumulates (owner,spender) tuples and allows clients to infer the accounts that token owners have $\mathbf{approve}$’d. The second accumulator, allowedBalancesAcc, accumulates (spender,tokens) tuples and allows clients to infer the token balance that $\mathbf{approve}$’d accounts are allowed to transfer from the owner’s account. Thus, we have a constant-sized and verifiable representation of account balances and allowances.

Our design’s security depends solely on that of the smart contract platform (Ethereum in our case) and the accumulator scheme. This allows us to employ a variety of primitives to realize the storage network, whose concrete specification we leave as future work. For instance, even centralized cloud storage services are a viable option. However, we believe that the best approach is a distributed file storage system, especially one that has “bridges” with the Ethereum network. Some notable examples are Swarm ([13]), Storj ([14]) and IPFS ([15]). The storage network’s state is assumed to be comprised of the memory data structure (see Section III) of each of the aforementioned accumulators. As we show below, the interaction with accumulator-based ERC20 smart contracts requires the construction of (non) membership and update witnesses by the clients which, subsequently, are subject to verification by the smart contract. Clients construct these witnesses by interacting with the storage network. We stress that clients do not need to download the entire memory of accumulators to construct these witnesses. The data that needs to be transmitted from storage nodes to clients are hash paths from the appropriate accumulators’ hash trees, i.e., they are of logarithmic complexity. Thus, from hereon in, we assume that clients can efficiently construct the witness values that are required to realize the ERC20 token interface.

Accumulator-based ERC20 token smart contracts cannot implement the $\mathbf{balanceOf}$ and $\mathbf{allowance}$ functions since they do not store account balances and allowances in their state. Instead, clients are able to infer the information obtained by these functions by interacting with the storage network. To infer the balance $y$ of account $x$, clients construct and verify a membership witness that the tuple $(x,y)$ is accumulated in balancesAcc. To infer the allowance $z$ of a spender’s account $x_{2}$ from an owner’s account $x_{1}$, clients construct and verify two membership witnesses. First, a membership witness that the tuple $(x_{1},x_{2})$ is accumulated in allowedAddressesAcc, which proves that the token owner $x_{1}$ has allowed the spender account $x_{2}$ to transfer some tokens from her account. Second, a membership witness that the tuple $(x_{2},z)$ is accumulated in allowedBalancesAcc, which proves the number of tokens the spender is allowed to transfer from the token owner’s account.

An account $x_{1}$ with balance $y_{1}$ that wishes to $\mathbf{transfer}$ $z$ tokens ($y_{1}\geq z$) to an account $x_{2}$ with balance $y_{2}$ produces the following proofs. First, a membership witness for the tuple $(x_{1},y_{1})$ in balancesAcc, which proves the owner’s account balance. Second, a membership witness for the tuple $(x_{2},y_{2})$, which proves the balance of the destination account. Third, an update witness for the deletion of the tuple $(x_{1},y_{1})$ from balancesAcc. Fourth, an update witness for the deletion of the tuple $(x_{2},y_{2})$ from balancesAcc. Fifth, an update witness for the addition of the tuple $(x_{1},y_{1}-z)$ to balancesAcc. Sixth, an update witness for the addition of the tuple $(x_{2},y_{2}+z)$ to balancesAcc. Notice that the sequence of the involved updates reflects the transfer of $z$ tokens from $x_{1}$ to $x_{2}$.

Due to space limitations, we are unable to describe how we realize the $\mathbf{approve}$ and $\mathbf{transferFrom}$ operations. To provide insight with regards to their complexity, we mention the proofs that are involved in each operation. The $\mathbf{approve}$ operation involves two update witnesses and either one non membership, or, one membership witness, depending on whether the token owner approves the spender’s account for the first time or not, respectively. The $\mathbf{transferFrom}$ operation involves four membership witnesses and six update witnesses. Thus, the $\mathbf{transferFrom}$ is the most expensive operation, followed by $\mathbf{transfer}$ and, lastly, by $\mathbf{approve}$.

In this section, we evaluate our accumulator-based ERC20 token construction. We ran our experiments on a private blockchain that is maintained by a single mining node. We use the latest, stable version of geth (v1.8.17, [16]), Ethereum’s official client, that was available at the time of this writing. We conducted our experiments via the truffle suite (v4.1.13, [17]) that employs solc-js (v0.4.24, [18]) to compile smart contracts with optimizations enabled.

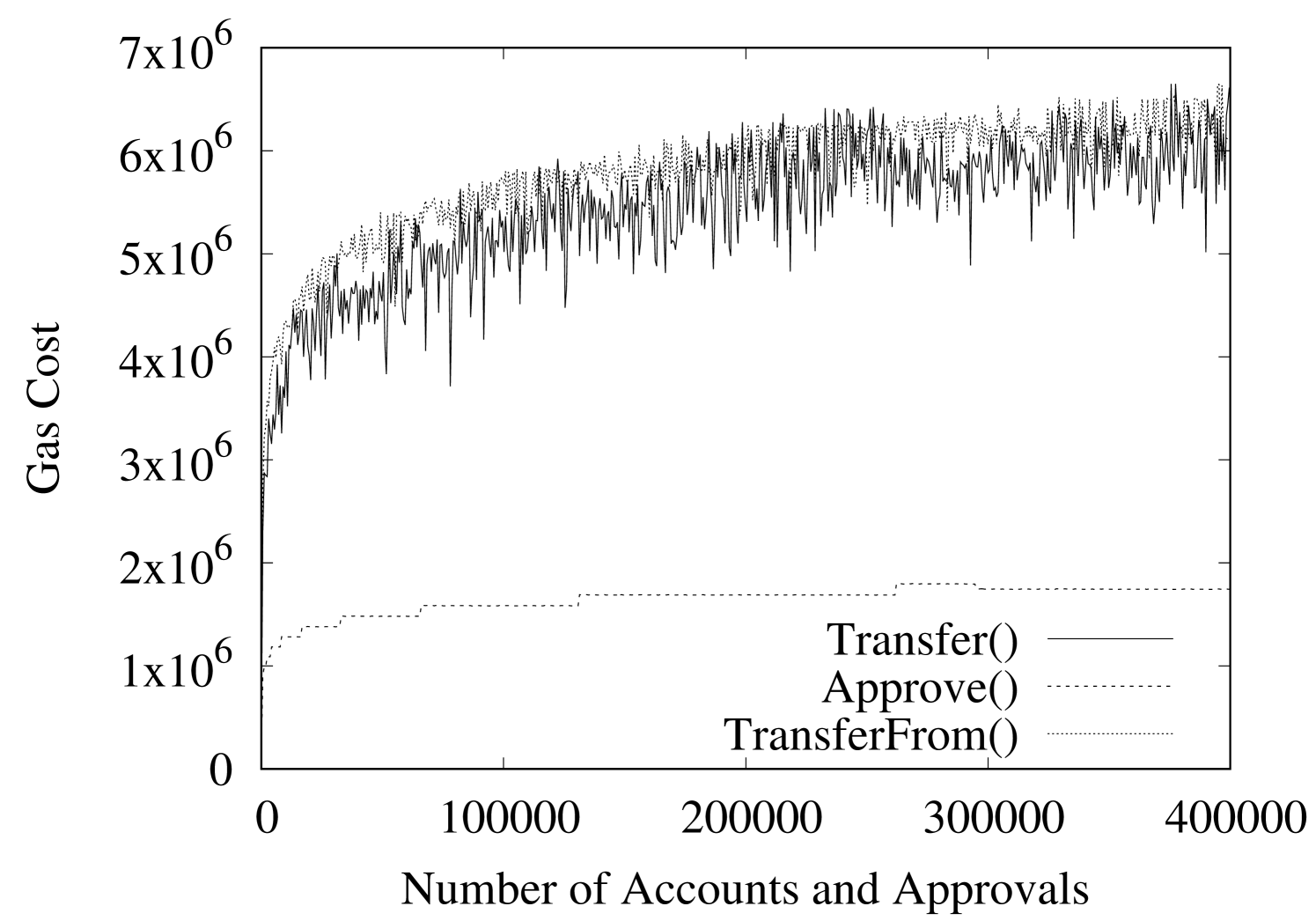
Figure 1 illustrates the gas cost of the $\mathbf{transfer}$, $\mathbf{approve}$ and $\mathbf{transferFrom}$ operations of our accumulator-based ERC20 token for up to a total of 400,000 accounts and 400,000 approvals. Results illustrate that transaction gas costs scale logarithmically, which is expected (same holds for the $\mathbf{approve}$ operation). Recall that all involved proofs are hash path(s) starting from some node(s) (not necessarily leaf node(s)) in the accumulator’s tree. Thus, their size and verification cost varies based on the position of those nodes in the tree. Our construction’s operations consume a large portion of the block’s limit which is, currently, about 8 million gas ([19]). In the following, we discuss a series of improvements that will diminish the cost of our construction’s operations.

The security property of the accumulator of Camacho et al. [12] is based on the presupposition that, prior to an invocation of $\mathsf{CheckUpdate}$ for the deletion or addition of some element $x$, $x\in X$ or $x\notin X$, respectively. Thus, prior to, e.g., verifying the addition of some element $x$ via the $\mathsf{CheckUpdate}$ algorithm, we have to make sure, via a non membership witness verification, that $x\notin X$. Part of an ongoing project is to provide a proof extension that will allow us to lift this assumption from the accumulator’s security property. Consequently, we will be able to eliminate one, two and four invocations of the accumulator’s $\mathsf{Belongs}$ algorithm from the $\mathbf{approve}$, $\mathbf{transfer}$ and $\mathbf{transferFrom}$ operations of the accumulator-based ERC20 token, respectively. Note that one invocation of $\mathsf{Belongs}$ costs, on average, 289,873.23 gas, when $|X|=400,000$ and will, thus, provide a substantial improvement.

Our implementation of the hash tree accumulator employs the SHA-256 hash function, which is exposed as a precompiled contract in Ethereum. Precompiled contracts reside on well-known, static addresses and constitute Ethereum’s “standard library”, similar to that of common programming languages. The advantage of precompiled contracts is that their computation incurs low gas costs because their code runs on the miner’s machine language. The computational cost of the SHA-256 hash function is 60 gas, plus 12 gas per input word (rounded up) and its implementation complies to the NIST standard. However, the KECCAK-256 hash function, whose computational cost is 30 gas, plus 6 gas per input word (rounded up), does not comply to the NIST standard and is, instead, implemented as an EVM opcode. Moreover, precompiled contracts, at each invocation, incur the extra gas cost of a message call, which is 700 gas. However, that is not the case for EVM opcodes. Thus, Ethereum promotes the use of a non-standard compliant hash function. Recently, a proposal has been submitted ([20]) that suggests the removal of the message call gas cost for precompiled contracts, which we believe is fair. Furthermore, we believe that the gas cost of these hash functions should be equalized. Assuming that both of the aforementioned suggestions are applied, the gas cost of the hashing operations will be reduced by $93.69\%$ and, as a result, will further diminish the gas cost of the accumulator-based ERC20 token operations.

To illustrate the overhead of our accumulator-based ERC20 token construction, we implemented a “bare-bones” ERC20 token (where account balances and allowances are stored in the contract’s state [21]) and repeated the same experiment. We measure an average cost of 33,193.12, 42,465.23 and 23,798.35 gas for the $\mathbf{transfer}$, $\mathbf{approve}$ and $\mathbf{transferFrom}$ operations, respectively. Thus, our accumulator-based construction is much more expensive, despite its constant and minimal space overhead on Ethereum’s state. The large discrepancy between the gas cost of the two constructions’ operations, as well as, the small and static gas cost of the bare-bones ERC20 token operations, are a by-product of Ethereum’s flat cost model. The fact that storage-related operations are underpriced ([9]) and that contracts do not pay a recurring fee proportional to the size of their state is one of Ethereum’s main incentive misalignments. This issue, if left unchecked, will have severe consequences to the future of, not only Ethereum, but any smart contract platform that employs a flat cost model. Next, we propose modifications to Ethereum’s cost model to deal with this issue.

Ethereum employs a flat cost model to price all EVM opcodes ([3]), including storage-related operations. There are two main issues with this approach. First, storing data on the state of smart contracts incurs a one time fee which is underpriced ([9]). To our knowledge, there is no other, real world system that provides such high levels of data replication and availability without a recurring fee that is proportional to the volume of the stored data. Furthermore, as there is no incentive for freeing storage, Ethereum is faced with a tragedy of the commons problem with regards to the monotonically increasing size of its state. Second, Ethereum’s flat cost model does not account for the complexity of executing storage-related operations, which is a function of the size of the state of smart contracts. We propose the following modifications to Ethereum’s pricing of storage to address these issues.

Recurring Storage Fees: The concept of introducing “storage rent”, i.e., a recurring fee that smart contracts have to pay based on the amount of storage they consume has been discussed over the years. Buterin’s original proposal ([22]) has spurred a lot of discussion and has led to the publication of several articles (e.g., [23, 24, 25]) which, in their vast majority, stress how important such a mechanism is for the longevity of public blockchains. An additional use of the rent mechanism is to clean up Ethereum’s state from accounts (contracts are accounts as well) that are not being used anymore.

Our proposal on the subject of storage rent is based on the following points. First, we believe that rent fees should not be rewarded to anyone as that could introduce new attack vectors. Second, since Ethereum is a global computer, it is rational to assume that it has a predefined storage capacity $S_{max}$ (e.g., Buterin has suggested 500 GB [26]). Naturally, this is a conceptual upper bound on the state’s size and will, essentially, reflect an estimate of what is considered reasonable for the average miner. Third, $S_{max}$ should be adjustable by the ones that maintain the network, i.e., the miners, to account for real world, storage trends. This could be achieved via a mechanism similar to the one that is already in use for adjusting block difficulty. We propose that up to a low utilization percentage of the system’s state, e.g., $U_{low}=25\%$, the rent per storage key of a contract’s state should be static to reflect the low burden imposed on miners. When the state’s utilization is between $U_{low}$ and, e.g., $U_{high}=80\%$, the rent per storage key of a contract’s state should increase logarithmically with the total number of keys in the system’s state. This reflects the fact that Ethereum’s state is organized on top of LevelDB whose complexity we elaborate more on the following paragraph. From thereon in, rent fees should be prohibitive, thus, they should scale linearly to the total number of keys in the system’s state. To derive a base rent fee per storage key, we considered real world examples of systems that are highly replicated, available and charge for storage. Cloud storage providers are a prime example. For instance, Amazon’s EFS ([27]) charges 0.30 USD per GB per month. At the time of this writing, one unit of Ether corresponds to 202.18 USD ([28]). Based on this analogy, we compute a base rent fee of $R_{base}=530,657,634.8$ Wei per storage key per year (1 Ether corresponds to $10^{18}$ Wei). Thus, we have an adaptable scheme for computing rent fees that follows the laws of supply and demand by considering the state’s overall utilization and the burden imposed on miners.

Scaling Storage Costs: A contract’s state is organized on an on-disk Merkle Patricia (MP) trie ([29]), which is referred to as the storage trie. This is a modified version of a typical radix tree with the added property of Merkle trees, i.e., the root hash uniquely identifies the (key,value) pairs in the tree. The nodes of the storage trie and the smart contract’s state (storage keys) are stored in a LevelDB ([30]) key-value store, whose underlying data structure is a multi-level Log Structured Merge (LSM) tree. As illustrated in a recent study ([31]), due to Ethereum’s authenticated storage (MP trie), one Ethereum read (e.g., reading the root node of a contract’s storage trie) can lead to 64 LevelDB $\mathsf{get()}$ (read) requests. Each $\mathsf{get()}$ may internally involve multiple disk reads due to the large amount of metadata that LevelDB maintains ([32]). Updates to a contract’s storage, e.g., adding/updating storage keys, result in updates to its storage trie that have to be committed on disk. In LevelDB, key-value updates are reinserted into a skip list with a monotonically increasing sequence number along with a “tombstone” flag that invalidates the pair’s prior version. To maintain key-value pairs in sorted order, LevelDB uses a compaction method. This process involves multiple merge sorts (one per LSM tree level) and incurs a write amplification factor, which is the ratio of the amount of data written to the amount of data requested for writing by users, of $\times 11$ ([32]).

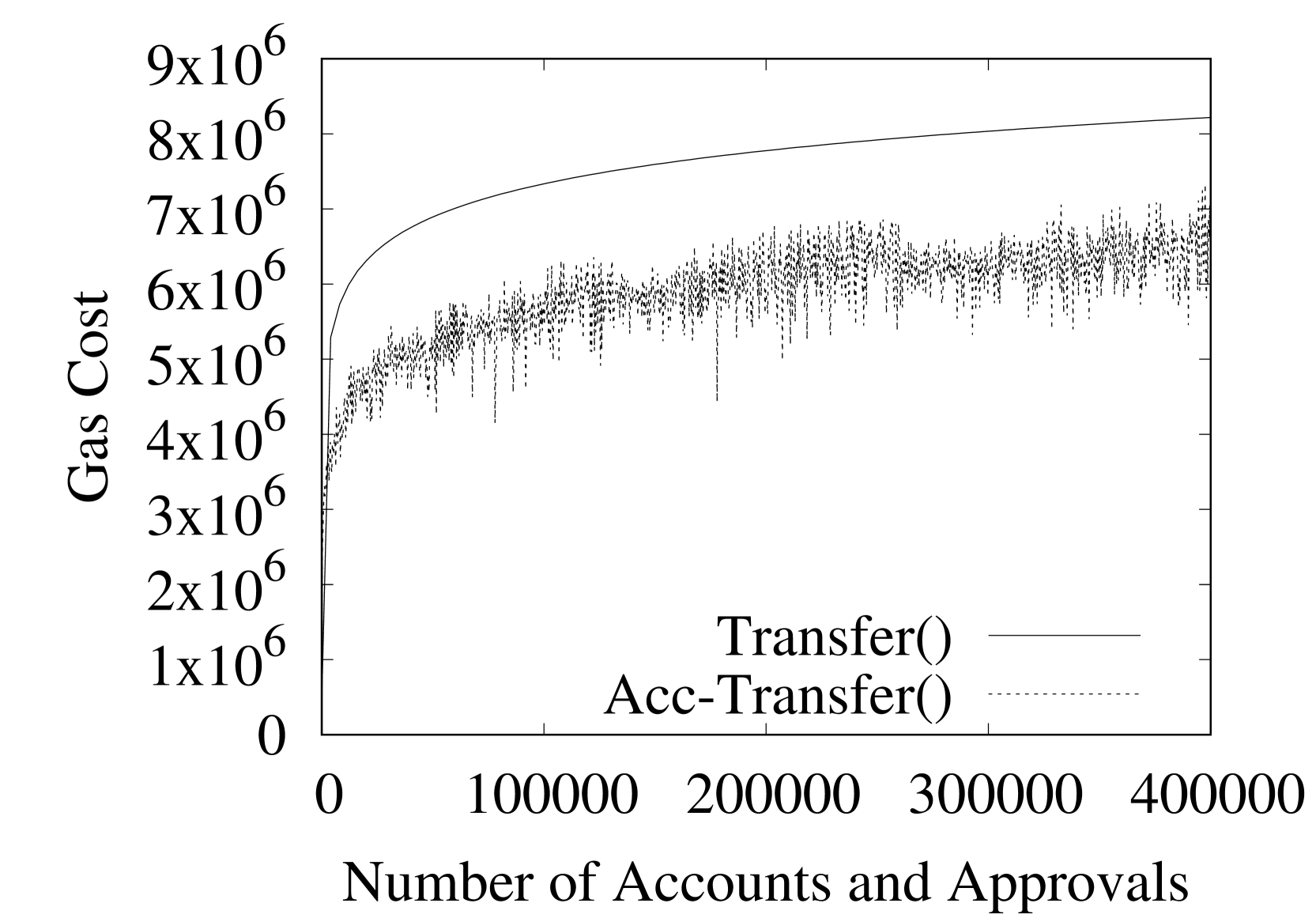
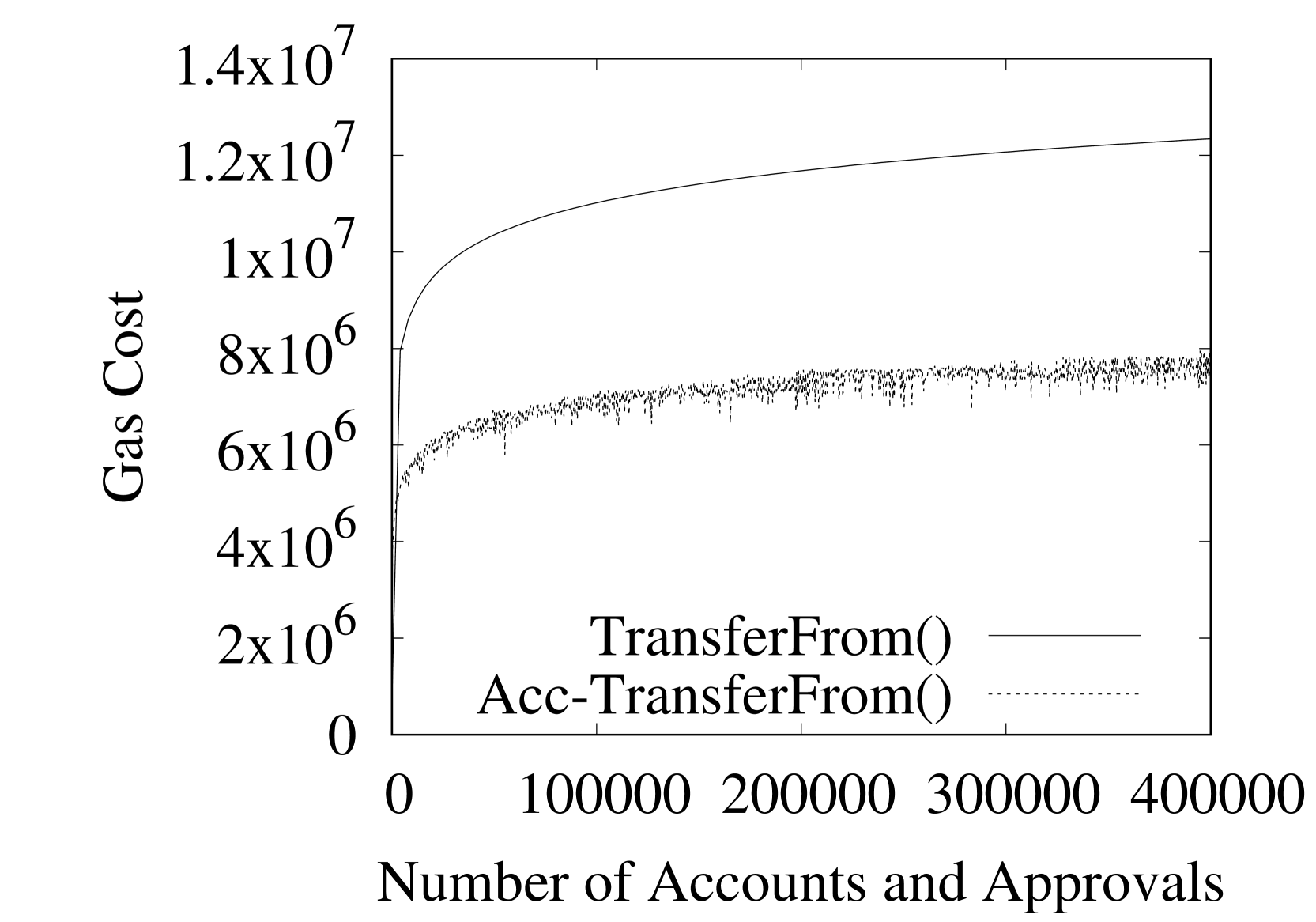
Ethereum’s flat cost model does not reflect the aforementioned complexity of storage-related operations. One might assume that an ideal scheme would scale the cost of these operations based on the number of incurred disk operations. However, this is not possible as Ethereum miners do not have a shared hardware configuration, e.g., their physical hard disks and their caches vary significantly. This would interfere with Ethereum’s consensus as the execution of the same transaction would lead to different gas costs across different miners. Instead, we propose a scheme where the cost of storage-related operations is computed on a per transaction basis and scales according to the number of operations to LevelDB’s LSM tree, which is the same across all miners. Fetching one key from a LSM tree involves two binary searches ([33]). Accessing the value of a smart contract’s storage key involves, at minimum, fetching one node of its storage trie and, subsequently, fetching the storage key itself. Thus, it requires a total of four binary searches, i.e., $4\log_{2}(n)$ accesses, where $n$ is the number of storage keys. Updating, or, adding a new storage key, involves the same number of accesses to infer the value of the tombstone flag. However, since updates are propagated to all levels of LevelDB’s LSM tree during its compaction process, they are subject to LevelDB’s write amplification factor, which we discussed above. Thus, updates incur a total of $11\times 4\log_{2}(n)=44\log_{2}(n)$ operations. Currently, reading, storing and updating storage keys costs 200, 20,000 and 5,000 gas, respectively. Thus, under our proposed scheme, the cost of, e.g., reading a storage key is $200\times 4\log_{2}(n)$.

Figure 2 illustrates the gas cost of the $\mathbf{transfer}$, $\mathbf{transferFrom}$ and $\mathbf{approve}$ operations of the bare-bones and our accumulator-based ERC20 token under our proposed cost model. Regarding the bare-bones ERC20 token, we only plot the storage-related cost of its operations, which are the dominant factor. The biggest discrepancy is in the $\mathbf{approve}$ operation (Figure 2(c)) where our accumulator-based construction provides an order of magnitude improvement. Overall, results illustrate that, under a pricing scheme that reflects the effort that miners have to expend to execute storage-related operations, the programming paradigm that we propose in this work provides reduced gas costs across all ERC20 token operations. Nevertheless, we believe that the most important property of our approach is that it aligns well with the future of smart contract platforms since it incurs constant storage overhead to miners.

We introduce an alternative programming paradigm for developing dApps that promotes diversity, scalability and aligns well with the future of smart contract platforms. Our approach can be adapted to any application that requires a verifiable representation of its application data. We propose a scheme for computing rent fees that follows the laws of supply and demand by considering the state’s overall utilization, as well as the burden imposed on miners. In addition, our scheme is adjustable to real world, storage trends. We introduce scaling of the cost of storage-related operations to account for the effort that miners have to expend to execute them. Lastly, we show that under such a pricing scheme that encourages economy in the state consumed by smart contracts, our ERC20 token adaptation reduces the incurred transaction fees by up to an order of magnitude.