An Easy-to-use Scalable Framework for Parallel Recursive Backtracking
Abstract
Supercomputers are equipped with an increasingly large number of cores to use computational power as a way of solving problems that are otherwise intractable. Unfortunately, getting serial algorithms to run in parallel to take advantage of these computational resources remains a challenge for several application domains. Many parallel algorithms can scale to only hundreds of cores. The limiting factors of such algorithms are usually communication overhead and poor load balancing. Solving NP-hard graph problems to optimality using exact algorithms is an example of an area in which there has so far been limited success in obtaining large scale parallelism. Many of these algorithms use recursive backtracking as their core solution paradigm. In this paper, we propose a lightweight, easy-to-use, scalable framework for transforming almost any recursive backtracking algorithm into a parallel one. Our framework incurs minimal communication overhead and guarantees a load-balancing strategy that is implicit, i.e., does not require any problem-specific knowledge. The key idea behind this framework is the use of an indexed search tree approach that is oblivious to the problem being solved. We test our framework with parallel implementations of algorithms for the well-known Vertex Cover and Dominating Set problems. On sufficiently hard instances, experimental results show linear speedups for thousands of cores, reducing running times from days to just a few minutes.
Index Terms:
parallel algorithms; recursive backtracking; load balancing; vertex cover; dominating set;I Introduction
Parallel computation is becoming increasingly important as performance levels out in terms of delivering parallelism within a single processor due to Moore’s law. This paradigm shift means that to attain speed-up, software that implements algorithms that can run in parallel on multiple cores is required. Today we have a growing list of supercomputers with tremendous processing power. Some of these systems include more than a million computing cores and can achieve up to 30 Petaflop/s. The constant increase in the number of cores per supercomputer motivates the development of parallel algorithms that can efficiently utilize such processing infrastructures. Unfortunately, migrating known serial algorithms to exploit parallelism while maintaining scalability is not a straightforward job. The overheads introduced by parallelism are very often hard to evaluate, and fair load balancing is possible only when accurate estimates of task “hardness” or “weight” can be calculated on-the-fly. Providing such estimates usually requires problem-specific knowledge, rendering the techniques developed for problem useless when trying to parallelize an algorithm for problem .
As it is not likely that polynomial-time algorithms can be found for NP-hard problems, the search for fast deterministic algorithms could benefit greatly from the processing capabilities of supercomputers. Researchers working in the area of exact algorithms have developed algorithms yielding lower and lower running times [1, 2, 3, 4, 5]. However the major focus has been on improving the worst-case behavior of algorithms (i.e. improving the best known asymptotic bound on the running time of algorithms). The practical aspects of the possibility of exploiting parallel infrastructures has received much less attention.
Most existing exact algorithms for NP-hard graph problems follow the well-known branch-and-reduce paradigm. A branch-and-reduce algorithm searches the complete solution space of a given problem for an optimal solution. Simple enumeration is normally prohibitively expensive due to the exponentially increasing number of potential solutions. To prune parts of the solution space, an algorithm uses reduction rules derived from bounds on the function to be optimized and the value of the current best solution. The reader is referred to Woeginger’s excellent survey paper on exact algorithms for further detail [6]. At the implementation level, branch-and-reduce algorithms translate to search-tree-based recursive backtracking algorithms. The search tree size usually grows exponentially with either the size of the input instance or, when the problem is fixed-parameter tractable, some integer parameter [7]. Nevertheless, search trees are good candidates for parallel decomposition. Given cores, a brute-force parallel solution would divide a search tree into subtrees and assign each subtree to a separate core for sequential processing. One might hope to thus reduce the overall running time by a factor of . However, this intuitive approach suffers from several drawbacks, including the obvious lack of load balancing.
Even though our focus is on NP-hard graph problems, we note that recursive backtracking is a widely-used technique for solving a very long list of practical problems. This justifies the need for a general framework to simplify the migration from serial to parallel. One example of a successful parallel framework for solving a different kind of problem is MapReduce [8]. The success of the MapReduce model can be attributed to its simplicity, transparency, and scalability, all of which are properties essential for any efficient parallel framework. In this paper, we propose a simple, lightweight, scalable framework for transforming almost any recursive backtracking algorithm into a parallel one with minimal communication overhead and a load balancing strategy that is implicit, i.e., does not require any problem-specific knowledge. The key idea behind the framework is the use of an indexed search-tree approach that is oblivious to the problem being solved. To test our framework, we use it to implement parallel exact algorithms for the well-known Vertex Cover and Dominating Set problems. Experimental results show that, on sufficiently hard instances, we obtain linear speedups for at least 32,768 cores.
II Preliminaries
Typically, a recursive backtracking algorithm exhaustively explores a search tree using depth-first search traversal and backtracking at the leaves of . Each node of (a search-node) can be denoted by for the depth of in and the position of in the left-to-right ordering of all search-nodes at depth . The root of is thus . We use to denote the subtree rooted at node . We say has branching factor if every search-node has at most children. An example of a generic serial recursive backtracking algorithm, Serial-RB, is given in Figure 1. The goal of this paper is to provide a framework to transform Serial-RB into an efficient parallel algorithm with as little effort as possible. For ease of presentation, we make the following assumptions:
-
-
Serial-RB is solving an NP-hard optimization problem (i.e. minimization or maximization) where each solution appears in a leaf of the search tree.
-
-
The global variable stores the best solution found so far.
-
-
The IsSolution() function returns true only if is a solution which is “better” than .
-
-
The search tree explored by Serial-RB is binary (i.e. every search-node has at most two children).
None of these assumptions are needed to apply our framework. In Section IV-C, we discuss how the same techniques can be easily adapted to any search tree with arbitrary branching factor. The only (minor) requirement we impose is that the number of children of a search-node can be calculated on-the-fly and that generating those children (using GetNextChild()) follows a deterministic procedure with a well-defined order. In other words, if we run Serial-RB an arbitrary number of times on the same input instance, the search trees of all executions will be identical. The reason for this restriction will become obvious later.
In a parallel environment, we denote by the set of available computing cores. The rank of is equal to and . We use the terms worker and core interchangeably to refer to some participating in a parallel computation. Each search-node in corresponds to a task, where tasks are exchanged between cores using some specified encoding. We use to denote the encoding of . When search-node is assigned to , we say is the main task of . Any task in sent from to some , , is a subtask for and becomes the main task of . The weight of a task, , is a numerical value indicating the estimated completion time for relative to other tasks. That is, when , we expect the exploration of to require more computational time than . Task weight plays a crucial role in the design of efficient dynamic load-balancing strategies [9, 10, 11]. Without any problem-specific knowledge, the “best” indicator of the weight of is nothing but since estimating the size of is almost impossible. We capture this notion by setting . We say a task is heavy if it has weight close to and light otherwise.
From the standpoint of high-performance computing, practical parallel exact algorithms for hard problems mean one thing: unbounded scalability. The seemingly straight-forward parallel nature of search-tree decomposition is deceiving: previous work has shown that attaining scalability is far from easy [12, 13, 14]. To the best of our knowledge, the most efficient existing parallel algorithms that solve problems similar to those we consider were only able to scale to less than a few thousand (or only a few hundred) cores [10, 11, 15]. One of our main motivations was to solve extremely hard instances of the Vertex Cover problem such as the 60-cell graph [16]. In earlier work, we first attempted to tackle the problem by improving the efficiency of our serial algorithm [17]. Alas, some instances remained unsolved and some required several days of execution before we could obtain a solution. The next obvious step was to attempt a parallel implementation. As we encountered scalability issues, it became clear that solving such instances in an “acceptable” amount of time would require a scalable algorithm that can effectively utilize much more than the 1,024-core limit we attained in previous work [11].
We discuss the lessons we have learned and what we believe to be the main reasons of such poor scalability in Section III. In Section IV, we present the main concepts and strategies we use to address these challenges under our parallel framework. Finally, implementation details and experimental results are covered in Sections V and VI, respectively.
III Challenges and Related Work
III-A Communication Overhead
The most evident overhead in parallel algorithms is that of communication. Several models have already been presented in the literature including centralized (i.e. the master-worker(s) model where most of the communication and task distribution duties are assigned to a single core) [15], decentralized [9, 11], or a hybrid of both [13]. Although each model has its pros and cons, we believe that centralization rapidly becomes a bottleneck when the number of computing cores exceeds a certain threshold. Even though our framework can be implemented under any communication model, we chose to follow a simplified version of our previous decentralized approach [11].
An efficient communication model has to (i) reduce the total number of message transmissions and (ii) minimize the travel distance (number of hops) for each transmission. Unfortunately, (ii) requires detailed knowledge of the underlying network architecture and comes at the cost of portability. For (i), the message complexity is tightly coupled with the number of times each runs out of work and requests more. Therefore, to minimize the number of generated messages, we need to maximize “work time”, which is achieved by better dynamic load balancing.
III-B Tasks, Buffers, and Memory Overhead
No matter what communication model is used, a certain encoding has to be selected for representing tasks in memory. An obvious drawback of the encoding used by Finkel and Manber [18] is that every task is an exact copy of a search-node, whose size can be quite large. In a graph algorithm, every search-node might contain a modified version of the input graph (and some additional information). In this case, a more compact task-encoding scheme is needed to reduce both the memory and communication overheads.
Almost all parallel algorithms in the literature require a task-buffer or task-queue to store multiple tasks for eventual delegation [11, 13, 15, 18]. As buffers have limited size, their usage requires the selection of a “good” parameter value for task-buffer size. Choosing the size can be a daunting task, as this parameter introduces a tradeoff between the amount of time spent on creating or sending tasks and that spent on solving tasks. It is very common for such parallel algorithms to enter a loop of multiple light task exchanges which unnecessarily consumes considerable amounts of time and memory [11]. Tasks in such loops would have been more efficiently solved in-place by a single core.
III-C Initial Distribution
Efficient dynamic load balancing is key to scalable parallel algorithms. To avoid loops of multiple light task exchanges, initial task distribution also plays a major role. Even with clever load-balancing techniques, such loops can consume a lot of resources and delay (or even deny) the system from reaching a balanced state.
III-D Serial Overhead
All the items discussed above induce some serial overhead. Here we focus on encoding and decoding of tasks, which greatly affect the performance of any parallel algorithm. Upon receiving a new task, each computing core has to perform a number of operations to correctly restart the search-phase, i.e. resume the exploration of its assigned subtree. When the search reaches the bottom levels of the tree, the amount of time required to start a task might exceed the time required to solve it, a situation that should be avoided. Encoding tasks and storing them in buffers also consumes time. In fact, the more we attempt to compress task encodings the more serial work is required for decoding.
For NP-hard problems, it is important to account for what we call the butterfly effect of polynomial overhead. Since the size of the search tree is usually exponential in the size of the input, any polynomial-time (or even constant-time) operations can have significant effects on the overall running times [17], by virtue of being executed exponentially many times. In general, the disruption time (time spent doing non-search-related work) has to be minimized.
III-E Load Balancing
Task creation is, we believe, the most critical factor affecting load balancing. Careful tracing of recursive backtracking algorithms shows that most computational time is spent in the bottom of the search tree, where is very large. Moreover, since task-buffers have fixed size, any parallel execution of a recursive backtracking algorithm relying on task-buffers is very likely to reach a state where all buffers contain light tasks. Loops of multiple light task exchanges most often occur in such scenarios. To avoid them, we need a mechanism that enables the extraction of a task of maximum weight from the subtree assigned to a , that is, the highest unvisited node in the subtree assigned to .
Several load-balancing strategies have been proposed in the literature [12, 19]. In recent work [10], a load-balancing strategy designed specifically for the Vertex Cover problem was presented. The algorithm is based on a dynamic master-worker model where prior knowledge about generated instances is manipulated so that the core having the estimated heaviest task is selected as master. However, scalability of this approach was limited to only 2,048 cores.
III-F Termination Detection
In a centralized model, the master detects termination using straightforward protocols. The termination protocol can be initiated several times by different cores in a decentralized environment, rendering detection more challenging. In this work, we use a protocol similar to the one proposed in [11], where each core, which can be in one of three states, broadcasts any state change to all other cores.
III-G Problem Independence
We need to address all the challenges listed above independently of the problem being solved. Moreover, we want to minimize the amount of work required for migrating existing serial algorithms to parallel ones.
IV The Framework
In this section, we present our framework by showing how to incrementally transform Serial-RB into a parallel algorithm. First, we discuss indexed search trees and their use in a generic and compact task-encoding scheme. As a byproduct of this encoding, we show how we can efficiently guarantee the extraction of the heaviest unprocessed task for dynamic load balancing. We provide pseudocode to illustrate the simplicity of transforming serial algorithms to parallel ones. The end result is a parallel algorithm, Parallel-RB, which consists of two main procedures: Parallel-RB-Iterator and Parallel-RB-Solver.
IV-A Indexed Search Trees
For a binary search tree , we let and denote the left child and the right child of node , respectively. We use the following procedure to assign an index, , to every search-node in (where denotes concatenation):
-
(1)
The root of has index 1 ()
-
(2)
For any node in :
-
and
-
-
An example of an indexed binary search tree is given in Figure 2. Note that this indexing method can easily be extended for arbitrary branching factor by simply setting the index of the child of to .
To incorporate the notion of indices, we introduce minor modifications to Serial-RB. We call this new version Almost-Parallel-RB (Figure 3). Almost-Parallel-RB includes a global integer array that is maintained by a single statement: . We let ; the encoding of a task under our parallel framework corresponds to its index and is of size. Combined with an effective load-balancing strategy which generates tasks having only small (i.e. heavy tasks), this approach greatly reduces memory and communication overhead. Upon receiving an encoded task, every core now requires an additional user-provided function ConvertIndex, the implementation details of which are problem-specific (Section V discusses some examples). The purpose of this function is to convert an index into an actual task from which the search can proceed. Since every index encodes the unique path from the root of the tree to the corresponding search-node and by assumption search-nodes are generated in a well-defined order, to retrace the operations it suffices to iterate over the index. Note that the overhead introduced by this approach is closely related to the number of tasks solved by each core. Minimizing this number also minimizes disruption time since the search-phase of the algorithm is not affected.
We use the functions GetHeaviestTaskIndex and FixIndex (Figure 4) to repeatedly extract the heaviest task from the array while ensuring that no search-node is ever explored twice. The general idea of indexing is not new and has been previously used for prioritizing tasks in buffers or queues [13]. However, our approach completely eliminates the need for task-buffers, effectively reducing the memory footprint of our algorithms and eliminating the burden of selecting appropriate size parameters for each buffer or task granularity as defined in [13].
In a parallel computation involving cores and in Figure 2, has main task and is currently exploring node (hence ). After receiving an initial task request from , calls GetHeaviestTaskIndex, which returns and sets . (We use to denote a subarray of starting at position and ending at position .) At the receiving end, calls FixIndex, after which . As seen in Figure 2, was in fact the heaviest task in . If subsequently requests a second task from while is still working on node , the resulting task is and the of is updated to .
Before exploring a search-node, every core must first use to validate that the current branch was not previously delegated to a different core (Figure 3, lines 2–3). Whenever discovers a negative value in , the search can terminate, since the remaining subtree has been reassigned to a different core.
IV-B From Serial to Parallel
The Almost-Parallel-RB algorithm is lacking a formal definition of a communication model as well as the implementation details of the initialization and termination protocols. For the former, we use a simple decentralized strategy in which any two cores can communicate. We assume each core is assigned a unique rank , for . There are three different types of message exchanges under our framework: status updates, task requests or responses, and notification messages. Each core can be in one of three states: active, inactive, or dead. Before changing states, each core must broadcast a status update message to all participants. This information is maintained by each core in a global integer array . Notification messages are optional broadcast messages whose purpose is to inform the remaining participants of current progress. In our implementation, notification messages are sent whenever a new solution is found. The message includes the size of the new solution which, for many algorithms, can be used as a basis for effective pruning rules.
In the initialization phase, for a binary search tree and the number of cores a power of two (), one strategy would be to generate all search-nodes at depth and assign one to each core. However, these requirements are too restrictive and greatly complicate the implementation. Instead, we arrange the cores in a virtual tree-like topology and force every core, except , to request the first task from its parent (stored as a global variable) in this virtual topology. is always assigned task . The GetParent function is given in Figure 5. The intuition is that if we assume that cores join the computation in increasing order of rank, must always request an initial task from where and there exists no such that and has a heavier task than . Figure 6 shows an example of an initial task-to-core assignment for . The parent of corresponds to the first encountered on the path from the task assigned to to the root. When joins the topology, although all remaining cores () have tasks of equal weight, selects as a parent. This is due to the alternating behavior of the GetParent function. When is even, the parent of corresponds to , where is the smallest even integer such that has a task of maximum weight. The same holds for odd , except that must pick as a parent. This approaches balances the number of cores exploring different sections of the search tree.
Once every core receives a response from its initial parent, the initialization phase is complete. After that, each core updates its parent to . During the search-phase, whenever a core requires a new task, it will first attempt to request one from its current parent. If the parent has no available tasks or is inactive, the virtual topology is modified by the GetNextParent function (Figure 5). In the global variable , we keep track of the number of times each core has unsuccessfully requested a task from all participants. The termination protocol is fired by some core whenever . goes from being active to inactive and sends a status update message to inform the remaining participants. Once all cores are inactive, the computation can safely end.
The complete pseudocode for Parallel-RB is given in Figure 7. The algorithm consists of two main procedures: Parallel-RB-Iterator and Parallel-RB-Solver. All communication must be non-blocking in the latter and blocking in the former.
IV-C Arbitrary Branching Factor
For search trees of arbitrary branching factor, the index of needs to keep track of both the unique root-to-node path as well as the number of unexplored siblings of (i.e. all the nodes at depth and position greater than ). Therefore, we divide an index into two parts, and . We let denote the child of and the set of all children of . The following procedure assigns indices to every search-node in :
-
(1)
The root of has and
-
(2)
For any node in :
-
and
-
-
An example of an indexed search tree is given in Figure 8. Each node is assigned two identifiers: (top) and (bottom). At the implementation level, the array is replaced by a array that can be maintained after every recursive call in a similar fashion to Parallel-RB-Solver as long as each search-node is aware of . The first non-zero entry in (the second row of the array), say , indicates the depth of all tasks of heaviest weight. Since there can be more than one unvisited node at this depth, we could choose to send either all of them or just a subset . In the first case, we can remember delegated branches by simply setting to . For the second case, is decremented by . Note that the choice of cannot be arbitrary. If , must include , and for any , it must be the case that is also in for all between and . The only modification required in Parallel-RB-Solver is to make sure that at search-node , GetNextChild is executed only times.
V Implementation
We tested our framework with parallel implementations of algorithms for the well-known Vertex Cover and Dominating Set problems.
| Vertex Cover | |
|---|---|
| Input: | A graph |
| Question: | Find a set such that is |
| minimized and the graph induced by | |
| is edgeless | |
| Dominating Set | |
|---|---|
| Input: | A graph |
| Question: | Find a set such that is |
| minimized and every vertex in is either | |
| in or is adjacent to a vertex in | |
Both problems have received considerable attention in the areas of exact and fixed parameter algorithms because of their close relations to many other problems in different application domains [20]. The sequential algorithm for the parameterized version of Vertex Cover having the fastest known worst-case behavior runs in time [3]. We converted this to an optimized version by introducing simple modifications and excluding complex processing rules that require heavy maintenance operations. For Dominating Set, we implemented the algorithm of [4] where the problem is solved by a reduction to Minimum Set Cover. We used the hybrid graph data-structure [17] which was specifically designed for recursive backtracking algorithms that combines the advantages of the two classical adjacency-list and adjacency-matrix representations of graphs with very efficient implicit backtracking operations.
Our input consists of a graph where , , and each vertex is given an identifier between and . The search tree for each algorithm is binary and the actual implementations closely follow the Parallel-RB algorithm. At every search-node, a vertex of highest degree is selected deterministically. Vertex selection has to be deterministic to meet the requirements of the framework. To break ties when multiple vertices have the same degree, we always pick the vertex with the smallest identifier. For Vertex Cover, the left branch adds to the solution and the right branch adds all the neighbors of to the solution. For Dominating Set, the left branch is identical but the right branch forces to be out of any solution. The ConvertIndex function is straightforward as the added, deleted, or discarded vertices can be retraced by iterating through the index and applying any appropriate reduction rules along the way. Every time a smaller solution is found, the size is broadcasted to all participants to avoid exploring branches that cannot lead to any improvements.
VI Experimental Results
All our code relies on the Message Passing Interface (MPI) [21] and uses the standard C language with no other dependencies. Computations were performed on the BGQ supercomputer at the SciNet HPC Consortium111SciNet is funded by the Canada Foundation for Innovation under the auspices of Compute Canada; the Government of Ontario; Ontario Research Fund - Research Excellence; and the University of Toronto. [22]. The BGQ production system is a generation Blue Gene IBM supercomputer built around a system-on-a-chip compute node. There are 2,048 compute nodes each having a 16 core 1.6GHz PowerPC based CPU with 16GB of RAM. When running jobs on 32,768 cores, each core is allocated 1GB of RAM. Each core also has four “hardware threads” which can keep the different parts of each core busy at the same time. It is therefore possible to run jobs on and cores at the cost of reducing available RAM per core to 500MB and 250MB, respectively. We could run experiments using this many cores only when the input graph was relatively small and, due to the fact that multiple cores were forced to share (memory and CPU) resources, we noticed a slight decrease in performance.
The Parallel-Vertex-Cover algorithm was tested on four input graphs.
-
-
p_hat700-1.clq: is a graph on vertices and edges with a minimum vertex cover of size
-
-
p_hat1000-2.clq is a graph on vertices and edges with a minimum vertex cover of size
-
-
frb30-15-1.mis is a graph on vertices and edges with a minimum vertex cover of size
-
-
60-cell is a graph on vertices and edges with a minimum vertex cover of size
The first two instances were obtained from the classical Center for Discrete Mathematics and Theoretical Computer Science (DIMACS) benchmark suite (http://dimacs.rutgers.edu/Challenges/). The frb30-15-1.mis graph is a notoriously hard instance for which the exact size of a solution was only known so far from a theoretical perspective. To the best of our knowledge, this paper is the first to experimentally solve it; more information on this instance can be found in [23]. Lastly, the 60-cell graph is a 4-regular graph (every vertex has exactly neighbors) with applications in chemistry [16]. Prior to this work, we solved the 60-cell using a serial algorithm which ran for almost a full week [17]. The high regularity of the graph makes it very hard to apply any pruning rules resulting in an almost exhaustive enumeration of all feasible solutions. For the Parallel-Dominating-Set algorithm we generated two random instances 201x1500.ds and 251x6000.ds where x.ds denotes a graph on vertices and edges. Both instances could not be solved by our serial algorithm when limited to 24 hours.
| Graph | Time | |||
| p_hat700-1.clq | 16 | 19.5hrs | 2,876 | 2,910 |
| p_hat700-1.clq | 32 | 9.8hrs | 2,502 | 2,567 |
| p_hat700-1.clq | 64 | 4.9hrs | 3,398 | 3,518 |
| p_hat700-1.clq | 128 | 2.5hrs | 4,928 | 5,196 |
| p_hat700-1.clq | 256 | 1.3hrs | 4,578 | 5,153 |
| p_hat700-1.clq | 512 | 38min | 4,354 | 5,451 |
| p_hat700-1.clq | 1,024 | 18.9min | 4,052 | 6,391 |
| p_hat700-1.clq | 2,048 | 9.89min | 3,781 | 8,117 |
| p_hat700-1.clq | 4,096 | 5.39min | 3,665 | 11,978 |
| p_hat700-1.clq | 8,192 | 2.9min | 2,714 | 19,183 |
| p_hat700-1.clq | 16,384 | 1.7min | 1,342 | 32,883 |
| p_hat1000-2.clq | 64 | 23.6min | 3,664 | 3,799 |
| p_hat1000-2.clq | 128 | 12.5min | 2,651 | 2,912 |
| p_hat1000-2.clq | 256 | 6.5min | 1,623 | 1,956 |
| p_hat1000-2.clq | 512 | 3.7min | 1,235 | 1,872 |
| p_hat1000-2.clq | 1,024 | 2.1min | 866 | 2,142 |
| p_hat1000-2.clq | 2,048 | 1.2min | 610 | 3,120 |
| frb30-15-1.mis | 1,024 | 14.2hrs | 13,580 | 15,968 |
| frb30-15-1.mis | 2,048 | 7.2hrs | 21,899 | 26,597 |
| frb30-15-1.mis | 4,096 | 3.6hrs | 28,740 | 37,733 |
| frb30-15-1.mis | 8,192 | 1.9hrs | 29,110 | 45,685 |
| frb30-15-1.mis | 16,384 | 55.1min | 28,707 | 59,978 |
| frb30-15-1.mis | 32,768 | 28.8min | 30,008 | 96,438 |
| frb30-15-1.mis | 65,536 | 16.8min | 25,359 | 158,371 |
| frb30-15-1.mis | 131,072 | 11.1min | 19,419 | 312,430 |
| 60-cell | 128 | 14.3hrs | 19 | 26 |
| 60-cell | 256 | 7.3hrs | 23 | 23 |
| 60-cell | 512 | 3.7hrs | 1,091 | 1,388 |
| 60-cell | 1,024 | 45.1min | 1,397 | 1,940 |
| 60-cell | 2,048 | 11.3min | 1,331 | 2,430 |
| 60-cell | 4,096 | 2.8min | 949 | 3,094 |
| Graph | Time | |||
| 201x1500.ds | 512 | 18.1hrs | 8,231 | 9,642 |
| 201x1500.ds | 1,024 | 9.2hrs | 10,315 | 12,611 |
| 201x1500.ds | 2,048 | 4.5hrs | 11,566 | 16,118 |
| 201x1500.ds | 4,096 | 2.3hrs | 14,070 | 23,413 |
| 201x1500.ds | 8,192 | 1.2hrs | 13,243 | 33,680 |
| 201x1500.ds | 16,384 | 36.2min | 10,295 | 41,795 |
| 201x1500.ds | 32,768 | 19.2min | 6,925 | 72,719 |
| 201x1500.ds | 65,536 | 11.8min | 4,221 | 109,346 |
| 251x6000.ds | 256 | 8.9hrs | 3,313 | 4,573 |
| 251x6000.ds | 512 | 4.7hrs | 3,865 | 4,985 |
| 251x6000.ds | 1,024 | 2.4hrs | 2,842 | 5,306 |
| 251x6000.ds | 2,048 | 1.2hrs | 1,528 | 5,396 |
| 251x6000.ds | 4,096 | 36.4min | 2,037 | 9,714 |
| 251x6000.ds | 8,192 | 18.7min | 1,445 | 10,497 |
| 251x6000.ds | 16,384 | 10.1min | 1,132 | 12,310 |
| 251x6000.ds | 32,768 | 5.5min | 934 | 13,982 |
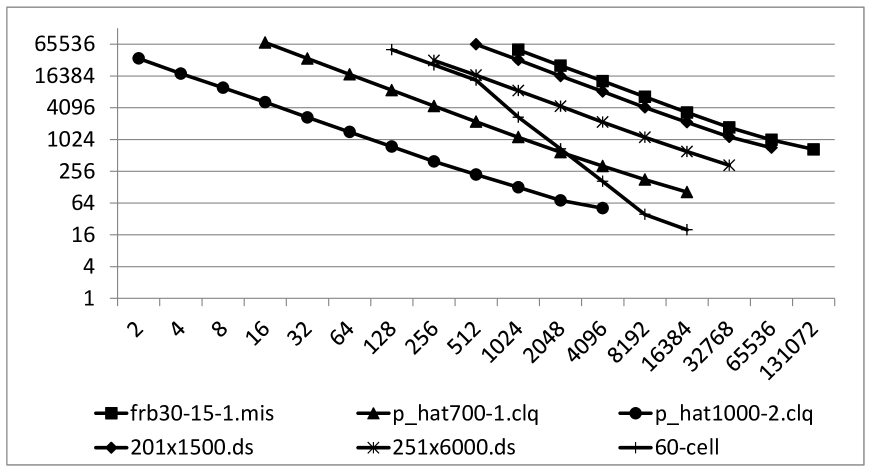
All of our experiments were limited by the system to a maximum of 24 hours per job. To evaluate the performance of our communication model and dynamic load balancing strategy, we collected two statistics from each run: and . denotes the average number of tasks received (and hence solved) by each core while denotes the average number of tasks requested by each core. In Table I, we give the running times of the Parallel-Vertex-Cover algorithm for every instance while varying the total number of cores, , from to (we only ran experiments on 65,536 or 131,072 cores when the graph was small enough to fit in memory or when the running time exceeded 10 minutes on 32,768 cores).
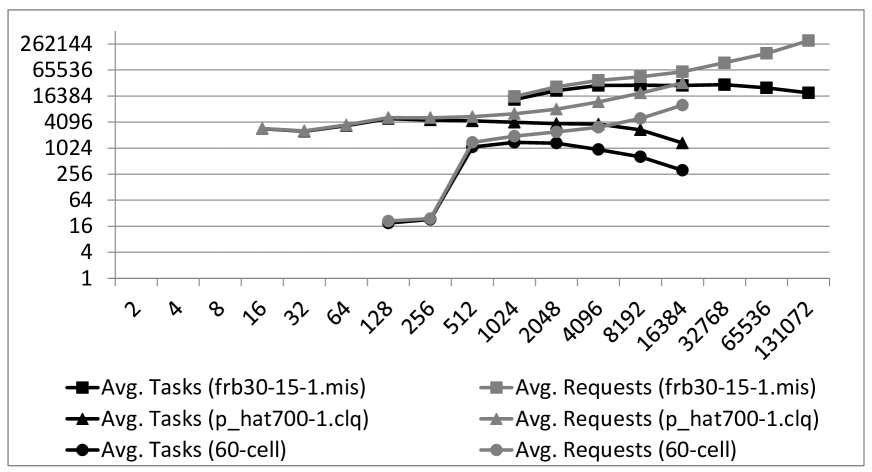
The values of and are also provided. Similar results for the Parallel-Dominating-Set algorithm are given in Table II. Due to space limitations, we omit some of the entries in the tables and show the overall behaviors in the chart of Figure 9. In almost all cases, the algorithms achieve near linear (super-linear for the 60-cell graph) speedup on at least 32,768 cores. We were not able to gather enough experimental data to characterize the behavior of the framework on 65,536 and 131,072 cores but results on 201x1500.ds and frb30-15-1.mis suggest a 10 percent decrease in performance. As noted earlier, cores were forced to share resources whenever was greater than 32,768. Further work is needed to determine whether this can explain the performance decrease or if other factors came into play. We also note that harder instances are required to fairly test scalability on a larger number of cores since the ones we considered were all solved in just a few minutes using at most 32,768 cores. In Figure 10, we plot the different values of and for a representative subset of our experiments. This chart reveals the inherent difficulty of dynamic load balancing. As increases, the gap between and grows larger and larger. Any efficient dynamic load-balancing strategy has to control the growth of this gap (e.g. keep it linear) for a chance to achieve unbounded scalability. The largest gap we obtained was on the frb30-15-1.mis instance using 131,072 cores. The gap was approximately 300,000. Given the number of cores and the amount of time ( 10 minutes) spent on the computation, the number suggests that each core requested an average of 2.5 tasks from every other core. One possible improvement which we are currently investigating is to modify our virtual topology to a graph-like structure of bounded degree. The framework currently assumes a fully connected topology after initialization (i.e. any two cores can communicate) which explains the correlation between and . By bounding the degrees in the virtual topology, we hope to make this gap weakly dependent on .
VII Conclusions and Future Work
Combining indexed search-trees with a decentralized communication model, we have showed how any serial recursive backtracking algorithm, with some ordered branching, can be modified to run in parallel. Some of the key advantages of our framework are:
-
-
The migration from serial to parallel entails very little additional coding. Implementing each of our parallel algorithms took less than two days and around 300 extra lines of code.
-
-
It completely eliminates the need for task-buffers and the overhead they introduce (Section III-B).
-
-
The input of both the serial and parallel implementations are identical. Running the parallel algorithms requires no additional input from the user (assuming every core has access to and ). Most parallel algorithms in the literature require some parameters such as task-buffer size. Selecting the best parameters could vary depending on the instance being solved.
-
-
Experimental results have showed that our implicit load-balancing strategy, joined with the concise task-encoding scheme, can achieve linear (sometimes super-linear) speedup with scalability on at least cores. We hope to test our framework on a larger system in the near future to determine the maximum number of cores it can support.
-
-
Although not typical of parallel algorithms, when using the indexing method and the ConvertIndex function, it becomes reasonably straightforward to support join-leave (i.e. cores leaving the computation after solving a fixed number of tasks) or checkpointing capabilities (i.e. by forcing every core to write its to some file).
We believe there is still plenty of room for improving the framework at the risk of losing some of its simplicity. One area we have started examining is the virtual topology. A “smarter” topology could further reduce the communication overhead (e.g. the gap between and ) and increase the overall performance. Another candidate is the GetNextParent function which can be modified to probe a fixed number of cores before selecting which to “help” next. Finally, we intend to investigate the possibility of developing the framework into a library, similar to [14] and [13], which will provide users with built-in functions for parallelizing recursive backtracking algorithms.
Acknowledgment
The authors would like to thank Chris Loken and the SciNet team for providing access to the BGQ production system and for their support throughout the experiments.
References
- [1] J. Chen, I. A. Kanj, and W. Jia, “Vertex cover: further observations and further improvements,” Journal of Algorithms, vol. 41, no. 2, pp. 280–301, 2001.
- [2] F. V. Fomin, D. Kratsch, and G. J. Woeginger, “Exact (exponential) algorithms for the dominating set problem,” in Graph-Theoretic Concepts in Computer Science, 2005, vol. 3353, pp. 245–256.
- [3] J. Chen, I. A. Kanj, and G. Xia, “Improved upper bounds for vertex cover,” Theor. Comput. Sci., vol. 411, no. 40-42, pp. 3736–3756, Sep. 2010.
- [4] F. V. Fomin, F. Grandoni, and D. Kratsch, “Measure and conquer: Domination a case study,” in Automata, Languages and Programming, 2005, vol. 3580, pp. 191–203.
- [5] J. M. M. Rooij, J. Nederlof, and T. C. Dijk, “Inclusion/exclusion meets measure and conquer,” in Algorithms - ESA 2009, 2009, vol. 5757, pp. 554–565.
- [6] G. J. Woeginger, “Exact algorithms for NP-hard problems: a survey,” in Combinatorial optimization - Eureka, you shrink!, 2003, pp. 185–207.
- [7] R. G. Downey and M. R. Fellows, Parameterized complexity. New York: Springer-Verlag, 1997.
- [8] J. Dean and S. Ghemawat, “MapReduce: simplified data processing on large clusters,” Commun. ACM, vol. 51, no. 1, pp. 107–113, Jan. 2008.
- [9] G. D. Fatta and M. R. Berthold, “Decentralized load balancing for highly irregular search problems,” Microprocess. Microsyst., vol. 31, no. 4, pp. 273–281, Jun. 2007.
- [10] D. P. Weerapurage, J. D. Eblen, G. L. Rogers, Jr., and M. A. Langston, “Parallel vertex cover: a case study in dynamic load balancing,” in Proceedings of the Ninth Australasian Symposium on Parallel and Distributed Computing, vol. 118, 2011, pp. 25–32.
- [11] F. N. Abu-Khzam and A. E. Mouawad, “A decentralized load balancing approach for parallel search-tree optimization,” in Proceedings of the 2012 13th International Conference on Parallel and Distributed Computing, Applications and Technologies, 2012, pp. 173–178.
- [12] L. V. Kale, “Comparing the performance of two dynamic load distribution methods,” in Proceedings of the 1988 International Conference on Parallel Processing, 1988, pp. 8–11.
- [13] Y. Sun, G. Zheng, P. Jetley, and L. V. Kale, “An adaptive framework for large-scale state space search,” in Proceedings of the 2011 IEEE International Symposium on Parallel and Distributed Processing Workshops and PhD Forum, 2011, pp. 1798–1805.
- [14] T. K. Ralphs, L. Ládanyi, and M. J. Saltzman, “A library hierarchy for implementing scalable parallel search algorithms,” J. Supercomput., vol. 28, no. 2, pp. 215–234, May 2004.
- [15] F. N. Abu-Khzam, M. A. Rizk, D. A. Abdallah, and N. F. Samatova, “The buffered work-pool approach for search-tree based optimization algorithms,” in Proceedings of the 7th international conference on Parallel processing and applied mathematics, 2008, pp. 170–179.
- [16] S. Debroni, E. Delisle, W. Myrvold, A. Sethi, J. Whitney, J. Woodcock, P. W. Fowler, B. de La Vaissiere, and M. Deza, “Maximum independent sets of the 120-cell and other regular polyhedral,” Ars Mathematica Contemporanea, vol. 6, no. 2, pp. 197–210, 2013.
- [17] F. N. Abu-Khzam, M. A. Langston, A. E. Mouawad, and C. P. Nolan, “A hybrid graph representation for recursive backtracking algorithms,” in Proceedings of the 4th international conference on Frontiers in algorithmics, 2010, pp. 136–147.
- [18] R. Finkel and U. Manber, “DIB - a distributed implementation of backtracking,” ACM Trans. Program. Lang. Syst., vol. 9, no. 2, pp. 235–256, Mar. 1987.
- [19] V. Kumar, A. Y. Grama, and N. R. Vempaty, “Scalable load balancing techniques for parallel computers,” J. Parallel Distrib. Comput., vol. 22, no. 1, pp. 60–79, Jul. 1994.
- [20] F. N. Abu-Khzam, M. A. Langston, P. Shanbhag, and C. T. Symons, “Scalable parallel algorithms for FPT problems,” Algorithmica, vol. 45, no. 3, pp. 269–284, Jul. 2006.
- [21] J. J. Dongarra and D. W. Walker, “MPI: A message-passing interface standard,” International Journal of Supercomputing Applications, vol. 8, no. 3/4, pp. 159–416, 1994.
- [22] C. Loken, D. Gruner, L. Groer, R. Peltier, N. Bunn, M. Craig, T. Henriques, J. Dempsey, C.-H. Yu, J. Chen, L. J. Dursi, J. Chong, S. Northrup, J. Pinto, N. Knecht, and R. V. Zon, “Scinet: Lessons learned from building a power-efficient top-20 system and data centre,” Journal of Physics: Conference Series, vol. 256, no. 1, p. 012026, 2010.
- [23] K. Xu, F. Boussemart, F. Hemery, and C. Lecoutre, “A simple model to generate hard satisfiable instances,” in Proceedings of the 19th international joint conference on Artificial intelligence, 2005, pp. 337–342.