An Efficient Algorithm for Enumerating Chordless Cycles and Chordless Paths
Abstract
A chordless cycle (induced cycle) of a graph is a cycle without any chord, meaning that there is no edge outside the cycle connecting two vertices of the cycle. A chordless path is defined similarly. In this paper, we consider the problems of enumerating chordless cycles/paths of a given graph and propose algorithms taking time for each chordless cycle/path. In the existing studies, the problems had not been deeply studied in the theoretical computer science area, and no output polynomial time algorithm has been proposed. Our experiments showed that the computation time of our algorithms is constant per chordless cycle/path for non-dense random graphs and real-world graphs. They also show that the number of chordless cycles is much smaller than the number of cycles. We applied the algorithm to prediction of NMR (Nuclear Magnetic Resonance) spectra, and increased the accuracy of the prediction.
1 Introduction
Enumeration is a fundamental problem in computer science, and many algorithms have been proposed for many problems, such as cycles, paths, trees and cliques[Ep90, KpRm00, MkUn04, RdTj75, tomita, Un01]. However, their application to real world problems has not been researched very much, due to the handling needed for the huge amount of and the high computational cost. However, this situation is now changing, thanks to the rapid increase in computational power, and the emergence of data centric science. For example, the enumeration of all substructures frequently appearing in a database, i.e., frequent pattern mining, has been intensively studied. This method is adopted for capturing the properties of databases, or for discovering new interesting knowledge in databases. Enumeration is necessary for such tasks because the objectives cannot be expressed well in mathematical terms. The use of good models helps reduce the amount of output, and the use of efficient algorithms enables huge databases to be more easily handled[InWsMt03, UNOT, seq]. More specifically, introducing a threshold value for the frequency, which enables controlling the number of solutions. In such areas, minimal/maximal solutions are also enumerated to reduce the number of solutions. For example, enumerating all cliques is usually not practical while enumerating all maximal cliques, i.e. cliques included in no other cliques, is often practical[tomita, MkUn04]. In real-world sparse graphs, the number of maximal cliques is not exponential, so, even in large-scale graphs, the maximal cliques can often be enumerated in a practically short time by a stand alone PC even for graphs with millions of vertices. However, the enumeration of maximum cliques, that have the maximum number of vertices among all cliques, is often not acceptable in practice, since the purpose of enumeration is to find all locally dense structures, and finding only maximum cliques will lose relatively small dense structures, thus it does not cover whole the data.
Paths and cycles are two of the most fundamental graph structures. They appear in many problems in computer science and are used for solving problems, such as optimizations (e.g. flow problems) and information retrieval (e.g. connectivity and movement of objects). Paths and cycles themselves are also used to model other objects. For example, in chemistry, the size and the fusing pattern of cycles in chemical graphs, representing chemical compounds, are considered to be essential structural attributes affecting on several important properties of chemical compounds, such as spectroscopic output, physical property, chemical reactivity, and biological activity.
For a path/cycle , an edge connecting two vertices of but not included in is called a chord. A path/cycle without a chord is called a chordless path/cycle. Since a chordless cycle includes no other cycle as a vertex set, it is considered minimal. Thus, chordless cycles can be used to represent cyclic structures. For instance, the size and fusing pattern of chordless cycles in chemical graphs as well as other properties of chemical structures are taken into account when selecting data for prediction of nuclear magnetic resonance (NMR) chemical shift values[St]. Most chemical compounds contain cycles. In chemistry, the term ‘ring’ is used instead of ‘cycle’, for example a cycle consisting of 5 vertices is called 5-membered ring. Since the character of ring structures of chemical compounds is assumed to be important to study the nature of the structure-property relationships, the ring perception is one of classical questions [chem-Bl, chem-Dw2, chem-Dw, chem-HsJfGf96] in the context of chemical informatics, so called chemoinformatics. Several kinds of ring structures, such as all rings and the smallest set of smallest ring (SSSR) are usually included in a basic dataset of chemical information. NMR chemical shift prediction is a successful case where the information about chordless cycles is employed to improve the accuracy of the prediction. The path/cycle enumeration is supposed to be useful also for analysis of network systems such as Web and social networks.
In this paper, we consider the problem of enumerating all chordless paths (resp., cycles) of the given graph. While optimization problems for paths and cycles have been studied well, their enumeration problems have not. This is because there are huge numbers of paths and cycles even in small graphs. However, we can reduce the numbers so that the problem becomes tractable by introducing the concept of chordless. The first path/cycle enumeration algorithm was proposed by Read and Tarjan in 1975[RdTj75]. Their algorithm takes as input a graph and enumerates all cycles, or all paths connecting given vertices and , in time for each. The total computation time is where is the number of output cycles/paths. Ferreira et al. [FGMPRS] recently proposed a faster algorithm, that takes time linear in the output size, that is the sum of the lengths of the paths.
The chordless version was considered by Wild[Wl08]. An algorithm based on the principle of exclusion is proposed, but the computational efficiency was not considered deeply. In this paper, we propose algorithms for enumerating chordless cycles and chordless paths connecting two vertices and (reported in 2003[Un03]). Note that chordless cycles can be enumerated by chordless path enumeration. The running time of the algorithm is for each, the same as the Read and Tarjan algorithm.
We experimentally evaluated the practical performance of the algorithms for random graphs and real-world graphs. The results showed that its practical computation time is much smaller than , meaning that the algorithms can be used for large-scale graphs with non-huge amount of solutions. The results also showed that the number of chordless cycles is drastically small compared to the number of usual cycles.
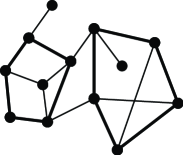
2 Preliminaries
A graph is a combination of a vertex set and an edge set such that each edge is a pair of vertices. A graph with vertex set and edge set is denoted by . An edge of pair and is denoted by . We say that the edge connects and , is incident to and , and and are adjacent to each other, and call and end vertices of . An edge with end vertices that are the same vertex is called a self-loop. Two edges having the same end vertices and are called multi-edges. We deal only with graphs with neither a self-loop nor a multi-edge. This restriction does not lose the generality of the problem formulation.
A path is a graph of vertices and edges composing a sequence
satisfying and .
The and are called the end vertices of the path.
If the end vertices of are and , the path is called an
- path.
When holds, a path is called a cycle.
Here we represent paths and cycles by vertex sequences,
such as .
An edge connecting two vertices of a path/cycle and not included in
is called a chord of .
A path/cycle such that the graph includes no chord of is called
chordless.
Figure 1 shows examples.
In a set system composed of the vertex sets of cycles (resp.,
- paths), the vertex set of a chordless cycle (resp., - path)
is a minimal element.
For a graph and a vertex subset of , denotes the graph obtained from by removing all vertices of and all edges incident to some vertices in . For a vertex , denotes the neighbor of , that is, the set of vertices adjacent to . For a vertex set and a vertex , and denote and , respectively. For a path and its end vertex , denotes the path obtained by removing from .
Property 1
There is a chordless - path if and only if there is an - path.
Proof
A chordless - path is an - path, thus only if part is true. If an - path exists, a shortest path from to is a chordless - path, and thus it always exists. ∎
Property 2
A vertex is included in a cycle if and only if is included in a chordless cycle.