an elementary proof of borsuk theorem

Dian Yang

(Date: July 30, 2025)

In 1933, Borsuk conjectured that any bounded $d$ -dimensional set of nonzero diameter can be broken into $d+1$ parts of smaller diameter[1]. This conjecture was disproved for large enough $d$ [2, 3, 4, 5, 6, 7], though it is true for low dimensional cases. The paper provides an alternative proof for $d=2$ case.

Theorem 1 (Borsuk).

Any bounded plane figure can be divided into three pieces of smaller diameters.

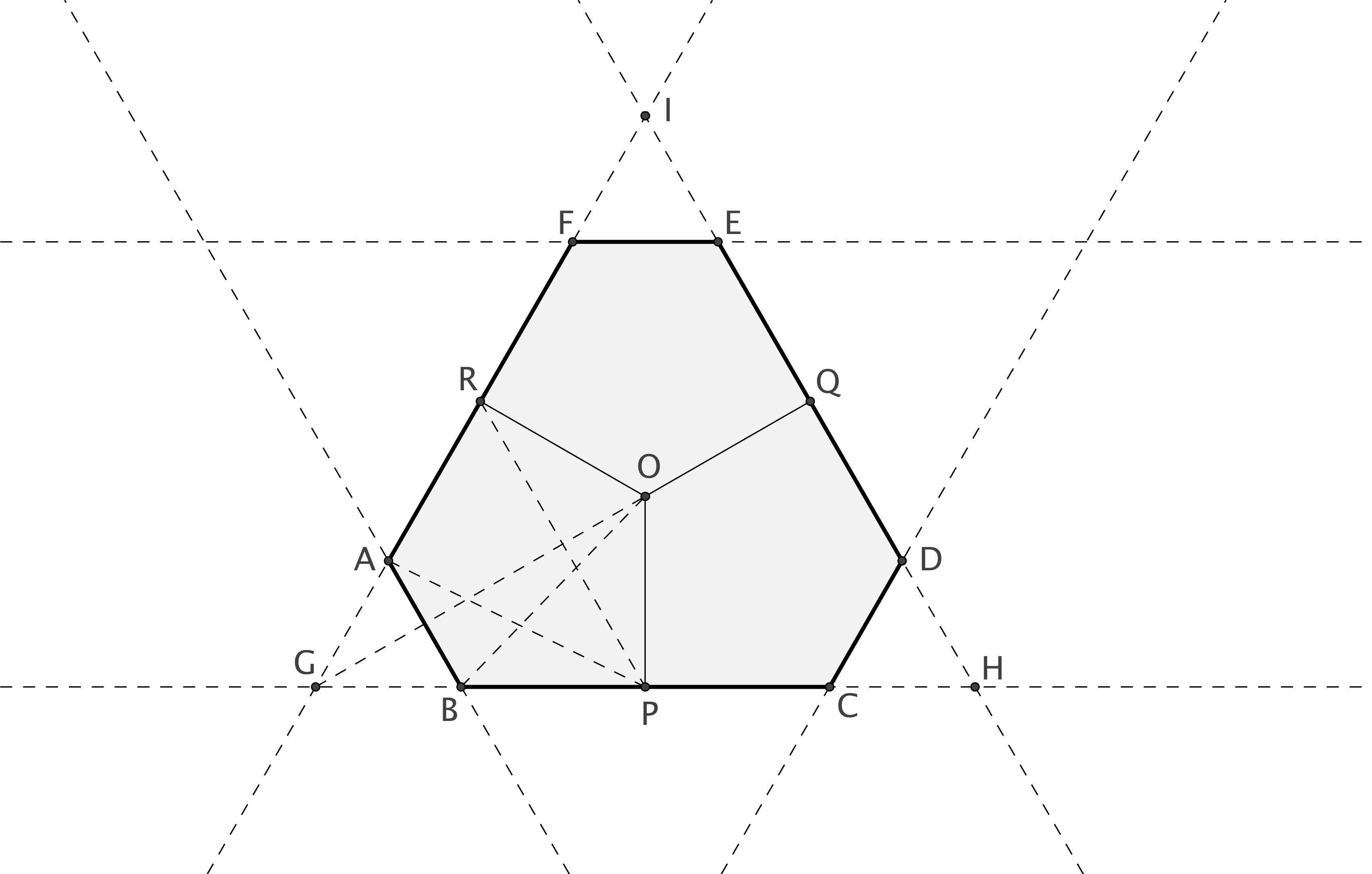
This theorem has a standard proof by first proving the plane figure (assume its diameter to be 1) can be bounded by a hexagon, with opposite sides parallel and separated by a distance no greater than 1, all of its angles being $120^{\circ}$ , arbitrarily chosen the direction of one of its sides. By considerations of continuity we may assume that the hexagon is regular. It can be easily partitioned into three congruent pentagons with diameter $\sqrt{3}/2$ . Instead of considerations of continuity, one can use the following lemma:

Lemma 2 (Main Lemma).

A hexagon with opposite sides parallel and separated by distance 1, all of its angles being $120^{\circ}$ , can be divided into 3 parts of diameter less than 1.

Proof.

(Hexagon $ABCDEF$ as shown in Figure 1.)

By construction, $|AB|=|CD|=|EF|$ , $|BC|=|DE|=|FA|$ . Without loss of generality we assume $|AB|\leq|BC|$ . Drop perpendiculars $OP$ , $OR$ . Hexagon $ABCDEF$ is partitioned into three pentagons congruent to $ABPOR$ . It suffices to prove that this pentagon has diameter smaller than 1, or equivalently: $|AP|<1$ , $|RP|<1$ , $|OB|<1$ . Extend $BC$ and $FA$ so that they intersect at $G$ . Since distances between opposite sides of $ABCDEF$ are 1’s, $|AB|+|BC|=|GC|=2/\sqrt{3}$ . Hence $|AB|\leq 1/\sqrt{3}$ .

On one hand, since $\Delta GPR$ is equilateral,

|AP|\leq|RP|=|PG|<|OG|;

(1)

and since $OP\bot GP$ ,

|OB|\leq|OG|.\quad\textnormal{($|OB|=|OG|$ iff. $|AB|=0$)}

(2)

On the other hand,

|OG|=\frac{2}{\sqrt{3}}|PG|=\frac{1}{\sqrt{3}}|HG|=\frac{1}{\sqrt{3}}\left(|AB|+\frac{2}{\sqrt{3}}\right)\leq 1

(3)

We conclude: $|AP|<1$ , $|RP|<1$ , $|OB|<1$ , thus the lemma is proven.

∎

Refer to caption — Figure 1. A hexagon with opposite sides parallel and separated by distance 1, all of its angles being $120^{\circ}$

Acknowledgement 3.

This note is one of the results of my participation in ‘Math in Moscow’ program. I would like to thank the program as well as prof. A. Skopenkov of Moscow State University for his support and help in making the note more succinct.

References

[1] K. Borsuk, Drei Sätze über die n-dimensionale euklidische Sphäre, Fund. Math. 20 (1933), 177-190.
[2] J. Kahn and G. Kalai. A counterexample to Borsuk’s conjecture, Bull. Amer. Math. Soc. (N.S.) 29 (1993), 60-62
[3] A. Nilli. On Borsuk’s problem. In Jerusalem combinatorics ’93, pages 209-210. Amer. Math. Soc., Providence, RI, 1994.
[4] Raigorodskii, A. M. On dimensionality in the Borsuk problem. Uspekhi Mat. Nauk 52 (1997), 181–182, engl. transl. in Russian Math. Surveys 52 (1997), 1324–1325
[5] Raigorodskii, A. M. On a bound in Borsuk’s problem. Uspekhi Mat. Nauk 54 (1999), 185–186, engl. transl. in Russian Math. Surveys 54 (1999), 453–454
[6] Weissbach, B. Sets with large Borsuk number. Beitra ̵̈ge Algebra Geom., 41 (2000), No. 2, 417-423.
[7] A. Hinrichs and C. Richter. New sets with large Borsuk numbers. Discrete Math., 270 (2003), 137–147.