An insight into strangeness with $\phi$(1020) production in small to large collision systems with ALICE at the LHC

Resonances are ideal candidates to probe the hadronic phase formed in heavy-ion collisions due to their short lifetimes. The lifetime of $\phi$ (46.3 fm/c) is longer compared to that of other hadronic resonances as well as the lifetime of the fireball produced in heavy-ion collisions. Thus it is expected that $\phi$ meson will not be affected by the re-scattering and re-generation processes [1] during the hadronic phase. Being the $\phi$ a bound state of a strange-antistrange quark pair (s$\bar{\rm{s}}$), a measurement of its production can help shed light on strangeness production mechanisms. Also, the study of $\phi$ in small colliding systems helps in the search for the onset of collectivity and provides a necessary baseline for heavy-ion collisions.

This article focuses on measurements of $\phi$ production with the ALICE detector at the LHC in pp collisions at $\sqrt{s}$ = 0.9, 2.76, 5.02, 7, 8 and 13 TeV, p–Pb collisions at 5.02 and 8.16 TeV, Xe–Xe collisions at $\sqrt{s_{\rm{NN}}}$ = 5.44 TeV and Pb–Pb collisions at $\sqrt{s_{\rm{NN}}}$ = 2.76 and 5.02 TeV. In particular, $p_{\mathrm{T}}$ spectra at different energies and colliding systems as well as $p_{\mathrm{T}}$-integrated particle ratios to long-lived hadrons are compared for minimum bias collisions and as a function of the charged particle multiplicity ($\langle\mathrm{d}N_{\mathrm{ch}}/\mathrm{d}\eta\rangle$). In this paper, we aim at addressing one of the major questions, namely whether $\phi$ behaves like a non-strange or strange particle. The strangeness of $\phi$ will be discussed in relation to its production mechanism, such as strangeness canonical suppression, non-equilibrium production of strange quarks and thermal models.

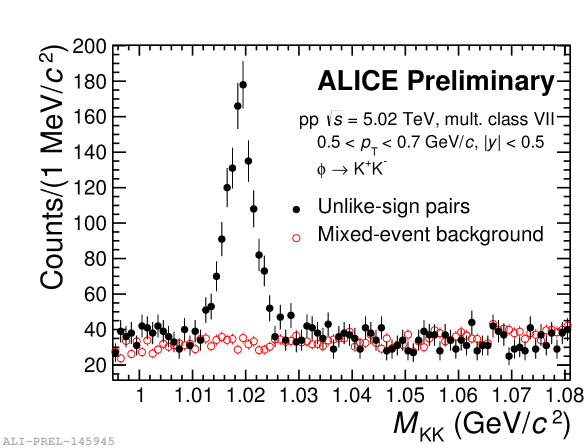
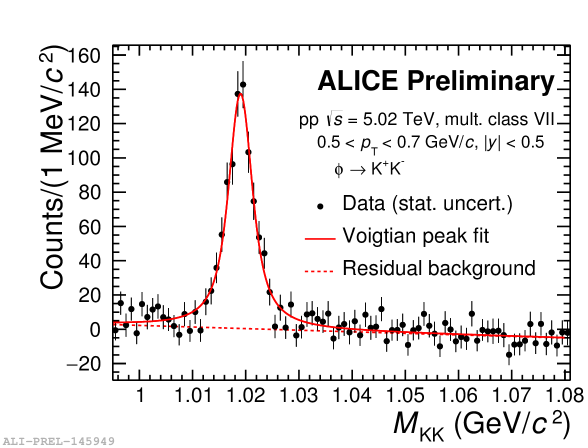
The $\phi(1020)$ is reconstructed at mid-rapidity ($|y|<$ 0.5) through an invariant mass analysis via its hadronic decay channel [2, 3] into K⁺K^- (branching ratio: 49.2%) [4]. Figure 1 shows the invariant-mass distribution for the $\phi$ in pp collisions at $\sqrt{s}$ = 5.02 TeV in the $p_{\mathrm{T}}$ range 0.5 $<$ $p_{\mathrm{T}}$ $<$ 0.7 GeV/$c$ in V0M Multiplicity class VII. The left plot of Fig. 1 shows the unlike-charge invariant-mass distribution with a combinatorial background. The event mixing and like-sign techniques are used to estimate the combinatorial background and after combinatorial background subtraction a residual background remains as shown in the right plot of Fig. 1, together with a fit used to describe the peak of $\phi$ and the residual background. The latter is mainly due to mis-identified particle decay products or from other sources of correlated pairs (e.g. mini-jets). The $\phi(1020)$ peak is fitted with a Voigtian function, a convolution of Breit-Wigner and Gaussian functions [2, 3]. For some cases, the $\phi$ peak is fitted without any combinatorial background subtraction when the combinatorial background shows large statistical fluctuation.

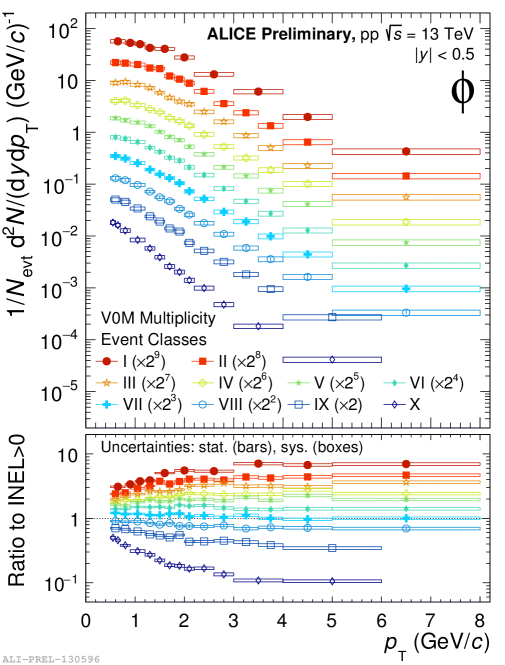
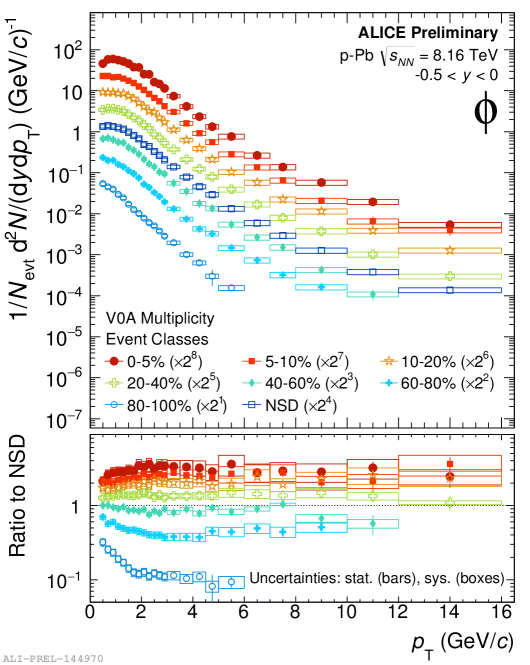
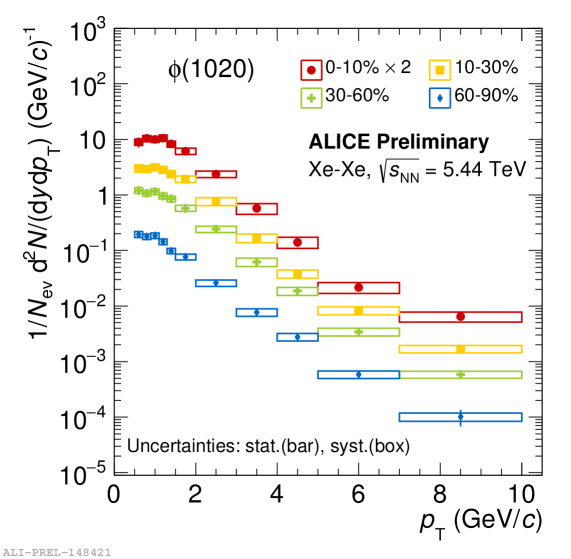
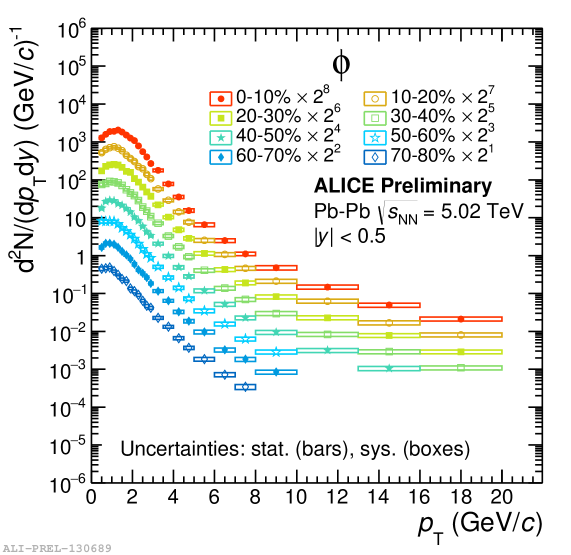
In each $p_{\mathrm{T}}$ intervals, raw yields are obtained from the fit to the signal peak and then corrected for the detector efficiency $\times$ acceptance and the branching ratio to determine the final $p_{\mathrm{T}}$ spectrum. Figure 2 shows the $p_{\mathrm{T}}$ spectra of $\phi$ mesons in pp collisions at $\sqrt{s}$ = 13 TeV (left) and p-Pb collisions at $\sqrt{s_{\rm{NN}}}$ = 8.16 TeV (right) in different V0 multiplicity classes. The lower panels show the ratio of the $p_{\mathrm{T}}$ spectra to the 0-100% $p_{\mathrm{T}}$ spectrum. Evolution of $p_{\mathrm{T}}$-spectra is observed at low-$p_{\mathrm{T}}$. For high-$p_{\mathrm{T}}$, the slopes of the spectra in different multiplicity classes seem to be similar to those observed in minimum bias pp collisions. Figure 3 shows the $p_{\mathrm{T}}$ spectra of $\phi$ mesons in Xe-Xe collisions at $\sqrt{s_{\rm{NN}}}$ = 5.44 TeV (left) and Pb-Pb collisions at $\sqrt{s_{\rm{NN}}}$ = 5.02 TeV (right) for different centrality classes.

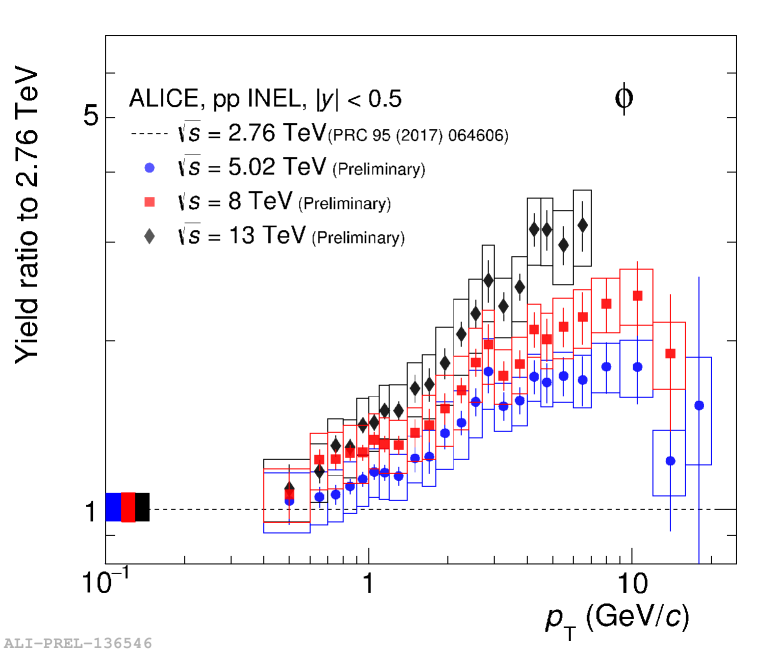
Figure 4 shows ratios of $p_{\mathrm{T}}$ spectra of $\phi$ in inelastic pp collisions at various center-of-mass energies to the spectrum obtained in pp collisions at $\sqrt{s}$ = 2.76 TeV. These ratios indicate that from 1-2 GeV/$\it c$, the yields increase as a function of collision energy, but the production at low $p_{\mathrm{T}}$ does not strongly depend on collision energy.

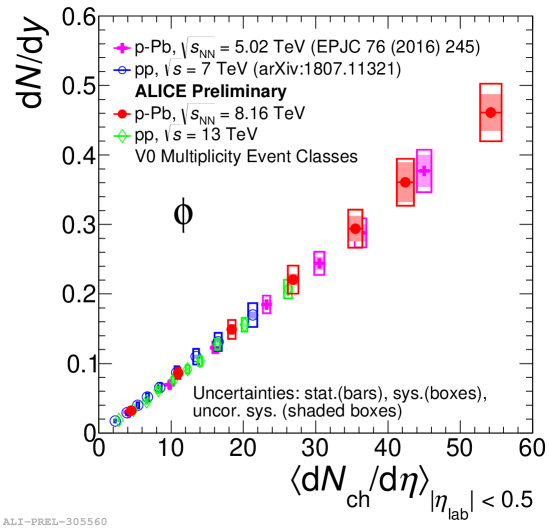
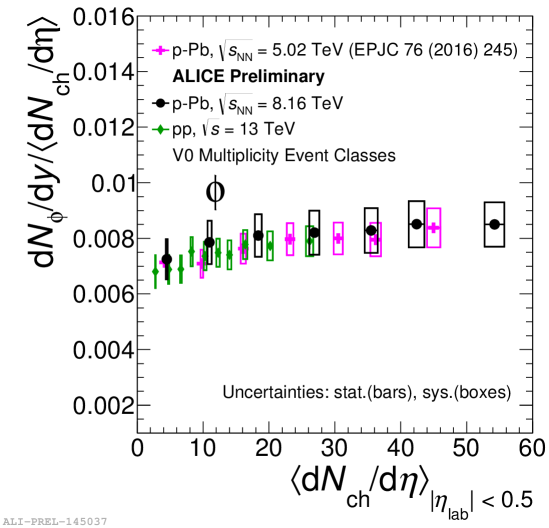
The left panel of Fig. 5 shows the integrated yield of $\phi$ in pp collisions at $\sqrt{s}$ = 7 and 13 TeV and p–Pb collisions at $\sqrt{s_{\rm{NN}}}$ = 5.02 and 8.16 TeV. The integrated yield shows a linear increase as a function of charged-particle multiplicity for both pp and p-Pb collisions. The right panel of Fig. 5 shows the $\phi$ yield normalized by the $\langle\mathrm{d}N_{\mathrm{ch}}/\mathrm{d}\eta\rangle$ value as a function of average charged particle multiplicity in pp collisions at $\sqrt{s}$ = 13 TeV and in p–Pb collisions at $\sqrt{s_{\rm{NN}}}$ = 5.02 and 8.16 TeV. The ratio is independent of collision energy, which suggests that the event multiplicity drives the particle production, irrespective of collision system type and energy.

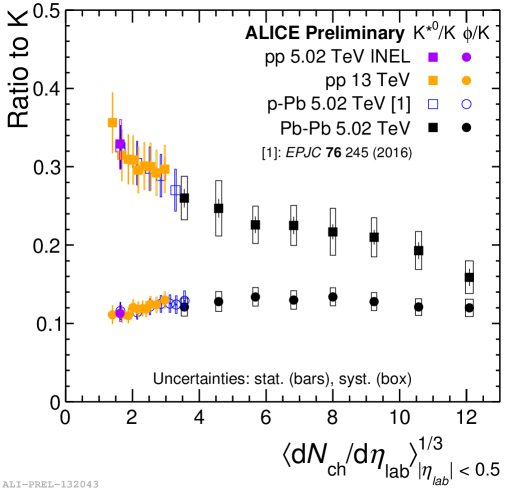
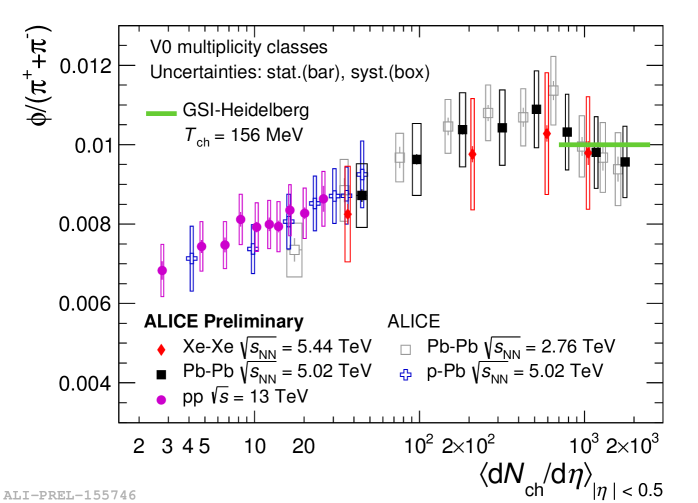
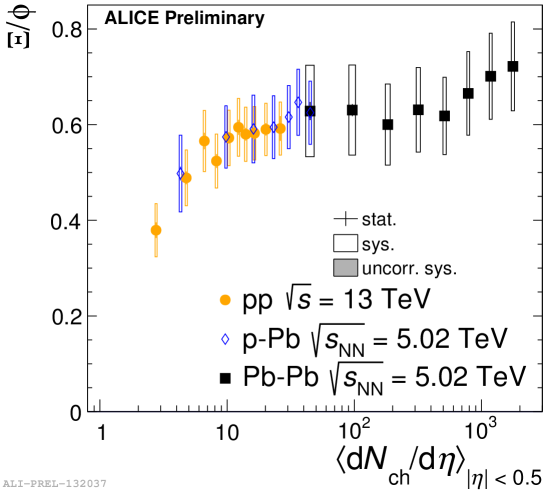
The top left panel of Fig. 6 shows the yield ratios of $\phi$ and K^∗0 to kaons as a function of charged particle multiplicity for different colliding systems at different collision energies. As the lifetime of K^∗0 is almost 10 times shorter compared to $\phi$, it is expected that K^∗0 is affected by the re-generation and/or re-scattering processes in a long-lasting hadronic phase of the expanding system. A decreasing trend in the K^∗0/K ratio is observed, suggesting that the re-scattering mechanism dominates over regeneration. As expected, the $\phi$/K ratio remains fairly flat, which indicates that either the regeneration and re-scattering are balanced or $\phi$ decays after the hadronic phase without being affected by these processes. The top right panel of Fig. 6 shows the $\phi$/$\pi$ ratio as a function of $\langle\mathrm{d}N_{\mathrm{ch}}/\mathrm{d}\eta\rangle$. The production of $\phi$ in Pb–Pb and Xe–Xe collisions is well described by a grand-canonical thermal model (GSI-Heidelberg) [5], while for small systems (pp and p–Pb collisions) the increase of the $\phi/\pi$ ratio with multiplicity is in contrast to the expectation from strangeness canonical suppression [6]. This behavior favors the non-equilibrium production of $\phi$ and/or strange particles. The bottom panel of Figure 6 shows the $\Xi$/$\phi$ ratio as a function of $\langle\mathrm{d}N_{\mathrm{ch}}/\mathrm{d}\eta\rangle$. The $\Xi/\phi$ ratio remains fairly flat or slightly increases across a wide multiplicity range. In addition, a multiplicity dependence of the ratio is observed, particularly at low multiplicities. Comparing the $\phi$ with particles with strange quark content 1 or 2, we observe that the $\phi$ behaves like a particle with open strangeness [8].

ALICE has studied $\phi$ production as a function of collision energy and charged particle multiplicity in different colliding systems. The event multiplicity seems to drive the production of hadrons, including $\phi$ production, irrespective of collision energy for pp and p-Pb collisions at the LHC. The $\phi$/K ratio remains rather flat across a wide range of multiplicity and across colliding systems, which indicates that either regeneration and re-scattering are balanced or that the $\phi$ decays after the hadronic phase in Pb–Pb collisions and is not affected by re-scattering and regeneration. The latter seems to be the likely scenario as $\phi$ has an almost 10 times longer lifetime than K^∗0. Looking at the $\phi$/$\pi$, $\phi$/K and $\Xi/\phi$ ratios, the $\phi$ meson seems to show a similar behavior to that of particles with open strangeness.

ST acknowledges the financial support by DST-INSPIRE program of the Government of India.