An Invariant of Virtual Trivalent Spatial Graphs

Evan Carr Elon University ecarr10@elon.edu , Nancy Scherich Elon University nscherich@elon.edu http://www.nancyscherich.com and Sherilyn Tamagawa Davidson College shtamagawa@davidson.edu http://sherilyntamagawa.com

Abstract.

We create an invariant of virtual $Y$ -oriented trivalent spatial graphs using colorings by virtual Niebrzydowski algebras. This paper generalizes the color invariants using virtual tribrackets and Niebrzydowski algebras by Nelson-Pico, and Graves-Nelson-T. We computed all tribrackets, Niebrzydowski algebras and virtual Niebrzydowski algebras of orders 3 and 4, and provide generative code for all data sets.

1. Introduction

A Y-oriented trivalent spatial graph is an oriented finite graph embedded in $\mathbb{R}^{3}$ and which contains only degree 3 vertices. The $Y$ -orientation forbids sources or sinks at the vertices, but requires vertex orientations with two-in-one-out or two-out-one-in. A virtual $Y$ -oriented trivalent spatial graph is a $Y$ -oriented trivalent spatial graph with an additional type of crossing, a virtual crossing. Virtual crossings were originally defined for virtual knots in [6], and we denote virtual crossings by a circle over the crossing in the diagram. Two virtual $Y$ -oriented trivalent spatial graphs are pictured below.

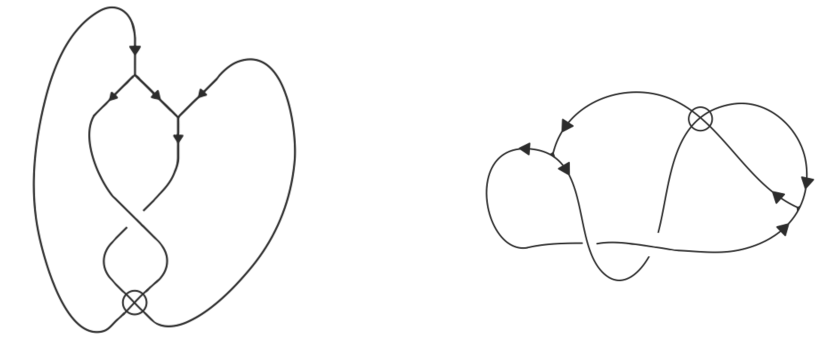
Refer to caption — Figure 1. Two virtual Y-oriented trivalent spatial graphs.

Virtual trivalent graphs have become increasingly important in finite type invariant theory since Bar-Natan and Dancso developed w-Foams to study certain types of knotted surfaces in $\mathbb{R}^{4}$ [1]. Murakami, Ohtsuki, and Yamada proved that the Reshetikhin-Turaev invariant of a link in $\mathbb{R}^{3}$ can be computed using (classical) oriented trivalent graphs [7]. Trivalent vertices are particularly useful in algebraic computations by labeling the edges of a trivalent graph. For example, the trivalent vertex orientated with two-in-one-out can be used as a visual representation of a Lie bracket, as was done in [2]. The two inputs label the inward oriented arcs of the vertex, and the output of the Lie bracket labels the outward oriented arc. Similarly, the vertex oriented with two-out-one-in can be used to represent a coproduct. In this paper, instead of labeling the arcs of a graph, we label/color the planar complement of the graph to attain an invariant.

Coloring invariants of knotted objects have been widely studied in various different contexts. For example, Niebrzydowski used an algebraic structure called a ternary quasigroup to color planar knot complements [9]. Nelson and Pico used virtual tribrackets to color planar complements of oriented virtual link diagrams [8]. Extending the ideas of Niebrzydowski and Nelson-Pico, Graves-Nelson-T. introduced Niebrzydowski algebras to color planar complements of $Y$ -oriented trivalent spatial graphs [5].

In the original definition of an Niebrzydowski algebra given in [5], there is a well-definedness issue related to the partial product structure. Partial products can lead to violations of the Reidemeister moves, which nullifies the use of an Niebrzydowski algebra to define a graph invariant. We offer a correction to this issue with the addition of an extra axiom to the definition of an Niebrzydowski algebra, as described in Section 4.

In this paper, we combine the ideas of a virtual tribracket and a Niebrzydowski algebra to define a virtual Niebrzydowski algebra, as stated in Definition 3.4 in Section 3. Virtual Niebrzydowski algebras can be used to color the planar complements of virtual $Y$ -oriented trivalent spatial graphs. Our main result proves that the number of colorings of a graph by a virtual Niebrzydowski algebra is an invariant of the graph.

Main result(Theorem 3.6) Let $X$ be a virtual Niebrzydowski algebra and $\Gamma$ a virtual $Y$ -oriented trivalent spatial graph. The number of $X$ -colorings of the planar complement of $\Gamma$ is invariant under the virtual $Y$ -oriented Reidemeister moves, and is therefore an integer-valued invariant of virtual $Y$ -oriented trivalent spatial graphs.

Organization of the paper. In Section 2, we discuss the virtual $Y$ -oriented Reidemeister moves for virtual $Y$ -oriented trivalent spatial graphs. Section 3 reviews the foundational definitions of tribrackets, virtual tribrackets, Niebrzydowski algebras, and the associated coloring invariants for these structures. We state our new definition of virtual Niebrzydowski algebras and prove our main result. In Section 4, we discuss the well-definedness issues of the original definition of an Niebrzydowski algebra and give a corrected definition of a partially defined Niebrzydowski algebra, and extend this notion to partially defined virtual Niebrzydowski algebras as well. Much of the work in this paper is computational, and in Section 5 we share the computational results and give links to generative code to use the data sets.

Acknowledgments. The authors would like to thank Sam Nelson for helpful conversations, and our anonymous referee for catching an important error. The second author was partially supported by the NSERC grant RGPIN-2018-04350. This project occurred in part as an undergraduate student research project through Elon University where the first author was mentored by the second author.

2. Virtual Y-oriented Reidemeister Moves

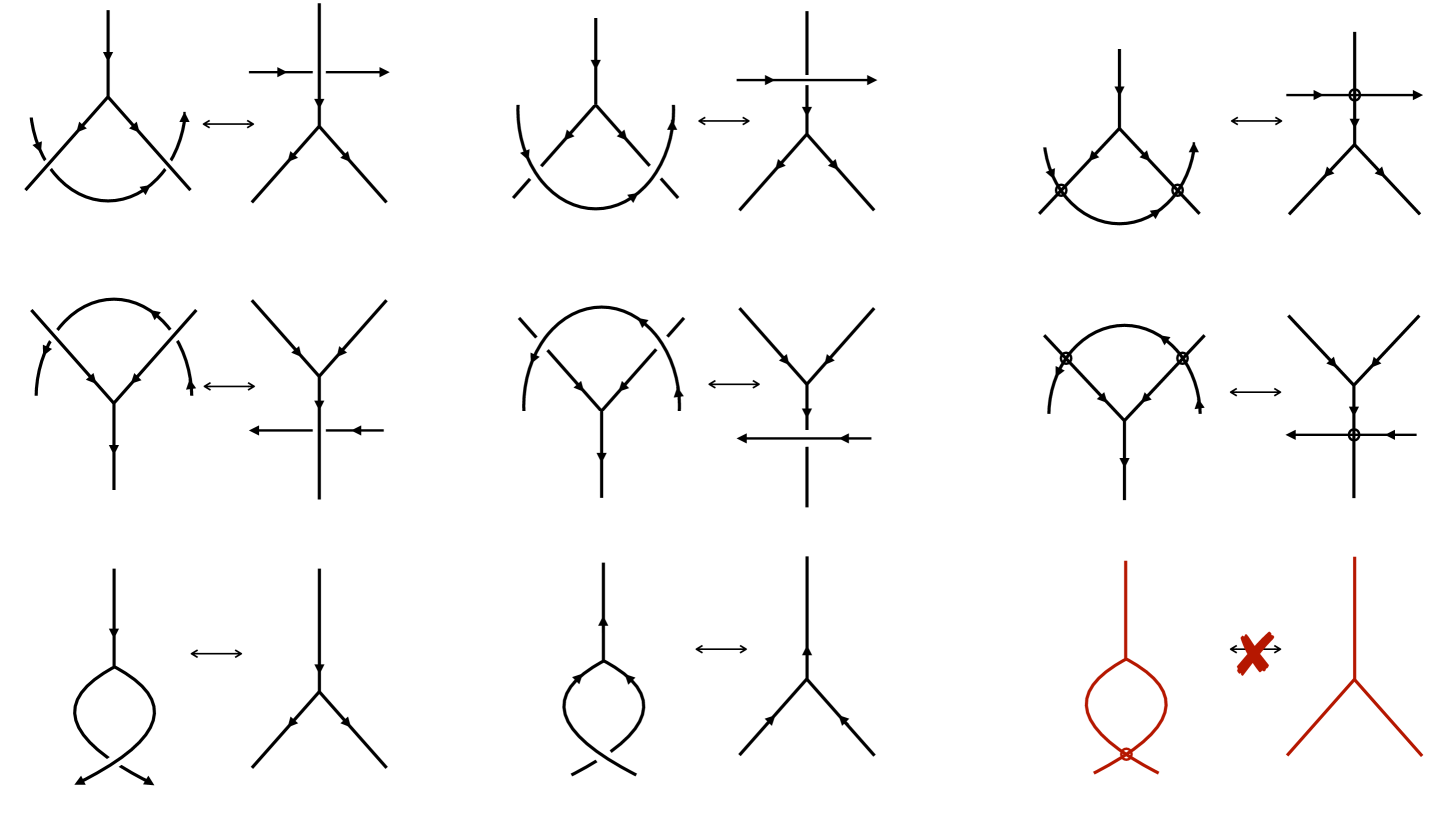
Graves, Nelson and the third author found a generating set of $Y$ -oriented Reidemeister moves for $Y$ -oriented trivalent spatial graphs [5]. Flemming and Mellor studied virtual graphs with arbitrary degree and found a generating set of virtual graph Reidemeister moves in [4]. Combining the results of Graves-Nelson-T. and Flemming-Mellor, gives a complete list of Reidemeister moves for $Y$ -oriented trivalent spatial graphs. Any set of generating Reidemeister moves for virtual knots (aka virtual Reidemeister moves) together with the moves in Figure 2 form a generating set of $Y$ -oriented Reidemeister moves for virtual $Y$ -oriented trivalent spatial graphs.

Notice, the virtual generalization of the $R4$ move is a forbidden move, and is not considered part of our virtual $Y$ -oriented Reidemeister move list.

3. From Tribrackets to Virtual Niebrzydowski Algebras

The new contributions of this paper are to synthesize two different generalizations of a tribracket, namely the virtual tribracket and the Niebrzydowski Algebra, to create the virtual Niebrzydowski algebra. In this section, we explain each of these objects and their associated coloring invariants. We state the new definition of the virtual Niebrzydowski algebra along with its associated coloring invariant.

The term tribracket was first coined by Nelson-Pico in [8] as an adaptation of the ternary quaisgroup defined in [9] by Niebrzydowski.

Definition 3.1.

(Niebrzydowski, Nelson-Pico) Let $X$ be a set. A tribracket on $X$ is a ternary operation $[-,-,-]:X\times X\times X\rightarrow X$ satisfying the following conditions.

(1)

In the equation $[a,b,c]=d$ , any three of the four elements in $\{a,b,c,d\}$ determine the fourth.

(2)

For all $a,b,c,d\in X$ the following equalities are true.

	$\displaystyle[a,b,[b,c,d]]$	$\displaystyle=[a,[a,b,c],[[a,b,c],c,d]]$	$\displaystyle\hfill(III.i)$
	$\displaystyle[[a,b,c],c,d]$	$\displaystyle=[[a,b,[b,c,d]],[b,c,d],d]$	$\displaystyle\hfill(III.ii)$

The axioms of a tribracket are derived from the Reidemeister moves and can be interpreted as instructions for how to color the planar complement of a link diagram, see Figure 3. Niebrzydowski proved that the number of colorings of the planar complement of an oriented link diagram by a tribracket is an integer-valued invariant for classical links [9, 8].

There are two natural extensions of classical link theory; virtual knot/link theory and trivalent spatial graphs. Nelson and Pico extend the notion of a tribracket to virtual knots in the form of a virtual tribracket.

Definition 3.2.

(Nelson-Pico) A virtual tribracket on a set X is two ternary operations $[-,-,-],\langle-,-,-\rangle:X\times X\times X\rightarrow X$ which satisfy the following rules.

(1)

Both $[-,-,-]$ and $\langle-,-,-\rangle$ are tribrackets on $X$ .
(2)

For all $a,b,c,d\in X$ , the following equalities are true.
1. (a)
  
  $\langle a,\langle a,b,c\rangle,c\rangle=b$ (vII)
2. (b)
  
  $[\langle a,b,c\rangle,c,d]=\langle[a,b,\langle b,c,d\rangle],\langle b,c,d\rangle,d\rangle$ (m.i)
3. (c)
  
  $[a,b,\langle b,c,d\rangle]=\langle a,\langle a,b,c\rangle,[\langle a,b,c\rangle,c,d]\rangle$ (m.ii)

The axioms of a virtual tribracket are derived from the virtual Reidemeister moves and can be interpreted as instructions for how to color the planar complement of a virtual link diagram, see Figure 3. The square bracket $``[-,-,-]"$ is used for classical crossings, and the angle bracket $``\langle-,-,-\rangle"$ is used for virtual crossings. Nelson-Pico proved that the number of colorings of the planar complement of an oriented virtual link diagram by a virtual tribracket is an integer-valued invariant for virtual links [8].

In another direction, Graves-Nelson-T. introduced the Niebrzydowski algebras as a tool to study $Y$ -oriented trivalent spatial graphs [5]. In a similar manner to the tribracket coloring invariant, one can also color the planar complement of a $Y$ -oriented trivalent spatial graph with Niebrzydowski algebras to get an invariant of $Y$ -oriented trivalent spatial graphs, see Figure 3.

Definition 3.3.

(Graves-Nelson-T.) Let $X$ be a set with a ternary operation $[-,-,-]:X\times X\times X\rightarrow X$ and a product structure $a,b\mapsto ab$ . $X$ is a Niebrzydowski algebra if the following conditions are satisfied.

(1)

Any two of the three $\{a,b,c\}$ in $ab=c$ determines the third.
(2)

$[-,-,-]$ is a tribracket on $X$ .
(3)
For all $a,b,c,d\in X$ ,the following equalities are true.
1. (a)
  
  $[a,ab,b]=ab$ (R4)
2. (b)
  
  $a[a,b,c]=[a,b,bc]$ (R5.1)
3. (c)
  
  $[a,b,c]=[[a,b,bc],bc,c]$ (R5.2)
4. (d)
  
  $[a,b,c]c=[ab,b,c]$ (R5.3)
5. (e)
  
  $[a,b,c]=[a,ab,[ab,b,c]]$ (R5.4)

The definition shown here is a slight modification of the definition given by Graves-Nelson-T. in [5]. In the original definition of the Niebrzydowski algebra, the product could be a partially defined binary operation. This leads to a welldefinedness issue for the coloring invariant, which we address in Section 4. The definition above requires the product to be fully defined on $X\times X$ , and this leads to a well defined coloring invariant.

The name algebra is slightly misleading. The Niebrzydowski algebras are not algebras in the sense of a module with multiplication. But instead, these Niebrzydowski algebras are like an algebra of the tribracket by adding a multiplication to the existing tribracket structure.

In the definition of a Niebrzydowski algebra, the relations $R4$ and $R5.1$ , $R5.2$ , $R5.3$ , $R5.4$ are derived from the $R4$ and $R5$ $Y$ -oriented Reidemeister moves. Coloring the planar complement of the arcs of the graph using the coloring rules in Figure 3 gives the relations $R4$ , $R5.1$ , $R5.2$ , $R5.3$ , and $R5.4$ . For more details, see Section 3 of [5].

In this paper, we combine the ideas of virtual tribrackets and Niebrzydowski algebras to get a virtual Niebrzydowski algebra. We can color the regions of the planar complement of virtual $Y$ -oriented trivalent spatial graph to obtain an invariant that generalizes both the tribracket and Niebrzydowski algebra color invariants.

Definition 3.4.

A virtual Niebrzydowski algebra is a set $X$ with virtual tribracket given by $[-,-,-]$ and $\langle-,-,-\rangle$ , a product $\cdot$ which maps $a,b\mapsto ab$ , and satisfies the following conditions.

(1)

$[-,-,-]$ and $\langle-,-,-\rangle$ are a virtual tribracket as in Definition 3.2.
(2)

$X$ together with $[-,-,-]$ and the product $\cdot$ is a Niebrzydowski algebra as in Definition 3.3.
(3)
For all $a,b,c\in X$ ,the following equalities are true.
1. (a)
  
  $a\langle a,b,c\rangle=\langle a,b,bc\rangle$ (vR5.1)
2. (b)
  
  $\langle\langle a,b,bc\rangle,bc,c\rangle=\langle a,b,c\rangle$ (vR5.2)
3. (c)
  
  $\langle a,b,c\rangle c=\langle ab,b,c\rangle$ (vR5.3)
4. (d)
  
  $\langle a,ab,\langle ab,b,c\rangle\rangle=\langle a,b,c\rangle$ (vR5.4)

Example 3.5. The following brackets and product structure form a virtual Niebrzydowski algebras on the set $X=\{1,2,3\}$ . The tribracket and multiplication structures are given in tables. For example, to determine $[a,b,c]$ , take the the $b,c$ -entry of the $a$ ’th matrix in $[-,-,-]$ .

	$\displaystyle[-,-,-]:$	$\displaystyle\left[\begin{array}[]{rrr}1&2&3\\ 3&1&2\\ 2&3&1\end{array}\right],\left[\begin{array}[]{rrr}2&3&1\\ 1&2&3\\ 3&1&2\end{array}\right],\left[\begin{array}[]{rrr}3&1&2\\ 2&3&1\\ 1&2&3\end{array}\right]$	$\displaystyle\cdot:\left[\begin{array}[]{rrr}1&3&2\\ 3&2&1\\ 2&1&3\end{array}\right]$
	$\displaystyle\langle-,-,-\rangle:$	$\displaystyle\left[\begin{array}[]{rrr}1&2&3\\ 3&1&2\\ 2&3&1\end{array}\right],\left[\begin{array}[]{rrr}2&3&1\\ 1&2&3\\ 3&1&2\end{array}\right],\left[\begin{array}[]{rrr}3&1&2\\ 2&3&1\\ 1&2&3\end{array}\right]$

Like the virtual tribrackets in [8], and Niebrzydowski algebras in [5], the equations in the definition of the virtual Niebrzydowski algebra are derived from coloring the planar complements of virtual $Y$ -oriented Reidemseister moves. Figure 3 shows how to color regions of the planar complements of graphs using the tribracket and product structure of a virtual Niebrzydowski algebra.

As proved by Nelson-Pico, the number of colorings of a virtual knot by a virtual tribracket is an invariant of virtual knots [8]. That is, the axioms of virtual tribrackets are derived from, and hence preserve, the virtual Reidemeister moves. Similarly, Graves-Nelson-T. proved that the number of Niebrzydowski algebra colorings of the planar complement of a $Y$ -oriented trivalent spatial graph is an invariant of $Y$ -oriented trivalent spatial graphs[5]. That is, all of the (classical) $Y$ -oriented Reidemeister moves and the classical Reidemeister moves are preserved by the axioms of a Niebrzydowski algebra. Virtual Niebrzydowski algebras are Niebrzydowski algebras with an extra virtual tribracket. Combining the two results for tribrackets and Niebrzydowski algebras, to show that the number of colorings of a virtual $Y$ -oriented trivalent spatial graph by a virtual Niebrzydowski algebra is an invariant, we only need to check that the two virtual $Y$ -oriented Reidemeister moves ( $vR5$ ) are preserved under these colorings.

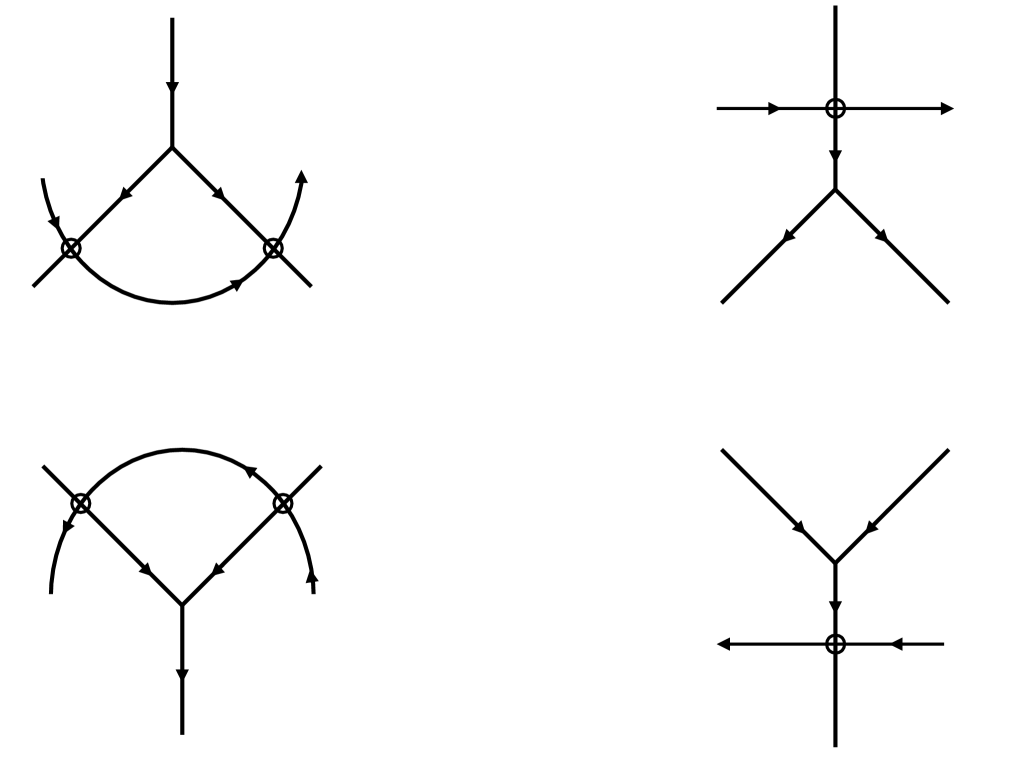
Figure 4 shows the two orientations of the virtual $Y$ -oriented Reidemeister move $vR5$ colored according to the rules of the product $\cdot$ and tribracket $\langle-,-,-\rangle$ . In the definition of a virtual Niebrzydowski algebra, axioms $vR5.1$ and $vR5.2$ can be seen by equating the two blue and two red quantities in the top diagrams in Figure 4. Axiom $vR5.4$ can be seen by equating the two red quantities in the bottom diagrams in Figure 4. By equating the blue quantities in the bottom diagram of Figure 4, we get the equation $\langle a,ab,\langle ab,b,c\rangle\rangle c=\langle ab,b,c\rangle$ . By substituting $\langle a,ab,\langle ab,b,c\rangle\rangle=\langle a,b,c\rangle$ from axiom $vR5.4$ , we get $vR5.3$ .

By construction, the following theorem is true.

Theorem 3.5.

Let $X$ be a virtual Niebrzydowski algebra and $\Gamma$ a virtual $Y$ -oriented trivalent spatial graph. The number $\Phi_{X}(\Gamma)$ of $X$ -colorings of the planar complement of $\Gamma$ is invariant under the virtual $Y$ -oriented Reidemeister moves, and is therefore an integer-valued invariant of virtual $Y$ -oriented trivalent spatial graphs.

Example 3.7. Using $X=\{1,2,3\}$ and the virtual Niebrzydowski algebra from Example 3.5, Figure 5 shows two virtual Y-oriented trivalent spatial graphs that are distinguished by the invariant $\Phi_{X}$ . For the graph $K_{1}$ , choosing the labels $a,b$ , and $c$ determines the colorings for every other region and is limited by one equation $a\langle a,ac,a\rangle=\langle a,ac,c\rangle c.$ There are three possible choices for $a,b$ , and $c$ from $X$ , which makes $\Phi_{X}(K_{1})=3$ .

For the graph $K_{2}$ , choosing the labels $a,b,c,d$ and $e$ determines the coloring of the entire planar complement and is limited by the following seven equations.

$\displaystyle bc$	$\displaystyle=b((bc)[bc,c,a])$	$\displaystyle\langle b,(bc)[bc,c,a],[bc,c,a]a\rangle$	$\displaystyle=c$
$\displaystyle[bc,c,a]$	$\displaystyle=((bc([bc,c,a])([bc,c,a]a)$	$\displaystyle[[bc,c,a]a,a\langle a,d,e\rangle,e]$	$\displaystyle=d$
$\displaystyle a$	$\displaystyle=([bc,c,a]a)(a\langle a,d,e\rangle)$	$\displaystyle[c,a,d]$	$\displaystyle=[bc,c,a]a$
$\displaystyle\langle a,d,e\rangle$	$\displaystyle=(a\langle a,d,e\rangle)e$

There are 9 possible choices for the labels $a,b,c,d$ and $e$ from $X$ , which makes $\Phi_{X}(K_{2})=9$ . Since $\Phi_{X}(K_{1})\neq\Phi_{X}(K_{2})$ , then $K_{1}\neq K_{2}$ .

4. Partial Products and Welldefinedness

In their original paper, Graves-Nelson-T. defined a Niebrzydowski algebra as in Definition 3.3 but where the product structure need only be partially defined. That is, if the product is written as a table, some entries of the table are left blank, as shown below. We will call a Niebrzydowski algebra with a partially defined product structure a partially defined Niebrzydowski algebra.

\left[\begin{array}[]{rrr}1&-&2\\ 3&2&-\\ -&-&3\end{array}\right]

Using a partially defined Niebrzydowski algebra to color the planar complement of a graph restricts the colorings to only include those that give rise to defined products. For example, in Figure 6, if $ab$ is not defined, then $a$ and $b$ cannot color regions on either side of a trivalent edge.

Figure 6. Partial products restrict possible colorings around a trivalent vertex.

There are several benefits of using a partially defined Niebrzydowski algebra. The partial product restricts the number of colorings of a graph, making the associated coloring invariant easier to compute. Also, there are not many examples of fully defined Niebrzydowski algebras, as will be described in Section 5. Allowing a partial product gives a much larger family of Niebrzydowski algebra coloring invariants. However, the use of a partially defined product structure can lead to a welldefinedness issue.

Suppose $X$ is a partially defined Niebrzydowski algebra where $b,c\in X$ but $bc$ is undefined. Consider the colorings in Figure 7 before and after a Reidemeister move. The coloring on the right does not use $bc$ , the undefined product, where the coloring on the left does use the product $bc$ . Therefore the coloring on the right is a valid coloring and the coloring on the left is not. This shows that coloring the planar complement by a partially defined Niebrzydowski algebra does not respect the Reidemeister moves and is not an invariant of the graph.

We give a solution to this welldefinedness issue. Keeping the definition of the Niebrzydowski algebra to include the partial products, we can instead define the coloring invariant associated to the partially defined Niebrzydowski algebra to count only admissible colorings of a graph. An admissible coloring is a coloring of the planar complement where an undefined product is never induced by a Reidmemeister move. This would of course lead to a well defined graph invariant, but it is very difficult to compute as it is difficult to prove a coloring is admissible, and would be very graph dependent.

To make this coloring invariant computable, we can add an axiom to the definition of an Niebrzydowski algebra that will force every coloring by that Niebrzydowski algebra to be admissible. At first glance, it is tempting to add to the definition of Niebrzydowski algebra that for every axiom, the left side of the equation is defined if and only the right side is defined. For example, $(3)(a)$ of Definition 3.3 states that

[a,ab,b]=ab.

In this example, it is true that $[a,ab,b]$ is defined if and only if $ab$ is defined. However, in axiom $(3)(c)$ ,

[a,b,c]=[[a,b,bc],bc,c],

$[a,b,c]$ is always defined for all $a,b,c$ , so $bc$ must always be defined. This would imply that the product structure is fully defined.

Instead, we focus on the the Reidemeister moves to derive the axiom. The axiom needs to ensure that the seemingly admissible coloring on the right side of Figure 7 never occurs. So if $bc$ is undefined, then $a$ and $a[a,b,c]$ cannot color regions on either side of a trivalent vertex. One way to ensure this is if $a[a,b,c]$ , the product of $a$ and $[a,b,c]$ , is also undefined. Taking into account the same Reidemeister move with the negative crossings, the new axiom is:

\text{For all $b$ and $c$, }bc\text{ is defined if and only if }a[a,b,c]\text{ and }[b,c,a]a\text{ are defined for all $a$}.

The corrected definition of a partially defined Niebrzydowski algebra with the new axiom is stated below.

Definition 4.1.

Let $X$ be a set with a ternary operation $[-,-,-]:X\times X\times X\rightarrow X$ and a partial product $a,b\mapsto ab$ structure. $X$ is a partially defined Niebrzydowski algebra if the following conditions are satisfied.

(1)

If the product $ab$ is defined, any two of the three $\{a,b,c\}$ in $ab=c$ determines the third.
(2)

$[-,-,-]$ is a tribracket on $X$ .
(3)
For all $a,b,c,d\in X$ , if both sides of the equations are defined, then the following equalities are true.
1. (a)
  
  $[a,ab,b]=ab$ (R4)
2. (b)
  
  $a[a,b,c]=[a,b,bc]$ (R5.1)
3. (c)
  
  $[a,b,c]=[[a,b,bc],bc,c]$ (R5.2)
4. (d)
  
  $[a,b,c]c=[ab,b,c]$ (R5.3)
5. (e)
  
  $[a,b,c]=[a,ab,[ab,b,c]]$ (R5.4)
(4)

For all $b$ and $c$ , $bc$ is defined if and only if $a[a,b,c]$ and $[b,c,a]a$ are defined for all $a$ .

The addition of the new axiom, axiom (4), ensures that any coloring by a partially defined Niebrzydowski algebra will be an admissible coloring and respect the Reidemeister moves.

Corollary 4.2.

Any coloring of the planar complement of a Y-oriented spatial graph by a partially defined Niebrzydowski algebra is an admissible coloring. The total number of admissible colorings by a partially defined Niebrzydowski algebra is a graph invariant.

Applying the same reasoning to the virtual analogue of the Reidemeister move shown in Figure 4, we can add the same axiom for the $\langle-,-,-\rangle$ bracket. This will ensure that every coloring by a partially defined virtual Niebrzydowski algebra is an admissible coloring.

Definition 4.3.

A partially defined virtual Niebrzydowski algebra is a set $X$ with virtual tribracket given by $[-,-,-]$ and $\langle-,-,-\rangle$ , a partial product $\cdot$ which maps $a,b\mapsto ab$ , and satisfies the following conditions.

(1)

$[-,-,-]$ and $\langle-,-,-\rangle$ are a virtual tribracket as in Definition 3.2.
(2)

$X$ together with $[-,-,-]$ and the product $\cdot$ is a partially defined Niebrzydowski algebra as in Definition 4.1.
(3)
For all $a,b,c\in X$ , if both sides of the equations are defined, then the following equalities are true,
1. (a)
  
  $a\langle a,b,c\rangle=\langle a,b,bc\rangle$ (vR5.1)
2. (b)
  
  $\langle\langle a,b,bc\rangle,bc,c\rangle=\langle a,b,c\rangle$ (vR5.2)
3. (c)
  
  $\langle a,b,c\rangle c=\langle ab,b,c\rangle$ (vR5.3)
4. (d)
  
  $\langle a,ab,\langle ab,b,c\rangle\rangle=\langle a,b,c\rangle$ (vR5.4)
(4)

For all $b$ and $c$ , $bc$ is defined if and only if $a\langle a,b,c\rangle$ and $\langle b,c,a\rangle a$ are defined for all $a$ .

Corollary 4.4.

Any coloring of the planar complement of a virtual Y-oriented spatial graph by a partially defined virtual Niebrzydowski algebra is an admissible coloring. The total number of admissible colorings by a partially defined virtual Niebrzydowski algebra is a graph invariant.

Example 4.5.

The set $X=\{1,2,3,4\}$ with the following tribracket and multiplicative structures forms a partially defined virtual Niebrzydowski algebra.

	$\displaystyle[-,-,-]:$	$\displaystyle\left[\begin{array}[]{rrrr}1&2&3&4\\ 4&1&2&3\\ 3&4&1&2\\ 2&3&4&1\end{array}\right],\left[\begin{array}[]{rrrr}2&3&4&1\\ 1&2&3&4\\ 4&1&2&3\\ 3&4&1&2\end{array}\right],\left[\begin{array}[]{rrrr}3&4&1&2\\ 2&3&4&1\\ 1&2&3&4\\ 4&1&2&3\end{array}\right],\left[\begin{array}[]{rrrr}4&1&2&3\\ 3&4&1&2\\ 2&3&4&1\\ 1&2&3&4\end{array}\right]$
	$\displaystyle\langle-,-,-\rangle:$	$\displaystyle\left[\begin{array}[]{rrrr}1&2&3&4\\ 4&1&2&3\\ 3&4&1&2\\ 2&3&4&1\end{array}\right],\left[\begin{array}[]{rrrr}2&3&4&1\\ 1&2&3&4\\ 4&1&2&3\\ 3&4&1&2\end{array}\right],\left[\begin{array}[]{rrrr}3&4&1&2\\ 2&3&4&1\\ 1&2&3&4\\ 4&1&2&3\end{array}\right],\left[\begin{array}[]{rrrr}4&1&2&3\\ 3&4&1&2\\ 2&3&4&1\\ 1&2&3&4\end{array}\right]$
	$\displaystyle\cdot:$	$\displaystyle\left[\begin{array}[]{rrrr}1&-&-&-\\ -&2&-&-\\ -&-&3&-\\ -&-&-&4\end{array}\right]$

5. Computational Results

How many different coloring invariants are there? That is, how many tribrackets, Niebrzydowski algebras, and virtual Niebrzydowski algebras are there? Using Latin squares and Latin cubes, we exhaustively generated lists of all tribrackets, Niebrzydowski algebras and virtual Niebrzydowski algebras on a set with 3 elements, and a set with 4 elements. All of the code to verify our results and to generate usable lists of tribrackets and Niebrzydowski algebras can be found on GitHub in [3].

5.1. Latin Squares and Cubes.

A Latin square of order $n$ is an $n\times n$ array filled with $n$ different symbols, each occurring exactly once in each row and exactly once in each column. Let $X$ be a set with $n$ elements and $\mathcal{N}$ a Niebrzydowski algebra on $X$ . Condition (1) in Definition 3.3 of a Niebrzydowski algebra sates for any two of the three $\{a,b,c\}\subseteq X$ in the equation $a\cdot b=c$ determines the third. This condition requires that any complete multiplication table for the product operation must be a Latin square. On the other hand, for a partially defined product, any two of the three $\{a,b,c\}\subseteq X$ in the equation $a\cdot b=c$ determines the third only implies no row or column of the multiplication table can contain a repeated entry. From this definition, a partially defined product does not need to be completable to a Latin square.

A Latin cube of order $n$ is an $n\times n\times n$ cube array filled with $n$ different symbols, each occurring exactly once in each row, exactly once in each column, and exactly once in each third dimension. Condition (1) in Definition 3.1 of a tribracket requires that any multiplication table for the tribracket operation must be a Latin cube of order $n$ .

The number of Latin squares of order $n$ has a closed formula, though not easily computable, and has been been computed up to $n=10$ in the Online Encyclopedia of Integer Sequences (OEIS) [10] as sequence A002860. There are 12 Latin squares order three, 576 Latin squares order four, and 161,280 Latin squares order five. There are 24 Latin cubes or order three, 55,296 Latin cubes or order four, and 2,781,803,520 Latin cubes of order five, as verified in sequence A098679 in the OEIS.

5.2. Tribrackets

To generate tribrackets, we first generated all Latin cubes of order 3 and 4, and then exhaustively checked which cubes satisfied the tribracket axioms. Our computations have revealed that there exist 12 distinct tribrackets order 3 and 168 distinct tribrackets order 4. We guess that there are 4680 tribrackets of order 5, and in general $n(n^{(n-1)}-1)\frac{(n-2)!}{(n-1)}$ tribrackets of order $n$ , based on the sequence A059522 from OEIS. Our computational approach was not efficient enough to exhaustively generate and search through the 2.7 billion Latin Cubes of order 5, but we encourage the reader to be more clever than we were.

By considering all pairs of tribrackets and checking to see which pairings satisfy the virtual tribracket axioms, we exhaustively computed all virtual tribrackets of order 3 and 4. We found all 24 distinct virtual Tribrackets order 3, and 1080 distinct virtual Tribrackets of order 4.

5.3. Niebrzydowski Algebras

Compared to the plethora of tribrackets, Niebrzydowski algebras are quite scarce. By exhaustively searching all pairings of a tribracket with a Latin square, we demonstrated there is a unique Niebrzydowski algebra of order 3 (the one shown in Example 3.5), and no Niebrzydowski algebras of order 4. We suspect this inductively implies there are no Niebrzydowski algebras of order $n>4$ , though we cannot prove it.

Loosening the restrictions to allow for a partially defined product, we determined there are 6 partially defined Niebrzydowski algebras of order 3. All instances used the same tribracket as in Example 3.5, and the 6 different partial products are listed below. It turns out that for order 3, every partial product square can be completed to a fully defined Latin square.

\left[\begin{array}[]{rrr}-&-&2\\ 3&-&-\\ -&1&-\end{array}\right],\left[\begin{array}[]{rrr}1&3&-\\ -&2&1\\ 2&-&3\end{array}\right],\left[\begin{array}[]{rrr}-&3&-\\ -&-&1\\ 2&-&-\end{array}\right],

\left[\begin{array}[]{rrr}1&-&2\\ 3&2&-\\ -&1&3\end{array}\right],\left[\begin{array}[]{rrr}1&-&-\\ -&2&-\\ -&-&3\end{array}\right],\left[\begin{array}[]{rrr}-&3&2\\ 3&-&1\\ 2&1&-\end{array}\right]

We also found 28 partially defined Niebrzydowski algebras of order 4. We only searched for partial squares that can be completed to a fully defined Latin square. It is possible that there are examples that we did not find that have a product which does not complete to a Latin square.

5.4. Virtual Niebrzydowski Algebras

Similarly to the Niebrzydowski algebras, we found there to be a unique virtual Niebrzydowski algebra of order 3 (as shown in Example 3.5), and since there is no Niebrzydowski algebra of order 4, there is no virtual Niebrzydowski algebra of order 4.

There are exactly 6 partially defined virtual Niebrzydowski algebras of order 3, all which come from the 6 examples of the partially defined Niebrzydowski algebras listed above.

Lastly, we found 52 partially defined virtual Niebrzydowski algebras of order 4. We only searched for partial products that can be completed to a fully defined Latin cube, so there could potentially be more examples than found here. The order $4$ partial squares have an entry for every row and for every column, and fit into one of the patterns shown below.

\left[\begin{array}[]{rrrr}*&-&-&-\\ -&*&-&-\\ -&-&*&-\\ -&-&-&*\end{array}\right],\left[\begin{array}[]{rrrr}-&-&*&-\\ -&-&-&*\\ &-&-&-\\ -&*&-&-\end{array}\right],\left[\begin{array}[]{rrrr}-&*&-&-\\ &-&-&-\\ -&-&-&*\\ -&-&*&-\end{array}\right],\left[\begin{array}[]{rrrr}-&-&-&*\\ -&-&*&-\\ -&*&-&-\\ &-&-&-\end{array}\right]

5.5. Small mysteries for the interested reader.

Our computational findings seem to beg more questions than they answer. We encourage the reader to consider the following questions. Why are there no Niebrzydowski algebras of order 4? Where is the contradiction in the axioms for $n=4$ that is not a contradiction for $n=3$ ? Does this contradiction apply to all $n>4$ ? Can one inductively prove that if there are no Niebrzydowski algebras of order $4$ , then there are no Niebrzydowski algebras of order $n>4$ ? For the virtual Niebrzydowski algebras of order 4, why are the missing entries in the product squares symmetric?

References

[1] Dror Bar-Natan and Zsuzsanna Dancso. Finite Type Invariants of w-Knotted Objects II: Tangles, Foams and the Kashiwara-Vergne Problem. Math. Ann., 367(3-4):1517–1586, 2017.
[2] Dror Bar-Natan, Zsuzsanna Dancso, and Nancy Scherich. Ribbon 2-knots, 1+1=2, and Duflo’s theorem for arbitrary Lie algebras. Algebraic and Geometric Topology, 20, 2020.
[3] Evan Carr, Nancy Scherich, and Sherilyn Tamagawa. Virtual Niebrzydowski algebras, a GitHub repository. https://github.com/ejrcarr/Virtual_N_Algebras, 2023.
[4] Thomas R. Fleming and Blake Mellor. Virtual spatial graphs. ArXiv article, arXiv:math/0510158(4), 2005.
[5] Paige Graves, Sam Nelson, and Sherilyn Tamagawa. Niebrzydowski algebras and trivalent spatial graphs. Internat. J. Math., 29(14):1850102, 16, 2018.
[6] Louis H. Kauffman. Virtual knot theory. European J. Combin., 20(7):663–690, 1999.
[7] H. Murakami, T. Ohtsuki, and S. Yamada. Homfly polynomial via an invariant of colored plane graphs. Enseign. Math, 44(3-4):325–360, 1998.
[8] Sam Nelson and Shane Pico. Virtual tribrackets. J. Knot Theory Ramifications, 28(4):1950026, 12, 2019.
[9] M. Niebrzydowski. On some ternary operations in knot theory. Fund. Math., 255:259–276, 2014.
[10] Online Encyclopedia of Integer Sequences. https://oeis.org/A002860.