An Optimal Transport approach to arbitrage correction: Application to volatility Stress-Tests
Abstract
We present a method based on optimal transport to remove arbitrage opportunities within a finite set of option prices. The method is notably intended for regulatory stress-tests, which impose to apply important local distortions to implied volatility surfaces. The resulting stressed option prices are naturally associated to a family of signed marginal measures: we formulate the process of removing arbitrage as a projection onto the subset of martingale measures with respect to a Wasserstein metric in the space of signed measures. We show how this projection problem can be recast as an optimal transport problem; in view of the numerical solution, we apply an entropic regularization technique. For the regularized problem, we derive a strong duality formula, show convergence results as the regularization parameter approaches zero, and formulate a multi-constrained Sinkhorn algorithm, where each iteration involves, at worse, finding the root of an explicit scalar function. The convergence of this algorithm is also established. We compare our method with the existing approach by [Cohen, Reisinger and Wang, Appl. Math. Fin. 2020] across various scenarios and test cases.
1CMAP, Ecole Polytechnique, Institut Polytechnique de Paris
2Société Générale, Global Risk Methodologies111This work was carried out as part of a collaboration (thèse CIFRE) between CMAP and Société Générale. The findings and conclusions presented in this paper are solely those of the authors and do not represent the views of Société Générale.
Contact author: Marius Chevallier, marius.chevallier@polytechnique.edu.
Acknowledgments: we thank Ghislain Essome-Boma, Quentin Jacquemart, Laurent Jullien, Claude Martini, Mohamed Sbai, Fabien Thiery, and Justine Yedikardachian for stimulating discussions and useful insights.
Keywords: Arbitrage, Volatility Stress-Tests, Optimal Transport, Entropic Regularization, Sinkhorn Algorithm.
Mathematics Subject Classification: 91G80, 49Q22.
JEL Classification: C18, C61, C65.
1 Introduction
In order to steer their risk/reward profile and maintain sufficient capital to face crises, financial institutions frequently compute several metrics to monitor the risks inherent to their activities. Among these risks, market risk refers to potential losses induced by market moves on the income of trading activities. Assessing market risk, besides being mandatory to compute regulatory capital requirements, is key to manage the activities of the front office. For instance, the Value-at-Risk (a quantile of the global short-term Profit-and-Loss or P&L) is a metric generally evaluated on a daily basis that helps firms identify trading desks that are the most at risk and thus steer their business. The computation of VaR, as for many other metrics, requires to generate scenarios for risk factors, i.e. quantities which determine the values of financial instruments (equity index levels, commodity prices, interest rates…). A fundamental risk factor that drives options values is the implied volatility surface (IVS). In order to estimate market risk carried by option portfolios, it is common for financial institutions to apply some stress-tests directly to the IVS (so to tailor design risky scenarios). This practice is even compulsory within the Fundamental Review of the Trading Book (FRTB), the most recent international regulation supervising minimum capital requirements for market risk (see [3], or Article 9 in [21]). However, from a modeling point of view, the IVS has shape constraints induced by the no-arbitrage assumptions. Stress testing often involves applying local deformations which may result in an IVS that does not fulfill these constraints, preventing the pricing functions of the institution from yielding meaningful results, especially on exotic products that rely on a global calibration. It is often a challenge for the industry to be compliant with both the regulation and a sound mathematical framework. In this paper, we investigate this problem and propose a novel approach to construct a solution.
1.1 Literature review
1.1.1 Detection and removal of arbitrage
An arbitrage opportunity is a trading strategy that has zero cost and a positive probability of making profit. A static arbitrage relates to a strategy consisting in fixed positions taken at present time on available assets (options and underlying), with the possibility to adjust the position on the underlying a finite number of times in the future (a situation often referred to as semi-static). Other arbitrages are called dynamic arbitrages. Carr & Madan [10] provided sufficient conditions to ensure absence of static arbitrages in a set of option prices on a rectangular grid, composed of a finite number of maturities, but countably many strikes. Davis and Hobson [17] extended their work to a more realistic framework, with a rectangular grid defined by a finite set of maturities and strikes. Cousot [14, 15] formulated a more general result for a finite but non-rectangular grid (even with solely bid/ask information), which corresponds to the real case in equity markets, where different strikes are typically quoted for different maturities. All these works formulate numerical tests to apply to a given set of option prices in order to check for the existence of a martingale process fitting those option prices, which is equivalent to no-arbitrage according to the First Fundamental Theorem of Asset Pricing. More recently, Cohen et al. [13], building on the aforementioned works, have formulated an algorithm to remove arbitrages from option price data (“arbitrage repair”) under the form of a linear program, with the possibility to use bid/ask prices as soft bounds. Removing arbitrages may also be addressed with smoothing techniques, which basically consist in fitting an arbitrage-free model to the data, by minimizing some criterion (see [22] for example).
Link with signed measures. While classical results link no-arbitrage with the existence of probability (hence positive) measures, a signed measure can be naturally associated (in the usual way, actually) to option prices with arbitrages, and this will be the starting point of our analysis. Concerning related literature, we note that Jarrow and Madan [25] extended the Second Fundamental Theorem of Asset Pricing to the case of an economy with infinitely many assets and where arbitrages may occur, establishing the equivalence between a certain notion of market completeness and the uniqueness of an equivalent signed local martingale measure.
1.1.2 Optimal Transport and applications to finance
The theory of optimal transport (OT) initiated by Monge and Kantorovitch (see the monographs [33, 34] for an extensive description of the theory and some of its applications) has been used to define metrics of Wasserstein-type between signed measures. Piccoli et al. [28] defined a Wasserstein norm on the space of finite signed measures on , relying on distances between unbalanced positive measures. They used it to prove well-posedness of a non-local transport equation with a source term given by a signed measure. Ambrosio et al. [2] give another definition, in the context of superconductivity modeling. We will use the latter to formulate the correction of arbitrage in option prices as a projection problem of a signed measure onto the subset of martingale measures. Wasserstein projections of probability measures have of course been considered in a variety of fields; in the context of finance, Alfonsi et al. [1] consider projections with respect to the usual -Wasserstein distance () as a tool to sample the marginal laws of a stochastic process while respecting the convex order condition, with a view on the numerical solvability of martingale optimal transport problems. In its turn, martingale optimal transport in finance was introduced by [5] with another goal, namely to derive model-independent bounds and hedging strategies for exotic options. Recently, another aspect of optimal transport was used in [35], where the author proposes to find suitable Monge maps that preserve convex order as a tool for data generation without arbitrage.
1.1.3 Entropic optimal transport and Sinkhorn’s algorithm
A popular method used in numerical OT is to penalize the cost functional involved in the minimization problem (the Wasserstein distance in our case) by an entropic term. This gives rise to the so-called entropic optimal transport (EOT) problem, which has gained much interest since the work of Cuturi [16], which allows for quick approximate numerical solutions. Cuturi’s solution is based on the renowned Sinkhorn’s algorithm [31], which consists of iterative projections on the marginal constraints (see [27] for a rich overview). Contrary to classical OT where the cost is linear, EOT is equivalent to minimizing a strictly convex functional known as the Kullback-Leibler divergence, or relative entropy. After the advent of EOT, extensions of Sinkhorn’s algorithm were designed to solve martingale optimal transport problems in finance [18, 19, 24, 7]. The projection approach we rely on to remove arbitrage can also be tackled with entropic regularization. Inspired by recent works of Benamou et al. [6] and Chizat et al. [12], we will formulate a “multi-constrained Sinkhorn” algorithm that incorporates more constraints than the usual ones in OT theory (i.e. the marginal constraints). Entropic projections (that is, the minimization of a relative entropy objective) have been exploited by De March and Henry-Labordère [19] as a tool to construct non-parametric fits of implied volatility smiles. Postponing precise definitions and discussions, let us point out a structural difference of our problem with theirs: [19] consider the projection of a given parametric model onto the set of martingale measures that fit some implied volatility market data. In this setting, the starting point (the probabilistic model) is arbitrage-free by construction, and, on the other side, one has to assume that the target market data satisfy the no-arbitrage condition; the whole operation takes place, then, within a set of probability measures. In our case, our starting point is an arbitrageable stressed smile (for which we know that the arbitrage condition is, in general, not satisfied) and the target is a martingale measure which is not required to fit market quotes — our main goal is precisely the creation of new data after the arbitrage removal. The mathematical framework of metric spaces of signed measures, which is the natural environment for our results and numerical methods, is therefore absent from [19].
1.2 Content of the article and our contributions
As addressed above, in this work we propose a new method based on OT to remove arbitrage from option data. In Section 2, we show how we can associate a discrete signed measure to option prices affected by arbitrage. In Section 3, we recall the concepts and results from OT that we use to define a Wasserstein metric between signed measures, following the notion already introduced in Ambrosio et al. [2]. Then, in Section 4, we define subsets of martingales in the space of discrete signed measures. Using the previously defined metric, we give the statement of our problem: the correction of arbitrage as a projection of the signed measure defined in Section 2 onto the martingale subsets. Next, we show that this problem is equivalent to an OT problem (i.e. a linear program on couplings). Section 5 is devoted to the entropic regularization of the minimization problem. We provide several results: we prove strong duality, dual attainment, and convergence when the regularization parameter tends to zero. In Section 6, we propose a multi-constrained Sinkhorn algorithm to approximate the solution of the regularized problem, for which we establish convergence as the number of iterates becomes large. The steps of the algorithm are either explicit, or boil down to finding the root of an explicit scalar function. Finally, Section 7 gathers several numerical applications to, first, showcase the theoretical results of convergence and, second, to illustrate the correction of stressed implied volatility smiles obtained with our method.
2 Setting and notations
We consider a finite set of call options written on the same underlying designated by . will stand for the value of at time . Present time is . The options can have different maturities . For a given maturity , available strikes are denoted by . Hence, the grid we are interested in may not be rectangular. The current price (i.e. at time ) of the option paying at time is which we assume to be positive. We suppose that interest rates and dividends paid by are deterministic. We denote by the discount factor associated to the maturity and will stand for the -forward price of at time . In the following, we will work with the normalized quantities , and . The vector of normalized prices is .
2.1 Checking for arbitrages
The feasibility to build a consistent martingale model can be checked with model-independent tests, relying only on the available data (see [14, 15] for the construction of a discrete model or [19] for a continuous model). This is equivalent to no-arbitrage by the First Fundamental Theorem of Asset Pricing. Cohen et al. showed (see [13, Section 2.4, Proposition 2]) that these tests boil down to verify that solves a linear system of inequalities: with 111See their github repository: https://github.com/vicaws/arbitragerepair for an implementation of and given arbitrary data.. If any inequality of the system is violated, then there is at least one (static) arbitrage in the data.
Definition 2.1.1 (Convex order).
Let and be a family of probability measures on , with finite moment of order 1. We say that is non-decreasing in the convex order (NDCO) if for all convex functions with linear growth and for all , one has
Being NDCO is in fact a necessary and sufficient condition for the existence of a martingale , on the product space , with marginals (see Strassen’s Theorem [32]).
Let us briefly emphasize Cousot’s procedure to build discrete marginals, NDCO and consistent with the data (assuming the tests mentioned above are passed). First, we need to artificially extend the (normalized) data with two more prices at each maturity: for all , at strike and at a strike carefully chosen (see [14, Section 4.2]). Note that it is possible to choose for all (see Lemma 4.1.2 for more details). Then, the (normalized) call pricing function , for the maturity , is defined as the decreasing and piecewise-affine function drawn by the lower boundary of the convex hull of the points (and zero after ). Under the no-arbitrage assumption, verifies for all . Furthermore, it defines a discrete probability measure , the second derivative of in the sense of distributions, supported on a subset of , satisfying , for all (see [14, Lemma 3.1]). Thus defined, the probability measures are NDCO and their support is included in
the collection of all strikes.
Remark 2.1.2.
The important fact here is that, up to a proper choice of , any system of call prices on the fixed grid that has no arbitrage can be attained by a discrete martingale on the finite product space (by Strassen’s Theorem). This is what motivated us to work in a discrete setting.
2.2 Signed measure associated to option prices with arbitrages
Assume now that there are some arbitrages in the data, meaning that c does not solve Cohen’s system of inequalities. For example, they may be due to a local stress-test applied to the associated IVS (initially arbitrage-free). In some applications, we will need to be able to control which part of the IVS must be preserved during the process of removing arbitrage opportunities. We denote by any vector of arbitrage-free (normalized) prices, on an arbitrary sub-grid of . For instance, could correspond to the prices that were not impacted by the hypothetical stress-test mentioned above. On the contrary, it could also consist of the ones that were actually impacted, as long as, ignoring the rest of the data, they are arbitrage-free. In order to identify the maturities and the (normalized) strikes of the sub-grid, we introduce and for any , , so that . Finally, we call the length of .
Even if there are arbitrages, we will see that it is still possible to associate discrete measures that are consistent with the data, through a simple adaptation of Cousot’s construction. However, the resulting measures might be signed or fail to be NDCO. Similarly, we can enlarge the data with additional prices for each : at and at (see Lemma 4.1.2 to see how should be chosen). As previously, we call the collection of all strikes, namely and, to ease notations, we rewrite it as , with , so that , and .
Definition 2.2.1 (Signed marginal).
For a given maturity , we define the discrete (signed) measure by
where is the Dirac mass located at and
Remark 2.2.2.
The ’s are always well defined and have a total mass of . Even though they can be true probability measures (in the case of calendar arbitrages only), we still use the terminology “signed” to emphasize that they are associated to some inconsistent data.
Definition 2.2.3 (Piecewise-affine continuous pricing function).
For a fixed , we define by
By construction, is piecewise-affine, continuous and .
Lemma 2.2.4 (Lemma 3.1 [14]).
For all and for all , we have
Remark 2.2.5.
Lemma 2.2.4 justifies why we allow ourself to employ the terminology “marginals” for the ’s, though they can be signed. Indeed, they sum up to one and calibrate the data with arbitrages.
Note that each has a finite support included in , but can be seen as a measure distributed on , with zero weights for the elements of that are not in its support. The ’s being specified, we can define what we call a “joint signed measure” , on the finite product space , with marginals . A simple choice would be to set , but this could be somehow unsatisfactory, for reasons that will become clearer in Section 4.2. From now, we just assume that is built. Note that it satisfies . In the following section, we will define a distance between signed measures with total mass equal to one, to formulate the correction of arbitrages as the projection of onto the subset of martingales. Just recall that, from Remark 2.1.2, it is sufficient to look for martingales on to get rid of arbitrages in the data (up to a choice of ).
3 Distance of Wasserstein-type between signed measures
In this part, we work with a Polish space , and we endow it with its Borel -algebra, denoted by . is the set of finite signed measures on . is the subset of consisting of all finite positive measures on . We recall that any element of admits a unique decomposition (the so-called Jordan decomposition) with , such that and . However, note that there are infinitely many decompositions of of the form . For instance, and with is one of them. The variation of is (it is an element of ). For , we also define and . Finally, for , we denote by the set (and similarly , with obviously whenever ).
3.1 Wasserstein distances for positive measures with finite mass
Wasserstein distances are usually defined for elements in i.e. for probability measures with finite moment of order (see the monographs [33, 34] for more details), but it extends naturally for positive measures with some fixed finite mass . Their definition is based on the theory of optimal transport.
Definition 3.1.1 (Transference plan).
Let and . A transference plan between and is a positive measure , on the product space , that satisfies
for all .
The set of transference plans is denoted by . We shall also refer to it as the set of couplings between and .
Definition 3.1.2 (Wasserstein distance of order ).
Let , and . The Wasserstein distance of order between and is defined by
Theorem 3.1.3 (See Theorem 7.3 in [33] for ).
For any , and any , the space is a metric space.
Theorem 3.1.4 (Kantorovich-Rubinstein duality formula, see [33] for the case ).
Let and . Then,
where is the set of Lipschitz functions on and .
3.2 A Wasserstein distance between signed measures
The following definition, motivated by Ambrosio et al. [2], extends the -Wasserstein distance to signed measures.
Definition 3.2.1 (Wasserstein distance between signed measures with unit mass).
Let and be two elements of . The Wasserstein distance between and is defined by
for any decomposition and of and .
Proposition 3.2.2.
is a well-defined functional. Moreover, we have the following duality formula
Proof.
Let and such that and .
Because , we have . Hence and are elements of . Then, from the duality formula 3.1.4, we obtain
From this duality, we see that the value of does not depend on the decomposition of and . ∎
Proposition 3.2.3.
The space is a metric space.
Proof.
From the duality in Proposition 3.2.2, is symmetric (with the change of variable ). Moreover, from Definition 3.2.1, is non-negative, as the classical -Wasserstein distance is. From the positivity of , we get . Finally, for , and for with , we have
Taking the supremum over all on the left-hand side and using Proposition 3.2.2 leads to the triangle inequality. ∎
4 Projection on subsets of martingales
Hereafter, we work with and a distance on . In the discrete case, and for all . Let be the cardinality of i.e. . For , there exists a unique -tuple such that (a slight reformulation of the decomposition of in the base ). With this one to one correspondence, we can define the path , identified to a vector in , that starts at and ends up at . We denote by the distance matrix . The state space being here, any element can either be written as or , with . Thus, we will identify signed measures on either by vectors in or -rank tensors in , depending on the situation. Finally, we denote by the canonical process: and we introduce the shorthand notations and .
4.1 Subsets of interest
Definition 4.1.1 (Martingale measures on ).
We call the subset of martingale measures centered at . An element must satisfy
Identifying to a -rank tensor , this translates equivalently to
| (1) | |||
| (2) | |||
| (3) | |||
| (4) |
where (4) must stand for all , for all ( equality constraints).
The total number of equality constraints is .
We also introduce , the subset of , where the elements (seen as -rank tensors) satisfy the additional calibration property
| (5) |
where (5) must stand for all , for all ( equality constraints).
Therefore, an element of must satisfy equality constraints.
All these constraints are linear in the variable . Hence, seeing now measures as vectors in , there exists a matrix and a vector (resp. a matrix and a vector ) such that (resp. ).
Lemma 4.1.2.
If one chooses , then is non-empty.
If
with
then, is non-empty.
Proof.
For the first part, define , for . The ’s are discrete probability measures on (because by definition) satisfying . Moreover, they are obviously NDCO because equal. From Strassen’s Theorem, there exists a martingale measure on , with these marginals, hence an element of .
The second part follows from Cousot’s construction [14] applied to the data formed by . We obtain probability measures NDCO, with support included in . By construction, they satisfy and , for all and . Then, we define
with and .
Thus defined, the ’s are still NDCO so, from Strassen’s Theorem, there exists a martingale measure on with these marginals, hence an element of . As the marginals also calibrate , is actually an element of . ∎
For the rest of the paper, we assume that is properly chosen, so that Lemma 4.1.2 always applies.
4.2 Choice of the joint signed measure
As discussed in 2.2, the signed marginals are uniquely defined in our setting. However, we have a degree of freedom in the choice of the joint signed measure with these marginals. Even though there are arbitrages, the choice would correspond, in some way, to an independent framework which is unsatisfactory. Indeed, recall that our aim is to project onto the subset of martingales. Martingales never have independent marginals (except for constant martingales). Consequently, choosing as the product measure would be somehow “very far” from (or ). Thus, we can try to build a signed measure that already looks like a martingale. We propose below a possible construction for this joint signed measure, but leave for future work the question of whether this choice can be improved.
Let us assume, for the moment, that are true probability measures NDCO. Then, from Strassen’s Theorem, there exists a discrete probability measure on satisfying (1), (2), (3), (4) and
| (6) |
for all , for all ( equality constraints), where is the -th coefficient of the vector . The constraint (6) is again linear in the variable . Therefore, we can write , with for some and . However, there is some redundancy in the constraints satisfied by . For instance, if (4) and (6) are verified, then (2) and (3) are automatically true by construction. Said differently, doesn’t have full rank. Removing the redundant rows (resp. coefficients) in (resp. ) and keeping the same notations for simplicity, we may assume that belongs to , with , , and .
From this remark and coming back to our setting, we could try to find in the set i.e. removing the positivity constraint (otherwise this set is empty because of arbitrages). It corresponds to the set of “signed martingales”, with fixed marginals . Besides, recall from the positive case that the product measure maximizes the entropy, or, said differently, the randomness among joint distributions with prescribed marginals. Because the entropy is not well defined for signed measures, an alternative could be to choose a signed martingale close to . To some extent, it corresponds to the least biased choice. Therefore, we choose to be the unique solution of the following quadratic constrained optimization problem
is closed and non-empty because has full rank. Moreover, is continuous and coercive, hence existence of a minimizer follows. Uniqueness comes from the strict convexity of .
will remain fixed for the rest of the paper. We define by and . Note that we have , because of the presence of arbitrages. Since does not depend on the decomposition of (see Proposition 3.2.2), we may add the same positive vector to and , to obtain a positive decomposition of . Keeping the same notations for simplicity, we assume from now that we work with such decomposition. Finally, we call the total mass of (which is nothing else than the -norm of ).
4.3 Projection of on and
Now that is defined, we have all the ingredients to formulate the correction of arbitrages as a projection problem. More specifically, we will be interested in:
and
These infima are finite since and are non-empty and .
Remark 4.3.1.
In the discrete setting, Definition 3.2.1 reduces to
where , , , and is the Frobenius dot product between matrices. We also define two sets of couplings that will play a major role in what follows
Proposition 4.3.2 (Equivalent minimization problems).
Proof.
Let . Since is non-empty, there exists such that
From standard arguments of optimal transport theory (see [33, 34]), there exists an optimal coupling such that . Consequently, and letting , we get the first inequality.
Similarly, there exists such that
Then, define . By definition of , . Then, using and letting , we obtain the second inequality.
The adaptation of the proof to 4.3 is just a matter of notations. ∎
Lemma 4.3.3 (Compactness).
The sets and are compact.
Proof.
is bounded by (for the Frobenius norm), where . Using the characterization of with the matrix and the vector , one can rewrite as
which is easily seen to be closed.
Again, the compactness of is obtained by adapting notations. ∎
Theorem 4.3.4 (Existence of minimizers).
Proof.
From Lemma 4.3.3 and the continuity of , there exists such that . Then, if we denote , we have and . From the definition of , we get . Using Proposition 4.3.2, we obtain . We are left with the proof of the first implication. Let . Again, from standard arguments of the theory of optimal transport, there exists such that , by Proposition 4.3.2. ∎
5 Entropic regularization
The linear program 4.3.2 can rapidly become intractable since we are optimizing variables. A common method in optimal transport to overcome this difficulty is to penalize the linear cost involved in the minimization problem, by an entropic term. As we will see, it brings strict convexity and its numerical resolution can be tackled efficiently, with an iterative algorithm of Sinkhorn-type. In this part, we will only focus on the regularization of the problem 4.3.2, but all the results will apply similarly when replacing by . Most of our definitions come from [27].
5.1 Entropic projection of on
Definition 5.1.1 (Entropy of a matrix).
The entropy of , is defined by
with the convention .
Let , the -regularized version of 4.3 is
The function is strictly convex, because its Hessian is which is symmetric positive-definite. Hence, from the compactness of , there exists a unique solution to 5.1.
Proposition 5.1.2 (Convergence of the entropic regularization).
If we denote by the set , then we have
Proof.
First, is a closed subset of , by continuity of . Consequently, is also compact. The entropy being continuous and strictly concave, there exists a unique such that .
Let be a sequence of positive real numbers converging to . Denote by the unique solution of . From the optimality of , and by definition of , one has:
| (6) |
It follows that . The latter set is closed by continuity of the entropy, hence compact (as a subset of ). Thus, up to a subsequence, converges to some cluster point and . Passing to the limit in (6), one obtains . As a consequence, and, by definition of , . The cluster point being unique, the whole sequence converges to .
Then, we immediately get
Finally, by continuity of the projection, one has . Since , we have by Theorem 4.3.4.
∎
Remark 5.1.3.
We believe one can not conclude that maximizes the entropy on the set . Indeed, it is not hard to build discrete couplings for which the order of the entropy is reversed after projection onto the first dimension. If one considers and , with respective first marginals and , then one can verify that , while . Of course, this simple example does not fit our framework. However, we were able to emphasize numerically this inversion of entropy in our setting (though we were not able to find a general counterexample).
Definition 5.1.4 (Kullback-Leibler divergence).
Let and be two squared matrices of size such that has positive entries. The relative entropy of with respect to is defined by
with the convention .
Note that for , we have , with . Thus, 5.1 is equivalent, up to a constant, to
By equivalent here, we mean different costs but same unique minimizer.
5.2 Duality formula for 5.1
Throughout the rest of the paper, , for some , is the shorthand notation for the vector . We will also rely on classical notions of convex analysis recalled in Appendix A. For a set , and denote, respectively, the relative interior and the indicator function of (see Definitions A.1 and A.2). For a function , , and are, respectively, its domain, convex conjugate and subdifferential (see Definitions A.3 to A.5).
Let . We introduce the closed convex sets defined by
where is the -th row of the matrix and denotes the -th coefficient of . Thanks to this notation, one has and we can rewrite 5.1 as
the positivity constraint being already contained in the definition of . Writing 5.2 in this specific form was highly motivated by the work of Chizat et al.[12], especially the section 4.5.
Theorem 5.2.1 (Strong duality).
Proof.
is a linear map and its adjoint is
We define and by
Each being proper, lower semicontinuous and convex, is itself proper, lower semicontinuous and convex by Proposition A.7. A similar statement holds for which is even continuously differentiable and strictly convex. By Theorem A.8, and after some calculations, one obtains and . Since is everywhere continuous and , we can apply Theorem A.9 which shows the strong duality.
It also proves the existence of a minimizer, but we already proved it at the end of Section 5.1 (as well as uniqueness). Let us call the unique solution of 5.2. Then, again by Theorem A.9, maximizes 5.2.1 if and only if and . being continuously differentiable, the latter condition writes and leads to (7). To obtain (6), recall that . As a consequence, and (or equivalently ). From this remark and using the definition of the subdifferential, we have
since whenever for some . As means , is zero. Subsequently, , so we can fix for all except one to conclude that implies (6). The converse is immediate by summation and the above equivalences. ∎
Proposition 5.2.2.
The dual problem 5.2.1 is attained.
Proof.
Let be the unique solution of
We recall that the constraints set can be written
Since the constraints are all affine in , constraint qualification boils down to the existence of a matrix . First, we have (where is the interior in ). Now, let and . since , and , so that . From the necessary condition of Kuhn-Tucker’s Theorem [26], there exists Lagrange multipliers , and such that is a saddle-point of the Lagrangian and the complementary slackness condition holds (pointwise). Since the Lagrangian is differentiable, being a saddle-point reduces to , from which we obtain , where is the -th column of . Now, define by for , and . We immediately see that satisfies (7). Furthermore, for , for , one has , since and are in . Finally, for , one can verify that the complementary slackness condition gives (recall that ). Hence, also satisfies (6) and is a maximizer by Theorem 5.2.1. ∎
6 Iterative scaling algorithm
Following the ideas of [12], we will propose an algorithm to approximate based on alternating maximization on the dual 5.2.1. These maximization will be closely related to Bregman projections [8] which are used in numerous applications of entropic optimal transport (see [6] for example). The algorithm will be suited for the resolution of 5.1, but it also applies if one replaces by .
In this part, we will use the notations and to denote the componentwise product and division between vectors or matrices. For any vector , will stand for the diagonal matrix whose diagonal is given by . Finally, for is the notation for the vector .
6.1 Dykstra’s algorithm
The solution of 5.1 is also called the KL-projection of onto the convex set . It is well-known (see [6]) that can be approximated using Dykstra’s algorithm [20], extended to the framework of Bregman divergences (KL being one of them). For , and for such that , we introduce the so-called “proximal operators”:
Let , and for all
with the conventions and for all . Hereafter, the index designates the -th iteration of Dykstra’s algorithm and the -th substep.
Under the constraint qualification which is verified here (see proof of Proposition 5.2.2), we have where
(see [4, 11] for a proof). Consequently, , for any sequence .
Lemma 6.1.1.
For all such that , one has
where is the unique root of .
Proof.
The form of the minimizers can be deduced by introducing Lagrange multipliers (see [8] for and [6] for ).
Thus, we only prove that for , there is only one root of . First, is continuously differentiable. Moreover, and . Hence, is increasing, since . Therefore, exists and is unique if and only if . There are three possibilities:
where . We only need to discuss the first two cases.
Case 1:
This happens for the rows of corresponding either to the mass constraint (2), the centering constraint (3), or to some of the martingality constraints (4) (for i.e. ). If corresponds to (2) or (3), then , otherwise . In any case, one has , since and , by assumption. Hence, belongs to .
Case 2:
This happens for some of the martingality constraints (4) (for i.e. ). If corresponds to such case, then . Hence, because and . Again, belongs to .
∎
6.2 A multi-constrained Sinkhorn algorithm
The duality 5.2.1, together with Proposition 5.2.2, show that is a diagonal scaling of the Gibbs kernel . It is a classical property of optimal couplings in entropic optimal transport. Instead of estimating with Dykstra’s algorithm, we will take advantage of its specific form and directly estimate the dual scalings , hereafter denoted by , with a Sinkhorn-type algorithm generalized to our setting.
For , we define by
We also introduce similar proximal operators to the ’s, that act on vectors in . For and , we define
Finally, we set and for ,
where the different scalings are defined by Algorithm 1 below. For consistency, we adopt the conventions and for all .
is the stopping criterion and measures the marginal constraints violation of . There are several ways to define . To obtain the results described in Section 7, we worked with
where is the standard sup norm in finite dimension.
We justify the choice of this convergence criterion in Section 6.2.3.
6.2.1 Link with alternating maximization on the dual
From the definition of , one has , for all , where .
One way to approach the dual scalings is to perform an alternating block dual ascent defined by and for all
where (uniqueness follows from strict concavity).
Applying Fenchel-Rockafellar’s Theorem A.9, one can prove that . Hence, recalling , we see that the ’s and the ’s satisfy the same scheme.
6.2.2 Link with Dykstra’s algorithm and convergence
In this section, we will prove that for all . Hence, the iterates defined in Algorithm 1 are sufficient to perform Dykstra’s algorithm. They are cheaper to manipulate as they lie in (instead of for ). Plus, recovering will just be a matter of scaling the kernel (as defined by ).
We begin with the following Lemma whose proof is essentially the same as the one of Lemma 6.1.1.
Lemma 6.2.1.
For such that , one has:
where is the unique root of .
Lemma 6.2.2.
Suppose that for some and for ,
Then, for all , one has and
Proof.
We start by proving for .
Case :
By assumption , so with our conventions: . Suppose for some . Then, according to Dykstra’s algorithm 6.1 and our hypothesis,
where . On the other hand, one has
By definition, , where . Thus, if , we have . From the definitions of and (see Lemmas above), this condition boils down to
Using the definition of , and , the latter condition holds true.
By induction, for all .
Case :
From Dystra’s algorithm 6.1:
Using the previous case and our hypothesis on , we get
Then, by noticing that , it follows from the expression of that
Case :
With similar arguments, one has
so in particular . Hence, from the -th substep of Dykstra’s algorithm 6.1:
Then, we prove that the ’s have the expected form. By definition of Dykstra’s algorithm (see Section 6.1), we have . Hence, considering the above, we have for
and
∎
Proposition 6.2.3 (Convergence of Algorithm 1).
For all , and, consequently, for any sequence .
Proof.
We proceed by induction. For , let be the statement
holds true by definition of and thanks to our conventions. The induction step is given by Lemma 6.2.2, so that holds for all . ∎
6.2.3 Convergence criterion of Algorithm 1
In this section, when , is the shorthand notation for the vector .
Lemma 6.2.4.
For , we have
Proof.
The case is trivial since, by definition of the convex conjugate, .
If , by definition, . If one decomposes into , we easily get that
Then, from the definition of the convex conjugate and again by decomposing into , , we obtain
which is whenever and otherwise. Thus, and , since .
Regarding the case , observe that for any and any , , where is the -th vector of the canonical basis of . Hence, if the -th coordinate of is positive, . Consequently, if . Conversely, if , it is not hard to verify that , for any . Thus, and . We conclude by noticing that , so that .
∎
Lemma 6.2.5.
Let , and . Then,
Proof.
First, and are proper convex functions on . From the separability of , we have and each domain being convex (since the ’s are), one also has , which is non-empty, from Lemma 6.2.4. is continuously differentiable on so, in particular, . Hence, Theorem A.6 applies: . Then, using once more the separability of , one obtains . We conclude using (again) the fact that is everywhere differentiable. ∎
Proposition 6.2.6 (Fixed point of Algorithm 1).
Proof.
If and are the functions defined in Lemma 6.2.5, we see that is the dual functional in 5.2.1. From the observation made at the beginning of Section 6.2.1, , where . Then,
where the first and third equivalences are just optimality conditions, the second follows from Lemma 6.2.5 and the last by applying Theorem A.9. ∎
Proposition 6.2.7.
Proof.
For the sake of clarity, we write to avoid confusion between and which corresponds to
, with the notation of Algorithm 1. Additionally, since come from substeps of Algorithm 1, there exists , such that .
Conversely, if , for any , since with equality if and only if . On the other hand, from Lemma 6.1.1 and , , where is the unique real number such that
From our first observation, the only possibility is , because and . However, , when . Hence,
Thus, from Lemma 6.2.1, we obtain
for .
Then, by definition of the -th substep of the -th iteration of Algorithm 1:
which immediately gives , because, with our notation, and .
Finally, can be written , which implies
∎
7 Numerical results
This section contains different numerical results, with the aim to either confirm our theoretical results or highlight the behavior of our method on real data. We use public SPX options data available on the CBOE delayed option quotes platform111https://www.cboe.com/delayed_quotes/spx/quote_table. We evaluate a mid-price for calls and puts from the bid and ask quotes. After a basic filtering (volume ), discount factors and forwards for the different maturities are determined by linear regression on the call-put parity. For the sake of clarity, we will use the following color and shape code:
-
• for SPX market data,
-
★ for stressed data, generated artificially from SPX market data,
-
+ for repaired data obtained with our method (possibly with a color gradient to emphasize different regularization levels),
-
• for repaired data obtained with the algorithm of Cohen et al. [13].
In the different experiments, we chose to be the Euclidean distance.
7.1 Convergence of the multi-constrained Sinkhorn algorithm
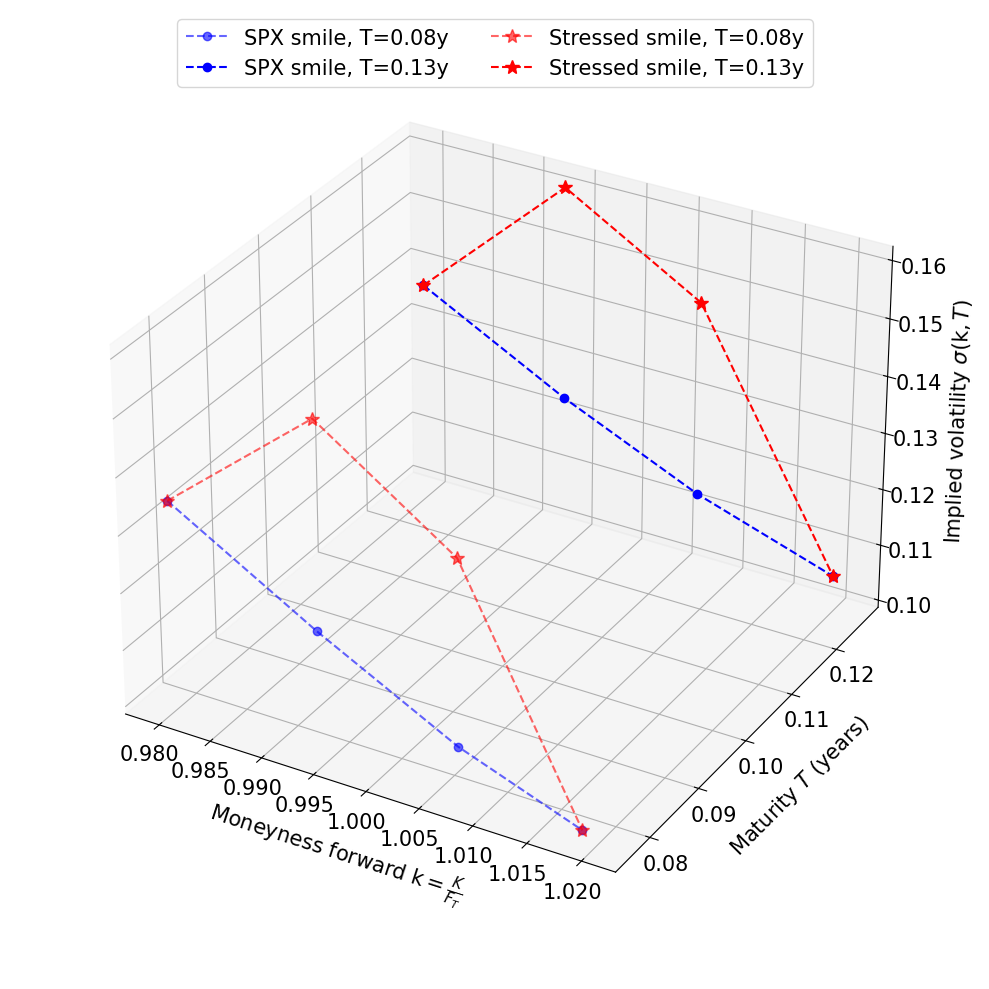
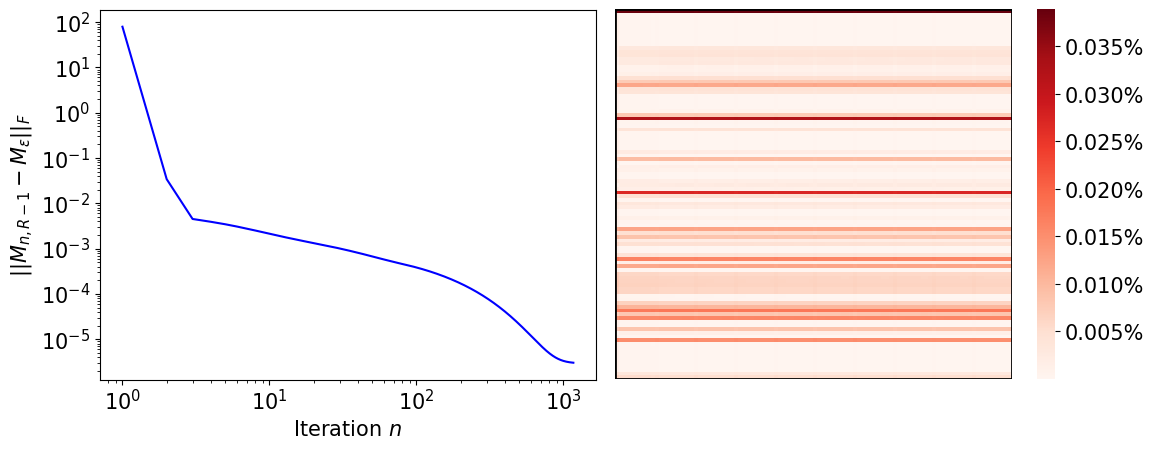
In Figure 1, we artificially created (butterfly) arbitrages by increasing the volatilities around the money by . Numerical illustration of Proposition 6.2.3 can be found in Figure 2. We performed Algorithm 1 starting from the stressed configuration described by Figure 1, with and . was obtained using SciPy’s solver minimize with the method SLSQP. In this toy example, . In Figure 2, on the left, we see that the distance between and is monotonically decreasing to zero. However, it is not clear that the rate of convergence is linear, as for the usual Sinkhorn algorithm. On the right, we see that if we zoom in residual errors between () and , both matrices are very close, confirming empirically that the algorithm estimates what is expected.
7.2 Convergence of the entropic regularization ()
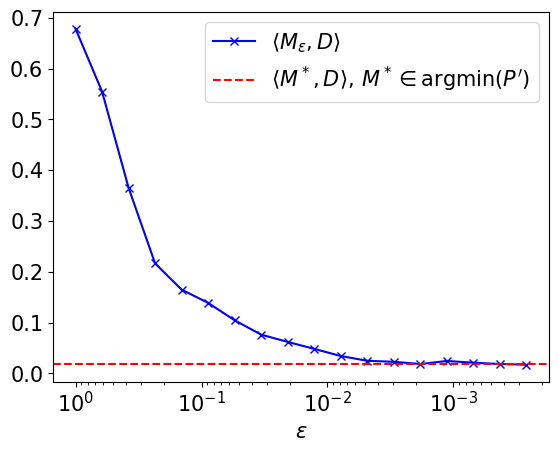
Figure 4 illustrates Proposition 5.1.2: when , converges to a minimizer of 4.3.2. We point out that, to obtain this graph, we used the Python library POT [23] to handle classical numerical errors appearing when solving EOT problems for small regularization parameters. Such difficulties are, for example, discussed in [12] Section 4.3.
7.3 Correction of stressed smiles: single maturity case
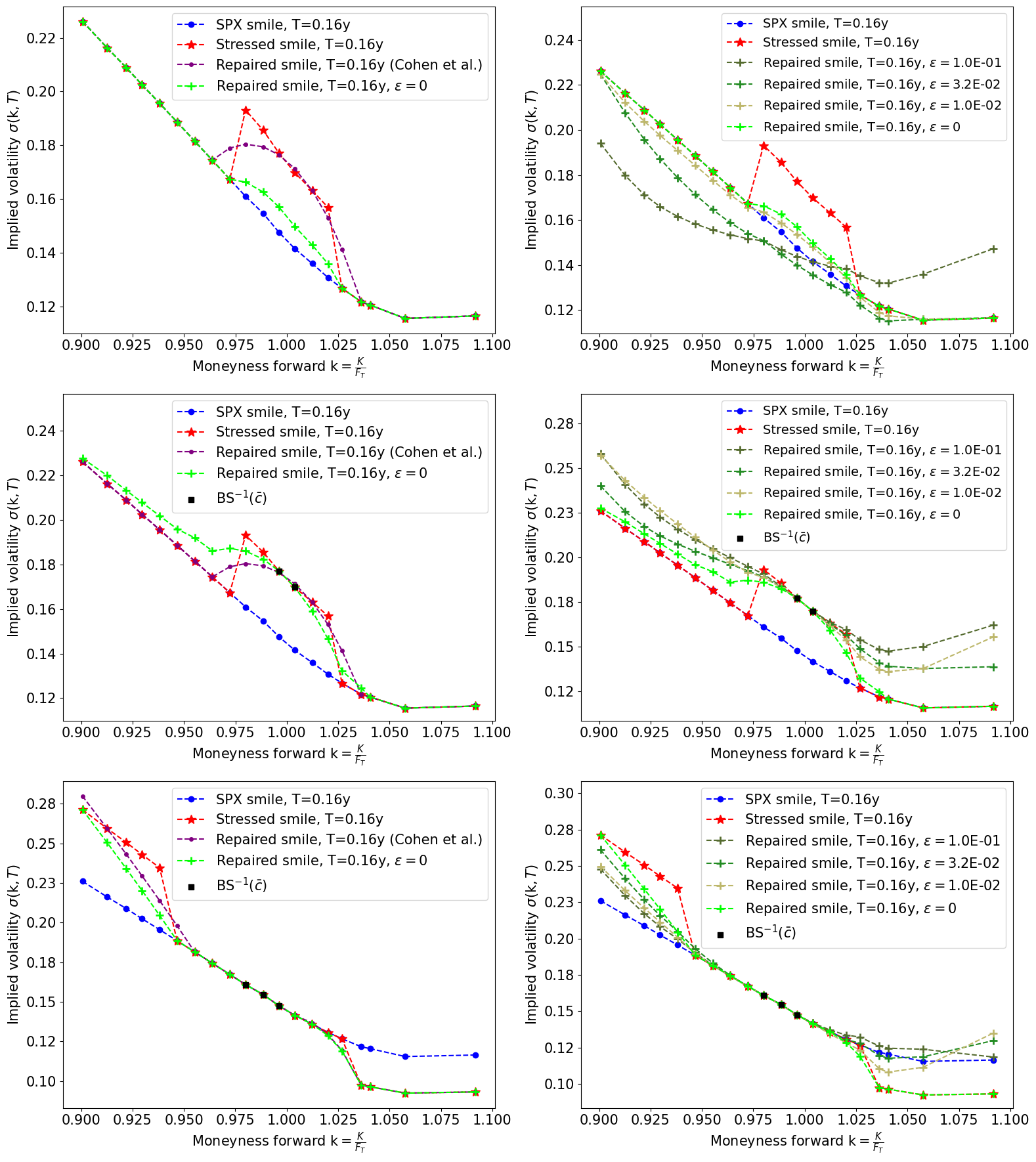
In this section, the SPX data we work with is dated 23-10-2024. Figure 5 highlights the differences between our method and the one proposed in [13], for three types of stress-test. In the first row, the volatilities with moneyness were increased by . Surprisingly, the green smile with , corresponding to a solution of 4.3, does not deviate from the original blue smile outside the interval , even though no calibration constraints were imposed. The increase is also more contained than Cohen et al.’s solution. The graph on the right displays the expected behavior of regularization: when approaches zero, the darker green smiles are getting closer to the one associated to . We also observe that higher tends to produce smoother and more U-shaped smiles. However, without constraints here, the average level of volatility is lost for high regularization.
Regarding the second row, the volatilities with were still increased by , but we also constrained our solutions to calibrate two prices that were impacted by the stress-test, to ensure high enough volatility at-the-money (see the black squares on the graphs). The green smile with corresponds then to a solution of 4.3. Again, we observe smoother smiles for greater and constraining seems to be an appropriate way to match a certain average level of volatility.
The last row was obtained with a more exotic stress-test of steepening: volatilities with were raised by , while the ones with were reduced by . This time, our solutions were constrained to fit some prices that were not affected by the stress-test, to keep the level of volatility around the money unaffected.
Note that all smiles appearing in Figure 5 are arbitrage-free (except of course the stressed ones) and were obtained with .
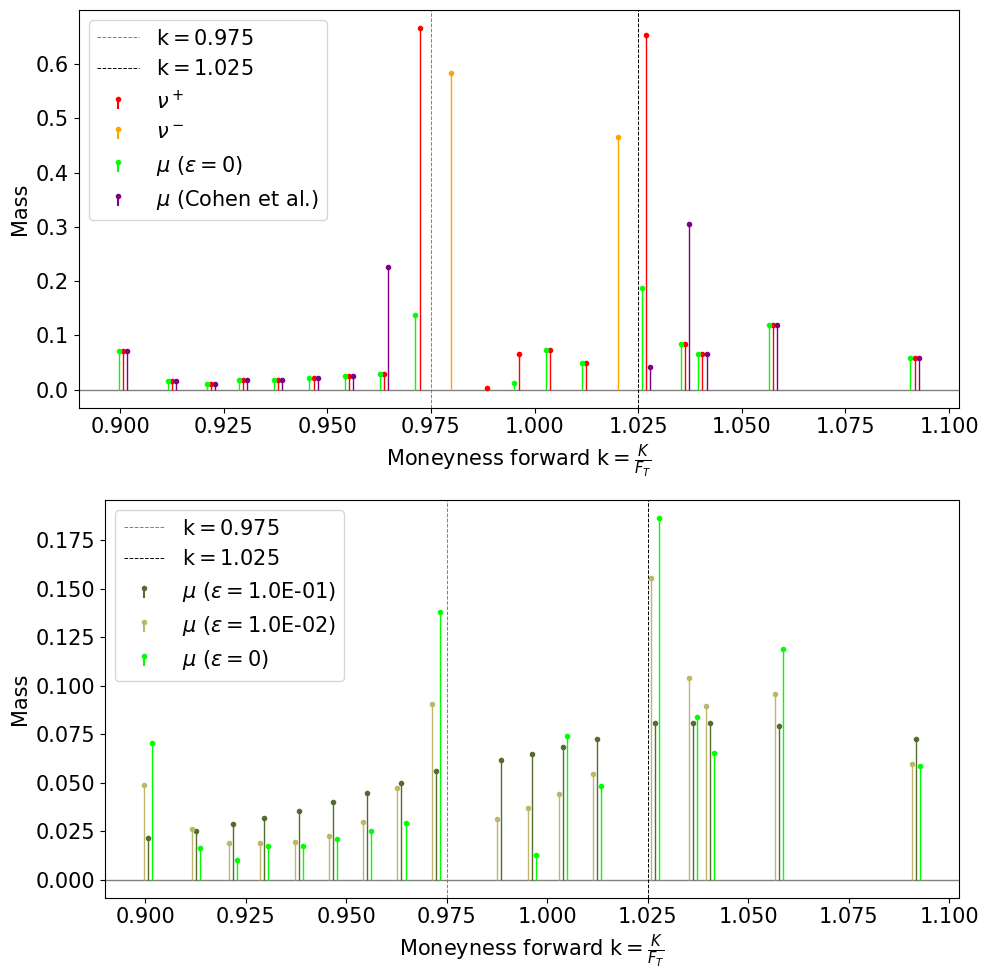
Figure 6 zooms in the distributions of mass (on , for the sake of graphs’ clarity) of the different marginals attained either by our method or Cohen et al’s, for the first stress-test of Figure 5. Note that, for visualization purposes, the sticks were slightly separated, but they correspond to the same atoms. Regarding the first row, we observe very unusual distributions, from a financial point of view, but still true probability measures. We believe there are two reasons for that. The first is the closeness with respect to the stressed configuration, which is economically not viable, because of arbitrages. The second is the general sparsity of solutions of linear programs (our case) and -norm minimization problems (Cohen et al’s case). About the second row, we recognize a typical property of solutions of EOT problems. They are more diffuse than the non-regularized solution and get sparser when approaches zero.
7.4 Correction of stressed smiles: two maturities case
In this section, we still use SPX data dated 23-10-2024, with two maturities to highlight the behavior of the projection method in a multidimensional framework.
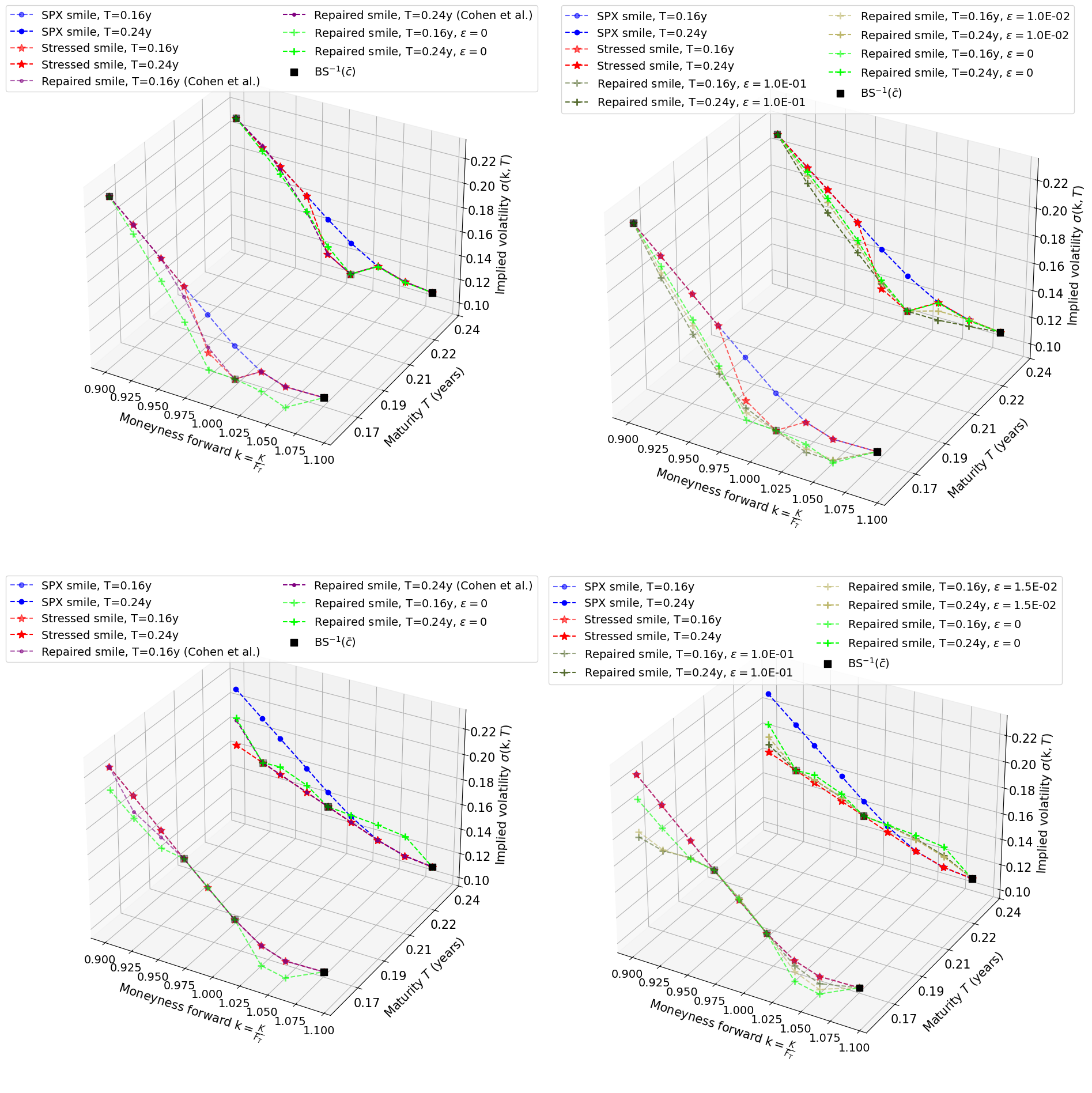
Figure 7 is nothing else but the extension of experiments described in Figure 5 to a two maturities setting. In the first row, the volatilities with moneyness were decreased by , for both maturities. To have sufficiently low volatility around the money, and to ensure that in and out-the-money volatilities remain, as much as possible, unaffected, we constrained our solution to calibrate a subset of arbitrage-free prices (see the black squares on the graph). In this experiment, the green and purple smiles at are very close, but our correction at deviates more from the red smile than Cohen et al’s. Regularization has again the property to smooth the correction. What is interesting about the second row is that we created calendar arbitrages only, by flattening the smile at the highest maturity. As a consequence, each smile is arbitrage-free when ignoring the other. For this second experiment, we wanted our solutions to preserve the average shape of the smile at and to be as flat as possible at . This is what motivated our choice of calibration subset (see the black squares). Both green and purple corrections are close. However, we observe again that Cohen et al’s output is closer than ours from the stressed surface. Note that we could not achieve a convergence criterion of for , in this second stress-test, due to numerical instabilities (overflow in exponentials) encountered in the root-finding procedures of certain substeps of Algorithm 1. This is why we only performed regularization up to . We believe handling these instabilities (addressed, for instance, in [12] Section 4.3) is out of the scope of this work.
As before, all the smiles appearing in Figure 7 are arbitrage-free (except the stressed ones) and were obtained with .
8 Conclusion
We have explored a novel approach to correct arbitrages in option portfolios, based on the projection of a signed measure onto the subset of martingales, with respect to a Wasserstein distance. We conducted an in-depth study of the associated entropic optimal transport problem and introduced an appropriate Sinkhorn algorithm, for which we proved convergence. We have validated this theoretical framework through numerical experiments, comparing the behavior of our method with existing ones. In future work, we aim at building on this approach to develop a method with an improved computational complexity.
References
- [1] A. Alfonsi, J. Corbetta, and B. Jourdain. Sampling of probability measures in the convex order by Wasserstein projection. Annales de l’I.H.P. Probabilités et Statistiques, 56(3):1706–1729, 2020.
- [2] L. Ambrosio, E. Mainini, and S. Serfaty. Gradient flow of the Chapman–Rubinstein–Schatzman model for signed vortices. Annales de l’I.H.P. Analyse non linéaire, 28(2):217–246, 2011.
- [3] Basel Committee on Banking Supervision. Minimum capital requirements for market risk, 2019. https://www.bis.org/bcbs/publ/d457.pdf.
- [4] H. H. Bauschke and A. S. Lewis. Dykstras algorithm with Bregman projections: A convergence proof. Optimization, 48(4):409–427, 2000.
- [5] M. Beiglböck, P. Henry-Labordere, and F. Penkner. Model-independent bounds for option prices—a mass transport approach. Finance and Stochastics, 17:477–501, 2013.
- [6] J.-D. Benamou, G. Carlier, M. Cuturi, L. Nenna, and G. Peyré. Iterative Bregman projections for regularized transportation problems. SIAM Journal on Scientific Computing, 37(2):A1111–A1138, 2015.
- [7] J.-D. Benamou, G. Chazareix, and G. Loeper. From entropic transport to martingale transport, and applications to model calibration. arXiv preprint arXiv:2406.11537, 2024. https://arxiv.org/pdf/2406.11537.
- [8] L. M. Bregman. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR computational mathematics and mathematical physics, 7(3):200–217, 1967.
- [9] H. Brezis. Analyse fonctionnelle. Théorie et applications, 1983.
- [10] P. Carr and D. B. Madan. A note on sufficient conditions for no arbitrage. Finance Research Letters, 2(3):125–130, 2005.
- [11] Y. Censor and S. Reich. The Dykstra algorithm with Bregman projections. Communications in Applied Analysis, 2(3):407–420, 1998.
- [12] L. Chizat, G. Peyré, B. Schmitzer, and F.-X. Vialard. Scaling algorithms for unbalanced optimal transport problems. Mathematics of Computation, 87(314):2563–2609, 2018.
- [13] S. N. Cohen, C. Reisinger, and S. Wang. Detecting and repairing arbitrage in traded option prices. Applied Mathematical Finance, 27(5):345–373, 2020.
- [14] L. Cousot. Necessary and sufficient conditions for no static arbitrage among European calls. Courant Institute, New York University, 2004.
- [15] L. Cousot. Conditions on option prices for absence of arbitrage and exact calibration. Journal of Banking & Finance, 31(11):3377–3397, 2007.
- [16] M. Cuturi. Sinkhorn distances: Lightspeed computation of optimal transport. Advances in neural information processing systems, 26, 2013.
- [17] M. H. Davis and D. G. Hobson. The range of traded option prices. Mathematical Finance, 17(1):1–14, 2007.
- [18] H. De March. Entropic approximation for multi-dimensional martingale optimal transport. arXiv preprint arXiv:1812.11104, 2018. https://arxiv.org/pdf/1812.11104.
- [19] H. De March and P. Henry-Labordere. Building arbitrage-free implied volatility: Sinkhorn’s algorithm and variants. arXiv preprint arXiv:1902.04456, 2019. https://arxiv.org/pdf/1902.04456.
- [20] R. L. Dykstra. An algorithm for restricted least squares regression. Journal of the American Statistical Association, 78(384):837–842, 1983.
- [21] European Banking Authority. Draft Regulatory Technical Standards on the capitalisation of non-modellable risk factors under the FRTB, 2020.
- [22] M. R. Fengler and L.-Y. Hin. Semi-nonparametric estimation of the call-option price surface under strike and time-to-expiry no-arbitrage constraints. Journal of Econometrics, 184(2):242–261, 2015.
- [23] R. Flamary, N. Courty, A. Gramfort, M. Z. Alaya, A. Boisbunon, S. Chambon, L. Chapel, A. Corenflos, K. Fatras, N. Fournier, L. Gautheron, N. T. Gayraud, H. Janati, A. Rakotomamonjy, I. Redko, A. Rolet, A. Schutz, V. Seguy, D. J. Sutherland, R. Tavenard, A. Tong, and T. Vayer. POT: Python Optimal Transport. Journal of Machine Learning Research, 22(78):1–8, 2021.
- [24] J. Guyon. Dispersion-constrained martingale Schrödinger problems and the exact joint S&P 500/VIX smile calibration puzzle. Finance and Stochastics, 28(1):27–79, 2024.
- [25] R. Jarrow and D. B. Madan. Hedging contingent claims on semimartingales. Finance and Stochastics, 3:111–134, 1999.
- [26] H. W. Kuhn and A. W. Tucker. Nonlinear programming. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, pages 481–492, Berkeley, CA, USA, 1951. University of California Press.
- [27] G. Peyré, M. Cuturi, et al. Computational optimal transport: With applications to data science. Foundations and Trends® in Machine Learning, 11(5-6):355–607, 2019.
- [28] B. Piccoli, F. Rossi, and M. Tournus. A Wasserstein norm for signed measures, with application to nonlocal transport equation with source term. Communications in Mathematical Sciences, 21(5):1279–1301, 2023.
- [29] R. Rockafellar. Duality and stability in extremum problems involving convex functions. Pacific Journal of Mathematics, 21(1):167–187, 1967.
- [30] R. Rockafellar. Convex Analysis. Princeton Landmarks in Mathematics and Physics. Princeton University Press, 1997.
- [31] R. Sinkhorn and P. Knopp. Concerning nonnegative matrices and doubly stochastic matrices. Pacific Journal of Mathematics, 21(2):343–348, 1967.
- [32] V. Strassen. The existence of probability measures with given marginals. The Annals of Mathematical Statistics, 36(2):423–439, 1965.
- [33] C. Villani. Topics in optimal transportation, volume 58. American Mathematical Soc., 2021.
- [34] C. Villani et al. Optimal transport: old and new, volume 338. Springer, 2009.
- [35] V. Zetocha. Volatility Transformers: an optimal transport-inspired approach to arbitrage-free shaping of implied volatility surfaces. Available at SSRN, 2023. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4623940.
Appendix A Reminders on convex analysis
We fix and denote by the usual scalar product in .
Definition A.1 (Affine hull and relative interior).
Let be a subset of . The affine hull of , , is the smallest affine set of containing . The relative interior of , , is the interior of , when is seen as a subset of its affine hull endowed with the subspace topology:
where is the open ball centered at , with radius .
Definition A.2 (Indicator function of a set).
Let be a subset of . The indicator function of is defined by
Recall that if is non-empty, closed and convex in , then is convex, lower semicontinuous and (i.e. is proper).
Definition A.3 (Domain of a function).
Let . The domain of , denoted by , is the set
Definition A.4 (Convex conjugate).
Let . The convex conjugate of is defined for each by
Definition A.5 (Subdifferential).
Let . The subdifferential of at the point is the set
Note that it might be empty (for instance when ). Whenever it is not, is said to be subdifferentiable at . An element of is called a subgradient of at . If is differentiable at , one can prove that . Besides, if and only if is subdifferentiable at and .
Theorem A.6 (Theorem 23.8 in [30]).
Let , be proper convex functions on and let . Then,
where the sum is to be understood in the Minkowski sense.
Furthermore, if , then the equality holds for all .
The following results are stated in a finite dimensional framework, which is sufficient for us, but they were also proved in more general settings.
Proposition A.7 (Proposition 1.9 in [9]).
Let . If is proper (i.e. ) lower semicontinuous and convex, then is also proper, lower semicontinuous and convex.
Theorem A.8 (Fenchel-Moreau, see Theorem 1.10 in [9]).
Let be a proper, lower semicontinuous and convex function. Then, .
Theorem A.9 (Fenchel-Rockafellar, [29]).
Let be a linear map and its adjoint. Let and be proper, lower semicontinuous and convex functions. If there exists such that is continuous at , then
i.e. the right-hand side is attained.
Moreover, is a maximizer of the left-hand side if and only if there exists a minimizer of the right-hand side, such that and .