An Unsupervised Learning Approach for Spectrum Allocation in Terahertz Communication Systems
Abstract
We propose a new spectrum allocation strategy, aided by unsupervised learning, for multiuser terahertz communication systems. In this strategy, adaptive sub-band bandwidth is considered such that the spectrum of interest can be divided into sub-bands with unequal bandwidths. This strategy reduces the variation in molecular absorption loss among the users, leading to the improved data rate performance. We first formulate an optimization problem to determine the optimal sub-band bandwidth and transmit power, and then propose the unsupervised learning-based approach to obtaining the near-optimal solution to this problem. In the proposed approach, we first train a deep neural network (DNN) while utilizing a loss function that is inspired by the Lagrangian of the formulated problem. Then using the trained DNN, we approximate the near-optimal solutions. Numerical results demonstrate that comparing to existing approaches, our proposed unsupervised learning-based approach achieves a higher data rate, especially when the molecular absorption coefficient within the spectrum of interest varies in a highly non-linear manner.
Index Terms:
Terahertz communication, machine learning, unsupervised learning, spectrum allocation, adaptive bandwidthI Introduction
Terahertz (THz) communication (THzCom) has been envisioned as a key wireless technology in the sixth-generation (6G) and beyond era [1]. The THz band has enormous potential to support tera-bits-per-second (Tbps) data rates and massive connections in 6G networks, due to the tens up to a hundred GHz bandwidth [2]. Thanks to the recent advancements in manufacturing THz transceivers and antennas, as well as the experimental licenses (95 GHz–3 THz) opened by the US Federal Communications Commission, increasing endeavors have been devoted to the design and development of practical THzCom systems over the past few years [3].
Despite the promise, THzCom encounters unique challenges that are different from those experienced at lower frequencies, e.g., severe spreading loss, higher channel sparsity, and the unique molecular absorption loss [4]. The molecular absorption loss is frequency-dependent, divides the whole THz band into several ultra-wide transmission windows, and introduces substantially varying distance-dependent path loss within transmission windows. These challenges need to be wisely tackled for developing practical THzCom systems.
There have recently been increasing endeavors to exploring novel and efficient THz spectrum allocation strategies, e.g., [4, 5, 2], due to its benefits of exploiting the potentials of the THz band. Specifically, multi-band-based spectrum allocation is envisioned as one promising solution to supporting micro- and macro-scale THzCom systems, since it can effectively assign spectral resources when the variation in molecular absorption loss among the users in multiuser systems is very high [6]. In this allocation, the spectrum of interest is divided into non-overlapping sub-bands, and the sub-bands are utilized to support the users in the system.
Although different designs have been proposed to optimize the performance of multi-band-based spectrum allocation, e.g., [6, 7, 8, 9], they all considered the spectrum of interest is divided into sub-bands with equal bandwidth. It is noted that the consideration of equal sub-band bandwidth (ESB) can lead to high variation in the molecular absorption loss among the sub-bands. Different from ESB, adaptive sub-band bandwidth (ASB), where the spectrum of interest is divided into sub-bands with unequal bandwidths, can effectively reduce the variation in molecular absorption loss among the users, thus leading to an overall improvement in the data rate performance. Motivated by this, the multi-band-based spectrum allocation with ASB was first proposed in our previous studies [10, 11]. We note that the design in [10] is only applicable when the molecular absorption coefficient within the to-be-allocated spectrum is simple such that it can be modeled as a piecewise exponential function of frequency with minimal approximation errors. In many spectrum regions within the THz band, the molecular absorption coefficient varies in a highly non-linear manner; thus, it cannot be modeled as a piecewise exponential function of frequencies in such spectrum regions. It follows that the designs in [10, 11] cannot be adopted in such spectrum regions. This motivates the current work.
In the current work, we study multi-band-based spectrum allocation with ASB to improve the spectral efficiency of THzCom systems. We formulate an optimization problem to determine the optimal sub-band bandwidth and optimal transmit power. We then propose an unsupervised learning-based approach to obtaining a near-optimal solution to the formulated optimization problem. In the proposed approach, we first train a deep neural network (DNN) where a loss function inspired by the Lagrangian of the formulated optimization problem is used. Thereafter, using the trained DNN, we approximate the near-optimal solution to the formulated optimization problem. Using numerical results, we demonstrate that when the values of the molecular absorption coefficient within the spectrum of interest can be modeled as an exponential function of frequency, the data rate obtained by our proposed unsupervised learning-based approach converges to the optimal data rate achieved by the existing spectrum allocation approach with ASB. We also demonstrate that when the values of the molecular absorption coefficient within the spectrum of interest change rapidly and thus cannot be modeled as an exponential function of frequency, our proposed unsupervised learning-based approach outperforms the existing approach.
Notations: Matrices and column vectors are denoted by uppercase and lowercase boldface symbols, respectively. Scalar variables are denoted by italic symbols. Given a matrix , denotes the th row vector of . Given a column vector , and denote the transpose and the th element of , respectively. Moreover, and denote identity matrix and lower triangular matrix with all non-zero values as 1, respectively. Furthermore, denotes the vector with all entries as 1. The curled inequality symbols, e.g., , denote generalized inequalities, i.e., componentwise inequality between vectors.
II System Model and Problem Formulation
We consider a three-dimensional (3D) indoor THzCom system where the high data rate demands of users are supported by a single AP. We consider that the users are stationary and distributed uniformly on the floor in the indoor environment. We denote as the communication distance vector of the AP-user channels. For notational convenience, we consider that the elements in are ordered such that .
II-A THz Spectrum
II-A1 Spectrum of Interest
We define the regions which generally exhibit an decreasing and increasing molecular absorption coefficient behaviour within an ultra-wideband THz transmission window as the negative absorption coefficient slope region (NACSR) and the positive absorption coefficient slope region (PACSR), respectively, as depicted in Fig. 1 [10]. It is noted that at the THz band, the available bandwidths in each NACSR and PACSR are in the order of tens of GHz [10, Table 1]. Considering this, we focus on the scenario where the to-be-allocated spectrum of interest fully exists in either an NACSR or a PACSR of a THz transmission window in this work111To fully utilize the potentials of the huge available bandwidths at the THz band, it would be more beneficial to focus on resource allocation when the to-be-allocated spectrum of interest spans across multiple NACSRs and/or PACSRs. This consideration will be addressed in our future work.. Without loss of generality, in the rest of the paper, we present spectrum allocation in an NACSR only since this spectrum allocation can be easily applied to a PACSR.
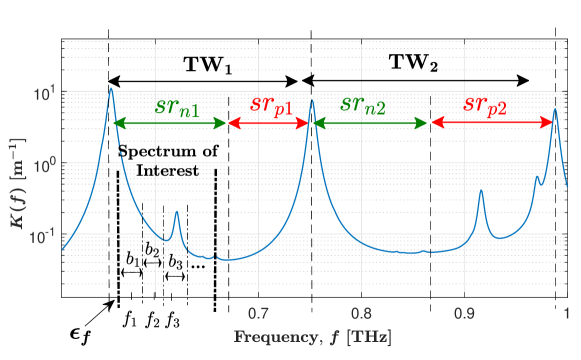
We focus on multi-band-based spectrum allocation with ASB. Thus, we divide the spectrum of interest into sub-bands that are of unequal bandwidths. We denote and as the vectors of the bandwidth and the center frequency of the sub-bands, respectively. For notational convenience, we label the sub-bands such that , as shown in Fig. 1. Thus, we have
| (1) |
where and is the start frequency of the spectrum of interest, as shown in Fig. 1. Here, is an matrix with . Considering this, we have . Due to the consideration of ASB, we have
| (2) |
where denotes the upper bound on bandwidth of the sub-band. We then denote as the total available bandwidth within the spectrum of interest and express it as
| (3) |
II-A2 Sub-band Assignment
In the considered system, we assume that the users in the system are served by separate sub-bands222A higher spectral efficiency can be achieved by utilizing sub-band reuse during spectrum allocation, which will be considered in our future work.. This assumption is made to (i) ensure the data transmission to be free of intra-band interference and (i) eliminate the signal processing overhead and hardware complexity caused by frequency reuse in the system, which is also adopted in [7, 6, 8, 10, 11]. Considering this assumption, we set the total number of sub-bands within the spectrum of interest to be equal to the total number of users in the system, i.e., . Also, following [8, 6, 9], we adopt distance-aware multi-carrier (DAMC)-based sub-band assignment to improve the throughput fairness among users. The DAMC-based sub-band assignment assigns (i) the sub-bands with high absorption coefficients to the users with shorter distances and (ii) the sub-bands with low absorption coefficients to the users with longer distances.
II-B Achievable Data Rate
We denote as the rate vector of users. Considering spreading and molecular absorption losses experienced by THz signal propagation, we obtain the rate achieved in the th sub-band as [12]
| (4) |
where , and are the antenna gains at the AP and users, respectively, is the noise power density, is the speed of light, and is the molecular absorption coefficient at . Furthermore, denotes the transmit power vector.
In this work, we focus on the line-of-sight (LoS) rays of THz signals [12, 13, 10, 11]. This is reasonable because when THz signals propagate, the direct ray dominates the received signal energy, while the non-line-of-sight rays are significantly attenuated due to high scattering and reflection losses. Also, we omit the impact of fading in the THz channel as the prior studies at the THz band [12, 13, 10, 11]. Moreover, following [6, 7, 8, 9, 11], we omit the impact of blockages in the THz channel. Finally, the impact of inter-band interference (IBI) is not considered in this work since prior studies have proposed designs to suppress IBI with minimal throughput degradation [14].
II-C Optimal Spectrum Allocation
We now design an efficient spectrum allocation strategy to harness the potential of the THz band. To this end, we study spectrum allocation with ASB to maximize the achievable data rate under given sub-band bandwidth and power constraints. Mathematically, this problem is formulated as
| (5a) | |||||
| s. t. | (5b) | ||||
| (5c) | |||||
| (5d) | |||||
| (5e) | |||||
In , is the objective function of the considered data rate maximization strategy. In this work, we consider proportionally-fair data rate maximization, which leads to . Moreover, (5b) and (5c) are the power budget at the AP and the upper bound on the power allocated to each user, respectively. Furthermore, the justifications on (5d) and (5e) are given by (3) and (2), respectively.
We note that it is extremely difficult, if not impossible, to analytically solve using the traditional optimization techniques [15]. This is due to the difficulty in obtaining a tractable expression for in terms of the design variables . On one hand, obtaining as per (4) involves an integral, the limits of which depend on . On the other hand, the values of for all frequencies within the spectrum of interest are required to obtain . However, there does not exist a tractable expression that maps to for all spectrum regions within the THz band. To tackle these challenges, we resort to unsupervised learning to obtain near-optimal solution to [16, 17], and present the solution in Section III.
III Unsupervised Learning-Based Solution
In this section, we present an unsupervised learning-based approach to solving problem in (4). In this approach, we first employ an offline training phase to train a DNN, utilizing (i) a loss function which is inspired by the objective function of the dual problem of and (ii) a batch of realizations of distance vectors. Thereafter, during the implementation phase, we use the trained DNN to approximate the optimal solution to for the given distance vector. Next, we will discuss the architecture of the adopted DNN in Section III-A, and the unsupervised learning model used in the training phase in Section III-B.
III-A Architecture of DNN
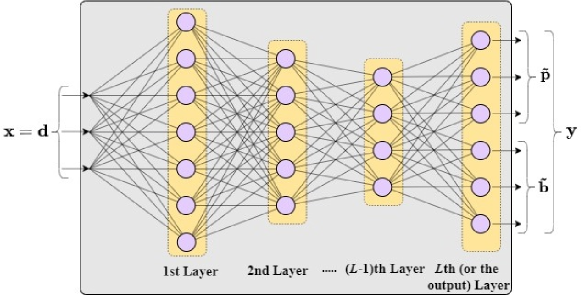
The general architecture of the adopted DNN is presented in Fig. 2. The DNN consists of fully-connected layers with multiple neurons in every layer. Each neuron in the network contains a linear operation, which is followed by a point-wise nonlinearity, also known as an activation function. Considering this, the output of the network, , is expressed as a non-linear function to the input of the network, , which is given by
| (6) |
Here, , denotes the set of parameters (i.e., weights and biases) of the DNN, and and are the weights vector and the bias of the th layer, respectively. Also, we have
| (7) |
where is the activation function of the th layer.
During the implementation phase, we provide as the input to the DNN and obtain the output as the approximated values of the optimization variables of , which are denoted by and . Therefore, we have
| (8) |
III-B Unsupervised Learning Model
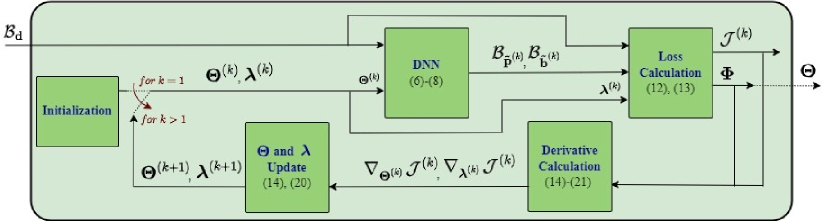
The block diagram representation of the unsupervised learning model used in the training phase is depicted in Fig. 3. The unsupervised learning model takes a batch of realization of the distance vector, , as the input, and delivers the trained as the output. We note that the unsupervised learning model iteratively updates to ensure the best mapping being obtained between and the near-optimal solution to for the given .
III-B1 Loss Function
The loss function of the unsupervised learning model is inspired by the objective function of the dual problem of . Specifically, the dual problem of is given by
| (9a) | ||||
| (9b) | ||||
where
| (10) |
is the Lagrangian of , and and are the Lagrange multipliers associated with the constraints of . In our unsupervised learning model, and are approximated as and using the DNN, respectively, which is parameterized by . Considering this, the problem can be regenerated into the following variable optimization as
| (11a) | |||||
| (11b) | |||||
where
| (12) |
In (III-B1), is obtained as a simplified version of given in (III-B1). This is because the satisfaction of constraints (5c) and (5e) can be guaranteed by carefully choosing appropriate activation functions for the neurons in the th (or the output) layer of the DNN, e.g., , where is the sigmoid function, and and for the first and the second neurons of the output layer, respectively.
We note that the optimal value of might be a loose global lower bound on the optimal value of , since is not a convex optimization problem. However, we also note that the design variables of are approximated using a DNN in our unsupervised learning model and aims to optimize the DNN parameters, . Thus, it can be concluded based on the universal approximation theorem that the optimal value of provides a tight lower bound on the optimal value of [16, 17]. Based on this conclusion and considering that a batch of realization of d, , is used during the training phase, we define the loss function of the unsupervised learning model, . Specifically, for each realization of d in , we obtained the corresponding , and then derive as the mean of values. Mathematically, is obtained as
| (13) |
where is the total number of realization of d in . We then iteratively update and with the objective of minimizing to arrive at the near-optimal solution to .
III-B2 Updating and
The DNN parameters, , are updated according to
| (14) |
where is the learning rate and is the th iteration value of , with . Considering the chain rule, we express in (14) as
| (15) |
In (15), and can be derived as
| (16) |
and
| (17) |
respectively. Note that in (16) and (17), it is impossible to analytically derive and , respectively. Hence, we numerically calculate the values of and when and by using
| (18) |
and
| (19) |
respectively, where is a very small positive number. We also note that in (15), can be calculated as a function of utilizing the chain rule.
As for the Lagrangian multiplier, , it can be updated according to
| (20) |
where is the learning rate. In (III-B2), can be derived as
| (21) |
IV Convex Optimization-based Solution for a Special Case
As mentioned in Section III, it is impossible to analytically solve the spectrum allocation problem using traditional optimization techniques for the generalized system model considered in this work. Despite so, for a special case of the considered system model, the solution to can be obtained using the convex optimization theory and standard convex problem solvers [10, 11]. We next present this special case system and its solution using convex optimization, the performance of which will be used as a benchmark in Section V for demonstrating the effectiveness and benefits of our proposed approach in Section III.
In the considered special case system, the molecular absorption coefficient within the spectrum of interest, , can be modeled as an exponential function of frequency with minimal approximation errors. We note that there indeed exist PACSRs and NACSRs within the THz band where can be modeled as an exponential function of frequency, e.g., between and , where the maximum modeling approximation error is .
For the considered special case system, the data rate, , can be approximated as a tractable expression in terms of b. Specifically, by modeling within NACSRs as an exponential function of frequency, we can approximate as
| (22) |
where is the model parameter vector. This enables us to obtain as a tractable expression of b as
| (23) |
With the simplified expression in (23), although becomes tractable, it is still non-convex. To overcome the non-convexity, we consider the following substitution for , given by
| (24) |
where is the new design variable vector that would replace in the optimization problem and is a vector with real constants as its elements. Using (24), the spectrum allocation problem for the special case system can be transformed into an equivalent standard convex problem given by
| (25a) | ||||
| (25b) | ||||
| (25c) | ||||
where , , and . The transformed problem for the special case system, , can be solved efficiently by using standard convex problem solvers [15]. The details of the convex optimization-based approach can be found in our previous work [10, 11].
V Numerical Results
The numerical results are obtained by considering a rectangular indoor environment of size where an AP, which is located at the center of the ceiling of the indoor environment, serves 15 users. We consider the spectrum with a bandwidth of 50 GHz that exist in either (i) the NACSR between and or (ii) the NACSR between and is used to serve the users. We clarify that on one hand, the molecular absorption coefficient, , in can be modeled as an exponential function of frequency with minimal approximation errors. Hence, the spectrum allocation problem in is a special case of the general spectrum allocation problem considered in this work. On the other hand, in cannot be modeled as an exponential function of frequency.
We implement the unsupervised learning model presented in Section III in Python. We utilize a five-layer DNN for the unsupervised learning model, which has 100, 100, 50, 25, and 30 neurons in the first, second, third, fourth, and fifth layers, respectively. The initial weights of the DNN are Gaussian random variables with zero mean and unit variance, and the initial biases are set to 0. The initial values of are set to a small constant of . The values of other system parameters, hyper-parameters of the unsupervised learning model, and the parameters of the convex optimization-based approach used for numerical results are summarized in Table I.
| Parameter | Value |
|---|---|
| System Parameters | |
| Difference between the heights of AP and | |
| users | |
| Antenna gains, , | , |
| Noise power density, | |
| Power budget, | -5 dBm |
| Upper bound on power per sub-band, | |
| Upper bound on sub-band bandwidth, | |
| Hyper-Parameters of the Unsupervised Learning Model | |
| Learning rates, | 0.05, 0.025 |
| Number of iterations | 500 |
| Total number of realization of d, | |
| Activation function of 1st to 4th layer, | ReLU |
| Activation function of the 5th layer, | sigmoid, |
| Parameters used for the Convex Optimization-based Approach | |
| Exponential model parameters in , | ,, |
| Exponential model parameters in , | ,, |
| Transformation model parameters, | ,, |
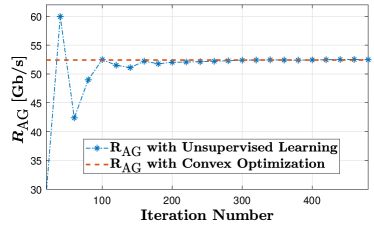
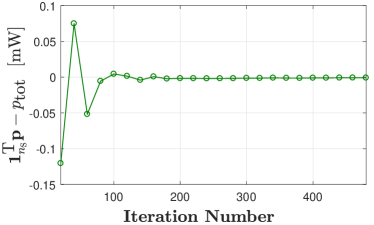
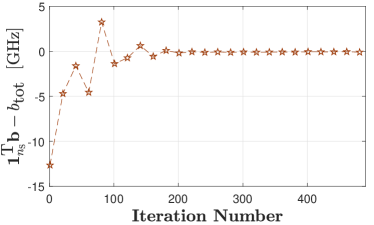
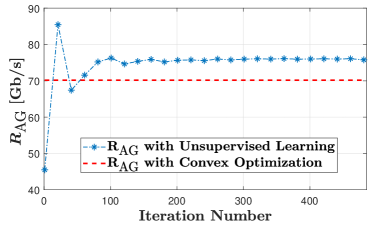
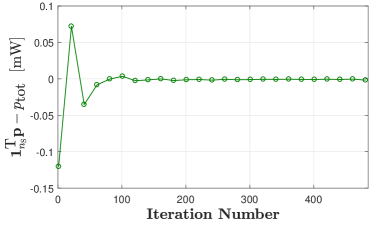
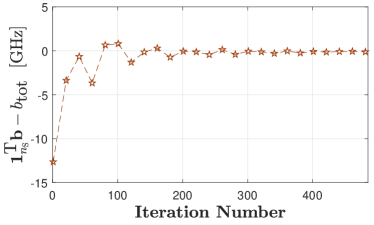
In Fig.4, we show the convergence of the proposed unsupervised learning-based approach when within the spectrum of interest can be modeled as an exponential function of frequency, i.e., considering the special case system investigated in Section IV. To this end, we plot the aggregated multiuser data rate, , the value of , and the value of obtained from the unsupervised learning-based approach in Figs. 4(a), 4(b), and 4(c), respectively, when the spectrum allocation problem is implemented in . Also, the value of obtained from the convex optimization-based approach is plotted in Fig.4(a). We first observe from Fig.4(a) that for several initial iterations, the value of obtained using the unsupervised learning-based approach is higher than that obtained using the convex optimization-based approach. This is due to the occasional violation of the constraints (5b) and (5d) that occur at corresponding initial iterations, which can be validated by observing and in Figs. 4(b) and 4(c), respectively. Moreover, after 200 iterations, we observe that the value of obtained using the unsupervised learning-based approach converges to the optimal value obtained using the convex optimization-based approach, which shows the correctness of our proposed unsupervised learning-based approach. Finally, we observe from Figs. 4(b) and 4(c) that after 200 iterations, the values of and of the proposed unsupervised learning-based approach are very close to zero, which reflects that constraints (5b) and (5d) are satisfied when the proposed unsupervised learning-based approach is used.
We next show the convergence of the proposed unsupervised learning-based approach when within the spectrum of interest cannot be modeled as an exponential function of frequency, i.e., considering the generalized system investigated in Sections II and III. To this end, we plot , , and in Figs. 5(a), 5(b), and 6(c), respectively, when the spectrum allocation problem is implemented in . We clarify that in , cannot be modeled as an exponential function of frequency with minimal approximation errors. However, for the sake of comparison, we obtain approximate solutions to the spectrum allocation problem in using the convex optimization approach while utilizing an inaccurate approximation for in , and plot the resulting in Fig.5(a). Once again, we observe the overshoot in , , and for several initial iterations and the satisfaction of the constraints (5b) and (5d) after 200 iterations in Figs. 5(a)-5(c), which are similar to Figs. 4(a)-4(c). Apart from them, we further observe that the value of obtained using the unsupervised learning-based approach converges to a value higher than that obtained using the convex optimization-based approach. This is because when the convex optimization-based approach is used, where an exponential function with high approximation errors is used to model , only the sub-optimal is obtained. This shows the significance of our proposed unsupervised learning-based approach, i.e., it gives much higher for the spectrum allocation problem when within the spectrum of interest cannot be modeled as an exponential function of frequency.
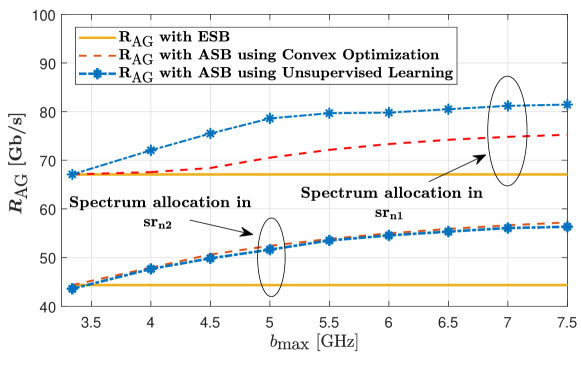
Finally, we plot achieved by the spectrum allocation strategy with ESB [6, 7, 8, 9] and the spectrum allocation strategy with ASB that is obtained from both convex optimization and unsupervised learning-based approaches, versus the upper bound on sub-band bandwidth, , in Fig.6. We first observe that the proposed spectrum strategy with ASB achieves a significantly higher compared to the strategy with ESB for different , which demonstrates the benefits of our proposed strategy with ASB. Second, we observe that in , the value of obtained using the unsupervised learning-based approach converges to values higher than that obtained using the convex optimization-based approach for all . This again shows the significance of our proposed unsupervised learning-based approach to obtain higher , especially when within the spectrum of interest cannot be modeled as an exponential function of frequency.
VI Conclusions
We investigated multi-band-based spectrum allocation with ASB for multiuser THzCom systems. We first formulated an optimization problem and then proposed an unsupervised learning-based approach to obtaining near-optimal sub-band bandwidth and transmit power. In the proposed unsupervised learning-based approach, we first employed an offline training phase to train a DNN while utilizing a loss function inspired by the Lagrangian of the formulated problem. Then using the trained DNN, we approximated the near-optimal solutions to the optimization problem for the given distance vector. Numerical results showed that when the values of the molecular absorption coefficient within the spectrum cannot be modeled as an exponential function of frequency, the data rate obtained by our proposed unsupervised learning-based approach outperforms that obtained by the existing convex optimization-based approach.
References
- [1] M. Giordani, M. Polese, M. Mezzavilla, S. Rangan, and M. Zorzi, “Toward 6G networks: Use cases and technologies,” IEEE Commun. Mag., vol. 58, no. 3, pp. 55–61, Mar. 2020.
- [2] A. Shafie, N. Yang, C. Han, J. M. Jornet, M. Juntti, and T. Kürner, “Terahertz communications for 6G and beyond wireless networks: Challenges, key advancements, and opportunities,” July 2022. [Online]. Available: https://arxiv.org/abs/2207.11021
- [3] H. Sarieddeen, N. Saeed, T. Y. Al-Naffouri, and M.-S. Alouini, “Next generation terahertz communications: A rendezvous of sensing, imaging, and localization,” IEEE Commun. Mag., vol. 58, no. 5, pp. 69–75, 2020.
- [4] M. Polese, J. M. Jornet, T. Melodia, and M. Zorzi, “Toward end-to-end, full-stack 6G terahertz networks,” IEEE Commun. Mag., vol. 58, no. 11, pp. 48–54, Nov. 2020.
- [5] V. Petrov, T. Kurner, and I. Hosako, “IEEE 802.15.3d: First standardization efforts for sub-terahertz band communications toward 6G,” IEEE Commun. Mag., vol. 58, no. 11, pp. 28–33, Nov. 2020.
- [6] C. Han and I. F. Akyildiz, “Distance-aware bandwidth-adaptive resource allocation for wireless systems in the terahertz band,” IEEE Trans. THz Sci. Technol., vol. 6, no. 4, pp. 541–553, July 2016.
- [7] A. Moldovan, P. Karunakaran, I. F. Akyildiz, and W. H. Gerstacker, “Coverage and achievable rate analysis for indoor terahertz wireless networks,” in Proc. IEEE Int. Conf. Commun. (ICC), Paris, France, May 2017, pp. 1–7.
- [8] C. Han, A. O. Bicen, and I. F. Akyildiz, “Multi-wideband waveform design for distance-adaptive wireless communications in the terahertz band,” IEEE Trans. Signal Process., vol. 64, no. 4, pp. 910–922, Feb. 2016.
- [9] X. Zhang, C. Han, and X. Wang, “Joint beamforming-power-bandwidth allocation in terahertz NOMA networks,” in Proc. Int. Conf. Sensing, Commun., Netw. (SECON), Boston, MA, USA, Sept. 2019, pp. 1–9.
- [10] A. Shafie, N. Yang, S. A. Alvi, C. Han, S. Durrani, and J. M. Jornet, “Spectrum allocation with adaptive sub-band bandwidth for terahertz communication systems,” IEEE Trans. Commun., vol. 70, no. 2, pp. 1407–1422, Jan. 2022.
- [11] A. Shafie, N. Yang, C. Han, and J. M. Jornet, “Novel spectrum allocation among multiple transmission windows for terahertz communication systems,” July 2022. [Online]. Available: https://arxiv.org/abs/2207.02401
- [12] J. M. Jornet and I. F. Akyildiz, “Channel modeling and capacity analysis for electromagnetic wireless nanonetworks in the terahertz band,” IEEE Trans. Wireless Commun., vol. 10, no. 10, pp. 3211–3221, Oct. 2011.
- [13] A. Shafie, N. Yang, S. Durrani, X. Zhou, C. Han, and M. Juntti, “Coverage analysis for 3D terahertz communication systems,” IEEE J. Sel. Areas Commun., vol. 39, no. 6, pp. 1817–1832, June 2021.
- [14] W. Gao, Y. Chen, C. Han, and Z. Chen, “Distance-adaptive absorption peak modulation for terahertz covert communications,” IEEE Trans. Wireless Commun., vol. 20, no. 3, pp. 2064–2077, Nov. 2020.
- [15] S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge, U.K.: Cambridge Univ. Press, 2004.
- [16] M. Eisen, C. Zhang, L. F. O. Chamon, D. D. Lee, and A. Ribeiro, “Learning optimal resource allocations in wireless systems,” IEEE Trans. Signal Process., vol. 67, no. 10, pp. 2775–2790, May 2019.
- [17] C. Li, C. She, N. Yang, and T. Q. S. Quek, “Secure transmission rate of short packets with queueing delay requirement,” IEEE Trans. Wireless Commun., vol. 21, no. 1, pp. 203–218, Jan. 2022.