Analog Circuit Design with Dyna-Style Reinforcement Learning
Abstract
In this work, we present a learning based approach to analog circuit design, where the goal is to optimize circuit performance subject to certain design constraints. One of the aspects that makes this problem challenging to optimize, is that measuring the performance of candidate configurations with simulation can be computationally expensive, particularly in the post-layout design. Additionally, the large number of design constraints and the interaction between the relevant quantities makes the problem complex. Therefore, to better facilitate supporting the human designers, it is desirable to gain knowledge about the whole space of feasible solutions. In order to tackle these challenges, we take inspiration from model-based reinforcement learning and propose a method with two key properties. First, it learns a reward model, i.e., surrogate model of the performance approximated by neural networks, to reduce the required number of simulation. Second, it uses a stochastic policy generator to explore the diverse solution space satisfying constraints. Together we combine these in a Dyna-style optimization framework, which we call DynaOpt, and empirically evaluate the performance on a circuit benchmark of a two-stage operational amplifier. The results show that, compared to the model-free method applied with 20,000 circuit simulations to train the policy, DynaOpt achieves even much better performance by learning from scratch with only 500 simulations.
1 Introduction
Although analog circuits are present as many different functional blocks in most integrated circuit (IC) chips nowadays, analog circuit design has been increasingly difficult for several reasons, e.g., growing complexity in circuit topology, tight tradeoffs between different performance metrics and so on [1]. Unlike digital circuit design that is aided by well standardized design flow with electronic design automation (EDA) tools [2], analog design requires a high level of application-specific customization and still resorts to domain knowledge by experienced designers. Manual optimization based on exhaustive search with simulation is a notoriously time consuming and labor intensive task. Particularly the post-layout design, in which the design objectives are verified after the layout creation, is much more challenging because it demands additional computationally costly simulations using EDA tools to reflect the layout parasitics to the circuit accurately. In addition, the circuit problem can have multiple different solutions which are distributed diversely in the search space. It can serve as crucial information fed back to designers such that they better understand the circuit operation under constraints. Unfortunately this generalization capability is mostly missing in prior methods. Automated analog design has drawn increasing attention to take human experts out of the optimization loop. Traditionally, population based methods (e.g., genetic algorithm [3] and particle swarm optimization [4]), and Bayesian optimization [5, 6] have been used. However, the former suffers from low sample efficiency and lacks reproducibility. The latter is sample efficient, but scales poorly in high dimensional problems.
In this work, we introduce a novel reinforcement learning (RL) [7] based optimization framework, DynaOpt, which not only learns the general structure of solution space but also ensures high sample efficiency based on a Dyna-style algorithm [8]. The contributions of this paper are as follows: First, the policy is trained through a noise source and learns a whole distribution of feasible solutions. Second, the reward is modeled using neural networks, which allows us to leverage model-based RL. Third, the post-layout circuit is optimized based on model-based RL, together with transfer learning from the schematic based design, and we achieves 300 higher sample efficiency than model-free approach. Finally, DynaOpt is implemented by taking advantage of both the model-free and model-baed methods to maximize the learning process from scratch. Even though we focus on analog circuit design, the methodology is expected to be readily applicable to a broad range of simulation based optimization problems in engineering.
2 Background
2.1 Circuit optimization problem
The objective of analog circuit design is to search over optimal circuit parameters (e.g., width and length of transistors, resistance and capacitance) that meet design constraints imposed on performance metrics (e.g., power, noise and voltage gain) given a circuit topology [1]. The performance metrics are measured by running a circuit simulator with input of candidate parameters, and this process repeats until all the required inequality constraints, which are application specific, are satisfied (e.g., voltage gain > 100 V/V and power consumption < 1mW).
The circuit optimization can be formulated as a RL problem. Generation of circuit parameters corresponds to the action, and the reward is determined by an estimate of circuit performance. The agent iterates sequential decision process by interacting with the environment (i.e., circuit simulation), and improves the policy to maximize the expected reward. We define the reward as a weighted sum of normalized performance metrics under measurement.
| (1) |
where the measured metric should be either larger than the lower bound or smaller than the upper bound , and denotes the weighting factor which is one in this work. Each normalized metric is set to be within a range of , which also helps regression of the reward model discussed in Section 3. The reward starts from the negative and reaches zero once all hard constraints are satisfied. The other minimization or maximization objectives can be also included in Equation 1 similarly without clipping values to be negative.
2.2 Related works
Recent rapid progress in machine learning has accelerated analog design automation with various learning based methods. For example, [9] combines evolutionary algorithms with a neural network discriminator to boost the sample efficiency. Recent works [10, 11] frame the optimization problem as a Markov decision process (MDP) and apply the RL method to learn the optimal policy. RL is also used together with graph convolutional neural networks to learn about the circuit topology representation [12]. However, the aforementioned RL based approaches all rely on model-free algorithms which require to run the circuit simulation for every training sample to evaluate the reward, and thus the sample efficiency inevitably degrades as the circuit complexity increases. In addition, [11] attempts to learn about the design space through a sparse subsampling technique (i.e., randomizing target specifications in a certain range), but it may not guarantee convergence to generalized solutions.
3 DynaOpt: reinforcement learning based optimization
In this section, we present a RL based optimization framework which can tackle both the sample efficiency and the solution generalization. The policy generator and the reward model are discussed in detail as important building blocks in the proposed architecture, and it is followed by a description of Dyna-style leaning based algorithm.
3.1 Policy generator
In this paper, we try to address the circuit optimization problem with RL. Even though the problem has no time component, RL can still be promising. For instance, RL has recently been used for the problem of network architecture search (NAS) with good results [13]. Our initial approach was to mirror their method: we used the recurrent neural network (RNN) controller where each RNN cell generates one circuit parameter at every time step, and it is then fed as input to the next cell at the next time step. However, our experiments indicated that the cell connections over time steps do not help for the problem (see more details in Supplementary Material).
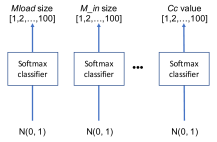
Therefore, we take a much simpler approach as illustrated in Figure 1 (left): each parameter is represented by its own distribution. Together these form a policy that is a product distribution: , where is a specification of all parameters. To allow flexible distributions for each parameter, we draw inspiration from generative adversarial networks (GANs) [14]and use a feedforward network which is fed by a Gaussian noise input such that it can ultimately learn a distribution of optimal actions. For implementation, this policy generator is trained using the REINFORCE policy gradient algorithm [15] with baseline, and the entropy bonus is added to encourage exploration [16].
3.2 Reward model
The reward evaluation with simulation is an expensive process in analog circuit design, and here we investigate if it can be replaced by a reward model built with learnable neural networks. The reward model is simply a regression model predicting a scalar valued reward as a function of actions. Alternately, it can be implemented to output each performance metric separately, from which the reward is calculated in the final stage. The neural network is designed to have different heads and one shared backbone like a multi-task regressor. It can serve to be better explainable to designers, but costs slightly increased complexity in the neural network. Furthermore, since the environment is fully represented by the reward model only, model-based RL can be directly applied to the problem without incorporating any other models. In this regard, the post-layout deign can greatly benefit from model-baed RL, as discussed in detail below.
Transfer learning
Design lifecycle of analog circuits generally involves two circuit optimization tasks. While the first preliminary design considers the schematic only, the post-layout design requires several costly EDA tools to take into account the layout effect, and it poses a major bottleneck. The overall design efficiency can be significantly improved by transferring knowledge between the two, based on the model-based approach. More specifically, it starts with optimizing the first design with model-free RL. The training data of action-reward pairs are reused to build up the reward model for the first design. Then the reward model is tweaked for the post-layout design with a minimal number of simulation based training samples. Finally the post-layout design is optimized based on full model-based RL.
3.3 Dyna-style optimization
In case that prior knowledge related to the problem is unavailable, model-based optimization can be implemented in a different way such that the policy generator and the reward model are improved alternately from scratch. At each training cycle, a small batch of action-reward pairs sampled from the policy and evaluated with simulation, i.e., real experience, is accumulated to the sample buffer which is in turn used to train the reward model. It is followed by the policy improvement with this updated reward model. This iteration continues until the optimal policy is reached. Moreover, since real experience is sampled from the on-policy distribution, the reward model can be effectively updated with much less training samples by focusing on the interested action space defined by the current policy [7]. Due to this advantage, the algorithm can be implemented in several different ways such that, for instance, the reward model is trained without using the off-policy sample buffer.
To further enhance the sample efficiency, a unified Dyna-style optimization scheme is proposed by intermixing both the model-free and model-based RL methods [8]. The algorithm needs one modification from the model-based one such that real experience is used to improve the policy by model-free RL as well as the reward model. The details are described in Algorithm 1.
Initialize policy generator , reward model and sample buffer
For number of training cycles do
. For do // Loop for model-free RL
. . Sample
. . Sample a vector of actions // : number of circuit parameters
. . Estimate reward using circuit simulation with
. . Update policy parameters based on REINFORCE rule
. . Store action-reward pair in
. End
. Update reward model parameters by regression on
. For do // Loop for model-based RL
. . Sample
. . Sample
. . Estimate using reward model
. . Update based on REINFORCE rule
. End
End
4 Experiments
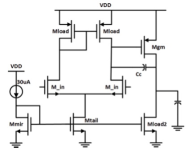
An experiment is carried out on the same design problem of a two-stage operational amplifier as found in [11]. The circuit schematic is shown in Figure 1 (right). The problem has 7 circuit parameters (6 transistor sizes, 1 capacitance) to optimize and 4 design constraints (voltage gain > 200 V/V, unity gain bandwidth > 1 MHz, phase margin > 60 degree, bias current < 10 mA) to satisfy. Each discretized circuit parameter can be selected from 100 possible values, and so the action space size is in total. The circuit is evaluated using 45nm BSIM model with NGSPICE simulator [17].
4.1 Analysis of policy generator
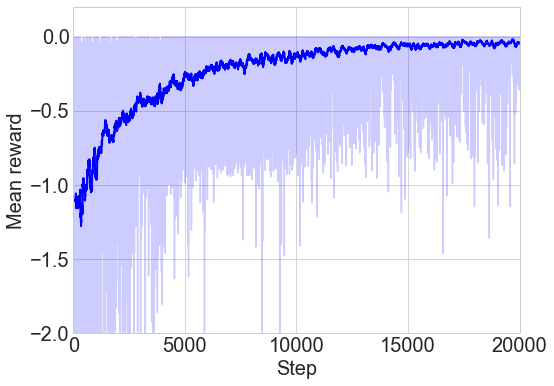
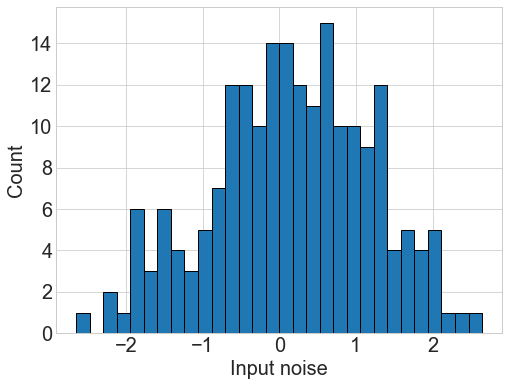
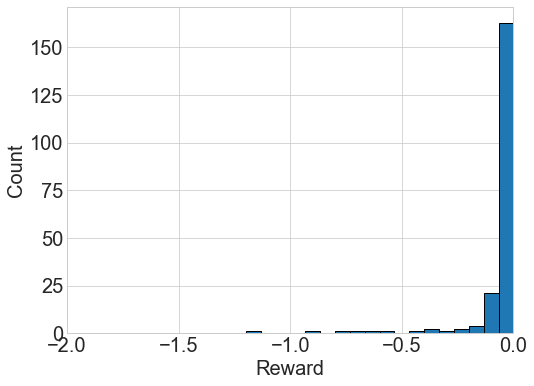
We train the policy generator in Figure 1 (left) based on the policy gradient method, using random noise input from the normal distribution for generalization. Figure 2 (left) shows a noisy reward trajectory to learn about the action space from the noise input, and the mean reward converges to zero around 20,000 steps111Because a minibatch size of one is used throughout this work, the training step in model-free algorithms is equal to the number of simulation. as the policy improves. For verification, this trained policy generator is evaluated with 200 simulation based samples given by the same noise source as found in Figure 2 (center). Figure 2 (right) shows the reward distribution of the corresponding actions generated by the trained policy and evaluated by simulation. The generated actions are distributed mostly near a reward of zero, and eventually the policy generator can learn to map the input noise to a distribution of optimal actions solving the problem.
4.2 Transfer learning for post-layout design
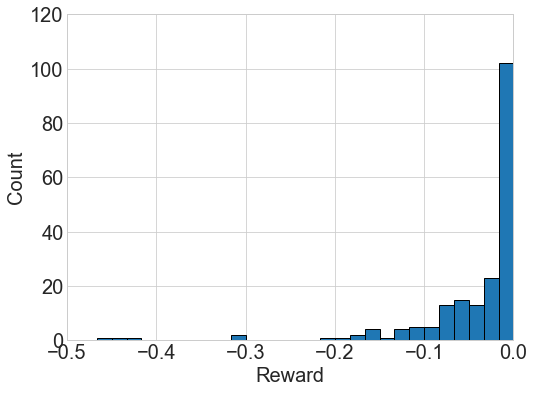
In the post-layout design, we simply assume that the layout effect introduces additional parasitic capacitance of 200 pF between all nodes to the circuit in Figure 1 (right). This value is likely to be much larger than actual ones like some worse-case scenario, and accurate assessment of the layout parasitics may not be critical here for proof-of-principle experiment. Figures 3 (left) shows the model-based optimization result. Initially the policy trained in the first schematic-only design as described above, generates low-quality actions unsuitable for this post-layout circuit. Only 100 simulation based training samples are used to update the reward model by transfer learning. The reward model is configured to have 3 hidden layers of size 16 with ReLU activation except the output layer. The policy is then updated from the pretrained policy and optimized for the post-layout circuit, based on model-based RL without involving simulation at all. The reward distribution is obtained by evaluating the trained policy with 200 input noise samples as before. For comparison, model-free optimization is also carried out by learning from scratch with 30,000 simulations, and the result is shown in Figure 3 (right). The model-based approach achieves comparable performance, with 300 improved sample efficiency.

4.3 DynaOpt based circuit optimization
DynaOpt is also applied to the problem in Figure 1 (right). The training is repeated over 5 cycles, and each cycle uses 100 simulations to update both the policy generator and the reward model, based on Dyna-style RL, as described in Algorithm 1. Figure 4 shows how the reward distribution evolves as the policy improves, when the agent starts learning without prior knowledge. As compared to Figure 2 (right) where the the model-free method is applied with 20,000 simulations, DynaOpt yields comparable results only after about 3 training cycles (300 simulations), and learns nearly optimal policy with merely 500 simulations.
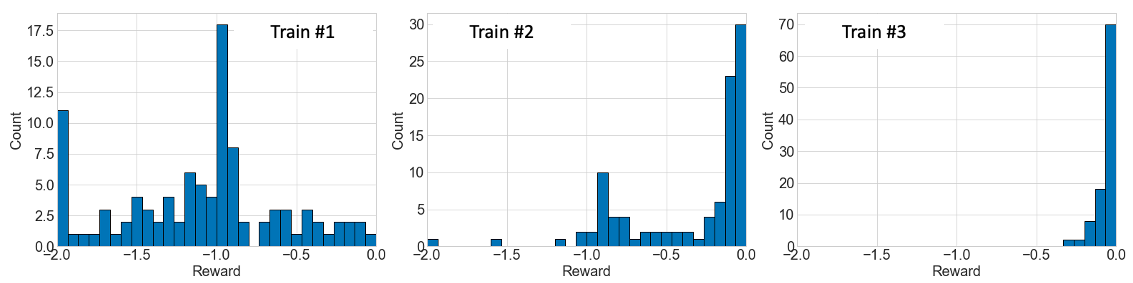
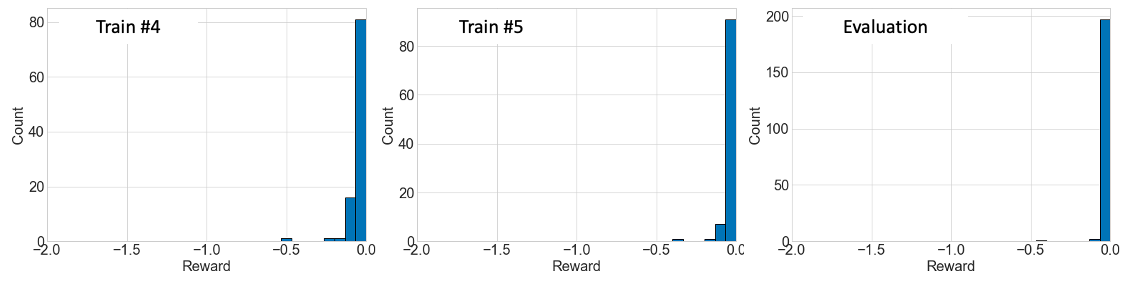
5 Conclusions
We propose DynaOpt for analog circuit design, which is a Dyna-style RL based optimization framework. It is built by intermixing both the model-free and model-based methods with two key components - the stochastic policy generator and the reward model. The policy generator learns to map the random noise input to the on-policy distribution of actions which eventaully move toward solutions as the policy improves, and the reward model allows to leverage sample efficient model-based RL by replacing expensive simulation with it. By putting them together, DynaOpt achieves both generalization capability and high sample efficiency, which is difficult with prior methods. Application to the design of a two-stage operational amplifier is demonstrated based on various implementation of the methodology such as model-based learning with knowledge transfer and Dyna-style learning, which all outperform the model-free approach with promising results.
Acknowledgments and Disclosure of Funding
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/19d494f7-89a0-49f4-8aac-445a72b62f7f/LOGO_ERC-FLAG_EU-cropped.jpg)
This project had received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 758824 —INFLUENCE).
References
- [1] P. E. Allen and D. R. Holberg. CMOS analog circuit design. Oxford University Press, 2002.
- [2] J. M. Rabaey, A. P. Chandrakasan, and B. Nikolic. Digital integrated circuits: a design perspective. Prentice Hall, 2003.
- [3] M. W. Cohen, M. Aga, and T. Weinberg. Genetic algorithm software system for analog circuit design. Procedia CIRP, 36:17–22, 2015.
- [4] P. P. Prajapati and M. V. Shah. Two stage CMOS operational amplifier design using particle swarm optimization algorithm. In IEEE UP Section Conference on Electrical Computer and Electronics, pages 1–5, 2015.
- [5] W. Lyu, P. Xue, F. Yang, C. Yan, Z. Hong, X. Zeng, and D. Zhou. An efficient Bayesian optimization approach for automated optimization of analog circuits. IEEE Transactions on Circuits and Systems I: Regular Papers, 65(6):1954–1967, 2018.
- [6] W. Lyu, F. Yang, C. Yan, D. Zhou, and X. Zeng. Batch Bayesian optimization via multi-objective acquisition ensemble for automated analog circuit design. In International Conference on Machine Learning, pages 3306–3314, 2018.
- [7] R. S. Sutton and A. G. Barto. Reinforcement learning: an introduction. MIT Press, 2018.
- [8] R. S. Sutton. Dyna, an integrated architecture for learning, planning, and reacting. ACM Sigart Bulletin, 2(4):160–163, 1991.
- [9] K. Hakhamaneshi, N. Werblun, P. Abbeel, and V. Stojanovic. BagNet: Berkeley analog generator with layout optimizer boosted with deep neural networks. IEEE/ACM International Conference on Computer-Aided Design, pages 1–8, 2019.
- [10] H. Wang, J. Yang, H.-S. Lee, and S. Han. Learning to design circuits. In NeurIPS Machine Learning for Systems Workshop, 2018.
- [11] K. Settaluri, A. Haj-Ali, Q. Huang, K. Hakhamaneshi, and B. Nikolic. AutoCkt: deep reinforcement learning of analog circuit designs. In Design, Automation & Test in Europe Conference & Exhibition, pages 490–495, 2020.
- [12] H. Wang, K. Wang, J. Yang, L. Shen, N. Sun, H.-S. Lee, and S. Han. GCN-RL circuit designer: transferable transistor sizing with graph neural networks and reinforcement learning. In ACM/IEEE Design Automation Conference, pages 1–6, 2020.
- [13] B. Zoph and Q. V. Le. Neural architecture search with reinforcement learning. In International Conference on Learning Representations, 2017.
- [14] I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio. Generative adversarial networks. Advances in Neural Information Processing Systems, 3(06), 2014.
- [15] R. J. Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning, 8(3-4):229–256, 1992.
- [16] M. Lapan. Deep reinforcement learning hands-on. Packt Publishing, 2018.
- [17] K. Settaluri. AutoCkt: deep reinforcement learning of analog circuit designs. https://github.com/ksettaluri6/AutoCkt, 2020.
6 Supplementary Material
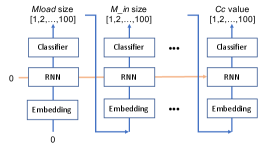
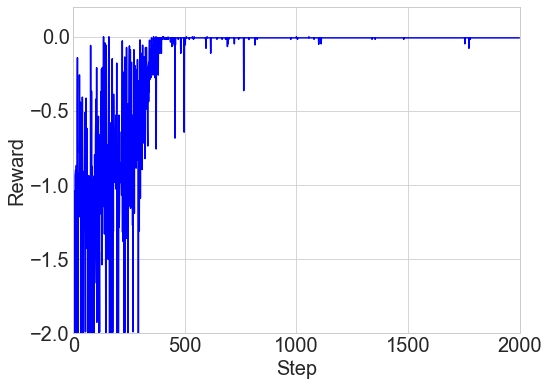
Due to similarity to the NAS problem, the RL based approach in [13] is directly applicable to the circuit optimization as long as the action space is discretized. As shown in Figure 5, the RNN controller is used as the policy network to sequentially sample a list of actions, i.e., circuit parameters, based on the current policy. The action generated in each RNN cell is fed to the next cell in an autoregressive way. After collecting the final action, the agent receives the corresponding reward by measuring the circuit performance with simulation. We first apply the RNN controller to the circuit problem in Figure 1 (right), and Figure 6 (left) shows the reward over training steps. The problem is solved, i.e., approaching a reward of zero, in < 500 steps, with producing one random combination of optimal parameters. Different orders of parameters assigned to RNN cells are tested, and they produce all similar learning curves without any preferred orders observed.
However, the controller still works similarly even when the cells are disconnected by deactivating the RNN (i.e., setting zero to all inputs and hidden states) and cutting off the autoregressive connection, as shown in Figure 6 (right). Each cell works as an independent learner like treating the circuit parameters as independent variables, and thus the policy network for the circuit optimization can be greatly simplified to the scheme presented in Figure 1 (left).