Analysis of Energy-Based Blended Quasicontinuum Approximations
Abstract.
The development of patch test consistent quasicontinuum energies for multi-dimensional crystalline solids modeled by many-body potentials remains a challenge. The original quasicontinuum energy (QCE) [28] has been implemented for many-body potentials in two and three space dimensions, but it is not patch test consistent. We propose that by blending the atomistic and corresponding Cauchy-Born continuum models of QCE in an interfacial region with thickness of a small number of blended atoms, a general quasicontinuum energy (BQCE) can be developed with the potential to significantly improve the accuracy of QCE near lattice instabilities such as dislocation formation and motion.
In this paper, we give an error analysis of the blended quasicontinuum energy (BQCE) for a periodic one-dimensional chain of atoms with next-nearest neighbor interactions. Our analysis includes the optimization of the blending function for an improved convergence rate. We show that the strain error for the non-blended QCE energy (QCE), which has low order where is the atomistic length scale [13, 29], can be reduced by a factor of for an optimized blending function where is the number of atoms in the blending region. The QCE energy has been further shown to suffer from a O error in the critical strain at which the lattice loses stability [16]. We prove that the error in the critical strain of BQCE can be reduced by a factor of for an optimized blending function, thus demonstrating that the BQCE energy for an optimized blending function has the potential to give an accurate approximation of the deformation near lattice instabilities such as crack growth.
Key words and phrases:
quasicontinuum, error analysis, atomistic to continuum2000 Mathematics Subject Classification:
65Z05,70C201. Introduction
Crystalline materials often have highly singular strain fields at crack tips, dislocations, and grain boundaries that require the accuracy of atomistic modeling only in small regions surrounding these defects. However, these localized defects interact through long-ranged elastic fields with a much larger region where the strain gradients are sufficiently small to allow accurate and efficient approximation by coarse-grained continuum finite element models. This has motivated the development of numerical methods that couple atomistic regions with continuum regions to compute problems with length scales that are sufficiently large for accurate and reliable scientific and engineering application [26, 7, 20, 23, 24, 32, 19, 10, 21, 28, 34, 38].
The quasicontinuum energy (QCE) [30] couples an atomistic model to a finite element continuum model based on the Cauchy-Born strain energy density. The Cauchy-Born strain energy density reproduces the atomistic energy density for a uniformly deformed lattice. The QCE atomistic-to-continuum coupling also reproduces the atomistic energy density for a uniformly deformed lattice simply by modifying the volume of the triangles or tetrahedra within the cut-off radius of the boundary of the atomistic region by using the Voronoi cell [28]. The QCE energy remains the most popular quasicontinuum energy since the modification of the volume of the triangles near the interface to reproduce the atomistic energy density can be explicitly achieved and has been implemented in the code [27] for multi-dimensional problems with many-body potentials.
A quasicontinuum energy is said to be patch test consistent if it reproduces the zero net forces at each atom for a uniformly deformed lattice. The fully atomistic and Cauchy-Born energies are patch test consistent by symmetry, but the symmetry is broken in the QCE atomistic-to-continuum interface. The nonzero forces in the QCE atomistic-to-continuum interface of a uniformly deformed lattice are called ghost forces [15, 11, 28, 35].
The ghost force correction method (GFC) was developed to improve the accuracy of QCE [35], and it has been shown to converge to the patch test consistent force-based quasicontinuum method (QCF) [9, 11]. GFC has been implemented in the code [27] and further developed to utilize the efficiency of atomistic-to-continuum modeling and continuum mesh a posteriori adaptivity [2, 1, 28, 35].
However, it has been shown that the force-based quasicontinuum method (QCF) gives a non-conservative force field [9, 11, 28], so the stability of a deformation that satisfies the QCF equations cannot be simply determined by checking whether it is a local minimum of a quasicontinuum energy [14]. The linearization of the QCF method has also been shown to be indefinite and to have unusual stability properties [15] which presents a further challenge to the notion of stability and to the development of efficient and reliable iterative methods [17, 25].
The potential for more reliable and efficient iterative solution methods and more direct extensions to finite temperature dynamical methods [18] make energy-based quasicontinuum methods more desirable than force-based quasicontinuum methods. Several quasicontinuum energies have been proposed which satisfy the patch test for a limited class of problems, but a quasicontinuum energy that satisfies the patch test for many-body potential interactions in several space dimensions with general coupling interfaces and coarsening has yet to be developed.
The quasi-nonlocal energy (QNL) [39] gives an explicit and implemented algorithm for close range interactions (up to next-nearest neighbor interactions for a chain and up to fourth-nearest neighbor interactions for a FCC lattice) by restoring the symmetry of the interactions. Ghost forces remain for nonplanar interfaces and coarsening [19]. The geometric consistency approach gives geometric and algebraic conditions to allow finite range interactions, but an implemented algorithm has only been given for low index planar interfaces. An efficient and implemented algorithm has yet to be given for a general nonplanar interface surrounding a defect. Ghost forces still remain for nonplanar interfaces and coarsening [19]. Further, the generalization of the geometric consistency approach to three-dimensional problems seems to depend on special decompositions of three-dimensional space into congruent tetrahedra (for example, the hexagonal lattice is such a special decomposition of two-dimensional space).
The QCE energy, on the other hand, can be implemented for any decomposition of three-dimensional space into tetrahedra (see (21) in [28]), and so can the blended quasicontinuum energy (BQCE) which we propose below. In fact, a code for the BQCE energy can be obtained by simply modifying any QCE code and suppressing the coarsening in the blending interface. We have done that for our two-dimensional QCE code [40]. The BQCE code will then be able to utilize any adaptive atomistic-to-continuum and continuum coarsening features of the QCE code.
More recently, generalizations have been given for the explicit extension of the QNL energy to allow finite range interactions [38, 22]. The consistent a/c coupling [38] gives an implemented patch test consistent quasicontinuum energy for two-dimensional problems with general pair potential interactions, atomistic-to-continuum coupling interface, and coarsening. No generalizations of these or other patch test consistent methods to three-dimensional crystals, multi-lattices, or multi-body potentials are yet known.
Since there remain important problems for which no patch test consistent methods are known, we feel it is important to develop general strategies for reducing the error of coupled energies which can be applied to a broad class of methods and problems. We propose that by blending the atomistic and corresponding Cauchy-Born continuum energies of QCE in an interfacial region with thickness of a small number of blended atoms, a blended quasicontinuum energy (BQCE) can be developed with the potential to significantly improve the accuracy of the QCE energy near lattice instabilities such as dislocation formation and motion. This blended quasicontinuum energy can be implemented for any problem for which a QCE energy has been developed, and we think that most existing codes for QCE could be easily modified to implement BQCE.
The blended quasicontinuum energy is not patch test consistent, but our error estimates in Section 3 show that the error due to the ghost force can be reduced significantly by optimizing the blending function over a blending region of small size Therefore, we think that the use of BQCE is a good strategy for reducing the error of QCE when applied to problems for which no patch test consistent methods are known. Moreover, patch test consistent quasicontinuum methods tend to be more complicated and more difficult to implement than QCE. Thus, even for problems for where a patch test consistent quasicontinuum energy is known, we think that the BQCE energy remains an attractive quasicontinuum energy.
The BQCE method is similar to many other methods in which atomistic and continuum energies are smoothly blended over an interfacial region, with some features specific to the quasicontinuum setting. We call such a region a blending region, and we call such a method a blended method. (Other authors call the blending region a “handshake region”, an “interface”, a “bridging region”, or an “overlap”.) We call the weights which blend the atomistic and continuum contributions to the energy blending functions. For example, the AtC coupling [3], the bridging domain method [6], and the Arlequin method for coupling particle and continuum models [5] are all energy-based blended methods which are similar to BQCE. By contrast, in other schemes, the atomistic and continuum models are coupled abruptly across a sharp interface consisting of only a few atoms. Such schemes include the energy-based quasicontinuum (QCE) method [30], the quasinonlocal quasicontinuum (QNL) method [39], the generalized QNL method [22], and the consistent a/c coupling [38].
In this paper, we present an error analysis of the blended quasicontinuum energy (BQCE). We determine precisely how the error of the BQCE method depends on the size of the blending region and how it depends on the blending functions. We analyze the accuracy of BQCE applied to the problem of a one-dimensional chain of atoms with periodic boundary conditions and a next nearest neighbor pair interaction model. Our choice of a one-dimensional analysis allows us to explicitly investigate the accuracy of the BQCE energy for deformations up to lattice instability [16], which is crucial for the computation of critical strains in lattice statics as well as for the computation of the dynamics of defect nucleation and movement.
We focus on modeling error and do not consider coarse-graining in our analysis. Instead, we assume that the continuum energy is a Cauchy-Born energy discretized by piecewise linear finite elements with nodes at every atom. We refer the reader to [32, 33] for an analysis of coarse-graining for a problem similar to our one-dimensional chain. In addition, we constrain the displacements of atoms in the blending region to exactly match the continuum displacement field. In some other methods, the displacements of atoms in the blending region are coupled weakly to the continuum displacement field using Lagrange multipliers or a penalty method. This is the case in the Arlequin method [5], in the bridging domain method [6], and in some implementations of the AtC Coupling [3, 4]. Computational experiments comparing various methods of weak coupling are given in [36, 4, 3, 6]. A numerical analysis of a mixed finite element method for a weakly coupled problem is given in [5].
Blending can also improve the accuracy of quasicontinuum energies which are more accurate than QCE, but may not satisfy the patch test for general interactions, nonplanar interfaces, or coarsening. We thus also define and analyze a blended generalization of QNL which we call the blended QNL (BQNL) energy. The BQNL method is an energy-based, blended coupling which passes the patch test for the one-dimensional problem analyzed in this paper, but does not generally satisfy the patch test as described above.
Our analysis extends the techniques developed in [31] for the patch test consistent QNL to obtain precise estimates of the error for BQCE, which does not satisfy the patch test. Most importantly, our estimates can be used to optimize the blending function and blending interface size of BQCE to obtain accurate solutions up to lattice instabilities. Our error estimate in Theorem 5.1 shows that the strain error for the BQCE method can be reduced by a factor of where is the number of atoms in the blending region. This result is suggested by the results of [13, 29] on the decay of the coupling error for QCE. It has been shown that the QCE method suffers from a O error in the critical strain at which the lattice loses stability (which models fracture or the formation of a defect) [16]. We prove in Theorem 4.1 that the error in the critical strain of BQCE can be reduced by a factor of where is the number of atoms in the blended interface region. In Remark 3.3, we use our modeling error estimates to derive blending functions for the BQCE method which minimize the error due to the ghost force. We give our a priori error estimate for BQNL in Theorem 5.2. In Theorem 5.2, we show that the strain error for the BQNL method can be reduced by a factor of . We prove in Theorem 4.1 that the BQNL method does not suffer from a critical strain error.
2. An atomistic model and its quasicontinuum approximations
2.1. The atomistic model problem
We begin by presenting a model of a one-dimensional lattice of atoms. Our reference configuration is the integer lattice with lattice spacing . The admissible deformations are N-periodic, mean-zero displacements of uniformly strained states of .
Precisely, for , we let
be the set of N-periodic, mean-zero displacements. For we let
be the uniformly deformed state with macroscopic strain , and we let
be the set of admissible deformations with fixed macroscopic strain . We will fix throughout the remainder of the paper, so that the reference length of a period is one, independently of . For notational convenience, we have let the deformations be functions of instead of even though we still think of as the reference configuration. We also remark that the “displacements” which appear in the definition of are not displacements measured relative to the reference lattice , but are instead displacements relative to the uniformly deformed state .
In the language of mechanics, one would say that our choice of the deformation space means that we have imposed “periodic boundary conditions with macroscopic strain .” Periodic boundary conditions are mathematically similar to Dirichlet boundary conditions in that constraints are applied to the space of admissible deformations. In our case, the constraint is given by the macroscopic strain which models the macroscopic scale stretching or contraction of the chain. Periodic boundary conditions are useful because they eliminate surface effects near the boundaries of the chain.
For a deformation we define a stored energy per period which we call . Our stored energy sums the energies of all the interactions between first nearest neighbors and second nearest neighbors in the lattice. We compute the energies of interaction using a potential which we assume satisfies
-
(1)
-
(2)
there exists so that for all , and for all
-
(3)
and its derivatives decay at infinity.
Examples of commonly used interaction potentials which satisfy the above conditions include the Lennard-Jones potential and the Morse potential. Specifically, we define
| (2.1) |
In (2.1), we call the terms of the form first nearest neighbor interactions, and we call terms of the form second nearest neighbor interactions.
The reader will observe that we have scaled the energy by and the interatomic distances by . This is done for two related reasons. First, quasicontinuum methods are only needed when when is large (equivalently, when is small). By introducing the scaling above, we are able to distinguish those parts of the error which are most significant in the practically relevant limit of large . The reader should bear this in mind when interpreting our error estimates in Sections 3, 4, and 5. Second, we desire that in the limit as tends to zero (equivalently, as tends to infinity), the atomistic energy converges to the fully continuum Cauchy-Born energy (2.5). This is explained in detail in Section 2.2 below. Roughly speaking, this ensures that the atomistic energy is compatible with the continuum energy to which it is coupled in the BQCE and BQNL schemes. The compatibility of the two energies is reflected in the fact that the modeling error of the Cauchy-Born energy (2.4) is of order (See Remark 3.2).
Now suppose we want to model the response of our lattice to a dead load. We let denote the algebraic dual of , and we equip the space with the inner product given by
| (2.2) |
Generally speaking, a dead load should be thought of as an element of . However, since is a Hilbert space with the inner product (2.2), any is represented by some . That is, for any there exists so that for all , . Thus, we will think of dead loads as elements of .
The total energy for an atomic chain subject to a dead load is then given by
and the equilibrium deformation of the atoms solves the minimization problem:
| (2.3) |
Let denote the first variation of the energy , and let denote the second variation. We will say that a solution of the minimization problem (2.3) is strongly stable if for all , and we will call a deformation an equilibrium if it solves
2.2. The Cauchy-Born approximation
We call an energy local if it can be written in the form
where is called a strain energy density. Otherwise, we say that an energy is nonlocal. Observe that energy (2.1) is nonlocal. The development and use of a strain energy density allows coarse-graining in the continuum region by utilizing the full range of algorithms, codes, and analysis developed for the continuum finite element method. (An alternative quasicontinuum approach uses quadrature to approximate the nonlocal coarse-grained energy without the construction of a strain energy density [21]. Peridynamics offer another promising fully nonlocal approach to coarse-graining [37].) Thus, it is useful to devise local energies which approximate (2.1). The key to developing such energies is to observe that as long as varies slowly between neighboring lattice points, we have
If we replace the second nearest neighbor terms by in (2.1), we then obtain the Cauchy-Born energy
| (2.4) |
which is a local energy commonly used to approximate (2.1).
An alternative derivation of the Cauchy-Born energy is as follows. Suppose that is a deformation of , and define . It can be shown that
where is called the Cauchy-Born strain energy density. We call the energy the fully continuum Cauchy-Born energy. We refer the reader to [8] for a detailed discussion of the convergence of to as goes to zero.
Now suppose that is in the Lagrange finite element space on with nodes at the reference position of each atom; so the nodes are for . In that case, it is easy to show that
| (2.5) |
Thus, we see that the Cauchy-Born energy is a finite element approximation of the fully continuum Cauchy-Born energy . Consequently, we will refer to as a “continuum” energy. We say that the energy is not coarse-grained since has the same number of degrees of freedom as the atomistic energy : both depend on the deformed position of each atom.
2.3. Quasicontinuum approximations
Suppose we want to approximate a solution to the minimization problem (2.3) which has defects in localized regions but which is smooth throughout most of the lattice. Efficiency requires that most of the lattice be modeled using the Cauchy-Born energy (2.4), while accuracy requires that the defects be treated using the nonlocal energy (2.1). Thus, we desire a coupling of the two models.
We distinguish two approaches to deriving coupled energies. We call these the strain-energy based approach and bond based approach. In the strain-energy based approach, one first defines an atomistic energy per atom. For our one-dimensional chain, an appropriate energy per atom is
| (2.6) |
We call the atomistic energy at atom . Observe that is half the total energy of all bonds involving atom , so . The energy per atom should be interpreted as the energy per length at atom ; thus, is analogous to a continuum strain-energy density.
To define a coupled energy we now blend the atomistic energy per atom with the continuum energy. Schematically, we choose some blending functions and . Then for a deformation with corresponding atomistic deformation , we define
| (2.7) |
In equation (2.7), one should imagine that the function is zero in a small region containing any defects, and one throughout the bulk of the lattice. One should imagine that is one near defects, and zero throughout the bulk of the lattice. For an abruptly coupled energy, one should imagine that is the characteristic function of the continuum region, and is the characteristic function of the atomistic region. By contrast, for a blended energy, one should imagine that and are more smooth. The energy-based quasicontinuum (QCE) method [28], the bridging domain method [6], and the Arlequin method [5] all take essentially the form (2.7). Moreover, although the AtC method [3] was derived in variational form, the equilibrium condition is the Euler-Lagrange equation of an energy similar to (2.7).
We will now explain the QCE energy in detail. Let be a partition of the domain into an atomistic region and a continuum region . Suppose that is in the Lagrange finite element space with nodes at every lattice site, and let be the corresponding deformation of the atomistic lattice . In this special case, the QCE energy reduces to
| (2.8) |
We call the continuum energy at .
Our blended energy-based quasicontinuum energy (BQCE) is based on a blend of the atomistic energy at (2.6) and the continuum energy at (2.8). Let be a blending function. For we define
| (2.9) |
We observe that the QCE energy is simply the BQCE energy whose blending function is the characteristic function of the continuum region. We will show in Theorem 3.1 that BQCE does not pass the patch test where we recall that a quasicontinuum energy passes the patch test if there are no forces under uniform strain; for our one-dimensional problem an energy passes that patch test if for all . We will call a method which passes the patch test patch test consistent.
We will now discuss the QNL and BQNL energies in detail. The atomistic and continuum energies of the bond between the nearest neighbors at reference positions and are taken to be . This is the same as the energy of that bond in the fully atomistic model (2.1). The atomistic energy of the bond between the second nearest neighbors at reference positions and is taken to be , and the continuum energy of that bond is taken to be . As discussed in Section 2.2, this choice of continuum bond energy is related to the Cauchy-Born rule. The coupled energy is then given by
| (2.10) |
where is a partition of .
Our blended quasinonlocal QC (BQNL) energy is based on a smooth blending of the atomistic and continuum bond energies used to define the QNL energy (2.10). Let be a blending function. We define
| (2.11) |
We remark that the QNL energy is the BQNL energy whose blending function is the characteristic function of the atomistic region .
We will now give a simple proof that BQNL passes the patch test. We discuss the modeling error of BQNL in more detail in Section 3. The patch test consistency of BQNL is a consequence of the following result.
Lemma 2.1.
The set of BQNL energies is the affine hull of the set of QNL energies. In particular, any BQNL energy may be expressed as an affine combination of QNL energies with different atomistic and continuum regions.
Proof.
The reader may verify that the set of BQNL energies is an affine space. Thus, to prove the Lemma it suffices to express every BQNL energy as an affine linear combination of QNL energies with different atomistic and continuum regions. Let be the BQNL energy with blending function , and let be the QNL energy with atomistic region and continuum region for . We compute
and so we derive
Then we have
This expresses as an affine combination of QNL energies, since we recall that the Cauchy-Born energy, , is the QNL energy whose continuum region is the entire domain. ∎
In light Lemma 2.1, one expects that BQNL will inherit many of the properties of the QNL energy. In particular, since any BQNL energy is an affine combination of QNL energies, and since the QNL energy is patch test consistent [39], the BQNL energy passes the patch test. Moreover, we show in Remark 4.2 that the BQNL energy predicts the critical strain of the atomistic energy as accurately as the QNL method.
Remark 2.1.
(Construction of Patch Test Consistent Blended Methods). Lemma 2.1 suggests a general method for constructing patch test consistent, blended methods from patch test consistent methods with a sharp interface: one can define a patch test consistent, blended method by taking a convex combination of patch test consistent energies with different atomistic and continuum regions. Of course, it may be that the method so constructed is not practical. Nevertheless, we feel that this observation could be useful in deriving patch test consistent, blended couplings.
For our analysis, it will be convenient to define a single energy which incorporates both BQCE and BQNL as special cases. We will use the blended quasicontinuum (BQC) energy
| (2.12) |
where are blending functions. We observe that the BQCE energy with blending function is the same as the BQC energy with blending functions
| (2.13) |
The BQNL energy with blending function is the BQC energy with blending functions
| (2.14) |
2.4. Summary of notation and auxiliary theorems
Here we collect all the notation and auxiliary theorems which we will use below. The reader may feel free to skim this section at first and return only as necessary.
For differences, we write
For means, we write
For , we will think of , , , and as N-periodic functions defined on the reference configuration.
We will also use certain bounds on the potential function and its derivatives:
We will denote the convex hull of the set by
We define the following norms
Correspondingly, we let denote the space equipped with the norm , and we let denote the space equipped with the norm . Additionally, let denote the topological dual of the Banach space , and let where with . We let denote the atomistic region, denote the continuum region, and denote the interface. We let be the norm taken over the set for . We denote the closed ball of radius at in by
for one of the spaces or .
We will write for the first variation of a differentiable energy functional . The first variation is a map from into ; we will let denote the first variation of at the deformation evaluated on the test function . We will use the letter to denote a test function belonging to throughout the remainder of the paper. The letter will be used to denote a deformation belonging to . We warn the reader that in expressions such as , denotes an arbitrary test function, not the displacement corresponding to the deformation . Similarly, we will let denote the second variation of . The second variation can be interpreted either as a map from into the space of bilinear forms on , or as a map from into . We will let denote the second variation of at evaluated on the test functions .
We will need the following version of the Inverse Function Theorem which appears as Lemma 1 in [31].
Theorem 2.1.
(Inverse Function Theorem) Let and be Banach spaces, let be an open subset of , and let be a function. Let and suppose:
-
(1)
, and
-
(2)
-
(3)
for all with ;
-
(4)
.
Then there exists so that and .
3. Modeling Error for the BQC method
In Theorem 3.1, we estimate the norms of the modeling errors of the BQCE and BQNL energies.
Theorem 3.1 (Modeling error in ).
Let with .
-
(1)
Let be the BQCE energy with blending function . Recall from equation (2.13) that is the BQC energy with blending functions , and . We have
(3.1) where , for
-
(2)
Let be the BQNL energy with blending function . We have
(3.2) where , for
Proof.
We begin by writing down the first variations of and . For and we have
The first variation of is a special case of the above. We have
Using these formulas we compute the modeling error
| (3.3) | ||||
Now we expand the terms
in (3.3) at using Taylor’s theorem. We obtain
| (3.4) | ||||
| (3.5) |
where , and . When we substitute (3.4) and (3.5) into (3.3), we obtain
| (3.6) |
Expanding the term of order on the right hand side of (3.6), we compute
| (3.7) |
We recall from equation (2.14) that the BQNL energy with blending function is the BQC energy with . In that case, we compute that for the BQNL energy , the term of order zero in equation (3.7) vanishes, and so
Therefore, by Hölder’s inequality,
where . Thus,
This proves the first claim made in the statement of the theorem.
On the other hand, for the BQCE energy there is a ghost force arising from the term of order zero on the right hand side of equation (3.7). Using formulas (2.13), we compute
| (3.8) |
Substituting this expression in equation (3.7), we derive
Thus,
This proves the first claim made in the statement of the theorem. ∎
Remark 3.1 (BQNL is patch test consistent and BQCE is not patch test consistent).
Estimate (3.2) implies that BQNL is patch test consistent. For observe that if is the uniform deformation, then for all . Thus, by (3.2), . On the other hand, observe that the term which appears on the right hand side of estimate (3.1) does not vanish under uniform strain. This reflects the fact that BQCE is not patch test consistent.
Remark 3.2 (Interpretation of modeling estimates).
We will now give a detailed interpretation of the each term in estimates (3.2) and (3.1). First, we consider the term
Observe that the function is supported in the interface and continuum, and that it is identically one throughout the continuum. This suggests that the term arises from the error of the Cauchy-Born model. Recall that the Cauchy-Born energy is the BQNL energy with blending function . Therefore, by the modeling estimate for BQNL given in Theorem 3.1 we have
Consequently, we will call the term the Cauchy-Born error.
Next, we consider the term . We observe that is supported in the interface. Thus, the term arises from the error caused by coupling the atomistic and continuum models in the interface. We will call this term the coupling error.
Finally, we consider the term which appears in the modeling estimate for BQCE but not in the estimate for BQNL. Let be the uniform deformation . We call the ghost force associated with the energy , and we observe that under uniform strain formula (3.7) reduces to
Thus, we see that is the norm of the ghost force. We will call the ghost force error.
Remark 3.3 (Dependence of ghost force error on interface size).
We will now analyze the dependence of the ghost force error on the size of the interface and the shape of the blending function. Our analysis will lead to an estimate for the rate at which the ghost force error decreases with the number of atoms in the interface, and to an optimal family of blending functions for the BQCE method. Consider the BQCE energy with blending function as depicted in Figure 1.
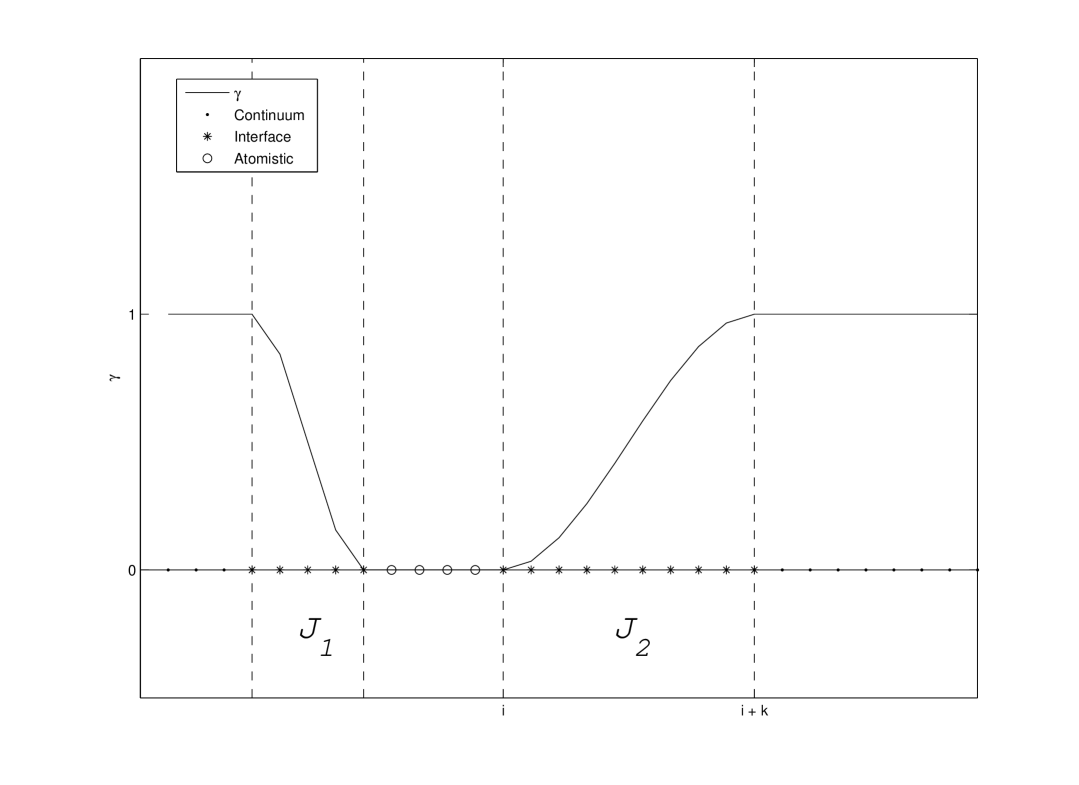
Each transition between the atomistic and continuum models results in some ghost force. We will consider the ghost force which arises from a single transition from the atomistic model to the continuum model. The total ghost force is, of course, the sum of the ghost forces due to each transition. Let be part of the interface, which we will denote simply as is the following. Assume that atoms and are in the atomistic region, and that atoms and are in the continuum. That is, suppose that for , and that for . We will estimate the ghost force due to the transition which occurs over region .
First, we construct a blending function which implements such a transition. Let be a twice continuously differentiable function such that , , and . Extend to a function defined on by taking for and for . Now let , and define by . We call the shape of the blending function .
We will show
for all . Suppose , and compute
| (3.9) |
By Taylor’s theorem,
| (3.10) |
where
We note that (3.10) holds for and only since we have assumed that . Now observe that is a non-negative function whose mass is one, and that is convex for . Therefore, Jensen’s inequality implies
This yields the estimate
for all . By a similar argument, one can show
Recall from Remark 3.2 that the ghost force error due to the transition over is
By Minkowski’s inequality and the estimates above, we have
| (3.11) |
for all . This gives the dependence of the ghost force error on , the blending function, and . We remark that inequality (3.11) is sharp. In fact, if is sufficiently smooth, then converges to as tends to infinity.
We pause here to explain why we assumed . It can be shown that no estimate of order holds unless . We leave the proof of this fact to the reader, and will instead give an illustrative example. Suppose that were the linear polynomial with and , so is not differentiable at or . Then
| (3.12) |
In Section 5, we use an estimate of the norm of the modeling error in order to obtain convergence results. Thus, we are particularly interested in the norm of the ghost force error. By estimate (3.11), if satisfies then the norm of the ghost force error decreases with as . On the other hand, if is the linear blending function then we see that the ghost force error decreases as . We conclude that if a large blending region is desired, it is best to choose a blending function which satisfies so that the faster rate of decrease is obtained. In particular, we suspect that the linear polynomial is a poor choice for the shape of the BQCE blending function.
We will now use estimate (3.11) to derive an optimal shape for the blending function of the BQCE energy. As discussed above, we will use the modeling estimate to prove our error results in Section 5. Thus, we would like to find a family of blending functions which minimizes the ghost force. Estimate (3.11) suggests that we should choose the shape which minimizes subject to , , and . The Euler-Lagrange equation for this minimization problem is
Thus, the optimal shape is the cubic polynomial which satisfies the constraints , , and .
Remark 3.4 (Dependence of coupling error on interface size).
Now we examine the dependence of the coupling error on the number of atoms in the interface and the shape of the blending function. First, we consider the coupling error of the BQNL energy. Following the notation established in Remark 3.3, let be contained in the interface. Let be a continuously differentiable function with and . Extend to a function defined on by taking for and for . Now let be defined by . Using an argument similar to the one given in Remark 3.3, one can show
for all . The result above yields the estimate
This gives the dependence of the coupling error of the BQNL energy on , the blending function, and the size of the interface.
We now address the coupling error of the BQCE method. Let the blending function, , of the BQCE energy be defined as in Remark 3.3. We recall from equation (2.13) that the BQCE energy with blending function is the BQC energy, , with
Thus, using Minkowski’s inequality and the result for the BQNL energy, we make the estimate
| (3.13) |
This gives the dependence of the coupling error of the BQCE method on , the blending function, and the size of the interface.
Remark 3.5 (Higher order estimates).
Remark 3.6 (Newton’s Third Law).
We observe that the forces arising on each atom due to the BQC energy can be decomposed into a sum of central forces which satisfy Newton’s Third Law. In particular, the forces arising from both the BQCE and BQNL energies satisfy Newton’s Third Law.
4. Stability of the BQC method
First we derive expressions for the second variations of the atomistic and BQC energies. We have
| (4.1) | ||||
where
| (4.2) |
The second variation of the atomistic energy is, of course, a special case of the above. We have
where
| (4.3) |
We begin our analysis with a lemma bounding . In Remark 3.2, we interpreted each term which appears in the estimate below, and in Remarks 3.3 and 3.4 we explained how each term depends on , the blending function, and the number of atoms in the interface. We concluded that
where is the number of atoms in the interface. The reader should keep these scalings in mind throughout Section 4.
Lemma 4.1.
-
(1)
Let be the BQCE energy with blending function . We have
where , and , for
-
(2)
Let be the BQNL energy with blending function . We have
where , for
Proof.
The proof of the lemma is extremely similar to the proof of our modeling estimate above. For the general BQC energy we compute
using formulas (4.2) and (4.3). Then we expand all terms above at using Taylor’s theorem. So,
| (4.4) |
where , and . Now we expand the second term in curly braces on the right hand side of (4.4). We obtain
| (4.5) |
We now consider the case of the BQCE energy. As a consequence of equation (3.8), we have
| (4.6) |
Thus, by substituting (4.6) into (4.5), we see that for the BQCE energy
This proves the first claim made in the statement of the lemma.
On the other hand, we recall from the proof of Theorem 3.1 that for the BQNL energy,
Therefore, for the BQNL energy, the first term in curly braces in equation (4.5) vanishes, and we have
This proves the second claim made in the statement of the lemma.
∎
Now we derive estimates relating the coercivity constants of the Hessians of and . Define
For our a priori error estimate, we would like to show that if is a strongly stable minimizer of then and . However, such a general result was not proved for the QNL method in [31]. Instead, a weaker stability result that is restricted to “elastic states” without defects [32] was proved. We now extend this a priori stability result to the BQC method.
Remark 4.1 (A bound on second neighbor interactions).
We will place an additional condition on the set of admissible deformations in order to prove our a priori and a posteriori stability estimates in Theorems 4.1 and 4.2. We will assume that
| (4.7) |
Under this assumption, the constants and in the expressions for the atomistic and BQC Hessians are nonnegative. Assumption (4.7) is justified since only under extreme compression, and in that case the second nearest neighbor pair interaction model (2.1) itself can be expected to be invalid. The authors of [31], [13], and [12] all consider energies similar to (2.1), and they all make assumptions similar to (4.7) (see Section 2.3 of [31] for further discussion of this point).
Theorem 4.1 (A priori stability).
Let . Assume that .
-
(1)
Let be the BQCE energy with blending function . We have
where , , and , for
-
(2)
Let be the BQNL energy with blending function . We have
where , for
Proof.
Let with . Recall that by formula (4.1) we have
for any BQC energy . Since we assume , all the coefficients are nonnegative, so
Now we assume that the energy is a BQCE energy. Then using the first part of Lemma 4.1 we have
This proves the first claim made in the statement of the theorem.
For the BQNL method, we make a similar estimate using the second part of Lemma 4.1. We have
| (4.8) |
This proves the second claim made in the statement of the theorem. ∎
Remark 4.2 (Accuracy of critical strain).
Let be the uniform deformation . Let be the strain at which the lattice loses stability in the atomistic model, so
We call the critical strain of the atomistic model, and we define the critical strains of the Cauchy-Born, BQCE, and BQNL energies similarly. The significance of the critical strain is discussed in [16].
Under uniform strain, the coercivity constant of the Cauchy-Born energy is
Furthermore, by formula (4.3), for the atomistic model under uniform strain . Thus, by Theorem 4.1, we see
| (4.9) |
where is the constant which arises in estimate (3.11), and is the number of atoms in the interface. In the language of [16], estimates (4.9) imply that there is no error in the critical strain of the BQNL energy, and that the error in the critical strain of the BQCE energy decreases as .
For an a posteriori existence result, one would like to show that if is a strongly stable minimizer of , then . We will not present an a posteriori existence result, but we give an a posteriori stability estimate anyway. Using this estimate, one can prove a posteriori existence theorems similar to Theorems 5.2 and 5.1.
Theorem 4.2.
(A posteriori stability) Assume that .
-
(1)
Let be the BQCE energy with blending function . We have
where , , and , for
-
(2)
Let be the BQNL energy with blending function . We have
where , for
5. A priori error estimates for the BQCE and BQNL methods
We are now ready to prove our a priori error estimates. Our results generalize Theorem 8 and its proof given in [31]. Before stating the theorem, it is convenient to establish some notation. Let be a minimizer of the energy . We will use Theorem 4.1 in the proof of Theorem 5.2. Thus, we must assume that is an elastic state. That is, we assume that for . See the discussion preceding Theorem 4.1 for more explanation. Now define the energy by .
We realize that the statement of Theorem 5.1 may seem slightly complicated, but the basic idea of the theorem is quite simple. In essence, Theorem 5.1 states that if is a stable minimizer of the atomistic energy which is sufficiently smooth in the continuum region, and if the ghost force error is sufficiently small, then there exists a stable minimizer of the BQCE energy which is close to . The conditions (5.1) and (5.2) make the hypotheses that must be sufficiently smooth in the continuum region and that the ghost force must be small precise.
Theorem 5.1 (A priori error estimate for the BQCE method).
Let , , and be as above. Assume that , and that . There exist constants and so that if
| (5.1) |
and
| (5.2) |
then there exists a locally unique minimizer of which satisfies
Proof.
Let by . We will apply Theorem 2.1 to with . In order to apply Theorem 2.1, we need to find a bound on the residual , a bound on , and a Lipschitz constant for on the ball . We will find using the modeling estimates given in Theorem 3.1, and we will find using the stability estimates given in Theorem 4.1 together with the condition (5.1). Once we have these constants, we must verify the condition . As we will see, this condition holds if and are taken sufficiently small. Once these facts are established, Theorem 2.1 implies that there exists such that and . Finally, we show that is a strongly stable minimizer of which proves Theorem 5.2.
2. Stability: . Second, we find so that
By Theorem 4.1, we have
| (5.3) |
Then if we take , we can combine (5.3) and (5.1) to find
In that case,
So we can use
| (5.4) |
3. Lipschitz bound of on . Now we bound the Lipschitz constant of on . The Lipschitz bound follows easily if we can assume that
| (5.5) |
for all with . We will choose so that (5.2) implies (5.5). To that end, observe that for we have
where . Then we need only choose to ensure that (5.5) holds.
To see the Lipschitz bound, let . Then expand
using formula (4.1). One sees easily that
where . In that case, we have
where
4. The fixed point condition: . We show that if is sufficiently small then . We have
| (5.6) |
Observe that (5.2) could be restated as with as defined in part (1) above. Thus, inequality (5.6) holds whenever .
5. The error estimate. Take , and . Then by Theorem 2.1 and the conclusions of parts (1-4) above, there exists with and
It remains only to show that the equilibrium is a locally unique minimizer of . We will show that is positive definite. We have
The second inequality follows from (5.4), the Lipschitz bound, and the error estimate
The third inequality follows from the condition . ∎
We will now restate Theorem 5.1 using the estimates given in Remarks 3.3 and 3.4. For simplicity, assume that all transitions between the atomistic and continuum models occur over regions which contain atoms. Let and be the blending functions so that . (See (2.13) for the precise definitions of and given .) Using the estimates given in Remarks 3.3 and 3.4, let be a constant so that
and let be a constant so that
In essence, Corollary 5.1 states that if is a stable minimizer of the atomistic energy which is sufficiently smooth in the continuum region and if the ghost force error is small, then there exists a minimizer of the BQCE energy which is close to .
Corollary 5.1.
Let , , and be as in Theorem 5.1, and let , , and be as above. There exist constants and so that if
and
then there exists a locally unique minimizer of which satisfies
We give a similar a priori error estimate for the BQNL method in Theorem 5.2. Following the notation adopted in Theorem 5.1, let be the energy given by . Let be a minimizer of the energy such that for .
Theorem 5.2 (A priori error estimate for the BQNL method).
Let , , and be as above. Assume that , and that . There exist constants and so that if
then there exists a locally unique minimizer of which satisfies
6. Conclusion
We have proposed a smoothly blended version of the quasicontinuum energy (QCE) which we call the blended quasicontinuum energy (BQCE). BQCE blends the atomistic and corresponding Cauchy-Born continuum energies used in the QCE method over an interfacial region whose thickness is a small number of blended atoms. We analyze the accuracy of BQCE applied to the problem of a one-dimensional chain with next-nearest neighbor interactions. For this test problem, we show how to choose the optimal blending function for weighting the atomistic and Cauchy-Born continuum energies. If BQCE is implemented using the optimal blending function, the critical strain error of BQCE can be reduced by a factor of . Thus, we believe that BQCE could be used to accurately compute the deformation of crystalline solids up to lattice instabilities.
We are continuing the development of the BQCE energy by modifying the code developed to study the accuracy of quasicontinuum methods for two benchmark problems — the stability of a Lomer dislocation pair under shear and the stability of a lattice to plastic slip under tensile loading [40]. We note that the potential to significantly improve the accuracy of existing quasicontinuum codes by easily implemented modifications is a very desirable feature of the BQCE approach. We think our theoretical analysis of the accuracy near instabilities for one-dimensional model problems can successfully explain most of the computational results for these multi-dimensional benchmark problems.
We expect that some form of the stability and error estimates in this paper can be generalized to atomistic models with finite range interactions by extending the techniques given in [22]. We are investigating the extension of our one-dimensional analysis to the multi-dimensional setting, but we expect that any multi-dimensional analysis would likely be restricted to perturbations from the ground state which are far from lattice instability. We will thus need to rely on our one-dimensional analysis to attempt to understand the computational results from our multi-dimensional benchmark studies [40].
7. Acknowledgments
We acknowledge the useful suggestions of Xingjie Li and Dr. Christoph Ortner.
References
- [1] M. Arndt and M. Luskin. Error estimation and atomistic-continuum adaptivity for the quasicontinuum approximation of a frenkel-kontorova model. SIAM J. Multiscale Modeling & Simulation, 7:147–170, 2008.
- [2] M. Arndt and M. Luskin. Goal-oriented adaptive mesh refinement for the quasicontinuum approximation of a Frenkel-Kontorova model. Computer Methods in Applied Mechanics and Engineering, 197:4298–4306, 2008.
- [3] S. Badia, P. Bochev, R. Lehoucq, M. L. Parks, J. Fish, M. Nuggehally, and M. Gunzburger. A force-based blending model for atomistic-to-continuum coupling. International Journal for Multiscale Computational Engineering, 5:387–406, 2007.
- [4] S. Badia, M. Parks, P. Bochev, M. Gunzburger, and R. Lehoucq. On atomistic-to-continuum coupling by blending. Multiscale Model. Simul., 7(1):381–406, 2008.
- [5] P. T. Bauman, H. B. Dhia, N. Elkhodja, J. T. Oden, and S. Prudhomme. On the application of the Arlequin method to the coupling of particle and continuum models. Comput. Mech., 42(4):511–530, 2008.
- [6] T. Belytschko and S. P. Xiao. Coupling methods for continuum model with molecular model. International Journal for Multiscale Computational Engineering, 1:115–126, 2003.
- [7] X. Blanc, C. Le Bris, and F. Legoll. Analysis of a prototypical multiscale method coupling atomistic and continuum mechanics. M2AN Math. Model. Numer. Anal., 39(4):797–826, 2005.
- [8] X. Blanc, C. Le Bris, and P.-L. Lions. Atomistic to continuum limits for computational materials science. M2AN Math. Model. Numer. Anal., 41(2):391–426, 2007.
- [9] W. Curtin and R. Miller. Atomistic/continuum coupling in computational materials science. Modell. Simul. Mater. Sci. Eng., 11(3):R33–R68, 2003.
- [10] M. Dobson and M. Luskin. Analysis of a force-based quasicontinuum approximation. M2AN Math. Model. Numer. Anal., 42(1):113–139, 2008.
- [11] M. Dobson and M. Luskin. Analysis of a force-based quasicontinuum approximation. Mathematical Modelling and Numerical Analysis, pages 113–139, 2008.
- [12] M. Dobson and M. Luskin. An analysis of the effect of ghost force oscillation on the quasicontinuum error. Mathematical Modelling and Numerical Analysis, 43:591–604, 2009.
- [13] M. Dobson and M. Luskin. An optimal order error analysis of the one-dimensional quasicontinuum approximation. SIAM. J. Numer. Anal., 47:2455–2475, 2009.
- [14] M. Dobson, M. Luskin, and C. Ortner. Sharp stability estimates for the force-based quasicontinuum approximation of homogeneous tensile deformation. SIAM J. Multiscale Modeling & Simulation, 8:782–802, 2010. arXiv:0907.3861.
- [15] M. Dobson, M. Luskin, and C. Ortner. Stability, instability, and error of the force-based quasicontinuum approximation. Archive for Rational Mechanics and Analysis, 197:179–202, 2010. arXiv:0903.0610.
- [16] M. Dobson, M. Luskin, and C. Ortner. Accuracy of quasicontinuum approximations near instabilities. Journal of the Mechanics and Physics of Solids, to appear. arXiv:0905.2914v2.
- [17] M. Dobson, M. Luskin, and C. Ortner. Iterative methods for the force-based quasicontinuum approximation. Computer Methods in Applied Mechanics and Engineering, to appear. arXiv:0910.2013v3.
- [18] L. M. Dupuy, E. B. Tadmor, R. E. Miller, and R. Phillips. Finite-temperature quasicontinuum: Molecular dynamics without all the atoms. Phys. Rev. Lett., 95(6):060202, Aug 2005.
- [19] W. E, J. Lu, and J. Yang. Uniform accuracy of the quasicontinuum method. Phys. Rev. B, 74(21):214115, 2006.
- [20] V. Gavini, K. Bhattacharya, and M. Ortiz. Quasi-continuum orbital-free density-functional theory: A route to multi-million atom non-periodic DFT calculation. J. Mech. Phys. Solids, 55:697–718, 2007.
- [21] M. Gunzburger and Y. Zhang. A quadrature-rule type approximation for the quasicontinuum method. Multiscale Modeling and Simulation, 8:571–590, 2010.
- [22] X. H. Li and M. Luskin. A generalized quasi-nonlocal atomistic-to-continuum coupling method with finite range interaction. IMA Journal of Numerical Analysis, to appear. arXiv:1007.2336v2.
- [23] P. Lin. Theoretical and numerical analysis for the quasi-continuum approximation of a material particle model. Math. Comp., 72(242):657–675, 2003.
- [24] P. Lin. Convergence analysis of a quasi-continuum approximation for a two-dimensional material without defects. SIAM J. Numer. Anal., 45(1):313–332, 2007.
- [25] M. Luskin and C. Ortner. Linear stationary iterative methods for the force-based quasicontinuum approximation. In B. Engquist, O. Runborg, and R. Tsai, editors, Numerical Analysis and Multiscale Computations, volume 82 of Lect. Notes Comput. Sci. Eng. Springer Verlag, to appear. arXiv:1104.1774.
- [26] C. Makridakis, C. Ortner, and E. Süli. Stress-based atomistic/continuum coupling: A new variant of the quasicontinuum approximation. preprint, 2010.
- [27] R. Miller and E. Tadmor. The QC code. http://www.qcmethod.com/.
- [28] R. Miller and E. Tadmor. Benchmarking multiscale methods. Modelling and Simulation in Materials Science and Engineering, 17:053001 (51pp), 2009.
- [29] P. Ming and J. Z. Yang. Analysis of a one-dimensional nonlocal quasi-continuum method. Multiscale Model. Simul., 7(4):1838–1875, 2009.
- [30] M. Ortiz, R. Phillips, and E. B. Tadmor. Quasicontinuum analysis of defects in solids. Philosophical Magazine A, 73(6):1529–1563, 1996.
- [31] C. Ortner. A priori and a posteriori analysis of the quasi-nonlocal quasicontinuum method in 1D, 2009. arXiv.org:0911.0671.
- [32] C. Ortner and E. Süli. Analysis of a quasicontinuum method in one dimension. M2AN Math. Model. Numer. Anal., 42(1):57–91, 2008.
- [33] C. Ortner and H. Wang. A priori error estimates for energy-based quasicontinuum approximations of a periodic chain. Mathematical Models and Methods in Applied Sciences, to appear.
- [34] S. Prudhomme, P. T. Bauman, and J. T. Oden. Error control for molecular statics problems. Int. J. Multiscale Comput. Eng., 4(5-6):647–662, 2006.
- [35] D. Rodney and R. Phillips. Structure and strength of dislocation junctions: An atomic level analysis. Phys. Rev. Lett., 82(8):1704–1707, Feb 1999.
- [36] P. Seleson and M. Gunzburger. Bridging methods for atomistic-to-continuum coupling and their implementation. Communications in Computational Physics, 7:831–876, 2010.
- [37] P. Seleson, M. L. Parks, M. Gunzburger, , and R. B. Lehoucq. Peridynamics as an upscaling of molecular dynamics. Multiscale Modeling and Simulation, 8:204–227, 2009.
- [38] A. V. Shapeev. Consistent energy-based atomistic/continuum coupling for two-body potential: 1D and 2D case. Multiscale Modeling and Simulation, to appear. arXiv:1010.0512.
- [39] T. Shimokawa, J. Mortensen, J. Schiotz, and K. Jacobsen. Matching conditions in the quasicontinuum method: Removal of the error introduced at the interface between the coarse-grained and fully atomistic region. Phys. Rev. B, 69(21):214104, 2004.
- [40] B. Van Koten, X. H. Li, M. Luskin, and C. Ortner. A computational and theoretical investigation of the accuracy of quasicontinuum methods. In I. Graham, T. Hou, O. Lakkis, and R. Scheichl, editors, Numerical Analysis of Multiscale Problems. Springer, to appear. arXiv:1012.6031.
- [41] A. F. Voter. Hyperdynamics: Accelerated molecular dynamics of infrequent events. Phys. Rev. Lett., 78:3908–3911, 1997.